Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 7 (2010) , Article ID: 2331 , 7 pages DOI:10.4236/jemaa.2010.27053
Wave Propagation in Nanocomposite Materials
![]()
Institut Henri Poincaré, Bis Route de Croissy, Le Vésinet, France.
Email: pierre.hillion@wanadoo.fr
Received February 9th, 2010; revised April 21st, 2010; accepted May 3rd, 2010.
Keywords: Composite materials, Maxwell-Garnett, Constitutive relations, TE TM Fields
ABSTRACT
Electromagnetic wave propagation is first analyzed in a composite material mde of chiral nano-inclusions embedded in a dielectric, with the help of Maxwell-Garnett formula for permittivity and permeability and its reciprocal for chirality. Then, this composite material appears as an homo-geneous isotropic chiral medium which may be described by the Post constitutive relations. We analyze the propagation of an harmonic plane wave in such a medium and we show that two different modes can propagate. We also discuss harmonic plane wave scattering on a semi-infinite chiral composite medium. Then, still in the frame of Maxwell-Garnett theory, the propagation of TE and TM fields is investigated in a periodic material made of nano dots immersed in a dielectric. The periodic fields are solutions of a Mathieu equation and such a material behaves as a diffraction grating.
1. Introduction
Nanotechnology is blossoming with in particular the inclusion of nano-particles (nano-dots) in some specific support [1,2]. Then, to analyze electromagnetic wave propagation such as light or X rays in these composite materials, we need a theory able to calculate average, macroscopic values from their granular microscopic properties. This job is performed by the Maxwell-Garett theory [3-6].
In this work, the support is a dielectric with permittivity e1, permeability m and we consider two situations according that nano-dots are chiral or periodically distributed along a direction of the structure.
In the first case (chiral nano-dots) the permittivity e of the composite material is according to the MaxwellGarett formula
[e – e1][e + 2e1]-1 = f [e2 – e1][e2 + 2e1]-1(1)
f is the filling factor of inclusions (their volume fraction) in the host material, the subscripts 1, 2 corresponding to host and inclusions respectively and we get from (1)
e = e1 (1 + 2af )(1 - af)-1a = (e1 - e2)(e1 + 2e2)-1,(2)
Permeability µ is assumed the same for nano-dots and dielectric.
The relation (2) has been generalized [7,8] to chirality x when both inclusions and host materials are chiral. But here, the situation is different since only inclusions have this property and the relation (1) with x, x1, x2 instead of e, e1, e2 has no meaning when x1 = 0. To cope with this difficulty, we introduce a reciprocal Maxwell-Garnett relation obtained by applying to (1) the transformation (x1, x2, f) Þ (fx2, x1, 1/f) which gives
[x – fx2][x + 2fx2]-1 = f -1[x1 – fx2][x1 + 2fx2]-1 (3)
reducing for x1 = 0 to x = -2fx2(1 - f)(1 + 2f)-1 (4)
From now on, we assume f << 1, e1 > 0, e2 < 0, a > 0 and x2 < 0 so that the 0(f 2) approximation of (2) and (4) gives e = e1(1 + 3af ) > 0 (5)
x = -2fx2 > 0(6)
So, this composite material made of nano-chiral particles included in a dielectic may be hand-led as an homogeneous chiral medium with permittivity and chirality (5) and (6) and permeabiity µ > 0 assumed to be the same for inclusions and dielectric.
In the second situation (periodically distributed nanorods), the relation (1) is still valid with f changed into a periodic function f (x). Assuming f (x) = f cos(2ax), we write the permittivity e (x) in the following form reducing to (5) to the 0(f 2) order e (x) = e1exp[3afcos(2ax)](7)
Using (5)-(7), we shall analyze harmonic plane wave propagation in both composite materials, chiral and periodic.
2. Harmonic Plane Wave Propagation in a Chiral Composite Medium
We suppose this chiral medium endowed with the Post constitutive relations in which e, x have the expressions (5) and (6) [9,10]
D = e E + ix B, H = B/µ + ix E, i =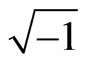 (8)
(8)
This choice is not arbitrary because the Post constitutive relations, in their general form, are covariant under the proper Lorentz group as Maxwell’s equations which guarantees a consistent theory with a simple mathematical formalism, in agreement with the statement that only covariant mathematical expressions have a physical meaning.
Plane wave scattering from a semi-infinite chiral medium was discussed some time ago by Bassiri et al [11], also using the Post constitutive relations, but we proceed differently from these authors working with the Fresnel reflection and transmission amplitudes.
2.1 Refractive Indices
We consider harmonic plane waves with amplitudes E, B, D, H
(E,B,D,H)(x,t) = (E,B,D,H)y(x,t)(9)
in which y (x,t) = exp[iw(t + nsinθ x/c + ncosθ z/c)] (10)
in which n is a refractive index to be determined.
Substituting (9) into the Maxwell equations
ÑÙE + 1/cθ t B = 0, Ñ.B = 0
ÑÙH - 1/cθ t D = 0, Ñ.D = 0(11)
and taking into account (10) give the equations for the amplitudes E, B, D, H
-ncosθ Ey + Bx = 0,
n(cosθ Ex - sinθ Ez) + By = 0,
nsinθ Ey + Bz = 0, (12)
ncosθ Hy + Dx = 0
n(cosθ Hx - sinθ Hz) - Dy = 0
nsinθ Hy - Dz = 0(13)
with the divergence equations sinq Bx + cosq Bz = 0, sinq Dx + cosq Dz = 0(14)
We get at once from (8) and (14), the divergence equation satisfied by the electric field sinq Ex + cosq Ez = 0(15)
Substituting (8) into (13) gives ncosq (By /m + ixEy) + eEx + ix Bx = 0 ncosq (Bx /m + ixEx) - nsinq (Bz /m + ixEz) - eEy - ixBy = 0 nsinq (By /m + ixEy) - eEz -ixBz = 0 (16)
Taking into account (12), these equations become ncosq By /m + eEx + 2ixBx = 0 ncosq Bx /m - nsinq Bz/m - eEy - 2ixBy = 0 nsinq By /m - eEz - 2ixBz = 0(17)
Then, eliminating B between (12) and (17) gives the homogeneous system of equations in which s = 2nx
(n2/m - e)Ex - iscosq Ey = 0
(n2/m - e)Ey - is(sinq Ez - cosq Ex) = 0
(n2/m - e)Ez + issinq Ey = 0(18)
This homogeneous system has nontrivial solutions if its determinant is null and a simple cal-culation gives
(n2/m - e)[(n2/m - e)2 - s2] = 0(19)
Deleting (n2/m - e) = 0 which would correspond to an a-chiral medium, we get from (11) two modes (n±2/m - e) = ± s in which which s = 2nx so that the refractive index depends not only on permittivity and permeability but also on chirality with the positive expressions n+ = xm + (x2m2 + em)1/2, (20)
n- = -xm + (x2m2 + em)1/2 (21)
Changing the square root into its opposite gives negative refractive indices.
Consequently, two modes with respectively the refractive indices n+, n- can propagate in the metachiral slab, they are independent as long as the medium is infinite, otherwise they become coupled at boundaries. The amplitudes of the field components in these two modes have now to be determined.
2.2 Electromagnetic Fields
1) We first suppose n+2/m - e = s and n+ = xm + (x2m2 + em)1/2 with e and µ > 0: fields and parameters are characterized by superscripts or subscripts + respectively.
Then, we get at once from (18) and (12) in terms of E+y
E +x = icosq+ E+y, E+z = - isinq+ E+yB+x = n+ cosq+ E+yB+y = -i n+ E+y, B+z = - n+ sin+ E+y (22)
and substituting (22) into (8)
D+x = icosq+ l+E+yD+y = l+E+yD+z = -isinq+ l+E+y (23)
H+x = cosq+ n+E+yH+y = -i n+E+yH+z = -sinq + n+E+y (24)
in which l+ = e + xn+, n+ = n+/m - x = (x 2 + e /m)1/2 (25)
2) For n-2/m - e = - s and n- = - xm + (x 2m 2 + em)1/2, we get at once with now super-scripts and subscripts -:
E-x = - i cosq- Ey, E-z = i sinq- E-yB-x = n- cosq- E-y, B-y = i n-E-yB-z = - n- sinq- E-y(26)
and substituting (26) into (8)
D-x = -icosq- l-E-y, D-y = l-E-y,
D-z = isinq- l-E-y(27)
H-x = cosq- n-E-y, H-y = i n-E-y,
H-z = - sinq- n-E-y (28)
with l- = e - xn-, n- = n-/m + x = (x 2 + e/m)1/2 = n+ (29)
Then, according to (9) and (10), the electromagnetic field of the plus and minus modes, each depending on an arbitrary amplitude E+y , E-y, is
(E±, B±, D±, H±) (x,t) = (E±, B±, D±, H±) y±(x, t) (30)
with the amplitudes given by (22)-(24) and (26)-(28) and the phase functions y±(x,t) = exp[iw (t + n± sinq± x/c + n± cosq± z/c)](31)
2.3 Plane Wave Scattering from a Semi-Infinite Chiral Composite Medium
We suppose that the chiral composite material fulfills the half space z < 0 on which impinges from z > 0 on the interface z = 0 an harmonic plane wave characterized by the phase factor y(qi)
y (qi) = exp[-iwn0(xsinqi + zcosqi)](32)
n0 is the refractive index in z > 0 and the components of the incident electromagnetic field are [12] with two amplitudes Mi, Ni:
Eix = -cosqi Mi y (qi), Eiy = Ni y (qi), Eiz = sinqi Mi y (qi)
Hix = -n0cosqi Ni y (qi), Hiy = -n0Mi y (qi)Hiz = n0sinqi Ni y(qi) (33)
The reflected field in the half-space z > 0 has a similar expression with (Mi, Ni, qi) changed into (Mr, Nr, qr) while the refracted field in z < 0 is supplied by (30).
According to (31) and (32), also valid for the reflected wave, the continuity of the phase at z = 0 implies the Descartes-Snell relations n0 sinqi = n0 sinqr = n+ sinq+ = n- sinq- (34)
The continuity of the components Ex,y, Hx,y, at z = 0 supplies four boundary conditions to de-termine in terms of Mi, Ni the amplitudes Mr, Nr of the reflected field and those E +y, E -y of the refracted field.
According to (22), (26) and (33) and taking into account (34), we get for the Ex,y components cosq i(Mr - Mi ) = icosq + E +y - icosq- E -y
Nr + Ni = E +y + E -y(35)
while for Hx,y, according to (24), (28) and (33), we have since n- = n+ (= n )
n0 cosqi(Nr - Ni ) = n (cosq+ E +y + icosq- E -y)
n0( Mr + Mi) = n(E +y - E -y )(36)
To make calculations easier, we introduce the notations Mr + Mi = M, Nr + Ni = NMr - Mi = M’, Nr - Ni = N’(37)
and a = n0/n (cosq+ + cosq-)-1 (38)
Then, we get at once from (36)
E +y = a(cosqi N’ + cosq- M)
E -y = a(cosqi N’ - cosq+ M) (39)
and, substituting (39) into (35) gives cosqi M’ = a11 N’ + a12 M N = a21 N’ + a22 M(40)
in which a11 = iacosqi (cosq + + cosq-), a12 = 2iacosq + cosq-
a21 = acosq i, a22 = a(cosq - + cosq + ) (41)
Taking into account (37) the system (40) becomes
(cosq i - a12)Mr + a11 Nr = (cosq i + a12) Mi - a11 Ni
a22Mr - (1 - a21) Nr = -a22Mi + (1 + a21)Ni(42)
from which we easily get the amplitudes Mr, Nr of the reflected field and consequently M’, N’ according to (37) to obtain finally the amplitudes Ey± of the refracted field from (39).
One has a simple result for a normal incidence qi = qr = q± = 0 since the Equations (35) and (36) reduce to Mr - Mi = i(E +y - E -y), Nr + Ni = E +y + E -y
-2n0 Ni = n (E +y + E -y), n0(Mr + Mi) = n (E +y - E -y) (43)
with the solution Mr = (n + in0) (n - in0)-1 Mi, Nr = -(1 + 2n0 /n)Ni (44)
E +y = n0(n - in0)Mi - n0/n Ni,
E -y = -n0(n - in0)Mi - n0 /n Ni (45)
Remark 1. If the angles q+, q- obtained from (34) are real, the plus and minus modes propa-gate in the chiral medium. If they are both purely imaginary, we get from (34)
cos(q±) = -i[(n0/n±)2 sin2qi - 1]1/2 (46)
the negative sign in front of the square root in (46) corresponds to the physical situation: refracted waves are evanescent and, incident waves undergo a total reflection, with as consequence for beams of plane waves a GoösHanken lateral shift and a Imbert-Fedorov transverse shift [13]. Of course with a single angle pure imaginary, only one mode propagates, the other mode giving rise to an evanescent wave.
Remark 2. At the expense of more intricacy, the present formalism may be generalized to wave propagation in a chiral slab located between z = 0 and z = - d. Then, two more fields exist respectively reflected at z = -d inside the slab and refracted outside in the z < -d region, supplying four supplementary amplitudes matched by the boundary conditions at z = -d. But, instead of a 4 ´ 4 system of equations to get the amplitudes of the electromagnetic field, we have to deal with a 8 ´ 8 system more difficult to solve.
3. Harmonic Plane Wave Propagation in a Two Dimensional Nano-Periodic Medium
With B = µH, D = e (x)E, and exp(-iwt) implicit, the Maxwell equations are for E(x,z), H(x,z)
θzEy - iwm/c Hx = 0, θzHy + iw e(x)/c Ex = 0
θzEx – θxEz + iwm/c Hy = 0θzHx – θxHz – iw e(x)/c Ey = 0
θxEy + iwm/c Hz = 0, θxHy – iwe(x)/c Ez = 0 (47)
with the divergence equations
[e’ + eθx]Ex + eθzEz(x,z) = 0, θxHx + θzHz = 0(48)
giving rise to TE (Ey, Hx, Hz) and TM (Hy, Ex, Ez) waves.
3.1 TE Wave Propagation
Assuming f << 1, we work with the Maxwell-Garnett 0(f2) approximation of (7)
e (x) = e1 + h f cos(2ax), h = 3ae1 (49)
The component Ey satisfies the Helmholtz equation in which ∆ = θx2 + θz2
[∆ + w2me (x)/c2]Ey(x,z) = 0(50)
We look for the solutions of this equation in the form, A being an arbitrary amplitude Ey(x,z) = A exp(ikzz) y (x) (51)
Substituting (51) into (50) and taking into account (49), gives the differential equation satisfied by y(x)
[θx2 + k02 + f ke2 cos(2ax)] y (x) = 0 (52)
in which k02 = w2me1/c2 - kz2, ke2 = w2mh /c2(53)
Using the variable z = k1 x , Equation (52) becomes a Mathieu equation [14,15]
[θz2 + c2 + f cos(2az/ke)]y (z) = 0, c2 = k02/ke2(54)
with solutions in the form [14,15,16] where v has to be determined y (z) = ∑m=-¥¥ cm exp([i(v + 2m) az/ke)](55)
Substituting (55) into (54) gives the following recurrence relation [15] for the coefficients cm
cm + gm(v) (cm-1 + cm+1) = 0 (56)
with gm(v) = -f /2 [(2m + v )2 - c2](57)
Now, the main difficulty [14,15] is to get v in terms of f and c, but f being small, the infinite determinant of the system (56) supplies v to the 0(f 3) order [15]
cos(vπ) = cos(cπ) + πf 2 [4c 2(1 - c 2)1/2] -1 sin(cπ) (58)
Once v known, the cm coefficients may be obtained by numerical methods based on the recurrence relations (36) or on some variant of it. It is shown [15] how for moderate values of c and f, these relations can be transformed into convergent continued fractions Rm(n) = cm/cm-1, Lm(n) = cm/cm+1.
So, according to (51) and (55), Ey(x,z) = Ey(x + π/a,z) and Ey(x,z) = A exp(ikzz) ∑m=-¥¥ cm exp[i(v + 2m)ax)]0 ≤ x < π/a(59)
and taking into account the Maxwell Equation (47), the other two components Hx, Hz of the TE field are obtained from θzEy and θxEy respectively. Writing (59)
Ey(x,z) = A∑m=-¥¥ cm exp(ikzz + ikmx)km = (v + 2m)a, 0 ≤ x < π/a (60)
Ey(x,z) appears as a periodic beam of plane waves propagating in the directions defined by the wave vectors with components (kz, km), their amplitude being weighted by the coefficients cm.
3.2 TM Wave Propagation
For TM waves (Hy, Ex, Ez), we start with the expression (7) of e (x). Then, according to the Maxwell Equation (47) the component Hy satisfied the equation
[∆ + w2me (x)/c2 - {e’(x)/e(x)}θx] Hy(x,z) = 0 (61)
We look for the solutions of (61) in the form Hy(x,z) = A exp(ikzz) y(x) (62)
y (x) = u(x) f (x), f (x) = exp[ f1/2 cos(2ax)]f1 = f h (63)
A simple calculation gives the first and second derivative of y (x)
y’(x) = [u’/u - af1 sin(2ax)]y (x)
y’’(x) = [u’’/u - 2a u’/u f1 sin(2ax)
- 2a2 f1 cos(2ax) + a2f12 sin2 (2ax)]y (x)(64)
and since e’/e = -2a f1 sin(2ax), we get to the 0( f12) order y’’ - e’/e y’ = [u’/u - 2a2 f1 cos(2ax)] y (x) + 0( f12) (65)
so that
[y’’- e’/e y’]Hy (x,z) = [u’/u - 2a2 f1 cos(2ax)]Hy(x,z)(66)
Then, according to (62) and (66), we get from (61), the differential equation satisfied by u(x)
[θx2 + w2me(x)/c2 - kz2 - 2a2 f1 cos(2ax)]u(x) = 0 (67)
which becomes with the Maxwell-Garnett approximation (49) of e (x)
[θx2 + k02 + f kh2 cos(2ax)]u(x) = 0(68)
with k02 given by (53) while kh2 = w2me1/c2 - 2a2h(69)
The comparison of (52) and (68) shows that, to the 0(f 2) order, one has just to change ke into kh to go from TE to TM waves so that all the calculations of Subsection 3.1 can be repeated mutatis mutandis.
3.3 TE Wave Scattering in a Semi Infinite Nano-Periodic Material
The granular material, made of nano dots immersed in a dielectric, lies in the z < 0 half-space and we suppose that a TE harmonic plane wave (Eyi, Hxi, Hzi) impinges from the upper half-space z > 0 with refractive index n and permeability m on the z = 0 interface.
The components Eyi, Eyr of the incident and reflected waves are Eyi(x,z) = Ai exp[iwn/c (x sinqi + z cosqi)]
Eyr(x,z) = Ar exp[iwn/c (x sinqi - z cosqi)](70)
and according to the Maxwell Equation (47), the components Hxi, Hxr involved in the boundary conditions are Hxi(x,z) = n /m cosqi Eyi(x,z)Hxr(x,z) = -n /m cosqi Eyr(x,z) (71)
Now, the refracted periodic field in z < 0 has the form (59)
Eyt(x,z) = At exp(ikzz) ∑m=-¥¥ cm exp[i(v + 2m) ax]0 ≤ x < π/a(72)
and, still using (47)
Hxt(x,z) = g Eyt(x,z), g = ckz /wm(73)
the boundary conditions impose the continuity on z = 0 of Ey and Hx, that is, according to (70)-(73)
(Ai + Ar) exp(iwn /c x sinqi)
= At ∑m = –¥¥ cm exp[i(v + 2m)ax]0 ≤ x < π/a (74)
n /m cosqi (Ai - Ar) exp(iwn /c x sinqi)
= gAt ∑m=-¥¥ cm exp[i(v + 2m)ax]0 ≤ x < π/a (75)
Let us write (74)
Ai + Ar = At W( b p)W(b p) = ∑m=-¥¥ cm exp[i(km - ki) ßπ](76)
in which according to (60) and (70)
km = (v + 2m)a, ki = wn /c sinqi(77)
with 0 ≤ ß < 1 since 0 ≤ x ≤ π/a.
So, taking into account (60), the granular periodic semi-infinite material behaves as a diffraction grating: the beam of plane waves propagating in the directions defined by the wave vectors with components (kz, km) have their amplitudes modulated by the coefficients cmexp(-iki ßπ). And, acccording to (76), the relations (74) and (75) become Ai + Ar = At W(b p), n/m cosqi (Ai - Ar) = gAt W(b p)0 ≤ ß < 1(78)
from which we get in terms of the incident amplitude Ai
Ar = -(gm - n cosqi) (gm + n cosqi)-1AiAt = 2n cosqi (gm + n cosqi)-1 W-1(b p) Ai(79)
So, the amplitude At is not constant on the interval (0, π/a).
4. Discussion
The relation (6), leads to a consistent formalism but further work is needed to prove or to amend it. In any case, two different modes of harmonic plane waves propagate in these chiral materials. The Post constitutive relations used to characterize such media, allow to get exact analytic expressions for the amplitude of the electromagnetic field in each mode, a note-worthy property due, as noticed in the introduction, to the covariance of Post’s relations under the proper Lorentz group. An excellent review of chiral nano-technology may be found in [17] with a discussion of two topics: nanoscale approaches to chiral technology and, corresponding to the situation considered here, nanotechnology that benefits from chirality. In particular, a section is devoted to chiral carbon nanotechnology and the authors conclude “possible applications of such materials in the field of biomedecine and biotechnology range from prepara-tion of novel antibacterial, cyclotonic and drug delivery agents to catalysis and materials science applications”.
Remark: The analysis of Section 2 may be performed in left-handed chiral materials with negative e, m: just change e, m into -|e|, |-m|.
Granular periodic materials are currently used in mechanical engineering and, with the ob-jective to appraise their properties, theoretical studies have been devoted to acoustic wave propagation in these structures [18]. In electrical engineering, photonic crystals [19,20] are the main illustration of periodic nanomaterials and they take an increasing importance in today technology. But, they are not composite with inclusions immersed in a dielectric structure. For instance, a one-dimensional photonic crystal with a permittivity periodic in the direction of propagation may be described by an expansion in which U is the unit step function e(z) = e1 ∑n [U(z - 2na) - U(z - {2n + 1}a)]
+ e2 ∑n [U(z - {2n + 1}a) - U(z - {2n + 2}a)] (80)
and, the solutions of Maxwell’s equations are the Bloch functions ∑m ck,m exp(ikz+2iπmz/a) to be compared with (59) (and (80) with (49)). Incidently, (80) has a simple expression in terms of the square-sine function e(z) = e + r sin(az) / |sin(az)| U(z)e1 = e + r, e2 = e - r(81)
which suggests to work with the Laplace transform of Maxwell’s equations since tanh(πp/2a) is the Laplace transform of the square-sine function [21]. People fluent with the Laplace transform, could think in terms of p instad of z as they use to do with w instead of t.
In opposite to photonic crystals, composite granular materials with a continuous filling factor have no lattice structure and, as shown in Section 3.3, they rather behave as a smooth dielectric grating [22]. Some of the restrictive assumptions on the filling factor f could be somewhat released at the expense of more intricacy:
1) It would be interesting to check what happens when a higher order approximation than 0( f 2) is used;
2) When f(x) = f cos(2ax) is changed into f (x) = ∑0¥ fm(cos2max), the Mathieu equation becomes a Hill equation [14,15] with solutions similar to (55) but the recurrence relations bet-ween the coefficients cm is more intricate;
3) Finally a generalization to a two-dimensional filling factor f (x,y), periodic in x and y would approach more closely a real physical situation.
To sum up, the application of the Maxwell-Garnett theory to nano composites deserves further research, taking into account the innocuity or not of such materials in biomedecine [23]. This theory is also used to analyze, in the frame of surface plasmon polaritons, the scattering of TE, TM light waves from a composite material made of metallic nano spherical particles immersed inside a metallic structure such as Ag particles in a Sio2 matrix [24].
The 0( f 2) Maxwell-Garnett approximation of the periodic permittivity in the nanodoped medium of Section 3 implies that TE, and TM fields are solutions of the Mathieu equation as if they were diffracted from a dielectric grating [25].
REFERENCES
- M. Khan, A. K. Sood, F. L. Deepak and C. N. R. Rao, “Nanorotors Using Asymmetric in Organic Nanorods in an Optical Trap,” Nanotechnology, Vol. 17, No. 11, 2006, pp. S287-S290.
- X. M. Guo, C. Jiang and T. S. Shi, “Prepared Chiral Nanorods of a Cobalt,” Inorganic Chemistry, Vol. 46, No. 12, 2007, pp. 4766-4768.
- J. C. Maxwell-Garnett, “Colours in Metal Glasses and Metallic Films,” Philosophical Transactions of the Royal Society of London A, Vol. 203, No. 359-371, 1904, pp. 385-420.
- C. A. Grimes, “Calculation of the Effective Electromagnetic properties of Granular Materials,” in: A. Lakhtakia, Ed., Essays on the Formal Aspects of Electromagnetic Theory, World Scientific, Singapore, 1993, pp. 699-746.
- L. Tsang and J. A. Kong, “Scattering of Electromagnetic Waves: Advanced Topics,” Wiley Series in Remote Sensing, Wiley, New York, 2001.
- P. Mallet, C. A. Guerin and A. Sentenac, “Maxwell-Garnett Mixing Rule in the Presence of Multiple Scattering,” Physical Review B, Vol. 72, No. 1, 2005, p. 014205.
- B. Shanker and A. Lakhtakia, “Extended Maxwell-Garnett Model for Chiral-in-Chiral Composites,” Journal of Physics D: Applied Physics, Vol. 26, No. 10, 1993, pp. 1746- 1758.
- A. Lakhtakia, V. K. Varadan and V. V. Varadan, “On the Maxwell-Garnett Model of Chiral Composite,” Journal of Materials Research, Vol. 8, No. 4, 1993, pp. 917-922.
- E. J. Post, “Formal Structure of Electromagnetics,” NorthHolland Publications, Amsterdam, 1962.
- A. Lakhtakia,V. K. Varadan and V. V. Varadan, “TimeHarmonic Electromagnetic Fields in Chiral Media,” Springer, Berlin, 1989.
- S. Bassiri, C. H. Papas and N. Engheta, “Electromagnetic Wave Propagation through a Dielectric-Chiral Interface and through a Chiral Slab,” Journal of the Optical Society of America A, Vol. 5, No. 9, 1988, pp. 1450-1459.
- M. Born and E. Wolf, “Principles of Optics,” Pergamon Press, Oxford, 1965.
- P. Hillion, “Light Beam Shifts in Total Reflection,” Optics Communications,Vol. 266, No. 1, 2006, pp. 336-341.
- E. T. Whittaker and G. N. Watson, “A Course of Modern Analysis,” University Press, Cambridge, 1962.
- A. Erdelyi, “Higher Transcendental Functions,” McGrawHill, New York, Vol. 3, 1955.
- P. Hillion, “Theoy of Electromagnetic Wave Propagation in a Longitudinally Periodic Cylinder,” European Physical Journal B, Vol. 62, No. 4, 2008, pp. 477-480.
- J. Zhang. M. T. Albelda, Y. Liu and J. W. Canary, “Chiral Nanotechnology,” Chirality, Vol. 17, No. 7, 2005, pp. 404-420.
- C. Inserra, V. Tournat and V. Gusev, “A Method of Controlling Wave Propagation in Initially Spatially Periodic Media,” Europhysics Letters, Vol. 78, No. 4, 2007, p. 44001.
- J. D. Joannopoulos, R. D. Meade and J. N. Wynn, “Photonic Crystals,” University Press, Princeton, 1995.
- C. Lopez, “Material Aspects of Photonic Crystals,” Advanced Materials, Vol. 15, No. 20, 2003, pp. 1679-1704.
- B. Van Der Pol and H. Bremmer, “Operational Calculus,” Academic Press, Cambridge, 1959.
- M. Neviere and E. Popov, “Light Propagation in Periodic Media,” Marcel Dekker, Basel, 2005.
- C. A. Poland, R. Duffin, I. Kinloch, A. Maynard, et al., “Carbon Nanotubes Introduced into the Abdominal Cavity of Mice Show Asbestos-Like Pathogenicity in a Pilot Study,” Nature Nanotechnology, Vol. 3, 2008, pp. 423-428.
- S. Kawata, “Near-Field Optics and Surface Plasmon Polariton,” Springer, Berlin, 2001.
- N. Yamaguchi, “High Order Bragg Diffraction by Dielectric Grating,” Electronics and Communications in Japan, Vol. 69, No. 8, 2007, pp. 112-121.

