Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 1 (2010) , Article ID: 1222 , 11 pages DOI:10.4236/jemaa.2010.21002
Voltage and Current Mode Vector Analyses of Correction Procedure Application to Clarke’s Matrix—Symmetrical Three-Phase Cases
![]()
1Department of Electrical Engineering, Faculty of Engineering of Ilha Solteira, The São Paulo State University, São Paulo, Brazil; 2Department of Electrical Engineering, The State University of Campinas, Campinas, Brazil.
Email: afonsojp@uol.com.br, kurokawa@dee.feis.unesp.br, pisso@dsce.fee.unicamp.br
Received September 4th, 2009; revised October 6th, 2009; accepted October 15th, 2009.
Keywords: Clarke’s Matrix, Eigenvector, Eigenvalue, Phase‑Mode Transformation, Error Analysis, Non‑Symmetrical Lines, Frequency Dependent Parameters
ABSTRACT
Clarke’s matrix has been applied as a phase-mode transformation matrix to three-phase transmission lines substituting the eigenvector matrices. Considering symmetrical untransposed three-phase lines, an actual symmetrical three-phase line on untransposed conditions is associated with Clarke’s matrix for error and frequency scan analyses in this paper. Error analyses are calculated for the eigenvalue diagonal elements obtained from Clarke’s matrix. The eigenvalue off-diagonal elements from the Clarke’s matrix application are compared to the correspondent exact eigenvalues. Based on the characteristic impedance and propagation function values, the frequency scan analyses show that there are great differences between the Clarke’s matrix results and the exact ones, considering frequency values from 10 kHz to 1 MHz. A correction procedure is applied obtaining two new transformation matrices. These matrices lead to good approximated results when compared to the exact ones. With the correction procedure applied to Clarke’s matrix, the relative values of the eigenvalue matrix off-diagonal element obtained from Clarke’s matrix are decreased while the frequency scan results are improved. The steps of correction procedure application are detailed, investigating the influence of each step on the obtained two new phase-mode transformation matrices.
1. Introduction
Modal transformations are applied to transmission line analyses because, in mode domain, it is easier to represent the frequency influence on the line parameters. Using phase-mode transformation matrices, all electrical parameters and all line representative matrices are obtained in mode domain [1–4]. The line representtative matrices become diagonal and the frequency influence can independently be introduced for every mode because the mutual phase couplings are independently included at every mode. Applying frequency dependent line parameters also leads to frequency dependent phasemode transformation matrices. Because of this, to obtain voltages and currents in phase domain after signal mode propagation, it is necessary to use a convolution procedure [5–10].
An alternative is to change the exact transformation matrices into single real ones. With these single real transformation matrices, any values can be determined in phase or mode domain using only a matricial multiplication [3,11]. The single real transformation matrices can obtain exact modes and diagonal line representative matrices for ideally transposed lines [12–14]. For untransposed lines, the results are not exact. The errors related to the eigenvalues (l) can be considered negligible for some untransposed three‑phase line analyses when Clarke’s matrix is applied as the transformation matrix. The data obtained with Clarke’s matrix are called quasi-modes. Increasing the asymmetrical geometrical line characteristics, even though the errors of quasi-mode matrix diagonal elements are negligible, the relative values of the quasi-mode matrix off‑diagonal elements can be significant when compared to the correspondent eigenvalues (l).
Based on these hypotheses, Clarke’s matrix application is analyzed considering a symmetrical three-phase line and a frequency range from 10 Hz to 1 MHz. The quasi-mode errors related to the eigenvalues (l) are studied as well as the off‑diagonal elements of the l quasi-mode matrix. Improving the analyses, frequency scans are also made using the characteristic impedance (ZC) and the propagation function (g) calculated from the exact mode values and the quasi-mode ones. Searching for the off-diagonal element relative value minimization, a perturbation approach corrector matrix is applied to Clarke’s matrix. The errors and frequency scan analyses are carried out again and the new results are compared to the previous error values. So, with a first-order approximation procedure, the l quasi-mode off-diagonal element relative values are highly decreased and the frequency spectrum of the processed signals is closer to that of the exact transformation. Neglecting the imaginary part of the new transformation matrix, frequency scan results similar to those from the first order matrix correction are obtained.
From the comparisons carried out using the 10 kHz frequency value, mode voltage and mode current vectors, it is suggested to extend the analyses shown in this paper considering one of the both modes that is not the homopolar reference of the system as the correction procedure application base. Another suggestion is to apply twice the correction procedure where the both modes related to the modal coupling for symmetrical threephase transmission lines are subsequently used.
2. Mathematical Bases
Searching for more simplicity for phase-mode transformation applied to transposed three-phase lines, single real transformation can be used. One sample of these matrices is Clarke’s matrix [3,11]. The exact differential equations that relate the transversal voltages and the longitudinal currents are described below. In this case, the phase-mode transformations (TV and TI), the per unit length longitudinal impedance (Z) and the per unit length transversal admittance (Y) matrices are included [1, 5, 7, 10, 12–14].
 (1)
(1)
uMD and iMD are the voltages and the currents in mode domain, respectively. For transposed three-phase lines, the TV and TI matrices are changed into Clarke’s matrix represented by TCL. So, the uMD and iMD values are:
 (2)
(2)
For exact eigenvectors (TV and TI), the phase-mode relations of Equation (2) are described by:
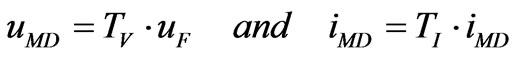 (3)
(3)
Using Equations (2) and (3) for transposed three-phase lines, the following relations are obtained:
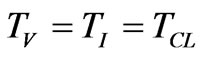 (4)
(4)
The inverse Clarke’s matrix is equal to its transposed one and the initial differential equations are changed into:
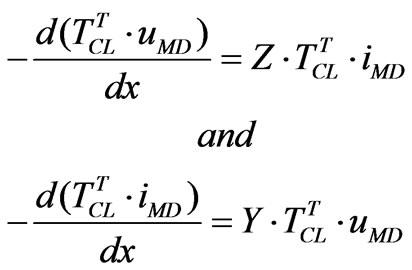 (5)
(5)
The Z and Y matrices in mode domain are:
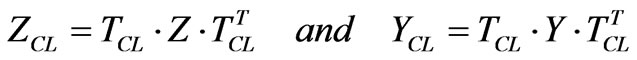 (6)
(6)
The Clarke’s matrix structure is [3, 11]:
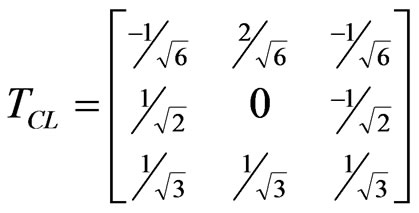 (7)
(7)
Based on Equations (4–7), the eigenvalues of a transposed three-phase line are determined by:
 (8)
(8)
In this case, the modes are called a, b and 0 (homopolar). The lCL is described by:
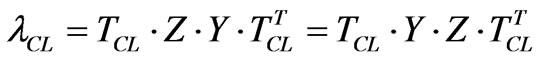 (9)
(9)
The impedance characteristic (ZC) is described by:
![]() (10)
(10)
The propagation function is described by:
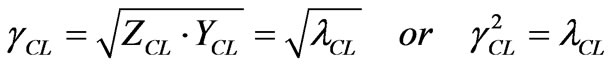 (11)
(11)
Considering a symmetrical untransposed three-phase line, lCL is not diagonal. The results are called quasimodes. There is a modal coupling between a and 0 modes and the lCL matrix becomes the following [3]:
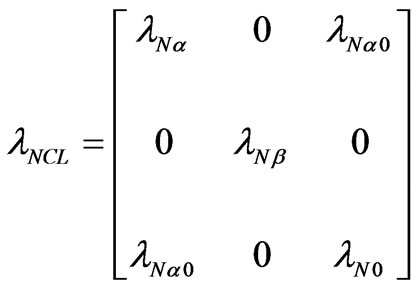 (12)
(12)
For the exact l matrix, the exact eigenvectors (TV and TI) are applied, obtaining the following:
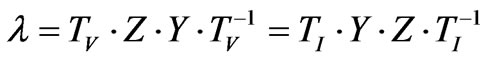 (13)
(13)
The exact Z and Y matrices in mode domain are:
 (14)
(14)
The exact modal ZC matrix is:
![]() (15)
(15)
The exact modal g matrix is:
 (16)
(16)
Applying Clarke’s matrix to an actual symmetrical untransposed three-phase line, the quasi-mode results are compared to the exact values through the following equations:
 (17)
(17)
The relative values of the lCL off-diagonal elements are obtained with the following:
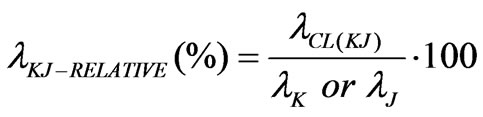 (18)
(18)
Regarding the frequency scan, the modal couplings among the quasi-modes are neglected. Every mode or quasi-mode is analyzed as in Figure 1 [7].
The propagation wave in Figure 1 is solved by the following system of equations where d is the line length [7].
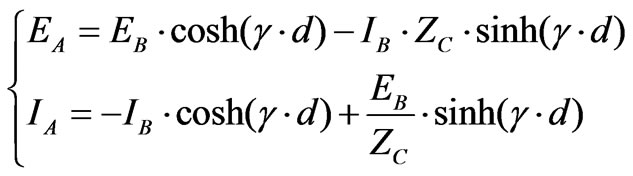 (19)
(19)
The system of Equations (19) is applied for every mode considering three situations in the line receiving terminal (the B terminal): opened line, short-circuit and infinite line. The infinite line is calculated using an impedance with the ZC value connected to the line receiving terminal. For the frequency scan, the line sending terminal is connected to a unitary step voltage source, considering the frequency domain. This voltage source is described by the next equation. The unitary step voltage
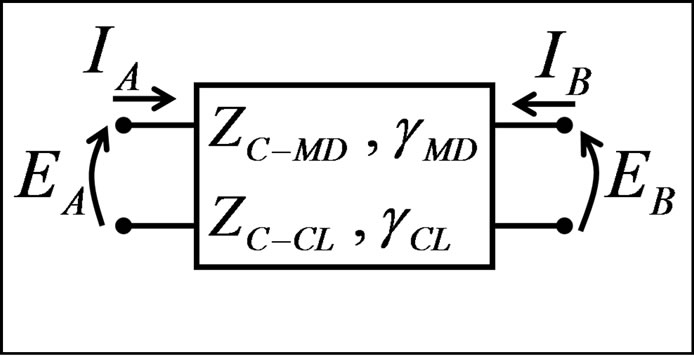
Figure 1. Frequency scan analyses
is chosen because it includes all frequency values. In the case of this paper, the frequency scan analyses are performed with a frequency range from 10 Hz to 1 MHz.
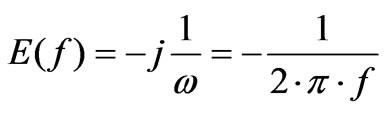 (20)
(20)
3. The Actual Symmetrical Three-Phase Line
The interactions between any transposed three-phase line and Clarke’s matrix produce exact mode results and the modal representative matrices are diagonal. In case of untransposed three-phase lines, the TCL results are not exact. These results are compared to the correspondent exact values using Equations (17) and (18) as well as the frequency scan.
The actual three-phase line analyzed in this paper has a vertical symmetry and shown in Figure 2.
The central phase conductor height is 27.67 m on the tower. The height of adjacent phase conductors is 24.07 m. Every phase is composed of four conductors distributed in a square shape with 0.4 m side length. Every conductor is an ACSR type one (ACSR‑26/7‑636 MCM). The phase conductor resistivity is 0.089899 W/m and the sag at the midspan is 13.43 m. The earth resistivity is considered constant (1000 W.m). The ground wires are EHS 3/8 with the resistivity of 4.188042 W/m. The height of these cables on the tower is 36.00 m. The sag of the ground wires at the midspan is 6.40 m.
4. The Error Analyses of the Clarke’s Matrix Application
From the Equations (8), (9), (12) and (13), the lNCL quasi‑modes are compared to the eigenvalues using Equation (17). In this case, firstly, the eigenvectors are calculated applying the iterative Newton-Raphson’s method. The initial values for this method are frequency of 10 Hz and the Clarke’s matrix elements. For this first frequency
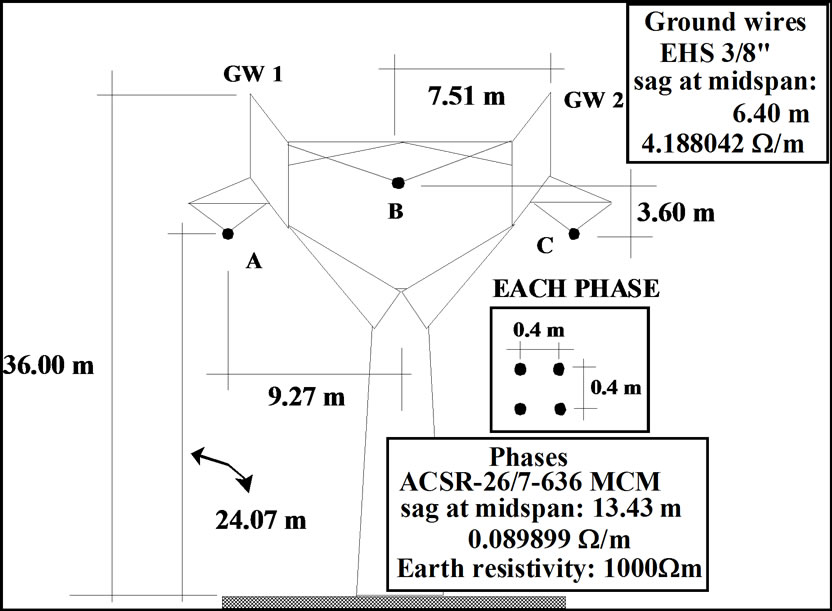
Figure 2. The actual symmetrical three-phase line of Brazil’s utilities
value, the iterative processing is started considering the eigenvectors equal to the Clarke’s elements. When the iterative processing converges to the exact values, it is restarted with the next frequency value and uses the exact values of the previous frequency value for the reinitialization of the new eigenvectors. After the determination of eigenvectors, the eigenvalues and the comparisons to the quasi-modes are performed for every frequency value [4].
The results of the comparisons between quasi-modes and the eigenvalues are shown in Figure 3. The β quasimode presents null errors because this is an exact mode. Also confirming the results of Equation (12), α and 0 quasi‑modes are not exact. The α quasi-mode presents the highest error peak among the three shown curves and this peak is about 10 kHz. The range of errors is from -0.3% to 0.2 %. There are inverse signals between the α and 0 quasi-mode error curves. The errors between the quasi-modes and eigenvalues can be considered negligible. These errors are determined using the modulus of the related values. Because of this, it is important to analyze the off-diagonal quasi-mode elements.
It is shown in Equation (12) that there is a modal coupling between the α and 0 quasi-modes. Because the line representative matrices are symmetrical independently of whether the line is symmetrical, or not, the off-diagonal element in the intersection between the matrix first line and the matrix third row is equal to the off-diagonal in the third line and the first row intersection. In Figure 4, this off‑diagonal element is compared to the correspondent eigenvalues (the α and 0 modes). If the Clarke’s matrix application does not obtain diagonal matrices, the modal coupling can interfere in the signal processing. It depends on the signal spectrum.
In Figure 4, the λNα0 off-diagonal element is compared to the correspondent eigenvalues from Equation (13). When it is compared to the λα eigenvalue, the λNα0 relative curve gets higher values than the curve obtained from the λ0 eigenvalue. The highest peak of the curve related to the λα eigenvalue is close to 18 % and it is associated to the initial frequency values of the consideredfrequency range. The curve related to the λ0 eigenvalue has softer variations than the other curve. Considering both curves presented in Figure 4, the λNα0 relative values decrease when the frequency increases. For low frequency values, the λNα0 modal coupling is more significant then for high frequency values. Based on these results, signal phase-mode transformation comparisons are carried out for analyzed frequency range using Clarke’s matrix and the eigenvectors (TV and TI). From phase vectors and with the Clarke’s matrix application, it is obtained mode vectors where only one mode has non-null value. It is shown in the following Equation:
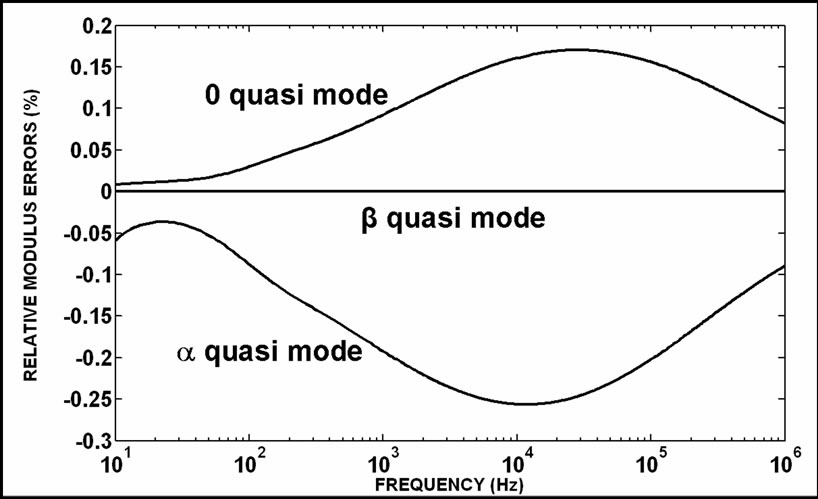
Figure 3. The λ error curves for an actual symmetrical threephase line
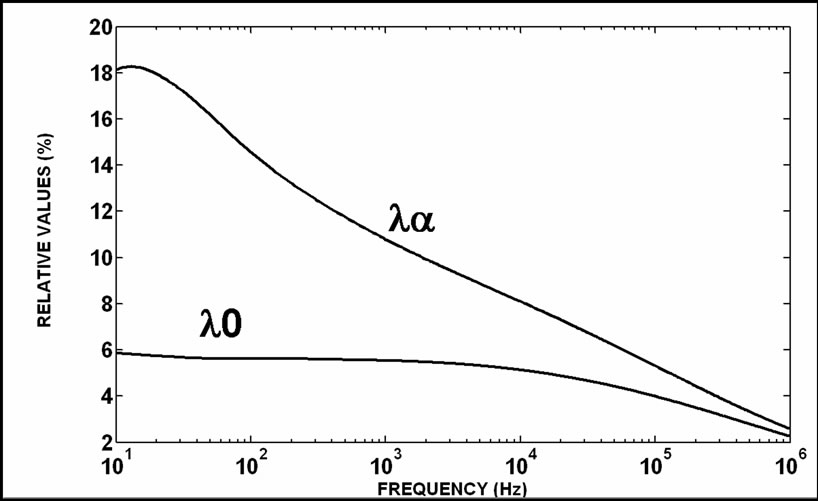
Figure 4. The quasi-mode off-diagonal element for the actual symmetrical three-phase line
 (21)
(21)
The non-null values are compared to the results obtained from the application of the eigenvectors:
 (22)
(22)
The results of comparisons between the non-null voltage values of Equation (21) and its correspondent values of Equation (22) are shown in Figure 5. The non-null current values of Equation (21) are compared to their correspondent eigenvector values in Figure 6. In these cases, the non-null values of the Clarke’s matrix application are compared to the results of the eigenvector application. The shown results are comparisons among modulus values. In Figure 7, it is shown the deviation angles related to the modal transformations using Clarke’s matrix and the TV eigenvector matrix. These are voltage vector transformations detailed in Equations (21) and (22). In case of Figure 8, the transformations are related to the current comparisons and also based on Equations (21) and (22).
For modal transformations of Z and Y matrices as well as for obtaining of eigenvalues, a transformation matrix and an inverse transformation one are used. Applying the modal transformations to the voltage and current vectors, only one transformation matrix, or its inverse matrix, is necessary. In this case, the transformation could increase the errors related to the quasi-modes. On the other hand, based on mentioned results, the use of quasi mode Z and Y matrices for determining other variables in mode domain could increase the errors observed in Figure 3. Investigating this supposition, the impedance characteristic and the propagation function are calculated from ZCL and YCL matrices and compared to the correspondent values obtained from ZMD and YMD matrices. The comparisons are made through Equation (17).
Figure 9 is associated to the ZC modulus. The ZC angle is null because this variable is real. Figures 10 and 11 are
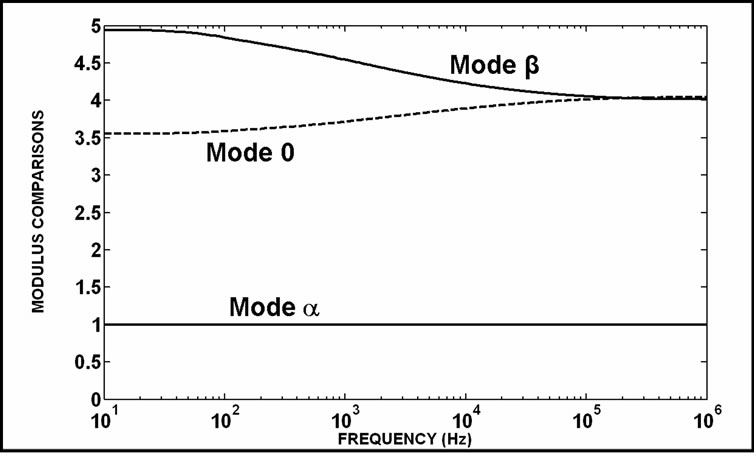
Figure 5. Non-null modulus comparisons among mode voltages (VCL/V) for the TCL matrix application
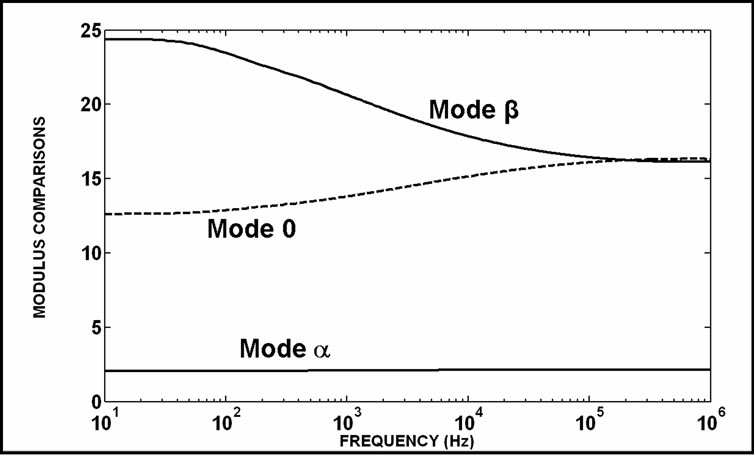
Figure 6. Non-null modulus comparisons among mode currents (ICL/I) for the TCL matrix application
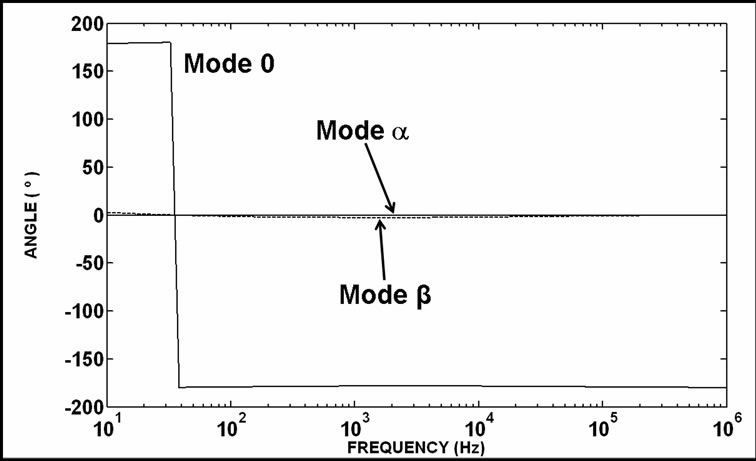
Figure 7. Non-null angle comparisons among mode voltages (VCL/V) for the TCL matrix application
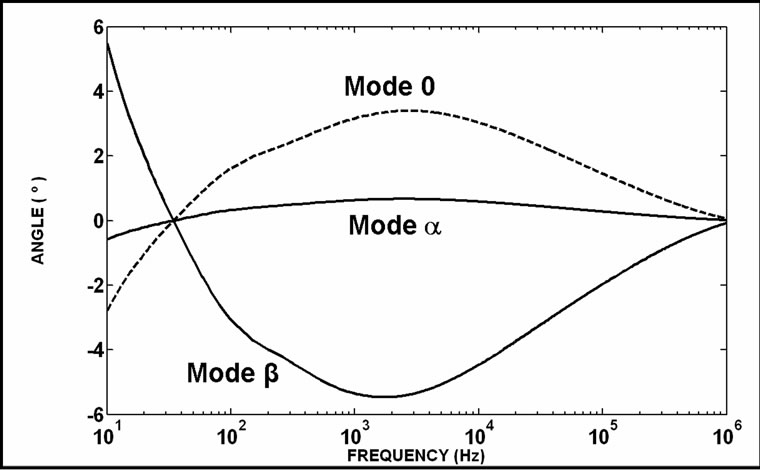
Figure 8. Non-null angle comparisons among mode currents (ICL/I) for the TCL matrix application

Figure 9. The ZC modulus errors for the actual symmetrical line
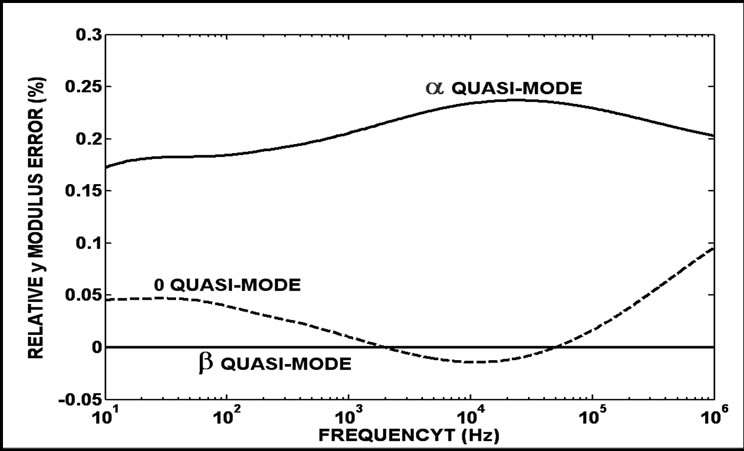
Figure 10. The γ modulus errors for the actual symmetrical line

Figure 11. The γ angle errors for the actual symmetrical line
associated to the γ modulus and the γ angle errors, respectively.
Considering the ZC modulus and the γ angle errors, there are curves with inverse signals (the α and 0 quasimodes). This characteristic can also be observed in Figure 3.
The range error for the ZC modulus (from -2 % to 2 %) is about 10 times higher than the γ modulus error range (from -0.05 % to 0.25 %) and it is about 100 times higher than the γ angle error range (from ‑0.015 % to 0.03 %). So, the ZC modulus is more sensitive to the errors introduced by Clarke’s matrix. The relative values of the off-diagonal element (the Nα0 modal coupling) for ZC modulus are shown in Figure 12. Based on these results, the ZC-Nα0 off-diagonal element influence is significant on the correspondent ZC quasi-modes.
In Figure 13 as much as in Figure 12, the curves have a crescent tendency from 10 kHz. In Figure 13, the relative values are in a much lower range than that of Figure 12. In Figure 14, the γNα0 angle relative values are in a similar range to the γNα0 modulus relative values. In this case, the values do not tend to be crescent ones.
5. Frequency Scan Analyses
Frequency scan analyses are based on Figure 1 and Equations (19) and (20) are used [7]. The EA voltage is described by Equation (20). Three situations of the line receiving terminal (the B terminal) are checked: open line (IB=0), short-circuit (EB=0) and infinite line. The infinite line is obtained with an impedance equal to the ZC value connected in the B terminal of Figure 1. For all these three situations, considering both line terminals, the modulus values of the voltages and the currents obtained

Figure 12. The ZC-Na0 modulus off-diagonal element relative values

Figure 13. The gNa0 modulus off-diagonal element relative values
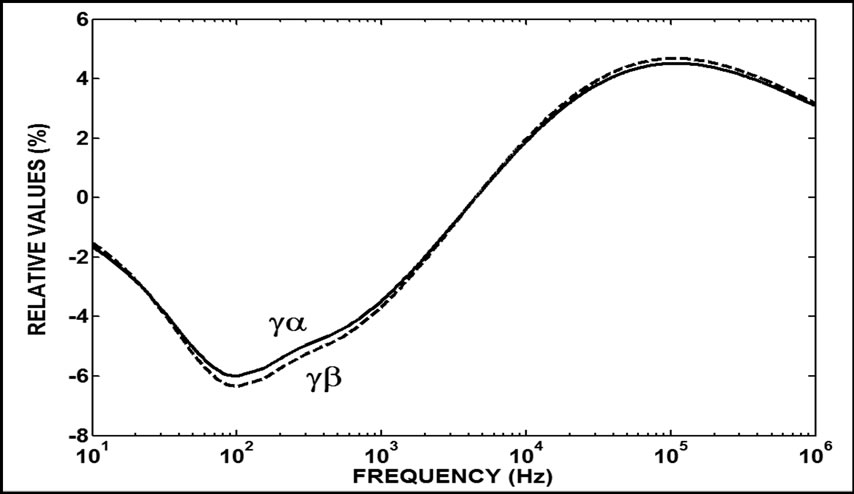
Figure 14. The gNa0 angle off-diagonal element relative values
from quasi-modes are equal or very close to the exact values obtained from eigenvectors. The main differences are related to the angle values and the a mode. Showing the results related to the modulus values, Figure 15 presents the B terminal currents for the a mode when this terminal is open. Similar values are presented in Figure 16 considering the 0 mode and the infinite line.
Considering the short-circuit analyses in Figure 17, it is shown that the a quasi-mode and exact angle values are superimposed for frequency values up to 10 kHz. From 10 kHz to 1 MHz, there are great differences between quasi-mode and exact angle values. In this case, the differences are great because the curves present inverse signals related to the horizontal axis.
When the infinite line is analyzed (Figure 18), the obtained results are similar to those present in Figure 17. The quasi‑mode and the exact angle values are superimposed for frequency values up to 10 kHz. Above 10 kHz, the differences are great and for some parts of the range, the curves are opposite and present inverse signals. Figure 18 shows results from 10 kHz to 1 MHz.
Based on frequency scan analyses, Clarke’s matrix could be applied to transient simulations considering symmetrical untransposed three-phase lines and phenomena with a frequency spectrum concentrated below 10 kHz. For general phenomena, there are classical solutions for
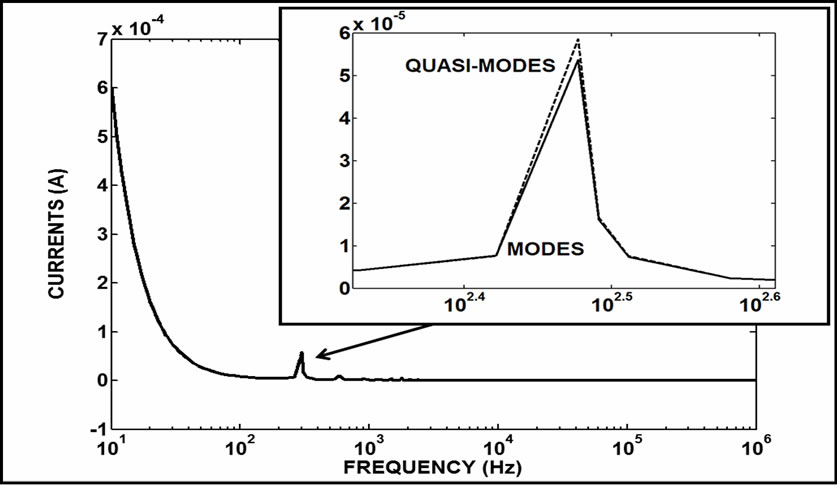
Figure 15. The B terminal currents for the a mode and the opened line
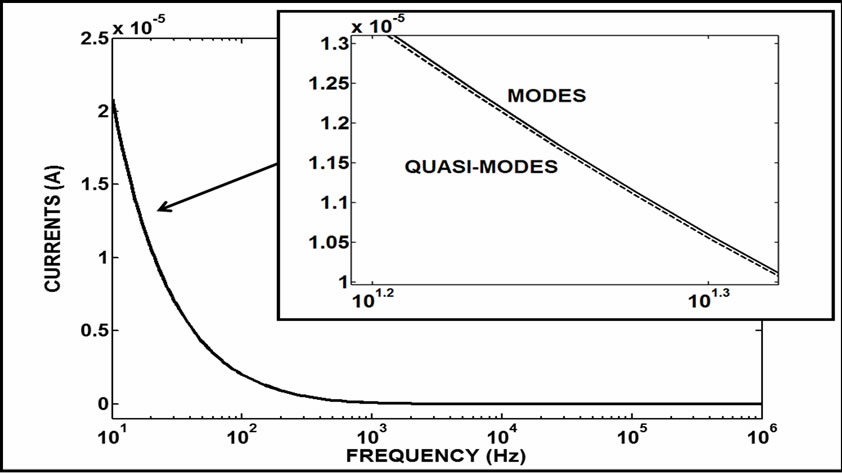
Figure 16. The B terminal currents for the 0 mode and the infinite line
this problem based on eigenvector applications. An alternative is to apply a perturbation approach corrector matrix, improving the results of the Clarke’s matrix application above 10 kHz. This alternative is described in the next item and based on the homopolar mode.
6. The Perturbation Approach Corrector Matrix
The procedure shown in this section is based on a first‑order perturbation theory approach [3]. This procedure is used to improve the quasi-mode results and obtain a better approximation to the exact values. Initializing this development, a normalization matrix is defined as:
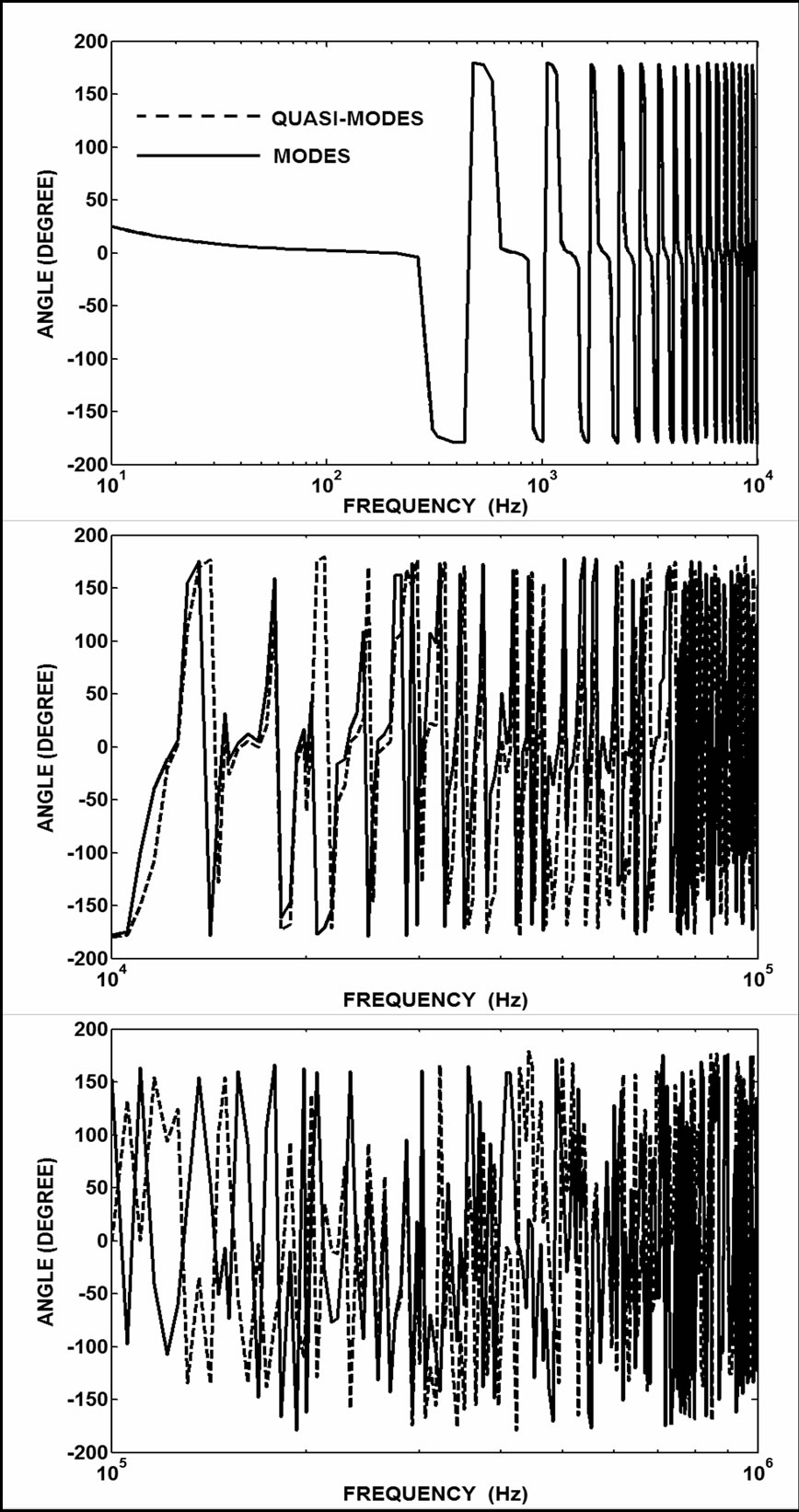
Figure 17. The current angle values for the B terminal with short-circuit (the a mode)

Figure 18. The current angle values for the B terminal with infinite line (the a mode)
 (36)
(36)
The N22 matrix is defined as:
 (37)
(37)
The normalization matrix is applied to the lNCL matrix:
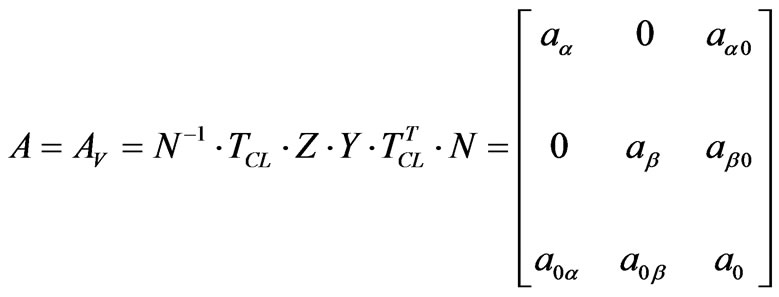 (38)
(38)
The described procedure is applied to the TV and the TI matrices. For the TI matrix, the procedure is similar to the TV one with a change in the position of the Z and Y matrices in Equation (38):
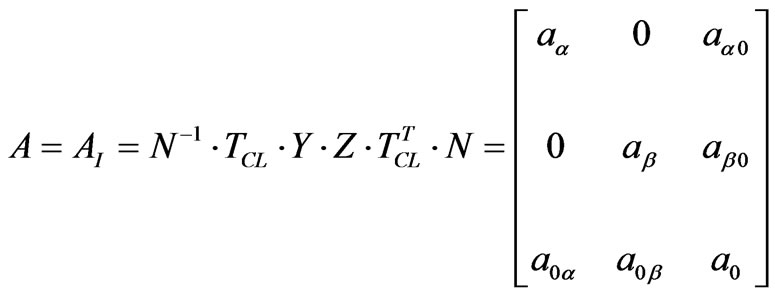 (39)
(39)
The structure of the A matrix is determined from:
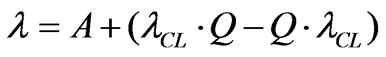 (40)
(40)
The last Equation leads to:
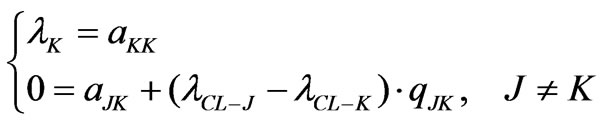 (41)
(41)
The lCL-a element is equal to the lCL-b. Because of this, the a12, a21, q12 and q21 elements are null. Dividing the lNCL matrix into blocks, the portioned structure can be described by:
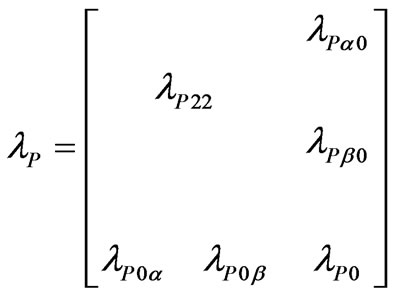 (42)
(42)
The lP22 is:
 (43)
(43)
In this case, despite the symmetry of the line representative matrices, small numeric differences are considered between symmetrical elements of the lP matrix. The small numeric values of the lPab and lPba are also considered. Using Equations (42) and (43), the aa and ab elements are determined by:
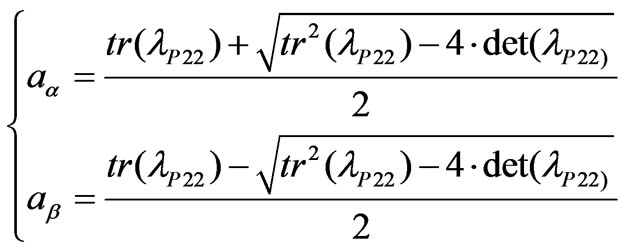 (44)
(44)
The N22 matrix elements are determined by:
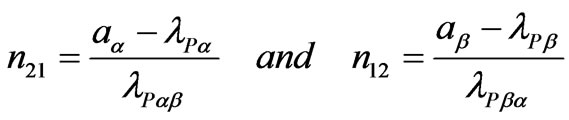 (45)
(45)
In this case, only the Q matrix elements of the third line and the third row can not be null. These elements correspond to the 0 mode and are calculated by:
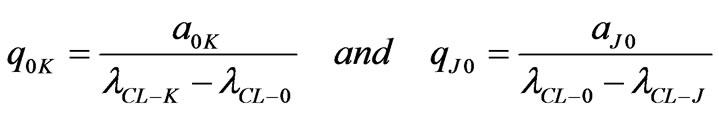 (46)
(46)
The perturbation approach corrector matrix is described by:
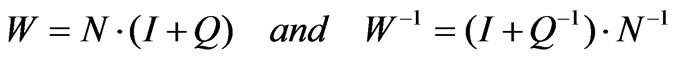 (47)
(47)
The corrected transformation matrix is described by:
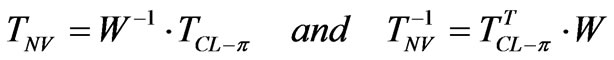 (48)
(48)
7. Obtained Results
Checking the changes into the Clarke’s matrix results carried out applying only the N matrix, it is used the flowchart shown in Figure 19.
The changes obtained from the N matrix application are mainly related to the mode coupling relative values. The peak value is decreased from 18 % to 2 %. It is about a 10 time reduction. The off-diagonal relative obtained after applying the N matrix are shown in Figure 20. On the other hand, there are no expressive changes for the l relative errors. These values are shown in Figure 21.
Completing the analysis of the influence of N matrixthe results of Figures 22–25 show that the application of this matrix balances equally the phase-mode transformation results obtained from Equation (26) where the TCL matrix is changed into the AV and AI matrices.
Another analysis about the correction procedure ap-

Figure 19. Flowchart for checking of AN and AI applications

Figure 20. The quasi-mode off-diagonal relative values after the N matrix application
plication to Clarke’s matrix is about the Q matrix application. In this case, Figure 26 shows the flowchart related to this matrix application. Figure 27 shows the off-diagonal relative values after the Q matrix application and Figure 28 shows the l errors for the same case.
In Figures 27 and 28, the shown values decrease when compared to the values presented in Figures 20 and 21. The peak value shown in Figure 27 is about 150 times lower than the correspondent values shown in Figure 4. Comparing Figures 27 and 20, the reduction is about 15 times for the peak values.
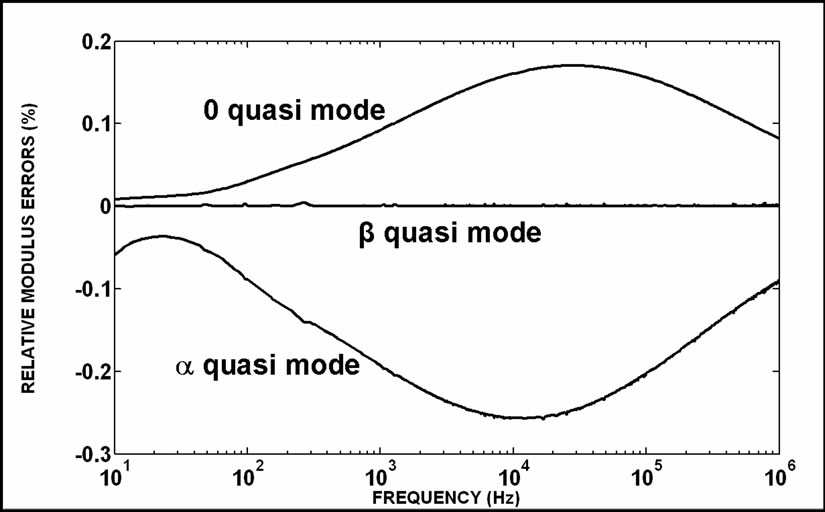
Figure 21. The λ error curves after the N matrix application
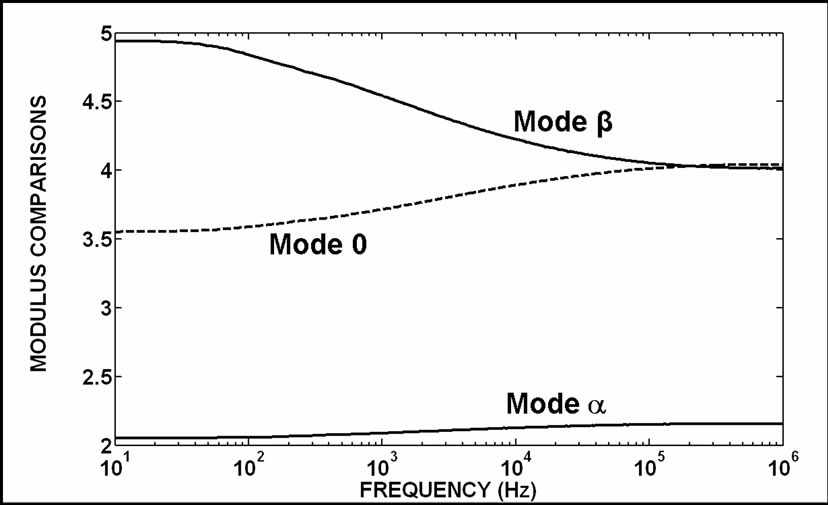
Figure 22. Non-null modulus comparisons among mode voltages (VCL/V) for the N matrix application

Figure 23. Non-null angle comparisons among mode voltages (VCL/V) for the N matrix application
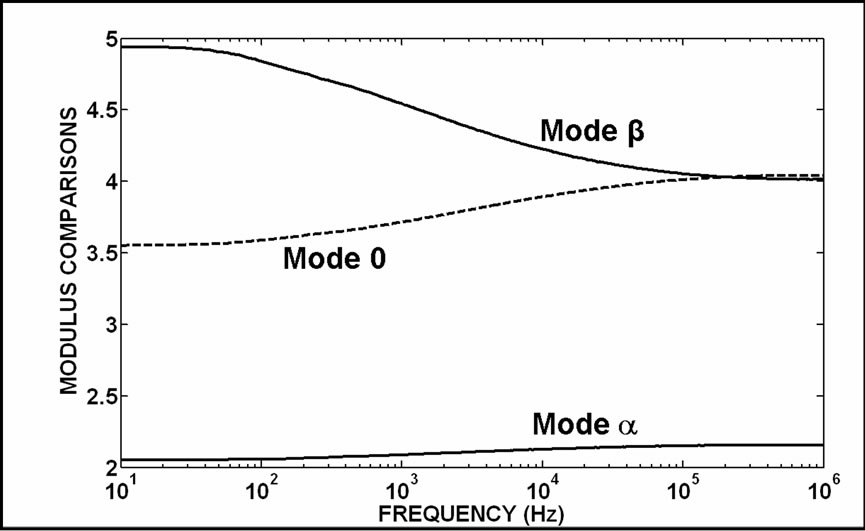
Figure 24. Non-null modulus comparisons among mode currents (ICL/I) for the N matrix application
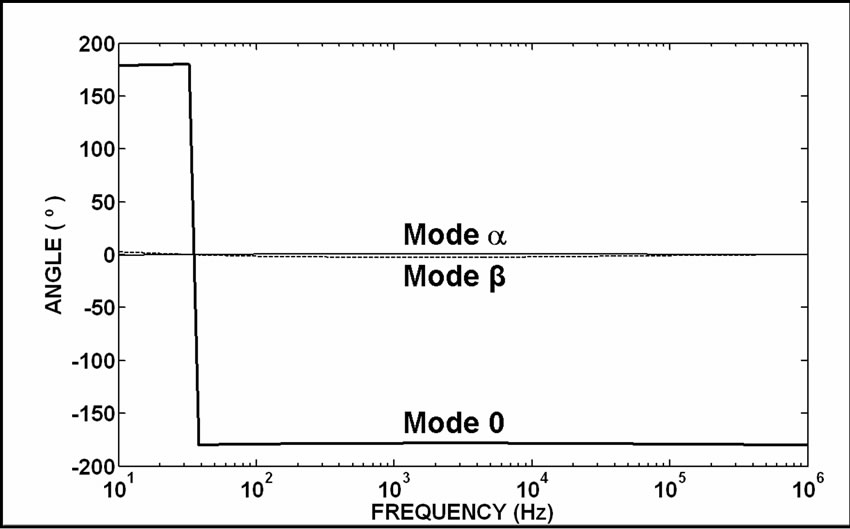
Figure 25. Non-null angle comparisons among mode currents (ICL/I) for the N matrix application
For the l errors, comparing Figures 3, 21 and 28, the reduction is about 150 times considering the negative peak values shown in these cases.
Applying the Q matrix, the off-relative and the l errors become negligible. Analyzing the results of both matrices applications, N and Q, it can be concluded that the N matrix mainly acts on the off‑diagonal relative values, decreasing them. On the other hand, the Q matrix acts on the λ error and the off-diagonal relative value decreasing.
Analyzing the results shown in Figures 27 and 28, these values can be considered negligible because they are in a very low range of relative values. The peak values reach 0.12 % and -0.002 % in mentioned figures. The shown curves also present some oscillations which, probably, are introduced by the used numeric method.
Based, on the results of Figure 29, where it is shown the B terminal a mode current angles for with the short-circuit in the line end, the influence of these numeric oscillations on the propagation wave results is not significant. On the other hand, for future development, if it is possible, these oscillations could be minimized, avoiding the numeric oscillation influence on the determination of ZC, g and other electrical variables.
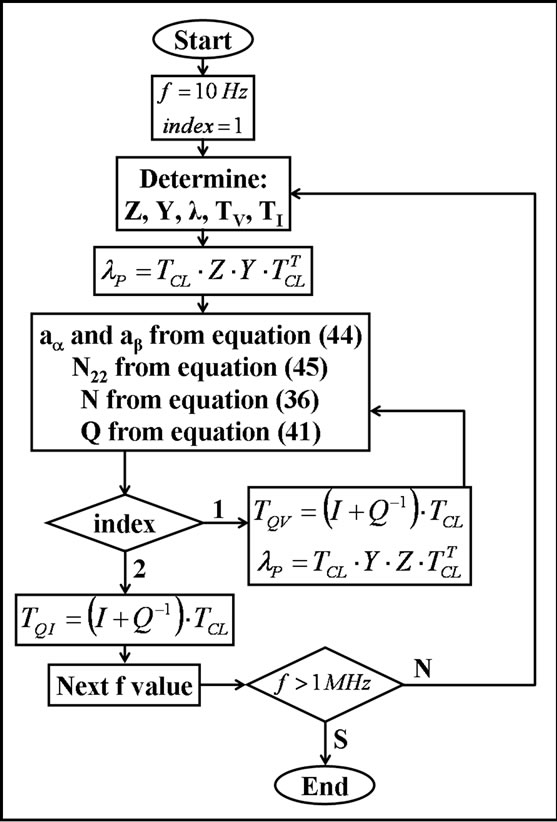
Figure 26. Flowchart for checking of Q matrix applications

Figure 27. The quasi-mode off-diagonal relative values after the Q matrix application

Figure 28. The λ error curves after the Q matrix application
8. Conclusions
Changing eigenvector matrices into Clarke’s matrix for untransposed symmetrical three-phase lines leads to small errors related to the exact modulus eigenvalues.
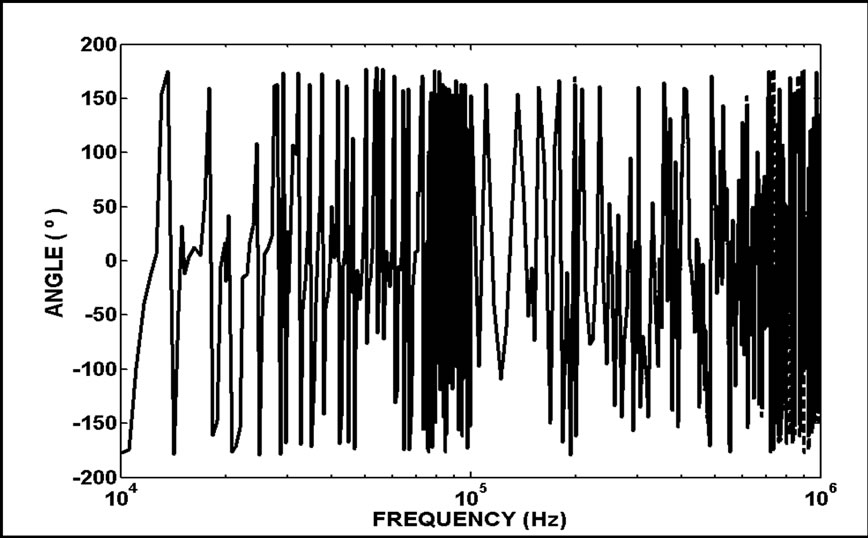
Figure 29. The current angle values for the B terminal with short-circuit (the a mode), considering the TNV and TNI transformation matrices
The off-diagonal element of the matrix obtained from the Clarke’s matrix application, the quasi-mode eigenvalue matrix, has high relative values when compared to the correspondent exact eigenvalues. Based on these element results, the frequency scan analyses are carried out, showing that there are great differences between the quasimode current angles and the exact ones for frequency values above 10 kHz. In this casse, three situations of the line receiving terminal are checked: open line, short-circuit and infinite line.
A correction procedure is applied and new phase‑mode transformation matrices are determined: one matrix for voltages and another one for currents.
It is detailed the steps of the correction procedure application, describing the influence of each step on the decreasing of the off-diagonal quasi-mode relative value elements and the quasi-mode matrix ones. One of these steps is the normalization matrix application that carries out balanced voltage and current vectors, obtaining a 150 time reduction of the off-diagonal quasi-mode eigenvalue matrix relative values when compared to the Clarke’s matrix application. After this step, the final one reduces about 150 times the l errors when compared to the Clarke’s matrix results. Using the new phase-mode transformation matrices, obtained from the applied correction procedure, the off-diagonal element relative values and the l errors are highly decreased and could be considered negligible.
REFERENCES
- H. W. Dommel, “Electromagnetic transients program— rule book,” Oregon, 1984.
- Microtran Power System Analysis Corporation, Transients Analysis Program Reference Manual, Vancouver, Canada, 1992.
- J. A. Brandão Faria and J. Briceño Mendez, “Modal analysis of untransposed bilateral three-phase lines—a perturbation approach,” IEEE Transactions on Power Delivery, Vol. 12, No. 1, January 1997.
- T. T. Nguyen and H. Y. Chan, “Evaluation of modal transformation matrices for overhead transmission lines and underground cables by optimization method,” IEEE Transactions on Power Delivery, Vol. 17, No. 1, January 2002.
- A. Morched, B. Gustavsen, and M. Tartibi, “A universal model for accurate calculation of electromagnetic transients on overhead lines and underground cables,” IEEE Transaction on Power Delivery, Vol. 14, No. 3, pp. 1032– 1038, July 1999.
- D. M. Nobre, W. C. Boaventura, and W. L. A. Neves, “Phase-domain network equivalents for electromagnetic transient studies,” The 2005 IEEE Power Engineering Society General Meeting, CD‑ROM, San Francisco, USA, June 12th-16th, 2005.
- A. Budner, “Introduction of frequency dependent transmission line parameters into an electromagnetic transients program,” IEEE Transaction on Power Apparatus and Systems, Vol. PAS-89, pp. 88–97, January 1970.
- S. Carneiro Jr., J. R. Martí, H. W. Domme1, and H. M. Barros, “An efficient procedure for the implementation of corona models in electromagnetic transients programs,” IEEE Transactions on Power Delivery, Vol. 9, No. 2, April 1994.
- T. F. R. D. Martins, A. C. S. Lima, and S. Carneiro Jr., “Effect of impedance approximate formulae on frequency dependence realization,” The 2005 IEEE Power Engineering Society General Meeting, CD‑ROM, San Francisco, USA, June 12th-16th, 2005.
- J. R. Marti, “Accurate modelling of frequency-dependent transmission lines in electromagnetic transients simulations,” IEEE Transaction on PAS, Vol. 101, pp. 147–155, January 1982.
- E. Clarke, “Circuit analysis of AC power systems,” Vol. I, Wiley, New York, 1950.
- L. M. Wedepohl, “Application of matrix methods to the solution of travelling-wave phenomena in polyphase systems”, Proceedings IEE, Vol. 110, pp. 2200–2212, December 1963.
- L. M. Wedepohl and D. J. Wilcox, “Transient analysis of underground power-transmission system—system model and wave propagation characteristics,” Proceedings of IEE, Vol. 120, No. 2, pp. 253–260, 1973.
- L. M. Wedepohl, H. V. Nguyen, and G. D. Irwin, “Frequency dependent transformation matrices for untransposed transmission lines using Newton-Raphson method”, IEEE Transaction on Power Systems, Vol. 11, No. 3, pp. 1538–1546, August 1996

