International Journal of Communications, Network and System Sciences
Vol.10 No.12(2017), Article ID:81522,75 pages
10.4236/ijcns.2017.1012019
Alloy Gene Sequence Project and System Science Philosophy
Youqing Xie1,2,3*, Xiaobo Li4, Xinbi Liu1,2,3, Hongjian Peng5, Yaozhuang Nie6
1School of Materials Science and Engineering, Central South University, Changsha, China
2Powder Metallurgy Research Institute, Central South University, Changsha, China
3State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China
4School of Materials Science and Engineering, Xiangtan University, Xiangtan, China
5School of Chemistry and Chemical Engineering, Central South University, Changsha, China
6School of Physical Science and Technique, Central South University, Changsha, China
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 31, 2017; Accepted: December 26, 2017; Published: December 29, 2017
ABSTRACT
System Science Philosophy is a knowledge system constructed of universal principle and law sequences. Alloy gene is a characteristic atom existing in the center of coordination cluster and occupying the lattice point of a lattice cell, and carries holographic information about valence electron structure, physical and thermodynamic properties obtained by alloy gene theory. Alloy gene potential energy curve function has developed traditional atom pair interaction potential functions into many atoms’ interaction function associated with valence electron structure, bond length, bond energy, which makes alloy gene Gibbs energy function can be established. Alloy gene Gibbs energy transmissive function has developed traditional partition function. Its equilibrium and sub-equilibrium transmissive modes produce alloy holographic network positioning bank, which is operable platform to achieve transformation from “trial and error” method to the “whole obtained from a few part” law for getting advanced alloys. It has become possible to launch alloy gene sequence project.
Keywords:
Alloy Gene Sequence, System Science Philosophy, Alloy Gene Theory, Alloy Gene Gibbs Energy Transmissive Function, Alloy Holographic Network Positioning Bank

1. Introduction
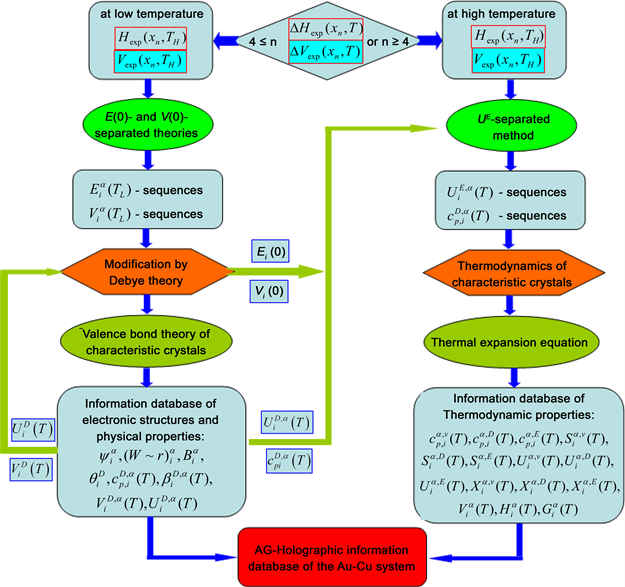
Materials are always one of the levers to propel the human society forward. There are 81 metal elements accounting for 79% in the Element Periodic Table, of which the 3240 kinds of binary alloy systems, 85,320 kinds of ternary alloy systems, and so on, can be composed. In these alloy systems there are a large number of potential advanced alloys to be discovered. Early in the 1937, Slater said that “the advance of physical metallurgy in the next few years is likely to be almost as dependent on the electron theory of metals as the advances of the last generation were dependent on thermodynamics” [1] . Nowadays, the biology has reached the level to be capable of transferring genes and “clone” creature, while in the same old and historical field of metal materials, the design of advanced alloys is still at the “trial and error” method stage. It is attributed to questionable thinking mode, theories and understanding of some experimental data in the QMAC (quantum mechanical ab initio calculations) electron theory [2] - [10] and CALPHAD (calculation of phase diagrams) thermodynamics [11] - [18] communities, and that there are very few scholars who regard seeking Alloy Gene (AG) as the first condition for realizing scientific design of advanced alloys. The System Science Philosophy (SSP) is a knowledge system constructed of universal principle and law sequences, which are integrated from theories and methods in biological, non-biological and societal systems. The SSP functions in the scientific practice are not only to be discovery, explanation and guide but also to strengthen scientific faith and courage of explorers. In order to quickly and efficiently discover, design and produce advanced alloys, we have discovered AG, established Systematic Metal Materials (SMM) science and created Alloy Holographic Network Positioning (AHNP) methods/techniques road by the SSP guide [19] - [24] . With these advances, it has become possible to launch the Alloy Gene Sequence Project (AGSP), of which the major goals are: Achieving transformation of the theoretic basis from Pauling’s chemical bond theory [25] [26] [27] and Lupis’s “central atoms” theory [28] to the SMM science, which drives further developments of the AG theory [29] - [35] , Alloy Phase (AP) theory [36] - [45] and Alloy Systems (AS) theory [46] [47] [48] , then provides theoretical support for the AGSP; Achieving transformation of technical law from “trial and error” method to “Whole Obtained from a few Parts (WOP)” law, which creates the AHNP techniques, including the methods of the AG holographic warehouse and AHNP warehouses of alloys, phases and alloy systems, as well as techniques of discovery, design, certification, manufacturing and deployment of advanced alloys. These techniques will significantly decrease drain on time, manpower, material, financial and energy resources, then provide technical support for the AGSP. The AGSP will create a new era of the SMM science and AG engineering, during the 21st century. This paper includes common description of theories chain in Text, explanation of methods chain and equations chain in Supplementary Information (1) and (2), respectively.
2. SMM Science
Creative SSP principles will evolve real systematic science theories! It can be explained by the SMM science and taking fcc-based lattice Au-Cu system with Au3Cu-, AuCu- and AuCu3-type ordered and disordered phases as an example, which has been considered to be a classical paragon studied nearly by almost alloy theories for one century.
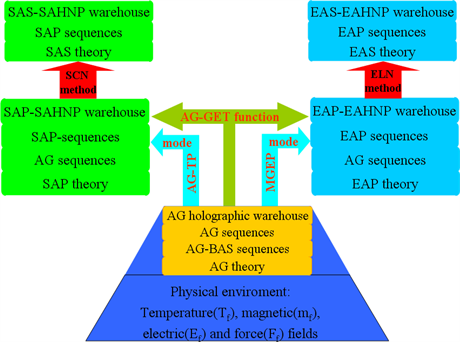
2.1. SMM Science Framework
According to the SSP-systematic globality principle, i.e., “The globality of a complex system is attributed to the multilevel of structures and properties and to the opening loop correlativity of structures, properties and environment.” The SMM science has been established (Figure 1). It includes three level theories: AG theory for determining AG-basic atom state (BAS) sequences and AG sequences, and establishing AG holographic warehouse; Equilibrium and Subequilibrium Alloy Phase (EAP, SAP) theories for determining EAP and SAP sequences, establishing EAP-EAHNP and SAP-SAHNP warehouses; Equilibrium and Subequilibrium Alloy System (EAS, SAS) theories for establishing EAS-EAHNP and SAS- SAHNP warehouses, based on EAP and SAP sequences, respectively.
The EAP and SAP theories are connected, respectively, with AG theory through the equilibrium Minimal Gibbs Energy Path (MGEP) and subequilibrium AG-Tracking Path (AG-TP) modes, based on AG-Gibbs Energy Transmissive (AG-GET) function, and associated with the EAS and SAS theories by Equilibrium Lever Numerical (ELN) and Subequilibrium Crosspoint Numerical
Figure 1. SMM science framework. It consists of alloy gene (AG) theory, equilibrium and subequilibrium alloy phase (EAP, SAP) theories, equilibrium and subequilibrium alloy system (EAS, SAS) theories, as well as AG-Gibbs energy transmissive (AG-GET) function, equilibrium minimal Gibbs energy path (MGEP) and subequilibrium alloy gene-tracking path (AG-TP) modes, and equilibrium lever numerical (ELN) and subequilibrium crosspoint numerical (SCN) methods.
(SCN) methods of isothermal Gibbs Energy (GE) curves, respectively. The SMM science is an integrated theory, in which the valence electron arranging structures and holographic properties in micro-AG theory, AG arranging structures and holographic properties in submicro-AP theory, AP arranging structures and holographic properties in macro-AS theory and environments have been linked up.
2.2. AG Sequences
The key step for establishing SMM science is to seek the AG sequences. According to the SSP-systematic genes (SG) universality principle, i.e., “Any system with appearing diversity of structures and properties possesses oneself of SG sequences.” We have discovered that, in the alloy system with gathering many atoms of some component elements, “a single AG is a characteristic atom existed in the center of the coordination cluster and occupied on the lattice point of a lattice cell.” In the fcc-based lattice Au-Cu system, the AG-sequences are the central - and -sequences respectively in the basic coordination clusters - and -sequences (Supplementary Information (1)), that are attributed to split of constituent atom states, under influence of coordinative configurations. The and coordinative clusters consist of the central and characteristic atoms respectively, and the nearest coordinative configuration . Here, I is the coordinative number and equal to 12; i is the number of Cu-atoms and can change from 0 to 12; is the number of Au-atoms. The diversity of alloy phase structures is attributed to combination and arrangement of alloy genes in the AG sequences. The diversity of alloy phase properties is attributed to AG properties and their transmissive modes.
2.3. AG Theory
AG theory includes AG separated theory and AG Characteristic Crystal (AGC) theory consisting of AGC-valence bond theory and AGC-thermodynamics. According to separable and functions in the AG separated theory, the , , and sequences of the Au-Cu system have been separated from experimental enthalpies and volumes of few alloys by WOP law (Supplementary Information (1) 1.1).
In order to determine AG holographic information about AG valence electron structures, physical and thermodynamic properties, and according to SSP combining rule of imaginal thinking and mathematic thinking, we have proposed the AGC concept , established AGC mixed model and additive law of AGC extensive properties ( , ) of alloy phases as functions of composition x, temperature and order degree :
(1)
(2)
where, denotes AGC concentration. Their magical effects are reflected in the following areas:
1) The AGC is a fictitious concept, which consists of the same alloy genes. Therefore, there are and sequences consisted with and sequences in the fcc-based lattice Au-Cu system [29] [30] . Among them, the primary and denote respectively the pure Au and Cu metals (Supplementary Information (1)). Then, the difficult problem to obtain AG holographic information may be resolved by the theory of single substances with known and sequences, i.e., AGC theory [31] [32] [33] [34] [35] .
2) The AGC mixed model may be imagined to be that when primary and characteristic crystals form an alloy, they are split into the and sequences at first, then to be mixed into the alloy [36] [37] [38] .
3) The AGC holographic information may be obtained by AGC theory. Each AG holographic information may be represented by corresponding AGC holographic information (Supplementary Information (1) 1.2-1.4).
2.4. AG ψi-Sequences
The diversity of AG valence electron structures ( ) is attributed to combination and arrangement of quantum valence electrons, that may be described by hybridization of some basic atom states in the basic atom state sequences (Supplementary Information (1) 1.2). In the AGC valence bound theory of the AGC theory, the AGC lattice constant equation and AGC potential energy equation as functions of valence electron structure , bond length and bond energy may be respectively used to translate the AG sequences into AGC sequences, and the AG sequences into AGC sequences. The AGC sequences may be calculated, through the crosspoint method of the equilattice constant -line and equipotential energy -line (Supplementary Information (1) 1.4) the essence of crystal symmetry and properties of AGC sequences may be explained by AGC sequences [39] [45] .
2.5. AG Gi-Sequences
In the AGC thermodynamics, AG Gibbs energy is the holographic energy state with multi-level thermodynamic properties. It may be divided into two parts [45] :
(3)
where, the AG interaction potential energy is responsible to make AG stabilization, the AG generalized action free energy is responsible to make AG suit variations in environments, under influences of temperature , magnetic , electric and force fields. Under the influence of field, the and sequences have been calculated by experimental enthalpies of few alloys (Supplementary Information (1) 1.3, 1.4).
2.6. AG Wi-Sequences
In the AGC valence bond theory, the AG potential energy curve function is of great significance: 1) It has developed traditional atom pair interaction potential functions, such as Mie potential and Lennard-Jones potential, into the MAI (Many Atoms Interaction)-AG function [31] , that makes AG theory have solid physical foundation and can establish the function worthy of the name. 2) It has developed elasticity: The force constant , bulk modulus , Young’s modulus and shear modulus equations associated with the and Debye temperature have been derived, that make function can respond to field. 3) It has developed Debye specific heat theory: The sequences may be calculated approximately by function, that make function can respond to field, through Debye vibration free energy and generalized attaching action free energy . 4) It has developed Grüneisen’s thermal expansion theory: The Grüneisen’s two constants and have been derived, which are useful to calculate AGC thermal expansion sequences, that make function can respond to and fields. 5) It has developed magnetism and electricity: The AGC total potential energy includes contributions of bond energies of covalent, magnetic and free electrons, that makes function can respond to , , and fields. These achievements have been tested by studies of some pure metals [32] [33] [34] [35] (Supplementary Information (1) 1.3, 1.4).
2.7. AG-GET Function
According to the SSP-systematic opening circuit evolution principle, i.e., “The sources of system are systematic genes, which determine structures of systems; structures determine properties; properties suit environments; environments optimize genes; genes optimize systems; systems optimize environments.” we have established the AG-Gibbs energy transmissive AG-GET function of alloy phases in field, which describes the systematic correlativity of the characteristic Gibbs energy (chemical potential of alloy phase), AG- probabilities ( , ) occupied at the AG-GE ( , ) levels and degeneracy g-factor of AG-probabilities occupied at the lattice points [37] [40] [45] [46] [47] [48] . It is the AG-GET function in the real sense of the term, which may be also called as the systematic opening evolution function (Supplementary Information (2) 4.1,4.2):
(4)
where, is Boltzmann’s constant, and may be obtained by the AG-GE additive law:
(5)
The first Gibbs energy function worthy of the name for alloy phases in the history has been derived:
(6)
The AG arranging configurational entropy -function is obtained from the degeneracy g-factor:
(7)
2.8. AG-GET Modes
The essential definition of equilibrium evolution described by AG-minimal Gibbs energy path (MGEP) equilibrium transmissive mode is that “the AG-GE ( , ) levels and AG-probabilities ( , ) occupied at the lattice points/AG-GE levels can respond immediately and change synchronously with each small variation in temperature, and proceed along the minimal Gibbs energy path, supposing to have no obstacle to atom movement”. The , , equilibrium path charts may be calculated by iso-order degree or isothermal path methods (Figure 2, Supplementary Information (1) 2.1). The MGEP mode leads to equilibrium EAP theory, which includes EAP thermodynamics [45] [46] [47] [48] , EAP valence bond theory [41] [42] [43] [44] and EAHNP phase diagrams of alloy phases (Figure 3). Then, the equilibrium EAS theory and EAHNP phase diagrams of Au-Cu system (Figure 4) have been established by Equilibrium Lever numerical NLN method of isothermal Gibbs energy curves.
The essential definition of subequilibrium evolution described by AG-tracking path (AG-TP) subequilibrium transmissive mode is that “the AG-Gibbs energy ( , ) levels can change immediately with each small variation in temperature, but AG-probabilities ( , ) occupied at the lattice point/AG-GE levels cannot change synchronously, due to exist potential well obstacle to atom
Figure 2. Path charts on disordering AuCu alloy. (a) Three dimension mixed Gibbs energy chart with equilibrium path and subequilibrium path; (b) Two dimension equilibrium path and subequilibrium path.
Figure 3. EAHNP diagrams of AuCu type phase. (a) Two dimension equilibrium isothermal phase diagram with phase boundary curves ; (b) Two dimension equilibrium iso-order degree phase diagrams with phase boundary curves and experimental jumping -temperatures [15] . The symbols “O”, “D”, “C” denote respectively ordered region, disordered region, stoechmetric compound.
Figure 4. Phase diagrams of Au-Cu system. (a) Equilibrium order degree EAHNP phase diagram with iso-order degree curves and experimental jumping -temperatures [15] ; (b) Subequilibrium order degree SAHNP phase diagram with iso-order degree curves and experimental jumping -temperatures [46] .
movement, and proceed along the higher path than path.” The , , subequilibrium path charts may be calculated by the AG-Tracking Path AG-TP mode of the experimental mixed enthalpy path (Figure 2, Supplementary Information (1) 3). This AG-TP mode leads to subequilibrium SAP theory, which includes SAP thermodynamics, SAP valence bond theory and SAHNP phase diagrams of alloy phases. Then, the SAS theory and SAHNP phase diagrams of Au-Cu system (Figure 4) have been established by the Subequilibrium Crosspoint Numerical SCN method of isothermal Gibbs energy curves.
2.9. AHNP Bank of Alloy Systems
The AHNP information bank of alloy systems consists of AG holographic warehouse (Supplementary Information (1) 1), equilibrium EAHNP and subequilibrium SAHNP warehouses of alloys, phases and systems (Supplementary Information (1) 2, 3), in which all of path charts and phase diagrams are calculated by steps , , and . As clicking one network point, the holographic information of the clicked alloy may be obtained immediately, that includes the AG valence electron arranging structures and holographic properties of its alloy genome, AG arranging structures and holographic properties of its alloy phases and alloy phase arranging structures and holographic properties of its alloy organization.
The AHNP bank is operable platform for researchers to achieve social road from the discovery to deployment of advanced alloys: AHNP intellectual discovery → AG arranging holographic design → AG tracking holographic certification → AG tracking high effectiveness manufacturing → AG tracking safe deployment, then allows us to significantly decrease drain on time, manpower, material, financial and energy resources for getting advanced alloys and provides information support for the AGSP.
3. Discussions
The SSP is a universality knowledge system to study relationships among components-genes-structures-properties-environments of various systems. It consists of principles of the globality, SG universality, opening circuit evolution, unity of opposites and so on, and laws of WOP, AG-TP, combination of probability and determinacy, and so on.
1) Discussion on SG universality principle
In the single level system, the correctness of AG universality can be directly explained. The genes of the free atoms system are the quantum state electron sequence described by four quantum numbers. The diversity of electronic structures of free atoms is attributed to combination and arrangement of quantum state electrons, and diversity of their properties is attributed to response of diverse structures to environments. The genes of musical compositions system are the musical note sequence. The diversity of structures of compositions is attributed to combination and arrangement of musical notes, and diversity of their properties is attributed to response of their structures to performers.
It is very difficult to seek genes of biologic system with multi-levels. Since Mendel’s pioneering investigation in genetic characters of peas to formally began the Human Genome Project (HGP), it took 125 years. It is also very difficult to seek alloy genes of alloy system with three levels. Since 1978, we began to seek alloy genes, and up to now we propose AGSP, which has taken 40 years. During the same period, we have discovered that the human social genes (HSG) are the characteristic people sequences. A single HSG is a characteristic people existing in the center of the clan cluster and occupying the professional position in the professional cluster, as well as carrying biological and social genetic information about structures and properties from one generation to the next.
2) Discussion on systematic globality principle
In the SSP, each level has its own structure unit sequences and corresponding properties sequences. Properties are that the structure unit sequences make response to environment act on the system. Relationship of the structures and properties of each level with environments is described by corresponding level theory. Relationship between two level theories is described by transmissive equation. Therefore, the SMM science based on the QMAC-electron theory of free atoms may be described by theories-, structure unit sequences- and equations- chains besides information-chain (Figure 1):
The theories chain: QMAC-electron theory → AG theory → EAP and SAP theories → EAS and SAS theories.
The structure units sequences chain: quantum state electron sequences → basic atom state sequences with quantum state valence electron sequences → AG sequences → EAP and SAP sequences.
The equations chain: Schrödinger equation of free atoms → AG separable functions, MAI-AG potential energy curve function, AG Gibbs energy function → AG-GET function, equilibrium MGEP and subequilibrium AG-TP modes → equilibrium ELN and subequilibrium SCN methods.
These achievements allow us to recognize that the QMAC-electron theory of alloys is a questionable alloy theory lacking of theories-, structure unit sequences- and equations-chains and that the quantum state electron sequences and Schrödinger equation in the QMAC-electron theory of free atom system are unreasonably used to establish electron theory of alloys, violating the matched rule of structure unit sequence and structure level theory.
These achievement allow us to recognize that the QMAC-cluster variation thermodynamics and CALPHAD-thermodynamics of alloy phases are the questionable theories, in which the “so-called Gibbs energy functions” established unreasonably by “constituent atoms”, “constituent atom pairs” and “constituent atom clusters”, carrying no valence electron structures, physical properties and Gibbs energies worthy of the name, contain a number of unknown parameters to be adjusted until the Gibbs energy function is capable of representing the chosen information well. They don’t know that the constituent atom states have split in the alloys. These advances allow us also to recognize that Prigogine’s dissipative structures thermodynamics is a phenomenological theory without genes. It can not reveal essence of chaotic phases (Supplementary Information (1) 3.4).
These advances allow us also to recognize that the “Materials Genome Initiative (MGI)” [18] [49] [50] is a questionable plan without materials gene (MG) sequences, MG-theory and MG-techniques. It is unthinkable that the MGI has been launched as a strategic plan in the United States America.
The SMM science established by guide of SSP-principles and laws will prove stimulating to researchers working on biologic, non-biologic and social systems, and who may well find values in using them as philosophic thinking modes for establishing applied system sciences. The AGSP will become a paragon to create a new era for establishing various kinds of applied system sciences and systematic gene engineerings.
Supplementary Information (1): Methods Chain
Creative SSP laws/rules evolve AHNP methods/techniques! The SSP laws/ rules mainly include the WOP law, combining rule of imaginal logic thinking and mathematical logic thinking, matched rule of structure unit sequence and structure level, determined rule for SG-sequence, united rule of probability and determinacy, integrated rule of analysis and synthesis, combining rule of theory and practice, and so on. These SSP laws/rules have been demonstrated to be very useful for establishing the SMM science and AHNP bank. Among the SSP laws/rules the WOP law has significant scientific, useful and economic values.
The WOP law means that a system can be reproduced from its few parts in the biosystems. Such as a tree can be reproduced from a seed, a branch and even a leaf of this tree; and an animal can be reproduced from its a egg cell and even a body cell. The secrets of these processes are deeply hided in the structures and properties of biological gene sequences, as well as their transmissive mode, that is attributed to natural selection. The WOP law also means that the holographic information of a system can be produced from its few parts. Due to discover AG sequences (Figure 5), the AHNP bank of the fcc-based lattice Au-Cu system, which includes the AG holographic warehouse, equilibrium EAHNP and subequilibrium SAHNP warehouses of alloys, phases and Au-Cu system, has been established based only experimental enthalpies and volumes of a few alloys. The secrets of this process are also hided in the structures and properties of AG sequences, as well as their transmissive principles and modes, that have been revealed by the AHNP methods/techniques road of the WOP law in the following sections.
1) AG-WOP methods
The establishment of AG-holographic warehouse is the first stage for establishing EAHNP bank of alloy systems. It can be explained by taking the fcc-based lattice Au-Cu system, which has been considered to be classical paragon studied nearly by almost conventional and modern measurement methods for one century [51] - [77] . The AG-WOP methods include the separated and chosen methods of AG potential energies and volumes sequences, and the calculated methods of AG valence electron structures, physical and thermodynamic properties [78] - [86] (Figure 6).
a) WOP methods of AG εi and vi sequences
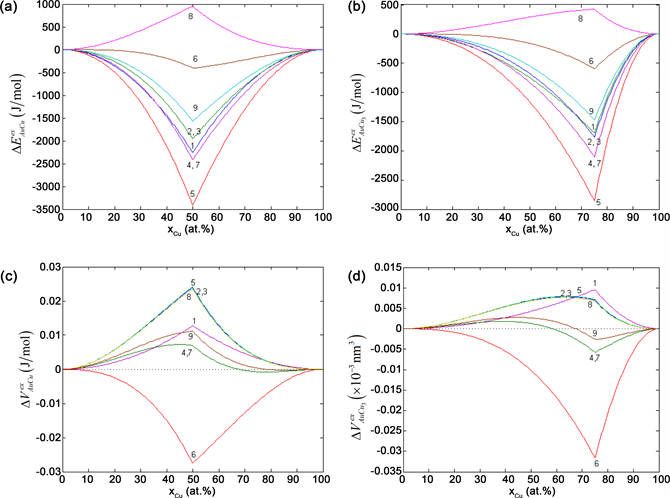
Determining AG potential energy and volume sequences is the first step to establish AG-holographic warehouse by the WOP law. In the functions of alloys, each function contains only four unknown parameters of primary states ( , ) and terminal states ( , ) of AG-sequences ( or ,). We have separated out the , , and sequences from only experimental enthalpies and volumes of pure Au and Cu metals, as well as AuCu and AuCu3 compounds, and chosen the 5th and 6th functions suitable for fcc-based lattice Au-Cu system by excess and excess of AuCu- and AuCu3-type sublattice alloys relative to disordered Au(1−x)Cux alloys [45] (Figure 7):
Figure 5. Three structural unit sequences. (a) Basic coordination cluster B-sequences and alloy gene A-sequences in fcc-based lattice Au-Cu system: , and , ; (b) AG-characteristic crystal C-sequences: , .
Figure 6. Theoretic road of AG-WOP methods. (a) AG-theory based on the experimental techniques or the first-principles electron theory of alloys; (b) (c) AG potential energies and volumes-sequences calculated by separated theory of potential energies and volumes of alloy genes; (d) (e) AG potential energy curves and physical properties calculated by valence bond theory of characteristic crystals; (f) (g) AG Gibbs energy curves and thermodynamic properties calculated by thermodynamics of characteristic crystals.
Figure 7. Choice among E- and V-functions. (a) (b) Excess potential energy differences and relative to disordered Au(1−x)Cux alloys; (c) (d) Excess volume differences and relative to disordered Au(1−x)Cux alloys.
(8)
(9)
where, the , , .
We have also calculated the potential energies and volumes of Au, Cu, Au3Cu, AuCu and AuCu3 by three methods with local density approximation in the QMAC electron theory of alloys for obtaining and functions. It has been discovered that the accuracies of both the potential energies and volumes at the same instant cannot allow correctly to determine and function [84] [85] . Perhaps there is “a uncertainty principle on relation between potential energy and volume” in the QMAC electron theory of alloys, that is likely to be similar to the “Heisenberg uncertainty principle”.
b) WOP methods of AG ψi sequences
Determining AG-VE structure sequences is the second step to establish AG-holographic warehouse based on AG and sequences. In the AGC valence bond theory, the AGC/AG-VE structure is described by one-atom valence electron y-hybrized by some basic atom states in the basic atom state sequences: . Each state is described by free electron ( ), covalent electron ( , , , ), magnetic electron ( , ) and non-valence electron ( , , ) (Table 1, Table 2). Then, the bond length and lattice constant equations, as well as bond energy
and potential energy equations have been established. The presive solutions of valence electron structures of AG and sequences have been calculated, through the crosspoint method of the equilattice constant -line and equipotential energy -line (Figure 8). The primary
Table 1. The basic atomic states (the number of free electrons (sf), covalent electrons (sc, dc), magnetic electrons (dm) and non-valent electrons (dn)) and the characteristic properties of some fcc and bcc pseudo-crystals of Fe metal [33] .
Table 2. The basic atomic states (the number of free electrons (sf, pf), covalent electrons (sc, dc) and non-valent electrons (dn)) and the characteristic properties (single bond radii (R), lattice constant (a) cohesive energy (Ec)) of some fcc pseudo-crystals of Au and Cu metals [86] .
Figure 8. AG-valence electron structures. (a) Hybridized compositions of three basic states and electronic structures for primary characteristic crystals at 0 K; (b) Hybridized compositions of three basic states and electronic structures for primary characteristic crystals at 0 K.
( , ) and terminal ( , ) valence electron structure in the and sequences (Table 3) are as follows [45] [86] :
; .
; .
where, ―Xenon electronic structure, ―Argon electronic structure.
According to potential surface forms and filling rules of , , and shells, the AG arranging crystallography of alloy phases may be established for revealing essence of crystalline structure categories of alloy phases.
According to energies, lengths and directions of , , and covalent bonds, the AG arranging covalent bond theory of alloy phases may be established for revealing essence of mechanical properties of alloy phases [41] [42] [43] [44] .
c) WOP methods of AG physical properties
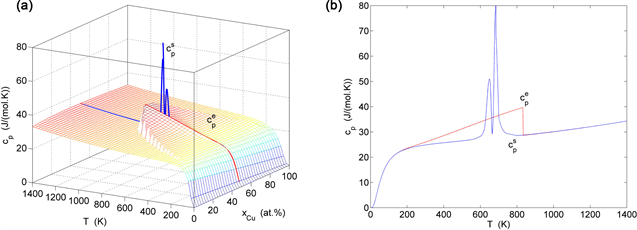
Determining AG physical properties sequences is the third step to establish AG-holographic warehouse based on AG , and sequences. In the AGC-VB theory, the AG potential curve equation has been established, besides bond length, lattice constant and potential energy equations. According to equation, the potential energy curves (Figure 6), cohesive energies ( ), Debye temperatures ( ), bulk moduli ( ) and so on of AGC crystals have been calculated (Table 3). The function has developed traditional atom pair interaction potential theory [87] [88] , Debye specific heat theory, Grüneisen’s thermal expansion theory, elasticity, magnetism and electricity, that makes function can respond to , , and fields [31] [32] [33] [34] [35] .
According to coupling energies and transmissive mode of magnetic and free electrons, the magnetic and electric conducting theories of alloy phases will be respectively established for revealing essence of magnetic and electric properties of alloy phases.
d) WOP methods of AG Gi-sequences
Determining AG Gibbs energy sequences is the fourth step to establish AG-holographic warehouse. Under the influence of temperature field, the AG may be simply rewritten as the , which may be described by two parts: a temperature independent potential energy and a temperature dependent generalized vibration/action free energy :
. (1)
The includes Debye vibration free energy and generalized attaching action free energy :
. (2)
The relationship of the with Debye vibration energy , Debye vibration entropy energy and Debye vibration specific heat is,
Table 3. The valence electron structures (the number of free electrons (sf), covalent electrons (sc, dc) and non-valent electrons (dn)), volumes(v), potential energies (ε) and single bond radii (R) of alloy genes, cohesive energy ( ), Debye temperatures ( ) and bulk moduli (B) of AG characteristic crystals in the fcc based Au-Cu system [45] .
(3)
The may be calculated by Debye theory.
The relationship of the with attaching action energy , attaching action entropy energy and attaching action specific heat is as following,
(4)
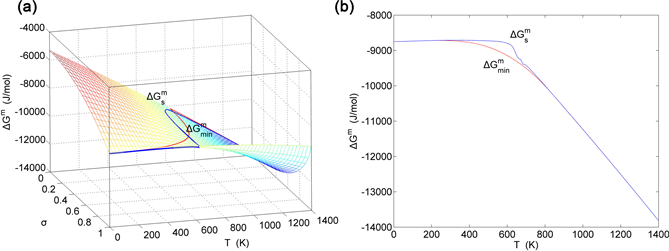
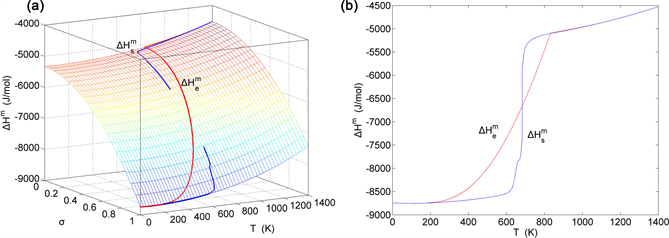
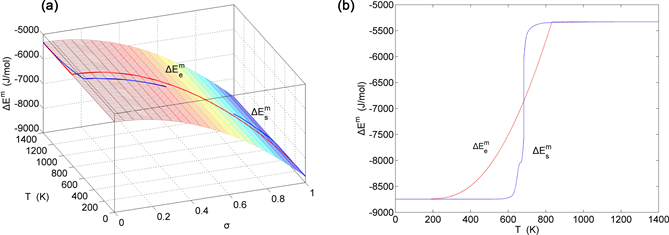
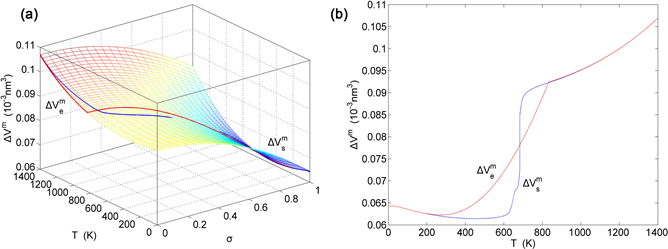
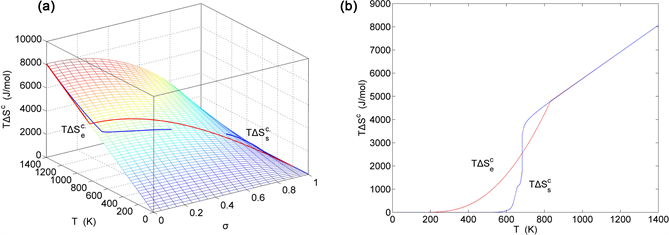
The may be obtained only by experimental enthalpies of few alloys (Supplementary Information (2) 3), which includes contributions of electron excitation, expansion work ( ) of volume, energy of formation of holes, variation of potential energy with temperature, and so on. For fcc-based Au-Cu system, the AG function with multi-level energetic functions in the real sense of the term have been established and shown in the Figure 9.
2) WOP methods of EAHNP warehouse
The establishment of equilibrium EAHNP path charts of single alloys and EAHNP phase diagrams of single phases and Au-Cu system is the second stage for establishing AHNP bank of the fcc-based lattice Au-Cu system only based on AG holographic warehouse, that needs no other experimental data.
a) WOP methods of EAHNP path of alloys
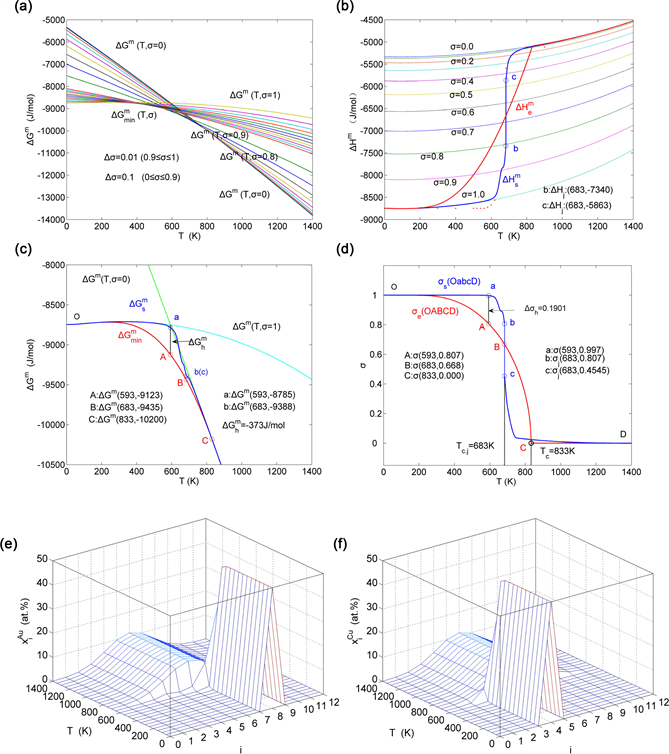
According to the and sequences, mixed Gibbs energy function and essential definition of equilibrium order disorder transition, the equilibrium , , and paths on equilibrium order disorder transition as function of temperature for the stoichiometric Au3Cu alloy have been calculated by the minimal Gibbs energy path MGEP method, which may be performed by the iso-order degree Gibbs energy path method or isothermal Gibbs energy path method (Figure 10), using calculated steps and (Figure 11). Then, EAHNP path charts of the Au3Cu alloy are calculated by and paths. It has following general behaviors: The order → disorder transition upon heating and disorder → order transition upon cooling proceed along the same minimal mixed Gibbs energy path. Namely, there exists no so-called hysteresis phenomenon between both transitions; The path is continuous and homogenous, and has stability and linearity without jumping phenomenon. The critical temperature is determined by the crosspoint method of and curves.
b) EAHNP phase diagrams of phases
By the path MGEP method, the , , and path charts on equilibrium order disorder transition as function of composition, temperature and order degree for all alloys in the Au3Cu-type sublattice phase may be calculated, using calculated steps , , . Then, the three-dimension and two-dimension , and EAHNP phase diagrams may be constructed [48] .
By analogous method, the EAHNP phase diagrams of the AuCu- and AuCu3-type sublattice ordered phases [45] [47] , as well as fcc-based lattice disordered phase may be established.
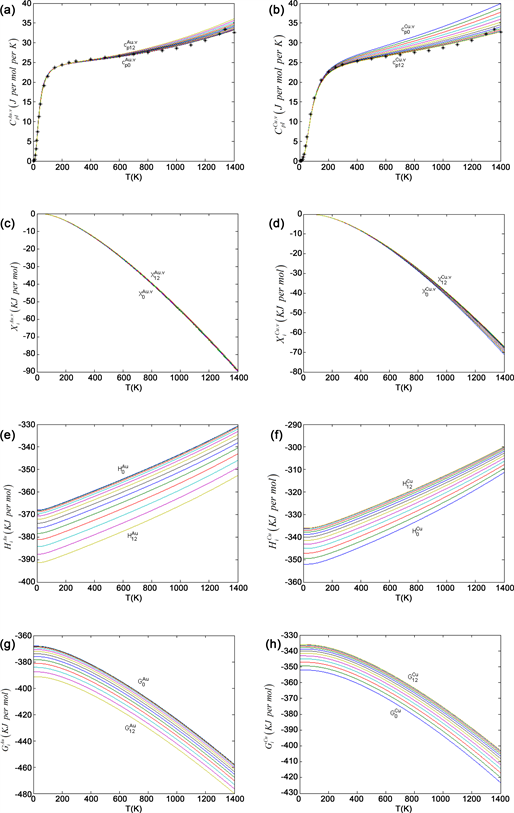
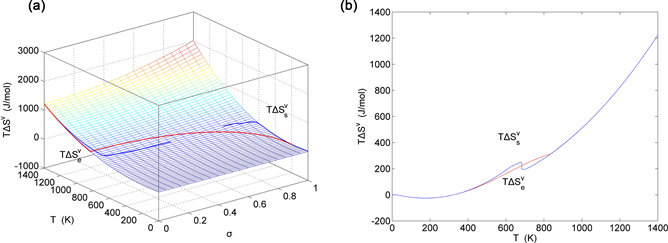
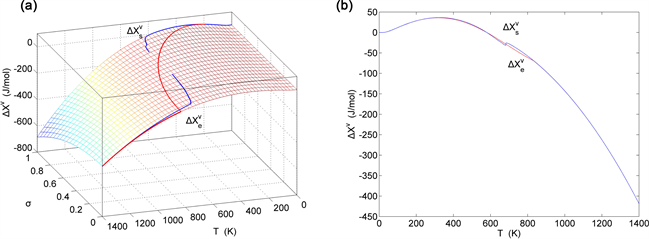
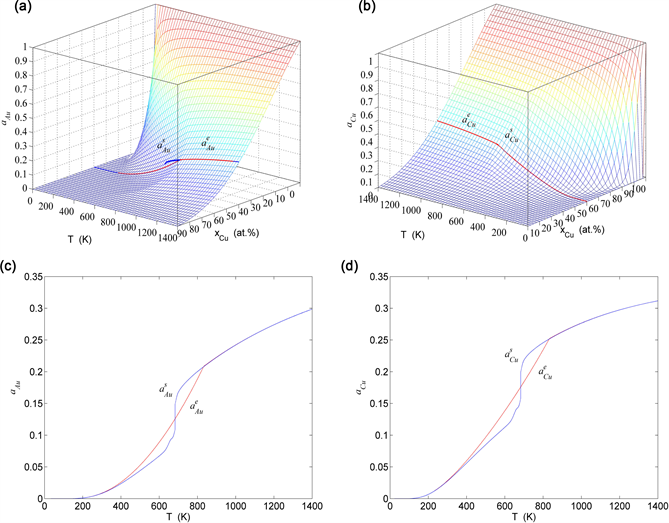
Figure 9. AG-thermodynamic properties. (a) (b) Generalized vibration heat capacity curves in Au-Cu system: , ; (c) (d) Generalized vibration free energy curves: , ; (e) (f) Enthalpy of formation curves: , ; (g) (h) Gibbs energy curves: , .
Figure 10. Minimal Gibbs energy path method. (a) The iso-order degree Gibbs energy path method; (b) The isothermal Gibbs energy path method; (c) path on equilibrium order disorder transition of stoichiometric Au3Cu alloy; (d) path on equilibrium order disorder transition of stoichiometric Au3Cu alloy; (e) (f) Three-dimension and path charts on disordering or ordering the stoichiometric Au3Cu alloy.
Figure 11. AG-tracking path method. (a) Minimal mixed Gibbs energy path on disordering AuCuI alloy obtained by the iso-order degree Gibbs energy equilibrium path method; (b) Experimental mixed enthalpy path method based on the network chart of the iso-order degree mixed enthalpies equilibrium paths, attaching equilibrium path; (c) (OABC) and (Oabc) paths of the equilibrium and subequilibrium order → disorder transitions, where denotes superheated driving Gibbs energy; (d) (OABCD) and (OabcD) paths of the equilibrium and subequilibrium order → disorder transitions, where denotes hysteresis order degree; (e) Three-dimension SAHNP chart; (f) Three-dimension SHNP chart.
c) EAHNP phase diagrams of alloy system
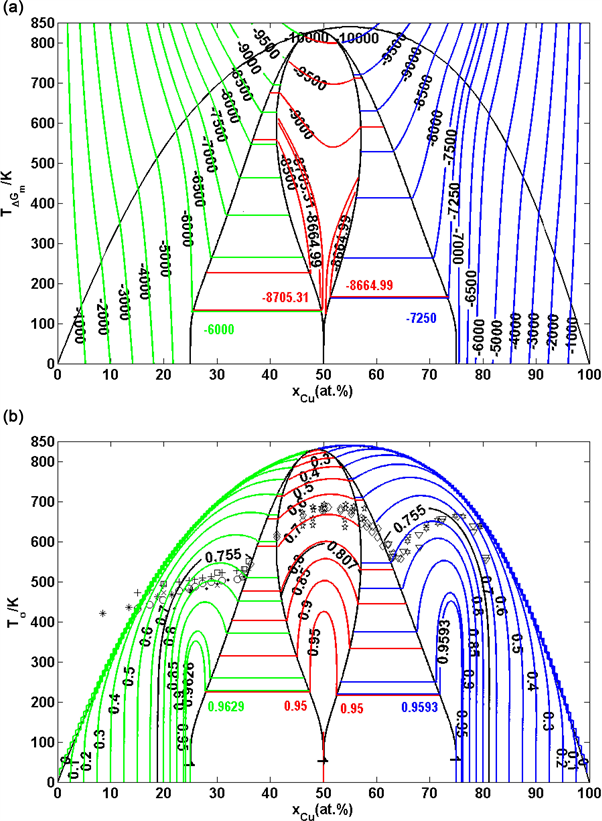
The solid fcc-based lattice Au-Cu system is a competitive system of the Au3Cu-, AuCu- and AuCu3-type sublattice ordered phases, as well as fcc-based lattice disordered phase. The equilibrium three dimension phase diagram may be established by the equilibrium lever numerical method of isothermal Gibbs energy curves [23] . Then, the EAHNP phase diagrams of fcc-based lattice Au-Cu system have been established (Figure 4).
3) WOP methods of SAHNP warehouses
The subequilibrium SAHNP warehouse established by the AG-tracking path AG-TP method is the third stage for establishing AHNP bank of the fcc-based lattice Au-Cu system only based on AG holographic warehouse, EAHNP warehouse and experimental mixed enthalpy or volume paths of alloys! It includes SAHNP path charts of single alloys [46] , and SAHNP phase diagrams of single phases and Au-Cu system [23] .
a) WOP methods of SAHNP path of alloys
The steps of the AG-TP method for subequilibrium SAHNP path charts of alloys may be presented by taking ordered AuCuI(AuCu) alloy as an example, which is a classic paragon (Figure 11):
i) To establish equilibrium path chart by the iso-order degree Gibbs energy method at first, then, the path and iso-order degree enthalpies path network chart may be drawn up (Figure 11(a), Figure 11(b)).
ii) To draw up the experimental mixed enthalpy path on the network chart of the path, then, the subequilibrium, , , , (Figures 11(c)-(f)) and SAHNP path charts of the AuCu alloy may be calculated.
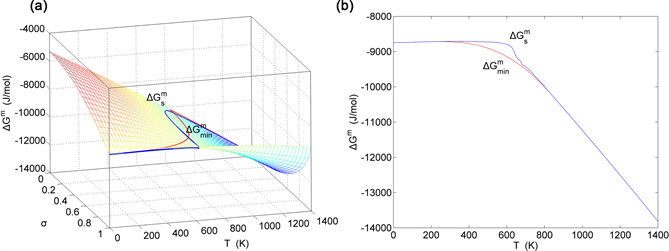
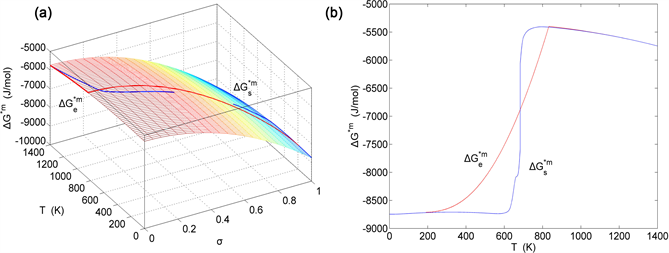
The common behaviors of the SAHNP charts are as follows: The order degree keeps unchanged in a broad temperature range from 0 K to 593 K by slow heating rate; There exists complex variation in order degree, during the temperature range from onset temperature ( ) to jumping -temperature, that is only about 100 K interval; Upon increasing heating rate, the -temperature increases, and the -temperature decreases, i.e., so called Retro-Effect [68] [70] ; The path is higher than the equilibrium path. Their difference ( ) is the superheated driving Gibbs energy of the subequilibrium alloy; There exists a thermal hysteresis Gibbs energy loop between the order → disorder and disorder → order transitions.
b) SAHNP phase diagrams of phases
By the AG-tracking path (AG-TP) method on experimental mixed enthalpy path, the , , and path charts on subequilibrium order → disorder transition as function of composition, temperature and order degree for all alloys in the AuCu-type sublattice phase may be calculated, using calculated steps , and . Then, the three-dimension and two-dimension , and SAHNP phase diagrams may be constructed [47] [48] .
By analogous method, the SAHNP phase diagrams of the Au3Cu- and AuCu3- type ordered phases may be established.
c) SAHNP phase diagrams of alloy systems
The subequilibrium three dimension phase boundries of solid fcc-based lattice Au-Cu system may be established by the crosspoint numerical method of isothermal Gibbs energy curves [23] . Then, the SAHNP phase diagrams of fcc-based lattice have been established (Figure 4).
d) Values of AG-TP method
The AG-TP method has special values. It can make us describe all real situations happened in evolutional progress of alloys, through tracking one property only. Then, we can reveal essence of chaotic phases, observe some new phenomena, discover some new mechanisms, explain some difficult questions left over by history and establish SAHNP path charts, that may be explained by the disordering path of AuCuI( ) compound [46] .
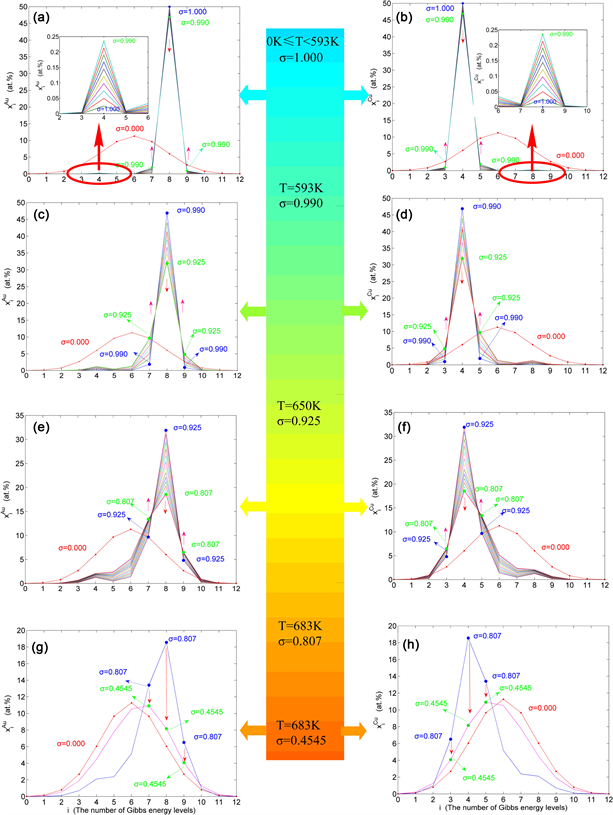
i) When , it is the subequilibrium unchanged period of the AuCuI( ), of which the behaviors as fellows (Figure 11): There exists no variation in order degree until , , other AG concentrations , and still occupied at the and energy levels, respectively; The superheated driving Gibbs energy ( ) between the equilibrium (OABC) and experiment (Oabc) paths increases with rising temperature, of which the difference (-373J/mol at 593 K) is very small (Figure 11(c)); The generalized action energies ( and ) increase with rising temperature, but their values are much smaller than their potential well depths. At 593K the , (Table 4, Table 5); The new knowledge is that only depending on superheated driving Gibbs energy and generalized action energy, the and “stem alloy genes” cannot change their lattice positions, if without a special mechanism.
ii) When and (Figure 12(a), Figure 12(b)), it is the unequilibrium growing period of the high order degree AuCu(H) alloy. According to the peculiar orders in AG concentrations (Table 6, Table 7): , , we have discovered the 3(RA-SA) mechanism, which is that three AG-pairs in a cell-scale region occur Resonance Activating (RA) to accumulate vibration energies and Synchro Alternating (SA) to change their lattice positions and energetic states by two manners (Figure 13(a), Figure 13(b)). The new knowledge is that there exists cell-scale heterogeneity in the AuCu(H) alloy, which includes early-3(RA-SA) cell region with more 3(RA-SA) cells, middle-3(RA-SA) cell region with less (RA-SA) cells and late-AuCuI ( ) cell region with no (RA-SA) cell, that lay a structural foundation for forming statistic periodic anti-direction (SPAD) region. The and are named as the “signal alloy genes of 3 (RA-SA) mechanism”.
iii) When and (Figure 12(c), Figure 12(d)), it is the unequilibrium growing period of the SPAD-AuCuII region. We
Table 4. The , , , , , , of the -alloy gene [46] .
1) The generalized vibration energy includes contributions of Debye vibration energy, existing energy of electrons, forming energy of holes, expansion work of volume and variation in potential energy with temperature; 2) The melting of pure Au metal; 3) The melting of pure Cu metal.
Table 5. The , , , , , , of the -alloy gene [46] .
1)The generalized vibration energy includes contributions of Debye vibration energy, existing energy of electrons, forming energy of holes, expansion work of volume and variation in potential energy with temperature; 2) The melting of pure Au metal; 3) The melting of pure Cu metal.
Figure 12. AG tracking structure path charts. (a) (b) As the and concentration distributions on disordering AuCuI( ); (c) (d) As , the and concentration distributions; (e) (f) As , the and concentration distributions; (g) (h) As , the and concentration distributions.
Table 6. Systematic correlativity of the equilibrium transition temperature , subequilibrium transition temperature , order degree and -alloy gene concentrations ( ) on disordering AuCuI( ) compound.
The denotes corresponding to or corresponding to .
Table 7. Systematic correlativity of the equilibrium transition temperature , subequilibrium transition temperature , order degree and -alloy gene concentrations ( ) on disordering AuCuI( ) compound.
The denotes corresponding to or corresponding to .
have discovered that as and , the concentrations and display the “emergent phenomenon”, which is defined as that their concentrations are larger than ones of the corresponding alloy genes in the disorder state: , . During this period, there exists “region- scale heterogeneity”: the original early-3(RA-SA) cell regions with more (RA-SA) cells grow into the early-(SPAD-AuCuII) regions, the original middle-(RA-SA) cell regions with less 3(RA-SA) cells grow into the middle-(RA-SA) cell regions with more 3(RA-SA) cells and the original late-AuCuI( ) regions with no (RA-SA) cell grow into the late-(RA-SA) cell regions with less (RA-SA) cells (Figure 13(c), Figure 13(d)). The new knowledge is that the AuCu(H) region and SPAP-AuCuII region are co-existed, two distinct x-ray diffraction patterns may be observed at the . This alloy with region-scale heterogeneity is called as the “Pseudo-Two-Phases (PTP)” AuCu alloy with the AuCu(H) regions and the SPAD-AuCuII regions. The use of the phrase “PTP” is intended to convey the impression that two heterogeneous subequilibrium regions have the same composition, different order degrees, and belong in the same ordered AuCu-type sublattice phase.
iv) When and (Figure 12(e), Figure 12(f)), it is the unequilibrium mature period of the SPAD-AuCuII alloy. During
Figure 13. The 3(RA-SA) mechanism. (a) AG arranging structure after A-manner alternating in 3(RA-SA) mechanism of three - pairs in a single cell on disordering AuCuI( ); (b) AG arranging structure after B-manner alternating in 3(RA-SA) mechanism of three - pairs in a single cell; (c) AuCu(H) alloy containing three regions with cell-scale heterogeneity; (d) PTP-[AuCuI(H) + PAP-AuCuII] alloy containing three regions with region-scale heterogeneity; (e) AG arranging structure of a early SPAP-AuCuII cell.
this period, the middle-(RA-SA) cell regions and late-(RA-SA) cell regions are respectively transferred into the middle- and late-SPAD-AuCuII regions. The new knowledge is “the SPAD-AuCuII alloy containing early-, middle- and late-SPAD-AuCuII regions is a statistic periodic anti-direction structure stacking of incommensurate tetragonal cells containing more and stem alloy genes and anti-direction boundary with (RA-SA) cells containing less and stem alloy genes along b axis.” It has no strict long periodic cell, and may be called as Prigogine’s dissipative structures or chaotic phase [89] [90] .
v) When and (Figure 12(g), Figure 12(h)), it is the unequilibrium jumping period of the SPAD-AuCuII alloy. We have discovered that as , and display the “maximum emergent phenomenon”: ; as , and display the “maximum emergent phenomenon”, . Therefore, the , , and , , are called as the first and second “jumping alloy genes”, “jumping order degrees”, respectively. As the -order degree less than the -order degree, the disordering begins to translate from a single splitting of the and stem alloy genes to a “universal splitting” or “snowslide splitting” of the stem and jumping alloy genes, which is an essential condition to happen a discontinuous jump change from the high order degree SPAD-AuCuII to the Low order degree AuCu(L) with low order degree ( ). After the -temperature, the AuCu(L) alloy is continuously unequilibrium transformed into the equilibrium Disordered AuCu (D) alloy. The new knowledge is that the heterogeneous successive transitions on disordering stoichiometric AuCuI( ) by slow heating rate are as follows: AuCuI ( ) → AuCu (H) → PTP-AuCu → SPAD-AuCuII → AuCu (L) → AuCu (D).
The AG-TP method may lead to the AG tracking holographic certification, AG tracking high effectiveness manufacturing and AG tracking safe deployment, as well as AG subequilibrium and unequilibrium kinemics.
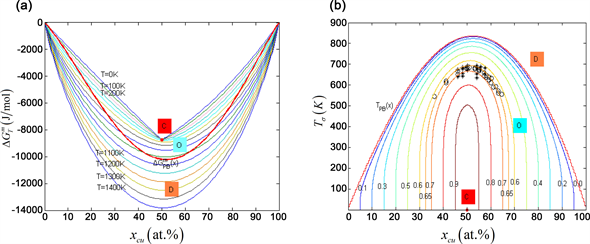
The fcc-based lattice Au-Cu system has been studied as a classical paragon with complete order-disorder transition for about one century. However, a equilibrium phase diagram of Au-Cu system in the real sense of the term has not been established, and numerous questions about order-disorder transition have been raised [73] [74] , because one of many reasons is that researchers have got used to recognizing experimental phenomena observed during very slow variation in temperature to be thermodynamic equilibrium phenomena: The experimental jumping -temperatures are erroneously considered as the -critical temperatures of equilibrium order-disorder transition of alloys, although the experimental jumping -order degrees are about 0.8 ~ 0.6 and the experimental short range order degrees exist at the temperatures considerable above the -temperature [53] [65] ; The experimental composition-dependent curve is erroneously considered as the phase boundary curve between ordered and disordered phases. The researchers in the CALPHAD- and QMAC-communities took these miss understandings of experimental phenomena as the selected information, then adjusted parameters in so-called Gibbs energy functions and established so-called equilibrium phase diagrams to achieve the best representation of the selected information [18] . These phase diagrams have no scientific significance as well as useful value [15] [91] [92] [93] [94] (Figure 14).
Figure 14. Phase diagrams of Au-Cu system calculated by CALPHAD- and QMAC-thermodynamics. (a) Experimental jumping Tj temperatures, erroneously considered as equilibrium critical Tc temperatures and experimental limit composition ranges of long range ordered (LRO) Au3Cu-, AuCu- and AuCu3-type at room temperature [60] [61] [91] [92] ; (b) Calculated Au-Cu phase diagrams by CALPHAD-thermodynamics [92] ; (c) Calculated Au-Cu phase diagram by CALPHAD-thermodynamics [15] ; (d) Calculated Au-Cu phase diagram by CALPHAD-thermodynamics [15] ; (e) Calculated Au-Cu phase diagram by CALPHAD- thermodynamics [93] ; (f) Calculated Au-Cu phase diagram by QMAC-thermodynamics [94] .
Supplementary Information (2): Equations Chains
The logical thinking in images is a foundation of the logical thinking in mathematics; while it is deepened by the logical thinking in mathematics. A clear and perfect theory can be created by comprehensive application of the two ways of thinking. The SMM science is the framework consisting of the correlated three-level theories. Each level theory is quantitatively described by main equations. We have encountered some difficult mathematical problems during the mathematization process. It has taken a few years or even more than ten years of effort to solve each of the problems, such as the AG separable functions, MAI-AGC potential energy curve function and the AG Gibbs energy transmissive AG-GET function. We have deeply realized that the “mathematization is a heavy storm fortification of establishing SMM science”.
1) Equations in AG separable theory
a) AG additive law
(1-1)
Where, the q denotes AG potential energy (E), volume (v) and other extensive properties, which are the functions of temperature (T) only; the and are AG concentrations; which are the functions of the composition (x), temperature (T) and order degree ( ); and denote compositions of the A and B components, respectively.
b) AG separable functions
The potential energies and volumes are the most basic properties of AG sequences. In order to make the Equation (1-1) become the simple, applicable and separable function performed by WOP law, three type relations of and with i have been designed [37] :
Type I of linear relation,
(1-2)
Type II of concave parabola relation,
(1-3)
Type III of convex parabola relation,
(1-4)
where, the q denotes AG potential energy or volume; I denotes coordinative number; the and denote, respectively, potential energy and or volume and of the primary state alloy genes; the and denote, respectively, and or and of the terminal state alloy genes.
By combining Equations (1-2)-(1-4) and substituting them into Equation (1-1), nine functions can be obtained. In Table 8, the nine general functions of alloy phases can be used to compounds, ordered and disordered alloy phases. In Table 9, the nine -functions can be used for the disordered alloy phases only.
c) Choices of E- and V-functions
The 5th E-function in Table 8 has been chosen for describing Au-Cu system, according to the excess potential energies of AuCu- and AuCu3-type sublattice ordered Au(1-x)Cux alloys with maximum order degrees calculated by nine E-functions at room temperature [45] (Figure 7(a), Figure 7(b)).
The 6th V-function in Table 8 has been chosen for describing Au-Cu system, according to the calculated values of the mixed volumes and
Table 8. Nine general -functions of alloy phases at T K.*
*: Here, the and ; or v; i is the number of B-atoms in the nearest coordinative configuration ; (I-i) is the number of A-atoms in the nearest coordinative configuration ; I is the coordinative number.
Table 9. -functions of disordered alloy phases ( ) at T K.*
*: Here, the and denote compositions of the A and B components; or v; I is the coordinative number.
excess volumes of the AuCu- and AuCu3-type sublattice ordered Au(1−x)Cux alloys with maximum order degrees calculated by the nine V-functions at room temperature (Figure 7(c), Figure 7(d)).
In the Au-Cu system, the correlative function between AG potential energies,
(1-5)
The potential energy function of alloys is,
(1-6)
The correlative function between AG volumes:
(1-7)
The volume function of alloys is,
(1-8)
where, , , , ; , , , , . The results calculated by Equations ((1-6) and (1-8)) are in good agreement with experimental values. Their essential features are as follows:
i) The decreases with increasing number i of Cu-atoms in the coordinative configuration: .
ii) The decreases with increasing number (I-i) of Au-atoms in the coordinative configuration: .
iii) The decreases with increasing number i of Cu-atoms in the coordinative configuration: .
iv) The increase with increasing number (I-i) of Au-atoms in the coordinative configuration: .
2) Equations of AGC valence bond theory
AGC valence bond theory of AGC theory includes the description of AG valence electron structures and three main functions: MAI-AGC lattice constant equation with many atoms interaction (MAI), MAI-AGC cohesive energy equation and MAI-AGC potential energy curve function , that have developed Pauling’s, Yu’s and Grigorovvich’s metallic bond theories [25] [26] [27] .
a) Description of AG ψ -sequences
An AG is represented by AGC of corresponding AGC crystal and formed by some basic atom states in the basic atom state sequences [32] [33] [34] [35] (Table 1, Table 2):
(2-1)
In our opinion the metallic bond is a mixed bond containing unsaturated covalent electron bond, free electron bond and magnetic electron bond, except non-valence electrons. The unsaturated covalent electron bond network is formed by covalent electrons ( ) of an atom with its neighbors. The number and symmetry of the overlapping hybrid orbitals directly determine the crystalline structure of the AGC crystal. These unsaturated covalent bonds are responsible for the most fraction of cohesive energy of the crystals. The free electron bond consists of near free electrons ( ), which uniformly fill the free space of the unsaturated covalent bond network and are responsible for the conductivity and plasticity. The magnetic electron bond consists of magnetic electrons ( ) responsible for the magnetism. Both the free electron bond and the magnetic electron bond have small contributions to cohesive energy of the crystal. The non-valence electrons ( ) can be treated as the “chemically inert” ion core.
The occupations of electrons in each basic atomic state obey Pauli Exclusion principles. If , and denote respectively the number of the covalent electrons of s, p and d shells in the k basic atomic state; , and denote respectively the numbers of free s electrons, magnetic d electrons and non-valence d electrons, then the state parameters of one-atom state of the AGC crystal can be obtained by the following equations:
(2-2)
where is the single bond radius which can be obtained by Pauling’s equation slightly modified by the authors.
For Fe-AGC crystal,
(2-3)
For Au-AGC crystal,
(2-4)
For Cu-AGC crystal,
(2-5)
From the state parameters of the basic state atoms, the characteristic properties (lattice constant, cohesive energy, and atomic magnetic moment) of the relative pseudo-crystal consisting of atoms in each kind of basic atomic state can be calculated by a series of equations presented in the following sections (Table 1, Table 2).
b) The MAI lattice constant equation
An AG volume may be described by lattice constant equation with many atoms interaction (MAI) of corresponding AGC crystal, which is the function of AG valence electron structure and bond length . Pauling’s bond length equation should be suitable to the various bond lengths in the AGC crystal [29] (in nm):
(2-6)
where denotes the length of the s neighboring bond, denotes the single bond radius, denotes the number of pairs of covalent electrons on the relative bond, is taken as 0.060 determined by Pauling. From Equation (2-6), the following equations may be derived as
(2-7)
where represents the number of the same kind of the s bond. For a AGC crystal, the lattice constant can be expressed by its bond length
(2-8)
For a crystal with fcc structure, , , and .
For a crystal with bcc structure, , , and .
Combining Equations ((2-7) and (2-8)), we have (in nm)
(2-9)
It has been proved that the is the convergent transcendental equation; and that there is a certain lattice constant for a pseudo-crystal with known basic atom state. It may be obtained by repeated calculation methods [29] (Table 1, Table 2).
c) AGC cohesive energy equation
Considering contributions of bond energies of covalent electrons, near free electrons, and magnetic electrons to cohesive energy of AGC crystal, the MAI-AGC cohesive energy equation has been established [31] [32] [33] [34] [35] ,
(2-10)
where, N is Avogardro’s number.
In the AGC crystal, the bond energy of a kind of bonds should be directly proportional to the number of covalent electron pairs on each bond and the number of the same kind of bonds and inversely proportional to its bond length, i.e.,
(2-11)
In Pauling’s and Yu’s opinion, the bonding capacities of s, p, d and f orbitals are , , and , respectively. If the number of covalent electrons of s, p, d and f orbitals in the hybrid orbital are respectively , , and , the bonding capacity of the hybrid orbital should be
(2-12)
where,
(2-13)
In the AGC crystal, there should be free electrons besides the covalent electrons. The free electrons are regarded as distributed through the whole crystal. If the average energy of the free electron bond is assumed directly proportional to the number of free electrons and inversely proportional to the effective average band length, i.e.
(2-14)
where is the average effective bond lengths of the AGC crystal in equilibrium,
(2-15)
In Yü’s opinion, the bonding capacity of free electrons should be
(2-16)
where,
(2-17)
For ferromagnetic AGC crystals, it also may be assumed that the average magnetic coupling energy is directly proportional to the number nm of magnetic electrons,
or (2-18)
where the denotes the bonding capacity of the magentic electrons.
Therefore, the MAI cohesive energy equation of AGC crystals may be written as (in KJ/mol) [31]
(2-19)
Where, the constant may be determined by experimental cohesive energies of primary AGC crystals, i.e., pure elements. The value may be determined by the experimental specific heat peak due to magnetic transformation of primary AGC crystal.
d) AGC potential energy curve function
Under the condition of homogeneous deformation, various bond lengths may be expressed by the following equations:
(2-20)
And their reduced bond lengths are identically equal:
(2-21)
where, the and r denote the shortest bond lengths of the AGC crystal in equilibrium and unequilibrium states, respectively.
Therefore, the MAI-AGC potential function with many atoms interaction (MAI) for one molar crystal may be simplified as [31]
(2-22)
In the equilibrium state, r = r0, the absolute value of molar potential energy is approximately equal to the molar cohesive energy, i.e., at 0K. The MAI-AGC potential energy curve function makes AG theory have solid physical foundation.
e) Equations of elasticities
i) The force constant
Suppose that the MAI-AGC crystal is subjected to a hydrostatic pressure, which produces a small deformation u. The potential function can be written as [31]
(2-23)
According to the principle of mechanics and Debye model, the force constant k and exponents x in MAI-AGC potential energy curve function can be obtained
(2-24)
(2-25)
where is Debye temperature; , Boltzman’s constant; , Planck’s constant; m, atomic mass; j and n, which are respectively the multiple of the half cutoff wave length and another exponent (n) of the MAI-AGC potential function, which can be obtained from two experimental values of the experimental linear thermal expansion coefficients at two temperatures of primary AGC crystals [33] .
ii) Bulk modulus
Suppose that the crystal is subjected to a hydrostatic pressure, which produces the Hookeian volume change . Then B, defined by [31]
(2-26)
is the bulk modulus of elasticity.
According to and functions,
(2-27)
iii) Young’s modulus, shear modulus and Poisson’s ratio
Suppose that the polycrystal undergoes a very small homogeneous extension along an arbitrary direction such as . Then, according to the definition of Young’s modulus, we have
(2-28)
The factor 1/3 is introduced due to dW/dV being the total differential and Young’s modulus being one-dimensional quantity.
Suppose the extension strain to be . Then, we have
(2-29)
According to and functions,
(2-30)
It is well known that there are the relationships among various moduli as follows
(2-31)
where, is the shear modulus, , the Poisson’s ratio.
f) Equations of specific heats
The specific heat of magnetic AGC crystals includes two ports: the normal specific heat caused by lattice vibration and magnetic specific heat caused by magnetic transformation [33] [34] [35] . They can be calculated from the Debye theory and Brillouin function respectively
(2-32)
where R is the gas constant; T is the temperature; , and are Debye temperature, potential energy and volume of primary AGC crystal, respectively.
When , the temperature dependence of the atomic magnetic moment can be expressed by Brillouin function
(2-33)
where is the Curie temperature, and is temperature at the experimental specific heat peak.
From this, it may be obtained that
(2-34)
When , we have chosen the following equation to express the temperature dependence of
(2-35)
From this, it may be obtained that
(2-36)
The values of a and b constants can be obtained by the conditions of boundary at temperature
(2-37)
g) Equations of thermal expansion
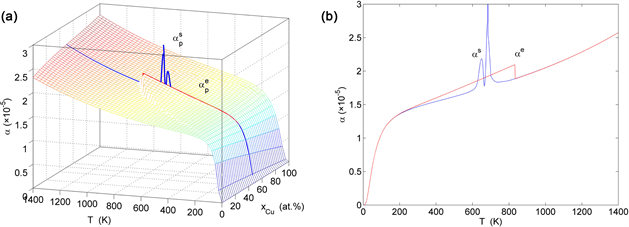
The linear thermal expansion coefficient of magnetic AGC crystals includes two parts: the normal linear thermal expansion coefficient arisen from inharmonic lattice vibration and the magnetic linear thermal expansion coefficient arisen from magnetic transformation [31] [33] [34] [35] .
The can be obtained by Grüneisen formula
(2-38)
(2-39)
The constants K and Q have been derived from function:
(2-40)
(2-41)
Considering influence of magnetic electrons on the bond length, the Equation (2-9) should be modified as
(2-42)
From this equation, the can be obtained by
(2-43)
where is given by Equations ((2-33) and (2-35)); the is given
by Equations ((2-34) and (2-36)). The value of constant can be obtained from an experimental value at a temperature near the Curie point of primary AGC crystals.
The correctness of these equations in this chapter were demonstrated by agreement between theoretical and experimental results of the primary AGC Fe, Co, Ni, Cu, Ag, Au crystals, i.e., pure metals [32] [33] [34] [35] . These achievements lead to establish AG Gibbs energy sequences and can make them respond to , , , and fields.
3) Equations of AGC Gibbs energy
Under the influence of temperature field, AG Gibbs energy function may be rewritten simply as the , which may be split into two parts: the AG temperature-independent potential energy and temperature-dependent generalized vibration/action free energy (Equation (3-1)). The AG enthalpy of each characteristic crystal may be also split into two parts: the AG potential energy and generalized vibration/action energy (Equation (3-2)). The generalized vibration/action free energy includes the generalized vibration energy , which include Debye vibration energy and attaching vibration energy , and generalized vibration/action entropy energy , which include Debye vibration entropy energy and attaching action entropy energy . The generalized vibration/action heat capacity includes Debye vibration heat capacity and attaching action heat capacity . The attaching includes contributions of electron excitation, energy of formation of holes, variation of potential energy and volume expansion work with temperature, and so on. Therefore, the is the AG holographic energy function with multi-level thermodynamic properties [45] [46] [47] [48] :
(3-1)
(3-2)
(3-3)
(3-4)
(3-5)
(3-6)
(3-7)
(3-8)
(3-9)
(3-10)
(3-11)
(3-12)
(3-13)
(3-14)
(3-15)
(3-16)
where, , , , .
It should be emphasized that the AG holographic warehouse of fcc-based lattice Au-Cu system has been established only based on experimental enthalpies and volumes of pure Au and Cu metals, as well as AuCu and AuCu3 compounds (Figure 15)!
Figure 15. Calculated road of AG-WOP methods. AG-holographic information includes AG potential energies ( ) and volumes ( ) of basic properties, as well as AG valence electron structures ( ) of basic structure; the AG physical property sequences (mechanical, magnetical, electric, optical and so on) obtained by AG-AGC valence bond theory; the AG Gibbs energy sequences with multi-level thermodynamic properties may be obtained by AG-AGC thermodynamics.
4) Equations of AG arranging thermodynamics
The AG arranging phase theory includes the AG arranging thermodynamics, which describes the AG arranging Gibbs energy band structures of alloy genes occupied at the Gibbs energy levels in the Gibbs energy space and thermodynamic properties of alloy phases; the AG arranging crystallography, which describes the AG arranging crystalline structures of alloy genes occupied at the lattice points in the crystalline space and crystalline symmetries of alloy phases; and AG arranging valence bond theory, which describes the AG arranging bond network structures of alloy genes occupied at the lattice points in the crystalline bond network space and physical and mechanical properties of alloy phases. Here, the main equations of the AG arranging thermodynamics are presented only, taking AuCu-type sublattice phase system as an example.
a) Equations chain of AG-GET function
The AG Gibbs energy transmissive AG-GET function produces alloy phase holographic energy Gibbs energy function and configurational entropy function [45] :
(4-1)
(4-2)
(4-3)
AG arranging characteristic (chemical potential) Gibbs energy function of alloy phases:
(4-4)
AG arranging degeneracy function of alloy phases:
(4-5)
Concentration equations of the AG and at the (1) and (2) sublattice points:
(4-6)
Concentration equations of the AG and occupied at the (1) and (2) sublattice points:
(4-7)
Probability equations of Au and Cu atoms occupied at (1) and (2) sublattice points:
(4-8)
Fractions of the (1) and (2) sublattice points for AuCu-type sublattice phase:
(4-9)
Definition of order degree:
(4-10)
The probability equation of the coordinative cluster surrounding the (1)-sublattice point:
(4-11)
In the equation, the probability of coordinative cluster occupied at the (2)-sublattice points, and the probability of coordinative cluster occupied at the (1)-sublattice points:
(4-12)
where, the i’ is the number of the Cu atoms occupied at the (2)-sublattice points.
The probability equation of coordinative cluster surrounding the (2)-sublattice point:
(4-13)
where, the i’ is the number of the Cu atoms occupied at the (1)-sublattice points
In the equation, the probability of coordinative cluster occupied at the (1)-sublattice points, and the probability of coordinative cluster occupied at the (2)-sublattice points:
(4-14)
In the Equations ((4-9) to (4-11)), k and K take their values, according to
(4-15)
The maximum order degree as function of composition :
For the stoichiometric alloy, due to , ;
For the alloys with , due to , ;
For the alloys with , due to , .
The methods for calculating and are listed in Table 10, Table 11.
The configurational entropy equations of the alloy and components:
(4-16)
The mole potential energy equations of the alloy and components:
(4-17)
The Debye vibration energy equations of alloy and components:
(4-18)
The attaching action energy equations of alloy and components:
(4-19)
Table 10. The methods for calculating the probability of coordinative cluster surrounding the (1)-sublattice point in AuCu-type order alloys.
Table 11. The methods for calculating the probability of coordinative cluster surrounding the (2)-sublattice point in AuCu-type order alloys.
The generalized action energy equations of the alloy and components:
(4-20)
The Debye vibration entropy equations of the alloy and components:
(4-21)
The attaching action entropy equations of the alloy and components:
(4-22)
The generalized action entropy equations of the alloy and components:
(4-23)
The generalized action free energy equations of the alloy and components:
(4-24)
The enthalpy equations of the alloy and components:
(4-25)
The characteristic Gibbs energy equations of the alloy and components:
(4-26)
The Gibbs energy equations of the alloy and components:
(4-27)
The mixed heat capacity equations of the alloy:
(4-28)
The activity equations of the components:
(4-29)
The volume equations of the alloy and components:
(4-30)
The mixed volume thermal expansion coefficient equations of the alloy:
(4-31)
It should be emphasized that the new -function can be used to describe both long-distance order and short-distance order states of alloy phases; and that, the thermodynamic properties of alloy components need no representatives by the partial molar properties. We have proved that the partial molar properties cannot represent the average properties of the corresponding components [21] . It should be emphasized again that the equilibrium EAHNP and subequilibrium SAHNP path charts on disordering AuCu( ) compound (Figures 16-27), the EAHNP phase diagrams of Au3Cu-, AuCu- and AuCu3-type sublattice systems (Figures 28-30) and the EAHNP and SAHNP phase diagrams of Au-Cu system (Figure 31, Figure 32) have been established only based on experimental enthalpies and volumes of pure Au and Cu metals, as well as AuCu and AuCu3 compounds! The composition ranges of long range ordered phases are shown in Figure 33.
Figure 16. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional mixed Gibbs energy EAHNP chart with and paths; (b) and paths.
Figure 17. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional mixed Gibbs energy EAHNP chart with and paths; (b) and paths.
Figure 18. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional mixed enthalpy EAHNP chart with and paths; (b) and paths.
Figure 19. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional mixed potential energy EAHNP chart with and paths; (b) and paths.
Figure 20. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional mixed volume EAHNP chart with and paths; (b) and paths.
Figure 21. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional mixed potential energy EAHNP chart with and paths; (b) and paths.
Figure 22. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional configurational entropy energy EAHNP chart with and paths; (b) and paths.
Figure 23. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional generalized vibration entropy energy EAHNP chart with and paths; (b) and paths.
Figure 24. EAHNP and SAHNP charts on disordering AuCuI( ). (a) Three-dimensional generalized vibration free energy EAHNP chart with and paths; (b) and paths.
Figure 25. Heat capacities on disordering AuCuI( ). (a) and paths on EAHNP phase diagram. (b) and paths. (These charts are calculated by temperature step and order degree step ).
Figure 26. Thermal expansion coefficient on disordering AuCuI( ). (a) and paths on EAHNP phase diagram. (b) and paths. (These charts are calculated by temperature step and order degree step ).
Figure 27. Activities on disordering AuCuI( ). (a) and paths on EAHNP phase diagram; (b) and paths on EAHNP phase diagram; (c) and paths; (d) and paths.
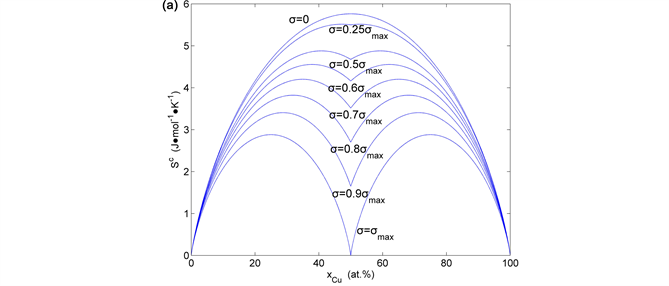
b) Choice of configurational entropy functions
In order to understand how to calculate the configurational entropy from the AG-probabilities occupied at the AG-Gibbs energy levels, we have calculated the EHNP-diagrams of the Au3Cu-, AuCu-, AuCu3-type sublattice systems by Equations ((4-32) to (4-37)), which are shown in Figures 34-36. In our opinion, the AG-probabilities occupied at the AG-Gibbs energy levels in the degeneracy g-function should be degenerated by the constituent atom probabilities occupied at the lattice points for calculating constituent atom arranging entropy, based on following reasons:
i) The AG generalized action entropy has been accounted in the -characteristic Gibbs energy (see Equations (4-16) to (4-27)). Therefore, the configurational entropy arisen from the AG-probabilities occupied at the lattice points should be degenerated by the constituent atom probabilities occupied at the lattice points.
Figure 28. EAHNP phase diagrams of sublattice systems. (a) Three-dimension EAHNP diagrams of Au3Cu-type sublattice system; (b) equilibrium phase diagram with iso-mixed Gibbs energy curves of Au3Cu-type sublattice system; (c) Three-dimension EAHNP diagrams of AuCu-type sublattice system; (d) equilibrium phase diagram with iso-mixed Gibbs energy curves of AuCu-type sublattice system; (e) Three-dimension EAHNP diagrams of AuCu3-type sublattice system; (f) equilibrium phase diagram with iso-mixed Gibbs energy curves of AuCu3-type sublattice system.
Figure 29. EAHNP phase diagrams of sublattice systems. (a) Three-dimension EAHNP diagrams of Au3Cu-type sublattice system; (b) equilibrium phase diagram with iso-order degree curves, top-points and experimental jumping -temperatures of Au3Cu-type sublattice system; (c) Three-dimension EAHNP diagrams of AuCu-type sublattice system; (d) equilibrium phase diagram with iso-order degree curves, top-points and experimental jumping - temperatures of AuCu-type sublattice system; (e) Three-dimension EAHNP diagrams of AuCu3-type sublattice system; (f) equilibrium phase diagram with iso-order degree curves, top-points and experimental jumping -tempera- tures of AuCu3-type sublattice system.
Figure 30. EAHNP phase diagrams. (a) (b) Three-dimension and diagrams of Au3Cu-type alloy; (c), (d) Three-dimension and diagrams of AuCu-type alloy; (e) (f) Three-dimension and diagrams of AuCu3-type alloy.
Figure 31. Equilibrium EAHNP phase diagrams of Au-Cu system. (a) Equilibrium EAHNP phase diagram with iso-mixed Gibbs energy curves of Au-Cu system; (b) Equilibrium EAHNP phase diagram with iso-order degree curves of Au-Cu system. (These diagrams are calculated by temperature step , composition step and ordered degree step ).
Figure 32. Subequilibrium SAHNP phase diagrams of Au-Cu system. (a) Subequilibrium SAHNP phase diagram with iso-mixed Gibbs energy curves of Au-Cu system; (b) Subequilibrium SAHNP phase diagram with iso-order degree curves of Au-Cu system. (These diagrams are calculated by temperature step , composition step and ordered degree step .)

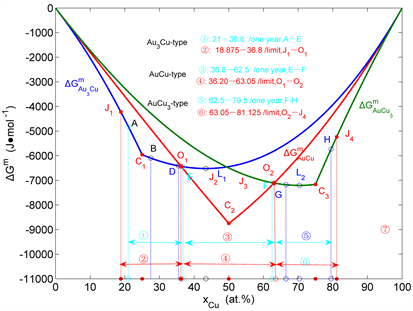
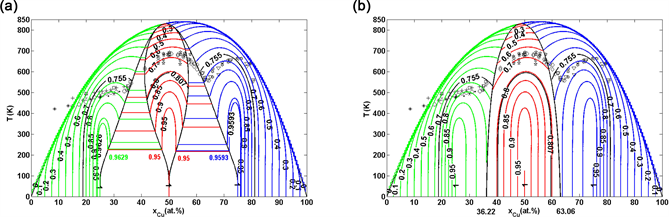
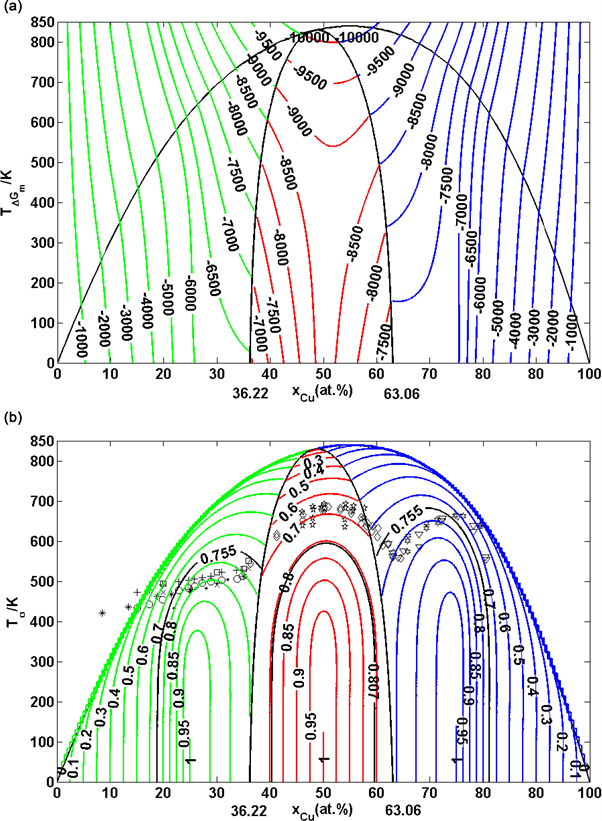
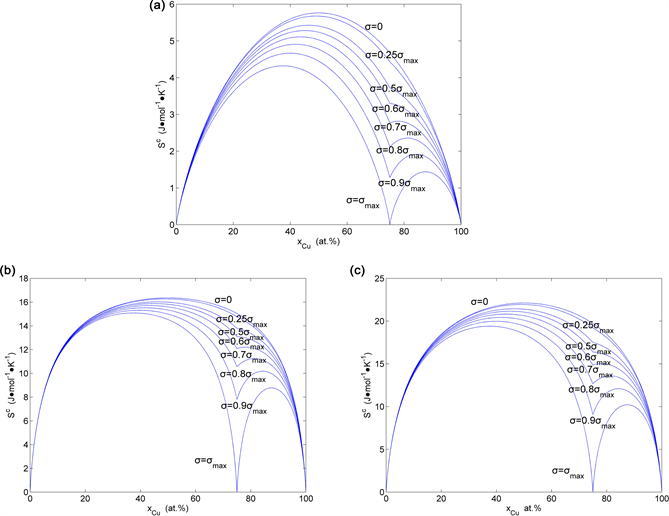
Figure 33. Ranges of long range ordered phases. (a) Composition ranges of ordered Au3Cu-type, AuCu-type and AuCu3-type in Au-Cu system calculated by their first jumping order degrees of Au3Cu- and AuCu3-type alloys and subequilibrium crosspint numerical method of isothermal Gibbs energy curves [47] [48] , together with experimental jumping points, which were erroneously considered as the equilibrium order-disorder transformation critical -temperatures from references given in [88] ; (b) Comparison of composition ranges of long range ordered phases. The alloys were annealed at appropriate temperature different periods (on six months and one year) and slowly cooled down to room temperature [60] [61] . For alloys on six months, the experimental composition range is B-D-G-H; For alloys on one year, the experimental composition range is A-E-F-H, which approachs to calculated limited composition range J1-O1-O2-J4. Each point is described by composition, mixed Gibbs energy and order degree: J1 (18.875, −4220.47, 0.7540), A (21.00, −4807.10, 0.8400), C1 (25.00, −5955.72, 1), B (27.50, −6094.93, 0.9667), D (35.50, −6411.03, 0.8600), O1 (36.20, −6428.97, 0.8507), E (36.80, −6443.06, 0.8427), J2 (43.375, −6518.13, 0.7553), L1 (43.40, −6518.13, 0.7547), C2 (50, −8746.23, 1), J3 (56.625, 0.7547), F (62.50, −7094.10, 0.8333), O2 (63.05, −7108.69, 0.8407), G (66.50, −7176.61, 0.8667), L2 (70.35, −7203.16, 0.9380), C3 (75, −7163.61, 1), H (79.50, −5726.05, 0.8200), J4 (81.125, −5320.59, 0.7550).
Figure 34. Congfiguration entropies of the Au3Cu-type sublattice system: (a) calculated by ; (b) calculated by ; (c) calculated by (the maximal order degree is the function of ).
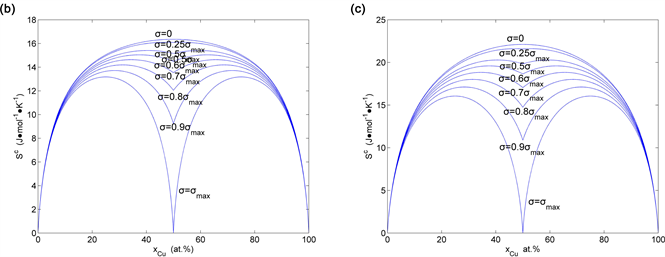
Figure 35. Congfiguration entropies of the AuCu-type sublattice system: (a) calculated by ; (b) calculated by ; (c) calculated by (the maximal order degree is the function of ).
Figure 36. Congfiguration entropies of the AuCu3-type sublattice system: (a) calculated by ; (b) calculated by ; (c) calculated by (the maximal order degree is the function of ).
ii) The configurational entropy of each ordered alloy calculated by a degeneracy function can change continually from the configurational entropy in the maximum order degree state to one in the perfectly disordered state.
iii) For binary alloy systems, the should lie in the range:
where, the upper limit is the value for a perfectly disordered equiatomic Au0.5Cu0.5 alloy.
The results show that the AG arranging degeneracy function and entropy function may be used [48] .
The AG arranging degeneracy function and entropy function :
(4-32)
(4-33)
The AG arranging degeneracy function and entropy function :
(4-34)
(4-35)
The AG arranging degeneracy function and entropy function :
(4-36)
(4-37)
The AHNP-social road is to turn the spiritual wealth of SMM science into the material wealth of advanced alloys. Therefore, the AGSP should add other three goals: We have to “surmount super era theory trap”, before we can start the AGSP. Because that the philosophic thinking mode and theoretical model of the SMM science are different from ones of QMAC electron theory and CALPHAD thermodynamics, specially due to social/interest factor, the SMM science has been inhibited; Achieving shift in social form to the AHNP-social organization, that drives deeper collaboration, vaster open, fuller utilization and fairer share, then provides social relations support for the AGSP; Achieving transformation of the human thinking mode from “reductionism” to the SSP, that drives well-qualified scientists, technicians and management personnel with SSP thinking mode, then provides human resources support for the AGSP.
Acknowledgements
This research was supported by the National Natural Science Foundation of China (51071181), the Natural Science Foundation of Hunan Province (2013FJ4043), Development and Reform Commission of Hunan Province (No.2016-01), China.
Cite this paper
Xie, Y.Q., Li, X.B., Liu, X.B., Peng, H.J. and Nie, Y.Z. (2017) Alloy Gene Sequence Project and System Science Philosophy. Int. J. Communications, Network and System Sciences, 10, 327-401. https://doi.org/10.4236/ijcns.2017.1012019
References
- 1. Slater, J.C. (1937) Electronic Structure of Alloys. Journal of Applied Physics, 8, 385-390. https://doi.org/10.1063/1.1710311
- 2. Hume-Rothery, W. (1962) Atomic Theory for Students of Metallurgy. Institute of metals, London.
- 3. Hohenberg, P. and Kohn, W. (1964) Inhomogeneous Electron Gas. Physical Review B, 136, 864-871. https://doi.org/10.1103/PhysRev.136.B864
- 4. Kohn, W. and Sham, L. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review A, 140, 1133-1138. https://doi.org/10.1103/PhysRev.140.A1133
- 5. Kikuchi, R.A. (1951) Theory of Cooperative Phenomemena. Physical Review, 81, 988-1003. https://doi.org/10.1103/PhysRev.81.988
- 6. Asta, M., Wolverton, C., de Fontaine, D. and Dreyssé, H. (1991) Effective Interaction from Cluster-Variation Formalism I. Physical Review B, 44, 4907-4913. https://doi.org/10.1103/PhysRevB.44.4907
- 7. Wolverton, C., Asta, M., Dreyssé, H. and de Fontaine, D. (1991) Effective Interaction from Cluster-Variation Formalism II. Physical Review B 44, 4914-4924. https://doi.org/10.1103/PhysRevB.44.4914
- 8. Asta, M. and de Fontaine D. (1993) First-Principles Study of Phase Stability of Ti-Al Intermetallic Compounds. Journal of Materials Research, 8, 2554-2568. https://doi.org/10.1557/JMR.1993.2554
- 9. Ellis, D.E. and Perdwew, J.P. (1994) Density Function Theory of Molecules, Clusters and Solids. Kluwer Academic, Holland.
- 10. Pettifor, D.G. (2003) Electron Theory in Materials Modeling. Acta Materialia, 51, 5649-5673. https://doi.org/10.1016/S1359-6454(03)00466-X
- 11. Bragg, W.L. and Williams E.J. (1934) The Effect of Thermal Agitation on Atomic Arrangement in Alloys. Proceedings of the Royal Society of London A, 145, 699-730. https://doi.org/10.1098/rspa.1934.0132
- 12. Bragg, W.L. and Williams E.J. (1935) The Effect of Thermal Agitation on Atomic Arrangement in Alloys-II. Proceedings of the Royal Society of London A, 151, 540-566. https://doi.org/10.1098/rspa.1935.0165
- 13. Bethe, H.A. (1935) Statistical Theory of Superlattices. Proceedings of the Royal Society of London A, 150, 552-575. https://doi.org/10.1098/rspa.1935.0122
- 14. Kaufman L. and Bernstein H. (1970) Computer Calculation of Phase Diagrams. Academic Press, New York.
- 15. Sundman, B., Fries, S.G. and Oates, W.A. (1999) A Calphad Assessment of the Au-Cu System Using the Cluster Variatiation Method. Zeitschrift für Metallkunde, 90, 267-273.
- 16. Hillert, M. (2001) The Compound Energy Formalism. Journal of Alloys and Compounds, 320, 161-176. https://doi.org/10.1016/S0925-8388(00)01481-X
- 17. Oates, W.A. (2006) Configurational Entropies of Mixing in Solid Alloys. Journal of Phase Equilibria and Diffusion, 28, 79-89. https://doi.org/10.1007/s11669-006-9008-3
- 18. Kaufman, L. and Agren, J. (2014) CALPHAD, First and Second Generation-Birth of the Materials Genome. Scripta Materialia, 70, 3-6. https://doi.org/10.1016/j.scriptamat.2012.12.003
- 19. Xie, Y.Q. (1998) Systematic Science of Metallic Materials. Central South University of Technology Press, Changsha. (In Chinese)
- 20. Xie, Y.Q. (1998) Development Course of Metallic Materials Science and Evolution of Human Thinking Mode. Materials Review, 12, 6-10. (In Chinese)
- 21. Xie, Y.Q. (2011) Relationship between Partial and Average Atomic Volumes of Components in Au-Ni Alloys. Transactions of Nonferrous Metals Society of China, 21, 1801-1807. https://doi.org/10.1016/j.scriptamat.2012.12.003
- 22. Xie, Y.Q. (2012) Systematic Science of Alloys. Central South University Press, Changsha. (In Chinese)
- 23. Xie, Y.Q., Liu X.B., Li, X.B., Peng, H.J. and Nie, Y.Z. (2015) Holographic Alloy Positioning Design System and Holographic Network Phase Diagrams of Au-Cu System. Transactions of Nonferrous Metals Society of China, 25, 885-906. https://doi.org/10.1016/S1003-6326(15)63678-0
- 24. Xie, Y.Q., Li X.B., Liu, X.B., Peng, H.J. and Nie, Y.Z. (2015) Alloy Gene, Holographic Alloy Positioning Design System. The Chinese Journal of Nonferrous Metals, 25, 2798-2843.
- 25. Pauling, L. (1960) The Nature of the Chemical Bonding. Conell University Press, Ithaca.
- 26. Yu, R.H. (1978) Empirical Electron Theory of Solids and Molecules. Science Bulletin, 23, 217-224.
- 27. Grigorovvich, V.K. (1989) The Metallic Bond and Structure of Metals. Nova Science, New York.
- 28. Lupis, C.H.P. and Elliott, J.F. (1967) Prediction of Enthalpy and Entropy Interaction Coefficients by the “Central Atoms” Theory. Acta Materialia, 15, 265-276. https://doi.org/10.1016/0001-6160(67)90202-7
- 29. Xie, Y.Q. and Ma, L.Y. (1985) Theoretical Lattice Parameters of Valence Electron Structures of Crystals. Journal of Central South Institute of Mining and Metallurgy, 1, 1-8. (In Chinese)
- 30. Xie, Y.Q. and Ma, L.Y. (1985) Generalized Vegard’s Law and Generalized Yü’s Law. Journal of Central South Institute of Mining and Metallurgy, 3, 1-7. (In Chinese)
- 31. Xie, Y.Q. (1993) A New Potential Function with Many-Atom Interactions in Solid. Science in China (Series E), 36, 90-99.
- 32. Xie, Y.Q., Zhang, X.D., Zhao, L.Y. and Ma, X.L. (1993) Electronic Structure and Properties of Cu Metal. Science in China (Series E), 36, 487-496.
- 33. Xie, Y.Q. (1994) Electronic Structure and Properties of Pure Iron. Acta Metallurgica et Materialia, 42, 3705-3715. https://doi.org/10.1016/0956-7151(94)90436-7
- 34. Xie, Y.Q., Zhang, X.D. and Chen, J.Y. (1996) Electronic Structure and Properties of Pure Cobalt. Science in China (Series E), 39, 394-403.
- 35. Xie, Y.Q., Lü, M.S. and Zhao, L.Y. (1993) Electronic Structure and Properties of Ni Metal. Science in China (Series A), 36, 495-503.
- 36. Xie, Y.Q., Zhang, X.D., Zou, P. and Zhao, L.Y. (1993) Microstructure and Properties of Cu-Ni Alloys. Science in China, A, 36, 612-623.
- 37. Xie, Y.Q. (1998) Atomic Energies and Gibbs Energy Functions of Ag-Cu Alloys. Science in China, Series E: Technological Sciences, 41, 146-156. https://doi.org/10.1007/BF02919677
- 38. Xie, Y.Q. and Zhang, X.D. (1998) Atomic Volume and Volume Functions of Ag-Cu Alloys. Science in China, Series E: Technological Sciences, 41, 57-168. https://doi.org/10.1007/BF02919678
- 39. Xie, Y.Q. and Zhang, X.D. (1998) Electronic Structure of Ag-Cu Alloys. Science in China, Series E: Technological Sciences, 41, 225-236. https://doi.org/10.1007/BF02919432
- 40. Xie, Y.Q. and Zhang, X.D. (1998) Phase Diagram and Thermodynamic Properties of Ag-Cu Alloys. Science in China, Series E: Technological Sciences, 41, 348-356. https://doi.org/10.1007/BF02917006
- 41. Xie, Y.Q., Peng, K. and Liu, X.B. (2004) Influences of xTi/xAl Atomic States, Lattice Constants and Potential-Energy Planes of Ordered FCC TiAl Type Alloys. Physica B, 344, 5-20. https://doi.org/10.1016/j.physb.2003.06.002
- 42. Xie, Y.Q., Liu, X.B. and Peng, K. (2004) Atomic State, Potential Energies, Volumes, Stability and Brittleness of Ordered FCC TiAl3 Type Alloys. Physica B, 353, 15-33. https://doi.org/10.1016/j.physb.2004.08.022
- 43. Xie, Y.Q., Peng, H.J., Liu, X.B. and Peng, K. (2005) Potential Energies, Volumes, Stability and Brittleness of Ordered FCC Ti3Al Type Alloys. Physica B, 362, 1-17. https://doi.org/10.1016/j.physb.2005.01.197
- 44. Xie, Y.Q., Tao, H.J., Peng, H.J., Li, X.B., Liu, X.B. and Peng, K. (2005) Atomic State, Potential Energies, Volumes, Stability and Brittleness of Ordered FCC TiAl2 Type Alloys. Physica B, 366, 17-37. https://doi.org/10.1016/j.physb.2005.04.041
- 45. Xie, Y.Q., Li, X.B., Liu, X.B., Nie, Y.Z. and Peng, H.J. (2013) Alloy Gene Gibbs Energy Partition Function and Equilibrium Holographic Network Phase Diagrams of AuCu-Type Sublattice System. International Journal of Communications, Network and System Sciences, 6, 415-442. https://doi.org/10.4236/ijcns.2013.610045
- 46. Xie, Y.Q., Peng, H.J., Liu, X.B., Li, X.B. and Nie, Y.Z. (2014) New Atom Movement Mechanism for Tracking Path on Disordering AuCuI(A8AuA4Cu) Compound. Transactions of Nonferrous Metals Society of China , 24, 3221-3256. https://doi.org/10.1016/S1003-6326(14)63464-6
- 47. Xie, Y.Q., Li, X.B., Liu, X.B., Nie, Y.Z. and Peng, H.J. (2014) Alloy Gene Gibbs Energy Partition Function and Equilibrium Holographic Network Phase Diagrams of AuCu3-Type Sublattice System. Transactions of Nonferrous Metals Society of China, 24, 3585-3610. https://doi.org/10.1016/S1003-6326(14)63505-6
- 48. Xie, Y.Q., Nie, Y.Z., Li, X.B., Peng, H.J. and Liu, X.B. (2015) Alloy Gene Gibbs Energy Partition Function and Equilibrium Holographic Network Phase Diagrams of Au3Cu-Type Sublattice System. Transactions of Nonferrous Metals Society of China, 25, 211-240. https://doi.org/10.1016/S1003-6326(15)63598-1
- 49. OSTP (2011) Materials Genome Intiative Strantegic for Global Competiveness.: Office of Science and Technology Policy, OSTP, Washington DC. OSTP (2014) Materials Genome Intiative Strantegic Plan. Office of Science and Technology Policy, Washington DC.
- 50. Zhao, J.C. (2014) A Perspective on Materials Genome Initiative. Chinese Journal of Nature, 36, 89-104.
- 51. Johannsson, C.H. and Linde, J.O. (1936) Roentgenographic and Electrical Investigations of the Cu-Au System. Annals of Physics, 25, 1-48.
- 52. Nix, F.C. and Macnair, D. (1941) A Dilatometric Study of the Order-Disorder Transformation in Cu-Au Alloys. Physical Review, 60, 320-329. https://doi.org/10.1103/PhysRev.60.320
- 53. Sutcliffe, C.H. and Jaumot Jr., F.E. (1953) Order-Disorder in Au-Cu Alloy. I. Short-Range Order in an Alloy Containing Atomic Percent Au. Acta Metallurgica, 1, 725-730. https://doi.org/10.1016/0001-6160(53)90032-7
- 54. Frank, E., Jaumot, J.R. and Charles, H.S. (1954) Order-Disorder in Au-Cu alloy II. The Nature of the Order-Disorder Transformation and Long-Range Order. Acta Metallurgica, 2, 63-74. https://doi.org/10.1016/0001-6160(54)90095-4
- 55. Kuczynski, G.C., Doyama, M. and Fine, M.E. (1956) Transformations in Disordered Gold Copper Alloys. Journal of Applied Physics, 27, 651-655. https://doi.org/10.1063/1.1722450
- 56. O’brien, J.L. and Kuczynski, G.C. (1959) X-Ray Study of the Kinetics of Ordering in AuCu. Acta Metallurgica., 7, 803-806. https://doi.org/10.1016/0001-6160(59)90096-3
- 57. Scott, R.E. (1960) New Complex Phase in the Copper-Gold System. Journal of Applied Physics, 31, 2112-2117. https://doi.org/10.1063/1.1735509
- 58. Orr, R.L., Luciat-Labry, J. and Hultgren, R. (1960) Energy of the Order-Disorder Transformation in AuCu. Acta Metallurgica, 8, 431-434. https://doi.org/10.1016/0001-6160(60)90029-8
- 59. Marcinkowski, M.J. and Zwell, L. (1963) Transmission Electron Microcopy Study of the Off-Staichiometric Cu3Au Superlattices. Acta Metallurgica, 11, 373-390. https://doi.org/10.1016/0001-6160(63)90162-7
- 60. Lu, S.S. and Liang, C.K. (1966) The Superlattice Formation and Lattice Spacing Changes in Copper-Gold Alloys. Acta Physica Sincica, 22, 639-696 (in Chinese).
- 61. Lu, S.S. and Liang, C.K. (1966) The Existence of the Superlattice CuAu3 in the Cu-Au System. Kexue Tongbao, 17, 395-396.
- 62. Marques, M.C., Pinheiro, M.F. and Braga, M.E. (1977) Electrical Resistivity and Phase Change in CuAu. Scripta Metallurgica, 11, 197-200. https://doi.org/10.1016/0036-9748(77)90052-7
- 63. Claeson, T. and Boyce, J.B. (1984) Order-Disorder Transformation in Au-Cu Alloys Studied by Extended X-Ray-Absorption Fine Structure. Physical Review, 29, 1551-1557. https://doi.org/10.1103/PhysRevB.29.1551
- 64. Lander, G.H. and Brown, P.J. (1985) A Neutron Diffraction Study of AuCu3 near the Order-Disorder Temperature. Journal of Physics C: Solid State Physics, 18, 2017-2024. https://doi.org/10.1088/0022-3719/18/10/007
- 65. Butler, B.D. and Cohen, J.B. (1989) The Structure of Cu3Au above the Critical Temperature. Journal of Applied Physics, 65, 2214-2219. https://doi.org/10.1063/1.342833
- 66. Potekaev, A.I. (1995) Long-Period States of Ordered Metal Alloys. 1. Analysis of Structural Features. Russian Physics Journal., 38, 549-562. https://doi.org/10.1007/BF00559919
- 67. Potekaev, A.I. (1996) Long-Period States of Ordered Metal Alloys. 2. Physical Properties. Russian Physics Journal, 39, 521-533. https://doi.org/10.1007/BF02437017
- 68. Sprusil, B. and Pfeiler, W. (1997) The Retro-Effect in Stoichiometric CuAu: A Resistometric Study. Intermetallics, 5, 501-505. https://doi.org/10.1016/S0966-9795(97)00019-8
- 69. Bogdanoff, P.D. and Fultz, B. (1999) Vibrational Entropy of L12 Cu3Au Measured by Inelastic Neutron Scattering. Physical Review B, 36, 3976-3981. https://doi.org/10.1103/PhysRevB.60.3976
- 70. Sprusil, B. and Pfeiler, W. (2000) The Retro-Effect in CuAu and Its Kinetic Limitations. Intermetallics, 8, 81-83. https://doi.org/10.1016/S0966-9795(99)00076-X
- 71. Pfeiler, W. and Sprusil, B. (2002) Atomic Ordering in Alloys: Stable States and Kinetics. Materials Science and Engineering A, 324, 34-42. https://doi.org/10.1016/S0921-5093(01)01280-1
- 72. Kubiak, R. and Janczak, J. (1991) X-Ray Study of Ordered Phase Formation in Au31.6Cu68.4, Au50Cu50 and Au75Cu25. Journal of Alloys and Compounds, 176, 133-140. https://doi.org/10.1016/0925-8388(91)90018-Q
- 73. Bonneaux, J. and Guymont, M. (1999) Study of the Order-Disorder Transition Series in AuCu by In-Situ Temperature Electron Microscopy. Intermetallics, 7, 797-805. https://doi.org/10.1016/S0966-9795(98)00128-9
- 74. Feutelais, Y., Legendre, B. and Guymont, M. (1999) New Enthalpies Determination and In Situ X-Ray Diffraction Observations of Order/Disorder Transitions in Au0.5Cu0.5. Acta Materialia, 47, 2539-2551. https://doi.org/10.1016/S1359-6454(99)00089-0
- 75. Volker, E., Williams, F.J., Calvo, E.J., Jacob, T. and Schiffrin, D.J. (2012) O2 Induced Cu Surface Segregation in Au-Cu Alloys Studied by Angle Resolved XPS and DFT Modelling. Physical Chemistry Chemical Physics, 14, 7448-7455. https://doi.org/10.1039/c2cp40565b
- 76. Miranda, G., Silva, F.S. and Soares, D. (2013) Solid State Transformations and Equilibrium Crystal Structures of an Au-Cu Alloy with Shape Memory Effect. Materials Science Forum, 732, 859-864.
- 77. Wu, J., Zou, L., Wang, T., Chen, Y. and Cai, J. (2016) Spin Hall Angle and Spin Diffusion Length in Au-Cu Alloy. IEEE Transactions on Magnetics, 52, 1-4. https://doi.org/10.1109/TMAG.2016.2522938
- 78. Xie, Y.Q., Li, X.B., Liu, X.B., Peng, H.J. and Nie, Y.Z. (2009) Potential Energy Sequences of Characteristic Atoms on Basis of Heats of Formation of Disordered Au(1−x)Cux Alloys (Part 1). Journal of Materials Science and Engineering, 3, 51-68.
- 79. Xie, Y.Q., Li, X.B., Liu, X.B., Peng, H.J. and Nie, Y.Z. (2009) Potential Energy Sequences of Characteristic Atoms on Basis of Heats of Formation of Disordered Au(1−x)Cux Alloys (Part 2). Journal of Materials Science and Engineering, 3, 44-57.
- 80. Xie, Y.Q., Li, X.B., Liu, X.B., Peng, H.J. and Nie, Y.Z. (2009) Volume Sequences of Characteristic Atoms Separated from Experimental Volumes of Disordered Au(1−x)Cux Alloys. Journal of Materials Science and Engineering, 3, 54-75.
- 81. Xie, Y.Q., Liu, X.B., Li, X.B., Peng, H.J. and Nie, Y.Z. (2009) Potential Energies of Characteristic Atoms Separated from Experimental Heats of Formation of AuCu and AuCu3 Compounds. Transactions of Nonferrous Metals Society of China, 19, 1243-1256. https://doi.org/10.1016/S1003-6326(08)60436-7
- 82. Xie, Y.Q., Liu, X.B., Li, X.B., Peng, H.J. and Nie, Y.Z. (2009) Volume of Characteristic Atoms Separated from Experimental Volumes of AuCu and AuCu3 Compounds. Transactions of Nonferrous Metals Society of China, 19, 1599-1617. https://doi.org/10.1016/S1003-6326(09)60077-7
- 83. Xie, Y.Q., Nie, Y.Z., Liu, X.B., Li, X.B., Peng, H.J. and Li, Y.F. (2012) Potential Energies of Characteristic Atoms Separated from First-Principles Calculated Heats of Formation of AuCu and AuCu3 Compounds. In: Xie, Y.Q., Ed., Systematic Science of Alloys, Central South University Press, Changsha, 405-427.
- 84. Xie, Y.Q., Nie, Y.Z., Liu, X.B., Li, X.B., Peng, H.J. and Li, Y.F. (2012) Volume of Characteristic Atoms Separated from First-Principles Calculated Volume of L10-AuCu and L12-AuCu3 Compounds. S In: Xie, Y.Q., Ed., Systematic Science of Alloys, Central South University Press, Changsha, 428-460.
- 85. Xie, Y.Q., Nie, Y.Z., Li, X.B., Liu, X.B., Peng, H.J. and Li, Y.F. (2011) Characteristic Atoms Potential Energy Partition Function of Au3Cu Type Ordered Alloys in FP-SSA Framework. The Chinese Journal of Nonferrous Metals, 21, 2489-2501.
- 86. Xie, Y.Q., Li, Y.F., Liu, X.B., Li, X.B., Peng, H.J. and Nie, Y.Z. (2011) Characteristic Atoms Occupation Patterns of Au3Cu, AuCu3, AuCuI and AuCuII Based on Experimental Data of Disordered Alloys. Transactions of Nonferrous Metals Society of China, 21, 1092-1104. https://doi.org/10.1016/S1003-6326(11)60827-3
- 87. Mie, G. (1903) Zur kinetischen theorie der einatomigen korper. Annals of Physics 316, 657-697. https://doi.org/10.1002/andp.19033160802
- 88. Lennard-Jones, J.E. (1931) Cohesion. Proceedings of the Physical Society, 43, 461-482. https://doi.org/10.1088/0959-5309/43/5/301
- 89. Prigogine, I. (1969) Structure, Disspipation and Life, First Conference on Theoretical Physics and Biology. North-Holland Publishing Company, Amsterdam.
- 90. Prigogine, I. (1967) Structure, Introduction to Thermodynamics of Irreversible Processes. 3rd Edition, Wiley-Interscience, New York.
- 91. Lu, S.S. and Liang, C.K. (1966) Experimental Evidence of Order-Disorder Transitions as of the Second Degree. Kexue Tongbao, 17, 441-443.
- 92. Sundman, B., Fries, S.G. and Oates, W.A. (1998) A Thermodynamic Assessment of the Au-Cu System. CALPHAD, 22, 335-354. https://doi.org/10.1016/S0364-5916(98)00034-0
- 93. Cao, W., Chang, Y.A., Zhu, J., Chen, S. and Oates, W.A. (2007) Thermodynamic Modeling of the Cu-Ag-Au System Using the Cluster/Site Approximation. Intermetallics, 15, 1438-1446. https://doi.org/10.1016/j.intermet.2007.05.003
- 94. Wei, S.H., Mbaye, A.A., Ferrira, L.G. and Alex, Z. (1987) First-Principles Calculations of the Phase Diagrams of Noble Metals: Cu-Au, Cu-Ag and Ag-Au. Physical Review B, 36, 4163-4185. https://doi.org/10.1103/PhysRevB.36.4163