International Journal of Communications, Network and System Sciences
Vol.09 No.04(2016), Article ID:65970,13 pages
10.4236/ijcns.2016.94007
Optimization of Leaky Feeder Slot Spacing for Better Beam Forming in Mines and Tunnels
Noha Hassan, Wisam F. Farjow, Xavier Fernando
Department of Electrical and Computer Engineering, Ryerson University, Toronto, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 March 2016; accepted 22 April 2016; published 27 April 2016
ABSTRACT
The radiating cable (or leaky feeder) is the leading solution for distributed broadband wireless access in underground mines and tunnels. The traditional radiating cable has equally spaced slots along its axis radiating evenly. However, with the new requirement for tracking and localization of miners, this paper shows how to modify the leaky feeder to function as a beam forming antenna array by appropriately optimizing the slot spacing. Optimizing the leaky feeder slot distances using Genetic algorithm has a good impact on the channel parameters, making it an excellent choice for leaky feeder antennas. Linear, as well as bent practical leaky feeder shapes, were considered, and we tested five different optimization algorithms and compared side lobe energies, varying the slot distance which had an impact on side lobe level. Also, we derived the expression for the BER, spectral efficiency and throughput considering a time-varying wireless channel. We observed that as the radius of curvature of the feeder increased (approaching a straight line), the spectral efficiency decreased as expected. Interestingly different optimization algorithms perform differently at different carrier frequencies. An optimization method should be chosen according to the required goal to be achieved (maintaining uniform equal power along the cable, or a more directed beam, or using a certain frequency of operation).
Keywords:
Beam-Forming Antenna, Leaky Feeder, Millimeter-Wave Frequencies, Optimization

1. Introduction
Leaky feeder (LF) cables are a particular type of transceivers widely used in tunnels and mines for two-way wireless access [1] [2] . The LF works in two ways. It acts as a cable carrying Radio Frequency (RF) signal from one place to another. Also, due to the slots along its way, it also acts as a linear antenna array enabling short- range broadband wireless communication up to 1.6 Gb/s [3] .
However, in addition to providing communications, there is a new interest for accurate tracking and localization of miners, vehicles, and explosives in mines and tunnels, with the advent of the recent MINER Act. The MINER Act mandates such monitoring to ease rescue operations in the light of a vast number of fatalities that somehow keep increasing.
The man used the LF for tracking and localization in the indoor and underground environment. For example, [4] demonstrated an LF based indoor positioning system. Authors of [5] show how the LF has a unique advantage for their Wireless Indoor Positioning System (WIPoS). They also propose an optimized LF cable that alleviates the effects of multi-coupling that reduces the positioning accuracy.
The LF is an array of slot antennas. Conventional LF has uniformly spaced (equidistance) slots along its longitudinal axis. There is a phase shift between the radiated signal from each slot as a function of the radio frequency and slot separation. The uniform slot separation provides higher side lobe energy.
Though different shapes of slots have been tried to control the amount of radiated RF energy, no effort has been reported to optimize the slot spacing systematically to monitor the radiation pattern of an LF. That is the focus of this paper. Concentrating the radiation in the desired direction realizes multiple benefits such as space division multiplexed communication, in addition to better tracking [6] .
In this paper, we study the optimization of LF slot spacing for beam forming. In our previous work [7] , we showed our modified Particle Swarm Optimization (PSO) algorithm significantly decreased the side lobe level. However, further investigation showed different optimization algorithms performed better at various carrier frequencies. Furthermore, it is intriguing to observe the behavior of an RF signal emanating from multiple slots with a phase difference travel through a time-varying wireless channel in a confined environment. The wireless channel in mines will have unique propagation characteristics with limited or no line of sight components [Wisam, Fernando]. In this paper, we have also studied the effect of varying the slot separation on spectral efficiency, average throughput, and Bit Error Rate (BER) using various evolutionary optimization methods.
We used the following optimization algorithms:
・ Genetic Algorithm (GE): This is a population-based search heuristic that mimics the process of natural selection. The aim is to find the fitness value of each member of a random population and to choose the individuals with the best fitness value for further reproduction [8] .
・ Particle Swarm Optimization (PSO): This is a stochastic optimization technique inspired by social behavior of bird flocking or fish schooling. PSO shares many similarities with GA. System initialization starts with a population of random solutions and searches for optima by updating generations. In PSO, the particles fly through the solution space by following the current optimum particles. However, unlike GA, PSO has no evolution operators such as crossover and mutation [9] .
・ Cat Swarm Optimization (CSO): This is an evolutionary method proposed less than one decade ago. In the recent years, it has been improved and applied in different fields by many researchers. CSO models the behavior of cats that rest mostly except when they are tracking some targets. Trying to find the next best position to move into, there are two modes in CSO: seeking mode and tracking mode [10] .
・ Differential Evolution (DE): It is a parallel search method that utilizes D-dimensional parameter vectors as a population for each generation. It was used to solve optimization problems where the objective function is non-differentiable, non-continuous, and non-linear [11] .
・ Legendre Polynomials (LEG): These are particular orthogonal functions used in the solution of physical problems. They are solutions to Legendre differential equation of the second order. The solutions are called Legendre functions [12] .
Studies showed that evolutionary algorithms usually had a better performance regarding sidelobe level reduction in antenna arrays more than the mathematical approaches. Besides, we analyzed an LF hooked up with different shapes, and the study of an LF considering the multi-path channel.
Related Work
The LF is a particular transceiver modeled as a linear slot-antenna array. The LF has higher average received signal level compared to a conventional omnidirectional antenna. Also, the LF has a higher average signal to noise ratio (SNR) because of the distributed transmission [13] .
In [14] Torrance et al. introduced the theoretical calculated leaky feeder channel impulse response. They considered the phase difference of the RF signal emanating from each slot and compared it with the measured series of impulse responses using a Swept Time Delay Cross Correlator (STDCC). Then, the BER of the leaky feeder of various modulation schemes was plotted experimentally, and compared with the performance of an omnidirectional antenna for coherent modulation.
In [15] Liao et al. suggested four designs for the unequally spaced resonant slotted waveguide antenna array. Varying the slot separation using the proposed models produced three different beam patterns and shapes. In their simulation, the excitation amplitude was varied, and the performance significantly improved. However, in this work, no systematic optimization method is followed, and they suggest random designs.
The rest of this paper is as follows. Section 2 discusses the leaky feeder channel model and the related equations to analyze the channel performance. Also, it highlights other LF models. Section 3 presents the simulation results. Finally, Section 4 ends with the conclusion and future work.
2. Leaky Feeder Channel Model
Consider the leaky feeder schematic diagram shown in Figure 1. Here, a leaky feeder is placed along the x-axis (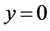 ) having slots along it. The distance between the origin and the
) having slots along it. The distance between the origin and the 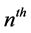 slot is
slot is 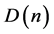 where
where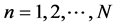 ; N is the total number of slots. The slots are either uniformly or non-uniformly spaced as considered later in this paper.
; N is the total number of slots. The slots are either uniformly or non-uniformly spaced as considered later in this paper.
In our model, we considered a single antenna receiver that is moving on the ground parallel to the x-axis at a position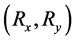 .
.
So the radial distance (range) from the 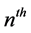 slot to the receiver will be:
slot to the receiver will be:
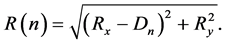 (1)
(1)
Consider, a signal injected into the cable that has an amplitude A and a general phase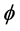 . The injected signal takes a mean time
. The injected signal takes a mean time 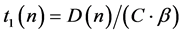 to reach the
to reach the 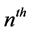 slot of the cable. Where C is the speed of light, K is the dielectric coefficient of the insulation material equal to
slot of the cable. Where C is the speed of light, K is the dielectric coefficient of the insulation material equal to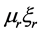 , and
, and 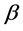 is the relative phase velocity equal to
is the relative phase velocity equal to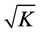 .
.
The attenuated and phase rotated signal at the 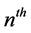 slot will be [14] :
slot will be [14] :
Figure 1. Schematic diagram of a slotted leaky feeder.

In this expression 



The signal that travels from each slot through free space take a mean time 



Therefore, the received impulsive signal at the receiver antenna is given by:

where 


We used Devasirvatham’s path loss model as it was more suitable for indoor and underground confined environments.
Therefore, the estimated impulse response of the channel can be written as the sum of signals emanating from all N slots. The total time is the time it takes the signal to travel through the LF plus the time in the air interface.

In general, this channel response is complex and has a magnitude and a phase component. Its magnitude is

By substitution, the impulse response is:

Expressing the two exponents in terms of


Since


Substituting for the common factor

The previous equation is the impulse response of the wireless channel followed by leaky feeder cable at time t.
Now, to compute the BER, let the input signal 



where 

Let the energy


The signal to noise ratio is 



The signal power is then the mean square value as follows:


After integrating, the received signal power is:

The total noise power 

The signal to noise ratio in dB is [17] ,

From the signal to noise ratio, we can calculate the spectral efficiency, the average throughput, and bit error rates.
The spectral efficiency is [18] :

The BER (

The average channel throughput (Th) in bits/secs is:

where 
Other Leaky Feeder Shapes
Practically the leaky feeder is not just hooked straight in the mine. There are some places where it is bent over or branched to provide coverage to different areas as shown in Figure 2. We shall also study the bent LF.
Consider the curved leaky feeder model shown in Figure 3. Now the distance between slots is different based on the radius. The calculated coordinates of a slot is as follows:


where r is the radius of the curved portion of the leaky feeder, 
The range from the each slot to the receiver is as follows:

Figure 2. Practical LF shapes.
Figure 3. Schematic model for a curved leaky feeder.

The distance between two slots along the circular path is the length of the arc subtended by the two slots.

where 
We can calculate



The branched LF consists of two branches, the horizontal arm and the vertical arm. There will be two coordinates for the slot distance along the x and y directions. For the horizontal branch, the slot coordinates can be calculated in the same way as done previously for the straight leaky feeder.

where n is the number of slots in the horizontal direction and
For the vertical branch, we assume that this branch emanates from the mid-point or the center slot. Therefore,

and,

where m is the number of slots along the y-axis.
Using these previous equations, 
3. Numerical Evaluation
Numerical evaluation is done using the model discussed in Section 2 and the parameters in Table 1.
PSO was applied based on the techniques used in [9] [10] . CSO and GE were applied using the techniques discussed in [10] , and [20] respectively.
The side lobe levels of the chosen optimization methods shown in Figures 4-6. We compared them with the uniformly slotted LF for five slots.
As for the mathematical methods like LEG and DE, we followed the same techniques discussed in [11] [12] .
From Figure 5 the Legendre optimization gave a sharply directed main lobe beam as expected [12] , but the side lobe level was not reduced significantly having a level of −16 to −20 dBm. In Figure 6 DE had a Side lobe level of about −23 dBm. In Figure 4 PSO had a side lobe level of about −22 dBm. CSO has a side lobe level of about −24 dBm as in Figure 4. Genetic optimization has the least side lobe level of about −30 dBm as shown in Figure 6.
In general, all the optimization methods reduced the side lobe levels to some extent, but they have different behavior at different frequencies as we will see later.
Figure 4. The radiation pattern of a Leaky Feeder with Uniform Slot Spacing and Optimized Slot Spacing using CSO and PSO Algorithms.
Table 1. Performance parameters.
Figure 5. The radiation pattern of a leaky feeder with uniform slot spacing and optimized Slot spacing using DE and LEG algorithms.
Figure 6. The radiation pattern of a leaky feeder with uniform slot spacing and optimized Slot spacing using DE and GE algorithms.
Table 2 shows the optimized slot distances used in our simulation for thirty slots based on various optimization methods normalized with wavelengths. We noticed that as the differences between slot distances is small, better performance is achieved.
Table 3 shows the SLL levels obtained with the simulation of thirty slots. Also, we calculated the mean, variance, and standard deviation of the SLL. The standard deviation for CSO, and DE are less than one, this corresponds to a low variance or less spreading of the data(data values are very close to the mean). We can conclude from this that the side lobe level values at different slot distances is very close to each other. Power coming from all the slots will be nearly the same(maintaining nearly a constant energy along the cable).
Besides, we calculated the minimum side lobe attenuation and the beam width angle deviation. Here minimum side lobe attenuation is −
Figure 7 shows a plot of the BER at a receiver that moves along the x-axis for all five optimization methods.
The genetic algorithm shows improvement in the BER by 2.5e−7 more than the equally spaced slots case at a position 5 m. The behavior is the same at all frequencies except the millimeter frequency range.
Studying the system throughput is crucial when changing the frequency especially when optimizing the slot spacing since the optimum spacing depends on the frequency.
To explore the effect of inter-slot interference on system throughput, a plot of throughput versus carrier frequency is shown in Figure 8. Here, the receiver is at 10 m away from the LF.
Figure 8 shows that the genetic algorithm has superior performance over all the other algorithms. GE has a high throughput for a large frequency range, and the curve starts to drop at the mm-wave spectrum. For other optimization methods, the throughput begins to fall at 0.5 GHz. GE also shows improvements in the received
Table 2. Slot distance of various optimization methods for 30 slots.
Table 3. SLL of various optimization methods in dBm for 30 slots.
Figure 7. Bit error rate with uniform and optimized slot spacings at 1 ghz carrier frequency.
Figure 8. Variation of throughput of a leaky feeder with frequency. The receiver is vertically below at 10 m.
power, spectral efficiency and, bit error rate independent of the used frequency, because, after optimization using the genetic algorithm according to [8] , the distance between slots became very tiny. The performance degrades when the distance between slots gets larger. The practicality of designing LF with such short slot spacing is subjected to further investigation.
Other algorithms, however, have inconsistent performance and, approach zero at certain frequencies. It is also worth to mention that the throughput goes to null at some frequencies. This vanishing happens even with the uniformly spaced LF. The explanation is that, at certain frequencies, the signal emanating from adjacent slots may destructively interfere causing the output signal to diminish.
We interpret the superior performance of the genetic algorithm in optimization is due to the following:
1) Most other optimization techniques can only explore the solution space to a problem in one direction at a time whereas GE moves in multiple directions at once.
2) GE performs well when the fitness function is complex.
Figure 8 shows that GE optimization for slot spacing improved the average throughput by about 1.4 bits/sec more than the equally spaced slots leaky feeder, whereas Legendre polynomials optimization decreased the throughput than the equally spaced case.
For the mm-wave frequencies, the performance fluctuates for all algorithms, but the PSO works better at 50 GHz. However, the GE can even work up to 100 - 200 GHz theoretically, although these frequencies may not be appropriate in LF systems. It is also worth to note that the signal amplitude has an effect on the fluctuation pattern, but still the GE outperforms other methods.
Figure 9 shows the spectral efficiency of a curved LF in a time varying channel. The spectral efficiency fluctuates due to the Rician distribution of the amplitude response 
Figure 10 shows the spectral efficiency for a curved LF for various radii from 1 m to 1000 m. The graphs show that as the radius increases (less curvature) the spectral efficiency decreases. At r = 1 m spectral efficiency is 45 bps/Hz, and at r = 1000 m (Nearly infinity) the spectral efficiency is about 30 bps/Hz.
4. Conclusions and Future Work
4.1. Conclusions
In this paper, we analyzed the spectral efficiency, received power (from all slots), and the BER of a leaky feeder based wireless communication system. The slot placement is optimized using various evolutionary and mathematical techniques. Simulation results show that varying the slot distance can significantly reduce side lobe level. Genetic algorithm optimization improved the leaky feeder channel parameters significantly regardless of the
Figure 9. Sample spectral efficiency of a time-varying curved LF channel, where receiver is moving along x-axis.
Figure 10. Sample spectral efficiency of a time-varying curved LF channel, where receiver is moving along x-axis.
used frequency, so we recommend it for use as a method for optimizing the leaky feeder slot spacing in all frequency bands. For mm-wave frequencies, it is better to use PSO up to 50 GHz and use GE beyond that band. If maintaining a constant energy along the cable is the requirement, then it is better to use CSO and DE. If a more directed beam is required to focus on the energy in a specific direction, then Legendre is better. Increasing the curvature of the LF also increases the received power and spectral efficiency.
4.2. Future Work
For our future work, we aim to apply the same five optimization techniques, but for a time-varying channel, we aim to check the effect of the varying slot spacing on the delay spread and other channel parameters. Furthermore, we will try to verify our simulation experimentally, taking measurements of different channel parameters by using various LF shapes.
Acknowledgments
This research paper came into the world with the help and support from everyone, including parents, family, and friends, especially engineers and staff from PBE Canada and Ryerson University.
Cite this paper
Noha Hassan,Wisam F. Farjow,Xavier Fernando, (2016) Optimization of Leaky Feeder Slot Spacing for Better Beam Forming in Mines and Tunnels. International Journal of Communications, Network and System Sciences,09,77-89. doi: 10.4236/ijcns.2016.94007
References
- 1. Quinlan, T.J., Dudley, S.E.M. and Walker, S.D. (2007) A High Data Rate Wireless Leaky Feeder System for Vehicular Tunnel Applications. 2007 Loughborough Antennas and Propagation Conference (LAPC 2007), Loughborough, 2-3 April 2007, 77-80.
http://dx.doi.org/10.1109/LAPC.2007.367435 - 2. Zhang, Y.P. (2001) Indoor Radiated-Mode Leaky Feeder Propagation at 2.0 Ghz. IEEE Transactions on Vehicular Technology, 50, 536-545.
http://dx.doi.org/10.1109/25.923065 - 3. Dudley, S.E.M., Quinlan, T.J. and Walker, S.D. (2007) 1.6 Gb/s Data Throughput Optically-Remoted Leaky Feeders for Underground Transport Environments. 2007 65th Vehicular Technology Conference, Dublin, 22-25 April 2007, 520-524.
http://dx.doi.org/10.1109/VETECS.2007.118 - 4. Engelbrecht, J., Collmann, R., Birkel, U. and Weber, M. (2010) Methodical Leaky Feeder Design for Indoor Positioning Considering Multipath Environments. 2010 IEEE Radio and Wireless Symposium (RWS), New Orleans, 10-14 January 2010, 164-167.
http://dx.doi.org/10.1109/RWS.2010.5434146 - 5. Weber, M., Birkel, U., Collmann, R. and Engelbrecht, J. (2010) Comparison of Various Methods for Indoor RF Fingerprinting Using Leaky Feeder Cable. 7th Workshop on Positioning Navigation and Communication (WPNC), Dresden, 11-12 March 2010, 291-298.
http://dx.doi.org/10.1109/WPNC.2010.5653786 - 6. Akbar, A., Jaseemuddin, M., Fernando, X. and Farjow, W. (2015) Energy-Efficient Scheduled Directional Medium Access Control Protocol for Wireless Sensor Networks. 2015 IEEE International Conference on Communications (ICC), London, 8-12 June 2015, 6258-6264.
http://dx.doi.org/10.1109/ICC.2015.7249321 - 7. Hassan, N. and Fernando, X. (2015) Reduced Side Lobe MM-Wave Leaky Feeder Transceiver by Slot Space Optimization. IEEE Global Symposium On Millimeter Waves (GSMM), Montreal, 25-27 May 2015, 1-3.
http://dx.doi.org/10.1109/GSMM.2015.7175463 - 8. Mandal, S.K., Mahanti, G.K. and Ghatakti, R. (2012) Genetic Algorithm for Reducing the Side Lobe Level of Main Beam of Uniformly Excited Time Modulated Linear Array Antenna. International Journal of Soft Computing and Engineering (IJSCE), 1, 168-172.
- 9. Khodier, M.M. and Al-Aqeel, M. (2009) Linear and Circular Array Optimization: A Study Using Particle Swarm Intelligence. Progress in Electromagnetics Research B, 15, 347-373.
http://dx.doi.org/10.2528/PIERB09033101 - 10. Pappula, L. and Ghosh, D. (2014) Linear Antenna Array Synthesis Using Cat Swarm Optimization. AEU-International Journal of Electronics and Communications, 68, 540-549.
http://dx.doi.org/10.1016/j.aeue.2013.12.012 - 11. Zhang, X. and Jia, P. (2012) Unequally Spaced Arrays Synthesis Based on Modified Differential Evolution. 2012 2nd International Conference on Consumer Electronics, Communications and Networks (CECNet), Yichang, 21-23 April 2012, 2229-2233.
http://dx.doi.org/10.1109/CECNet.2012.6202147 - 12. Preetham Kumar, B. and Branner, G. (1997) Synthesis of Unequally Spaced Linear Arrays by Legendre Series Expansion. 1997 Digest Antennas and Propagation Society International Symposium, Montreal 13-18 July 1997, 2236-2239.
- 13. Farahneh, H. and Fernando, X. (2014) Modeling the Leaky Feeder as a Multi-Antenna Array. 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, 4-7 May 2014, 1-5.
http://dx.doi.org/10.1109/CCECE.2014.6901150 - 14. Torrance, J., Keller, T. and Hanzo, L. (1996) Multi-Level Modulation in the Indoors Leaky Feeder Environment. IEEE 46th Vehicular Technology Conference, 1996. Mobile Technology for the Human Race, Atlanta, 28 Apr-1 May 1996, 1554-1558.
http://dx.doi.org/10.1109/vetec.1996.504019 - 15. Liao, S., Wang, J., Chen, Y., Tang, W., Wei, J., Xu, J. and Zhao, Z. (2012) Synthesis, Simulation and Experiment of Unequally Spaced Resonant Slotted-Waveguide Antenna Arrays Based on the Infinite Wavelength Propagation Property of Composite Right/Left-Handed Waveguide. IEEE Transactions on Antennas and Propagation, 60, 3182-3194.
http://dx.doi.org/10.1109/TAP.2012.2196922 - 16. Devasirvathan, D. (1991) Multi-Frequency Propagation Measurements and Models in a Large Metropolitan Commercial Building for Personal Communications. IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, 23-25 September 1991, 98-103.
http://dx.doi.org/10.1109/PIMRC.1991.571472 - 17. Smith, R.C. and Lange, R.C. (2001) Signal to Noise Ratio. Critical Reviews in Computed Tomography, 42, 135-140.
http://dx.doi.org/10.3109/20014091086711 - 18. Verdu, S. and Han, T.S. (1994) A General Formula for Channel Capacity. IEEE Transactions on Information Theory, 40, 1147-1157.
- 19. Wolcott, T.J. and Osborne, W.P. (1995) A Comparison of Modulation Schemes in Bandlimited AWGN Channels. Conference Record IEEE Military Communications Conference, MILCOM’95, San Diego, 7 November 1995, 538-542.
- 20. Das, S., Bhattacherjee, S., Mandal, D. and Bhattacharjee, A.K. (2010) Optimal Sidelobe Reduction of Symmetric Linear Antenna Array Using Genetic Algorithm. 2010 Annual IEEE India Conference (INDICON), Kolkata, 17-19 December 2010, 1-4.
http://dx.doi.org/10.1109/indcon.2010.5712742 - 21. Nongpiur, R.C. and Shpak, D.J. (2014) Synthesis of Linear and Planar Arrays with Minimum Element Selection. IEEE Transactions on Signal Processing, 62, 5398-5410.
http://dx.doi.org/10.1109/TSP.2014.2350966












