ABSTRACT

Diagnoses of heart diseases can be done effectively on long term recordings of ECG signals that preserve the signals’ morphologies. In these cases, the volume of the ECG data produced by the monitoring systems grows significantly. To make the mobile healthcare possible, the need for efficient ECG signal compression algorithms to store and/or transmit the signal efficiently has been rising exponentially. Currently, ECG signal is acquired at Nyquist rate or higher, thus introducing redundancies between adjacent heartbeats due to its quasi-periodic structure. Existing compression methods remove these redundancies by achieving compression and facilitate transmission of the patient’s imperative information. Based on the fact that these signals can be approximated by a linear combination of a few coefficients taken from different basis, an alternative new compression scheme based on Compressive Sensing (CS) has been proposed. CS provides a new approach concerned with signal compression and recovery by exploiting the fact that ECG signal can be reconstructed by acquiring a relatively small number of samples in the “sparse” domains through well-developed optimization procedures. In this paper, a single-lead ECG compression method has been proposed based on improving the signal sparisty through the extraction of the signal significant features. The proposed method starts with a preprocessing stage that detects the peaks and periods of the Q, R and S waves of each beat. Then, the QRS-complex for each signal beat is estimated. The estimated QRS -complexes are subtracted from the original ECG signal and the resulting error signal is compressed using the CS technique. Throughout this process, DWT sparsifying dictionaries have been adopted. The performance of the proposed algorithm, in terms of the reconstructed signal quality and compression ratio, is evaluated by adopting DWT spatial domain basis applied to ECG records extracted from the MIT-BIH Arrhythmia Database. The results indicate that average compression ratio of 11:1 with PRD₁ = 1.2% are obtained. Moreover, the quality of the retrieved signal is guaranteed and the compression ratio achieved is an improvement over those obtained by previously reported algorithms. Simulation results suggest that CS should be considered as an acceptable methodology for ECG compression.

Keywords:

Compressed Sensing, ECG Signal Compression, Sparsity, Coherence, Spatial Domain

1. Introduction

Heart disease is the leading cause of mortality in the world. The ageing population makes heart diseases and other cardiovascular diseases (CVD) an increasing heavy burden on the healthcare systems of developing countries. The electrocardiogram is widely used for the diagnoses of these diseases because it is a noninvasive way to establish clinical diagnosis of heart diseases. It reveals a lot of important clinical information about the heart, and it is considered as the gold standard for the diagnosis of cardiac arrhythmias. Long-term records have become commonly used to detect information from the heart signals; thus the volume of the ECG data produced by monitoring systems can be quite large over a long period of time. In these cases, the quantity of data grows significantly and compression is required for reducing the storage space and transmission times. Thus, ECG data compression is often needed for efficient storage and transmission for telemedicine applications. Recently, to make the mobile healthcare possible, the need for an efficient ECG signal compression algorithms has been raising exponentially [1] [2] .

In technical literature, many compression algorithms have shown some success in ECG compression; however, algorithms that produce better compression ratios and less loss of data in the reconstructed data are needed. These algorithms can be classified into two major groups: the lossless and the lossy algorithms. The traditional approach of compressing and reconstructing signals or images from measured data follows the well-known Shan- non sampling theorem, which states that the sampling rate must be twice the highest frequency. Similarly, the fundamental theorem of linear algebra suggests that the number of collected samples (measurements) of a discrete finite-dimensional signal should be at least as large as its length (its dimension) in order to ensure reconstruction. In recent years, CS theory [3] has generated significant interest in the signal processing community because of its potential to enable signal reconstruction from significantly fewer data samples than suggested by conventional sampling theory. The novel theory of compressive sensing-also known compressed sensing, compressive sampling or sparse recovery-provides a fundamentally new approach to data acquisition and compression simultaneously [4] . Compared to conventional ECG compression algorithms, CS has some important advantages: 1) It transfers the computational burden from the encoder to the decoder, and thus offers simpler hardware implementations for the encoder; 2) the location of the largest coefficients in the wavelet domain does not need to be encoded.

Compressed sensing is a pioneering paradigm that enables to reconstruct sparse or compressible signals from a small number of linear projections. CS research currently advances in three major fronts: 1) the design of CS measurement matrices, 2) the development of new and efficient reconstruction techniques, and finally 3) the application of CS theory to novel problems and hardware implementations. The first two topics have already achieved a certain level of maturity, and many advanced methods have been developed. Currently, very high efficiency CS measurement systems have been developed with different characteristics (deterministic/non-de- terministic, adaptive/non-adaptive) that can be adopted in a variety of signal acquisition applications. On the other hand, reconstruction methods span a wide range of techniques that include Matching Pursuit/Greedy, Basis Pursuit/Linear Programming, Bayesian, Iterative Thresholding, among others [5] . Which method is selected de- pends on the application of interest performance and speed needs.

The application of CS in ECG compression is still at its early stages, it has already led to important results [6] . For example, in [7] the ability of CS to continually and blindly compress ECG signals at compression factors of 10× has been demonstrated. In [8] several design considerations for CS-based ECG telemonitoring, including the encoder architecture and the design of the measurement matrix has been studied by Dixon et al. Their results show high compression ratios using a 1-bit Bernoulli measurement matrix. In [9] [10] new contributions to the area include CS-based algorithms for ECG compression with focus on algorithms enabling joint reconstruction of ECG cycles by exploiting correlation between adjacent heartbeats. In addition, a CS-based method to reconstruct ECG signals in the presence of EMG noise using symmetric α-stable distributions to model the EMG interference [11] was proposed as an extension to the work presented in [9] [10] . A hidden problem when trying to reconstruct ECG signals using CS-based methods is the inability to accurately recover the low-magnitude coefficients of the wavelet representation [12] . To alleviate this problem, the prior information about the magnitude decay of the wavelet coefficients across subbands in the reconstruction algorithm was incorporated [13] . More precisely, a weighted l₁-minimization algorithm with a weighting scheme based on the standard deviation of the wavelet coefficients at different scales was derived. In addition, the weighting scheme also takes into consideration the fact that the approximation subband coefficients accumulate most of the signal energy.

In this paper, a single-lead compression method has been proposed. It is based on improving the signal sparisty through the extraction of the significant ECG signal features. The proposed method starts with a preprocessing stage that detects the peaks and periods of the Q, R and S waves of each beat. Then, the QRS-complex for each signal beat is estimated. The estimated QRS -complexes are subtracted from the original ECG signal and the resulting error signal is compressed using CS technique. Throughout this process DWT sparsifying dictionaries have been adopted. The performance of the proposed algorithm in terms of the amount of compression and the reconstructed signal quality is evaluated using records extracted from the MIT-BIH Arrhythmia Database. Simulation results validate the superior performance of the proposed algorithm compared to other published algorithms. The rest of the paper is organized as follows. Section 2 introduces the compressed sensing Framework. Section 3 details the compressed sensing of ECG signal. Controlling the ECG signal sparisty using DWT basis is explained in Section 4. The solutions of CS problem including greedy algorithms, l₁-minimization, and TV minimization are presented in Section 5. Section 6 introduces the methodology used for improving the ECG signal sparisty using QRS-complex estimation. Section 7 details the metrics adopted for measuring the performance of the proposed CS ECG signal compression algorithm. Sections 8 and 9 present the simulation results and the main conclusions respectively.

2. Compressed Sensing Problem

In a traditional ECG acquisition system, all samples of the original signal are acquired. Thus the number of signal samples can be in the order of millions. The acquisition process is followed by compression, which takes advantage of the redundancy (or the structure) in the signal to represent it in a domain where most of the signal coefficients can be discarded with little or no loss in quality. Hence, traditional acquisition systems first acquire a huge amount of data, a significant portion of which is immediately discarded. This creates important inefficiency in many practical applications. Compressive sensing addresses this inefficiency by effectively combining the acquisition and compression processes. Traditional decoding is replaced by recovery algorithms that exploit the underlying structure of the data [3] [4] [14] .

CS has become a very active research area in recent years due to its interesting theoretical nature and its practical utility in a wide range of applications; especially in wireless telemonitoring of ECG signals. Compared to traditional data compression technologies, it consumes much less energy thereby extending sensor lifetime, making it attractive to wireless body-area networks. In the following we provide a brief overview of the basic principles of CS, since they will form the basis of the proposed ECG compression algorithms. The basic CS framework is an underdetermined inverse problem, which can be expressed as

(1)

where, in the context of data compression, 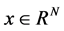is the vector representing the ECG signal, 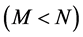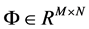is a user designed sensing matrix or measurement matrix, is sensor noise, and is the compressed signal. The matrix here plays as a sensor that acquire information from the input signal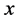. The compressed signal, 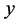, is sent to the receiver side where the original signal is recovered by a CS algorithm using yand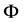. To successfully recover the ECG signal, is required to be sparse. When 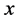is not sparse, one generally seeks a sparsifying matrix or sparsifying dictionary such that can be sparsely represented with the dictionary matrix, i.e., , where the representation coefficients z are sparse. Generally, is constructed using some bases. In this paper, DWT basis is considered. Then a CS algorithm can first recover using the available and the matrix. Then can be recoverd according to. The basic CS framework has been widely used for ECG signals [6] [15] . Thus, equation (1) can be rewritten in terms of the sparse signal coefficients as

(2)

In fact, the measurement process is not adaptive, meaning that is fixed and does not depend on the signal. The problem consists of designing a) a stable measurement matrix such that the salient information in any K-sparse or compressible signal is not damaged by the dimensionality reduction from to and b) a reconstruction algorithm to recover from only measurements (or about as many measurements as the number of coefficients recorded by a traditional transform coder). The key properties of the acquisition system in (2) are:

a) Instead of point evaluations of the signal, the system takes M inner products of the signal with the basis vector;

b) The number of measurements is considerably smaller than the number of signal coefficients.

If, can be recovered from in a straightforward manner by inverting. However, a reconstruction process is needed when . In this case, the system is underdetermined, and there are an infinite number of feasible solutions for. However, if the signal to be recovered is known to be sparse, then the sparsest solution (most 0’s) out of the infinitely possible is often the correct solution. The central result of the CS is that when the signal has a sparse representation, and the measurements are incoherent, the signal can be reconstructed from with a very high accuracy even when (in the order of). The measurement matrix can be chosen as noise-like, random matrix, which generally exhibits low-cohe- rence with any representation basis. The savings in the number of measurements in practice are generally around

to in typical acquisition systems, but much higher savings are achieved when the signals of interest have

a highly sparse representation [3] [4] .

After the acquisition process, an estimate of the signal is obtained by a reconstruction algorithm. A common and practical approach used to determine the sparse solution is to solve this problem as a convex optimization problem. The original work on CS employed regularization based on -norms and linear programming, such that the signal is reconstructed using the following optimization problem [3] [4] :

(3)

where denotes the -norm of a vector reinforcing a sparse solution, is the basis matrix and zis the coefficient vector. From (3), the recovered signal is then where is the optimal solution.

The -norm cost function serves as a proxy for sparseness as it heavily penalizes small coefficients so the optimization drives them to zero. The problem of minimizing the -norm in (3) has been shown to be solved efficiently and requires only a small set of measurements to enable perfect recovery [16] . The implication of these results is that an N-dimensional signal can be recovered from a lower order number of samples, M, provided that the signal is sparse in some basis. We rely on this result from CS theory to reduce the data that the sensor must transmit. Many other reconstruction algorithms have been proposed in the literature [17] - [19] .

3. Measurement Matrices

The measurement matrix must allow the reconstruction of the length-N signal x from measurements (the vector y). Since, this problem appears ill-conditioned. If, however, x is K-sparse and the K locations of the nonzero coefficients in z are known, then the problem can be solved provided. A necessary and sufficient condition for this simplified problem to be well conditioned is that, for any vector v sharing the same K nonzero entries as z and for some

(4)

That is, the matrix must preserve the lengths of these particular K-sparse vectors. Of course, in general the locations of the K nonzero entries in z are not known. However, a sufficient condition for a stable solution for both K-sparse and compressible signals is that satisfies (4) for an arbitrary 3K-sparse vector. This condition is referred to as the Restricted Isometry Property (RIP). The RIP characterizes matrices when operating on sparse vectors. The concept was introduced in [4] and is used to prove many theorems in the field of compressed sensing. There are no known large matrices with bounded restricted isometry constants, but many random matrices have been shown to remain bounded. In particular, it has been shown that with exponentially high probability, random Gaussian, Bernoulli, and partial Fourier matrices satisfy the RIP with number of measurements nearly linear in the sparsity level. Notice that the sensing matrix does not depend on the signal. To guarantee robust and efficient recovery of the K-sparse signal, the sensing matrix must obey the key restricted isometry property given by Equation (4).

A related condition, referred to as incoherence, requires that the rows of cannot sparsely represent the columns of (and vice versa). The concept of coherence was introduced in a slightly less general framework by Donoho [3] , and has since been used extensively in the field of sparse representations of signals. In particular, it is used as a measure of the ability of suboptimal algorithms such as matching pursuit and basis pursuit to correctly identify the true representation of a sparse signal. Current assumptions in the field of compressed sensing and sparse signal recovery impose that the measurement matrix has uncorrelated columns. To be formal, the coherence or the mutual coherence of a matrix is defined as the maximum absolute value of the cross-correla- tions between the columns of. Formally, let be the columns of the matrix, which are assumed to be normalized such that. The mutual coherence of is then defined as

(5)

with a lower bound given by

(6)

We say that a dictionary is incoherent if is small. Standard results then require that the measurement matrix satisfy a strict incoherence property, as even the RIP imposes this. If the dictionary D is highly coherent, then the matrix AD will also be coherent in general.

Direct construction of a measurement matrix such that has the RIP requires verifying (4) for

each of the possible combinations of nonzero entries in the vector v of length. However, both the

RIP and incoherence can be achieved with high probability simply by selecting as a random matrix. For instance, let the matrix elements be independent and identically distributed (iid) random variables from a Gaussian probability density function with mean zero and variance [3] [4] . Then the measurements y are merely M different randomly weighted linear combinations of the elements of, as illustrated in Figure 1. The Gaussian measurement matrix has two interesting and useful properties:

Ÿ The matrix is incoherent with the basis of delta spikes with high probability. More specifically, an iid Gaussian matrix can be shown to have the RIP with high probability if, with c a small constant [3] [4] . Therefore, sparse and compressible signals of length can be recovered from only random Gaussian measurements.

Ÿ The matrix is universal in the sense that will be iid Gaussian and thus has the RIP with high probability regardless of the choice of the orthonormal basis.

4. Signal Recovery from Incomplete Measurements

CS theory also proposes that rather than acquire the entire signal and then compress, it should be possible to capture only the useful information to begin with. The challenge then is how to recover the signal from what

would traditionally seem to be an incomplete set of measurements. The ECG signal has to be recovered from the measurement vector, with being defined as in Equation (2). This poses a classical linear algebra problem. When does a unique solution exist to the set of linear equations? Generally, a solution might exist for , i.e., for a determined or over-determined system. Our case is one of a heavily under- determined system of equations and there are infinite solutions as a consequence. However, with additional known structure present in ECG signal, recovery can be attempted. In this case, with knowledge of signal sparsity, a good approximation can be found, provided there are enough measurements. Again, the sparseness of the signal is relied upon to make this possible. So far, we have seen that if the signal of interest is sparse, then it is possible to recover it from a number of measurements. In this case, the system is underdetermined and there are an infinite number of feasible solutions for. However, if the signal to be recovered is known to be sparse, then the sparsest solution (most 0’s) out of the infinitely possible is often the correct solution. A common and practical approach used to determine the sparse solution is to solve the convex optimization problem:

The question is now how we can actually recover (or an estimate of it) from, the problem being ill- posed. A common method, which is used for over determined systems of linear equations, is the Least Square (LS) approach, which is based on minimizing the residual energy. To enforce the a priori knowledge about signal sparsity in the recovery algorithm, one should search for a solution with minimum -norm. Since the - norm counts the number of non-zero elements in a vector, minimizing it is equivalent to looking for the sparsest optimal solution which is in agreement with the measurements. Unfortunately, this problem not only does not have a closed form solution, but it is also NP-hard to solve (combinatorial complexity). However, if we replace -norm with -norm, then the problem is convex and can be solved using standard convex optimization routines [20] . For this purpose, in this paper the solution to Equation (3) is found using -magic software developed in [21] .

It has been proven that computing the sparsest solution directly generally requires prohibitive computations of exponential complexity [22] , so several heuristic methods have been developed in literature, such as Matching Pursuit (MP) [23] , Basis Pursuit (BP) [24] , log barrier method [20] , iterative thresholding method [25] , and so forth. Most of these methods or algorithms fall into three distinct categories: greedy algorithms, -minimiza- tion, and TV minimization.

4.1. Greedy Algorithms

Generally speaking, a greedy algorithm refers to any algorithm following the metaheuristic of choosing the best immediate or local optimum at each stage and expecting to find the global optimum at the end. It can find the global optimum for some optimization problems, but not for all [20] . This algorithm decomposes any signal into a linear combination of waveforms in a redundant dictionary of functions so that selected waveforms optimally match the structure of the signal. MP is easy to implement and has an exponential rate of convergence and good approximation properties. However, there is no theoretical guarantee that MP can achieve sparse representations. In [26] , the authors proposed a variant of MP, Orthogonal Matching Pursuit (OMP), which guarantees the nearly sparse solution under some conditions. A primary drawback of MP and its variants is the incapability of attaining truly sparse representations. The failure is usually caused by an inappropriate initial guess. This shortcoming also motivated the development of algorithms based on -minimization.

4.2. l₁-Minimization Algorithms

In [3] some early results related to -minimization for signal recovery have been introduced. The question why -minimization could work in some special setups was further investigated and answered in [20] [21] . Specifically, a signal which is K-sparse under some basis can be exactly recovered from c K linear measurements by - minimization under some conditions, where c is a constant. The new CS theory has significantly improved those earlier results. How big the constant c is here directly decides the size of linear measurements, important information needed to encode or decode a signal. The introduction of the concept RIP for matrices [4] [5] showed that if the measurements satisfy the RIP of a certain degree, it is sufficient to recover the sparse signal exactly from its decoded signal. However, it is extremely difficult to verify the RIP property in practice. Fortunately, Cand’es et al. in [15] showed that RIP holds with high probability when the measurements are random. Usually -minimization algorithms require fewer measurements than greedy algorithms. Basis Pursuit algorithm which seeks the solution that minimizes the -norm of the coefficients, is a prototype of -minimization. BP can simply be comprehended as linear programming solved by some standard methods. Furthermore, BP can compute sparse solutions in situations where greedy algorithms fail. All this work enriches the significance of studying and applying -minimization and compressive sensing in practice.

The solution to the above problem can be found with relative ease. There are methods that will find the solution to the BP problem but does it lead to a sparse solution? The answer in general is no but under the right conditions it can be guaranteed that BP will find a sparse solution or even the sparsest solution. This is because - norm is only concerned with the value of entries not the quantity. A vector with a small could have very small valued non zero entries in every position which would give it a large -norm. There are numerous algorithms to solve the problems involving the. One of these algorithms that has been used to solve this convex optimization problem is implemented in the Matlab software package CVX, a package for solving convex problems [27] . Simplex and interior-point methods offer an interesting insight into these optimization problems and will be introduced in the following. The standard simplex method starts by forming a new matrix consisting of linearly independent columns of A. Since all the columns of are independent b can be uniquely represented (or approximated) with respect to. Then an iteration process takes place, where at each iteration a column vector of is swapped with a column vector of A. Each swap improves the desired property of the solution. In this case a reduction of the value of the -norm. The interior method starts with a solution where. Then goes through an iteration process changing the entries in to form a new solution while maintaining the condition. A transformation is then applied to which effectively sparsifies. Eventually a vector is reached that meets the preset stopping conditions and by forcing all extreme small entries to zero, the final solution is obtained.

4.3. TV Minimization Algorithms

In the broad area of compressive sensing, -minimization has attracted intensive research activities since the discovery of equivalence [3] - [5] . However, for image restoration, recent research has confirmed that the use of Total Variation (TV) regularization instead of the term in CS problems makes the recovered image quality sharper by preserving the edges or boundaries more accurately, which is essential to characterize images. The advantages of TV minimization stem from the property that it can recover not only sparse signals or images, but also dense staircase signals or piecewise constant images. In other words, TV regularization would succeed when the gradient of the underlying signal or image is sparse. Even though this result has only been theoretically proven under some special circumstances [4] , it stands true on a much larger scale empirically. A detailed discussion on TV models has been reported by Chambolle et al. [28] . However, the properties of non-differentia- bility and non-linearity of TV functions make them far less accessible computationally than solving -mini- mization models. In 2004, Chambolle [29] proposed an iterative algorithm for TV denoising and proved the linear convergence. Furthermore, Chambolle’s algorithm can be extended to solve image reconstruction problems with TV regularization while the measurement matrix is orthogonal. Due to the powerful application of TV regularization in the edge-detection and many other fields, researchers kept trying for several years to explore algorithms for solving TV minimization problems. However, these algorithms are still either much slower or less robust compared with algorithms designed for -minimization.

5. Sparse Representation of ECG Signal

The time-domain representation of the ECG signal has low signal sparisty. Thus, ECG signal is not the true signal itself but its representation under a certain basis is sparse or compressible. Various researchers have reported ECG signals to be sparse in other bases [6] , [15] . A variety of compression algorithms represent ECG signals in suitable or thogonal basis and exploit signal redundancy in the transformed domain. Indeed, success of a compression algorithm depends on how compactly the signal is represented upon transformation. In this context, many transforming methods for representing signals in sparsity bases are proposed recently, for instance, FFT, DWT and DCT, etc. Generally, the biophysical signals are continuous and regular in nature. Hence, it can be represented by aforementioned transforms. To testify this, we exploit the DWT to guarantee the signal sparsity. Every transformation basis is able to provide a way of recovering the signal and should provide a way for re- trieving diagnostic information from the signal to form patient’s report of the medical case study. All the data we used are from MIT-BIH online distribution, a standard ECG database for arrhythmia diagnosis and research. This section introduces the wavelet transformation technique used for controlling the ECG signal sparisty.

The wavelet transform describes a multi-resolution decomposition process in terms of expansion of a signal onto a set of wavelet basis functions. Wavelet transforms have become an attractive and efficient tool in many applications especially in coding and compression of signals because of multi-resolution and high-energy compaction properties. Wavelets allow both time and frequency analysis of signals simultaneously because of the fact that energy of wavelet is concentrated in time and still possesses the wave like characteristics. As a result wavelet representation provides a versatile mathematical tool to analyze ECG signals.

Discrete Wavelet Transformation (DWT) has its own excellent space frequency localization property. The key issues in DWT and inverse DWT are signal decomposition and reconstruction, respectively. The basic idea behind decomposition and reconstruction is low-pass and high-pass filtering with the use of down sampling and up sampling respectively. The result of wavelet decomposition is hierarchically organized decompositions. One can choose the level of decomposition based on a desired cutoff frequency. Figure 2(a) shows an implementation of a three-level forward DWT based on a two-channel recursive filter bank, where and are low-pass and high-pass analysis filters, respectively, and the block $2 represents the down sampling operator by a factor of 2. The input signal is recursively decomposed into a total of four subband signals: a coarse signal, and three detail signals, , , and, of three resolutions. Figure 2(b) shows an implementation of a three-level inverse DWT based on a two-channel recursive filter bank, where and are low-pass and high-pass synthesis filters, respectively, and the block #2 represents the up sampling operator by a factor of 2. The four subband signals, , and, are recur- sively combined to reconstruct the output signal. The four finite impulse response filters satisfy the fol- lowing relationships:

(7)

(8)

(9)

so that the output of the inverse DWT is identical to the input of the forward DWT. In this environment, ECG signal representation using a wide variety of wavelets, drawn from various families including symlets and Daubechies’ bases has been adopted. In this context, the transform coefficients are arranged in decreasing order of magnitude, and count the number of coefficients accounting for 99% of the signal energy (as parser representation requires less number). “Symlet” and “Daubechies” families generally offer more compact representation com- pared to Meyer wavelet as well as biorthogonal and reverse biorthogonal families. In particular, the sparsest re-

presentation is provided by the “sym4” (closely followed by the “db4”) wavelet basis for abroad class of ECG signals [30] - [32] .

6. Improving ECG Signal Sparisty Using QRS-Complex Estimation

The correlation between the consecutive ECG beats can be exploited to improve the ECG signal sparisty. For this purpose, in this paper, the QRS-complex has been estimated based on the peaks and locations of Q, R and S waves. Then the estimated QRS-complex is subtracted from the original ECG signal and the resulting differential signal is manipulated using CS technique. The proposed compression scheme is presented in Figure 3. The details of the purposed compression algorithm are illustrated in subsequent steps as follows.

1) The signal is decomposed into windows; each of length 1024 samples. This short window length is considered in order to generate an approximate real time transmission. At the same time, many heartbeats in the window are incorporated to recover the signal with fewer samples.

2) The signal is preprocessed to determine the amplitudes and locations of the Q, R and S peaks. These parameters are used to estimate the QRS-complexes.

3) From the estimated QRS-complexes and the locations of the R-peaks locations, the error signal with more sparisity compared to the original ECG signal is determined as the difference between the original ECG signal and the estimated QRS-complexes.

4) Fewer measurements are determined from the resulting error signal and the sensing matrix.

5) The amplitudes and locations of the Q, R and S peaks and the measurement matrix are quantized.

6) The resulting quantized values are packetized for possible storage and/or transmission.

6.1. Preprocessing

In this section, the signal sparisty is controlled through the extraction of the significant ECG signal features. These features are extracted by estimating the QRS-complex for each signal beat. Then, the estimated QRS -complex is subtracted from the original ECG signal. After that, the resulting error signal is transformed into DWT domain and the resulting transformed coefficients are compressed using CS technique. A typical scalar ECG heartbeat is shown in Figure 4. The significant features of the ECG waveform are the P, Q, R, S and T waves and the duration of each wave. A typical ECG tracing of electrocardiogram baseline voltage is known as the isoelectric line. It is measured as the portion of the tracing following the T wave and preceding the next P wave. In addition to the QRS -complex, the ECG waveform contains P and T waves, 50-Hz noise from power line interference, EMG signal from muscles, motion artifact from the electrode and skin interface, and possibly other interference from

electro surgery equipment. The power spectrum of the ECG signal can provide useful information about the QRS -complex estimation. Figure 5 summarizes the relative power spectra, based on the FFT, of the ECG , QRS - complex, P and T waves, motion artifact, and muscle noise taken for a set of 512 sample points that contain approximately two heartbeats [33] . It is visible that QRS -complex power spectrum involves the major part of the ECG heartbeat. Normal QRS -complex is 0.06 to 0.1 sec in duration and not every QRS -complex contains a Q wave, R wave, and S wave. By convention, any combination of these waves can be referred to as a QRS-com- plex. This portion can be represented by Q, R and S values, the Q-R and R-S durations and the event time of R as shown in Figure 4. These values can be extracted from the original signal.

6.2. The QRS-Complex Detection and Estimation

The aim of the QRS -complex estimation is to produce typical QRS -complex waveform using parameters extracted from the original ECG signal [34] . The estimation algorithm is a Matlab based estimator and is able to produce normal QRS waveform. A single heartbeat of ECG signal is a mixture of triangular and sinusoidal wave- forms. The QRS -complex waveform can be represented by shifted and scaled versions of these waveforms. Figure 6 illustrates a sinc function that looks like the QRS-complex. However, in QRS-complex the QR-dura- tion is not equal to the RS-duration. So, the QRS estimation is divided into two parts: QR part and RS part. The QR part can be generated using a sinc function described by

(10)

where, is the QR duration and is a scaling factor determined as the difference between the R-peak and the Q-peak. Similarly, the RS part is generated using a sinc function described by

(11)

where, is the RS duration and is a scaling factor determined as the difference between the R-peak and the S-peak. The two parts are combined beside each other to form the estimated QRS signal. Finally, using the R occurrence time the estimated signal is time shifted to fit the occurrence time of the original signal.

To illustrate the QRS-complex estimation process, consider 1200 samples ECG signal extracted from record 103 of MIT-BIH arrhythmia database [35] . Investigation of this signal shows that its mean is 0.6973 and its maximum value is 1394. Figure 7(a) illustrates the signal after normalization and mean removal. This signal has 4 periods and the Q, R, and S values together with QR, and RS periods as given in Table 1. The first R-peak is located at 266 and durations between the four successive peaks are 311, 301 and 304 respectively. From these data and Equations (10) and (11) the QRS-complexes can be estimated. Figure 7(b) and Figure 7(c) illustrate the estimated ECG signal and the difference between the original signal and the estimated one respectively. Comparison between Figure 7(a) and Figure 7(c) show that the difference between the original and estimated ECG signals is much sparser compared to the original signal.

7. Performance Metrics & Quality Measurement

A practical compression algorithm should not focus totally on compression itself. Many applications have requirements for the quality of the de-compressed signal. A robust compression algorithm should have the ability to maintain the quality of the de-compressed signal while achieving reasonable compression ratio. This is because only good quality signal reconstruction makes sense in reality. The evaluation of performance for testing ECG compression algorithms includes three components: compression efficiency, reconstruction error and com- putational complexity. All data compression algorithms minimizes data storage by reducing the redundancy wherever possible, thereby increasing the Compression Ratio (CR). Thus, the compression efficiency is measured by the CR. The compression ratio and the reconstruction error are usually dependent on each other. The computational complexity component is part of the practical implementation consideration. The following evaluation metrics were employed to determine the performance measures of the proposed method [1] [2] . The CR is defined as the ratio of the number of bits representing the original signal to the number of bits required to store the compressed signal.

(12)

where and represent the numbers of bits required for the original and compressed signals, respectively. A high compression ratio is typically desired. A data compression algorithm must also represent the data with acceptable fidelity while achieving high CR.

Quality of lossy compression schemes is usually determined by comparing the de-compressed data and the original data. If there are no differences at all, then the compression is lossless. Conventional measurements are based on mathematical distortions, such as percentage root mean square difference (PRD) and signal-to-noise ratio (SNR), etc. These measurements are not specific for ECG signals; they reflect the distortion of signal by statistics criteria. They are of general purpose, so the criteria may not be very accurate to describe the characteristics of a specific signal type.

For example, the ECG signal is for medical use, so what concerns medical specification most is the diagnostic feature, which is not covered in the general mathematical descriptions. Thus, in [37] the Weighted Diagnostic Distortion (WDD) is proposed. It uses diagnostic features as criteria and has better feedback from the perspective of medical specialists than other measurements. However, WDD may not bring the benefit and it is far more complex. Table 2 shows a comparison between different quality measures. Among those, PRD is the most widely used measure in ECG data compression. PRD, SNR and STD are mathematically related. PRD is derived from RMSE, which measures the power of errors between the original data and the reconstructed data and is used frequently for prediction. The advantage of the PRD over RMS is its scale-independence. That makes PRD more accurate across different data sets. The PRD indicates the error between the original ECG samples and the reconstructed data. This metric is commonly used for measuring the distortions in reconstructed biomedical sig- nals such as ECG signals and EEG signals. There are subtle differences in calculation; PRD has 3 types for ECG data compression, which are numbered 0, 1, and 2. The definitions are described by Equations (13), (14) and (15) for signal x of length N samples.

(13)

(14)

(15)

where, is the sampled values of the original signal, is the sampled values of the reconstructed/predicted signal and is the mean value of. Compare to, is optimized by subtracting the offset, which is usually added from database for data storage. For the MIT-BIH database the offset is 1024. is further optimized by subtracting the mean value (approximately the DC component). The result is thus more accurate removing a lot of effects from DC offset. It should be noticed that is more popular in literature because of its simplicity but is preferred because it is more accurate. Table 3 shows the connection between the quality indication and the PRD values [37] .

The CR and PRD have the close relationship in the lossy compression algorithms. In general, the CR goes higher with the higher lossy level, while the error rate goes up. The final goal of the proposed compression algorithm is to keep the PRD value smaller than that of the conventional methods while maintaining the similar CR. Thus, quality score defined as the ratio between CR and PRD (QS = CR/PRD) is sometimes used to quantify the overall performance of the compression algorithm, considering both the CR and the error rate. A high score represents a good compression performance. Another distortion metric is the root mean square error (RMSE). In data compression, we are interested in finding an optimal approximation for minimizing this metric as defined by the following formula:

(16)

Since the similarity between the reconstructed and original signal is crucial from the clinical point of view, the cross correlation (CC) is used to evaluate the similarity between the original signal and its reconstruction.

(17)

where and are the mean values of the original and reconstructed signals, respectively. In or-

der to understand the local distortions between the original and the reconstructed signals, two metrics, the maximum error (MAXERR) and the peak amplitude related error (PARE), should be computed. The maximum error metric is defined as

(18)

and it shows how large the error is between every sample of the original and reconstructed signals. This metric should ideally be small if both signals are similar. The PARE is defined as

(19)

By plotting PARE, one will be able to understand the locations and magnitudes of the errors between the original and reconstructed signals.

8. Experimental Results

Compressive sensing directly acquires a compressed signal representation without going through the intermediate stage of acquiring N samples, where N is the signal length. Since CS-based techniques are still in early

stages of research and development, specially the development of Analog to Information Conversion (AIC) hardware, signals that are used for experimentation are acquired in the traditional way. The CS measurements of these data are computed from the original ECG signal. Tests were conducted using 10-min long single-lead ECG signal extracted from records 100, 107, 115 and 117 in the MIT-BIH Arrhythmia database. Record 115 is included in the data set to evaluate the performance of the algorithm in the case of irregular heartbeats. The data are sampled with 360 Hz and each sample is represented with 11-bit resolution. The records are split into non- overlapping 1024 samples windows that are processed successively. Then the characteristic points of the ECG waveforms are detected using the procedure introduced in Section 6.2. It relies on the extraction of Q, R and S peaks and locations and the estimation of the QRS-complex. We begin by first detecting the R peaks, since they yield modulus maxima with highest amplitudes. This enables the segmentation of the original ECG record into individual beats. Then, multi scale wavelet decomposition is performed on the difference between the given ECG window, and the estimated QRS-complexes.

To evaluate the performance of the proposed method concerning the amount of data compression, the sparisity of the ECG signal in both the time-domain and the wavelet-domain are measured. As it has been mentioned before, the sparisity of an array x is defined as the number of non-zero entries in x. For this purpose two ECG signals, each of length 6 seconds, extracted from records 100 and 106 of the MIT-BIH database are considered. Figure 8 illustrates the time-domain representation of the two ECG signals, their estimated QRS-complexes and the differences between them. Figure 9 illustrates the threshold wavelet coefficients of the original ECG signal, and that of the differences between the original signal and the estimated QRS-complex for the two records. The bi-orthogonal wavelet filter “bior4.4” has been adopted in the wavelet transformation process where the decomposition has been carried out up to the 8^th level. Thresholding is performed such that 98% of the total coefficients’ energy is kept and small coefficients are thrown away.

Figure 10 illustrates the effect of varying the signal length on the sparisity of the time-domain representation of ECG signals and the signals differences of the records after thresholding each of them such that 98% of the total energy is kept and small samples are thrown away. From this Figure it can be concluded that increasing the signal length increases its sparisity. Moreover, the signals differences are sparser compared to the original signals. Figure 11 shows the effect of varying the signal length on the sparisity of the wavelet representation of the ECG signals and the signals differences of the two records after thresholding both of them. Comparing the results presented in Figure 10 and Figure 11 shows that the wavelet transformed signals are sparser compared to the signal in time-domain.

Figure 12 illustrates the effect of varying the number of decomposition levels on the sparisity of the wavelet- domain representation of the original ECG signals and the signal differences of two MIT-BIH records. It shows that for record 100, the original signal is sparser than the signal differences for decomposition levels below 7. Otherwise, the signal differences are sparser. However, for record 106, the original signal is sparser than the signal differences for decomposition levels below 5. Otherwise, the signal differences are sparser. This indicates that the sparisity of the signal differences depends on the number of decomposition levels.

Figure 13 illustrates the effect of selecting the wavelet filters on the sparisity of the wavelet-domain representation of the original ECG signals and the signal differences extracted from two MIT-BIH records. It shows that for both records, the signal differences are sparser compared to the original signal for all Daubechies’ filters (from db2 up to db10). Comparing the results presented in Figure 13(a) and Figure 13(b) shows that the sparisity of the wavelet transformed signals depends on the ECG record to be analyzed. This has been checked by considering other MIT-BIH records.

To explore the effect of controlling the signal sparisity using other wavelet families, sparse representation is checked using bi-orthogonal (bior4.4) DWT filters and compared with that using Daubechies (db6) filters. In both cases the transformation is performed with four detailed levels and one approximation level. Another important process is also considered to improve the signal sparasity; that is by thresholding the wavelet coefficients in different decomposition levels according to the energy content in each subband. In this case, the wavelet coefficients have been thresholded to preserve 98%, 96%, 94% and 90% of the coefficients energy in the 1^st, 2^nd, 3^rd, and 4^th details subbands respectively. Moreover, the coefficients in the approximation subband are kept without threshold. After that, the resulting wavelet coefficients are mapped into significant and insignificant coefficients by ones and zeros respectively.

Figure 14 illustrates wavelet coefficients before and after thresholding of the transformed difference between

the original ECG signal and the estimated QRS-complex together with the mapping of the significant and insignificant coefficients for the two wavelet filters. The ECG signal considered here is of length 1200 samples extracted from record 103.

Next, the performance of the proposed compression method has been compared with traditional wavelet based ECG compression techniques. Table 4 illustrates the comparison between the performances of the proposed method and two other methods for the compression of four MIT-BIH ECG records (100, 107, 115 and 117) [15] [36] . The proposed method is tested for the compression of the original signal and the signal differences using the CS technique and bior4.4 wavelet filters and eight decomposition levels. For all cases, the same signal length of 1024 samples is used. As illustrated in the table, the proposed method achieves better results in terms of the CR and PRD. Moreover, the results of the proposed indicate that the signal differences is compressed more than the original signal and smaller. Figure 15 shows the performance of the proposed CS compressor

in compressing 1024 samples of the signal differences. This figure indicates that the proposed method achieved low reconstruction error. This corresponds to high quality recovered ECG signal and even outperforms the two other techniques [15] [36] .

9. Conclusion

This paper investigates CS approach as a revolutionary acquisition and processing theory that enables reconstruction of ECG signals from a set of non-adaptive measurements sampled at a much lower rate than required by the Nyquist-Shannon theorem. This results in both shorter acquisition times and reduced amounts of ECG data. At the core of the CS theory is the notion of signals sparseness. The information contained in ECG signals is represented more concisely in DWT transform domain and its performances in compressing ECG signals are evaluated. By acquiring a relatively small number of samples in the “sparse” domain, the ECG signal can be reconstructed with high accuracy through well-developed optimization procedures. Simulation results validate the superior performance of the proposed algorithm compared to other published algorithms. The performance of the proposed algorithm, in terms of the reconstructed signal quality and compression ratio, is evaluated by adopting DWT spatial domain basis applied to ECG records extracted from the MIT-BIH Arrhythmia Database. The results indicate that average compression ratio of 11:1 with are obtained. Moreover, the advantage of the proposed method is that the quality of the retrieved signal is guaranteed and the compression ratio achieved is an improvement over those obtained by previously reported CS based algorithms. Simulation results suggest that CS should be considered as an acceptable methodology for ECG compression.

Cite this paper

Mohammed M. Abo-Zahhad,Aziza I. Hussein,Abdelfatah M. Mohamed, (2015) Compression of ECG Signal Based on Compressive Sensing and the Extraction of Significant Features. International Journal of Communications, Network and System Sciences,08,97-117. doi: 10.4236/ijcns.2015.85013

References