International Journal of Communications, Network and System Sciences
Vol.08 No.06(2015), Article ID:57347,11 pages
10.4236/ijcns.2015.86022
A Hybrid Method for Compression of Solar Radiation Data Using Neural Networks
Bharath Chandra Mummadisetty, Astha Puri, Ershad Sharifahmadian, Shahram Latifi
Department of Electrical & Computer Engineering, University of Nevada, Las Vegas, NV, USA
Email: mummadis@unlv.nevada.edu, puri@unlv.nevada.edu, esahmadian@netscape.net, shahram.latifi@unlv.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 December 2014; accepted 19 June 2015; published 24 June 2015
ABSTRACT
The prediction of solar radiation is important for several applications in renewable energy research. There are a number of geographical variables which affect solar radiation prediction, the identification of these variables for accurate solar radiation prediction is very important. This paper presents a hybrid method for the compression of solar radiation using predictive analysis. The prediction of minute wise solar radiation is performed by using different models of Artificial Neural Networks (ANN), namely Multi-layer perceptron neural network (MLPNN), Cascade feed forward back propagation (CFNN) and Elman back propagation (ELMNN). Root mean square error (RMSE) is used to evaluate the prediction accuracy of the three ANN models used. The information and knowledge gained from the present study could improve the accuracy of analysis concerning climate studies and help in congestion control.
Keywords:
Data Compression, Predictive Analysis, Artificial Neural Network, Compression Ratio, Machine Learning, Climate Data Prediction

1. Introduction
The earth radiation consists of the energy entering the surface, absorbed, emitted, and reflected by earth system. Solar radiation is the portion of the sun’s radiation which falls at the earth’s surface. There are many applications associated with it in different fields like transportation and reconnaissance, water heating, water treatment, photovoltaics, fuel production, artificial photosynthesis, etc. Solar energy is ecofriendly and available on the earth throughout the year. The information about potential for solar energy at a particular location on earth can be provided using solar radiation data during a specific period of time. This information is very important for designing the size of solar energy systems. Due to the high cost and installation difficulties of measurement, these data are not always available. Therefore, there is a demand to develop alternative ways of predicting these data [1] .
The solar radiation components are measured generally using pyranometer etc. with the data acquisition system. The prediction of solar radiation has generated a renewed interest in recent years, mostly due to its relevance in renewable energy research and applications. There are a large number of meteorological and geographical variables which affect solar radiation and various researchers have used different variables for solar radiation prediction [2] .
Incoming ultraviolet, visible, and a limited portion of infrared energy (together sometimes called “shortwave radiation”) from the sun drives the earth’s climate system. Some of this incoming radiation is reflected off clouds, some is absorbed by the atmosphere, and some passes through to the earth’s surface. Larger aerosol particles in the atmosphere interact with and absorb some of the radiation, causing the atmosphere to warm up. The heat generated by this absorption is emitted as longwave infrared radiation, some of which radiates out into space.
Heat resulting from the absorption of incoming shortwave radiation is emitted as long wave radiation. Radiation from the warmed upper atmosphere, along with a small amount from the earth’s surface, radiates out to space. Most of the emitted longwave radiation warms the lower atmosphere, which in turn warms our planet’s surface.
The rest of this paper is organized as follows. Section 2 looks into the related work. Section 3 describes the methods adopted. In Section 4, the new algorithm is introduced. Section 5 presents the experimental results and analysis. Section 6 is the conclusion.
2. Related Work
The ANN models use different geographical parameters of a location as inputs for the prediction of solar radiation as discussed in [3] . Al-Alawi and Al-Hinai [4] discussed multi-layer feed forward network, back propagation (BP) training algorithm for global radiation prediction in Seeb, Oman. The inputs used in network were location, month, mean pressure, mean temperature, mean vapor pressure, mean relative humidity, mean wind speed and mean sunshine hours. Sözen et al. [5] [6] used meteorological and geographical data as input variables in the ANN model for solar radiation estimation in Turkey. The transfer function for model is logistic sigmoid and learning algorithm is Scaled conjugate gradient, Pola-Ribiere conjugate gradient Levenberg-Mar- quardt.
In the study undertaken by AbdAlKader and AL-Allaf, 2008 BPNN models were developed to predict the day soil temperature for the present day by using various previous day meteorological variables in Nineveh-Iraq. The BPNN models (M4: BP, M5: Cascade BP, and M6: NARX) consisting of the combination of the input variables were constructed to obtain the best fit input structure. After ANN training, testing the model M4: BP gave a soil temperature prediction correctly by 75%. Whereas the model M5: Cascade BP gave predict correctly by 80%. While the model M6: NARX gave soil temperature prediction correctly by 95% [7] .
In the research work done by Tamer Khatib, Azah Mohamed, K. Sopian, M. Mahmoud , prediction of hourly solar radiation values for Kuala Lumpur was performed. This prediction was performed using the GRNN, FFNN, CFNN, and ELMNN artificial neural networks. Prediction results show that GRNN has a higher efficacy compared to the other proposed networks. The FFNN and CFNN are still efficient at predicting solar radiation but do not predict well in poor radiation conditions such as the first and final hour of the solar day. The ELMNN was the worst at predicting the solar radiation among the proposed methods. Based on our results, GRNN is recommended for such purposes in Malaysia and other nearby regions [1] .
In the research work done by Bharath Chandra Mummadsietty and Astha Puri, the problem of lossless, offline compression of climate data was addressed. They proposed a method for compression solar radiation, photo synthetically active radiation, and data logger power system voltage data using combination of differential encoding and Huffman coding [8] .
3. Radiation Prediction through Artificial Neural Networks (ANNs)
Artificial neural networks are computational models which are non-algorithmic and process information iteratively. They learn the relationship between the input and output variables by mastering previously recorded data [1] . ANNs consist of a system of interconnected “neurons” which can compute values from inputs. The neurons are connected by a large number of weighted links which pass signals or information. A neuron receives and combines inputs and then generates the final results in a nonlinear operation. There are various types of neural networks, such as probabilistic neural networks (PNN), general regression neural networks (GRNN), radial basis function networks (RBF), cascade correlation and hybrid networks [1] . The advantages of ANN are speed, simplicity and the ability to train past data to provide the necessary predictions. ANNs are used to solve complex functions in various applications such as control, data compression, forecasting, pattern recognition etc [9] .
In our study, three commonly used neural network models were used to predict the solar radiation data for the location “Sheep Range Black brush” in Nevada from Nevada Climate Change portal. The models used were the Multi-layer perceptron neural network (MLPNN), the cascade-forward back propagation neural network (CFNN), and the Elman back propagation neural network (ELMNN). The input variables selection is the first step for developing the ANN model. The nine input parameters chosen for training the data set were: “time (in minutes), day, month, incoming short wave radiation, outgoing short wave radiation, incoming long wave radiation, outgoing long wave radiation, photo synthetically active radiation , humidity\wind speed and temperature data” and the output is solar radiation data for the year 2012. We used ANN model to predict the solar radiation data for the year 2013 which is then used to compress the actual solar radiation data for the year 2013.
3.1. Multi-Layer Perceptron Neural Network (MLPNN)
MLP model consists of multiple layers of nodes, with each layer connected to the next one usually in a feed- forward way. It consists of either three or more than three layers: input layer, one or more hidden layers, and an output layer of nonlinearly-activating nodes. It is thus considered a deep neural network. Figure 1 describes a basic MLP neural network model. Each node in one layer connects with a certain weight Wij to every node in the following layer. This model maps sets of input data onto a set of appropriate outputs. Each neuron in one layer has direct connections to the neurons of the subsequent layer [10] . Except for the input nodes, each node is a neuron (or processing element) with a nonlinear activation function. In our work the sigmoid function is used as the activation function which is used widely in many applications. MLP is a modification of the standard linear perceptron and can distinguish data that are not linearly separable.
The weight of the connection is updated after every data entry in the input data is handled. This process is called supervised learning. The amount of learning depends on how small the error is or how close the predicted value is to the expected result. Using this information, the algorithm adjusts the weights of connections so that error function’s value is reduced by a small amount. This process is performed multiple times until the error reduces to small number. In our experiment we have applied gradient descent non-linear optimization. For this, the derivative of the error function with respect to the network weights is calculated, and the weights are then changed such that the error decreases [10] .
MLP utilizes back propagation algorithm, which is the standard algorithm for supervised learning pattern recognition process. Also, it is the subject of ongoing research in computational neuroscience and parallel distributed processing. These are widely used in research activities due to their ability to solve problems to get approximate solutions for extremely complex problems.
The algorithm works as below:
Given a set of k-dimensional inputs represented as a column vector as given below:
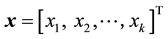 (1)
(1)
Figure 1. A basic MLP neural network model (Wikipedia) [11] .
And a nonlinear neuron with synaptic weights from the inputs:
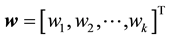 (2)
(2)
Then the output of the neuron is defined as follows:
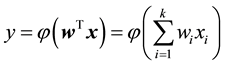 (3)
(3)
We will assume that the sigmoidal function is the simple logistic function as below:
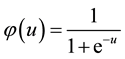 (4)
(4)
This function has the useful property that such that:
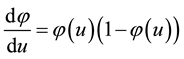 (5)
(5)
Feed forward back propagation is typically applied to multiple layers of neurons, where the inputs are called the input layer, the layer of neurons taking the inputs is called the hidden layer, and the next layer of neurons taking their inputs from the outputs of the hidden layer is called the output layer. There is no direct connectivity between the output layer and the input layer.
If there are inputs, hidden neurons, and output neurons, and the weights from inputs to hidden neurons are (i being the input index and j being the hidden neuron index), and the weights from hidden neurons to output neurons are (i being the hidden neuron index and j being the output neuron index), then the equations for the network are as follows:
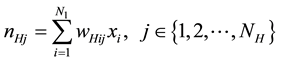 (6)
(6)
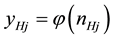 (7)
(7)
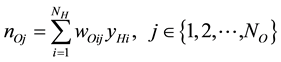 (8)
(8)
 (9)
(9)
If the desired outputs for a given input vector are, then the update rules for the weights are as follows:
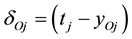 (10)
(10)
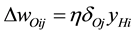 (11)
(11)
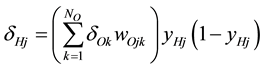 (12)
(12)
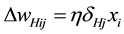 (13)
(13)
where η is some small learning rate, δOj is an error term for output neuron j and δHj is a back propagated error term for hidden neuron j.
In our work we have used ten inputs for the input layer, 4 hidden layers each layer having 27 neurons, and one output. The inputs used were day, month, time (in minutes), incoming longwave, outgoing longwave, incoming shortwave, outgoing shortwave, photo synthetically active radiation, temperature and humidity. The output is solar radiation. We have obtained a mean square error of 25 from this method.
3.2. Cascade Feed Forward Neural Networks (CFFNN)
This model of neural networks is similar to the feed forward neural networks in a way that the output from every layer is connected to the next layer. The components include input layers, hidden layers and output layers like
other neural networks [1] . In this case, each input is connected to every other hidden layer in the form of cascade, because of which it can learn associations of high complexity. Figure 2 illustrates the basic cascade feed forward neural network model.
The input layer consists of multi-dimensional vectors. Apart from the inputs, the bias is fed into each of the hidden and output neurons. In the hidden layer, each input neuron is multiplied by a weight, and the resulting weighted values are added together to produce a combined value. The weighted sum is fed into a transfer function, which then outputs a value. The outputs from the hidden layer are distributed to the output layer that receives values from all of the input neurons (including the bias) and all of the hidden layer neurons. Each value presented to an output neuron is multiplied by a weight, and the resulting weighted values are added together again to produce a combined value [1] .
In our experiment we have used a total of nine inputs namely time (in minutes), day, month, incoming short wave radiation, outgoing short wave radiation, incoming long wave radiation, outgoing long wave radiation, photo synthetically active radiation, humidity and temperature data for the year 2012.
3.3. Elman Back Propagation Neural Network (ELMNN)
Elman neural network was proposed by Elman in 1990. This network type consists of an input layer, a hidden layer, and an output layer. In this way it resembles a three layer feed forward neural network. However, it also has a context layer. This context layer is fed, without weighing the output from the hidden layer. These values are then sent, using a trainable weighted connection, back into the hidden layer. This model is a type of recurring neural networks in which a context layer is added in the feed forward network’s hidden layer [13] . Figure 3 shows a basic structure of Elman neural networks which typically have an input layer, hidden layer, an additional context layer and output layer.
Figure 2. Cascade feed forward neural network (The cascade Correlation Algorithm) [12] .
Figure 3. A simple representation of Elman neural networks [15] .
The function learned by the network is based on the current inputs plus a record of the previous state and outputs of the network. In other words, the Elman net is a finite state machine that learns what state to remember or what is relevant. The context layer is treated as another set of inputs and thus standard back propagation techniques can be used [14] .
The experimental values are given to the input units. Hidden units compute their values which is the weighted sum of inputs and context units. Context units get their value and thus, output units compute their value.
The mathematical model of Elman neural networks is analyzed as follows:



where k represents the moment, y(k), x(k), u(k), xc(k) are separately representing a dimension vector of output node, m dimension vector of hidden layer nodes, n dimension input vector and m dimension feedback state vector. Then w3, w2, w1 are separately representing connection weight matrix from hidden layer to output layer, from input layer to hidden layer and from association layer to hidden layer. f(.) is a transfer function of the neuron of hidden layer, which uses log sig function, and g(.) is a transfer function of output layer, which using tansig function. Then b1 and b2 are separately as the threshold of input layer and output layer [16] .
In the learning algorithm of this method, a back propagation algorithm with adaptive learning speed is used. The learning purpose is to use the difference between actual output and the output sample to modify the weight and bias values, and to make the error sum of squares of output layer minimize.
For this model, we used 4 layers and 26 neurons to train the data. The maximum number of epochs to train was 1000. After training the data for all the months of the year 2012, we obtained the mean square error of 102.
The trained data was used to simulate the month wise data for the year 2013, and the result gave us the predicted values of solar radiation data for each month. After we receive the predicted values of the data set, we apply a compression algorithm to compress the data. The compression ratios for all the months of the year were noted and presented in the Results section of this paper.
4. Algorithm
In this paper, we have used a hybrid method to combine artificial neural networks with data compression algorithms to better compress the data. The steps followed are as below:
Step 1: The inputs (day, month, time, incoming longwave, incoming shortwave, outgoing longwave, outgoing shortwave radiation data, photo synthetically active radiation, wind speed/humidity and temperature) are presented to the neural networks. After training the data, prediction of solar radiation for next year is obtained.
Step 2: The solar radiation data consists of leading zeros, non-zero data points and trailing zeros; this enables us to store the positions of starting and ending non-zero data points.
Step 3: The indices of non-zero data points were used to concatenate the actual data as well as the predicted data.
Step 4: For the pre-processing of the data we took the difference between the actual data and the predicted data.
Step 5: The result of this pre-processing technique is differentially encoded, and Huffman coding is applied in the last stage.
With this lossless compression of solar radiation data is achieved.
5. Results and Discussion
The above mentioned ANN models were trained with the solar radiation data obtained from the Nevada Climate Change Portal for the year 2012. The chosen input parameters were: day, month, time (in minutes), temperature, incoming longwave radiation, outgoing longwave radiation, incoming shortwave radiation, outgoing shortwave radiation, photo synthetically active radiation data and wind speed/humidity. A compression scheme was applied to the predicted values to obtain the corresponding compression ratio. The Evaluation criteria used for various ANN models are given in Table 1.
Root mean square error (RMSE) statistics were used to evaluate and compare the proposed neural network models. RMSE is a measure of the variation of the predicted values around the measured data and provides the efficiency and performance of the model. A large positive RMSE implies a big deviation in the predicted value from the measured value. Hence, the value of RMSE should be as small as possible. It is defined as follows:

where Ia is the measured value, Ip is the predicted value, and n is the number of observations.
The actual and predicted values for Multi-layer perceptron model is given in Figure 4, the actual and predicted values for Cascade feed forward model is given in Figure 5 and the actual and predicted values for Elman neural network is given in Figure 6.
The below figures give the actual and predicted values for 1 month of the year. For the month of January 2013, the values for MLP model is given in Figure 7. For the month of May 2013, the values for CFF model is given in Figure 8 and for December 2013, the values for Elman model is given in Figure 9.
Compression Ratio’s for the experiment performed is given in tables below. Table 2 gives the values for MLP model, Table 3 for CFF model and Table 4 for ELMAN model.
6. Conclusion
In this paper we have presented a hybrid method for compression of solar radiation data for the year 2013. Three models of ANN, namely Multi-layer perception, Cascade feed forward back propagation, and Elman back
Table 1. Evaluation criteria for various ANN models.
Figure 4. Actual and predicted values for MLP neural network.
Figure 5. Actual and predicted values for CFF neural network.
Figure 6. Actual and predicted values for ELM neural network.
propagation were used for prediction of solar radiation data. The year 2012 data was used as training data set and the year 2013 data was used for testing the trained ANN. RMSE was used as the evaluation parameter to test the performance of the tree models. The RMSE values of multi-layer perceptron, cascade feed forward back propagation and Elman back propagation are 5, 5.25, and 9.21, respectively. MLP provided the best results for
Figure 7. Actual and predicted values for MLP neural network model for month of January 2013.
Figure 8. Actual and predicted values for CFF neural network model for month of May 2013.
Figure 9. Actual and predicted values for ELM neural network model for month of December 2013.
Table 2. Compression Ratio’s with MLP neural network model.
predictive analysis. The predicted data was used for the compression of solar radiation data for the year 2013. The highest compression ratios using multi-layer perceptron, cascade feed forward back propagation and Elman back propagation are 9.8, 9.66, and 7.47, respectively.
Acknowledgements
This work is supported (in part) by the Defense Threat Reduction Agency, Basic Research Award # HDTRA1- 12-1-0033, National Science Foundation (NSF) award #EPS-IIA-1301726 and Nevada Space Grant Consortium
Table 3. Compression ratio’s with cascade neural network model.
Table 4. Compression Ratio’s with Elman neural network model.
Grant. Any findings, conclusions, or recommendations expressed in the material are those of the authors and do not necessarily reflect the views of NSF.
References
- Khatib, T., Mohamed, A., Sopian, K. and Mahmoud, M. (2012) Assessment of Artificial Neural Networks for Hourly Solar Radiation Prediction. International Journal of Photoenergy, 2012, Article ID: 946890. http://dx.doi.org/10.1155/2012/946890
- Yadav, A.K., Malik, H. and Chandel, S.S. (2014) Selection of Most Relevant Input Parameters Using WEKA for Artificial Neural Network Based Solar Radiation Prediction Models. Renewable and Sustainable Energy Reviews, 31, 509-519. http://dx.doi.org/10.1016/j.rser.2013.12.008
- Yadav, A.K. and Chandel, S.S. (2014) Solar Radiation Prediction Using Artificial Neural Network Techniques: A Review. Renewable and Sustainable Energy Reviews, 33, 772-781. http://dx.doi.org/10.1016/j.rser.2013.08.055
- Al-Alawi, S.M. and Al-Hinai, H.A. (1998) An ANN-Based Approach for Predicting Global Radiation in Locations with No Direct Measurement Instrumentation. Renewable Energy, 14, 199-204. http://dx.doi.org/10.1016/S0960-1481(98)00068-8
- Sözen, A., Arcaklioǧlu, E., Özalp, M. and Kanit, E.G. (2004) Use of Artificial Neural Networks for Mapping of Solar Potential in Turkey. Applied Energy, 77, 273-286. http://dx.doi.org/10.1016/S0306-2619(03)00137-5
- Sözen, A., Arcaklioǧlu, E. and Özalp, M. (2004) Estimation of Solar Potential in Turkey by Artificial Neural Networks Using Meteorological and Geographical Data. Energy Conversion and Management, 45, 3033-3052.
- AbdAlKader, S.A. and AL-Allaf, N.A. (2011) Backpropagation Neural Network Algorithm for Forecasting Soil Temperatures Considering Many Aspects: A Comparison of Different Approaches. The 5th International Conference on Information Technology, Amman, 11-13 May 2011, 11-13.
- Mummadisetty, B.C., Puri, A., Sharifahmadian, E. and Latifi, S. (2014) Lossless Compression of Climate Data. Proceedings of the 23rd International Conference on Systems Engineering, Vol. 330, 391-400.
- Xu, K., Song, J.D., Zhao, Y.W., Bi, Q. and Liu, Y. (2013) Forecasting Model Based on an Improved Elman Neural Network and Its Application in the Agricultural Production. IEEE International Conference on Granular Computing, Beijing, 13-15 December 2013, 202-207. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=6740408
- Rosenblatt, F. (1962) Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Spartan Books, Washington DC. http://catalog.hathitrust.org/Record/000203591
- Basic MLP Neural Network Model. http://en.wikibooks.org/wiki/Artificial_Neural_Networks/Activation_Functions
- Cascade Feed Forward Neural Network. http://www.cs.cornell.edu/boom/2004sp/projectarch/appofneuralnetworkcrystallography/NeuralNetworkCascadeCorrelation.htm
- Paraskevas, T., Dimitrios, R. and Andreas, B. (2014) Use of Artificial Neural Network for Spatial Rainfall Analysis. Journal of Earth System Science, 123, 457-465. http://dx.doi.org/10.1007/s12040-014-0417-0
- Al Shamisi, M.H., Assi, A.H. and Hejase, H.A. (2011) Using MATLAB to Develop Artificial Neural Network Models for Predicting Global Solar Radiation in Al Ain City―UAE. Engineering Education and Research Using MATLAB. http://www.intechopen.com/books/engineering-education-and-research-using-matlab/using-matlab-to-develop-artificial-neural-network-models-for-predicting-global-solar-radiation-in-al
- Representation of Elman Neural Network. http://mnemstudio.org/neural-networks-elman.htm
- Lina, R., Liu, Y.X., Rui, Z.Y., Li, H.Y. and Feng, R.C. (2009) Application of Elman Neural Network and MATLAB to Load Forecasting. Proceedings of the International Conference on Information Technology and Computer Science, Kiev, 25-26 July 2009, 55-59.











