Int'l J. of Communications, Network and System Sciences
Vol.7 No.3(2014), Article ID:43725,7 pages DOI:10.4236/ijcns.2014.73010
Improved Alamouti STBC Multi-Antenna System Using Hadamard Matrices
K. O. O. Anoh1, O. Ochonogor2, R. A. A. Abd-Alhameed1, S. M. R. Jones1, T. T. Mapuka1
1Mobile and Satellite Communications Research Centre, University of Bradford, Bradford, UK
2Department of Electronic Engineering, University of Westminster, Westminster, UK
Email: o.anoh@bradford.ac.uk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 25 January 2014; revised 25 February 2014; accepted 4 March 2014
ABSTRACT
To achieve multiple input multiple output (MIMO) in wireless communication, the orthogonal space-time block coding (OSTBC) is evaluated next. At first, the OSTBC design is extended to include Hadamard matrix, referred to in this work, as traditional Hadamard OSTBC. Next, the Hadamard matrix is imposed on the conventional OSTBC, which is referred to, in this work as, Alamouti-Hadamard STBC. Both the traditional Hadamard OSTBC and the conventional STBC are compared with the Alamouti-Hadamard STBC. It will be shown that imposing the Hadamard conditions over the conventional OSTBC, the performance of the OSTBC 2-transmit antenna scheme can be significantly improved in terms of BER performance. All propositions are well supported with analytical derivations.
Keywords:STBC; MIMO; Hadamard

1. Introduction
When signals traverse multipath environment, they are intercepted and then distorted due to non-uniformity of the surfaces on which they impinge. During reception, the signals can be received in error if the channel attenuation is large. The quality of information received in this case will be heavily degraded. Suppose that replicas of this information are transmitted over many different fading channels, then the probability, p, that all the information will fade simultaneously at each time instance, will be reduced considerably [1] -[3] . Methods of transmitting replicas of a signal, mostly, over different antenna branches are discussed as diversity. Since each transmission branch is independent of another, then the likelihood that all branches will fade critically is reduced. Three well-known diversity techniques are the frequency, time and space diversities [4] . Over the same bandwidth and without coding redundant overheads that constrain spectral efficiency, multi-antennas can be applied. One of the most adopted multi-antenna techniques is the STBC [5] . STBC exploits the space and time diversity gains to improve a multi-antenna system performance for MIMO systems.
In the recent time, MIMO technology has improved as a way of achieving a very dependable broadband network in wireless communication systems. For instance, MIMO technology can transfer high data rate depending on the number of transmission branches (diversities). For two transmit diversities, STBC is used [6] . This technique exploits full transmission power for orthogonal codes as long as the transmitter diversity order is no more than two [7] . In transmissions involving more than two antennas, the full rate power is not attainable [6] .
It was mentioned in [8] that the Alamouti STBC can as well be discussed using the Hadamard matrices. In [9] , the cyclic quasi-orthogonal codes were used to discuss QO-STBC for four-transmitter antennas. In that work, the quasi-orthogonal cyclic codes were used in conjunction with the Hadamard matrices to diagonalize the decoding matrix, for higher order matrices. Recently, [10] has applied Hadamard conditions to design up to 4-trasnmit antenna system. In orthogonal STBC that attains full diversity which has been reported in [6] , full transmission rate with full diversity can be attained without the use of the diagonalizing eigenvectors [7] , rotation of the code matrix elements constellation [11] -[13] or the Hadamard matrices [9] . However, it will be shown later in this work that imposing the Hadamard criteria on the STBC codes can improve the performance in the order of transmitting elements.
In this work, the construction of 2-transmit antenna system based on the Hadamard matrix properties is considered first. Then, the Alamoutiorthogonal STBC is extended to include the Hadamard property for improved diversity gain. Again, a consideration will be given to the code construction discussed for higher antenna order in [9] , but for 2-trasnmit antennas only. Results will be compared with the traditional 2-transmit Alamouti code. In all cases, the system model will be limited to BPSK and QPSK only. Further studies can build on these.
We have organised the remaining parts of this paper as follows: system model is discussed in Section 2, with the OSTBC presented in Section 3. Simulation results are discussed in Section 4 and the conclusion in Section 5.
2. System Model
A 2-two transmit diversity system model is involved and will be constructed from the Alamouti code. In Alamouti case, the code was discussed for frequency flat fading channel, h. If the signal of the system to be processed is s, then the received signal after traversing the channel will be of the form:
 (1)
(1)
where z is the noise term of the additive white Gaussian noise (AWGN). h is constructed from the multipath Rayleigh model as:
 (2)
(2)
where u is the gain corresponding to kth path, N is the maximum number of the resolvable multipath,  is the phase and NT is the maximum number of transmit antennas. The channel, h, in Equation (1) is a matrix containing
is the phase and NT is the maximum number of transmit antennas. The channel, h, in Equation (1) is a matrix containing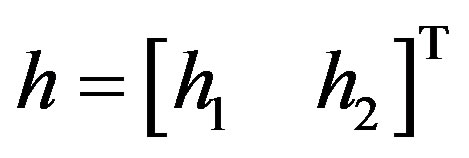 , where
, where  is the transpose operator. Since the model considers a frequency flat channel, the amplitude
is the transpose operator. Since the model considers a frequency flat channel, the amplitude 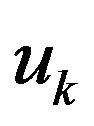 for all N-paths of each channel is therefore uniform.
for all N-paths of each channel is therefore uniform.
3. Space-Time Block Coding (STBC)
The most pioneering work on STBC was introduced by [6] . This diversity technique provides transmitter diversity for up to a maximum of 2-transmit antennas. The scheme exploits the space and time diversities (see [4] , Ch. 10). It involves transmitting the information-bearing signals over two different time slots over 2 antenna spaces. For instance, let the information-bearing signal be 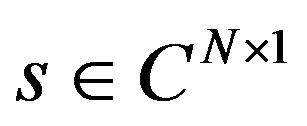 where
where  is a complex matrix of N × 1 dimension. The signals can be demultiplexed and transmitted over two antenna spaces as
is a complex matrix of N × 1 dimension. The signals can be demultiplexed and transmitted over two antenna spaces as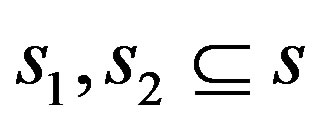 , where
, where 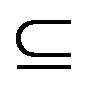 shows that s1 and s2 are proper subsets of the encoding matrix s. These can be obtained as [14] .
shows that s1 and s2 are proper subsets of the encoding matrix s. These can be obtained as [14] .
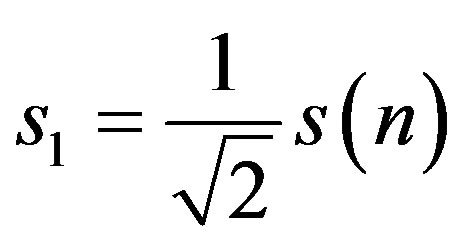 (3a)
(3a)
 (3b)
(3b)
 ,
, . Equation (3) represents a demultiplexing that volunteers equal power sharing with n as the prevailing discrete signal block under consideration.
. Equation (3) represents a demultiplexing that volunteers equal power sharing with n as the prevailing discrete signal block under consideration.
3.1. Conventional STBC
In [6] , it was shown that s1 and s2 will be transmitted during the first time slot and the conjugates 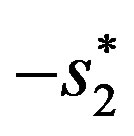 and
and  will be transmitted in the second time slot. Then the encoding matrix containing the above formulation can be described as:
will be transmitted in the second time slot. Then the encoding matrix containing the above formulation can be described as:
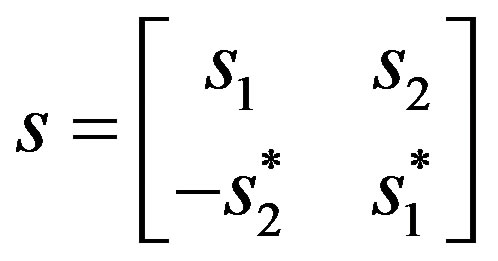 (4)
(4)
If signal energy on each antenna branch is normalized to unity, then the matrix s is an orthogonal matrix. Since there are NT transmitting elements, then each of the codes (and their respective conjugates) will be characterized as , where NR is the number of receive elements. For simplicity, NR is limited to 1. The construction above permits that the system attains full transmission rate and full diversity. For instance, there are two time slots, and there exist two antenna spaces over which the transmissions would take place. A system with T time slots and K antenna spaces attains full transmission rate if T/K = 1. In the code structure shown in Equation (4), there exist full transmission rate.
, where NR is the number of receive elements. For simplicity, NR is limited to 1. The construction above permits that the system attains full transmission rate and full diversity. For instance, there are two time slots, and there exist two antenna spaces over which the transmissions would take place. A system with T time slots and K antenna spaces attains full transmission rate if T/K = 1. In the code structure shown in Equation (4), there exist full transmission rate.
Now, recall Equation (1): The s is the orthogonal STBC from Equation (4), and will be transmitted over two antenna spaces. In that case, the channel over which the signals are transmitted will be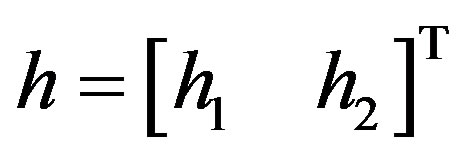 , where
, where 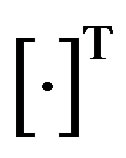 is the Hermitian transpose. In this case there are a maximum of 2 transmit branches (i.e. NT = 2).
is the Hermitian transpose. In this case there are a maximum of 2 transmit branches (i.e. NT = 2).
Figure 1 shows the architecture for implementing OSTBC. A part of the orthogonal codes (i.e. s1 and s2) is transmitted over antennas T1 and T2 in the first time slot (ts1), while the other part of the codes ( and
and ) is transmitted in the second time slot (ts2).
) is transmitted in the second time slot (ts2).
In the receiver, the decoding can proceed. Meanwhile, for an orthogonal matrix with complex entries, say:
 (5)
(5)
Then, the decoding matrix will be of the form [1] :
 (6a)
(6a)
or, in an expanded form:
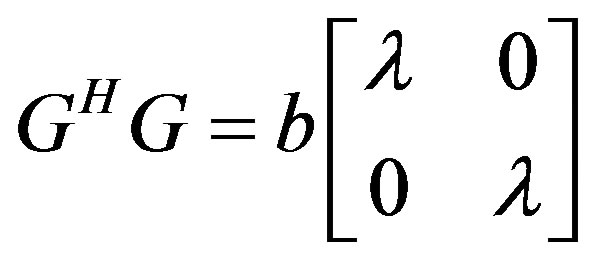 (6b)
(6b)
where  is an identity matrix for NT = 2 and b is a constant volunteered by multiplexing the input signal over NT antenna branches. So, the decoding matrix for the OSTBC following Equation (6) criteria will become:
is an identity matrix for NT = 2 and b is a constant volunteered by multiplexing the input signal over NT antenna branches. So, the decoding matrix for the OSTBC following Equation (6) criteria will become:
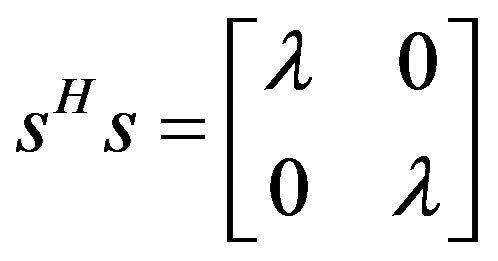 (7)
(7)
where  represents a Hermitian transposition operation and
represents a Hermitian transposition operation and . The decoding matrix is a diagonal matrix with no off-diagonal terms. Recall the channel matrix
. The decoding matrix is a diagonal matrix with no off-diagonal terms. Recall the channel matrix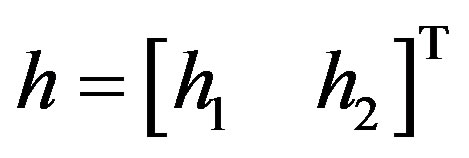 , and Equation (7) such that Equation (1) becomes:
, and Equation (7) such that Equation (1) becomes:

Figure 1. Architecture for implementation of OSTBC.
 (8)
(8)
Now, expanding a part of this result:
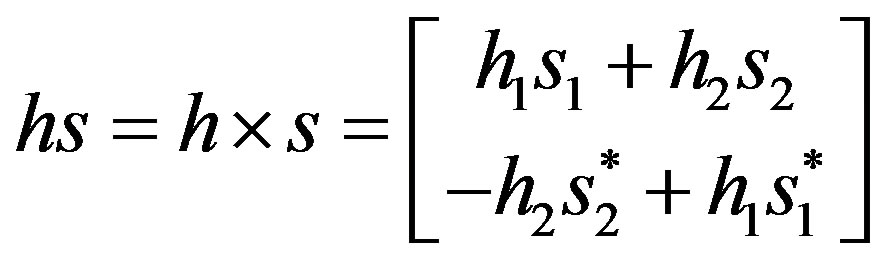 (9)
(9)
From Equation (9), it is easy to isolate the equivalent channel matrix of Equation (4) as:
 (10)
(10)
Then, with s1 and s2 each antenna branch will transmit for the two different time slots:
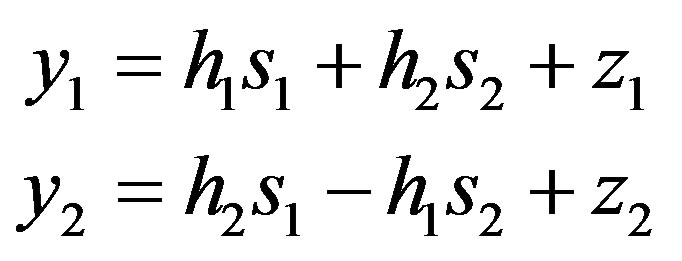 (11)
(11)
where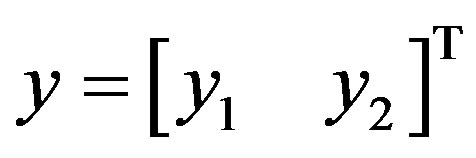 . Equation (11) is the case for one receiver. So, using the decoding criteria of Equations (18) and (19) in Equation (1), then:
. Equation (11) is the case for one receiver. So, using the decoding criteria of Equations (18) and (19) in Equation (1), then:
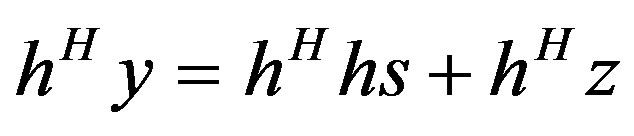 (12)
(12)
Equation (12) provides some coding gain according to the amplitude of the channel shown in Equation (2), where:
 (13)
(13)
In Equation (13), the decoding matrix shows the gain due to the channel as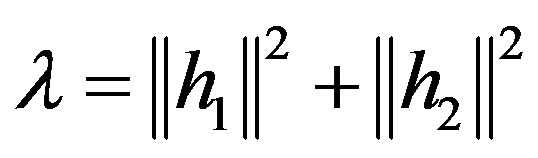 . However, the noise term is amplified by the hH term. Wherein there are more than one receive antenna, then each of the h1 and h2 can be treated respectively as a vector of the forms:
. However, the noise term is amplified by the hH term. Wherein there are more than one receive antenna, then each of the h1 and h2 can be treated respectively as a vector of the forms:
 (14)
(14)
where NR is the maximum number of receivers.
3.2. Quasi-Cyclic Hadamard Matrix Codes
The quasi-cyclic Hadamard matrix orthogonalizes a given code by using the Hadamard matrix of the order of the cyclic matrix. This is the case for higher order matrix. For matrix order of NT = 2, the cyclic matrix can be written as:
 (15)
(15)
Since the Hadamard matrix is a matrix of 1s and -1s, and usually discussed the eigenvectors of an orthogonal matrix, the Hadamard matrix for Equation (15) will be:
 (16)
(16)
Equation (16) is the eigenvector which can orthogonalize Equation (15). Combing Equations (15) and (16), we obtain:
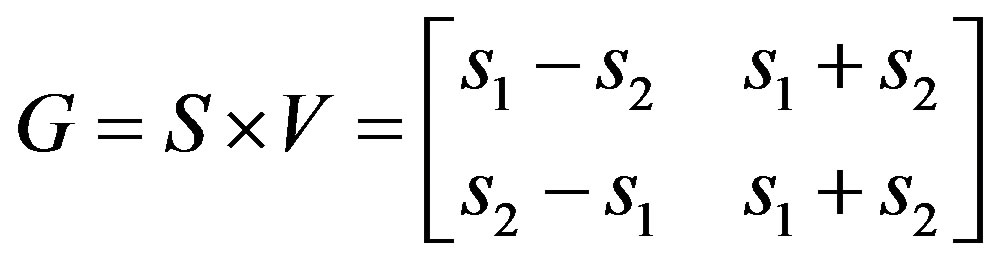 (17)
(17)
Equation (17) is the encoding matrix to be transmitted. In the receiver, the decoding matrix will be characterized as:
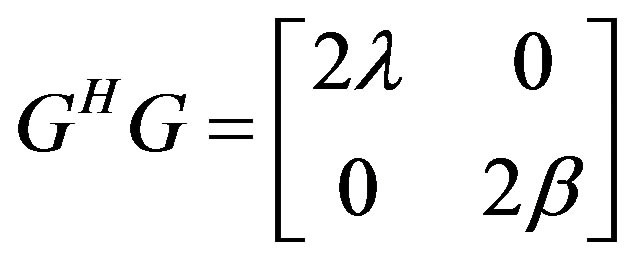 (18a)
(18a)
where 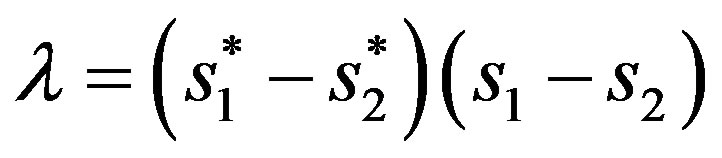 and
and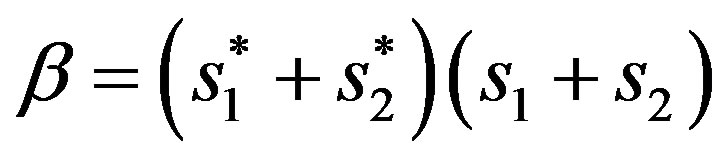 . Expanding
. Expanding  and
and , it can be noticed that:
, it can be noticed that: 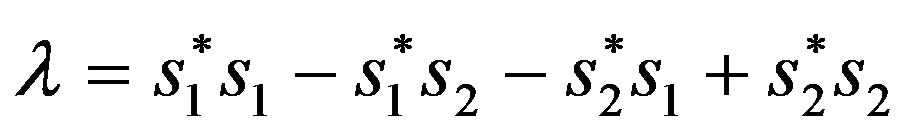 and,
and, 
In the  case,
case,  deplete the gain. Also, in
deplete the gain. Also, in  case,
case,  is also residual.
is also residual.
Notice also that the converse is also true:
 (18b)
(18b)
Equation (18) can easily be corroborated with the Hadamard criteria identified in [10] , although, in this case, the exact full diversity is not attained as the terms of Equation (15) are complex elements. This will be reflected in the result.
3.3. Combined Traditional-STBC and Hadamard Codes
It can be seen that the decoding matrix revealed by Equation (7) does not provide the b term of Equation (6b). The performance gain of the above technique can be improved by exploiting the Hadamard property of the quasi-cyclic Hadamard codes already discussed in [8] [9] for higher order matrix. To do that, recall that the Hadamard matrix is a matrix of 1 s and −1 s that provide the eigenvector which can diagonalize a matrix with some power gain in the order of code structure [10] . For instance, the Alamouti space time codes shown in Equation (4) which is, in this case, an orthogonal STBC, has 2-antenna elements that is a 2 × 2 matrix. The Hadamard matrix for a 2 × 2 matrix can be written as:
 (19)
(19)
Equation (19) can be regarded as the eigenvector of Equation (4) and can be combined as:
 (20)
(20)
Equation (20) is then the encoding matrix of the codes to be transmitted. Notice that Equations (4) and (19) form, independently, orthogonal codes. In the receiver, the decoding matrix will be characterized as:
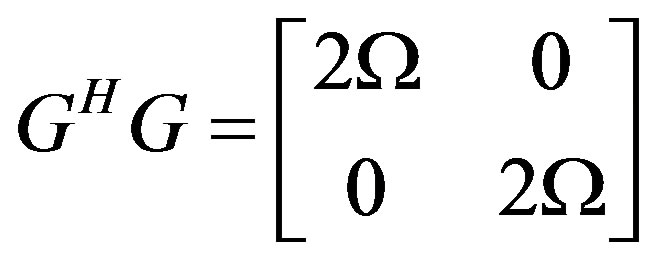 (21)
(21)
where,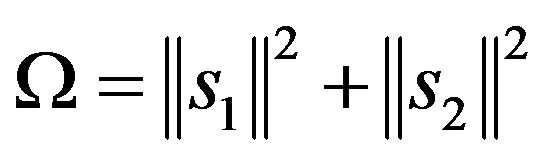 . If the residual terms identified in the case of Equation (18) can be zero, then full diversity can be attained. Only the Alamouti STBC codes satisfy these criteria. Equation (21) provides some processing gain to improve the diversity performance of the system in the order of the number of transmitting elements, in this case, 2. Thus by imposing the Hadamard matrix criteria on the design of orthogonal space time block codes, the system performance can be increased up to the number of transmitter diversity order.
. If the residual terms identified in the case of Equation (18) can be zero, then full diversity can be attained. Only the Alamouti STBC codes satisfy these criteria. Equation (21) provides some processing gain to improve the diversity performance of the system in the order of the number of transmitting elements, in this case, 2. Thus by imposing the Hadamard matrix criteria on the design of orthogonal space time block codes, the system performance can be increased up to the number of transmitter diversity order.
Like in Section 3.1, the equivalent channel matrix (of Equation (20)) can be constructed such as:
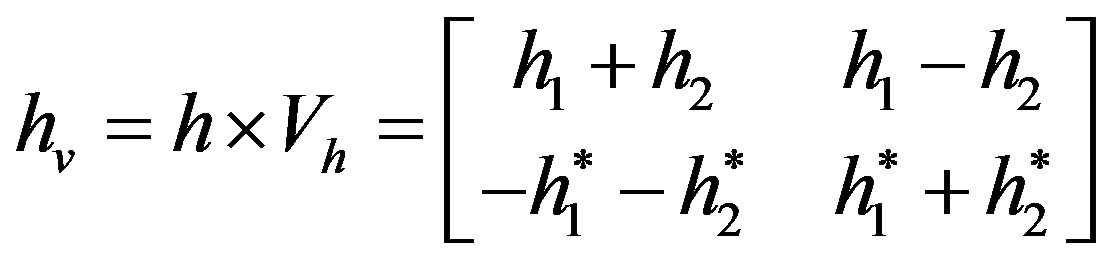 (22)
(22)
From the channel matrix in Equation (10), Vh is formed as:
 (23)
(23)
Equation (22) is realized by multiplying the channel matrix of the OSTBC and the equivalent eigenvectors of Equation (23). In that case, the decoding matrix (in the receiver) can be seen as:
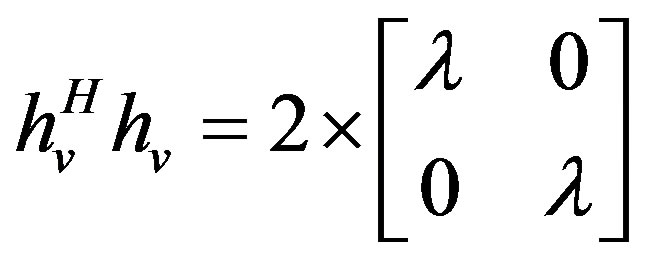 (24)
(24)
The constant 2 can be traced to the theory of orthogonal STBC discussed in [1] . These conditions are used to implement the scheme for one receive antenna only (i.e. 2 × 1).
4. Numerical Simulations Results and Discussion
We demonstrate the realization of the above propositions using some computer simulations performed in a MATLAB® environment. The demonstration is a test of error probability of the combined Alamouti-Hadamard system (depicted as in Figures 2 and 3 “AlamHad”) comparable to the traditional Hadamard STBC (depicted in Figures 2 and 3 as “Traditional”) and conventional STBC (also depicted in Figures 2 and 3 as “Alam”). It involves two system models, namely, BPSK and QPSK. Using the above design conditions, we demonstrate the simulation of the 2-antenna system for BPSK and QPSK mapping schemes.
The simulation is for Rayleigh frequency flat channel model, although each transmission channel branch is independent of another. In one case, the traditional Hadamard STBC model for 2 × 1 system is simulated. The second case involved the conventional Alamouti space-time coding structure for 2 × 1 system. The third case

Figure 2. Comparisons of traditional Hadamard STBC and conventional OSTBC with Almouti-Hadamard STBC for a BPSK system.
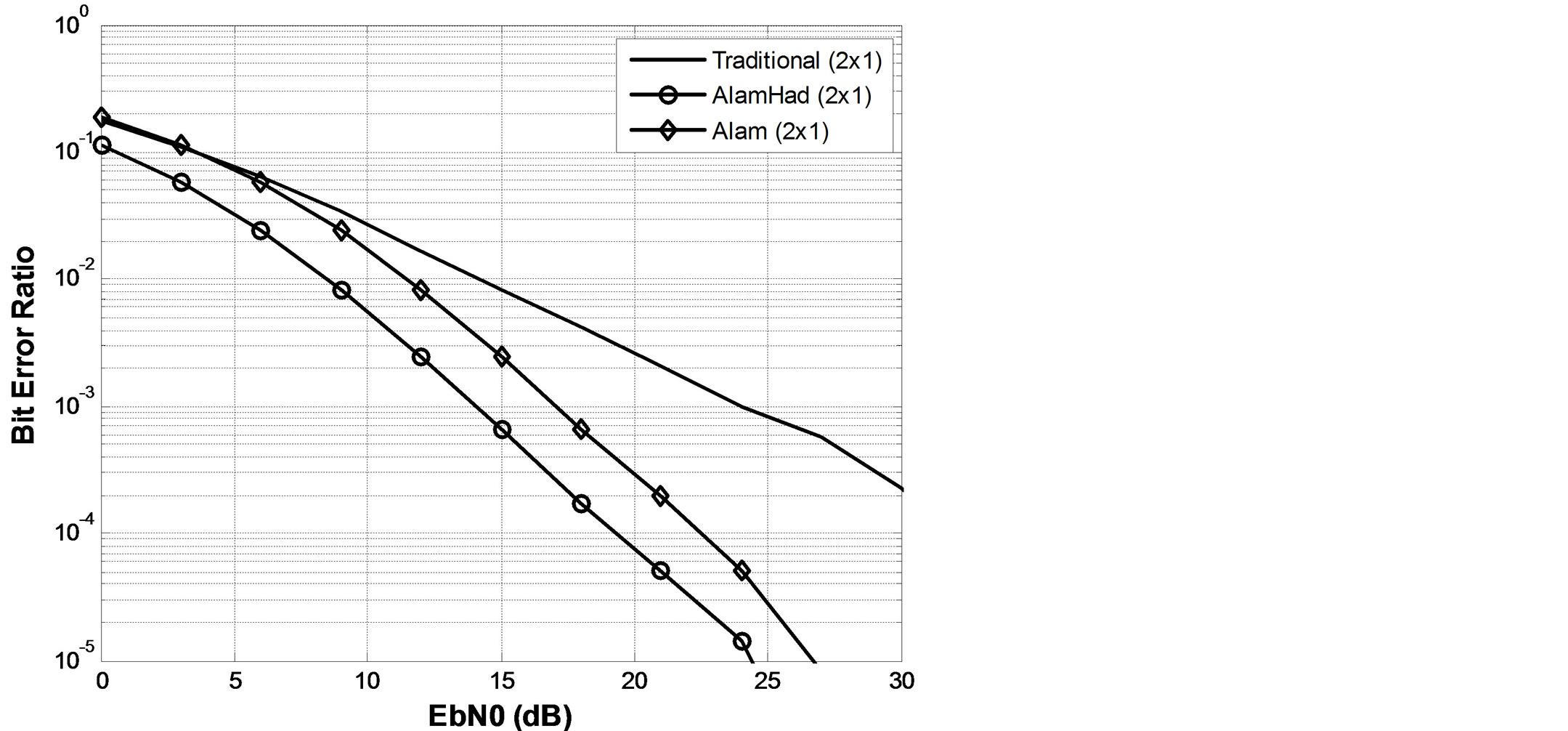
Figure 3. Comparisons of the Hadamard based OSTBC and Alamouti STBC using QPSK.
is a combination of the Alamouti code structure with the Hadamard matrix.
From Figure 2, results show that Alamouti code structure with Hadamard matrices provides better performance than both the Hadamard STBC and the conventional STBC code. This result corroborates the mathematical formulation discussed in this work. From Equation (18), although the Hadamard matrix orthogonalizes the quasi-cyclic codes, however the exact gain expected of the construction was not attained. This is evident in the performance of the traditional Hadamard STBC system. At first (in Figure 2), both the conventional STBC and traditional Hadamard STBC performed alike at low EB/N0, but the performance does not improve at increased EB/N0 since the residual terms (from Equation (18)) are irreducible so that the gain be depleted.
In Figure 3, the proposed code structure is extended to include the QPSK mapping scheme. Results obtained also support the fact that the proposed code structure is better than the conventional Alamouti and the traditional-Hadamard codes for OSTBC.
5. Conclusion
An approach to improve the design of multi-antenna system for a maximum of 2-antenna diversity branch scheme has been presented and evaluated. It exploited the Hadamard matrix codes in the construction of the 2-transmit antenna system. Two performance scenarios have been shown for BPSK and QPSK systems with a maximum of one-receiver antenna diversity. Results obtained well support the mathematical proposition obtained when the Hadamard matrix is used. This study can then be extended for multiple receiver diversity.
References
- Proakis, J. and Salehi, M. (2008) Digital Communications. 5th Edition, McGraw-Hill, Asia.
- Zhang, W., Xiang-Gen, X. and Ben Letaief, K. (2007) Space-Time/Frequency Coding for MIMO-OFDM in Next Generation Broadband Wireless Systems. IEEE Wireless Communications, 14, 32-43.
- Anoh, K.O., Abd-Alhameed, R.A., Chukwu, M., Buhari, M. and Jones, S.M. (2013) Towards a Seamless Future Generation Network for High Speed Wireless Communications. International Journal of Advanced Computer Science & Applications, 4.
- Garg, V. (2010) Wireless Communications & Networking: Morgan Kaufmann.
- Jafarkhani, H. (2005) Space-Time Coding: Theory and Practice. Cambridge University Press, Cambridge.
- Alamouti, S.M. (1998) A Simple Transmit Diversity Technique for Wireless Communications. IEEE Journal on Selected Areas in Communications, 16, 1451-1458.
- Dama, Y.A.S., Abd-Alhameed, R.A., Jones, S.M.R., Migdadi, H.S.O. and Excell, P.S. (2011) A New Approach to Quasi-Orthogonal Space-Time Block Coding Applied to Quadruple Mimo Transmit Antennas. 4th International Conference on Internet Technologies & Applications, September 2011.
- Fazel, F. and Jafarkhani, H. (2008) Quasi-Orthogonal Space-Frequency and Space-Time-Frequency Block Codes for Mimo OFDM Channels. IEEE Transactions on Wireless Communications, 7, 184-192.
- Dama, Y., Abd-Alhameed, R., Ghazaany, T. and Zhu, S. (2013) A New Approach for OSTBC and QOSTBC. International Journal of Computer Applications, 67, 45-48.
- Anoh, K., Dama, Y., Abd-Alhameed, R. and Jones, S. (2014) A Simplified Improvement on the Design of QO-STBC Based on Hadamard Matrices. International Journal of Communications, Network and System Sciences, 7, 37.
- Sharma, N. and Papadias, C.B. (2003) Improved Quasi-Orthogonal Codes through Constellation Rotation. IEEE Transactions on Communications, 51, 332-335.
- Wang, D. and Xia, X.-G. (2005) Optimal Diversity Product Rotations for Quasiorthogonal STBC with MPSK Symbols. IEEE Communications Letters, 9, 420-422.
- Xian, L. and Liu, H. (2005) Optimal Rotation Angles for Quasi-Orthogonal Space-Time Codes with PSK Modulation. IEEE Communications Letters, 9, 676-678.
- Anoh, K.O.O., Abd-alhameed, R.A., Noras, J.M. and Jones, S.M.R. (2013) Wavelet Packet Transform Modulation for Multiple Input Multiple Output Applications. IJCA, 63, 46-51.

