Int'l J. of Communications, Network and System Sciences
 Vol. 6  No. 9 (2013) , Article ID: 36446 , 7 pages DOI:10.4236/ijcns.2013.69042

Proposal of PAPR Reduction Method for OFDM Signal by Re-Ordering of Clusters in Frequency Domain

Tanairat Mata1, Katsuhiro Naito1, Pisit Boonsrimuang2, Kazuo Mori1, Hideo Kobayashi1

1Division of Electrical and Electronic Engineering, Graduate School of Engineering, Mie University, Tsu, Japan

2Department of Telecommunication Engineering, Faculty of Engineering, KMITL, Bangkok, Thailand

Email: tanairat@com.elec.mie-u.ac.jp

Copyright © 2013 Tanairat Mata et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received July 25, 2013; revised August 22, 2013; accepted August 29, 2013

Keywords: OFDM; PAPR; Re-Ordering of Clusters; Cluster ID Number; Packet-Switched Transmission

ABSTRACT

One of the limitations of using OFDM technique is its higher PAPR in the time domain signal. The higher PAPR OFDM signal would cause the fatal degradation of BER performance and undesirable spectrum regrowth in the nonlinear channel. One of the promising PAPR reduction methods for OFDM signal is the Partial Transmit Sequence (PTS) method which can achieve better PAPR performance with reasonable computation complexity. However the PTS method is required to inform the phase coefficients of PTS as the side information to the receiver for the correct demodulation of data information through the data or separate channels. To simplify the transceiver of OFDM system with the PTS method, the phase coefficients of PTS are usually embedded in the data information. However since the phase coefficients of PTS are obtained after the PTS processing only for the data information at each OFDM symbol, it is hard to embed the phase coefficients of PTS in the data information separately without degradation of PAPR performance. To solve this problem, this paper proposes a new PAPR reduction method based on the packet-switched transmission systems in which all the clusters within the certain number of OFDM symbols have the sequential cluster ID numbers embedded in the header of each cluster. The salient features of the proposed method are to reduce the PAPR performance by re-ordering of clusters (ROC) in the frequency domain at the transmitter and to reconstruct the original ordering of clusters by using the cluster ID number demodulated from each cluster at the receiver. This paper also proposes a reduction technique of computation complexity for the proposed ROC method by using the feature of IFFT processing. This paper presents various computer simulation results to verify the effectiveness of the proposed ROC method with the reduction technique of computation complexity.

1. Introduction

The OFDM (Orthogonal Frequency Division Multiplexing) technique has received a lot of attention especially in the field of wireless communications because of its efficient usage of frequency bandwidth and robustness to the multi-path fading. From these advantages, the OFDM technique has already been adopted as the standard transmission technique in the wireless LAN [1], the terrestrial digital TV broadcasting [2] and the next generation of mobile communication system (LTE: Long Term Evolution) [3,4]. One of the limitations of using OFDM technique is the larger peak to average power ratio (PAPR) of its time domain signal [5,6] as compared with the single carrier transmission method. The OFDM signal with larger PAPR would lead the severe degradation of bit error rate (BER) performance and the larger adjacent channel interference due to the undesirable spectrum regrowth which are caused by the intermodulation noise occurring at the non-linear amplifier.

To solve the PAPR problem in OFDM systems, various PAPR reduction methods have been proposed up to today including such as the Clipping and Filtering method [7,8], Selected Mapping method (SLM) [9,10], and Partial Transmit Sequence method (PTS) [11,12]. One of the promising methods among these methods is the PTS method which can achieve the better PAPR performance with reasonable computation complexity. In the PTS method, each transmission OFDM symbol is divided into several clusters in the frequency domain and all subcarriers in each cluster are weighted by one of the predetermined phase coefficients in the time domain so as to reduce the PAPR performance. Although the PTS method can achieve the better PAPR performance with reasonable computation complexity, this method is required to inform the phase coefficients of PTS to the receiver as the side information through the data or separate channels. To simplify the transceiver of OFDM system with the PTS method, the phase coefficients of PTS obtained after the PTS processing are usually embedded in the data information separately. However since the phase coefficients of PTS are obtained after the PTS processing only for the data information, the PTS method is unable to reduce the PAPR performance both for the data information and phase coefficients of PTS simultaneously. From this fact, the PAPR performance after embedding the information of phase coefficients into the data information would be degraded from the original PAPR performance.

To solve the problem of conventional PTS method as mentioned above, this paper proposes a new PAPR reduction method for the OFDM signal based on the packet-switched transmission systems. In the proposed OFDM system, one packet is composed of all the clusters over the certain number of OFDM symbols in which each cluster has the sequential cluster ID number embedded in the header of each cluster. The reduction of PAPR performance is performed for each packet by ReOrdering of Clusters (ROC) in the frequency domain. The proposed ROC method can reduce the PAPR performance over the certain number of OFDM symbols simultaneously which include both the data information and the cluster ID numbers. At the receiver, the proposed ROC method enables the correct demodulation of data information for each cluster independently, because the ROC method only changes the locations of clusters in the frequency domain over the certain number of OFDM symbols at the transmitter. From this fact, the cluster ID number embedded in the header of each cluster can be identified from the demodulated data information for each cluster. By using the demodulated cluster ID number for each cluster, the original ordering of clusters over the certain number of OFDM symbols can be reconstructed correctly at the receiver. The proposed ROC method is completely different from the PTS method which is required to inform the phase coefficients of PTS as the side information to the receiver separately. This paper also proposes a low computation complexity technique for the ROC method which enables the re-ordering of clusters in the time domain by using the feature of IFFT algorithm.

In this paper, Section 2 presents PAPR properties of OFDM signal. Section 3 presents the proposed ROC method of using the low computation complexity technique. Section 4 presents the various computer simulation results to verify the effectiveness of the proposed method as compared with the conventional OFDM, and finally Section 5 concludes this paper.

2. PAPR Properties of OFDM Signals

Let 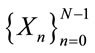denotes the frequency domain OFDM signal, where N is the number of FFT/IFFT points and n is the frequency index. The discrete time domain OFDM signal is obtained by taking the N-point Inverse Discrete Fourier Transform (IDFT) for Xn as given by the following equation:

. (1)

where k is the discrete time index, WN=e−j2π/N (known as the twiddle factor of IFFT), and j2 = −1. From (1) it can be seen that the time domain signal is generated by summation of complex independent random information data of. From this fact, the distribution of time domain signal has the property of Gaussian which has larger peak amplitude as compared with the single carrier transmission signal. To evaluate the envelop variations of OFDM time domain signal, the peak to average power ratio (PAPR) is usually employed as given by:

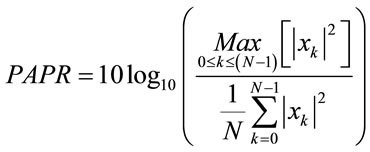. (2)

Here it should be noted that the discrete time PAPR can be evaluated precisely by taking more than four times oversampling ratio for the OFDM signal [13].

3. Proposal of Re-Ordering of Clusters (ROC) Method

This section proposes the ROC method [14] which can improve the PAPR performance with low computation complexity.

3.1. Re-Ordering of Clusters

Figure 1 shows the structure of OFDM symbol in the frequency domain to be used in the proposed ROC method. The OFDM symbol consists of M data sub-carriers and (N − M)/2 null sub-carriers (zero padding) inserted at the both ends of M data sub-carriers. M data sub-carriers are divided into V clusters in which each cluster has M/V sub-carriers.

In the proposed ROC method, one packet is constructed by all the clusters within the certain number of OFDM symbols which have the sequential cluster ID numbers based on the packet-switched transmission systems. The cluster ID number for assigning each cluster is ordered sequentially from the 1-st to the (P∙V)-th when the number of clusters in one OFDM symbol is V and the re-ordering of clusters is performed over P OFDM symbols. In the ROC method, the processing for the reduc-

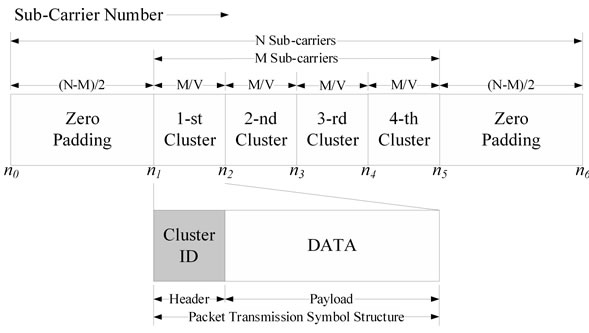
Figure 1. Structure of frequency domain OFDM symbol for the proposed ROC method.

tion of PAPR performance is conducted over the consecutive P OFDM symbols by changing the order of clusters in the frequency domain. Figure 2 shows an example of the proposed ROC method when V = 4 and P = 2. In this example for the proposed ROC method, the locations of 8 clusters are changed over two OFDM symbols in the frequency domain so as to achieve the better PAPR performance at the transmitter. From Figures 1 and 2, it can be observed that the proposed ROC method can reduce the PAPR performance both for the data information and cluster ID numbers simultaneously. This is completely different from the conventional PTS method which can reduce the PAPR performance only for the data information and the obtained phase coefficients of PTS is required to inform the receiver separately.

3.2. Low Computation Complexity Technique for ROC Method

In the proposed ROC method, the re-ordering of clusters is conducted in the frequency domain as mentioned above. However, when employing the frequency domain approach, the IFFT processing is required for each reordering of clusters in the frequency domain because the PAPR performance is required to evaluate in the time domain. This means that the computation complexity for the proposed ROC method becomes larger to achieve the better PAPR performance, because the computation complexity increases proportionally to the required number of IFFT processing. To solve this problem, this paper proposes a low computation complexity technique for the ROC method which can perform the re-ordering of clusters in the time domain by using the feature of IFFT algorithm.

When the number of clusters in one OFDM symbol is 4 (V = 4) and the re-ordering of clusters is performed over two symbols (P = 2) as shown in Figures 1 and 2, the data information including the cluster ID number for each cluster in the frequency domain is given by the following equation:

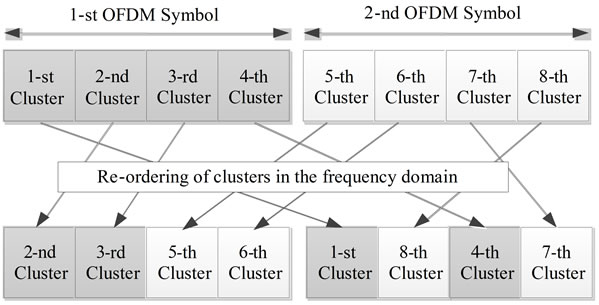
Figure 2. An example of ROC method when the number of clusters V and P are 4 and 2, respectively.

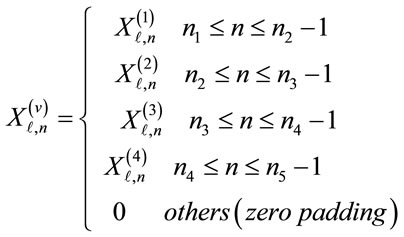. (3)

where 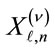is the data information at n-th sub-carrier of -th symbol (1 ≤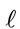≤ 2) for the v-th cluster (1 ≤v ≤ 4). In the proposed method, the time domain signal for each cluster is firstly calculated by the following equation:

. (4)

where nv (1 ≤ v ≤ 4) is the first sub-carrier number for the cluster v as given in (3). The time domain signal given in (4) corresponds to that the data information for the cluster v is located from the sub-carrier number 0 to M/V − 1 in the frequency domain. By using (4), the time domain signal for all clusters (1 ≤ v ≤ 4) over two symbols (1 ≤≤ 2) can be obtained. By using these time domain signals, the re-ordering of clusters can be conducted in the time domain. When the i-th cluster is changed to the j-th cluster in the frequency domain, its time domain signal can be given by the following equation:

. (5)

where is the time domain signal for the i-th cluster given in (4) and is the time domain coefficient for changing the location of cluster to the j-th cluster which is given by the following equation:

. (6)

From (5), it is concluded that the re-ordering of clusters in the frequency domain can be conducted in the time domain by using (6). The required number of computation processing for the proposed method is N times multiplications as shown in (5) which is smaller computation complexity than Nlog2N when using the IFFT processing. This means that the proposed method can reduce the computation complexity by log2N times as compared with that for using the IFFT processing.

As mentioned above, the proposed ROC method can reduce the PAPR performance by using the time domain signal obtained after IFFT processing for each cluster as given in (4). From this fact, the computation complexity required in the proposed ROC method would increase as increasing the number of clusters V. To solve the above problem, this paper employs the sprit-radix DIF-IFFT technique [15] for the ROC method to reduce the computation complexity required in the IFFT processing.

Table 1 shows the computation complexity for the processing of IFFT when using the various radix techniques [15]. From the table, it can be observed that the split-radix IFFT which is combined by the radix-2 and radix-4 IFFTs can reduce the computation complexity by 33.3% as compared with the conventional IFFT. From these results, this paper employs the split-radix IFFT for the proposed ROC method to reduce the computation complexity of IFFT processing.

Figure 3 shows the block diagram of the proposed ROC method with the reduction of computation complexity technique when V = 4 and P = 2. In the proposed method, the time domain signals for all clusters which are re-ordered in the frequency domain, are calculated over two OFDM symbols by using (5) with small computation complexity. And the time domain signals for the 1-st and 2-nd symbols after re-ordering of clusters over two OFDM symbol can be obtained by the summation of time domain signals over 4 clusters which is given by the following equation:

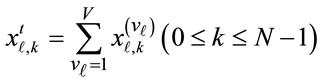. (7)

where 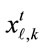is the aggregate time domain signal of 4 clusters for the ℓ-th symbol and vℓ is the cluster number in the ℓ-th symbol after re-ordering of clusters over two OFDM symbols.

In the proposed ROC method, the maximum number of iterations (MAXite) for changing the re-ordering of clusters and the threshold level of PAPR (THPAPR) are pre-determined to reduce the computation complexity.

Figure 4 shows the flow chart for the proposed ROC method when employing MAXite and THPAPR. Firstly, all the sequence patterns for re-ordering of clusters are generated of which the number of sequences is the same as the maximum number of iterations MAXite. The sequence patterns are generated by changing the order of clusters

Table 1. Comparisons of computation complexity for varous Radix IFFT techniques.

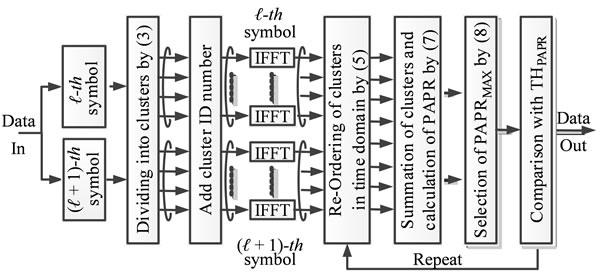
Figure 3. Block diagram of the proposed ROC method.

Figure 4. Flow chart for the low computation complexity technique for the proposed ROC method.

over two symbols randomly. By using the time domain signal given by (7) for each sequence pattern, the PAPR1 and PAPR2 are calculated for the 1-st and 2-nd symbols, respectively. The maximum PMAXite at the ite-th iteration is selected by:

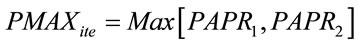. (8)

Then the PMAXite is compared with the given threshold level of THPAPR. If the PMAXite is smaller than the THPAPR, the iteration is stopped and the time domain signals both for the 1-st and 2-nd symbols are transmitted to the channel. If not the iteration is continued by using the next sequence pattern for the re-ordering of clusters. The above procedures are performed up to either the PMAXite is smaller than the THPAPR or the iteration number is reached to the MAXite. If the iteration number is reached to the MAXite, the time domain signals corresponding to the minimum PMAXite obtained among all iterations are transmitted to the channel.

By following the above procedures, the average number of iterations to satisfy the THPAPR would become relatively smaller than the MAXite and consequently the computation complexity which can achieve the better PAPR performance would become smaller.

3.3. Demodulation of Data Information for ROC Method

At the receiver the received time domain signal is converted to the frequency domain signal by FFT which is given by the following equation:

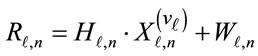. (9)

where is the received signal, 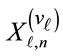is the data information given in (3), 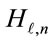is the channel frequency response, 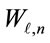is the AWGN at the n-th sub-carrier of the -th symbol, and 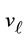is the cluster number within the 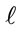-th symbol after re-ordering of clusters at the transmitter. After the frequency domain equalization for (9), all the sub-carriers within each cluster can be demodulated correctly, because the proposed method changes only the location of clusters in the frequency domain at the transmitter. Therefore the cluster ID number embedded in the header of each cluster as shown in Figure 1 can be demodulated without any side information. By using the obtained cluster ID numbers, the original order of clusters over two OFDM symbols can be reconstructed and the data information over two symbols can be demodulated correctly.

4. Performance Evaluation of Proposed ROC Method

This section presents the various computer simulation results to verify the effectiveness of the proposed ROC method as compared with the conventional PTS method. Table 2 shows the list of simulation parameters to be used in the following evaluations.

The computation complexity both for the conventional PTS and proposed ROC methods when employing the predetermined PAPR threshold level THPAPR and the maximum number of iterations MAXite can be given by the following equations:

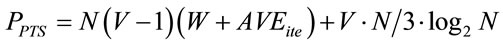(10)

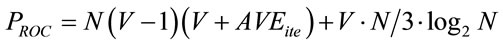(11)

where the computation complexity of the ROC method is evaluated per one OFDM symbol. In (10) and (11) both

Table 2. Simulation parameters.

for the PTS and ROC methods, the first term of the right hand is the required number of multiplication processing. In (10), W is the number of predetermined phase coefficients for the PTS. The second term and the third term both for (10) and (11) are the required number of addition processing and the required processing load when using the sprit-radix IFFT technique as shown in Table 1, respectively. From (10) and (11), it can be seen that when the number of phase coefficients W for the PTS method is the same as the number of clusters V both for the PTS and proposed ROC methods, the computation complexities both for the PTS and ROC become the same.

Table 3 shows the computation complexity for achieving the PAPR performance of 7 dB at CCDF = 10−2 for the proposed ROC and the conventional PTS methods when using the conventional IFFT and the sprit-radix IFFT techniques. The computation complexity is evaluated based on the averaged iteration numbers (AVEite) which is required to satisfy the predetermined threshold level of PAPR (THPAPR). In Table 3, “Improvement from PTS” shows the percentage of reduction in the computation complexity as compared with the PTS method with the conventional IFFT technique when all possible combinations of phase coefficients over V clusters (MAXite = 64) are performed which can achieve the best PAPR performance. From the table, it can be observed that the AVEite for the proposed ROC method would be increasing as decreasing the THPAPR. This is the reason that the required number of iterations to satisfy the lower THPAPR becomes larger. The proposed ROC method with THPAPR = 6.5 dB and the conventional PTS method with THPAPR = 6.1 dB can reduce the computation complexity by 48% from the conventional PTS method with the conventional IFFT technique.

Figure 5 shows the PAPR performance for the pro-

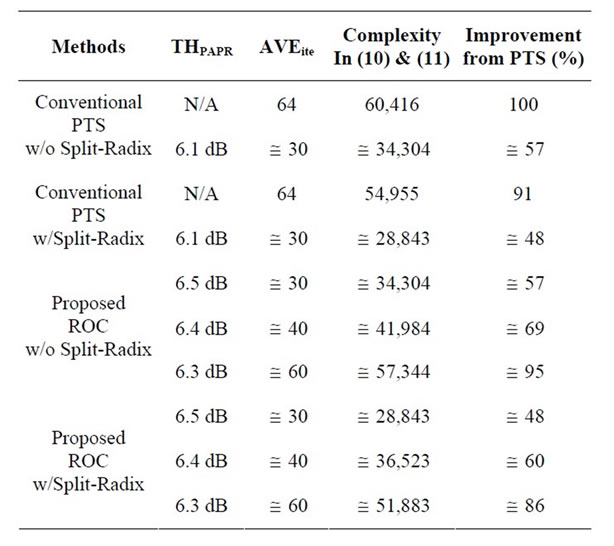
Table 3. Comparisons of Computation complexity for the proposed ROC and conventional PTS methods.

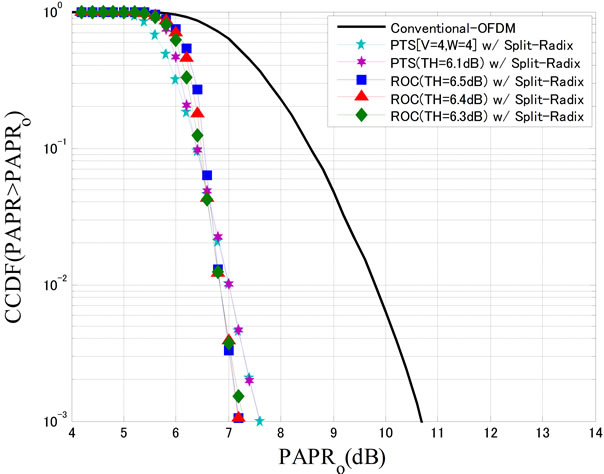
Figure 5. PAPR Performance for the proposed ROC method with sprit-radix IFFT technique.

posed ROC method with the proposed low computation complexity and the split-radix IFFT techniques. In the figure, the conventional OFDM and the PTS methods with the sprit-radix IFFT techniques are also shown. The modulation technique is 16QAM, the number of IFFTpoints N is 256, the number of data subcarriers M is 64 and the number of zero padding Z is 192. The over sampling ratio is taken by 4 to evaluate the PAPR performance precisely. The PAPR performances for the proposed ROC method are evaluated when the MAXite is 256 and the THPAPR are 6.3, 6.4, and 6.5 dB, respectively. In the figure, the PAPR performance is evaluated by using the Complementary Cumulative Distribution Function (CCDF). From the figure, it can be observed that the proposed ROC method with THPAPR = 6.5 dB shows better PAPR performance than the conventional OFDM by 2.8 dB at CCDF = 10−2 and almost the same PAPR performance as the conventional PTS method with THPAPR = 6.1 dB. From Table 3 and Figure 5, it can be concluded that the proposed ROC method with the low computation complexity technique can achieve almost the same PAPR performance with the same computation complexity as that for the conventional PTS method. The advantage of proposed ROC method is to reduce the PAPR performance both for the data information and cluster ID numbers simultaneously which is completely different from the conventional PTS method. In the conventional PTS method, the phase coefficients of PTS are obtained after the PTS processing only for the data information at each OFDM symbol which leads the difficulty to embed the phase coefficients of PTS into the data information separately without degradation of PAPR performance.

5. Conclusions

This paper proposes the new PAPR reduction method based on the packet-switched transmission systems in which all the clusters within the certain number of OFDM symbols have the sequential cluster ID numbers embedded in the header of each cluster. The salient features of the proposed method are to improve the PAPR performance both for the data information and cluster ID numbers simultaneously by re-ordering of clusters in the frequency domain at the transmitter and to reconstruct the original order of clusters by using the cluster ID numbers embedded in the data information at the receiver. This paper also proposes the computation complexity reduction technique for the ROC method by using the feature of IFFT processing. The proposed ROC method is completely different from the PTS method which is required to inform the phase coefficients obtained after the PTS processing as the side information to the receiver separately. From this fact, The PTS method has a difficulty to embed the phase coefficients of PTS into the data information separately without the degradation of PAPR performance.

From the computer simulation results, it is concluded that the proposed ROC method can achieve almost the same PAPR performance and the computation complexity as those for the conventional PTS method. The advantage of the proposed ROC method is to reduce the PAPR performance both for the data information and cluster ID numbers simultaneously which enables the realization of transmitter and receiver much simpler than that for the PTS method.

6. Acknowledgements

The authors would like to thank to the Japanese Government (Monbukagakusho: MEXT) Scholarships who supported this research.

REFERENCES

  1. IEEE Std. 802.11a, “High-Speed Physical Layer in the 5 GHz Band,” 1999. doi:10.1109/IEEESTD.1999.90606
  2. H. Sari, G. Karam and I. Jeanclaude, “Transmission Techniques for Digital Terrestrial TV Broadcasting,” IEEE Communications Magazine, Vol. 33, 1995, pp. 100- 109. doi:10.1109/35.350382
  3. A. Molisch, “3GPP Long Term Evolution,” Wireless Communication, Wiley-IEEE Press, 2011, pp. 665-698.
  4. J. Gozalvez, “Long-Term Evolution advanced Demonstrations [Mobile Radio],” IEEE Vehicular Technology Magazine, Vol. 6, 2011, pp. 4-9. doi:10.1109/MVT.2011.943338
  5. D. Dardari, V. Tralli and A. Vaccari, “A Theoretical Characterization of Nonlinear Distortion Effects in OFDM Systems,” IEEE Transactions on Communications, Vol. 48, No. 10, 2000, pp. 1775-1764. doi:10.1109/26.871400
  6. J. Tellado, “Multicarrier Modulation with Low PAR,” Kluwer Academic Publishers, Dordrecht, 2000. doi:10.1007/b117134
  7. X. Zhong, J. Qi and J. Bao, “Using Clipping and Filtering Algorithm to Reduce PAPR of OFDM System,” Proceedings ICECC International Conference on Electronics, Communications and Control, Ningbo, 2011, pp. 1763- 1766. doi:10.1109/ICECC.2011.6067790
  8. X. D. Zhu, W. S. Pan, H. Li and Y. X. Tang, “Simplified Approach to Optimized Iterative Clipping and Filtering for PAPR Reduction of OFDM Signals,” IEEE Transactions on Communications, Vol. 61, No. 5, 2013, pp. 1891-1901. doi:10.1109/TCOMM.2013.021913.110867
  9. H. B. Mishra, M. Mishra and S. K. Patra, “Selected Mapping Based PAPR Reduction in WiMAX without Sending the Side Information,” Proceedings RAIT Recent Advances in Information Technology, Dhanbad, 15-17 March 2012, pp. 182-184. doi:10.1109/RAIT.2012.6194502
  10. B. Kitaek, S. Changyong and E. J. Powers, “Performance Analysis of OFDM Systems with Selected Mapping in the Presence of Nonlinearity,” IEEE Transactions on Wireless Communications, Vol. 12, No. 5, 2013, pp. 2314-2322. doi:10.1109/TWC.2013.040213.120968
  11. J. Gao, J. Wang, B. Wang and X. Song, “Minimizing PAPR of OFDM Signals Using Suboptimal Partial Transmit Sequences,” Proceedings ICIST International Conference on Information Science and Technology, Hubei, 23-25 March 2012, pp. 776-779. doi:10.1109/ICIST.2012.6221753
  12. M. Gouda and M. Hussien, “Partial Transmit Sequence PAPR Reduction Method for LTE OFDM Systems,” Proceedings ISMS Intelligent Systems Modeling & Simulation, Bangkok, 29-31 January 2013, pp. 507-512. doi:10.1109/ISMS.2013.78
  13. C. Tellambura, “Computation of the Continuous-Time PAPR of an OFDM Signal with BPSK Sub-Carriers,” IEEE Communications Letters, Vol. 5, No. 5, 2001, pp. 185-187. doi:10.1109/4234.922754
  14. T. Mata, K. Naito, P. Boonsrimuang, K. Mori and H. Kobayashi, “Proposal of PAPR Reduction Method for OFDM Signal by Re-Ordering of Clusters,” Proceedings APCC Asia-Pacific Conference on Communications, Bali, 2013 (to be published).
  15. P. Boonsrimuang, P. Reangsuntea, P. Boonsrimuang and H. Kobayashi, “Proposal of Improved PTS Method Based on Split-Radix IFFT for OFDM Signal,” Computer Technology and Application, Vol. 3, 2012, pp. 425-230.

Journal Menu >>