Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 4 (2012) , Article ID: 18519 , 5 pages DOI:10.4236/ijcns.2012.54026
Improved Balas and Mazzola Linearization for Quadratic 0-1 Programs with Application in a New Cutting Plane Algorithm
Department of Computer Science, College of Computer Science & Information Systems, Jazan University, Jazan, KSA
Email: gharibi@jazanu.edu.sa
Received December 9, 2011; revised December 26, 2011; accepted January 20, 2012
Keywords: Quadratic Program; Integer program; Linearization; Cutting plane algorithm
ABSTRACT
Balas and Mazzola linearization (BML) is widely used in devising cutting plane algorithms for quadratic 0-1 programs. In this article, we improve BML by first strengthening the primal formulation of BML and then considering the dual formulation. Additionally, a new cutting plane algorithm is proposed.
1. Introduction
In this article, we consider the generalized quadratic 0-1 program given as follows
 (1.1)
(1.1)
where 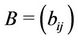 is an
is an  nonnegative matrix. Without loss of generality we assume
nonnegative matrix. Without loss of generality we assume 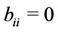 since
since 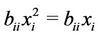 . Problem (P) is a generalization of unconstrained zero-one quadratic problems, zero-one quadratic knapsack problems, quadratic assignment problems and so on. It is a classical NP-hard problem [1].
. Problem (P) is a generalization of unconstrained zero-one quadratic problems, zero-one quadratic knapsack problems, quadratic assignment problems and so on. It is a classical NP-hard problem [1].
Linearization strategies are to reformulate the zero-one quadratic programs as equivalent mixed-integer programming problems with additional binary variables and/or continuous variables and continuous constraints, see [2- 8]. Recently, Sherali and Smith [9] developed small linearizations for more generalized quadratic 0-1 programs. Gueyea and Michelon [10] proposed a framework for unconstrained quadratic 0-1 programs. These linearizations are standard for employing exact algorithms such as branch and bound. Balas and Mazzola proposed a small-size linearization [11] and then successfully applied it to devise exact or heuristic cutting plane algorithms.
In this article, we focus on new small-size tight linearizations. We first propose a primal version of Balas and Mazzola linearization (BML). By strengthening the linearization and then considering the dual model, we obtain a new linearization which improves BML. As a direct application, a new cutting plane algorithm is proposed.
This article is organized as follows. In Section 2, we discuss Balas and Mazzola linearization (BML) [11] and the related primal linearization. In Section 3, we create a new approach to obtain a tighter linearization. It improves the primal linearization of BML in the sense that the linear programming relaxation often give tighter lower bound. In Section 4, we apply this dual linearization to devise cutting plane algorithm and compare the efficacy with that of BML. Concluding remarks are made in Section 5.
2. The Primal Model of Balas and Mazzola Linearization
In this section, we show that Balas and Mazzola Linearization has a primal model.
Define a column vector  with components
with components
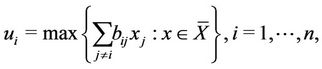 (2.1)
(2.1)
where 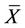 is any suitable relaxation of
is any suitable relaxation of 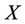 such that the problems (1) can be solved relatively easily.
such that the problems (1) can be solved relatively easily.
We rewrite the objective function of (P) as
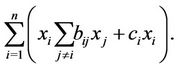
Introducing 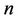 continuous variables
continuous variables
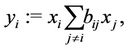 (2.2)
(2.2)
we can obtain the following mixed 0-1 linear program
 (2.3)
(2.3)
where the two series inequality constraints follow from the fact  and
and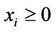 ,
,  , respectively.
, respectively.
Theorem 2.1. Problems (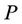 ) and (
) and (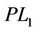 ) are equivalent in the sense that for each optimal solution to one problem, there exists an optimal solution to the other problem having the same optimal objective value.
) are equivalent in the sense that for each optimal solution to one problem, there exists an optimal solution to the other problem having the same optimal objective value.
The proof is found in Appendix 1.
Remark 2.1. If we restrict (P) as the quadratic assignment problem, the proposed linearization (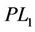 ) reduces to Kaufman-Broeckx linearization [12,13].
) reduces to Kaufman-Broeckx linearization [12,13].
Below we apply Benders’ decomposition approach to Problem (P), as in [14]. Firstly, (P) can be decomposed in the following way
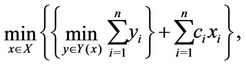 (2.4)
(2.4)
where
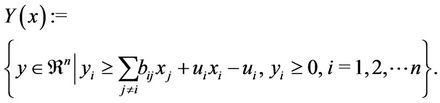 (2.5)
(2.5)
For fixed , we dualize the first series constraints of the problem
, we dualize the first series constraints of the problem 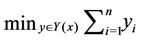 using Lagrangian multipliers
using Lagrangian multipliers  (
( ). We obtain the subproblem
). We obtain the subproblem
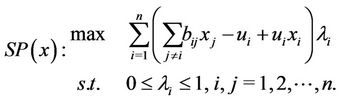 (2.6)
(2.6)
Note that the feasible solution region  of SP(x) does not depend on the chosen vector
of SP(x) does not depend on the chosen vector . Let
. Let  be the incidence vectors of the extreme points of
be the incidence vectors of the extreme points of  (which is unit hypercube in
(which is unit hypercube in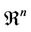 ). Introducing
). Introducing
 (2.7)
(2.7)
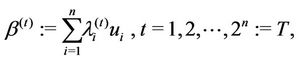 (2.8)
(2.8)
we can see that Problem (4) is equivalent to
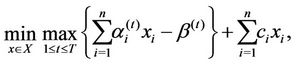 (2.9)
(2.9)
by the fact that for any fixed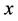 , the second-stage problem
, the second-stage problem  of (4) is a linear programming whose dual formulation is just (6) and the fact that one of the optimal solutions to the linear programming problem (6) is attained at an extreme point of
of (4) is a linear programming whose dual formulation is just (6) and the fact that one of the optimal solutions to the linear programming problem (6) is attained at an extreme point of . Problem (9) yields now the following mixed 0-1 linear program
. Problem (9) yields now the following mixed 0-1 linear program
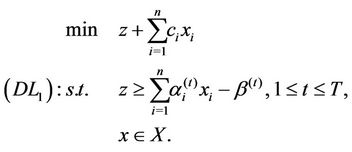 (2.10)
(2.10)
In some sense, linearization ( ) can be regarded as the dual formulation of (PL1). Above we also obtained the equivalence between (PL1) and (
) can be regarded as the dual formulation of (PL1). Above we also obtained the equivalence between (PL1) and (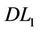 ):
):
Theorem 2.2. Problems (PL1) and (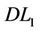 ) are equivalent in the sense that for each optimal solution to one problem, there exists an optimal solution to the other problem having the same optimal objective value.
) are equivalent in the sense that for each optimal solution to one problem, there exists an optimal solution to the other problem having the same optimal objective value.
Combining Theorem 2.1 with Theorem 2.2, we can see ( ) is equivalent to (P). In literature, linearization (
) is equivalent to (P). In literature, linearization (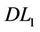 ) is known as Balas and Mazzola linearization (BML) [11].
) is known as Balas and Mazzola linearization (BML) [11].
3. New Tight Primal and Dual Linearizations
In this section, we propose a new approach to establish new tight linearizations.
Define
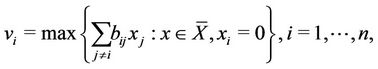 (3.1)
(3.1)
 (3.2)
(3.2)
Let  and
and  be the vectors with components
be the vectors with components 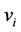 and
and 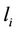 respectively,
respectively, .
.
Lemma 3.1. [15] Let . For all
. For all 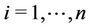 ,
,
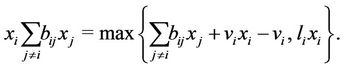 (3.3)
(3.3)
Therefore, the new linearization reads
 (3.4)
(3.4)
Under the linear transformations  the above linearization becomes
the above linearization becomes
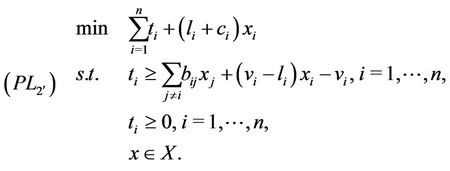 (3.5)
(3.5)
As a corollary of Lemma 3.1, we have Theorem 3.1. Problems ( ) (or (
) (or (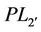 )) and (P) are equivalent in the sense that for each optimal solution to one problem, there exists an optimal solution to the other problem having the same optimal objective value.
)) and (P) are equivalent in the sense that for each optimal solution to one problem, there exists an optimal solution to the other problem having the same optimal objective value.
Continuously relaxing linearizations ( ) and (
) and ( ), i.e., replacing
), i.e., replacing 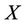 with
with , we obtain linear programming lower bounds for (P), denoted by
, we obtain linear programming lower bounds for (P), denoted by  and
and  respectively. (
respectively. (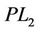 ) is not weaker than (
) is not weaker than ( ) in the following sense.
) in the following sense.
Theorem 3.2.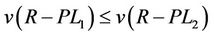 .
.
Proof. It is sufficient to show any feasible solution of (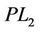 ) is also feasible in (
) is also feasible in (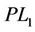 ), which follows from the fact that
), which follows from the fact that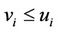 ,
, 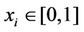 and
and 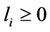 since
since 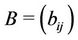 is nonnegative. □
is nonnegative. □
Next, we consider the dual model of (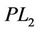 ). As the formulation of (
). As the formulation of (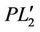 ) is similar to that of (
) is similar to that of ( ), we immediately have the dual model based on (
), we immediately have the dual model based on ( ).
).
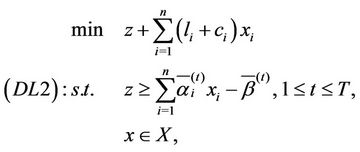 (3.6)
(3.6)
where
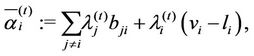 (3.7)
(3.7)
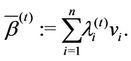 (3.8)
(3.8)
Similarly to Theorem 2.2, we have Theorem 3.3. Problems (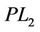 ) (or (
) (or (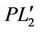 ) and (
) and (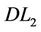 ) are equivalent in the sense that for each optimal solution to one problem, there exists an optimal solution to the other problem having the same optimal objective value.
) are equivalent in the sense that for each optimal solution to one problem, there exists an optimal solution to the other problem having the same optimal objective value.
4. Cutting Plane Algorithms Based on Dual Linearizations
We first establish cutting plane algorithm based on ( ). As in any decomposition approach the master problem (
). As in any decomposition approach the master problem (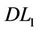 ) is not solved for all restrictions
) is not solved for all restrictions 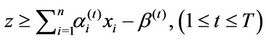 , but only for a subset
, but only for a subset 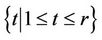 of indices. We denote the restricted master problem by
of indices. We denote the restricted master problem by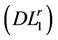 .
.
Getting a solution  for the restricted master problem, the subproblem
for the restricted master problem, the subproblem 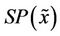 is solved, which yields
is solved, which yields
 (4.1)
(4.1)
 is an optimal solution of the subproblem
is an optimal solution of the subproblem  because of the definition of the constants
because of the definition of the constants  and the constraints
and the constraints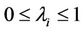 .
.
A new cut
 (4.2)
(4.2)
is added to the current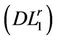 . Thus we get
. Thus we get .
.
The objection function value 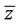 of
of 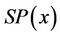 is an upper bound for (P), whereas the objective function value
is an upper bound for (P), whereas the objective function value 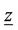 of the master problem
of the master problem  is a lower bound. If
is a lower bound. If , stop and return an optimal solution.
, stop and return an optimal solution.
This is the flow of cutting plane algorithm. Below we show the finite convergence. The proof is found in Appendix 2.
Lemma 4.1. Assume that 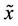 is an optimal solution of
is an optimal solution of 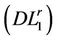 and
and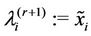 . For any
. For any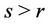 ,
, 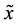 cannot be an optimal solution of
cannot be an optimal solution of 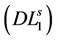 unless it is the optimal solution of (P).
unless it is the optimal solution of (P).
From the above lemma, we have the convergence result proved in Appendix 3.
Theorem 4.1. The above cutting plane algorithm stops in a finite number of steps and returns the optimal solution of (P).
Cutting plane algorithm based on (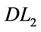 ) can be similarly devised. To compare with (
) can be similarly devised. To compare with ( ) conveniently, instead of (
) conveniently, instead of ( ), we use the following equivalent model
), we use the following equivalent model
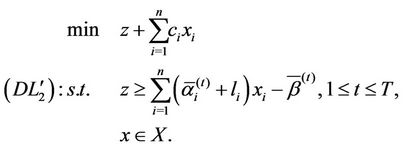 (4.3)
(4.3)
Theorem 4.2. Assume 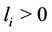 for all
for all . The restricted master program (
. The restricted master program (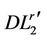 ) gives a lower bound strictly better than that of (
) gives a lower bound strictly better than that of (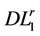 ) until the cutting plane algorithm stops.
) until the cutting plane algorithm stops.
5. Conclusion
In this article, we focus on the generalized quadratic 0-1 program, denoted by (P). We propose a linearization (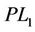 ) for (P) and show that it can be regarded as a dual formulation of Balas and Mazzola linearization (BML), denoted (
) for (P) and show that it can be regarded as a dual formulation of Balas and Mazzola linearization (BML), denoted (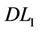 ). By applying a new approach, we establish a tight linearization (
). By applying a new approach, we establish a tight linearization ( ) of the same size. We proved (
) of the same size. We proved ( ) is not weaker than (
) is not weaker than (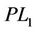 ) in the sense that the continuous linear programming relaxation of (
) in the sense that the continuous linear programming relaxation of (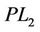 ) gives tighter lower bound than that of (
) gives tighter lower bound than that of (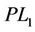 ). The dual linearizations of (
). The dual linearizations of (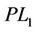 ) and (
) and (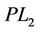 ), (
), (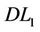 ) and (
) and ( ) are successfully used in devising cutting plane algorithms, respectively. We showed that the cutting plane algorithm based on (
) are successfully used in devising cutting plane algorithms, respectively. We showed that the cutting plane algorithm based on ( ) is strictly better than that of (
) is strictly better than that of (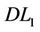 ) under some weak assumptions.
) under some weak assumptions.
REFERENCES
- M. R. Garey and D. S. Johnson, “Computers and Intractability: A Guide to the Theory of NP-Completeness,” WH Freeman & Co., New York, 1979.
- W. Chaovalitwongse, P. M. Pardalos and O. A. Prokopyev, “A New Linearization Technique for Multi-Quadratic 0-1 Programming Problems,” Operations Research Letters, Vol. 32, No. 6, 2004, pp. 517-522. doi:10.1016/j.orl.2004.03.005
- S. Elloumi, A. Faye and E. Soutif, “Decomposition and Linearization for 0-1 Quadratic Programming,” Annals of Operations Research, Vol. 99, No. 1-4, 2000, pp. 79-93. doi:10.1023/A:1019236832495
- R. Fortet, “L’algebre de Boole et ses Applications en Recherche Operationnelle,” Cahiers du Centred Études de Recheche Operationnelle, Vol. 1, No. 4, 1959, pp. 5-36.
- F. Glover, “Imporved Linear Integer Programming Formulations of Nonlinear Integer Problems,” Management Science, Vol. 22, No. 4, 1975, pp. 455-460. doi:10.1287/mnsc.22.4.455
- F. Glover and E. Woolsey, “Further Reduction of ZeroOne Polynomial Programming Problems to Zero-One Linear Programming Problems,” Operations Research, Vol. 22, No. 1, 1973, pp. 156-161. doi:10.1287/opre.21.1.156
- F. Glover and E. Woolsey, “Converting the 0-1 Polynomial Programming Problem to a 0-1 Linear Program,” Operations Research, Vol. 22, No. 1, 1974, pp. 180-182. doi:10.1287/opre.22.1.180
- L. Liberti, “Compact Linearization of Binary Quadratic Problems,” 4OR, Vol. 5, No. 3, 2007, pp. 231-245.
- H. D. Sherali and J. C. Smith, “An Improved Linearization Strategy for Zero-One Quadratic Programming Problems,” Optimization Letters, Vol. 1, No. 1, 2007, pp. 33- 47. doi:10.1007/s11590-006-0019-0
- S. Gueyea and P. Michelon, “A Linearization Framework for Unconstrained Quadratic (0-1) Problems,” Discrete Applied Mathematics, Vol. 157, No. 6, 2009, pp. 1255- 1266. doi:10.1016/j.dam.2008.01.028
- E. Balas and J. B. Mazzola, “Quadratic 0-1 Programming by a New Linearization,” The TIMS/ORSA Meeting, Washington DC, 1980.
- L. Kaufman and F. Broeckx, “An Algorithm for the Quadratic Assignment Problem Using Bender’s Decomposition,” European Journal of Operational Research, Vol. 2, No. 3, 1978, pp. 204-211.
- Y. Xia and Y. Yuan, “A New Linearization Method for Quadratic Assignment Problems,” Optimization Methods and Software, Vol. 21, No. 5, 2006, pp. 803-816.
- R. E. Burkard and U. Derigs, “Assignment and Matching Problems: Solution Methods with FORTRAN-Programs,” Springer-Verlag, Berlin, 1980.
- W. Gharibi and Y. Xia, “A Tight Linearization Strategy for Zero-One Quadratic Programming Problems,” in press, 2012.
Appendix
1) Proof of Theorem 2.1 Let 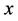 be any feasible solution to (P). It is easy to verify that
be any feasible solution to (P). It is easy to verify that  is feasible in (
is feasible in (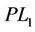 ) with the same objective value, where
) with the same objective value, where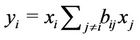 . As a consequence, the optimal objective value of (
. As a consequence, the optimal objective value of ( ) gives a lower bound for (P). It is sufficient to show that if
) gives a lower bound for (P). It is sufficient to show that if 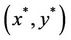 is an optimal solution to (
is an optimal solution to (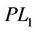 ),
),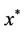 is optimal in (P) with the same objective value. We notice that
is optimal in (P) with the same objective value. We notice that
 . If
. If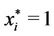 , we have
, we have , otherwise,
, otherwise,  ,
,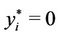 . As a conclusion,
. As a conclusion,  which implies
which implies
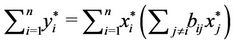 . That is,
. That is, 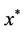 is a feasible solution to (P) whose objective value equals a lower bound. Therefore,
is a feasible solution to (P) whose objective value equals a lower bound. Therefore, 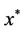 is optimal in (P) and both the optimal objective values are equal.
is optimal in (P) and both the optimal objective values are equal.
2) Proof of Lemma 4.1 Denote the optimal objective function value of any master problem 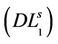 by
by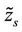 , which is a lower bound for (P). If
, which is a lower bound for (P). If 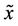 is also an optimal solution of
is also an optimal solution of  for some
for some , it follows that
, it follows that
 (2.1)
(2.1)
since 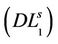 contains the constraint (2). The left-hand side of (4) is a lower bound for (P) while the right-hand side of (4) corresponds to a feasible objective function value of (P), which can be shown as follows:
contains the constraint (2). The left-hand side of (4) is a lower bound for (P) while the right-hand side of (4) corresponds to a feasible objective function value of (P), which can be shown as follows:
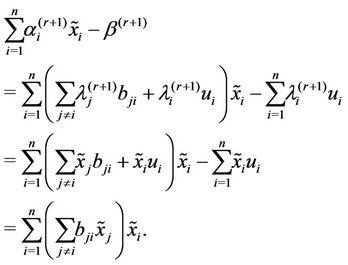
Therefore (4) holds as equality and  must be the optimal solution of (P).
must be the optimal solution of (P).
3) Proof of Theorem 4.2 If the cutting plane algorithm based on (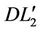 ) has not stopped at step
) has not stopped at step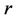 , the optimal solution
, the optimal solution  must be different from
must be different from 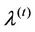 for any
for any , i.e., there exist index
, i.e., there exist index  such that
such that . Then the righthand side of (
. Then the righthand side of (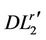 ) satisfies
) satisfies
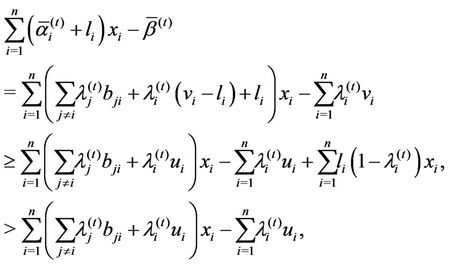 (3.1)
(3.1)
for any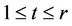 . Therefore the objective function value of (
. Therefore the objective function value of (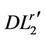 ) is strictly larger than that of
) is strictly larger than that of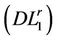 .
.

