Int'l J. of Communications, Network and System Sciences
Vol.4 No.2(2011), Article ID:4022,6 pages DOI:10.4236/ijcns.2011.42010
Performance of Block Diagonalization Scheme for Downlink Multiuser MIMO System with Estimated Channel State Information
School of Information Technology and Electrical Engineering, The University of Queensland, Brisbane, Australia
E-mail: {fwang, meb}@itee.uq.edu.au
Received December 7, 2010; revised January 8, 2011; accepted January 10, 2011
Keywords: MIMO, Block Diagonalization, Sum Rate
Abstract
In this paper, we study the performance of block diagonalization (BD) scheme for a downlink multiuser multi-input multi-output (MIMO) system with imperfect channel state information (CSI). At each mobile user, information about the channel is obtained by applying the minimum mean-square-error (MMSE) channel estimation method. The channel state information is fed back to the base station through error-free uplink channels. A theoretical analysis is performed showing that channel estimation errors contribute to co-channel interferences thus deteriorating sum rate capacity. Computer simulations are performed to evaluate the impact of channel estimation errors on the sum rate capacity. The results show that if the MSE of the channel estimation is not less than 10-2, the impact of channel estimation errors is significant and cannot be neglected. To combat this adverse effect, a proper transmit power level is required for the training signals.
1. Introduction
In the last decade, wireless MIMO communication systems employing multiple antennas at transmitter and receiver have received a considerable attention. The main reason is that MIMO technology is capable of improving significantly the signal transmission quality in rich scattering environment without the need for extra operational frequency bandwidth [1]. Recently, a significant shift of research focus has been observed from peer-to-peer links to multiuser MIMO systems [2]. A multiuser MIMO system typically consists of a base station equipped with multiple antennas and a number mobile users, each possibly equipped with multiple receive antennas. The base station transmits data to these mobiles users. To eliminate or reduce interference, the base station is required to employ orthogonalization techniques. These orthogonalization techniques distribute signals to mobile users among different dimensions of resources and thus obtain a minimum interference between them. One of the popular orthogonalization techniques is the time division multiple access (TDMA) technique. With TDMA, the base station transmits to a mobile user on a particular time slot. Alternatively, the base station can transmit to multiple users simultaneously by employing other orthogonalization techniques such as dirty-paper-coding (DPC) [3] or multiple beamforming [4]. DPC pre-cancels interference at the base station by using the perfect channel state information (CSI) and the full knowledge of the transmitted signals. Information theoretic works have proved that DPC is capable of achieving sum capacity [5,6]. However, it is not suitable for implementation in practical systems because of its complexity. Due to this reason, researchers have investigated a number of sub-optimal approaches. Among them, BD has been proved to have the ability of achieving a large fraction of DPC capacity with much reduced complexity [4] In this approach, the base station transmits signals to multiple mobile users by applying orthogonal beamforming weights. As a result, each mobile user’s beamforming weights lie in the null space of all other mobile users’ channels. This is equivalent to having orthogonal channels between different mobile users.
BD scheme is an attractive orthorgonalization scheme for its low complexity and acceptable sum capacity. Attention has been focused on improving the performance of BD under realistic scenarios. In [7], an improved BD algorithm that accounts for the presence of other cell interferences is proposed under the assumption that the transmitter has full CSI and the information about the interference plus noise covariance matrix for in-cell users. Researchers have also considered an impact of an antenna array configuration and mutual coupling on the sum capacity promised by BD. In [8], the impact of mutual coupling on BD performance in terms of sum rate capacity is addressed. In, [9] comparisons between BD schemes employing uniform circular array (UCA) and uniform linear array (ULA) are given. To further improve the sum capacity, a fast antenna selection scheme at base station is presented in [10]. However, most of the existing research results are based on the assumption of perfect channel state information at mobile users. In practical situations, the mobile users obtain CSI by applying channel estimation schemes. In this paper, we assume that the mobile users employ the training-based MMSE channel estimation [11]. Based on this assumption, we evaluate the impact of channel estimation errors on the performance of a multiuser MIMO system employing BD scheme in terms of sum rate capacity.
The paper is structured as follows. Section 2 presents the system model. In Section 3, the BD scheme is introduced. Section 4 is devoted to the channel estimation by mobile users. We introduce the channel estimation errors into the BD scheme and present an analysis of the impact of channel estimation errors on the system capacity in Section 5. Section 6 presents numerical results accompanied by discussion. Section 7 concludes the paper.
2. System Model
Figure 1 illustrates a multiuser MIMO system model. We consider a downlink scenario, where the base station broadcasts information to L mobile users. We assume that K out of L mobile users are scheduled by higher layers scheme, and each selected mobile user receives multiple data streams. The base station employs Nt transmit antennas and the kth mobile user is equipped with nk receiving antennas. The downlink complex channel matrix

Figure 1. Multiuser MIMO system model.
between the base station and the kth mobile terminal is denoted by  The elements of Hk are described by zero-mean circular symmetric complex Gaussian random variables, which are appropriate for a narrow-band system operating in a non-line-of-sight (NLOS) rich scattering environment. The (p,q)th elements of Hk represent the channel fading between the qth transmitting antennas at base station and the pth receiving antenna at the kth mobile user. The mobile terminals are spatially separated As they do not share the same scattering environment, it is assumed that they experience independent fading.
The elements of Hk are described by zero-mean circular symmetric complex Gaussian random variables, which are appropriate for a narrow-band system operating in a non-line-of-sight (NLOS) rich scattering environment. The (p,q)th elements of Hk represent the channel fading between the qth transmitting antennas at base station and the pth receiving antenna at the kth mobile user. The mobile terminals are spatially separated As they do not share the same scattering environment, it is assumed that they experience independent fading.
By assuming  denotes the transmitted signal vector intended for the kth mobile user, and ηk ∈ CMk×1 represents the zero-mean additive white Gaussian noise vector with variance
denotes the transmitted signal vector intended for the kth mobile user, and ηk ∈ CMk×1 represents the zero-mean additive white Gaussian noise vector with variance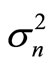 , the Mk × 1 received signal vector at the kth mobile terminal is given as
, the Mk × 1 received signal vector at the kth mobile terminal is given as
 (1)
(1)
It is assumed that there are Lk data streams intended for the kth mobile terminal. Assuming that the beamforming process takes place at the base station, the transmitted signals can be written as
 (2)
(2)
where 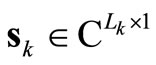 represents the data streams for the kth mobile terminal and
represents the data streams for the kth mobile terminal and 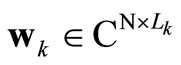 denotes the beamforming matrix for the for the kth mobile terminal.
denotes the beamforming matrix for the for the kth mobile terminal.
3. Linear Beamforming Schemes
The received signal at the kth MS, given as (1), is rewritten as
 (3)
(3)
where the second term represents the co-channel interference (CCI) caused by the multiuser sharing the downlink resources. The principal idea of the block diagonalization is to find the beamforming vectors which can zero-force the CCI. To enable the users to receive their own data with a zero co-channel interference, the base station has to apply the transmit beamforming weights such that
 (4)
(4)
With the beamforming vectors satisfying (4), the CCI is completely eliminated and thus the kth MS observes a point-to-point MIMO link with the base station.
By defining
 (5)
(5)
the constraint of (4) can be rewritten as
 (6)
(6)
Equation (6) indicates that the beamforming vectors for the kth mobile user should lie in the null space of (5). By applying singular value decomposition (SVD), the following is obtained
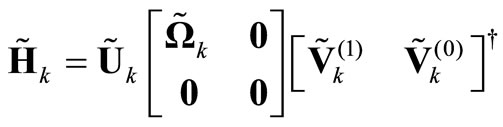 (7)
(7)
where  is the diagonal matrix with all non-negative singular values.
is the diagonal matrix with all non-negative singular values. 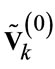 contains vectors corresponding to the zero singulars. They form an orthogonal basis for the space of (5). The columns are the candidate beamforming vectors.
contains vectors corresponding to the zero singulars. They form an orthogonal basis for the space of (5). The columns are the candidate beamforming vectors.
By using the beamforming vectors generated by (7), the CCI is completely eliminated and the mobile users observe point-to-point MIMO links with the base station. As a result, the effective MIMO link for the kth mobile user is described by
 (8)
(8)
Therefore, the broadcasting sum rate capacity for a downlink multiuser MIMO system employing block diagonalization scheme can be written as
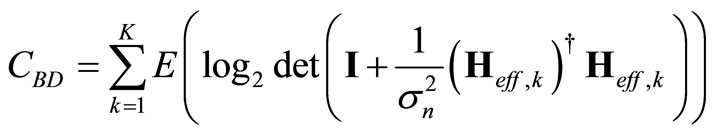 (9)
(9)
4. Channel Estimation Errors
We assume that training-based MIMO channel estimation methods are employed by the multiuser MIMO system, where the base station is broadcasting pilot signals to mobile users and all the mobile users perform channel estimation independently. The mobile users send the estimated channel state information to the base station via uplink feedback channels. Based on these channel state information, the base station performs beamforming, interference cancellation and downlink data transmission. In Figure 2" target="_self"> Figure 2, a basic downlink information frame structure is shown.
Assuming M ≥ N represent the number of the training signal vectors, the training sequences can be given as
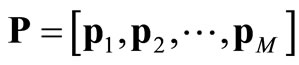 (10)
(10)
All the elements of the optimal training matrix should have the same magnitude. One of the most popular training matrices is given as [12]
 (11)
(11)
where  and
and  is the transmitted training power constraint. As a result, the received signals at the kth mobile user can be expressed as
is the transmitted training power constraint. As a result, the received signals at the kth mobile user can be expressed as
 (12)
(12)
The task of the mobile users at this stage is to recover the channel matrix between the base station and the kth mobile user based on the knowledge of the received signals Sk and the training matrix P. Different methods, including least squares (LS), minimum mean-squareerror (MMSE) and their improved versions [11], can be employed by the MIMO channel estimator at the kth mobile user. We assume that the output of the channel estimator at the kth mobile user is . The channel estimation error can be expressed by an error matrix, which is given as
. The channel estimation error can be expressed by an error matrix, which is given as
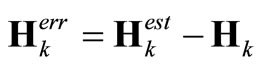 (13)
(13)
The performance of the channel estimator is characterized by the error matrix given by (13) and evaluated in terms of mean-square-error (MSE). The MSE of the channel estimator at the kth mobile user is expressed by
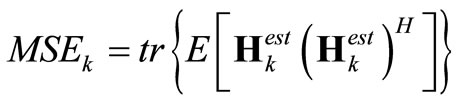 (14)
(14)
where tr(∙) represents the trace operation over a matrix and (∙)H is the conjugate transpose of a matrix. Smaller values of MSE indicate a higher accuracy of the channel estimation. For a given MIMO channel estimator, the MSE of the channel estimator is decided by a few factors, including transmitted power to noise ratio (TPNR) in the training mode, and the number of antenna elements at the transmitter and receiver.
5. Sum-Rate Capacity with Channel Estimation Errors
We assume that the uplink CSI feedback channels are error-free. Consequently, the base station has an access to the same channel estimation results as the active mobile

Figure 2. Frame structure of downlink information.
users. Based on these CSI, the base station performs beamforming, power allocation and data transmission. By using the estimated CSI, the Formula (3) can be rewritten as
 (15)
(15)
We can see that in (15), the kth mobile user is receiving the signals inclusive the co-channel interference (CCI) from other mobile users, white additive noise and the interference caused by channel estimation errors. With the channel estimation errors taken into account, the overall estimated channel matrices are given as
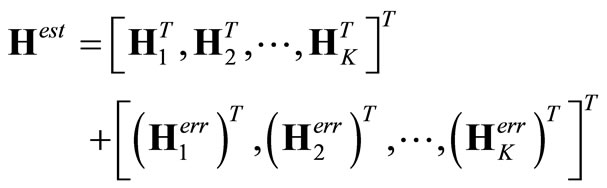 (16)
(16)
Following (16), the co-channel mobile users’ they can be expressed as
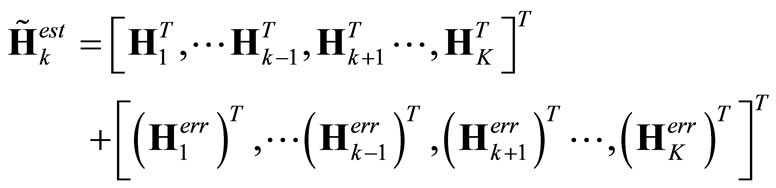 (17)
(17)
To cancel the co-channel interference, the weights for the kth mobile user should be lying in the null space of (17). By performing SVD over the co-channel mobile users’ overall channel, we have
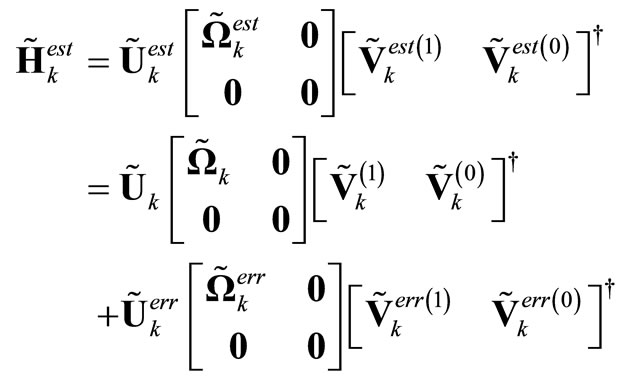 (18)
(18)
The first term in (18) is the SVD result of the error-free overall matrix and the second term represents the SVD result of the channel estimation error matrix. As a result of (18), the candidate beamforming vectors for the kth mobile user are given as . By setting the beamforming vectors as
. By setting the beamforming vectors as
 (19)
(19)
The effective MIMO link with the channel estimation errors taken into account for the kth mobile user is described by
 (20)
(20)
However, due to the existing channel estimation errors, the constraint shown by (6) is obviously not held any more, and has been changed to
 (21)
(21)
Formula (21) shows that the channel estimation errors contribute to co-channel interference. The channel capacity between the base station and the kth mobile user can then be written as
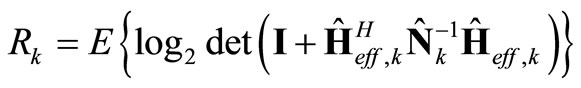 (22)
(22)
where 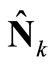 is the noise and coherent channel interference matrix for the kth mobile terminal. It can be represented by
is the noise and coherent channel interference matrix for the kth mobile terminal. It can be represented by
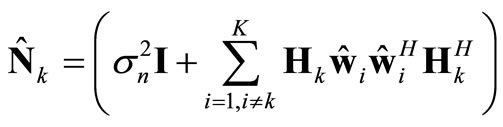 (23)
(23)
6. Numerical Results
In this section, we evaluate the performance of the linear beamforming schemes for the downlink multiuser MIMO system with the imperfect channel state information, which is obtained by the channel estimators at the mobile users. We assume that the mobile users employ the same channel estimator and they perform channel estimation independently. We assume that all the mobile users employ the MMSE channel estimator. We refer a multiuser MIMO system as 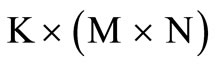 system, where K represents the number of mobile users, M is the number of receive antennas at the mobile user and N refers to the number of antennas at the base station. As Monte Carlo approach is applied, each point in the presented results is obtained from an average of 10000 independent simulation runs.
system, where K represents the number of mobile users, M is the number of receive antennas at the mobile user and N refers to the number of antennas at the base station. As Monte Carlo approach is applied, each point in the presented results is obtained from an average of 10000 independent simulation runs.
Figure 3 displays the channel estimation MSE of MMSE estimator for the kth mobile user. Two situations are included, in where the numbers of transmit antenna are fixed to 8 and 4, while the number of receive antenna at the kth mobile user is varied.
It can be seen in Figure 3 that when the number of transmit antenna is fixed to 8 or 4 and the performance of the MMSE channel estimator deteriorates with the number of the receiving antennas. At the same time, it can also be noted that if number of receiving antennas at the mobile users is fixed, a decreased number of transmit antenna at the base station results in an increased performance of MMSE channel estimator. More specifically, at SNR=20dB, the MMSE channel estimator at a mobile user with 2 receive antennas achieves MSE = 0.725 for the situation where the number of transmit antennas is 8 and MSE = 0.240 when the number of transmit antenna is 4.
In Figures 4 and 5, the impact of channel estimation error on the performance of multiuser MIMO system in terms of sum rate capacity is investigated. The sum rate of the block diagonalization is illustrated as a function of data SNR and channel estimation MSE. It can be seen from these figures that the presence of channel estimation errors deteriorates the sum rate capacity. In the region of low SNR, the noise has a dominating impact on the performance of the block diagonalization while the co-channel interference introduced by channel estimation errors has a limited impact. As a result, the sum rate capacity varies slightly with MSE. In the region of high SNR, the co-channel interference introduced by channel estimation errors takes the dominating role and has a significant impact on the sum rate capacity.
When the MSE is greater or equal to 10-1, the existence of channel estimation errors significantly decreases

Figure 3. Channel estimation MSEs of the MMSE estimator versus SNR.
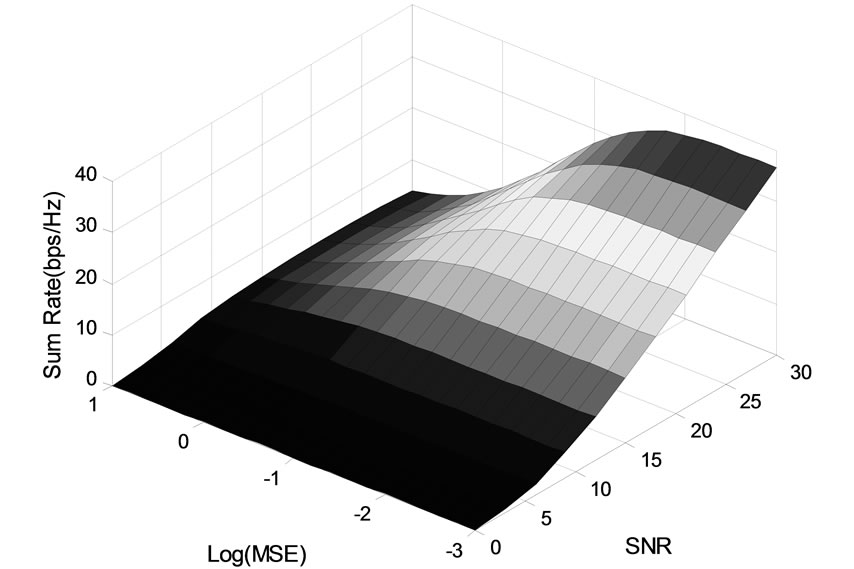
Figure 4 Impact of channel estimation error on the sum rate capacity of 2× (2 × 4) system.

Figure 5. Impact of channel estimation error on the sum rate capacity of 4 × (2 × 8) system.
the sum rate capacity. When the MSE is smaller or equal to 10-2, the impact of channel estimation errors is small and can be neglected. The simulation results also indicate that a reasonable transmit power (or SNR) is required for the training signals to make sure that the channel estimator at mobile users have a channel estimation MSE as low as 10-2.
Figure 6 and Figure 7 present the cumulative distribution of the sum rate capacity for 2× (2 × 4) and 4 × (2 × 8) systems, respectively.
These two figures further confirm the results shown earlier in Figures 5 and 6. The presence of channel estimation errors has a negative impact on the sum rate capacity of a multiuser MIMO system. It can be observed from the presented results that the gaps between the sum rates for the same MSE with different SNR levels (15 dB for red plots and 30 dB for blue plots) decrease with the MSE. To combat the negative impact brought by channel estimation errors, a higher transmit power is required for data transmission. In Figure 6, it can be seen that the 2× (2 × 4) system achieves similar capacity when the channel

Figure 6. CDF of sum rate capacity for a 2 × (2 × 4) system.
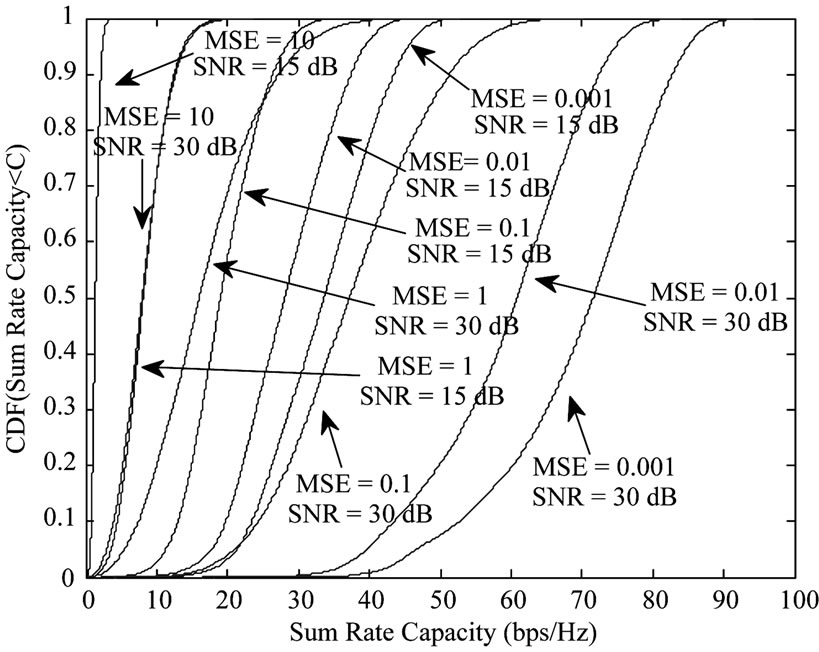
Figure 7. CDF of sum rate capacity for a 4 × (2 × 8) system.
estimation error MSE = 1 at SNR = 15 dB and MSE = 10 at SNR = 30 dB. These results indicate that to combat the increased MSE from 1 to 10, an increased transmit data SNR from 15 dB to 30 dB is required. In Figure 7, it can be seen that the 4× (2 × 8) system achieves similar capacity for the situations when channel estimation MSE = 1 at SNR = 15 dB and channel estimation MSE = 10 at SNR = 30 dB. These results show that to combat the increased MSE from 1 to 10, an increased transmit SNR from 15 dB to 3dB is required.
7. Conclusions
In this paper, we have investigated the impact of channel estimation errors on the performance of block diagonalization scheme for a multiuser MIMO system. Theoretical analysis has been presented showing that the presence of channel estimation error contributes to co-channel interference of the mobiles users, thus rendering deteriorated sum rate capacity of the system. Monte Carlo simulations have been carried out to evaluate the impact of channel estimation errors on the performance of multiuser system in terms of sum rate capacity. The results have shown that to combat the negative impact brought by channel estimation errors, an extra power is required for data transmission. The results also have shown that when the MSE is not less than 10-2, the impact of channel estimation errors is reduced to a very low level. The simulation results have also revealed that a reasonable transmit power is required for the training signals to make sure that the channel estimator at mobile users offers channel estimation MSE as low as 10-2.
8. References
[1] E. Telatar, “Capacity of Multi-Antenna Gaussian Channels,” European Transactions on Telecommunications, Vol. 10, No. 6, November 1999, pp. 585-596. doi:10.1002/ett.44 60100604
[2] D. Gesbert, M. Kountouris, R. W. Heath Jr., C. Chae and T. Salzer, “Shifting the MIMO Paradigm,” Signal Processing Magazine, Vol. 24, No. 5, September 2007, pp. 36-46.
[3] M. Costa, “Writing on Dirty Paper,” IEEE Transactions on Inforamtion Theory, Vol. 29, No. 3, May 1983, pp. 439- 441. doi:10.1109/TIT.1983.1056659
[4] Q. H. Spencer, A. L. Swindlehurst and M. Haardt, “ZeroForcing Methods for Downlink Spatial Multiplexing in Multi-User MIMO Channels,” IEEE Transactions on Information Theory, Vol. 42, No. 3, February 2004, pp. 461-471.
[5] W. Weingarten, Y. Steinberg and S. Shamai, “The Capacity Region of the Gaussian Multiple-Input Multiple-Output Broadcast Channel,” IEEE Transactions on Information Theory, Vol. 52, No. 9, September 2006, pp. 3936-3964. doi:10.1109/TIT.2006.880064
[6] W. Yu and J. Cioffi, “Sum Capacity of Gaussian Vector Broadcast Channels,” IEEE Transactions on Information Theory, Vol. 50, No. 9, September 2004, pp. 1875-1892. doi:10.1109/TIT.2004.833336
[7] S. Shim, J. S. Kwak, R. W. Heath and J. Andrews, “Block Diagonalization for Multi-User MIMO with Other-Cell Interference,” IEEE Transactions on Wireless Communications, Vol. 7, No. 7, July 2008, pp. 2671-2681. doi:10. 1109/TWC.2008.070093
[8] F. Wang and M. E. Bialkowski, “Performance of Block Diagonalization Broadcasting Scheme for Multiuser MIMO System Operating in Presence of Spatial Correlation and Mutual Coupling,” International Journal of Communications, Network and System Sciences, Vol. 3, No. 3, March 2010, pp. 266-272. doi:10.4236/ijcns.2010.33034
[9] F. Wang, X. Liu and M. E. Bialkowski, “Performance of Block Diagonalization for Multiuser MIMO System with Uniform Circular Array and Uniform Linear Array: A Compare,” Proceedings of 6th International Conference on Wireless Communications, Networking and Mobile Computing, Chengdu, 23-25 September 2010, pp. 1-4.
[10] F. Wang and M. E. Bialkowski, “Fast Transmit Antenna Selection Scheme Employing Block Diagonalization for Multiuser MIMO System,” Proceedings of Asia-Pacifia Microwave Conference, Yokohama, 7-10 December 2010, pp. 1-5.
[11] M. Biguesh and A. B. Gershman, “Training-Based MIMO Channel Estimation: A Study of Estimator Tradeoffs and Optimal Training Signals,” IEEE Transactions on Signal Processing, Vol. 54, No. 3, March 2006, pp. 884-893. doi:10.1109/TSP.2005.863008
[12] M. Biguesh and A. B. Gershman, “Downlink Channel Estimation in Cellular Systems with Antenna Arrays at Base Station Using Channel Probing with Feedback,” EURASIP Journal of Applied Signal Procesing (Special Issue on Adcances in Smart Antennas), May 2003, pp. 1330-1339.

