Int'l J. of Communications, Network and System Sciences
Vol.3 No.6(2010), Article ID:2001,4 pages DOI:10.4236/ijcns.2010.36068
Efficiency Improvement of Space Time Block Codes
1Université de Limoges-Ecole Nationale Supérieure d'Ingénieurs de Limoges (ENSIL), Rue Atlantis-Parc ESTER-BP Limoges cedex, France
2Balochistan University of Engineering & technology, Khuzadar, Pakistan
3Universiti Teknologi Petronas, Bandar Seri Iskandar, Malaysia
E-mail: zahoor.ahmed@ensil.unilim.fr, musman@buetk.edu.pk, nhussain@petronas.com.my
Received March 24, 2010; revised April 29, 2010; accepted May 30, 2010
Keywords: Space Time Block Code, Spectral Efficiency
Abstract
Unlike most of the existing methods in Space Time coding (STC) system which focus on design of STC gaining full rate and/or maximum diversity, we propose an approach to improve spectral efficiency of the code. The proposed scheme carries more information symbols in each transmission block as compared to its counterpart code, and yet retains the property of simple decoding. Simulation results show that transmit diversity is retained with improvement of code efficiency. We mainly focus on Four transmit antenna scheme but it can be generalized for any number of transmit antennas.
1. Introduction
Since 1998 when Alamouti in [1] presented the idea of Space Time Coding, significant progress has been made in code design for achieving better diversity and code rate over multiple wireless communication channels. Space Time Coding (STC) system is one of the compromising scheme to meet the fast growing challenges for reliable and high data rate communication over multiple input multiple out (MIMO) channels. In [2,3] V.Tarokh et el discusses in detail the design of different classes of ST codes for achieving maximum diversity and full rate. However to counter the problem of unfeasibility/impracticability of having multiple receiver antennas at end users has put the researchers on work for alternates. In [2] it was shown that code rate cannot be greater than one. In fact even the maximum diversity and full rate codes do not exploit high efficiency. For example, if we look at (1), which is a Space Time Block Code (STBC) transmission matrix for four transmit antennas.
 (1)
(1)
where only the four symbols of first row of the matrix 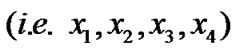 have been taken from a particular constellation (QPSK) while the other symbols are redundant and totally depend on four useful symbols. In other words out of sixteen symbols, only four symbols are carrying useful information.
have been taken from a particular constellation (QPSK) while the other symbols are redundant and totally depend on four useful symbols. In other words out of sixteen symbols, only four symbols are carrying useful information.
In [4], Foschini proposed BLAST coding technique, which offers higher spectral efficiency by exploiting the spatial multiplexing to transmit independent data streams over Multiple-Input Multiple-output channels. Such type of scheme outperforms to its counterpart STBC having multiple antennas at both transmitter and receiver, but contrary in [5] it was shown that the decoding of such a scheme does not work well if the numbers of receiver antennas are less than that of number of transmit antennas.
In [6] a scheme for increasing the spectral efficiency of Alamouti code has been presented. But such a scheme does not contribute significant improvement in code efficiency for more than two transmit antennas.
In this paper we propose a technique to improve the spectral efficiency of STBC for four transmit antennas retaining maximum diversity, full rate and simple maximum likelihood (ML) decoding characteristics of original code. Although the main focus of this paper is to design efficient code for four transmit antennas scenario, but same idea can be extended in a straightforward manner for STBC having more than four antennas.
The rest of the paper is organized as follow: Section 2 presents the system model. In Section 3, different techniques for increasing the code efficiency are discussed. Simulation results are given in Section 4 and finally conclusion in Section 5.
2. System Model
We consider a wireless communication system having four transmit antennas and one receiver antenna. We assume that transmission at the base band employs a real constellation  with
with 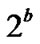 elements. The input binary stream is first split into two sub-stream by a serial to parallel converter. Each binary sub stream then passes through a QPSK constellation denoted by
elements. The input binary stream is first split into two sub-stream by a serial to parallel converter. Each binary sub stream then passes through a QPSK constellation denoted by  to map binary bits into symbols, i.e. setting
to map binary bits into symbols, i.e. setting  for
for , We arrive at a matrix
, We arrive at a matrix 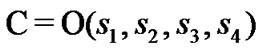 with entries
with entries . At each time slot
. At each time slot 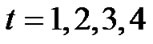 signals
signals 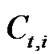 are transmitted simultaneously from four transmit antennas. Clearly the rate of transmission is b bit/s/Hz.
are transmitted simultaneously from four transmit antennas. Clearly the rate of transmission is b bit/s/Hz.
The fading coefficients from first to last transmit antennas to receiver antenna at time t are denoted by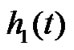 ,
, 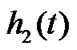 ,
,  and
and 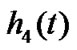 respectively. Assuming that the fading coefficients are constant across four consecutive symbols transmission periods, and are expressed as
respectively. Assuming that the fading coefficients are constant across four consecutive symbols transmission periods, and are expressed as
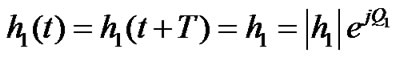

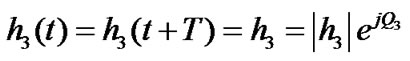
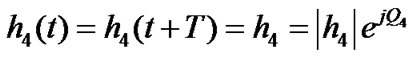
where 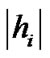 and
and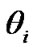 , for
, for 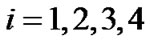 are the amplitude gain and phase shift for the path from transmit antenna i to the receive antenna, and T is the symbol duration.
are the amplitude gain and phase shift for the path from transmit antenna i to the receive antenna, and T is the symbol duration.
At the receive antenna, the received signals over four consecutive symbol periods, denoted by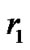 ,
,  ,
, 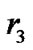 and
and 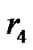 for
for 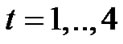 respectively, can be expressed as
respectively, can be expressed as
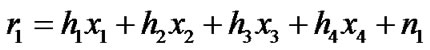
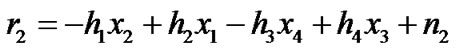
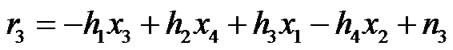
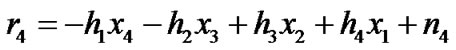
where ,
,  ,
,  and
and  respectively from time 1 to 4 are independent complex variable with zero mean power spectral density No/2 per dimension, representing additive white Gaussian noise. We may re-write Equation (3) into matrix form as:
respectively from time 1 to 4 are independent complex variable with zero mean power spectral density No/2 per dimension, representing additive white Gaussian noise. We may re-write Equation (3) into matrix form as:

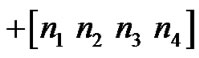
or more precisely
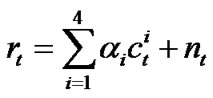
where 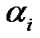 denotes channel coefficients. Assuming perfect channel state information is available at receiver, the receiver computes the decision metric
denotes channel coefficients. Assuming perfect channel state information is available at receiver, the receiver computes the decision metric
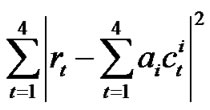
The maximum likelihood decoding for 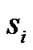 can be achieved by decoupling the signals transmitted from different antennas, [4,6].
can be achieved by decoupling the signals transmitted from different antennas, [4,6].
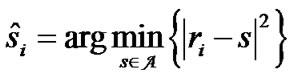
For  and decide in favour of
and decide in favour of  among all the constellation symbols.
among all the constellation symbols.
3. Efficiency Improvement Code
Assume that all the symbols in (1) are drawn from a QPSK constellation with gray constellation as shown in Figure 1. Although the code given in (1) is full rate code but its efficiency is too low. To find out the code efficiency over a QPSK constellation, we represent (1) by its corresponding bit representation. There might be 256 different patterns, and each pattern comprises of 32 bits. To lay down all 256 different patterns is a fatigable and un-necessary work. To save space we lay down just one such pattern below in (8), by assuming
 ,
, 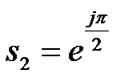 ,
, 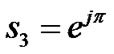 and
and 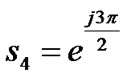

Now if we look at (8), the useful or informative bits are only 8 bits enumerated in first row of (8) while all other 24 (in 2nd, 3rd and 4th rows of (8)) bits are redundant and totally depends on 8 useful bits. We define the code efficiency η as the ratio of the number of useful bits and the total number of bits in each pattern of code matrix. In this particular case, the code efficiency is η = 8/32 = 0.25.
All full rate Space Time Block Codes having 4 or more than 4 transmit antennas do not gain code efficiency more than 0.25, even the case is worse for non-full rate codes.
Here we discuss some technique to improve the spectral efficiency of the code for four transmit antennas.
One way is to split the original data bit stream into group of 4 × 8 like that in (8), i.e. the redundant bits have dual function, at the same time they represent as redundant bits and information bits. In this case we can have full efficient code η = 1. But as our original data is random, so the probability of getting such a code pattern is  which is too small and practically near to zero probability.
which is too small and practically near to zero probability.
Another way to improve the code efficiency η is the technique very similar to that used in [6] for two transmit antenna Alamouti code. The original data stream is divided into group of nine bits. The first eight bits are arranged as useful bits in matrix form as in (8) and the ninth bit is used to decide which constellation to choose between the two constellation schemes shown in Figure 1 and Figure 2, for transmission of eight useful bits. For example if ninth bit 1, we choose the constellation A, shown in Figure 1, otherwise constellation B shown in Figure 2. It turns out that the transmission matrix has the same format as that in (8) but each transmission block now contains nine information bits instead of eight bits. The code efficiency increases to 9/32 = 0.28125.
As in this technique the code efficiency increases by a single bit we call this technique, bit efficient Eb code.
Another way to increase the code efficiency is to first divide the source binary data in to group of ten bits and then convert them into two binary sub-stream by a serial to parallel converter. For simplicity we show these five, 2-bits parallel bit stream by following symbols.
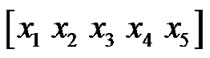 (9)
(9)
Before passing the symbol through constellation we tally the fifth symbol with other four symbols in (9) by its corresponding bit representation and find out the symbol which is same as fifth symbol. In case if there are more than one matching symbols, then we take the first one in that vector and in case if there is no any matching symbol then we ignore the fifth symbol for that specific transmission.
We use two type of constellation (as shown in Figure 1 and Figure 2). In transmitting the useful symbols , the symbol which is same as x5 is transmitted from constellation A whereas the rest of the symbols are transmitted from constellation B.
, the symbol which is same as x5 is transmitted from constellation A whereas the rest of the symbols are transmitted from constellation B.
As our source data stream is random, so it difficult to calculate the matching probability between fifth and other symbols. However for large data size we expect

Figure 1. QPSK Constellation ‘A’ with gray coding.
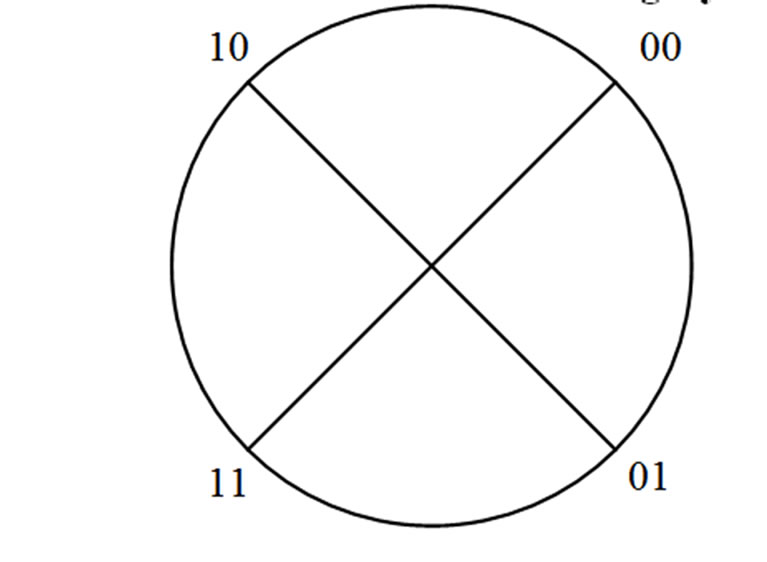
Figure 2. QPSK Constellation ‘B’ with gray coding.
maximum probability. If first four symbol in (9), in its corresponding bit representation, are different to each other, then the probability that the fifth symbol will match with one of the other four symbols is 100%, if any three symbols are different then the probability that the fifth symbol will match with one of the other four symbols is 75%, so probability is 50% if two symbols are different and it is 25% if one symbol is different.
We assume that in each block of transmission we find a matching symbol. In this case the code efficiency is 10/32 = 0.3125. As code efficiency is increased by a symbol, we call this technique as symbol efficient Es code Let 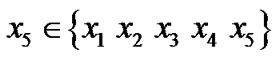 denote the fifth symbol and
denote the fifth symbol and 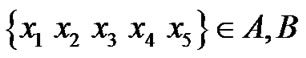
Then the transmission matrix (1) can be represented as
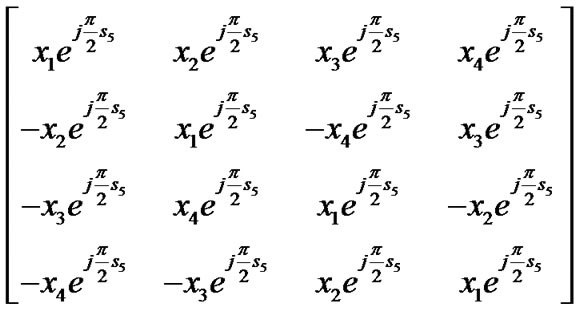 (10)
(10)
S5 is decided by the location of  which is closer to the decision boundary. Maximum likelihood decoding of
which is closer to the decision boundary. Maximum likelihood decoding of 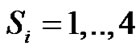 can be decoupled
can be decoupled
 (11)
(11)
4. Simulation Results
At transmitter two types of QPSK constellation are used. The minimum Euclidean distance between two QPSK constellations is the same as that of 8PSK constellation. Therefore in worse case the BER performance of the symbol efficient STBC code will be slightly worse due to additional error of symbol S5, as compare to 8PSK modulation. On the contrary, if the recovery of S5 is perfect i.e. the number of errors related to S5 is zero, then the selection of the QPSK constellation at the receiver is always correct, and the minimum Euclidean distance turns out to be the same as that of a QSPK constellation. Thus in the best case, the BER performance of symbol efficient STBC will be slightly better as compare to ordinary STBC code.
Our simulation results in Figure 3 prove our claim of better spectral efficiency of symbol efficient Es STBC code as compare to conventional STBC.
Table 1 shows some specific results of a neat comparison between STBC, Bit efficient STBC, symbol efficient STBC and 8PSK.

Table 1. Performances of QPSK modulation under different scenarios.
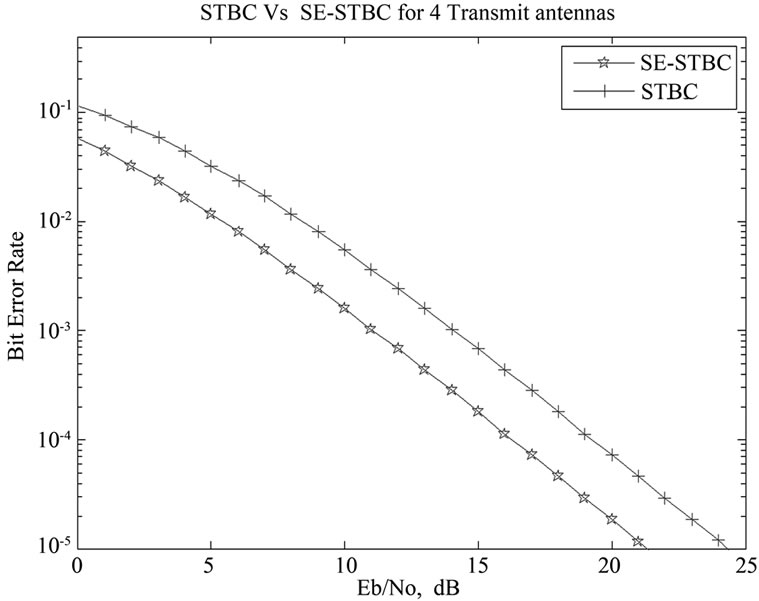
Figure 3. BER performance of STBC and spectral efficiency STBC with 4 -Transmit antennas.
5. Conclusions
Unlike most of the recent work, which are concentrated on design to achieve full rate and full diversity codes. We tried to invite researchers’ concentration to explore new techniques to augment the spectral efficiency of STB Codes. We presented a technique which enables us to send more symbols per transmission as compared to ordinary STB Codes. This approach also achieves full transmit diversity and allows maximum likelihood decoding for signals. The additional plus point of this technique is its flexibility to any number of transmit antennas.
6. References
[1] S. M. Alamouti, “A Simple Transmit Diversity Technique for Wireless Communication,” IEEE Journal on Selected Areas in Communications, Vol. 16, No. 8, 1998, pp. 1451-1458.
[2] V. Tarokh, H. Jafarkhani and A. R Calderbank, “Space Time Block Codes from Orthogonal Designs,” IEEE Transactions on Information Theory, Vol. 45, No. 5, 1999, pp. 1456-1467.
[3] V. Tarokh, H. Jafarkhani and A. R. Calderbank, “Space Time Block Coding for Wireless Communication: Performance Result,” Journal on Selected Areas in Communications, Vol. 17, No. 3, 1999, pp. 451-462.
[4] G. J. Foschini, “Layered Space-Time Architecture for Wireless Communication in a Fading Environment When Using Multi-Element Antennas,” Bell Labs Technical Journal, Vol. 1, No. 2, 1996, pp. 41-59.
[5] G. D. Golden, G. J Foschini, R. A. Valenzuela and P. W. Wolniansky, “Detection Algorithm and Initial Laboratory Results Using V-BLAST Space Time Communication Architecture,” Electronics Letters, Vol. 35, No. 1, 1999, pp. 14-16.
[6] Q. Ling and T. T. Li, “Efficiency Improvement for Alamouti Codes,” IEEE 40th annual conference on Information Sciences and systems, Princeton, 22-24 March 2006, pp. 569-572.

