Journal of Intelligent Learning Systems and Applications
Vol.06 No.04(2014), Article ID:50484,13 pages
10.4236/jilsa.2014.64013
Application of the Adaptive Neuro-Fuzzy Inference System for Optimal Design of Reinforced Concrete Beams
Jiin-Po Yeh, Ren-Pei Yang
Department of Civil and Ecological Engineering, I-Shou University, Kaohsiung, Taiwan
Email: jpyeh@isu.edu.tw
Academic Editor: Dr. Steve S. H. Ling, University of Technology Sydney, Australia
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 September 2014; revised 6 October 2014; accepted 14 October 2014
ABSTRACT
Using a genetic algorithm owing to high nonlinearity of constraints, this paper first works on the optimal design of two-span continuous singly reinforced concrete beams. Given conditions are the span, dead and live loads, compressive strength of concrete and yield strength of steel; design variables are the width and effective depth of the continuous beam and steel ratios for positive and negative moments. The constraints are built based on the ACI Building Code by considering the strength requirements of shear and the maximum positive and negative moments, the development length of flexural reinforcement, and the serviceability requirement of deflection. The objective function is to minimize the total cost of steel and concrete. The optimal data found from the genetic algorithm are divided into three groups: the training set, the checking set and the testing set for the use of the adaptive neuro-fuzzy inference system (ANFIS). The input vector of ANFIS consists of the yield strength of steel, compressive strength of concrete, dead load, span, width and effective depth of the beam; its outputs are the minimum total cost and optimal steel ratios for positive and negative moments. To make ANFIS more efficient, the technique of Subtractive Clustering is applied to group the data to help streamline the fuzzy rules. Numerical results show that the performance of ANFIS is excellent, with correlation coefficients between the three targets and outputs of the testing data being greater than 0.99.
Keywords:
Continuous Reinforced Concrete Beams, Genetic Algorithm, Adaptive Neuro-Fuzzy Inference System, Correlation Coefficients

1. Introduction
Genetic algorithms are search algorithms based on the mechanics of natural selection and natural genetics. They have been developed and were formally introduced in 1970s by Professor John Holland at the University of Michigan, who in 1975 published the ground-breaking book “Adaptation in Natural and Artificial System” [1] . In 1989, Goldberg described in more detail the theory of genetic algorithms and their applications [2] . From then on, genetic algorithms become more attractive and popular. Genetic algorithms have a number of applications in many fields, such as engineering, economics, chemistry, manufacturing, mathematics, physics and so on. Especially in the areas of civil engineering, there are reinforced concrete beams [3] , multiobjective optimization of trusses [4] , reliability analysis of structures [5] , global optimization of grillages [6] , global optimization of trusses with a modified genetic algorithm [7] and optimization of pile groups using hybrid genetic algorithms [8] , to name just a few.
The artificial neural network was originated by McCulloch and Pitts in 1943 [9] , who claimed that neurons with binary inputs and a step-threshold activation function were analogous to first-order systems. In 1986, Rumelhart et al. [10] proposed the theory of parallel distributed processing and developed the most famous learning algorithm in ANN-backpropagation, which uses a gradient descent technique to propagate error through a network to adjust the weights in an attempt to reach the global error minimum, marking a milestone in the current artificial neural networks.
Fuzzy sets were introduced by Zadeh [11] and Klaua [12] in 1965 as an extension of the classical set, where the membership of elements in a set is assessed in binary terms according to whether the element belongs to the set or not. In contrast, fuzzy set theory permits the gradual assessment of the membership of elements in a set, which is described with the degree of a membership function whose value is in the real interval [0, 1]. Fuzzy set theory is used now in many areas, such as clustering [13] , building group decision [14] and linguistic expressions [15] , etc.
Neuro-fuzzy systems are fuzzy systems which use ANNs theory in order to determine their membership functions and fuzzy rules by processing data samples. A specific approach in neuro-fuzzy development is the adaptive neuro-fuzzy inference system (ANFIS) first proposed by Jang [16] , which has shown significant results in modeling nonlinear functions. ANFIS integrates both neural networks and fuzzy logic principle, whose inference system corresponds to a set of fuzzy rules [17] that have learning capability to approximate nonlinear functions. Successful implementations of ANFIS in many fields have been reported, such as prediction of water level in the reservoir [18] [19] , forecasting of water discharge in a river [20] , sea level prediction considering tide-generating forces and oceanic thermal expansion [21] , prediction of flow through rockfill dams [22] , downstream water level forecasting [23] , flood forecasting [24] , generation of customer satisfaction models [25] , speech recognition [26] , chaotic traffic volumes forecasting [27] , etc.
Distinct from other authors’ works, this paper tries to combine the techniques of the genetic algorithm and ANFIS to optimally design reinforced two-span continuous reinforced concrete beams with rectangular cross- section. Based on the provisions of the ACI Building Code Requirements for Structural Concrete and Commentary [28] , the constraints are built, considering the strength requirements of the maximum positive and negative moments and shear, the development length of reinforcement as well as the serviceability requirement of deflection. Design variables are the width and effective depth of the continuous beam and the steel ratios for positive and negative moments. The objective function is to find the minimum cost of steel and concrete in the continuous beam.
2. Genetic Algorithms
Genetic algorithms were inspired by the evolution theory of “survival of the fittest”, proposed by Charles Darwin in 1860s. They simulate the survival of the fittest among individuals over consecutive generation and can solve both constrained and unconstrained optimization problems according to the “natural selection”. Genetic algorithms are less susceptible to getting stuck at local optima than traditional gradient search methods. This paper uses the Global Optimization Toolbox based on MATLAB [29] to carry out the genetic algorithm. It begins by creating a random initial population, and then creates a sequence of new populations. At each step, the algorithm uses the individuals in the current generation to create the next population. To create the new population, the algorithm performs the following steps: 1) score each member of the current population by computing its fitness value; 2) scale the raw fitness scores to convert them into a more usable range of values; 3) select members, called parents, based on their fitness. The lower the value of the fitness function, the more opportunity it has to be selected; 4) choose some elites from the current population that have lower fitness function values. These elite individuals are just passed to the next population; 5) produce children from the parents. Children are produced either by making random changes to a single parent―mutation―or by combining the vector entries of a pair of parents―crossover; 6) replace the current population with the crossover and mutation children and elites to form the next generation. The algorithm stops when one of the stopping criteria is met, such as the number of generation, the weighted average change in the fitness function value over some generations less than a specified tolerance, no improvement in the best fitness value for an interval of time, etc.
Supposed that 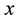 is the vector of design variables. The optimization problem of two-span continuous reinforced concrete beams can generally be described as
is the vector of design variables. The optimization problem of two-span continuous reinforced concrete beams can generally be described as
Minimize 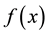 (the fitness function)
(the fitness function)
Such that
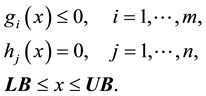 (1)
(1)
where 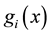 represents the inequality constraints and
represents the inequality constraints and 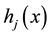 represents the equality constraints,
represents the equality constraints, 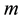 is the number of inequality constraints and
is the number of inequality constraints and 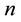 is the number of equality constraints,
is the number of equality constraints, 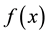 is the total cost of concrete and tension steels in the continuous beam, and
is the total cost of concrete and tension steels in the continuous beam, and 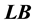 and
and 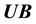 are vectors of lower and upper bounds of design variables, respectively. The constraints divide the design space into two domains, the feasible domain where the constraints are satisfied, and the infeasible domain where at least one of the constraints is violated. In most practical problems the minimum is found on the boundary between the feasible and infeasible domains, that is at a point where
are vectors of lower and upper bounds of design variables, respectively. The constraints divide the design space into two domains, the feasible domain where the constraints are satisfied, and the infeasible domain where at least one of the constraints is violated. In most practical problems the minimum is found on the boundary between the feasible and infeasible domains, that is at a point where  for at least one
for at least one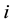 . In most structural optimization problems the inequality constraints prescribe limits on sizes, stresses, displacements, etc. These limits have great impact on the design, so that typically several of the inequality constraints are active at the minimum.
. In most structural optimization problems the inequality constraints prescribe limits on sizes, stresses, displacements, etc. These limits have great impact on the design, so that typically several of the inequality constraints are active at the minimum.
Most of the constraints built in this paper are nonlinear. The Global Optimization Toolbox based on MATLAB uses the augmented Lagrangian genetic algorithm [30] [31] to solve nonlinear constraint problems with bounds. A subproblem is formulated by combining the fitness function and nonlinear constraint functions using the Lagrangian and the penalty parameters. When the subproblem is minimized to a required accuracy, the Lagrangian multiplier estimates are updated, or the penalty parameter is increased by a penalty factor. These steps are repeated until one of the stopping criteria of the genetic algorithm is met.
3. The Adaptive Neuro-Fuzzy Inference System
The adaptive neuro-fuzzy inference system (ANFIS) consists of two components: fuzzy inference systems and neural networks. Using a given input/output data set, ANFIS constructs a fuzzy inference system whose membership function parameters are adjusted by a hybrid learning algorithm to approximate the precise value of the model parameters [16] [32] . The hybrid algorithm is a combination of gradient descent and the least-squares method. The gradient descent updates the premise parameters; the least squares method finds a proper set of consequent parameters. For an ordinary fuzzy inference, the parameters associated with a given membership function are usually predetermined by the user’s experience or the trial-and-error method. Rather than choosing the membership function parameters at random, ANFIS can scientifically obtain the parameters through the process of learning to tailor the membership functions to the input/output data to account for variations in the data values. This learning methods work similarly to those of neural networks. The fuzzy inference ANFIS operates on is the first- or zeroth-order Sugeno-type system [33] . For example, if there are only two inputs x and y, the general first-order Sugeno-type fuzzy inference has rules of the form
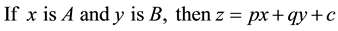 (2)
(2)
where A and B are the linguistic values defined by fuzzy sets in the antecedent, while ,
,  and
and 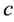 are constants. In Equation (2), the output
are constants. In Equation (2), the output 


where 





If the fuzzy inference is zeroth-order, then 
Data clustering specifying each data point belonging to a cluster to some degree by a membership grade can identify natural groupings of data from a large data set to produce a concise representation of a system’s behavior. Based on the cluster information, a Sugeno-type fuzzy inference system that best models the data behavior can be generated. The data clustering technique adopted in this paper is “Subtractive Clustering” [34] [35] . Based on the density of surrounding data points, it can estimate the number of clusters and the cluster centers in a set of data. The fuzzy rules found by clustering data are more tailored to the input data; therefore, the fuzzy inference system will have much fewer rules than that without data clustering. This algorithm works like a pre-processor to ANFIS for determining the initial rules. When the fuzzy inference system is generated, four parameters for “Subtractive Clustering” need to be specified [29] [34] : 1) range of influence 




4. Design of Two-Span Continuous Reinforced Concrete Beams
The two-span continuous reinforced concrete beams with a rectangular section are subjected to a uniformly distributed load


Figure 1. The structure of the adaptive neuro-fuzzy inference system.


Figure 2. The two-span continuous beam. (a) Shear and moment diagrams; (b) Reinforcement for the positive and negative moments.
4.1. Shear
Suppose that 

1) Region I: If

2) Region II: If

needs to be provided, where 


3) Region III: If

has to be provided to carry the difference and the spacing s must not be larger than
4) Region IV: If

The above statements can be summarized in Figure 3. From the maximum spacing limitations in different regions computed by the self-written MATLAB program, the total number of vertical stirrups can be obtained.
Because the reaction, in the direction of applied shear, introduces compression into the end regions of a member, the critical section can be assumed at a distance of 





4.2. Bending Moment
For simplicity, this paper assumes that the strain in the tension reinforcement is equal to 0.005; therefore, the section is tension-controlled, that is, the strength reduction factor for moment is fixed at 0.9, not a function of strain in the tension reinforcement any more. Accordingly, the constraint for both positive and negative moment takes the form

where 

Figure 3. Maximum spacing limitations for vertical stirrups in different regions.
itive moment 




When the strain in the tension reinforcement is equal to 0.005, the area of the reinforcement is of the form

where 

where

and


4.3. Development of Reinforcement
According to the ACI Code, at least one-third of the total tension reinforcement provided for negative bending moment at the support should extend beyond the inflections point not less than the effective depth 





where 

4.4. Deflections
The ACI Code indicates that wherever excessive deflection may adversely affect the service-ability of the structure at service loads, deflections under service load conditions must be computed. Creep and shrinkage will magnify the magnitude of deflection with time. Consequently, design engineers have to evaluate immediate as well as long-term deflection in order to ensure their values satisfy the maximum permissible criteria for the particular structure and its particular use. The additional deflection under sustained loading and long-term shrinkage in accordance with ACI procedure can be calculated by multiplying the immediate deflection by a factor

where 


where 

5. Numerical Results
The given conditions for the optimal design of two-span continuous singly reinforced rectangular concrete beams with a rectangular cross-section are the span length L, uniformly distributed dead 













5.1. Genetic Algorithms
To run the genetic algorithm of the MATLAB software, some parameters need to be selected. Here are the values used in this paper: after a number of trials, the population size is set to be 20, crossover rate 0.8, and elite number 2. Furthermore, all the individuals are encoded as real numbers; “Rank” is used as the scaling function that scales the fitness values based on the rank of each individual; “Roulette” is the selection function to choose parents for the next generation; “Two-Point Crossover” is used as the crossover method to form a new child for the next generation; the “Adaptive Feasible Function” is chosen as the mutation function to make small random changes in the individuals and ensure that linear constraints and bounds are satisfied. The genetic algorithm is executed 30 times for each case, from which the best is selected. For the use of ANFIS, the total 108 cases of data are divided into 3 groups randomly by a computer algorithm: 64 cases of training data (60%), 22 cases of checking data (20%) and 22 cases of testing data (20%).
5.2. Adaptive Neuro-Fuzzy Inference Systems
When using ANFIS with MATLAB, there are some restrictions: 1) only first- or zeroth-order Sugeno-type systems are supported; 2) there is only one single output; 3) each rule is of unit weight. The inputs of the adaptive neuro-fuzzy inference system consist of six elements:







Table 1. The linear regression results of the steel ratio ρ1 for the testing data.
Table 2. The linear regression results of the steel ratio ρ2 for the testing data.





Table 3. The linear regression results of the minimum cost for the testing data.
Figure 4. The scatter plot of the steel ratio 
intercept b approximately equals 0.
Based on Figures 4-6 and Tables 1-3, the performance of ANFIS is satisfactory and considered to be excellent. Table 4 lists the number of fuzzy rules for the three outputs with the influence ranges changing, which indicates that the larger the influence range of a cluster center becomes, the fewer fuzzy rules ANFIS results in. Taken as example, the inputs, targets and outputs of ANFIS for some cases of the testing data are shown in Table 5.
Figure 5. The scatter plot of the steel ratio ρ2 for the testing data.
Figure 6. The scatter plot of the minimum cost (103 NT$) for the testing data.
Table 4. The number of fuzzy rules for the three outputs: steel ratios ρ1 and ρ2 and the minimum cost with the influence range changing.
Table 5. Inputs, targets and outputs of ANFIS for some cases of testing data.
6. Conclusion
This paper first uses the genetic algorithm to work on the optimal design of two-span continuous reinforced concrete beams with a rectangular section. The adaptive neuro-fuzzy inference system (ANFIS) is then built based on the data of the given conditions and optimal results of the genetic algorithm. The inputs of this model are the yield strength of steel, compressive strength of concrete, dead load (live load is fixed) and span length, width and effective depth of the beam; targets are the minimum cost, the steel ratios for the positive and negative moments. The inputs of ANFIS are different from the given conditions of the genetic algorithm, which makes ANFI more useful and flexible in the design of beams. This paper proves that ANFIS has excellent performance with correlation coefficients between outputs and targets of the steel ratios for positive and negative moments and the minimum cost of the testing data being 0.9983, 0.9984 and 0.9996, respectively. In addition, the influence ranges of a cluster center from 0.1 to 1.5 for “Subtractive Clustering” to estimate the number of clusters and the cluster centers are explored, among which the value of 1.4 can lead to the best results as a whole, as far as the performance of ANFIS is concerned. In the future, once the input data are provided, ANFIS could quickly yield the minimum cost, steel ratios for the positive and negative moments as well as the spacing of vertical stirrups in each region with high precision, which automatically accomplish the design of the continuous reinforced concrete beams. The ANFIS model for the design of beams is easily implemented and timesaving, because it does not need to build the tedious and complex constraints.
References
- Holland, J.H. (1975) Adaptation in Natural and Artificial Systems. The University of Michigan Press, Ann Arbor.
- Goldberg, D.E. (1989) Genetic Algorithms in Search, Optimization and Machine Learning. Addison Wesley, Reading.
- Coello, C.C., Hernandez, F.S. and Farrera, F.A. (1997) Optimal Design of Reinforced Concrete Beams Using Genetic Algorithms. Expert Systems with Applications, 12, 101-108. http://dx.doi.org/10.1016/S0957-4174(96)00084-X
- Coello, C.A. and Christiansen, A.D. (2000) Multiobjective Optimization of Trusses Using Genetic Algorithms. Computers and Structures, 75, 647-660. http://dx.doi.org/10.1016/S0045-7949(99)00110-8
- Cheng, J. and Li, Q.S. (2008) Reliability Analysis of Structures Using Artificial Neural Network Based Genetic Algorithms. Computer Methods in Applied Mechanics and Engineering, 197, 3742-3750. http://dx.doi.org/10.1016/j.cma.2008.02.026
- Belevičius, R. and Šešok, D. (2008) Global Optimization of Grillages Using Genetic Algorithms. Mechanika, 6, 38-44.
- Šešok, D. and Belevičius, R. (2008) Global Optimization of Trusses with a Modified Genetic Algorithm. Journal of Civil Engineering Management, 14, 147-154. http://dx.doi.org/10.3846/1392-3730.2008.14.10
- Chan, C.M., Zhang, L.M. and Jenny, T.N. (2009) Optimization of Pile Groups Using Hybrid Genetic Algorithms. Journal of Geotechnical and Geoenvironmental Engineering, 135, 497-505. http://dx.doi.org/10.1061/(ASCE)1090-0241(2009)135:4(497)
- McCulloch, W.S. and Pitts, W. (1943) A Logical Calculus of Ideas Immanent in Nervous Activity. Bulletin of Mathematical Biophysics, 5, 115-133. http://dx.doi.org/10.1007/BF02478259
- Rumelhart, D.E., McClelland, J.L. and The PDP Research Group (1986) Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Volume 1: Foundations. MIT Press, Cambridge.
- Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Klaua, D. (1965) Über einen Ansatz zur mehrwertigen Mengenlehre. Monatsberichte der Deutschen Akademie der Wissenschaften zu Berlin, 7, 859-876.
- Bezdek, J.C. and Harris, J.D. (1978) Fuzzy Partitions and Relations: An Axiomatic Basis for Clustering. Fuzzy Sets and Systems, 1, 111-127. http://dx.doi.org/10.1016/0165-0114(78)90012-X
- Kuzmin, V.B. (1982) Building Group Decisions in Spaces of Strict and Fuzzy Binary Relations. Nauka, Moscow.
- De Cock, M., Bodenhofer, U. and Kerre, E.E. (2000) Modelling Linguistic Expressions Using Fuzzy Relations. Proceedings 6th International Conference on Soft Computing, Iizuka, 1-4 October 2000, 353-360.
- Jang, J.S.R. (1993) ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Transactions on Systems, Man and Cybernetics, 23, 665-685. http://dx.doi.org/10.1109/21.256541
- Klir, G.J. and Yuan, B. (1995) Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice-Hall International, Inc., Englewood Cliffs.
- Chang, F.J. and Chang, Y.T. (2006) Adaptive Neuro-Fuzzy Inference System for Prediction of Water Level in Reservoir. Advances in Water Resources, 29, 1-10. http://dx.doi.org/10.1016/j.advwatres.2005.04.015
- Valizadeh, N., El-Shafie, A., Mukhlisin, M. and El-Shafie, A.H. (2011) Daily Water Level Forecasting Using Adaptive Neuro-Fuzzy Interface System with Different Scenarios: Klang Gate, Malaysia. International Journal of the Physical Sciences, 6, 7379-7389. http://dx.doi.org/10.5897/IJPS11.1314
- Folorunsho, J.O., Iguisi, E.O., Mu’azu, M.B. and Garba, S. (2012) Application of Adaptive Neuro Fuzzy Inference System (Anfis) in River Kaduna Discharge Forecasting. Research Journal of Applied Sciences, Engineering and Technology, 4, 4275-4283.
- Lin, L.C. and Chang, H.K. (2008) An Adaptive Neuro-Fuzzy Inference System for Sea Level Prediction Considering Tide-Generating Forces and Oceanic Thermal Expansion. Terrestrial Atmospheric and Oceanic Sciences, 19, 163-172.
- Heydari, M. and Talaee, P.H. (2011) Prediction of Flow through Rockfill Dams Using a Neuro-Fuzzy Computing Technique. The Journal of Mathematics and Computer Science, 2, 515-528.
- Wang, A.P., Liao, H.Y. and Chang, T.H. (2008) Adaptive Neuro-Fuzzy Inference System on Downstream Water Level Forecasting. 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery, 3, 503-507. http://dx.doi.org/10.1109/FSKD.2008.671
- Mukerji, A., Chatterjee, C. and Raghuwanshi, N.S. (2009) Flood Forecasting Using ANN, Neuro-Fuzzy and Neuro-GA Models. Journal of Hydrologic Engineering, 14, 647-652. http://dx.doi.org/10.1061/(ASCE)HE.1943-5584.0000040
- Kwong, C.K., Wong, T.C. and Chan, K.Y. (2009) A Methodology of Generating Customer Satisfaction Models for New Product Development Using a Neuro-Fuzzy Approach. Expert Systems with Applications, 36, 11262-11270. http://dx.doi.org/10.1016/j.eswa.2009.02.094
- Leung, K.F., Leung, F.H.F., Lam, H.K. and Ling, S.H. (2007) Application of a Modified Neural Fuzzy Network and an Improved Genetic Algorithm to Speech Recognition. Neural Computing and Applications, 16, 419-431. http://dx.doi.org/10.1007/s00521-006-0068-4
- Yeh, J.P. and Chang, Y.C. (2012) Comparison between Neural Network and Adaptive Neuro-Fuzzy Inference System for Forecasting Chaotic Traffic Volumes. Journal of Intelligent Learning Systems and Applications, 4, 247-254. http://dx.doi.org/10.4236/jilsa.2012.44025
- ACI (2008) Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary (ACI 318R-08). American Concrete Institute, Farminton Hills.
- The MathWorks Inc. (2012) Global Optimization Toolbox: User’s Guide. The MathWorks, Inc., Natick.
- Conn, A.R., Gould, N.I.M. and Toint, Ph.L. (1991) A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds. SIAM Journal on Numerical Analysis, 28, 545-572. http://dx.doi.org/10.1137/0728030
- Conn, A.R., Gould, N.I.M. and Toint, Ph.L. (1997) A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds. Mathematics of Computation, 66, 261-288. http://dx.doi.org/10.1090/S0025-5718-97-00777-1
- Jang, J.S.R., Sun, C.T. and Mizutani, E. (1997) Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence. Prentice-Hall, Upper Saddle River.
- Sugeno, M. (1985) Industrial Applications of Fuzzy Control. Elsevier Science Pub. Co., Amsterdam.
- Chopra, S., Mitra, R. and Kumar, V. (2006) Analysis of Fuzzy PI and PD Type Controllers Using Subtractive Clustering. International Journal of Computational Cognition, 4, 30-34.
- Chiu, S. (1994) Fuzzy Model Identification Based on Cluster Estimation. Journal of Intelligent and Fuzzy Systems, 2, 267-278.







