ABSTRACT

In the new competitive electricity market, the accurate operation management of Micro-Grid (MG) with various types of renewable power sources (RES) can be an effective approach to supply the electrical consumers more reliably and economically. In this regard, this paper proposes a novel solution methodology based on bat algorithm to solve the optimal energy management of MG including several RESs with the back-up of Fuel Cell (FC), Wind Turbine (WT), Photovoltaics (PV), Micro Turbine (MT) as well as storage devices to meet the energy mismatch. The problem is formulated as a nonlinear constraint optimization problem to minimize the total cost of the grid and RESs, simultaneously. In addition, the problem considers the interactive effects of MG and utility in a 24-hour time interval which would increase the complexity of the problem from the optimization point of view more severely. The proposed optimization technique is consisted of a self adaptive modification method compromised of two modification methods based on bat algorithm to explore the total search space globally. The superiority of the proposed method over the other well-known algorithms is demonstrated through a typical renewable MG as the test system.

1. Introduction

In recent years, high utilization of renewable power sources (RESs) in the form of distributed generations (DGs) has experienced rapid growth especially in the voltage level of distribution networks. Some of the main benefits of using RESs can be named as lower cost, cleaner power generation mechanism, more reliability, better power quality, high flexibility, etc. [1]. However, from the operation management point of view, the high penetration of renewable DGs can bring some unwanted challenges which a significant part is covered in the form of Micro-Grid (MG) problem. MG problem is defined as the aggregation of DGs, electrical loads and generation interconnected among themselves and with the distribution network as well [2]. In the area of MG operation management, the solution techniques are experiencing continuous changing so that to keep these networks at the optimal operating point and control with different targets. In this regard, in recent years, several researches have been implemented to investigate the MG problem under different loading with different targets.

In [3], the author studied the recent progresses in the area of PV-based MGs in the multi-managing systems. In [4], the MG problem is investigated as a mix integer linear optimization problem to find the optimal operating point of renewable MG. The interactive effect of the MG and the upper network is assessed through the minimization of the total power generation cost in [5]. In [6], a test renewable MG is simulated in the lab to see the performance of the new methodology which is proposed to operate the MG in the next week time horizon. With the target of cot minimization, in [7], the author proposed a new method to handle the optimal sizing and management of RESs in a typical MG. In [8], a linear programming-based approach is proposed to reduce the total cost of a solar-wind MG. In [9], the direct effect of utilization of storage devices on the cost of the MG was investigated through a linear programming technique. Similar work based on participation method was proposed in [10] to solve the unit commitment problem in a renewable MG including storage devices. An integer optimization method based on Genetic Algorithm (GA) was proposed to formulate a three step methodology of prediction, storage and management to handle the MG problem in [11]. As it can be seen, wide rages of studies have been implemented to handle the complex and nonlinear MG operation management problem properly. Especially, considering different types of RESs such as Photovoltaics (PV), Fuel Cells (FCs), Wind Turbines (WTs), Micro Turbines (MTs), etc. as well as the storage devices can increase this complexity more than before. In addition, since most of the MGs are in alternation with the above network, the problem should be studies in the grid-connected mode which can result in a competitive electrical market. This situation dictates the necessary of new researches to find more reliable and powerful solution methodologies to handle the renewable MG appropriately.

According to the above discussion, this paper proposes a new solution methodology based on bat algorithm to investigate the optimal management of MG from the energy cost point of view. The bat algorithm is a population based metaheuristic optimization algorithm which was first inspired from the behavior of the bat animals to find food. The existence of some especial characteristics such as simple concept, easy implementation, the ability to both local and global, etc. makes the BA as suitable optimization tool. The MG investigated is consisted of several RESs with the back-up of FC, WT, PV, MT as well as storage devices to preserve the required energy mismatch. In this regard, the problem is formulated in a 24-hour time interval (next day) considering the interactive effect of the utility and MG on each other at each hour during the day. In order to see the constructive role of storage devices on the renewable MG operating mode, Nickel-Metal-Hydride Battery (NiMH-Battery) is also considered in the problem. In order to escape from premature convergence as well as the existing local optimal solution in the problem, a new self adaptive modification approach is proposed sufficiently. The proposed self adaptive modification technique is consisted of two submodification method which each of them can be chosen by each bat according to its positive influence. In order to see the superiority of the proposed method over the other well-known methods in the area, a typical renewable MG is considered as the test system.

2. Problem Formulation

In this section, the objective function and the relevant constraints are discussed sufficiently.

2.1. Objective Function

The operation management problem of a typical MG is defined as the problem of allocating optimal power generation set points as well as suitable ON or OFF states of RESs/DGs in the situation that the operating cost of the MG inside the grid are minimized while satisfying several equality and inequality constraints [12]. The total energy cost is consisted of the fuel cost for DGs, the start up and shut down cost and the cost of power exchange between the utility and the MG. The cost objective function tries the adjust the optimal power output of the RESs and the utility (as the upper network) as well as the ON/OFF statuses of all DGs. Therefore, the mathematiccal formulation of the cost objective function is as follows:

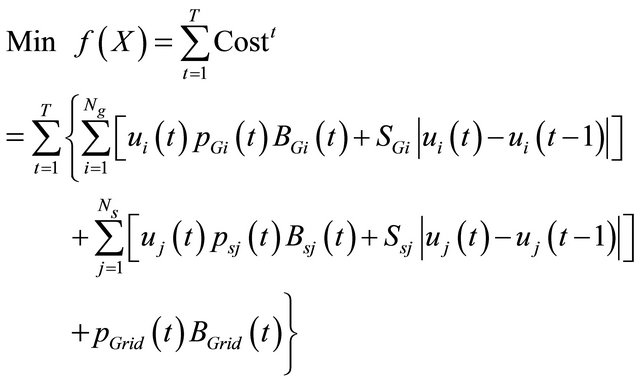(1)

where B_Gi(t) is the i^th DG bid at time t; X is the state variables vector; B_Sj(t) is the j^th storage device bid at time t; S_Sj(t) is the Start-up/Shut down cost of j^th storage device at time t; S_Gi(t) is the Start-up/Shut down cost of i^th DG at time t; p_grid(t) is the Active power bought (sold) from (to) the utility at time t; B_grid(t) is the utility bid at time t; U_i (t) is the State of the i^th unit denoting ON/OFF statuses; N_g is the number of generating units; N_s is the Number of storage devices; T is the Number of time intervals; P_G,i(t) is the active power production of i^th power unit at time t. In the above equation, X is the control vector which includes the output power generation of all units and their relevant ON/OFF statues as follows:

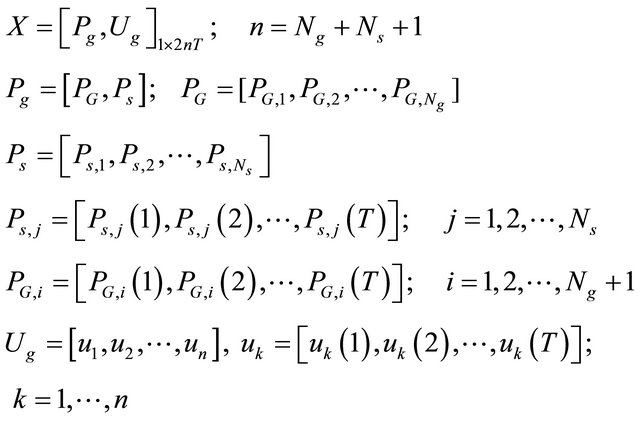(2)

where P_g is the vector including the power generation of all units; U_g is the vector including ON/OFF statuses of all units; n is the number of the state variables. Also, u_k(t) = 0 & u_k(t) = 1 show the OFF & ON status of k^th power unit at time t, respectively.

2.2. Problem Constraints

The problem constraints include both security and limitation constraints which are described bellow.

2.2.1. DG and Storage Devices Generation

Each power unit can generate in the range of its nominal power generation maximum and minimum capacity as follows:

(3)

where P_G,i,min(t) is the minimum active power production of i^th power unit at t; P_G,i,max(t) is the maximum active power production of i^th power unit at t ; P_s,j,min(t) is the minimum active power production of j^th storage device at t; P_s,j,max(t) is the maximum active power production of j^th storage device; P_Grid,min(t) is the minimum active power production of the grid at t; P_Grid,max(t) is the maximum active power production of the grid at t.

2.2.2. Load and Power Balance

The total amount of power produced by the power units and storage devices should supply all electrical loads as follows:

(4)

where P_L,l(t) is the amount of l^th load value at time t and N_L is the number of loads.

2.2.3. Battery Charging/Discharging Limits

Battery as the storage device is able to supply loads at each hour. However, the amount of power which is produced by the battery at each hour is limited to the amount of energy which is stored in it in the last hours. This limitation is preserved at each time interval as follows:

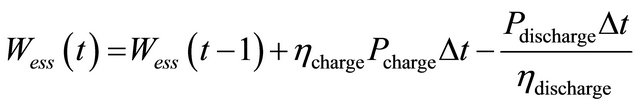(5)

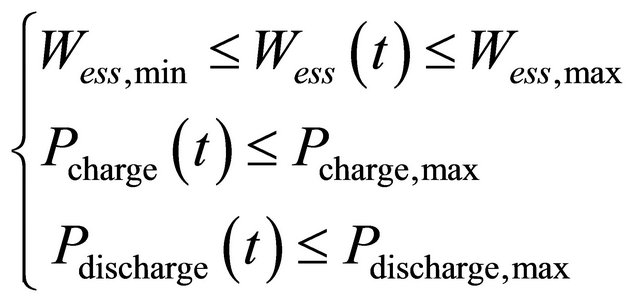(6)

where W_ess(t) is the amount of stored energy inside the battery at time t; W_ess,max is the maximum stored energy inside the battery; W_ess,min is the minimum stored energy inside the battery; P_charge is the permitted rate of charge during a finite time period (∆t); P_discharge is the permitted rate of discharge during a finite time period (∆t); η_charge is the battery efficiency during charge period; η_charge is the battery efficiency during charge period; η_discharge is the battery efficiency during discharge period; P_charge,max is the maximum permitted rate of charge during a finite each time period (∆t) ; P_{discharge,max}  is the is the minimum permitted rate of charge during a finite each time period (∆t).

3. Self Adaptive Modified Bat Algorithm (SAMBA)

In this section, the original bat algorithm as well as the proposed self adaptive modification method is described completely.

3.1. Bat Algorithm

Bat Algorithm (BA) is a metaheuristic population based optimization algorithm which was first inspired from the search of bats to find their food [13]. Bats send some signals to the environment and ten listen to its echo which is called echolocation process. BA is mainly constructed by the use of 4 main ideas [13]: 1) the difference between the prey and food is distinguished through the use of echolocation process; 2) Each bat in the position X_i flies with the velocity of V_i producing a especial pulse with the frequency and loudness of f_i and A_i respectively; 3) the loudness of A_i changes in different ways such as reducing from a large value to a low value; and 4) the frequency f_i and rate r_i of each pulse is regulated automatically. Initially, all bats fly randomly in the search space producing random pulses. After each fly, the position of each bat is updated as follows:

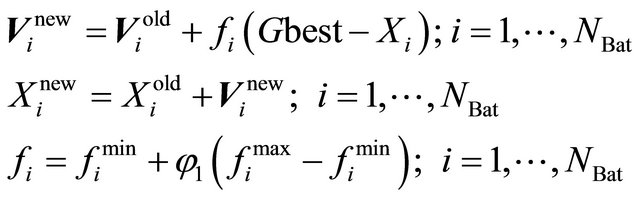(7)

where Gbest is the best bat from the objective function point of view; N_Bat is the number of bats in the population; 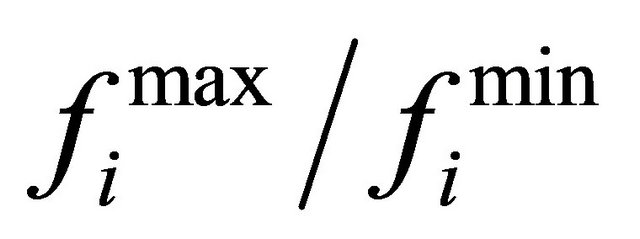are the maximum/minimum frequency values of the i^th bat and φ₁ is a random value in the range [0,1]. In order to reach a better random walking, another random fly is also simulated. In this regard, a random number β is generated randomly. In each iteration, if the random value β is larger than r_i then a new solution around X_i is generated as follows:

(8)

where ε is a random value in the range of [−1,1] and 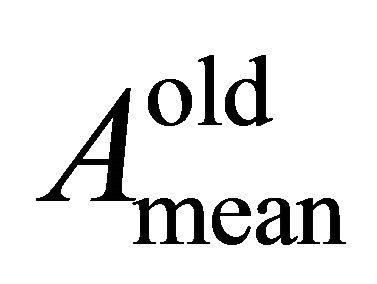is the mean value of the loudness of all bats. If the random value β is less than r_i then a new position 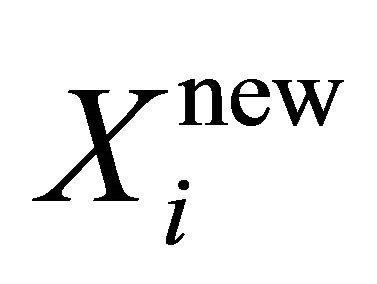is generated randomly. The new position 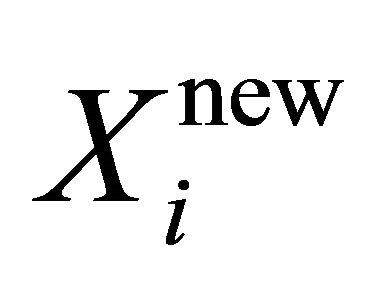is accepted if the bellow equation is satisfied:

(9)

Also, the values of loudness and rate are updated as follows:

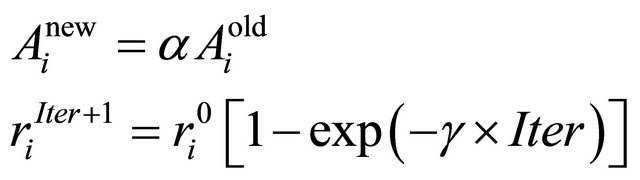(10)

where α and γ are constant values and Iter is the number of the iteration during the optimization process.

3.2. Self Adaptive Modification Method

In this part, a new self adaptive modification method is proposed to improve the total ability of the BA sufficiently. The main idea behind the proposed modification is to escape from local optima as well as avoiding premature convergence. The proposed self adaptive modification method is consisted of two sub-modification methods which each of them can be chosen during the optimization process according to its fitness. The proposed two sub-modification methods are as follows:

3.2.1. Sub-Modification Method 1

This modification approach will update the value of α during the optimization adaptively.

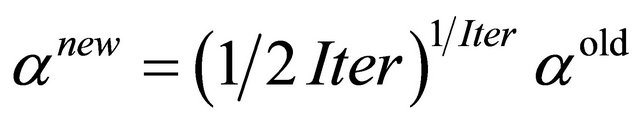(11)

The above equation is obtained by several running of the BA experimentally.

3.2.2. Sub-Modification Method 2

This modification approach will increase the variety of the bat population. The satisfying performance of this modification method in the optimization applications is demonstrated in several studies [14-17]:

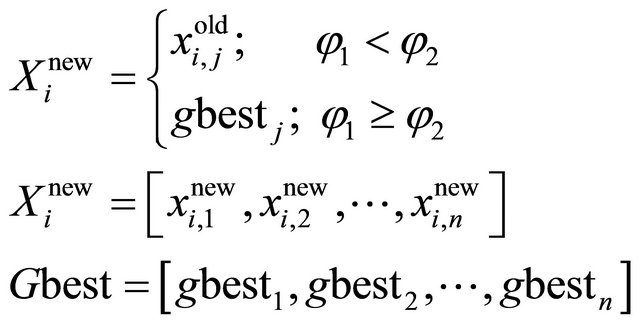(12)

where n is the length of the control vector and φ₂ is a random value in the range [0,1]. At the beginning, the probability of each sub-modification method is supposed to be equal (Prob_ω = 0.5 & ω = 1, 2). Each of the sub-modification methods can be a suitable modification method during the optimization process. Each bat would choose the ω^th modification method as the proper modification method with the use of roulette wheel mechanism (RWM). After each iteration, the population is sorted and the probability of each sub-modification method is updated as follows:

(13)

where SR_ω is the successful rate of ω^th modification method in producing more optimal bats in the population. Each bat 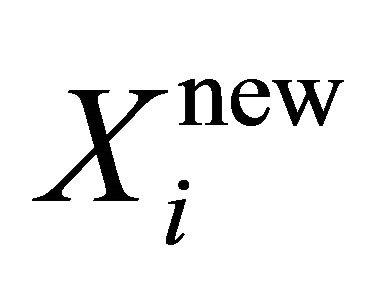is supposed to be more optimal if it reaches less objective function than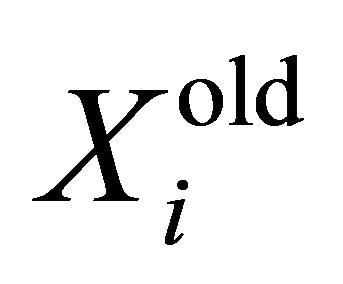. After updating the probability of each modification method, a random value φ₃ is generated in the range [0,1]. The process of choosing ω^th modification method to produce the next bat generation is by the use of roulette RWM. It is evident that the modification method with larger probability Prob_ω has more chance to be chosen for the next iteration. The process of choosing each modification method is shown in Figure 1.

4. Application of SAMBA to Solve MG Energy Management Problem

The following steps are required to apply the proposed SAMBA to solve the MG problem:

Step 1: Defining the input data.

Step 2: Converting the constrained problem to an unconstrained problem using penalty factors.

Step 3: Generate of the initial population and velocity.

Step 4: Evaluate the objective function values for the population.

Step 5: Find the best particle Gbest and store it.

Step 6: Improve the position of bats as in the original BA.

Step 7: Apply the proposed self adaptive modification method as explained in section 3 to each of the bats.

Step 8: Update the bat population and the best bat Gbest.

Step 9: Check the termination criterion. If the termination criterion is satisfied finish the algorithm, else return to Step 6.

5. Simulation Results

In this section, the proposed method is applied on a typical grid-connected MG including several types of RESs such as FC, PV, WT and MT as well as NiMH-Battery as the storage device. The single line diagram of the test system is shown in Figure 2. As it can be seen from Figure 2, the MG test system supplies three types of loads of 1) Residential loads; 2) Industrial loads; and 3) Commercial loads. It is supposed that there is no thermal load in the MG. Also, it is supposed that all the active power produced by the PV and WT power sources are

bought by the MG. The analysis is in a 24-hour time interval. All the power units are working at unit power factor. The forecast values of the hourly load consumption and WT and PV power production as well as the utility power production bid can be found in [12]. The bid data of the power units are shown in Table 1. The initial charge of the NiMH-Battery is zero. Therefore, the NiMH-Battery has to first be charged to be able to discharge at later hours. All the RESs can change between ON/OFF modes according to the economical benefits of the MG central controller. In order to have more reliable analysis, the effect of forecast error of load value, the PV and WT output generation and the cost coefficient are modeled through the probabilistic load flow as in [18,19] published by the author. The simulation results are implemented for the test system and the cost value is shown in Table 2. In order to reach better understanding of the powerful ability of the proposed method, some of the other well-known methods in the area are also shown in Table 2.

Table 2 shows the optimal value of cost function evaluated by different values for 25 trails. As it can be seen from Table 2, the proposed method has reached to much more optimal value for the cost function than the other methods. In fact, the proposed algorithm has reached to a new optimal value by escaping from the local optimal solutions. Columns 2-5 show the worst, the best, the standard deviation and the CPU time, respectively. Here, again the superiority of the proposed method over the other algorithms is evident. From the standard deviation point of view, the high stability of the proposed SAMBA can be deduced. Also, by comparing the CPU time, it is deduced that the convergence ability of the proposed method is better than that of the others. The corresponding optimal operating points of the RESs, the utility and the NiMH-Battery for all hours are shown in Table 3. As it can be seen from Table 3, at the first hours of the day which the load value and so the cost of energy is low, the NiMH-Battery is charging (in time interval of 1 - 8). However, at later times which the cost of buying power from the utility increases, the NiMH-Battery starts to discharge to reduce the role of utility in supplying the

Table 1. The limitations and bids of RESs & the utility.

Table 2. The simulation results for cost function for 25 trails.

Table 3. Output power of RESs evaluated by the proposed method.

load. In the case of MT, as it can be seen, it is ON in all hours except at hour 24. In fact, at hour 24, the algorithm has deduced to turn the MT off to reduce the total cost. Similar analysis can be made for the other RESs at different hours. According to the results of Tables 2 and 3, the superiority of the proposed method is evident

6. Conclusions

This paper proposes a new method based on BA to solve the nonlinear MG energy management problem properly. In this regard, a new self adaptive modification method based on BA was proposed to empower the BA to escape from the promising local optima as well as the premature convergence. The proposed algorithm is consisted of 2 sub-modification methods which each of them can be selected according to its usefulness during the optimization process. The investigated problem covers the renewable MG with the back-up of FC, WT, PV and MT as well as the NiMH-Battery as the storage device. The simulation results showed the feasibility and superiority of the proposed method over the other well-known methods in the area. Also, the positive role of NiMH-Battery to reduce the total cost of the MG was shown. According to the simulation results, the proposed method has suitable ability from both convergence speed and global searching ability points of view.

Although this work has investigated the MG operation management problem from the Energy reduction point of view, the other aspects of the problem such as amount of pollution and reliability analysis can be considered in the future works. Also, a complete comparison between the stochastic frameworks to capture more the uncertainty effects can be considered in future works too.

7. Acknowledgements

The authors wish to acknowledge Prof. Taher Niknam for his useful and constructive comments to empower the paper containing structure. In addition, they wish to thank the Islamic Azad University, Sarvestan Branch for supporting helps to yield the opportunity of having such a research in the MG area.

REFERENCES

NOTES

^*Corresponding author.