Journal of Intelligent Learning Systems and Applications
Vol.4 No.2(2012), Article ID:19254,10 pages DOI:10.4236/jilsa.2012.42009
Wisdom of Artificial Crowds—A Metaheuristic Algorithm for Optimization
![]()
Department of Computer Engineering and Computer Science Department, University of Louisville, Louisville, USA.
Email: {roman.yampolskiy, lhashb01, lwhass01}@louisville.edu
Received August 6th, 2011; revised March 27th, 2012; accepted April 5th, 2012
Keywords: NP-Complete; Optimization; TSP; Bio-Inspired
ABSTRACT
Finding optimal solutions to NP-Hard problems requires exponential time with respect to the size of the problem. Consequently, heuristic methods are usually utilized to obtain approximate solutions to problems of such difficulty. In this paper, a novel swarm-based nature-inspired metaheuristic algorithm for optimization is proposed. Inspired by human collective intelligence, Wisdom of Artificial Crowds (WoAC) algorithm relies on a group of simulated intelligent agents to arrive at independent solutions aggregated to produce a solution which in many cases is superior to individual solutions of all participating agents. We illustrate superior performance of WoAC by comparing it against another bio-inspired approach, the Genetic Algorithm, on one of the classical NP-Hard problems, the Travelling Salesperson Problem. On average a 3% - 10% improvement in quality of solutions is observed with little computational overhead.
1. Introduction
A large number of important problems have been shown to be NP-Hard [1]. Problems in that computational class are believed to require exponential time, in the worst case, to be solved. Since it is not feasible to practically solve such problems using Turing/Von-Neumann computational architecture optimal methods are replaced with heuristic algorithms that usually need polynomial time to provide approximate solutions [2].
Heuristic algorithms capable of addressing an array of diverse problems are known as metaheuristics. Such algorithms are computational methods that attempt to find a close approximation to an optimal solution by iteratively trying to improve a candidate answer with regard to a given measure of quality. Metaheuristic algorithms don’t make any assumptions about the problem being optimized and are capable of searching very large spaces of potential solutions. Unfortunately, metaheuristic algorithms are unlikely to arrive at an optimal solution for the majority of large real world problems. However, research continues to find asymptotically better metaheuristic algorithms for specific problems.
Most metaheuristic algorithms in optimization and search have been modeled on processes observed in biological systems [3-5]: Genetic Algorithms (GA) [6], Genetic Programming (GP) [7], Cellular Automata (CA) [8], Artificial Neural Networks (ANN), Artificial Immune System (AIS) [9], or in the surrounding environment:
Intelligent Water Drops (IWD) [10], Gravitational Search Algorithm (GSA) [11], Stochastic Diffusion Search (SDS) [12], River Formation Dynamics (RFD) [2], Electromagnetism-Like Mechanism (EM) [13], Particle Swarm Optimization (PSO) [14], Charged System Search (CSS) [15], Big Bang-Big Crunch (BB-BC) [16]. Continuing this trend of nature-inspired solutions a large number of animal or plant behavior-based algorithms have been proposed in recent years: Ant Colony Optimization (ACO) [17], Bee Colony Optimization (BCO) [18], Bacterial Foraging Optimization (BFO) [19], Glowworm Swarm Optimization (GSO) [20], Firefly Algorithm (FA) [21], Cuckoo Search (CS) [22], Flocking Birds (FB) [23], Harmony Search (HS) [24], Monkey Search (MS) [25] and Invasive Weed Optimization (IWO) [26]. In this paper we propose a novel algorithm modeled on the natural phenomenon known as the Wisdom of Crowds (WoC) [27].
Wisdom of Crowds
In his 1907 publication in Nature, Francis Galton reports on a crowd at a state fair, which was able to guess the weight of an ox better than any cattle expert [28]. Intrigued by this phenomenon James Surowiecki in 2004 publishes: “The Wisdom of Crowds: Why the Many are Smarter than the Few and How Collective Wisdom Shapes Business, Economies, Societies and Nations” [27]. In that book Surowiecki explains that “Under the right circumstances, groups are remarkably intelligent, and are often smarter than the smartest people in them. Groups do not need to be dominated by exceptionally intelligent people in order to be smart. Even if most of the people within a group are not especially well-informed or rational, it can still reach a collectively wise decision” [27]. Surowiecki further explains that for a crowd to be wise it has to satisfy four criteria:
• Cognitive diversity—individuals should have private information.
• Independence—opinions of individuals should be autonomously generated.
• Decentralization—individual should be able to specialize and draw on local knowledge.
• Aggregation—a methodology should be available for arriving at a common answer.
Since the publication of Surowiecki’s book, the WoC algorithm has been applied to many important problems both by social scientists [29,30] and computer scientists [31-36]. However, all such research used real human beings either in person or via a network to obtain the crowd effect. In this work we propose a way to generate an artificial crowd of intelligent agents capable of coming up with independent solutions to a complex problem.
Overall, the paper is organized as follows: in Section 2 we introduce the developed Wisdom of Artificial Crowds algorithm. In Section 3 the Traveling Salesman Problem is motivated as the canonical NP-Complete problem. In Section 4 we provide a detailed description of the Genetic Algorithm which is used to generate the intelligent crowd for the post-processing algorithm to operate on. In Section 5 we explain how the aggregate of the crowds’ decision is computed. Finally in Section 6 we report the results of our experiments and in Section 7 we look at potential future directions for research on Wisdom of Artificial Crowds.
2. Wisdom of Artificial Crowds
Wisdom of Artificial Crowds (WoAC) is a novel swarmbased nature-inspired metaheuristic algorithm for optimization. WoAC is a post-processing algorithm in which independently-deciding artificial agents aggregate their individual solutions to arrive at an answer which is superior to all solutions present in the population. The algorithm is inspired by the natural phenomenon known as the Wisdom of Crowds [27]. WoAC is designed to serve as a post-processing step for any swarm-based optimization algorithm in which a population of intermediate solution is produced, for example in this paper we will illustrate how WoAC can be applied to a standard Genetic Algorithm (GA).
The population of intermediate solutions to a problem is treated as a crowd of intelligent agents. For a specific problem an aggregation method is developed which allows individual solutions present in the population to be combined to produce a superior solution. The approach is somewhat related to ensemble learning [37] methods such as boosting or bootstrap aggregation [38,39] in the context of classifier fusion in which decisions of independent classifiers are combined to produce a superior meta-algorithm. The main difference is that in ensembles “when combing multiple independent and diverse decisions each of which is at least more accurate than random guessing, random errors cancel each other out, correct decisions are reinforced [40]”, but in WoAC individual agents are not required to be more accurate than random guessing.
3. Travelling Salesperson Problem
Travelling Salesperson Problem (TSP) has attracted a lot of attention over the years [41-43] because finding optimal paths is a requirement that frequently appears in real world applications and because it is a well-defined benchmark problem to test newly developed heuristic approaches [2]. TSP is a combinatorial optimization problem and could be represented by the following model [17]: 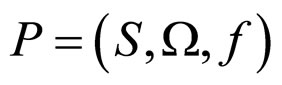 in which S is a search space defined over a finite set of discrete decision variables Xi, i = 1,…, n; a set of constraints
in which S is a search space defined over a finite set of discrete decision variables Xi, i = 1,…, n; a set of constraints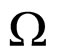 ; and an objective function f to be minimized.
; and an objective function f to be minimized.
TSP is a well-known NP-Hard problem meaning that an efficient algorithm for solving TSP will be an efficient algorithm for other NP-Complete problems. In simple terms the problem could be stated as follows: a salesman is given a list of cities and a cost to travel between each pair of cities (or a list of city locations). The salesman must select a starting city and visit each city exactly once and return to the starting city. His problem is to find the route (also known as a Hamiltonian Cycle) that will have the lowest cost. In this paper we will use TSP as a nontrivial testing ground for our algorithm.
Dataset
Data for testing of our algorithm has been generated using a piece of software called Concorde [44]. Concorde is a C program written for solving the symmetric TSP and some related network optimization problems and is freely available for academic use. The program also allows one to generate new instances of the TSP of any size either with random distribution of nodes, or with predefined coordinates. For problems of moderate size, the software could be used to obtain optimal solutions to specific TSP instances. Appendix contains an example of a Concorde data file with 7 cities.
4. Genetic Algorithms
Inspired by evolution, genetic algorithms constitute a powerful set of optimization tools that have demonstrated good performance on a wide variety of problems including some classical NP-complete problems such as the Traveling Salesperson Problem (TSP) and Multiple Sequence Alignment (MSA) [45]. GAs search the solution space using a simulated “Darwinian” evolution that favors survival of the fittest individuals. Survival of such population members is ensured by the fact that fitter individuals get a higher chance at reproduction and survive to the next generation in larger numbers [6].
GAs have been shown to solve linear and nonlinear problems by exploring all regions of the state space and exponentially exploiting promising areas through standard genetic operators, eventually converging populations of candidate solutions to a single global optimum. However, some optimization problems contain numerous local optima which are difficult to distinguish from the global maximum and therefore result in sub-optimal solutions. As a consequence, several population diversity mechanisms have been proposed to delay or counteract the convergence of the population by maintaining a diverse population of members throughout its search.
A typical GA follows the following steps [46]:
1) A population of N possible solutions is created.
2) The fitness value of each individual is determined.
3) Repeat the following steps N/2 times to create the next generation.
a) Choose two parents using tournament selection.
b) With probability pc, crossover the parents to create two children; otherwise simply pass parents to the next generation.
c) With probability pm for each child, mutate that child.
d) Place the two new children into the next generation.
4) Repeat new generation creation until a satisfactory solution is found or the search time is exhausted.
Implemented GA for Solving TSP
Solutions are encoded as chromosomes which traditionally are represented by data arrays, but can be represented in other ways. Each solution is rated according to its fitness which is based on the quality of the solution. A population of chromosomes that are initially generated randomly, continually goes through processes of inheritance, mutation, selection, and crossover based on fitness of the individual chromosomes. Hamiltonian cycles or paths traveling all nodes only once are encoded as a list of nodes in chromosomes. An initial population is generated randomly. Successive populations, generated by operations of mutation and crossover on a prior population, will replace the prior population. Each generation is likely to yield chromosomes more similar to chromosomes representing optimal solutions based on fitness.
This experimental code was implemented as a Windows Presentation Foundation (WPF) Application using C#. Net 4.0 framework in Visual Studio 2010 running on Windows 7. The application has an “Open” menu item to show a dialog box to browse for .tsp files and load them. The application initializes from the data provided by the file and displays the data graphically. The “Settings” menu item will open a dialog allowing a user to set parameters of the genetic algorithm. The user can start the process with a new population by pressing “Start” or continue with the existing population by pressing “Continue”. The best, average, worst, or any combination can be selected to be graphed as the algorithm is processing. Any of the parameters may be changed during the execution of the algorithm.
The application domain is divided into several classes for representing the TSP, and the genetic algorithm. FileData and Node classes are used to read a TSP file and represent the graph of the TSP. Class Solver implements the genetic algorithm. Solver is a strategy pattern with the method, Solve, relying on implementations of interfaces defining parts of an algorithm. A combination of concrete implementations that would make up a running instance of Solver is grouped together by an instance of EAConfiguration. The EAConfiguration object is passed to the constructor of Solver. The combination includes instances of Population, IChromosomeFactory, ICrossoverPolicy, ICrossoverOperator, IMutationPolicy, IMutationOperator, and ITerminationCriteria classes.
The method, Solve, first takes the instance of Population and adds instances of IChromosome created by the instance of IChromosomeFactory. Population is a container for ICromosome instances and keeps track of the sum of all chromosome fitness and current generation. IChromosome is an interface, defining that chromosomes need to provide read-only properties of the underlying data, the fitness and path distance, and provide methods to be able to clone its type but with different data, and to convert its data to a standard format to representing the path. IChromosomeFactory is an interface for factories that produce IChromosome. Next Solve reduces the size of Population. If a new EAConfiguration was created, and it required the size to be smaller than the previous generation of Population. This is only to allow change of population size in runtime and not necessarily a general part of the genetic algorithm. Now that an initial population is generated, Solve enters a while loop terminating on criteria defined by an instance of ITerminationCriteria.
For each iteration of the loop, an instance of ICrossoverPolicy performs a transformation on Population producing a new Population, and an instance of IMutaionPolicy, also performs a transformation on Population producing a new Population. ICrossoverPolicy and IMutationPolicy are strategy patterns themselves. ICrossoverPolicy takes an instance of ICrossoverOperator and defines how that operator is applied to the entire population. ICrossoverOperator itself is a strategy pattern which if given two chromosomes produces two new chromosomes based on the ones given. Similarly, IMutationPolicy is an interface for instances to define how to perform IMutationOperator instances on the entire population. IMutationOperator is an interface for instances to mutate a given chromosome.
To clarify, there are three tiers of strategy patterns. At the bottom ICrossoverOperator and IMutationOperator provide interfaces for instances, to define operations on interfaces of IChromosome. The next tier, ICrossoverPolicy and IMutationPolicy are interfaces for instances to define “policies” on how the operations are applied to the entire population. The top tier is the skeleton layout of the genetic algorithm Solver itself. The loop also fires an event at each generation so that a handler may analyze or display data as the algorithm is running. The use of events allows UI code to be decoupled with the genetic algorithm. This describes the general outline of the application presenting many interfaces to allow concrete implementations to “plug into”.
IChromosome is the interface for a solution representtation for which two concrete classes are implemented; OrderedPath and NumberedPermutation. Both OrderdPath and NumberedPermutation use classes, Permutation [47] and BigInteger [48]. OrderedPath simply describes a solution to the TSP as an array of the nodes in the order traveled. NumberedPermutation represents a solution as a number that maps to a specific permutation of the set of nodes. Given a set of size n, there is n! permutations of that set. In a Hamiltonian cycle, starting from any node in the cycle and maintaining all the edges in the cycle results in equivalent length of the path. Eliminating equivalent cycles will yield a search space of size (n – 1)!. Also, traveling a cycle in reverse will have the same distance. Removing the reverses will reduce the number of cycles in a set to ((n – 1)/2)!. In the creation of a NumberedPermutation chromosome, a number between 1 and (n – 1)! is given to reduce the solution space as any number above that will represent a permutation that is equivalent to a permutation represented by a number below or equal to (n – 1)!.
A similar affect is used on the OrderedPath chromosomes by always setting the first node traveled as node 0. The creation of chromosomes is abstracted away by the use of an abstract factory IChromosomeFactory. OrderedPathFactory and NumberedPermutation implement the interface by simply calling the constructor of their respected product classes and returning the created instance. OrderedPathFirstNodeZeroFactory produces OrderedPath chromosomes with the first node set to zero. NoRepeats implements ICrossoverOperator by taking the given chromosomes, the parents, and splicing both at some random mark. The first half or each is copied directly to the two chromosomes to be returned to the children. The second half of the two parents is read one gene at a time and the nodes are added to the end of the respected child as long as the node has not occurred already in the chromosome. If it has, a node that does not occur in the child chromosome is added by reading from the beginning of the parent chromosome. NoRepeatsFirstNodeZero does the exact same, but ensures that the first node is zero. This is to be used with OrderedPathNodeZeroFactory and SwapBitsFirstNodeZero, but not necessarily enforced. IMutatorOperator guarantees that implementations provide method Operated which will produce one chromosome based on the chromosome given. SwapBits implements IMutatorOperator by taking the given chromosomes and selecting two genes at random and simply swapping them. SwapBitsFirstNodeZero does exactly the same but ensures that the first node is zero.
The next level is the policies. Policies define how the selected operator is to be used on the entire population. ICrossoverPolicy implementations have the method Evaluate and the property PercentageRate. Evaluate takes as parameters Population, and ICrossoverOperator and returns a new Population. RouletteWheel implements ICrossoverPolicy by taking the population and selecting two parent chromosomes at random but with chromosomes with higher fitness being more likely to be selected. This is done by taking the summation of fitness in the population, and multiplying it by a random value between zero and one. This will be a value between zero and the summed fitness. For each chromosome in the population the value calculated is tested to see if it is lower than that of the chromosome’s fitness. If it is, then that chromosome is selected; if not, the calculated value is subtracted and the chromosome’s fitness value is reduced for the next iteration.
This process yields a chromosome chosen with a probability of fitness/total fitness. After two parents are selected this way, they have a probability defined in PercentageRate property of being operated on by the ICrossoverOperator. If the operator is not applied, the two selected parents are simply added to the new population. If the operator is applied, the ICrossoverOperator method, Operate, is used on the two parents, yielding two children. If the child’s fitness is greater than the parents’ the child is placed in the population; if not the parents are chosen instead. This tends to keep chromosomes with higher fitness and kills off those with lower fitness.
Once the new population is filled, it is returned back as the next generation. KeepElite is another implementation of ICrossoverOperator. This implementation will keep the best chromosomes in a given population, and apply the same roulette wheel selection on the rest of the population. The number of best chromosomes selected from the population is given by PercentageRate. OccurrenceRate implements IMutationPolicy by simply applying its mutation operator for each chromosome, by a probability given by PersentageRate.
A population of solutions produced by a GA tends to quickly converge on a local maxima point [45] resulting in a population of almost identical solutions (Figure 1). Two countermeasures against this problem have been developed. One is an early termination of the GA just prior to the point of solution convergence, and cognitive diversity elimination. The other way to maximize diversity of solutions present in the crowd of intelligent agents provided to the WoAC algorithm by the GA algorithm is to conduct multiple runs of the GA on the same dataset. Resulting populations are then merged and provide necessary cognitive diversity for the WoAC algorithm.
5. WoAC Aggregation Method
Building on the work of Yi et al. [30] who used a group of volunteers to solve instances of TSP and aggregated their answers, we have developed an automatic aggregation method which takes individual solutions and produces a common solution which reflects frequent local structures of individual answers. The approach is based on the belief that good local connections between nodes will tend to be present in many solutions, while bad local structures will be relatively rare. After constructing an agreement matrix, Yi et al. [30] applied a nonlinear monotonic transformation function in order to transform agreements between answers into costs. They focused on the function:
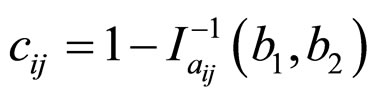 , (1)
, (1)
where
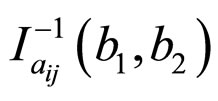 (2)
(2)
is the inverse regularized beta function with parameters b1 and b2 both taking a value of at least 1 [30].
In our implementation of the aggregation function we continue working with agreements between local components of the solutions. The process in which this implementation aggregates chromosomes is via recording the number of occurrences of edges, creating a new path traveling along edges that have occurred the most in the population of the solutions. First, an occurrence matrix is created to accumulate the number of times each edge shows up. This is done by constructing an n × n matrix with ni, where 0 < i ≤ n. Each cell stores the number of edge occurrences with the cell’s row number corresponding to one node of the edge and the cell’s column number corresponding to the other node in the edge. This matrix ends up being a symmetric matrix, and to save memory, only the lower triangle is stored. An example, of only two paths on 11 nodes can be seen in Figure 2.
To get every value of a row as if the entire matrix was completed, values of the column that lie on the last displayed value of the row, are used to complete the row. This is possible because of matrix symmetry. Figure 3 demonstrates this concept, highlighting what is to be considered the entire row five. Now that the number of edge occurrences has been tallied, a new path is to be constructed using the most occurring edges. The algorithm starts with the most occurring edge. In the case of multiple max occurrences being equal, as in this example, the first one is used. In our example, the new path will start using the

Figure 1. Paths get shorter with successive generations.
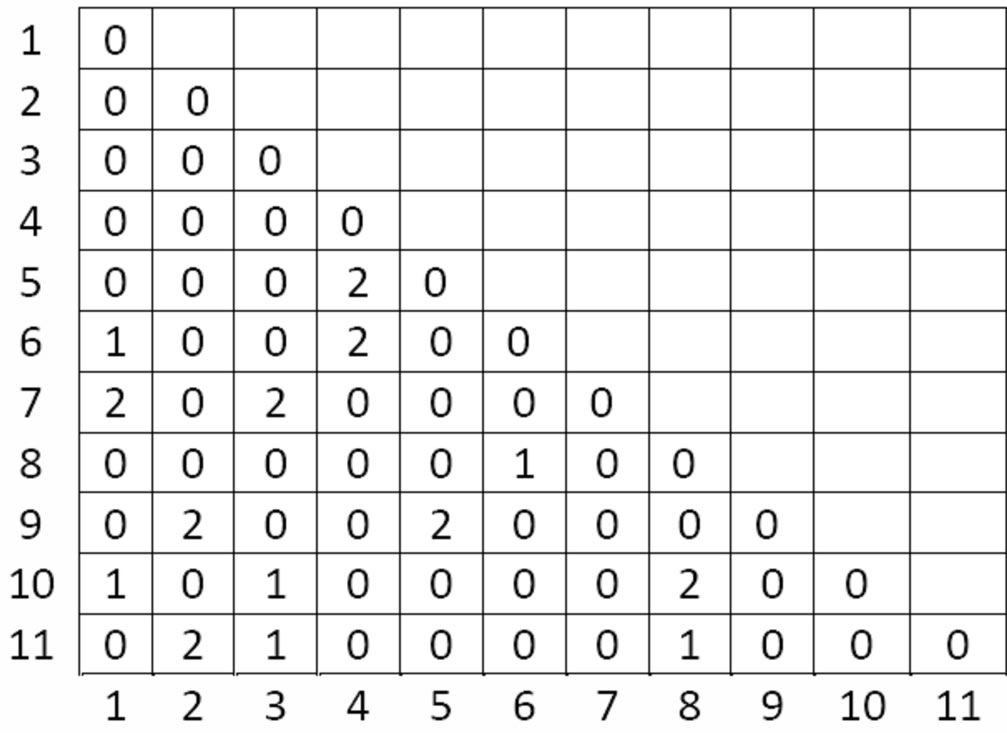
Figure 2. An example matrix with two paths shown.

Figure 3. Representative selection of the entire row five.
cell (5,4) meaning that the nodes 5 and 4 make the most frequently occurring edge. To find the next node, the algorithm searches the most occurring edge that shares one of the nodes used in the last step. This is done by looking at all the cells that share either the same row or same column. As mentioned earlier, a row’s data is completed by using the data of the column of the last cell in the row. This implies that any column’s data is part of some row.
To continue this example, in order to find the next node connecting to the edge (5,4), the cells that make up the row and column of (5,4) are examined. This can be seen in Figure 4. This process is continued until all nodes are connected to construct a new path. To make sure that a node is not used twice, a checklist is used to mark which rows have been used; nodes in these rows will be ignored. As the algorithm is run, sometimes a node cannot be found. In this case a node with the closest distance to the last node inserted into the new path, and that is not checked off, is used to continue the process.
6. Experimental Results
The GA was run 10 times, on 6 data sets, producing 60 populations. WoAC was applied to each of these populations, using all chromosomes of the population. Figure 5 shows 6 tables, each listing the best, average, worst, and WoAC for each population that resulted from the genetic algorithm. The results of WoAC are highlighted light blue if the results are equal to the best or highlighted dark blue if the results of WoAC are better than the best.

Figure 4. The cells that make up row and column of (5,4).
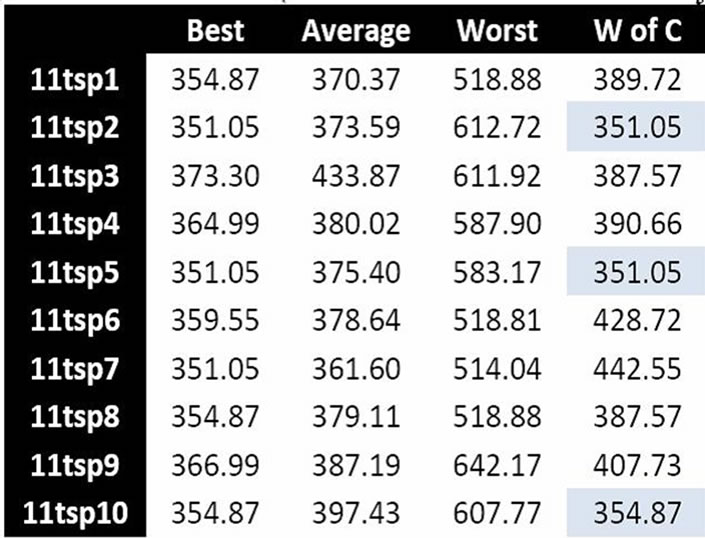



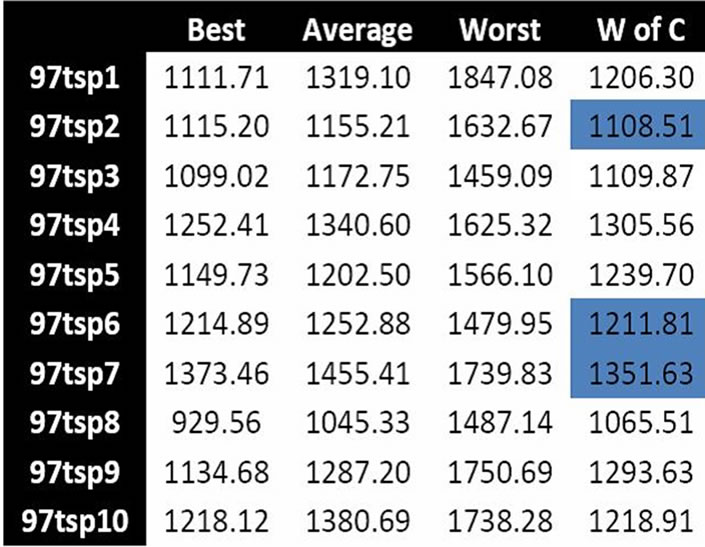

Figure 5. Comparison of GA vs. WoAC on six progressively larger TSP instances.
Figure 6 shows scatter plots graphing similarity to distance. Proportion of coincidence of path with other subjects was calculated by counting the number of edges a solution has in common with other solutions, and then dividing the number of agreeing edges by the number of cities to get the percentage of agreement. These are then averaged for all the cities to find the final value. WoAC was then applied to all populations of each given data set. This was done for the best chromosome from each population starting with top 5, then top 10, and so on incrementing by 5 up to the total population size of 100. Figure 7 shows a table displaying the best results from the genetic algorithm alone, result of applying WoAC to all chromosomes from the population, result of applying WoAC to the top 1 percent of chromosomes from the population, result of applying WoAC to the best number of chromosomes from the population, and the best number that was used. Highlighted in blue are the best results from all cases. On average a 3% - 10% improvement could be seen in cases where WoAC had improvement over standalone GA. Graphical representations of the best WoAC results for different datasets are displayed in Figures 8-13. The blue dots represent the nodes, gray lines are paths from the chromosomes, and orange lines are the path generated from WoAC.
We have performed additional experiments to verify cross-domain applicability of WoAC and the results are encouraging. In solving instances of NP-Complete game —Light Up, improvement due to WoAC over pure GA varied from 3.5% to 35% [4]. For another canonical NPComplete problem—Knapsack, improvements as a result of postprocessing by WoAC varied from 1.0% to 1.8% [3].


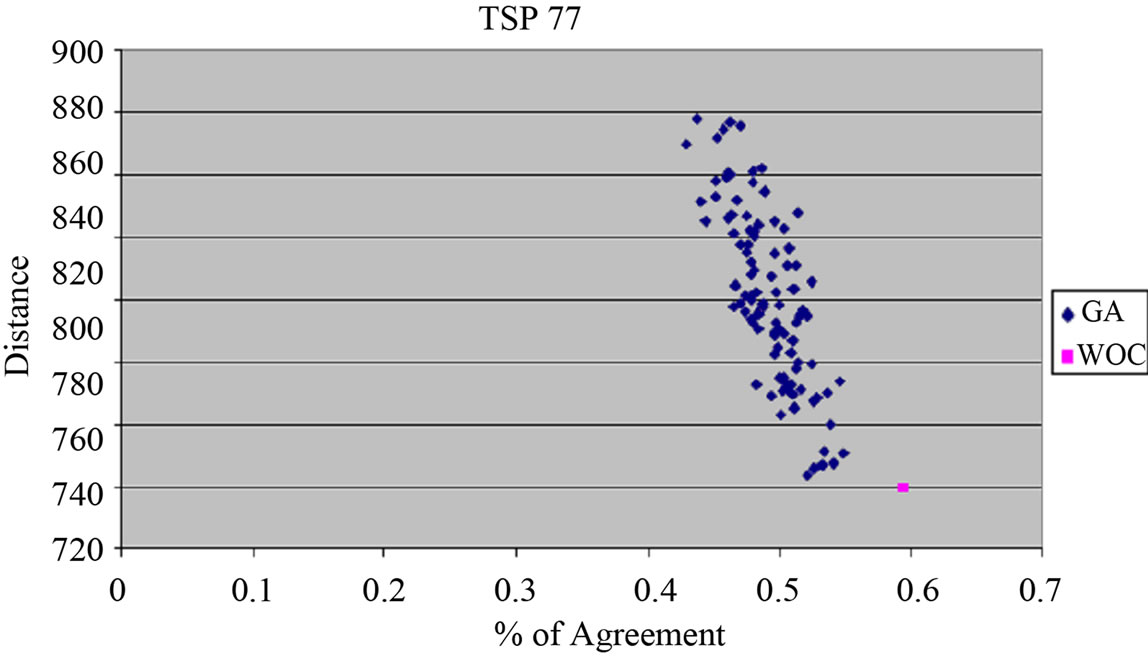


Figure 6. Scatter plots for 22, 44, 77, 97 and 222 city TSP.

Figure 7. Best results from GA and expert agents.
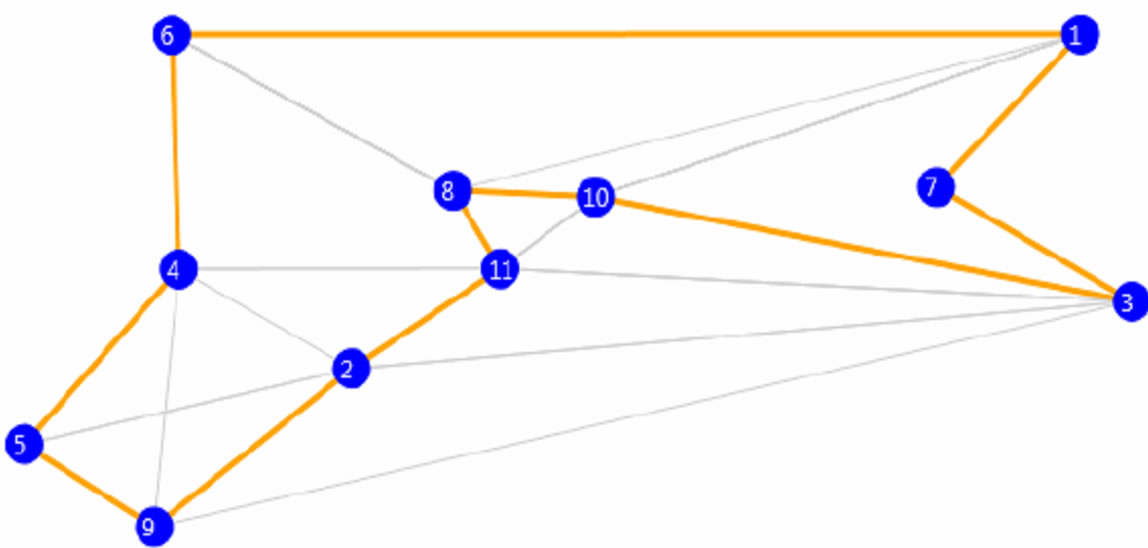
Figure 8. 11 nodes: top 30 from each population.

Figure 9. 22 nodes: top 80 from each population.
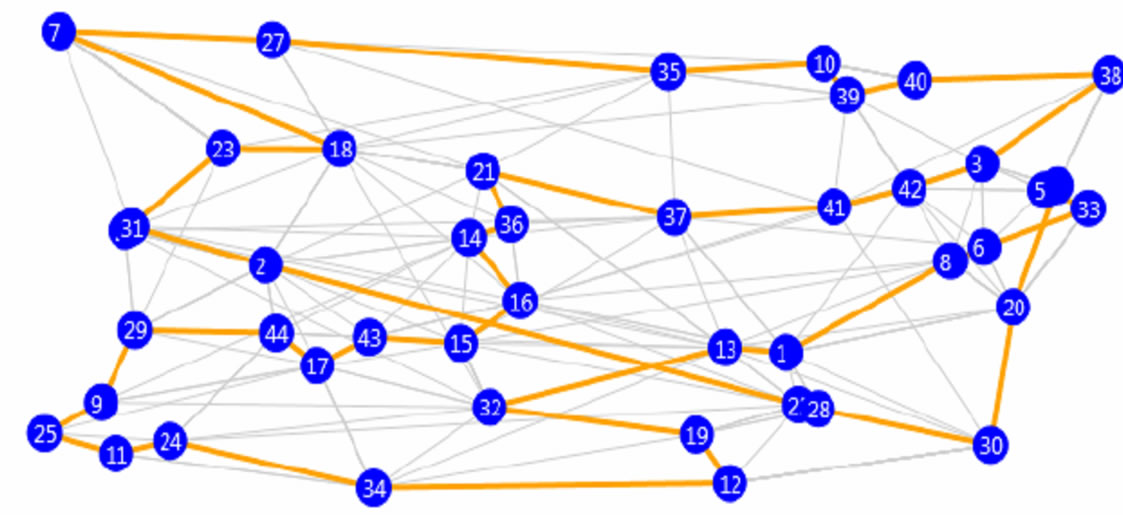
Figure 10. 44 nodes: top 90 from each population.
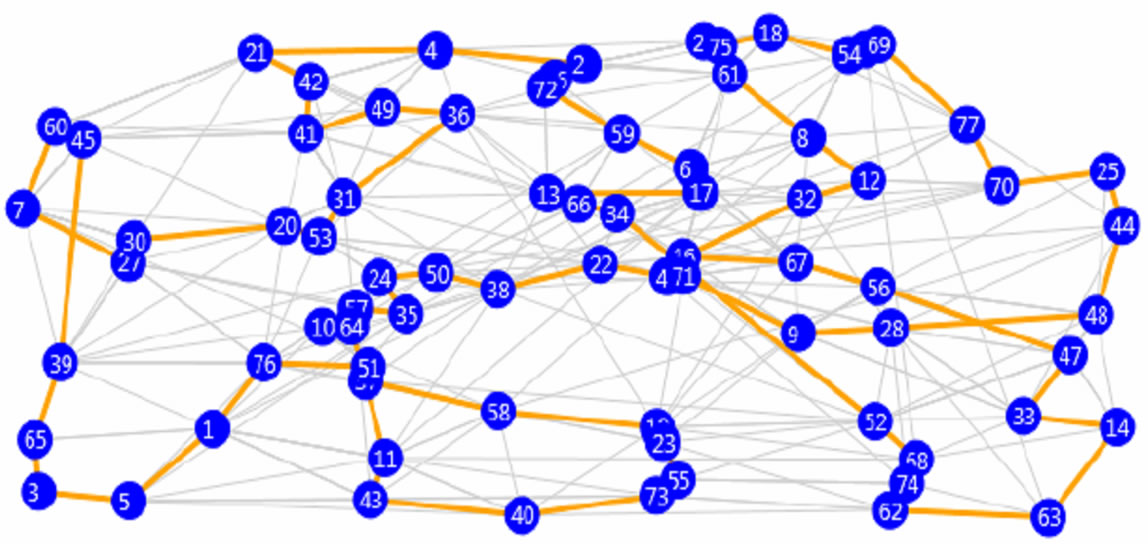
Figure 11. 77 nodes: top 10 from each population.
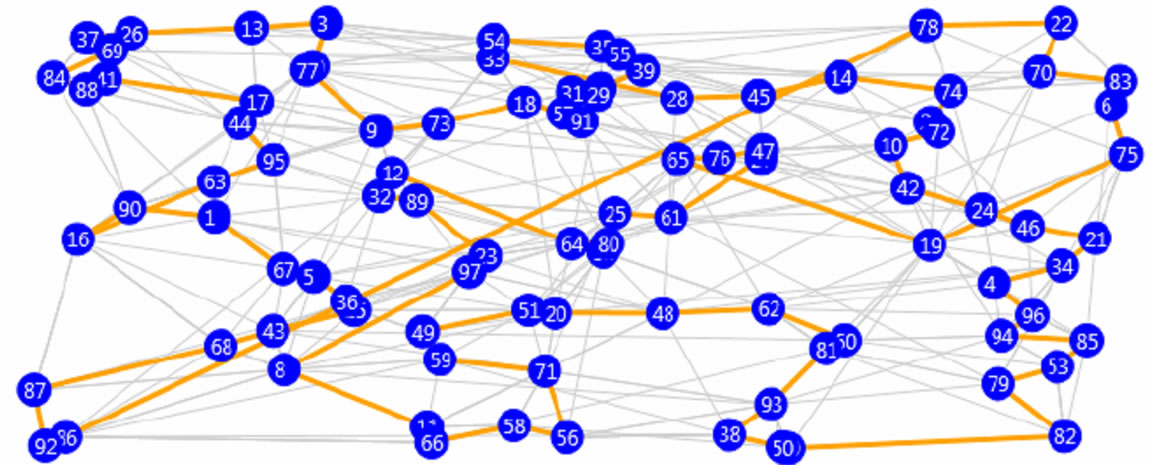
Figure 12. 97 nodes: top 45 from each population.

Figure 13. 222 nodes: top 15 from each population.
7. Conclusions
We have presented a novel swarm-based nature-inspired metaheuristic algorithm for optimization. In many cases WoAC outperformed even the best solutions produced by the genetic algorithm. In the case of running WoAC on a single population, better results seemed to appear more frequently in the larger data sets. Improved results are also seen in the case of running WoAC on groups of populations after reducing the number of chromosomes to use from each population. In both cases, the larger independent variance in the set used for WoAC, whether a single population or multiple, seemed to yield better results. On the small instances of TSP, the genetic algorithm is quick to find good solutions and the entire population tends to converge on best chromosome in the population. This gives poor independent variance and WoAC results in equal or worse results after processing the population.
As the data sets increase in size, the genetic algorithm performs worse, but this allows more room for improvement for WoAC. In using WoAC on multiple populations, the analysis gave varying results on different percentages of best chromosomes in each population. This parameter can be changed and WoAC tested to compare results, but a common value does not seem to generalize across different size data sets. This is due to high dependence on the data used. The larger data sets used with multiple populations did show more consistent improvement after the application of WoAC. Running WoAC on datasets with several hundred cities and subsampling any number of top chromosomes yielded better results than the best result from the genetic algorithm alone. Even running WoAC on each single population seemed to show improvement, giving better results on 5 of the 10 populations generated.
WoAC is a postprocessing algorithm with running time in milliseconds which is negligible in comparison to the algorithm it attempts to improve, genetic search. While, WoAC does not always produce a superior solution, in cases where it fails it can be simply ignored since the GA itself provides a better solution in such cases. Consequently, WoAC is computationally efficient and can only improve the quality of solutions, never hurting the overall outcome.
In the future we plan on conducting additional experiments aimed at improving overall performance of the WoAC algorithm. In particular we are going to investigate how WoAC could be combined with non-GA, swarm-based approaches such as ACO [17], BCO [18], (BFO) [19], or (GSO) [20]. Special attention should be given to discovering better aggregation rules and optimal ways of achieving diversity in the populations. An important question to ask, deals with an optimal percentage of the population to be used in the crowd. In other words, should the whole population be used or is it better to select a sub-group of “experts”. Finally we are very interested in applying WoAC to other NP-Hard problems.
REFERENCES
- R. M. Karp, “Reducibility among Combinatorial Problems,” In: R. E. Miller and J. W. Thatcher, Eds., Complexity of Computer Computations, Plenum, New York, 1972, pp. 85-103.
- P. Rabanal, I. Rodriguez and F. Rubio, “Using River Formation Dynamics to Design Heuristic Algorithms,” Lecture Notes in Computer Science, vol. 4618, 2007, pp. 163-177. doi:10.1007/978-3-540-73554-0_16
- R. V. Yampolskiy and A. EL-Barkouky, “Wisdom of Artificial Crowds Algorithm for Solving NP-Hard Problems,” International Journal of Bio-Inspired Computation, vol. 3, No. 6, 2011, pp. 358-369. doi:10.1504/IJBIC.2011.043624
- L. H. Ashby and R. V. Yampolskiy, “Genetic Algorithm and Wisdom of Artificial Crowds Algorithm Applied to Light Up,” the 16th International Conference on Computer Games, Louisville, 27-30 July 27, 2011, pp. 27-32.
- A. B. Khalifa and R. V. Yampolskiy, “GA with Wisdom of Artificial Crowds for Solving Mastermind Satisfiability Problem,” International Journal of Intelligent Games & Simulation, vol. 6, No. 2, 2011, pp. 12-17.
- D. E. Goldberg, “Genetic Algorithms in Search, Optimization and Machine Learning,” Addison Wesley Publishing Company, Boston, 1989.
- J. R. Koza, “Genetic Programming: A Paradigm for Genetically Breeding Populations of Computer Programs to Solve Problems,” Technical Report, Stanford University. Stanford, 1990.
- S. Wolfram, “A New Kind of Science,” Wolfram Media Inc., Champaign, 2002.
- J. D. Farmer, N. Packard and A. Perelson, “The immune System, Adaptation and Machine Learning,” Physica D, vol. 2, No. 1-3, 1986, pp. 187-204. doi:10.1016/0167-2789(86)90240-X
- H. Shah-Hosseini, “The Intelligent Water Drops Algorithm: A Nature-Inspired Swarm-Based Optimization Algorithm,” International Journal of Bio-Inspired Computation, vol. 1, No. 1-2, 2009, pp. 71-79. doi:10.1504/IJBIC.2009.022775
- E. Rashedi, H. Nezamabadi-Pour and S. Saryazdi, “GSA: A Gravitational Search Algorithm,” Information Sciences, vol. 179, No. 13, 2009, pp. 2232-2248. doi:10.1016/j.ins.2009.03.004
- J. M. Bishop, “Stochastic Searching Networks,” 1st IEE International Conference on Artificial Neural Networks, London, 16-18 October 1989, pp. 329-331.
- X.-J. Wang, L. Gao and C.-Y. Zhang, “Electromagnetism-Like Mechanism Based Algorithm for Neural Network Training,” Lecture Notes in Computer Science, vol. 5227, 2008, pp. 40-45. doi:10.1007/978-3-540-85984-0_5
- J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” IEEE International Conference on Neural Networks, Perth, 27 November-1 December 1995, pp. 1942- 1948.
- A. Kaveh and S. Talatahari, “A Novel Heuristic Optimization Method: Charged System Search,” Acta Mechanica, vol. 213, No. 3-4, 2010, pp. 267-289. doi:10.1007/s00707-009-0270-4
- O. K. Erol and I. Eksim, “A New Optimization Method: Big Bang-Big Crunch,” Advances in Engineering Software, vol. 37, No. 2, 2006, pp. 106-111. doi:10.1016/j.advengsoft.2005.04.005
- M. Dorigo, M. Birattari and T. Stutzle, “Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique,” IEEE Computational Intelligence Magazine, vol. 1, No. 4, 2006, pp. 28-39. doi:10.1109/MCI.2006.329691
- D. T. Pham, A. Ghanbarzadeh, E. Koc, S. Otri, S. Rahim and M. Zaidi, “The Bees Algorithm—A Novel Tool for Complex Optimisation Problems,” Virtual International Conference on Intelligent Production Machines and Systems, Cardiff, 13-14 July 2006, pp. 454-459.
- K. M. Passino, “Biomimicry of Bacterial Foraging for Distributed Optimization and Control,” Control Systems Magazine, vol. 22, No. 3, 2002, pp. 52-67. doi:10.1109/MCS.2002.1004010
- K. N. Krishnanand and D. Ghose, “Detection of Multiple Source Locations Using a Glowworm Metaphor With Applications to Collective Robotics,” IEEE Swarm Intelligence Symposium, Pasadena, 8-10 June 2005, pp. 84-91.
- X. S. Yang, “Firefly Algorithms for Multimodal Optimization,” Lecture Notes in Computer Sciences, vol. 5792, 2009, pp. 169-178. doi:10.1007/978-3-642-04944-6
- X.-S. Yang and S. Deb, “Cuckoo Search via Levy Flights,” World Congress on Nature & Biologically Inspired Computing, Coimbatore, 9-11 December 2009, pp. 210-214.
- C. W. Reynolds, “Flocks, Herds, and Schools: A Distributed Behavioral Model,” 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, 27-31 July 1987, pp. 25-34.
- Z. W. Geem, J. H. Kim and G. V. Loganathan, “A New Heuristic Optimization Algorithm: Harmony Search,” Simulation, vol. 76, No. 2, 2001, pp. 60-68. doi:10.1177/003754970107600201
- A. Mucherino and O. Seref, “Monkey Search: A Novel Metaheuristic Search for Global Optimization,” AIP Conference on Data Mining, Systems Analysis and Optimization in Biomedicine, Gainesville, 28-30 March 2007, pp. 162-173.
- A. R. Mehrabian and C. Lucas, “A Novel Numerical Optimization Algorithm Inspired from Weed Colonization,” Ecological Informatics, vol. 1, No. 4, 2006, pp. 355-366. doi:10.1016/j.ecoinf.2006.07.003
- J. Surowiecki, “The Wisdom of Crowds: Why the Many Are Smarter than the Few and How Collective Wisdom Shapes Business, Economies, Societies and Nations,” Doubleday, New York, 2004.
- F. Galton, “Vox Populi,” Nature, vol. 75, No. 1949, 1907, pp. 450-451.
- S. K. M. Yi, M. Steyvers, M. D. Lee and M. Dry, “Wisdom of Crowds in Minimum Spanning Tree Problems,” Proceedings of the 32nd Annual Conference of the Cognitive Science Society, Austin, 2010, pp. 1840-1845.
- S. K. M. Yi, M. Steyvers, M. D. Lee and M. Dry, “Wisdom of the Crowds in Traveling Salesman Problems,” 2011. socsci.uci.edu/~mdlee/YiEtAl2010.pdf
- C. Wagner, C. Schneider, S. Zhao and H. Chen, “The Wisdom of Reluctant Crowds,” 43rd Hawaii International Conference on System Sciences, Honolulu, 5-8 January 2010, pp. 1-10.
- M. C. Mozer, H. Pashler and H. Homaei, “Optimal Predictions in Everyday Cognition: The Wisdom of Individuals or Crowds?” Cognitive Science, vol. 32, No. 7, 2008, pp. 1133-1147. doi:10.1080/03640210802353
- F. Bai and B. Krishnamachari, “Exploiting the Wisdom of the Crowd: Localized, Distributed Information-Centric VANETs,” Communications Magazine, vol. 48, No. 5, 2010, pp. 1-8.
- T. Moore and R. Clayton, “Evaluating the Wisdom of Crowds in Assessing Phishing Websites,” Lecture Notes in Computer Science, vol. 5143, 2008, pp. 16-30. doi:10.1007/978-3-540-85230-8_2
- K. Shiratsuchi, S. Yoshii and M. Furukawa, “Finding Unknown Interests Utilizing the Wisdom of Crowds in a Social Bookmark Service,” IEEE/WIC/ACM International Conference on Intelligence and Intelligent Agent Technology, Hong Kong, 18-22 December 2006, pp. 421-424.
- F. C. C. Osorio and J. Whitney, “Trust, the Wisdom of Crowds, and Societal Norms,” 1st International Conference on Security and Privacy for Emerging Areas in Communication Networks, Athens, 5-9 September 2005, pp. 199- 208.
- D. Opitz and R. Maclin, “Popular Ensemble Methods: An Empirical Study,” Journal of Artificial Intelligence Research, vol. 11, 1999, pp. 169-198.
- P. Melville and R. J. Mooney, “Diverse Ensembles for Active Learning,” 21st International Conference on Machine Learning, Banff, 4-8 July 2004, pp. 584-591.
- P. Melville and R. J. Mooney, “Constructing Diverse Classifier Ensembles Using Artificial Training Examples,” 18th International Joint Conference on Artificial Intelligence, Acapulco, 9-15 August 2003, pp. 505-510.
- R. J. Mooney, “Machine Learning: Ensembles,” 2011. cs.utexas.edu/~mooney/cs391L/slides/ensembles.ppt
- M. Bellmore and G. L. Nemhauser, “The Traveling Salesman Problem: A Survey,” Operations Research, vol. 16, No. 3, 1968, pp. 538-558. doi:10.1287/opre.16
- M. Dorigo and L. M. Gambardella, “Ant Colonies for the Traveling Salesman Problem,” Biosystems, vol. 43, No. 2, 1997, pp. 73-81. doi:10.1016/S0303-2647(97)01708-5
- R. E. Burkard, V. G. Deineko, R. V. Dal, J. A. A. V. D. Veen and G. J. Woeginger, “Well-Solvable Special Cases of the Traveling Salesman Problem: A Survey,” SIAM Review, vol. 40, No. 3, 1998, pp. 496-546.
- W. Cook, “Concorde TSP Solver,” 2010. tsp.gatech.edu/concorde/index.html
- R. V. Yampolskiy, “Application of Bio-Inspired Algorithm to the Problem of Integer Factorisation,” International Journal of Bio-Inspired Computation, vol. 2, No. 2, 2010, pp. 115-123. doi:10.1504/IJBIC.2010.032127
- R. Yampolskiy, et al., “Printer Model Integrating Genetic Algorithm for Improvement of Halftone Patterns,” Western New York Image Processing Workshop, Rochester, 2004.
- J. McCaffrey, “Using Permutations in NET for Improved Systems Security,” 2003. msdn.microsoft.com/en-us/library/Aa302371
- C. K. Tan, “C# BigInteger Class-CodeProject,” 2002. http://www.codeproject.com/KB/cs/biginteger.aspx
Appendix: Concorde Data File
NAME: concorde7 TYPE: TSP DIMENSION: 7 EDGE_WEIGHT_TYPE: EUC_2D NODE_COORD_SECTION
1) 87.951292 2.658162
2) 33.466597 66.682943
3) 91.778314 53.807184
4) 20.52674947.633290
5) 9.006012 81.185339
6) 20.032350 2.761925
7) 77.181310 31.922361

