Wireless Sensor Network
Vol.07 No.12(2015), Article ID:61941,14 pages
10.4236/wsn.2015.712014
Enhancing Performance of Multi-Rate WLANs: Ant Colony Approach
Qiang Ma, Abdullah Al-Dhelaan, Mznah Al-Rodhaan
Department of Computer Science, College of Computer & Information Sciences, King Saud University, Riyadh, Saudi Arabia

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 15 November 2015; accepted 13 December 2015; accepted 16 December 2015

ABSTRACT
The trade-off between users’ fairness and network throughput may be unacceptable in a multi- rate 802.11 WLAN environment. In this paper, we will design a new intuitive simplified mathematical model called simplified coefficient of variation (SCV) to closely reflect our topic. Through controlling the power of Access Points, SCV can optimize and improve the performance. Since our topic is a NP-hard problem, we use Ant Colony Algorithm to solve our model in a practical scenario. The simulation shows excellent results indicating that our model is efficient and superior to an existing method. Also we use software SAS to further reveal the relationships among the three indicators to illustrate the essence of our approach and an existing algorithm.
Keywords:
Power Control, Proportional Fairness, Ant Colony, Optimization, Coefficient of Variation, Heuristic Function

1. Introduction
The rapid development of the Internet and the progress of wireless technology are making wireless networks play an increasingly important role in many areas. This is particularly true for the IEEE 802.11 wireless local area network (WLAN) technology. With its development, the increasing demands of service quality and a sharp rise in the number of user groups, the fairness and congestion etc. problems have become heavily concentrated in some places like offices, meeting rooms and other crowded places. In this case, many access points may be allocated, but without an overall channel or power planning, this will result in a large amount of co-channel interference, load imbalance, and network throughput decline, which will degrade the user experience.
Currently, many valuable solutions have been developed to solve above problems of WLAN, and are mainly focused on the following two aspects:
(a) Wireless channel planning. Through different methods, the limited channel resources will be reasonably assigned to all access points (APs) to make it possible to reduce co-channel interference and network overhead in order to improve overall network throughput.
(b) Power control to achieve load balancing. Through increasing or decreasing the AP’s power to adjust the signal strength of the AP, thus it changes the access topology of the user-AP in the network in order to reduce the scheduling overhead, and improve load balance, fairness etc.
This paper involves both aspects above. The rest of the paper is organized as follows: related work is discussed in Section 2, and Section 3 shows our motivation. After that, a brief introduction of ant colony algorithm as background will be provided in Section 4. Then we start to explain the new model SCV and implement it using ant colony algorithm, the simulation modeling using Matlab is explained in Section 5. After this, we give comparison and SAS analysis in Section 6 and then draw the conclusions in Section 7.
2. Related Work
According to IEEE 802.11, a high-density WLAN deployment environment offers a short distance between APs and users since each user will be surrounded by many APs. In this case, each user will connect with the AP by the strongest received signal strength indicator (RSSI) by default. We know that the users are not uniformly distributed in an area, which makes some APs connect more users than the other APs. This will produce the load imbalance problem, as some APs are hungry while some APs are overloaded. This situation results in unfair use of resources.
As a part of our research, the basic solution has been introduced in [1] .
To solve interference problem, the author in [2] proposed an adaptive neuro fuzzy distributed power control algorithm to maximize the minimum Carrier to Interference Ratio (CIR) among all of co-channel users in each channel of system. The simulation results showed better performance comparing with a classical method in terms of convergence.
To solve congestion problem, the authors in [3] proposed an adaptive load balance allocation strategy for small antenna based wireless networks that can enhance the traffic-carrying capacity for variations in traffic. Their simulation results were confirmed to be efficiency.
In order to improve the throughput, the authors in [4] introduced three strategies which were Dirty Paper Coding (DPC) strategy, Noise strategy, and Opportunistic Interference Cancellation (OIC) strategy. Also they proposed corresponding optimal power control algorithms for each strategy. The simulation results showed their aims were achieved.
The popular 802.11 MAC protocol provides equal transmission chances to all users, which may achieve throughput-based fairness if all users have the same frame size during a cycle [5] - [8] . Recent studies have shown that time-based fairness is much better than throughput-based fairness in multi-rate WLANs [9] .
So far, we have two fairness criteria factors that are widely used in network management: proportional fairness [7] which allocates bandwidth to users in proportion to their bit rates to maximize the sum of the bandwidth utilities of the users, and max-min fairness [10] which allocates throughput as equally as possible through maximizing the minimum throughput. Proportional fairness and time-based fairness are equivalent in multi-rate WLANs when all users have the same weight [11] . The equivalence of max-min fairness and throughput-based fairness under the same condition (integral association) was proved in [12] .
The authors in [13] proposed a new algorithm called Power Control for AP (PCAP) to optimize the network utility by maximizing the average of the AP utility and minimizing the variance of the AP utility, the result directly maximized the “throughput” as its target, and then they started to calculate the users’ fairness indicator― “J” (Jain’s fairness index [14] ) as their byproduct. Though the result showed significant improving, the “J” is unreasonable to be a dependent variable. We will analyze the relationship between these two variables.
According to IEEE802.11, AP’s transmission power can be changed in an allowable range, this technique is called power control. Some previous studies, such as [15] [16] , have assumed that the user-AP associated topology will not change when adjusting the power of APs, this assumption is not the reality. On the contrary, some papers have noticed this phenomenon and developed techniques called cell breathing [17] .
To enhance load-balancing and network throughput, a variable polyhedron genetic algorithm (GA) is proposed in [18] . Which not only provides an AP service availability guarantee but also yields a near-optimal beacon range for each AP when the number of evolutions is large enough. Their simulation study indicates that the algorithm is superior over the default 802.11 AP association model.
Also the problem researches like oblem. Similarly, in order to solve such trade off problem, there are many researches, such as [19] , the authors proposed an algorithm that transformed the trade off problem into a monotonic optimization problem. Also the problem was solved with geometric programming in [20] , but it is not suitable for the low Signal to Interference Ratio (SIR) case. While in [21] , the authors proposed a centralized algorithm called Non-Linear Approximation Optimization for Proportional Fairness to derive the user-AP association via relaxation, and also gave a distributed heuristic algorithm called Best Performance First which provides an AP selection criterion for new comers.
Regarding the tradeoff problem, also some other valuable solutions are given. Like [22] , the authors derived the stability region of a multiuser multichannel WLAN system and determined the throughput optimal channel switching scheme within a certain class of schemes. In [23] , the authors proposed an extension of the AP aggregation algorithm to ensure the minimum average throughput for each host in the field.
In [24] , the authors proposed a novel AP association approach LBAA, taking AP’s load-balancing, Wireless Mesh Networks’ (WMNs’) multi-hop characteristic, and user’s RSSI into consideration to solve network congestion and performance degradation problem in Wireless Mesh Networks (WMNs).
In [25] , to solve the fairness problem in Wireless Mesh Networks (WMNs), the authors proposed a probabilistic approach to provide proportional fairness without solving global non-linear and non-concave optimization. Their simulation result showed that the proposed scheme works better than the standard IEEE 802.11 based EDCA MAC in terms of fairness and throughput.
In summary, there are many valuable research papers related to the above trade off problem. Up to date, none of those researches in term of the tradeoff between fairness and throughput could offer a rational, clearly designed mathematical model which can be easily and widely implemented using the well known AI algorithms. Thus our research aims to fill such gap; we will design a reasonable mathematical model, which is SCV. It should have a simple form, easy to be understood. The model itself should be highly effective and efficient to match our topic, and should be a bridge to link our topic with AI algorithms. So we choose one of representative AI algorithms―Ant Colony, and design its detail to implement the SCV model. At the end, we will compare its performance with an existing algorithm-PCAP in [13] , also through SAS analysis, we will reveal the essence of our approach which has not been discussed at such micro level in the previous research.
In this paper, the contributions are listed as follows: 1) we describe the “trade-off” using “J of user” and “J of AP”, which refer to the fairness of users and fairness of APs respectively. Then we design our target function using many skills to deal with those complex formulas, after that we get our simplified coefficient of variation (SCV) model, which is a clear mathematical function to solve such trade-off problem. This is the core contribution of our paper; 2) we define the problem as an informed search NP-hard problem and apply Ant Colony algorithm to solve the SCV model; 3) we use multi-channel allocation to improve the transmission rate; 4) we use Statistical Analysis System (SAS) for analysis to reveal the relationships of three indicators and the essence of algorithms; 5) SCV opens a door for many AI algorithms; it is a bridge between Network & AI.
3. Motivation
3.1. The Essence of PCAP: throughput
From our SAS analysis in Figure 3, three indicators (Juser: J of user; Jap: J of AP; Tpt: relative throughput) show that J of AP can represent throughput (value > 0.8, so it is highly linear related).
Through our statistics calculation, PCAP focus on J of AP only, which means it only focus on throughput. This is a deficiency of Target Function design, which is not well reflecting our topic.
3.2. The Essence of SCV
The problem is defined as a NP-hard problem since we apply a practical scenario that includes 20 APs, each AP has 10 levels of power, so the state space of the problem will be 1020, making it neither solvable nor verifiable in polynomial time, so it is NP-hard.
From the computation theory, we know that we cannot get an accurate solution. Comparing with other NP- hard problems such as TSP (Traveling Salesman Problem), we get some heuristic methods. Since existing models either using complex definition such as utility or involving many parameters such as channel gain, those models are not clear enough to apply informed search techniques, so first we need to build a clear, simplified model SCV, and then apply the Ant Colony algorithm to solve the model.
Since our topic is: “J of user (fairness of users) & throughput”, which means to make balance between these two parameters. Obviously the two parameters have different units, then we have to convert the “throughput” to “J of AP” (already explained, it can represent throughput, with high linear relation).
Then our SCV gives a new designed target function:
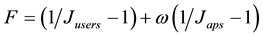
which reflects the balance of two parameters (J of user & throughput), and we will rewrite to get its final form f.
4. Ant Colony Algorithm
This part is clearly explained in [26] . The Ant Colony algorithm is a method from the field of Swarm Intelligence. Ant Colony Algorithm, Elite Ant System, and Rank-based Ant System compose the Ant Colony Optimization methods.
The Ant Colony algorithm is inspired by the foraging behavior of ants, specifically the pheromone communication among ants regarding a short path between the living place and a food source.
Ants initially wander randomly around their environment. Once the food is located, the ants that pass by the food will begin laying down pheromone in the environment. Numerous trips between the food and the living place are performed, and if the same path is followed that leads to food then additional pheromone is laid down. And also at the same time, the pheromone decays in the environment, so that older paths are less likely to be followed. Other ants may discover the same path that has strongest pheromone and also lay down pheromone when they are passing by. The positive feedback process makes more ants produce paths that are further refined through use.
The goal of this strategy is to exploit heuristic information to construct candidate solutions and hold the information as the history. Paths are constructed in a probabilistic step-wise manner. The probability of selecting a path is determined by both heuristic contribution and historical contribution. History is updated proportional to the quality of candidate paths and is uniformly decreased ensuring the most recent and useful information is retained. We will use 2 important formulas:
(a) After each ant conducts its tour of the trail, the pheromone is updated using the following formula:
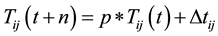
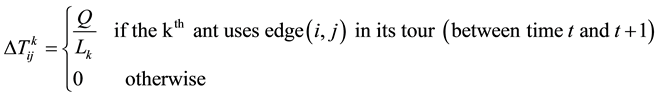
Q is a constant and Lk is the tour’s length of the kth ant.
(b)Transition probability:
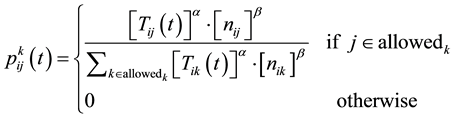
where α and β are controlling parameters that control the relative importance of trail versus visibility.
5. Model Design and Simulation
Now we are going to explain our SCV model and implement it in Ant Colony Algorithm.
5.1. The Way APs Attract Users
The user will select the strongest Received Signal Strength Indicator (RSSI) as default. In the model [27] , 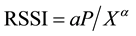 where “a” is a constant factor, “P” is received power by user, “X” is distance between user and selected AP, while “
where “a” is a constant factor, “P” is received power by user, “X” is distance between user and selected AP, while “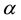 ” has different value in different scenarios, generally between 1.6 and 6.5 [28] . The formula only determines the association matrix of user-AP. In practice, the general power range of the AP is 10 dBm - 30 dBm, i.e. 1 mw ~1 w, here we adopt
” has different value in different scenarios, generally between 1.6 and 6.5 [28] . The formula only determines the association matrix of user-AP. In practice, the general power range of the AP is 10 dBm - 30 dBm, i.e. 1 mw ~1 w, here we adopt 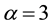 for indoor case. From the formula, the value of “a” does not affect the association results, to simplify the mathematical form, we take
for indoor case. From the formula, the value of “a” does not affect the association results, to simplify the mathematical form, we take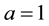 , so our model adopts a simplified form:
, so our model adopts a simplified form:
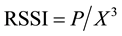 (1)
(1)
5.2. Study the SINR [rij] of the User [i]
We use rij to denote SINR (Signal to Interference plus Noise Ratio). Assuming the user [i] connects to AP[j], the power of AP[j] is Pj. Wherein “g” are channel gains, Ai is a set of all APs within the same channel of AP[j]. N0j is an additive white Gaussian noise generated by AP[j].
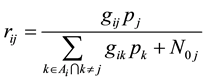 (2)
(2)
It is worth noting that N0j can be adjusted to an exact value [29] [30] . So we can set a constant ,
,
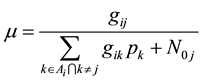 (3)
(3)
5.3. Study the Relationship between User [i]’s Transmission Rate vi and Its SINR [rij]
From Table 1 in [13] , vi denotes user’s transmission rate and rij is SINR. We see the monotonically increasing relationship between the two variables. Here we might assume that two variables meet the linear relationship as an approximation, 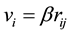 ,
, 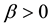 is a constant of proportionality. Then connect this to (2) and (3) we have:
is a constant of proportionality. Then connect this to (2) and (3) we have:
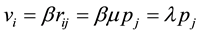 (4)
(4)
So λ is a constant:

5.4. Study the Effective Speed V̅i
Let N[j] denote the total number of users which connect with AP[j]. Pj is AP[j]’s power. Because the users are time based sharing the chance of AP[j], so we use 

5.5. Study the AP’s Power
According to the simulation result in [13] , we know that usually 10 Levels of AP power will be enough to achieve a good result. Therefore, in our model, pmax and pmin have relationship as following: pmax/pmin=10, pmax will be the basis of calculation, since we need to increase the pj, so the 10 APs’ power value is in Table 2.
Note here the unit of power is “mw”, not “dBm”. Since 

Table 1. vi - rij relationship.
Table 2. Level-value relationship.

Let M be the total number of users and N be the total number of APs. From statistics we know that the Expectation of V̅i for all users is denoted as E(V̅i), and Variance of V̅i for all users is denoted as S2(V̅i). We have the following (



Let b[i] denote the effective transmission speed from user[i] to AP[j], we have b[i] = V̅i. Moreover, let U[j] denote the transmission speed from the AP[j] to backbone. The Expectation of b[i] is denoted as:







Here cvusers denotes the coefficient of variation of transmission speed of all users, and cvAPs denotes the coefficient of variation of transmission speed of all APs, we have:


Note, here we adopt the definition of J in [13] , where we have
5.6. Cost Function Construction
According to our topic, we need a function that can describe the tradeoff between fairness of users and throughput of network. In [13] , the algorithm is divided into two steps: increase average value and decrease variance value of AP utility to increase throughput of network. They are equal to decreasing 


Let F denote a target function as follows:

Here we do some mathematical derivation to illustrate how we get a reasonable value of



From the above, it means 




where in

Note that M and N are constants as defined before. M is total number of users, N is total number of APs. When “F” goes to minimum, it is equal to “
5.7. Throughput
From Formula (12) we know that:


throughputreal is real throughput, and throughputrelative is relative throughput. Since the λpmin is constant, we use throughputrelative to represent throughputreal.
5.8. Ant Colony Design & Simulation
In this part we are going to place a total number of N = 20 APs on a 4 by 5 grid, with each AP on a grid point. The coverage area of each AP can stretch across the whole area. The distance between two adjacent APs is set to 100 meters. The maximum transmission power of each AP is set to 20 dBm (100 mw), so the minimum transmission power of each AP is set to 100/10 = 10 mw = 10 dBm.
We arrange M = 200 users randomly distributed in the whole area. According to [31] , a separation of four channels can be used without reducing the performance, so the possibilities could be opened to channels 1, 5, 9 and 13. In this paper we decide to use these channels in order to get a bigger
Let APj → Ci denote APj using channel i, we use 1, 5, 9, 13 these channels to configure the network as in Table 3.
5.9. Ant Colony Algorithm Design
(a) To initialize 200 users’ and 20 APs’ coordinates. NC_max is the maximum number of iterations, m is the number of ants, Alpha is a parameter to characterize the importance of pheromone, Beta is a parameter to characterize the importance of heuristic information, and Rho is a pheromone evaporation coefficient. Also we need to initialize pheromone matrix Tau: Tau = ones (10, 10, 19). We calculate the average distance for each AP to all users then to construct a row vector called xaverage (1 × 20): xaverage = sum (Distance)/200.
(b) Heuristic Matrix Eta Design: 
ratio of the two
× 10 × 19), from the 1st AP to 20th AP, which has total of 19 pages, and each page is a matrix (10 level × 10 level) describing the heuristic information from all power levels of current AP to all power levels of the next AP, and we set the value of these heuristic transition points as “1”. We introduce a new mechanism: we give such heuristic matrix a quantitative parameter defined as “similar”, namely the degree of similarity between non-heuristic points and the heuristic points, and we set the value of non-heuristic points in the heuristic matrix as “similar×1”. Then we finish the design of heuristic matrix Eta.
Table 3. AP-channel relationship.
(c) We set totally 10 ants at





(d) Repeat step(c) until reaching the NC_max (a constant), and output all cycles’ results.
6. Result Analysis
In this part, some definitions are as following. m is the number of ants, Alpha is a parameter to characterize the importance of pheromone, Beta is a parameter to characterize the importance of heuristic information, and Rho is a pheromone evaporation coefficient. NC_max is a constant that describes the number of iterations. Q and “similar” are constants according to the algorithm.
Let m = 10; Alpha = 1; Beta = 2; Rho = 0.1; NC_max = 200; Q = 100; similar = 0.9.
6.1. Simulation Analysis
(a) The solution of ant colony algorithm has many parameters, so we need to run multiple times on the same data set and same parameters and select the average result, also to search for the more suitable parameters’ values. Here we use 



(b) All parameters can affect the calculation result. Generally, it is suitable to set Alpha = 1; Beta = 2; Rho = 0.1; and similar = 0.9 to get better results.
(c) Strictly speaking the convergence of ant colony algorithm is defined as that the pheromone in the iteration process without change, or at least the obtained path without change. This is usually in the theoretical analysis. In practical applications due to a number of random factors, it is very difficult to achieve this status. So as long as the actual optimal solutions have vibration around the average straight line after each iteration, this is considered as convergence, and such average line is called convergence line. It can be seen from Figure 1 and Figure 2, after traveling 200 times, all of the parameters have been around the horizontal line with slight vibration, and these mean convergence.
Figure 1. {Max J of user, Max J of AP}-times plot.
Figure 2. {Relative throughput, Min value of cost function}-times plot.
6.2. SAS Analysis
We use the samples from experimental data to study the correlation coefficients among these indicators. Wherein Juser denotes J of user, Jap denotes J of AP, Tpt denotes
Figure 3 shows that at Alpha = 0.05 significance level, all the p-values are less than 0.05, we reject the H0 and accept H1 that these variables are linearly related, wherein the Tpt-(Jap, Juser) have highly significant linear correlations, while correlations of Jap-Juser is weak. We compared the degree of concentration of those data points in Figure 4 and Figure 5. It is clear that data points are more concentrated in Figure 5. This means the linear correlation of Tpt-Jap is much higher than the linear correlation of Tpt-Juser, which also proves the effectiveness of SCV model (coefficient of Tpt-Jap > 0.8, Tpt-Juser = 0.17, so it is more effective to use J of AP whereas not J of user to represent the throughput).
6.3. Comparison Analysis
We select average case in Figure 1, at the 100th time, the J of User is almost equal to 0.75, and corresponding J of AP is almost equal to 0.94, the 
Here we want to compare our solution with PCAP in Table 4 from [13] , since we use different definitions to denote throughput of AP and throughput of network, we have to use the indirect method to illustrate some issues. According to [13] , we can transfer and calculate their J of AP and their throughput percentage of network bandwidth:

So their

And we have:
Figure 3. Correlation coefficients.
Figure 4. Tpt-Juser linear regression.
Figure 5. Tpt-Jap linear regression.
Table 4. The statistics of the results.

Then their throughput percentage of network bandwidth is:

In Figure 1, our J of AP is superior to theirs in (22). From the throughput point of view, our throughput percentage of network bandwidth is 72.5% > 61.3% in (24), so our method is better than PCAP. But from the fairness of users (J of user) point of view, PCAP is better than ours since 0.75 < 0.9 in (22).
According to (17), we convert (22) into our function F, we have:


So the overall performance depends on the requirement of administrators, which indicator they most concern. We define the value of “F” as the overall performance criteria of algorithm, note smaller “F” is better, and then from (25) and (26) we know that our SCV model is much better than PCAP. The above comparison analysis result is in Table 5.
Theoretically, our design of target function “F” in (17) is more simple and rational than PCAP algorithm, since we joint consider the J of user and throughput (represented by J of AP), we regard them as two variables to reflect our topic which is a balance problem. While the target of PCAP is the throughput, the authors used two sub-algorithms to achieve J of AP only, and then got their by-product: J of user.
Technically, our SCV math model is a door that leads this problem to AI algorithms. The clear target function “F” is easy to be applied to other AI algorithms, while PCAP cannot.
7. Conclusions
The objective of this paper is to improve the trade-off between user fairness (J of user) and network throughput (represented by J of AP) via power control in multi-rate WLANs.
In this article, we first construct a new simplified model called SCV. The goal of the model is to derive a target function “F” in (17) and its simplified form “
SCV (Target function F) opens a door for many AI algorithms to apply in this problem; it is a bridge between Network & AI.
Our future work is to derive a more accurate target function, and adjusts the values of parameters to find more suitable combination so that to improve the performance. Also we are working on other AI solutions based on SCV model.
Table 5. Comparison result.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through research group No. RGP-264.
Cite this paper
QiangMa,AbdullahAl-Dhelaan,MznahAl-Rodhaan, (2015) Enhancing Performance of Multi-Rate WLANs: Ant Colony Approach. Wireless Sensor Network,07,157-170. doi: 10.4236/wsn.2015.712014
References
- 1. Ma, Q., Al-Dhelaan, A. and Al-Rodhaan, M. (2015) Using Hopfield Neural Network to Improve the Performance of Multi-rate WLANs. Proceedings of 4th WSEAS International Conference on Circuits, Systems, Communications, Computers and Applications, Kuala Lumpur, May 2015, 170-178.
- 2. Asoodeh, S. (2008) New Algorithm for Power Control in Cellular Communication with ANFIS. WSEAS Transactions on Communications, 7, 8-14.
- 3. Chen, J.-S., Wang, N.-C., Hong, Z.-W. and Chang, Y.-W. (2009) An Adaptive Load Balance Allocation Strategy for Small Antenna Based Wireless Networks. WSEAS Transactions on Communications, 8, 588-597.
- 4. Hu, Q. and Tang, Z.Z. (2010) Study on Power and Rate Control Algorithm for Cognitive Wireless Networks. WSEAS Transactions on Communications, 9, 281-289.
- 5. Tan, G. and Guttag, J. (2004) Time-Based Fairness Improves Performance in Multi-Rate WLANs. Proceedings of Usenix Annual Technical Conference, USENIX Association Berkeley, 23.
- 6. Heusse, M., Rousseau, F., Berger Sabbatel, G. and Duda, A. (2003) Performance Anomaly of 802.11b. Proceedings of IEEE INFOCOM, San Francisco, 30 March-3 April 2003, 836-843.
http://dx.doi.org/10.1109/infcom.2003.1208921 - 7. Kelly, F.P. (1997) Charging and Rate Control for Elastic Traffic. European Transactions on Telecommunications, 8, 33-37.
http://dx.doi.org/10.1002/ett.4460080106 - 8. Banchs, A., Serrano, P. and Oliver, H. (2007) Proportional Fair Throughput Allocation in Multi-Rate IEEE 802.11e Wireless LANs. Wireless Networks, 13, 649-662.
http://dx.doi.org/10.1007/s11276-006-6972-9 - 9. Babu, A.V. and Jacob, L. (2005) Performance Analysis of IEEE 802.11 Multi-Rate WLANs: Time Based Fairness vs. Throughput Based Fairness. Proceeding of IEEE International Conference on Wireless Networks, Communications, and Mobile Computing, Sheraton Maui Resort Maui, June 2005, 203-208.
- 10. Bertsekas, D. and Gallager, R. (1987) Data Networks. Prentice-Hall, Upper Saddle River.
- 11. Li, W., Cui, Y., Wang, S.L. and Cheng, X.Z. (2010) Approximate Optimization for Proportional Fair AP Association in Multi-Rate WLANs. Proceedings of 5th International Conference on Wireless Algorithms, Systems, and Applications, Beijing, 15-17 August 2010, 36-46.
- 12. Bejerano, Y., Han, S.J. and Li, L. (2007) Fairness and Load Balancing in Wireless LANs Using Association Control. IEEE/ACM Transactions on Networking, 15, 560-573.
http://dx.doi.org/10.1109/TNET.2007.893680 - 13. Li, W., Cui, Y., Cheng, X.Z., Al Rodhaan, M.A. and Al Dhelaan, A. (2011) Achieving Proportional Fairness via AP Power Control in Multi-Rate WLANs. IEEE Transactions on Wireless Communications, 10, 3784-3792.
http://dx.doi.org/10.1109/twc.2011.091411.101899 - 14. Jain, R., Chiu, D.M. and Hawe, W.R. (1984) A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer System. Digital Equipment, Tech. Dec-Tr-301.
- 15. Mhatre, V.P., Papagiannaki, K. and Baccelli, F. (2007) Interference Mitigation through Power Control in High Density 802.11 WLANs. 26th IEEE International Conference on Computer Communications, INFOCOM, Anchorage, 6-12 May 2007, 535-543.
http://dx.doi.org/10.1109/infcom.2007.69 - 16. Hasu, V. and Koivo, V. (2006) Fair Transmission Rate Allocation: A Power Control Feasibility Approach. 10th IEEE Singapore International Conference on Communication Systems, ICCS, Singapore, 30 October-1 November 2006, 1-5.
http://dx.doi.org/10.1109/iccs.2006.301457 - 17. Bejerano, Y. and Han, S.J. (2009) Cell Breathing Techniques for Load Balancing in Wireless LANs. IEEE Transactions on Mobile Computing, 8, 735-749.
http://dx.doi.org/10.1109/TMC.2009.50 - 18. Wang, S.L., Huang, J.H., Cheng, X.Z. and Chen, B. (2014) Coverage Adjustment for Load Balancing with an AP Service Availability Guarantee in WLANs. Wireless Networks, 20, 475-491.
http://dx.doi.org/10.1007/s11276-013-0615-8 - 19. Qian, L.P. and Jun, Y. (2009) Monotonic Optimization for Non-Concave Power Control in Multiuser Multicarrier Network Systems. Proceedings of IEEE INFOCOM 2009, Rio de Janeiro, 19-25 April 2009, 172-180.
http://dx.doi.org/10.1109/INFCOM.2009.5061919 - 20. Chiang, M., Tan, C.W., Palomar, D.P., O’Neill, D. and Julian, D. (2007) Power Control by Geometric Programming. IEEE Transactions on Wireless Communications, 6, 2640-2651.
http://dx.doi.org/10.1109/TWC.2007.05960 - 21. Li, W., Wang, S.L., Cui, Y., Cheng, X.Z., Xin, R., Al-Rodhaan, M.A. and Al-Dhelaan, A. (2014) AP Association for Proportional Fairness in Multirate WLANs. IEEE/ACM Transactions on Networking, 22, 191-202.
http://dx.doi.org/10.1109/tnet.2013.2245145 - 22. Wang, Q.S. and Liu, M.Y. (2013) Throughput Optimal Switching in Multichannel WLANs. IEEE Transactions on Mobile Computing, 12, 2470-2482.
http://dx.doi.org/10.1109/tmc.2012.228 - 23. Islam, M.E., Funabiki, N., Nakanishi, T. and Watanabe, K. (2013) An Extension of Access-Point Aggregation Algorithm to Ensure Minimum Host Throughput for Wireless Local Area Networks. 2013 1st International Symposium on Computing and Networking, Matsuyama, 4-6 December 2013, 141-147.
http://dx.doi.org/10.1109/CANDAR.2013.27 - 24. Cui, Y., Ma, T.Z., Liu, J.C. and Das, S. (2013) Load-Balanced AP Association in Multi-Hop Wireless Mesh Networks. The Journal of Supercomputing, 65, 383-409.
http://dx.doi.org/10.1007/s11227-010-0519-7 - 25. Chakraborty, S., Swain, P. and Nandi, S. (2013) Proportional Fairness in MAC Layer Channel Access of IEEE 802.11s EDCA Based Wireless Mesh Networks. Ad Hoc Networks, 11, 570-584.
http://dx.doi.org/10.1016/j.adhoc.2012.08.003 - 26. Brownlee, J. (2011) Clever Algorithms: Nature Inspired Programming Recipes. LuLu, Raleigh.
- 27. Ding, X.L., Li, F.H., Li, H.W., Jiang, Y. and Wu, J.P. (2007) Dynamic Load Balancing Mechanism in WLAN Based on Power Control and Location Information. Journal of Xiamen University (Natural Science), 46, 150-155.
- 28. Goldsmith, A. (2004) Wireless Communications. Stanford University, Stanford.
- 29. Yin, Z.Q., Shi, C.H., Chen, M.S. and Liu, S.Z. (2008) A White and Gaussian White Noise Generator with Adjustable Parameters. Fire Control and Command Control, 33, 109-111.
- 30. Wang, P.Y., Zhai, L.L. and Shi, J.F. (2013) Design of Gaussian White Noise Generator with Adjustable Parameters Based on FPGA. Shipboard Electronic Countermeasure, 36, 113-115.
- 31. Villegas, E.G., López-Aguilera, E., Vidal, R. and Paradells, J. (2007) Effect of Adjacent-Channel Interference in IEEE 802.11 WLANs. 2nd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Orlando, 1-3 August 2007, 118-125.
http://dx.doi.org/10.1109/CROWNCOM.2007.4549783










