Wireless Sensor Network
Vol.06 No.10(2014), Article ID:51140,8 pages
10.4236/wsn.2014.610021
Experimental Assessment of the Battery Lifetime in WSN Based on the Duty-Cycle Current Average Method
Leonardo Barboni1, Maurizio Valle2
1Facultad de Ingenieria, Universidad de la Republica, Montevideo, Uruguay
2Department of Naval, Electrical, Electronic and Telecommunications Engineering, University of Genova, Genova, Italy
Email: lbarboni@fing.edu.uy, maurizio.valle@unige.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 August 2014; revised 25 September 2014; accepted 24 October 2014
ABSTRACT
A great amount of work addressed methods for predicting the battery lifetime in wireless sensor systems. In spite of these efforts, the reported experimental results demonstrate that the duty-cycle current average method, which is widely used to this aim, fails in accurately estimating the battery life time of most of the presented wireless sensor system applications. The aim of this paper is to experimentally assess the duty-cycle current average method in order to give more effective insight on the effectiveness of the method. An electronic metering system, based on a dedicated PCB, has been designed and developed to experimentally measure node current consumption profiles and charge extracted from the battery in two selected case studies. A battery lifetime measurement (during 30 days) has been carried out. Experimental results have been assessed and compared with estimations given by using the duty-cycle current average method. Based on the measurement results, we show that the assumptions on which the method is based do not hold in real operating cases. The rationality of the duty-cycle current average method needs reconsidering.
Keywords:
Battery Lifetime, Current Consumption, TinyOS, Measurement, Duty-Cycle Current Average Method

1. Introduction
Nowadays, WSNs are used for many different applications, but systems are designed in a rather ad-hoc manner without unified and systematic battery lifetime analysis. Since the quantity of battery charge is limited, it is desirably the longest possible lifetime.
For instance, in [1] authors present an ad-hoc WSN for motor energy monitoring but the node lifetime estimation method is not discussed. In [2] authors discuss WSN design for industrial automation applications; technical aspects and design approach are remarked, but issues related to node lifetime estimation are not addressed. In [3] authors introduce a solar energy self-powered wireless sensor network. Issues regarding the devices for energy storing are discussed but the node current consumption is not modeled. In [4] , authors highlight the need of achieving reduced current consumption in order to maximize battery lifetime but a systematic methodology for achieving is not proposed. In [5] a WSN application for pedestrian tracking and localization is presented, but the node lifetime estimation is not addressed. On the other hand, nowadays WSNs are also used as part of precision agriculture tools [6] [7] , but methods related to node lifetime estimation still remain omitted. To the extent of our knowledge, after reviewing the state of the art (by means of well-known bibliographic and citation database of peer-reviewed scientific literature like SCOPUS, EBSCO, JSTOR, IOP science, and IEEE Xplore), we argue that WSN designers avoided carrying out long-term measurements in order to validate battery depletion estimate models for WSN applications. Designers use the duty-cycle current average method, which is nowadays the most accepted method. However, designers often report that batteries are depleted prematurely with respect to the estimation given by such method (e.g. [8] -[12] ).
The aim of this paper is to experimentally assess the duty-cycle current average method in order to give more effective insight on the effectiveness of the method. We present a counterexample based on measurements in order to show how the duty-cycle current average method can fail the battery lifetime estimation. As we need a solid understanding of the battery current consumption profile, we have designed an electronic metering system based on a dedicated PCB, which visualizes the node current consumption profile and charge extracted from the battery during the wireless sensor node operation (e.g. transmission, signal sampling). The node used in the experiments is the MICAz [13] running applications developed by using nesC language [14] . The TinyOS [15] version is provided by the software platform MOTEWORK [16] and the radio transceiver is the Chipcon CC2420 [17] . The node is powered by two non-rechargeable alkaline IEC-LR6 cells, size AA.
By using the proposed electronic metering system, measurements of two case studies have been performed; the experimental results provide evidence to explain why the duty-cycle current average method is not reliable for the estimation of the battery lifetime. An experimental battery full-depletion time measurement has been conducted to compare the result against the estimation given by the duty-cycle current average method.
2. Wireless Sensor Task and Duty-Cycle Definition
The TinyOs operating system manages the node hardware resources; it is based on the hardware abstraction layers software model (TEP 2 [15] ), where each level gives services to upper layers through interfaces. The bottom layer is named Hardware Presentation Layer (HPL) and it is responsible for accessing hardware resources. This is explained in the documented TinyOS Enhancement Proposals also named TEPs (in this case see TEP 2 from [15] ). By using this software model, designers can develop programs by using customized interfaces through which the lower hardware abstraction layers are invisible. The WSN application is implemented at the top level (Hardware Interface Layer or HIL). In this framework, the tasks represent applications performed by the wireless sensor node: e.g. sensor signal sampling, radio transmission and signal processing. The node wakes up (from power down state) in order to execute the task and afterwards goes into sleep mode (power down). In other words, a task is the activity that the node performs between two power down states. Each task is executed at the rate
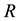 (number of tasks per second) and the task time duration is defined as the active period
(number of tasks per second) and the task time duration is defined as the active period
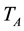 (each task has its own
(each task has its own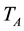 ). The node duty-cycle time interval
). The node duty-cycle time interval
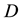 is defined as
is defined as
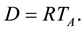 During the execution of a
During the execution of a
task, the node circuit consumes the battery charge
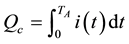 which is named task charge cost hence-
which is named task charge cost hence-
forth. Figure 1 shows the current consumption profile for a transmission task, where the marked time inter-
vals are: interval A
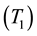 node wake up; interval B
node wake up; interval B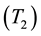 , radio transceiver start-up; interval C
, radio transceiver start-up; interval C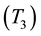 , MAC layer functions such as channel assessment and backoff-time calculations and receiver system calibration; interval D
, MAC layer functions such as channel assessment and backoff-time calculations and receiver system calibration; interval D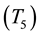 , transmission; interval E
, transmission; interval E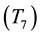 , reception mode according to the MAC protocol [17] , waiting for ACK packets. At the end, the node gets power down state (P.D.), waiting for the next timer interruption for next task execution.
, reception mode according to the MAC protocol [17] , waiting for ACK packets. At the end, the node gets power down state (P.D.), waiting for the next timer interruption for next task execution.
3. Battery Lifetime Estimation Approach
As Figure 2 shows, we need to estimate the time
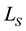 (node lifetime or service hours) at which the battery vol-
(node lifetime or service hours) at which the battery vol-
Figure 1. Battery current profile at −25 dBm output power. Time values are: ,
,
 ,
,
 ,
,





Figure 2. Battery voltage profile;





tage







There has been a lot of effort for building models capable of predicting the current consumption profile
On the other hand, see for instance [22] -[25] , there is no consensus about the description of the battery voltage












The coefficient


Figure 3. Battery service hours for different constant current consumption values (figure from [29] ).
Then:


Some node platforms vendors provide electronic sheets based on this method; see for example the Mote Battery Life Calculator from Crossbow Technology [26] and other examples given by [27] [28] . For examples, in Equation (4) if: 1)




To summarize, the hypotheses for using the duty-cycle current average method are the following:
・ H1) the node current consumption profile as function of the given application is known. It is a deterministic waveform that can be always approximated by a step-shaped waveform. The node duty-cycle will be constant during the node lifetime.
・ H2) superposition principle: let’s assume that a node performs task 1 with charge cost





We aim to demonstrate that H1) and H2) hypotheses do not always hold. In the next section, we present the metering system that has been used to experimentally assess the two hypotheses.
4. Electronic Metering System
The metering system is based on a dedicated PCB: it visualizes the node current consumption and the task’s charge cost

The value of





Figure 4. Block diagram of the experimental setup.
executes








The error is given by Equation (6) where

We use the following example to illustrate the methodology. If the node performs packet transmissions at the rate





As a final remark, we observe that the best set of values






5. Battery Lifetime Time Measurement
The MICAz node has been programmed to transmit one packet with a payload of 25 bytes, at the output power level of −25 dB∙m. The transmission rate is

Table 1. Measured charge Qc.
Power voltage supply: 3 V; Output power: −25 dB∙m∙$, payload size 25 bytes.
The transmission rate value has been selected to perform the experiment in a reasonable time (i.e. some days, no more than one month). The node could be considered not working when the voltage power supply drops value below 2.4 V (i.e. individual cell voltage value of 1.2 V). We daily measured the battery voltage and the result is shown in Figure 5; the voltage value 2.4 V has been achieved in 30 days.
The current consumption profile has been measured during transmission; it is shown in Figure 1. The resulting duty-cycle is


6. Assessment of H1 Hypothesis
Differently to the previously presented lifetime estimate, we use Qc = 0.042 μAh (see Table 1). The average current consumption is







Therefore, without a reliable value of the duty cycle value, the duty-cycle current average method can estimate the lifetime value very roughly. In fact, it is not possible to assume a priori node current consumption profile and the experimental characterization should be done for every given application. The node tasks are controlled by the program that runs inside the microcontroller under the supervision of an operating system like TinyOS [14] . Most of the time, the operating system asynchronously manages hardware resources in order to provide services to asynchronous events related to the wireless communication. More specifically, the origin of this non deterministic behavior is given by the method used for the clear channel assessment in most of the MAC layer protocols (see Chapter 5 MAC Protocols in [20] ). Therefore, generally speaking, the node awakes and sleeps in a non-deterministic way and the battery is forced to deliver current patterns which are not easily predictable, neither the duty-cycle value. The duty-cycle current average method requires the knowledge of the deterministic node current consumption, but we assessed that it is not possible.
7. Assessment of H2 Hypothesis
Table 1 shows charge costs for the tasks 1 and 2. Task 3 is defined as the sampling plus the transmission tasks, i.e. the node performs signal sampling and then packet transmission. The H2 hypothesis states that the expected battery charge cost



The measurements show that H2 hypothesis does not hold. The results are presented in Table 2; they are sig-
Figure 5. Measured battery voltage during node transmissions.
Figure 6. Three different measurements that show the time-varying node current profile behavior because of the random nature of backoff-time calculation for the MAC layer. Please, note how the TA value varies. Case A:



Table 2. Measured charge Qc.
nificantly different with respect to the expected ones.
The reason behind this result is due to the effects of node programming methods and compilers features which have a strong influence on the node current consumption profile. In fact, the operating system behavior and how hardware resources are managed, make unreliable the application of the superposition principle.
No withstanding the fact that programs are written in nesC, i.e. they are based on customized interfaces and modules which provide modularity, encapsulation and re-usability features; such benefits are counterbalanced by the impossibility of using the duty-cycle current average method for battery lifetime estimation.
8. Conclusions
The WSNs are comprised of battery-powered embedded electronic devices. A great amount of research has been devoted to the development of methods capable of predicting battery lifetime. Regardless of such efforts, most of the wireless sensors applications have prematurely depleted batteries, contrary to the estimations based on the widely adopted duty-cycle current average method. Our work experimentally assesses such discrepancy. An electronic metering system, based on a dedicated PCB to experimentally measure node current consumption profiles and charge extracted from the battery for two selected case studies, has been designed and implemented. Based on the measurement results, we demonstrate that the hypotheses on which the method is based are not reliable. The concluding remarks to be taken into account for the development of WSN applications are: 1) the software architecture and how to develop the application program have strong influence on the node current consumption profile and hence, on the battery lifetime; 2) the node current consumption profile as function of the given application as well as the duty-cycle is not deterministic. The duty-cycle current average method has another hypothesis which has not been considered: the battery operating temperature, which would have significant effect on the graph constant current discharge vs. hours service. It should be addressed as future research trend.
Cite this paper
LeonardoBarboni,MaurizioValle, (2014) Experimental Assessment of the Battery Lifetime in WSN Based on the Duty-Cycle Current Average Method. Wireless Sensor Network,06,212-220. doi: 10.4236/wsn.2014.610021
References
- 1. Lu, B. and Gungor, V.C. (2009) Online and Remote Motor Energy Monitoring and Fault Diagnostics Using Wireless Sensor Networks. IEEE Transactions on Industrial Electronics, 56, 4651-4659.
http://dx.doi.org/10.1109/TIE.2009.2028349 - 2. Gungor, V.C. and Gerhard, P.H. (2009) Industrial Wireless Sensor Networks: Challenges, Design Principles, and Technical Approaches. IEEE Transactions on Industrial Electronics, 56, 4258-4265.
http://dx.doi.org/10.1109/TIE.2009.2015754 - 3. Dondi, D., et al. (2008) Modeling and Optimization of a Solar Energy Harvester System for Self-Powered Wireless Sensor Networks. IEEE Transactions on Industrial Electronics, 55, 2759-2766.
http://dx.doi.org/10.1109/TIE.2008.924449 - 4. Agha, K.A., et al. (2009) Which Wireless Technology for Industrial Wireless Sensor Networks? The Development of OCARI Technology. IEEE Transactions on Industrial Electronics, 56, 4266-4278.
http://dx.doi.org/10.1109/TIE.2009.2027253 - 5. Ahn, H.-S. and Ko, K.H. (2009) Simple Pedestrian Localization Algorithms Based on Distributed Wireless Sensor Networks. IEEE Transactions on Industrial Electronics, 56, 4296.
http://dx.doi.org/10.1109/TIE.2009.2017097 - 6. Pierce, F.J. and Elliott, T.V. (2008) Regional and On-Farm Wireless Sensor Networks for Agricultural Systems in Eastern Washington. Computers and Electronics in Agriculture, 61, 32-43.
http://dx.doi.org/10.1016/j.compag.2007.05.007 - 7. Lopez, J.A., et al. (2009) Development of a Sensor Node for Precision Horticulture. Sensors, 9, 3240-3255.
http://dx.doi.org/10.3390/s90503240 - 8. Torvmark, K.H. Low Power Systems Using the CC1010. Chipcon Application Note AN017.
- 9. Baleri, G. Guidelines for WSN Design and Deployment.
- 10. The Battery Life Estimator. A Web-Based Calculator to Help Optimize Low-Power Applications.
http://www.silabs.com/support/pages/batterylifeestimator.aspx - 11. Yang, O. and Heinzelman, W.B. (2012) Modeling and Performance Analysis for Duty-Cycled MAC Protocols with Applications to S-MAC and X-MAC. IEEE Transactions on Mobile Computing, 11, 905-921.
http://dx.doi.org/10.1109/TMC.2011.121 - 12. Jiang, X., Taneja, J., Ortiz, J., Tavakoli, A., Dutta, P., Jeong, J., et al. (2007) An Architecture for Energy Management in Wireless Sensor Networks. Special Issue on the Workshop on Wireless Sensor Network Architecture, 4, 31-36.
- 13. Technical Data MPR-MIB Users Manual Revision B, June 2006 PN: 7430-0021-07. Technical Data MTS/MDA Sensor Board Users Manual Revision A, June 2007 PN: 7430-0020-05.
http://www.xbow.com/ - 14. Gay, P., Welsh, M., Levis, P., Brewer, E., Von Behren, R. and Culler, D. (2003) The nesC Language: A Holistic Approach to Networked Embedded Systems. Proceedings of the ACM SIGPLAN 2003 Conference on Programming Language Design and Implementation, San Diego, 9-11 June 2003.
- 15. http://tinyos.stanford.edu/tinyos-wiki/index.php/TinyOS_Documentation_Wiki
- 16. MoteWork Crossbow—Platform for the Development of Wireless Sensor Network from Crossbow. www.willow.co.uk/MoteWorks_OEM_Edition.pdf
- 17. CC2420 2.4 GHz IEEE 802.15.4 ZigBee-Ready RF Transceiver Chipcon, Product from Texas Instruments.
http://focus.ti.com/docs/prod/folders/print/cc2420.html - 18. Kan, B., Cai, L., Zhao, L. and Xu, Y. (2007) Energy Efficient Design of WSN Based on an Accurate Power Consumption Model. Proceedings of the Wireless Communications, Networking and Mobile Computing (WiCom 2007), Shanghai, 21-25 September 2007, 2751-2754.
- 19. Barberis, A., Barboni, L. and Valle, M. (2007) Evaluating Energy Consumption in Wireless Sensor Networks Applications. Proceedings of the 10th Euromicro Conference on Digital System Design Architectures, Methods and Tools, Lubeck, 29-31 August 2007, 455-462.
http://dx.doi.org/10.1109/DSD.2007.4341509 - 20. Holger, K. and Willig, A. (2005) Protocols and Architectures for Wireless Sensor Networks. John Wiley & Sons, Hoboken.
- 21. Bougard, B., Daly, D.C., Chandrakasan, A. and Dehaene, W. (2005) Energy Efficiency of the IEEE 802.15.4 Standard in Dense Wireless Microsensor Networks: Modeling and Improvement Perspectives. Proceedings of the Conference on Design, Automation and Test, 1, 196-201.
- 22. Rao, R., Vrudhula, S. and Rakhmatov, D. (2003) Battery Modeling for Energy-Aware System Design. IEEE Computer Society, 36, 77-87.
http://dx.doi.org/10.1145/860176.860179 - 23. Rakhmatov, D. and Vrudhula, S. (2003) Energy Management for Battery-Powered Embedded Systems. ACM Transactions on Embedded Computing Systems, 2, 277-324.
http://dx.doi.org/10.1145/860176.860179 - 24. Rao, R., Vrudhula, S. and Chang, N. (2005) Battery Optimization vs Energy Optimization: Which to Choose and When? Proceedings of Conference on Computer-Aided Design, ICCAD IEEE/ACM, San Jose, 6-10 November 2005, 439-445.
- 25. Panigrahi, D., Chiasserini, C., Dey, S., Rao, R., Raghunathan, A. and Lahiri, K. (2001) Battery Life Estimation of Mobile Embedded Systems. Proceedings of 14th International Conference on VLSI Design (VLSID 01), Bangalore, 3-7 January 2001, 57-63.
- 26. Expected Battery Life vs. System Current Usage and Duty Cycle, PowerManagement.xls. Excel Worksheet from Crossbow Technology.
http://www-db.ics.uci.edu/pages/research/quasar/PowerManagement.xls - 27. Kyaw, Z.T. and Sen, C. (2008) Using the CC2430 and TIMAC for Low-Power Wireless Sensor Applications: A Power Consumption Study.
http://focus.ti.com.cn/cn/lit/an/slyt295/slyt295.pdf - 28. Application Note AN053 Measuring Power Consumption with CC2430 and Z-Stack.
http://focus.ti.com/lit/an/swra144/swra144.pdf - 29. Product Datasheet Energizer E91, Alkaline Battery AA. Energizer Holdings, Inc. Form No. EBC-1202M.
http://www.energizer.com/ - 30. High-Side Measurement Current Shut Monitor INA 139, Datasheet Burr-Brown Products from Texas Instruments.
http://focus.ti.com/ - 31. Coulomb Counter—Battery Gas Gauge LTC4150. Linear Technologies IC Product.
http://www.linear.com/









