Journal of Water Resource and Protection
Vol.09 No.07(2017), Article ID:76780,22 pages
10.4236/jwarp.2017.97048
A Time-Based Framework for Evaluating Hydrologic Routing Methodologies Using Wavelet Transform
Mohamed ElSaadani*, Witold F. Krajewski
IIHR―Hydroscience & Engineering, The University of Iowa, Iowa City, IA, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 6, 2017; Accepted: June 6, 2017; Published: June 9, 2017
ABSTRACT
In this study we explore a method which provides an insight into the effectiveness of various hydrologic models’ routing components based on their ability to accurately represent flood peak times and shapes. The method is based on using Cross-Wavelet Transforms to estimate the phase (time) difference between the time series of the observed and the simulated discharges. In this article we evaluate two routing components, the Routing Application for Parallel Computation of Discharge (RAPID), which is based on the simplified Muskingum routing method, and the routing component of the non- linear Hillslope-Link hydrologic Model (HLM) produced in the Iowa Flood Center (IFC). Both routing components are driven by the same source of runoff and used the same channel network to ensure that the discrepancies between the simulated stream discharges are due to channel routing alone. We also explore the suitability of different wavelet shapes for our application, and how the difference in wavelet shape can affect our evaluation results. Unlike the conventional statistical skill scores used to evaluate model performance (e.g. Root Mean Squared Error, correlation coefficient, and Nash Sutcliff efficiency index), which give an estimate of the overall hydrograph performance, our method conveniently provides time-localized information with higher resolution at peak location. We perform our evaluation at multiple stream gauge locations, covering a wide range of scales (700 to 16,862 km2), located in the eastern part of the state of Iowa. Our results show that the proposed wavelet method is effective in evaluating the performance of the routing components in simulating peak times across spatial scales. Generally, the non-linear routing method employed in the HLM outperformed the Muskingum based method employed in RAPID. In addition, our results suggest that the Paul wavelet is more effective in detecting and separating individual peaks than the Morlet wavelet, which in turn leads to a more accurate evaluation of the routing components.
Keywords:
Hydrologic Routing, Wavelet Transform, Peak Timing

1. Introduction
Distributed hydrologic models usually consist of two major components that together produce stream discharge estimates. The first component is a Land Surface Model (LSM) that decomposes the terrain into a regular (e.g. rectangular or triangular) or irregular (e.g. terrain-fit polygons outlining hillslopes) grid where the energy and mass exchange between the land and the atmosphere are modeled. This process produces estimates of the potential excess surface and subsurface runoff depths that will enter the stream channels. It also provides estimates for evapotranspiration (ET), snowmelt, and the amount of water that is stored in the soil, and would affect the discharge estimates in the short or the long term. The second component is a water routing component, which is responsible for delivering the excess runoff into the channels through surface and subsurface lateral flow motions, then transporting the runoff downstream as stream discharge ( [1] [2] ).
In this article we evaluate two hydrologic routing components: first, the Routing Application for Parallel Computation of Discharge (RAPID) introduced in ( [1] [3] ), which is a storage-based simplified Muskingum linear routing method. Similar to other hydrologic routing approximations, the Muskingum method relies on discharge continuity alone and does not take the momentum equation into account. The Muskingum method uses the two parameters k and x to accumulate the discharge downstream, where k is a storage parameter that has units of time, and x is a weighting parameter that is relative to the discharge inputs and outputs of the channel. The estimation of these parameters is explained in [1] and [4] and the estimated values can be improved through optimization. Examples of possible cost functions that can be used to optimize these parameters are found in [1] [3] and [5] . The second routing component we evaluate in this study is the one implemented in the Hillslope-Link hydrologic Model (HLM) developed and used by the Iowa Flood Center (IFC). This routing component is nonlinear and accounts for the momentum equation in a simplified form ( [6] [7] and [8] ), and the stream velocity is determined based on the nonlinear relationship between the discharge and the served area ( [9] [10] ). Similar to [1] [11] and [5] we do not account in this study for lateral flows to the channel in our calculation for the sake of simplicity and since our sub-catchment sizes are small. This means we assume the runoff depth immediately enters the streams in their corresponding upstream junctions before the channel routing takes place.
Our study area is a moderately monitored average-sized basin called the Cedar River Basin located in the eastern part of the state of Iowa in the United States. The stream discharges of the basin are not affected by any artificial storages (e.g. dams and reservoirs) and are monitored by eleven United States Geological Survey (USGS) stream gauges that cover various connected and unconnected sub-catchments located within our basin of interest. In order conduct inter-comparisons between the observed and simulated stream discharges (hourly), we obtained the output of the two routing components at these USGS gauge locations for a whole warm season (March through October with a two month spin-up period). Both routing components were derived by the same runoff estimates which were generated by the community Land Surface Model (LSM) called Noah Multi-Parameter (Noah-MP) [2] , the model inputs are discussed later in this article. Afterwards, the discharge is aggregated over the same stream network by each routing component; for our application we used the digital stream network called the National Hydrography Dataset Plus Version 2 (NHDPlus V2, available at http://www.horizon-systems.com/nhdplus/).
Statistical skill scores such as root mean squared error, correlation coefficient, and Nash Sutcliff efficiency index are widely used to evaluate the performance of hydrologic models. However, comparing two time series with such indices reduces the features of the complete time series to one value that does not provide information about the variation of the model’s performance across the time series. One can decide to inspect individual parts of the time series separately, but this division of the time series can be either arbitrary if done using a fixed time window, or difficult to automate if the important features in the time series are to be located precisely in time. This implies that detecting features of interest in the time series is also a significant part of the evaluation problem. In this article to evaluate our routing components we use a method that offers solutions to both of these problems: first, detecting features of interest, and second, evaluating the model’s performance during the time period when they occurred.
We perform this time-based evaluation using Continuous Wavelet Transform (CWT) and Cross-Wavelet Transform XWT ( [12] [13] ). Wavelet transform analysis provides information about a given time series by filtering its frequencies in a time-localized manner. This information cannot be obtained using the traditional statistical skill scores such as RMSE and correlation coefficient due to their generality and inability to locate time series’ significant features in time. CWT provides information about the significant frequencies that exist in a time series and XWT provides information about where these detected frequencies coincide in two time series. This event matching is determined by computing the phase difference between the CWTs of the different time series. [12] and [14] are excellent references for a detailed description of CWT and XWT. We will briefly review the concepts behind CWT and XWT and elaborate on the use of different wavelets, and their advantages and disadvantages in our application.
Accurate peak time prediction for stream discharge is crucial in hazardous situations such as flash floods. Our method and results provide an insight regarding a more effective procedure to evaluate routing components in particular and hydrologic models in general based on their ability to forecast peak times. The evaluation framework we propose in this study should help decision makers and ground responders in making a more informed decision regarding peak time occurrence based on the performance of the hydrologic model which they receive their information from.
The rest of this article is organized as follows. First, we introduce our study area and describe the data obtained from the two routing components. Second, we review CWT and XWT and different types of wavelets that we used in this study and why we used them. Third, we show the results of the study. Lastly, we discuss our conclusions and findings.
2. Study Area, Data Inputs, and Routing Components
2.1. Study Area
We apply our wavelet-based evaluation method to the stream discharge estimates from RAPID and HLM routing components at eleven USGS gauge locations in the Cedar River basin. A map of the stream gauge locations is shown in Figure 1 and the areas they serve are listed in Table 1. As represented in Figure 1, our study area mostly fall in the “dry land crop” USGS land cover category, with a small area under “developed with low intensity category”. There is little to no river regulation effect at our basin, this insures that there is no delay in discharge due to storage. The areas served by the USGS stream gauges range from 766 km2 at Little Cedar River near Ionia, IA (USGS ID 05458000) to 16,862 km2 covered by the station at the basin outlet Cedar River at Cedar Rapids, IA (USGS ID 05464500). In this study we used hourly stream gauge observations to com-
Figure 1. USGS Land cover is plotted over the study area. The USGS stream gauges are represented by green dots. The legend of the four major land cover types is shown in the top right corner where 1 is dry land crop, 2 is urban and built-up, 3 is cropland/grassland, and 4 is water body. The labels of the USGS gauges correspond to the rankings in Table 1.
Table 1. A list of USGS gauges and their served area.
pare to our hourly model outputs, and stream gauge observation were available throughout our study period.
2.2. Data Inputs
We applied the same runoff estimate which we obtained from the WRF-Hydro hydrologic framework [15] to both routing components. WRF-Hydro utilizes the Noah-MP LSM [2] to estimate the runoff depths. We used the Stage IV [16] product as the rainfall input to WRF-Hydro; the rainfall estimates are projected on an HRAP [17] grid with a spatial resolution of approximately 4 km × 4 km and a temporal resolution of 1 hour. We also used the NLDAS V2 atmospheric forcings [18] [19] to drive WRF-Hydro; the dataset is available in a spatial resolution of 1/8˚ and hourly temporal resolution. We ran the model for the whole 2014 warm season (March through October), allowing a proper spin-up period starting from December 2013 with a proper initialization for channel states. We then ingested this runoff in both routing components allowing two months of spin-up period for routing. Consequently, our stream discharge estimates cover the period between May through October, 2014.
2.3. Routing Components
The methodologies on which each routing component is based can be found in [6] [7] and [3] . In short, RAPID is based on the linear Muskingum routing method, which is a storage-based method that does not account for flow momentum. The finite difference form of the Muskingum method can be written as shown in [1] . This method relies on two key parameters, 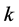 and
and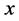 , where
, where 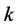 is a storage parameter and has units of time and
is a storage parameter and has units of time and 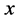 is a dimensionless weighting parameter. The
is a dimensionless weighting parameter. The 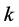 and
and 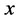 parameters were determined as described in [4] .
parameters were determined as described in [4] .
On the other hand, the HLM is based on the methodology described in [8] . In this method the channel velocity exhibits non-linear behavior in relationship with the upstream served area. As a simplification for the momentum equation the velocity v corresponding to a discharge 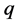 can be determined as follows,
can be determined as follows,
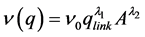 (1)
(1)
then the flow transport can be described as
 (2)
(2)
where at a certain time 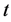 the corresponding surface and subsurface lateral inflows are
the corresponding surface and subsurface lateral inflows are 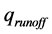 and
and  respectively. The discharge inflow into a stream channel (link) from the upstream served area
respectively. The discharge inflow into a stream channel (link) from the upstream served area 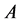 is
is 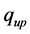 and the total discharge at the outlet junction of a stream is
and the total discharge at the outlet junction of a stream is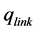 . The parameters
. The parameters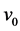 ,
, 

3. Methodology
Wavelet transform is a useful tool to extract information about time localization of certain frequencies in a time series, unlike Fourier transform which does not provide any time localization information ( [12] [13] ). One can consider wavelet transform as an extension to the Windowed Fourier Transform (WFT), where CWT extracts information about the signal structure through a filter of scaled and translated wavelet instead of an infinite sinusoid.
3.1. Continuous Wavelet Transform
Decomposing a signal into its constituent frequencies can be done in multiple ways. First, one can perform the Discrete Fourier Transform, (DFT) on the signal.DFT can give us an accurate measure of all the frequencies in a discrete signal






where 



where 




The compliance of CWT with the window size uncertainty is done by offering good time localization for the important sharp features by using low scale wavelets. Similarly the mild features that cover the wide range of the signal will be detected by high scale wavelets that do not offer good time localization. Another advantage of using wavelet analysis rather than Fourier transform is the ability to use confined “mother wavelets” that can have different shapes based on their functional form, and not an infinite sinusoid. As shown in Figure 2, some wavelets such as the Morlet wavelet are more suitable for detecting frequency properties, while others such as the Derivative of Gaussian (DOG) wavelet or Paul wavelet are better for detecting sharp features. One of the main goals of this article is to stress the significance of the selected wavelet shape, and that it can lead to a different interpretation of the properties of our signal.
One can use either directional wavelets (a wavelet with an imaginary component), such as the Morlet or Paul wavelets, or a real valued wavelet such as the DOG wavelet to estimate the CWT. This is not the case for XWT since it solely relies on estimating the phase difference between two CWTs. Given a mother
Figure 2. Unscaled wavelet function 
wavelet 



where 






For our CWT analysis we chose three of the most commonly used wavelets. The first is the real DOG wavelet in the second order (also called the Mexican hat wavelet or Marr wavelet), given by the equation

where m is the derivative and is equal to 2 and 


where m is the order and is equal to 4. Lastly is the directional Morlet wavelet,

where 
We estimated the 5% significance levels of the wavelets power spectrum following [12] by comparing the power spectrum to a background red noise. In short, the significance levels were estimated based on the hypothesis that our signal can be modeled as a univariate autoregressive with lag-1 AR(1) process. Before we proceed with the significance level calculation we had to test our signal’s power spectrum decay against that of a theoretical red noise with the same lag-1 correlation. As an example, we present in Figure 3 the power spectrum decay of our signal (hydrograph) at the outlet of the basin (Cedar River at Cedar Rapids), where the blue line represents our signal and the red line represents the theoretical red noise, the lag-1 auto correlation was estimated from the data. One can see that a red noise process is a good approximation for our process; this was expected since many geophysical processes follow a red noise model. The Fourier power spectrum of the wavelets and the corresponding confidence intervals are then calculated as described in [12] .
Another important feature in our CWT calculations is the Cone of Influence (COI).Similar to [12] , in order to perform the integral in Equation (5) efficiently we chose to perform our calculations in the Fourier space, then calculate the wavelet transform using a reverse Fourier transform of the convolution of the Fourier transform of the signal over the Fourier transform of the wavelet. We followed a zero padding procedure (adding zeros with a proper length to both ends of our series) since our signal is confined in time, which in turn results in artifacts in the wavelet transform at the edges of our signal. The COI helps us know where the effect of these artifacts is negligible, where all values outside of the COI are reliable. In this article, the COI as well as the transform-normalized
Figure 3. Power spectrum decay of a theoretical AR1 process (red) plotted against the power decay obtained from the data. Lag one correlation was estimated using the hourly hydrographs data.
powers are plotted against the Fourier periods of the wavelets and not their scales. The Fourier period λ for the same scale s is different from one wavelet shape to another; for the Morlet wavelet the Fourier period λ = 1.03 s, while for the Paul wavelet λ = 1.4 s, and finally for the Mexican hat wavelet λ = 3.97 s. For the sake of consistency in our analysis we are going to refer to the Fourier periods instead of the scales of the wavelets.
3.2. Cross-Wavelet Transform and Phase-Time Analysis
The next step after calculating the CWT is to relate these CWTs to each other to detect the similarities between our signals. This is done by calculating the CWT of the observed and simulated stream discharges, and then the XWT between each simulated flow and the observed flow. The XWT is calculated using Equation (9):

the Cross-Wavelet power is

where 





As shown in Equation (11), the time differences are associated with certain scales. However, some scales are more important than others based on the magnitude of the XWT at this scale over the locations of our interest. Similar to [20] we decided to represent the time difference between the simulated and observed signals using the 
Naturally, we are interested in the performance of the routing components during extreme events; thus, we estimate the time difference between simulated and observed flows at peak locations. This also makes sense since as we have explained earlier, the wavelet transform offers good time localization for small scales and not large scales, where small scales are associated with sharp peaks. We also had to add more constraints to make sure we are getting reliable time difference estimates. First, we only consider the periods corresponding to the
Figure 4. Morlet wavelet (top) and Paul wavelet (bottom) with Fourier periods of 400 hours plotted against the observed hydrograph at Cedar River at Cedar Rapids (black line). The vertical grey line shows the location of center of the wavelet, which coincides with a hydrograph peak.
maximum power at the peak locations and within the COI. In Figure 4 we show both the Paul and Morlet wavelets with Fourier period 400 on top of the hydrograph at the outlet of the basin, where both the wavelets and the hydrographs are normalized to have maximum value of 1. One can see that at this Fourier period, the wavelet is intersecting with multiple features in the hydrograph, and as the period increases the resulting power will have very poor time localization. In other words, the incoming power will result from the convolution of the wavelet with multiple features. For this reason we impose our second condition, which is limiting our search for maximum power to a maximum Fourier periods of 400 if the COI is not already covering this region. This seemed as a good limit as shown in Figure 4, since the peaks presented in it are the largest peaks, and all other peaks upstream must be smaller.
4. Results
We start our evaluation of RAPID and the HLM routing by visually comparing their CWTs against the CWT we obtained from the observed flow. In this article we only show the CWT for the hydrographs at the outlet of the basin in order to show the effect of the wavelet shape. This example will enable us to observe the different resulting power spectra associated with the hydrograph peaks and their time localization with regard to wavelet shape. The reasons we only show the CWT at the basin outlet are: first, CWT is only implicitly included in our main evaluation method, which is the time difference between simulated and observed flows; second, since we have eleven stations to analyze, this will result in an overwhelming amount of figures. Therefore, the details of the CWT performance across scales can be indirectly explained by our time difference analysis.
In Figure 5 we show the observed and simulated hydrograph at the outlet (a), the CWTs of the observed (b), HLM routing (c), and RAPID (d), using the Mexican hat wavelet. One can see in Figure 5(b) that the two peaks in the hydrograph were accurately detected: the first peak ranges between periods of 128 hours to 400 hundred hours and the second peak is wider with period ranging from about 150 to 500 hours. Starting from the period of about 500 hours, we can see that the power spectrum from both peaks becomes connected, since at this time scale both peaks are covered with one large wavelet. This is a good example to show why we enforced our second restriction by not considering periods larger than 400. The power spectrum values around 1000 hours and 2000 hours on the x axis, before and after the peaks, are caused by the negative correlation between the sinking parts of the wavelet and the peaks. If we look at the wavelet transform value alone, these regions have negative wavelet transform value. However, it is important to understand that we look at the wavelet transform power instead of the transform original value because in the case of directional wavelets there is an imaginary component that we will either have to look at separately from the real component, or otherwise combine the two components together by calculating the power. By looking at the HLM routing hydrograph, it is clear that the first peak is larger and occurred earlier in comparison to the observed flow; the second peak, however, is smaller in magnitude and duration. This is reflected in the CWT power values in Figure 5(c): the first spike in power occurred earlier than that of the observation and the signal is much stronger all the way to the period of 500. On the other hand, the second peak is located approximately between the 128 and 300 periods. For RAPID, we can see that the wavelet power occurred earlier for the first peak which is in agreement with the hydrograph, and the second peak caused a larger than observation spike in the CWT power. Interestingly, because the two RAPID peaks are well separated, due to a very early first peak and generally flashy behavior, the connection between the two peaks in CWT occurred in a much larger period (about 700 instead of 500).
Figure 6 and Figure 7 are the same as Figure 5 but for the Morlet and Paul wavelet CWT respectively. These figures suggest the same qualitative conclusions derived from Figure 5. However, one can see that the Morlet wavelet maximum power is located between the two peaks, since the maximum correlation between the Morlet wavelet and the hydrograph occurs when two humps from the wavelet are co-located with the two hydrograph peaks. Nevertheless, this power is shifted to the left because when the wavelet is far left (e.g. the first major wavelet hump is located over the second peak), the rest of the wavelet peaks do not correlate with the rest of the hydrograph. In the case of the Paul wavelet, we can see that the peaks are well confined with a weak connection resulting from the imaginary part of the wavelet. It is also interesting to observe how the negative correlation due to the sinking part of the wavelet is not separated from the positive part happening over the peak, contrary to what happened in the Mexican hat wavelet case. This is due to the overlapping of the sinking part of the wavelet with the rising imaginary part of the wavelet. This however resulted in a wider continuous base of power values at large period. Also, the power peaks are slightly shifted to the left because the imaginary component is always ahead of the real component.
Before we proceed to the XWT calculation, it is important to keep in mind that the XWT estimates common power activity locations in both CWTs involved,
Figure 5. CWT power outside the COI for the Mexican hat wavelet, observed (top), HLM routing (middle), and RAPID (bottom). The x axis unites are Time in hour, and the color bar unit is normalized square power.
Figure 6. CWT power outside the COI for the Morlet wavelet, observed (top), HLM routing (middle), and RAPID (bottom). The x axis unites are Time in hour, and the color bar unit is normalized square power.
Figure 7. CWT power outside the COI for the Paul wavelet, observed (top), HLM routing (middle), and RAPID (bottom). The x axis unites are Time in hour, and the color bar unit is normalized square power.
regardless of how strong these activities are. So even if we focus our interests on the 95% significant values within the COI and a period less than 400, we still have quite a range of agreement between the two CWTs. In order to decide which XWT value at the peak locations is going to be used in time difference estimation, we follow the approach described in [20] . The challenge in choosing the appropriate Fourier period to estimate the time difference at is the fact that the larger the wavelet is, the more power it produces. This means that if the peak was not strongly detected at the proper smaller period (e.g., due to the simulated peak looking very different from the observed peak in small periods or due to the wavelet shape), the agreement will instead be reached at a large period with bad time localization (this is why we stop our search at Fourier period of 400). In most cases agreement between the CWTs of the observed and simulated flows was reached in the proper scales, but in a few instances however we had to choose the power at period 400 or near the edge of the COI. Nevertheless, this limitation will not affect our conclusions, because we are not intending to use the time difference values to modify the simulated hydrographs, e.g. [20] ; the values we get will still be an accurate representation of the relative performance between the two routing components.
We now focus our attention to the major peaks in the hydrograph. As shown in previous figures, the 2014 season experienced two major events at the Cedar River basin. We have estimated the XWT transform at each station using both directional wavelets. In Figure 8 we show the hydrographs (top), time difference estimated using Equation (11) (middle), and the XWT (bottom) at the basins outlet. The two vertical grey lines over the hydrograph peak locations are where we extracted the power and time information. The left column is for RAPID re-
Figure 8. Morlet wavelet XWT analysis. The hydrographs (top) with their corresponding estimated time differences in hours (middle), and the log2 of the XWT power (bottom). The left column represents RAPID results and the right column represents the HLM routing results.
sults and the right column represents the HLM routing results. We can see how the maximum power is located around the 256 period band for both routing components. Also, it is clear that the corresponding time difference from RAPID at this region at peak locations is much higher in RAPID that it is in HLM routing. We show a detailed cross section at peak locations in Figure 9. The top panel is for the first event’s cross section and the bottom panel is for the second event’s cross section. The dashed lines represent RAPID and the solid lines represent the HLM routing; we represent the power with blue color and the corresponding time difference with the red color. We see that maximum power convergence for both routing components in both events occurred at periods less than 300. Additionally, one can see how the behavior of the time (phase) difference is unstable in regions apart from the maximum power. Another important observation is how the magnitude of the power is generally larger for the first event than it is for the second event, and how the maximum power occurred in a larger period in the first event than it did in the second event. As we have mentioned earlier, the power profile indicates common activity between the observed and simulated flows; although we have only picked one point (maximum power) to estimate the time difference, it is evident that the HLM routing performed better across a wide range of periods.
We then expanded our analysis using the Morlet wavelet upstream by doing the same analysis shown in Figure 8 and Figure 9 at all ten upstream gauge locations. Figure 10 and Figure 11 show the time difference (top), Maximum power (middle), and corresponding scale (bottom) for the first and second events respectively using the Morlet wavelet at all stream gauge location. The red
Figure 9. Morlet wavelet XWT analysis. Cross-section profile at the event 1 top and event 2 bottom for power (blue) and time difference (red). The solid lines represent the HLM results while the dashed lines represent RAPID results.
Figure 10. Morlet wavelet XWT analysis. Time differences in hours (top), XWT power (middle), corresponding period (bottom) for event 1 at all stations. The x-axis is the station number, and the green color represents RAPID, while the red color represents the HLM routing.
Figure 11. Morlet wavelet XWT analysis. Time differences in hours (top), XWT power (middle), corresponding period (bottom) for event 2 at all stations. The x-axis is the station number, and the green color represents RAPID, while the red color represents the HLM routing.
color represents the HLM routing and the green color represents RAPID. Although the chosen periods are the same or similar at all stations for both routing components, the time differences are sometimes significantly different with the HLM outperforming RAPID in both events at all locations. We plot the final estimates of the time differences using the Morlet wavelet spatially in Figure 12, where positive values indicate that the simulated flow is ahead of the observed flow and vice versa. The results show that both routing components performed better in the second event, compared to their performance during the first event. What is curious, however, about Figure 12 is how the time difference values obtained for the first and the second event are not as different as one would have expected them to be by visually inspecting the hydrographs. This is of course because one can judge by looking at the hydrographs that both routing components performed much better in simulating the peak time during the second event than they did for the first event, especially in the case of RAPID.As we will see later, this is not the case with the Paul wavelet and is mainly caused by the shape of the Morlet wavelet. This is due to the fact that the Morlet wavelet at this
Figure 12. Morlet wavelet XWT analysis. Spatial plot of time differences. Top row represents the HLM routing while the bottom row represents RAPID routing. The left column shows the results of the first event while the right column is for the estimates of the second event.
range of periods (200 to 300) intersects with both peaks, and the phase difference at the location of one peak is affected by the performance at the other peak as well.
Figure 13 and Figure 14 are the same as Figure 8 and Figure 9 respectively but for the Paul wavelet. In this case we can see how the difference between the time difference estimates of the two events is enlarged. This is due to the better time localization of the Paul wavelet where the effect of one event on the XWT at the location of the other event is small. On the other hand one can also see in Figure 15 and Figure 16 that the maximum power did not occur before the period of 400 in few locations. Although the time differences are different from those obtained for the Morlet wavelet (Figure 10 and Figure 11), generally we reach the same conclusions by using the Paul wavelet. We lay down the time difference spatially in Figure 17. In this case the performance between the first and second events is distinguished properly. We can see how RAPID performed much better in the second event in comparison to the first event; similar behavior is observed for the HLM routing as well. One can also see how the performance for the first event deteriorated when using the Paul wavelet as the contribution from the well-detected second peak diminished.
5. Conclusions and Recommendations
In this article we introduced a wavelet-based evaluation method of two hydrologic routing components. By looking at the hydrographs it was clear that the simplified Muskingum-based routing component RAPID exhibits flashy behavior with sharp peaks in comparison to the non-linear HLM routing component.
Figure 13. Paul wavelet XWT analysis. The hydrographs (top) with their corresponding estimated time differences in hours (middle), and the log2 of the XWT power (bottom). The left column represents RAPID results and the right column represents the HLM routing results.
Figure 14. Paul wavelet XWT analysis. Cross-section profile at the event 1 top and event 2 bottom for power (blue) and time difference (red). The solid lines represent the HLM results while the dashed lines represent RAPID results.
Figure 15. Paul wavelet XWT analysis. Time differences in hours (top), XWT power (middle), corresponding period (bottom) for event 1 at all stations. The x-axis is the station number, and the green color represents RAPID, while the red color represents the HLM routing.
Figure 16. Paul wavelet XWT analysis. Time differences in hours (top), XWT power (middle), corresponding period (bottom) for event 2 at all stations. The x-axis is the station number, and the green color represents RAPID, while the red color represents the HLM routing.
Figure 17. Paul wavelet XWT analysis. Spatial plot of time differences. Top row represents the HLM routing while the bottom row represents RAPID routing. The left column shows the results of the first event while the right column is for the estimates of the second event.
Traditional statistical skill scores such as RMSE and correlation coefficient can characterize the overall performance of a time series without providing any localized information in time about the significant features in the time series. In addition, these skill scores do not provide any information regarding the ability of the models to predict an accurate peak time, and peak time prediction is of great value to decision makers. Thus, we used the wavelet analysis which is widely used in the application of signal processing. CWT allowed us to filter the constituent frequencies of the hydrographs and also provided us with the locations of high frequency activities which correspond to significant peak locations. We also calculated the XWT, which provided us with the locations where both the observed and simulated discharges from each routing component experience similar power activity. The XWT also has a phase component which is the same as the phase difference between the CWTs of the observed and simulated flows. Then we calculated the time difference between the simulated and observed flows at peak locations using the Fourier period of the wavelet. A unique aspect of our study is that have analyzed the same hydrographs using different wavelet shapes. Although we have reached the same qualitative conclusion that the HLM routing outperformed RAPID in simulated peak times, there were differences in the interpretation of the routing component performance event wise. The significance of these differences is solely dependent on the shape of the hydrograph. For example, if we only had one peak in the hydrograph or if the peaks were well separated, the choice of wavelet would have been of less importance. On the other hand if we had many closely located peaks, the results from the Morlet wavelet would have been very hard to analyze since the computed power at one peak location is affected by the performance at surrounding peaks. Nevertheless, although the Paul wavelet offers better time localization, the location and Fourier period of the maximum power does not exactly correspond to the location and width of the feature we would like to detect due to the wavelet shape (the imaginary component of the wavelet). Hence, it is recommended to always look at the XWTs from different wavelets, especially for the purpose of applications such as the time series modification performed in [20] .
Acknowledgements
We gratefully thank the Iowa Flood Center (IFC) for funding this study. The authors would like to thank staff engineer Radoslaw Goska of the IFC for his help in organizing the models’ inputs. Cross wavelet transform codes were provided by Aslak Grinsted and are available at https://github.com/grinsted/wavelet-coherence.
Cite this paper
ElSaadani, M. and Krajewski, W.F. (2017) A Time-Based Frame- work for Evaluating Hydrologic Routing Methodologies Using Wavelet Transform. Journal of Water Resource and Protection, 9, 723-744. https://doi.org/10.4236/jwarp.2017.97048
References
- 1. David, C.H., Maidment, D.R., Niu, G.-Y., Yang, Z.-L., Habets, F. and Eijkhout, V. (2011) River Network Routing on the NHDPlus Dataset. Journal of Hydrometeorology, 12, 913-934.
https://doi.org/10.1175/2011JHM1345.1 - 2. Niu, G.-Y., et al. (2011) The Community Noah Land Surface Model with Multiparameterization Options (Noah-MP): 1. Model Description and Evaluation with Local-Scale Measurements. Journal of Geophysical Research, 116, D12109.
https://doi.org/10.1029/2010JD015139 - 3. David, C.H., Yang, Z.L. and Famiglietti, J.S. (2013) Quantification of the Upstream-to-Downstream Influence in the Muskingum Method and Implications for Speedup in Parallel Computations of River Flow. Water Resources Research, 49, 2783-2800.
https://doi.org/10.1002/wrcr.20250 - 4. Snow, A.D. (2015) A New Global Forecasting Model to Produce High-Resolution Stream Forecasts. Master’s Thesis, BYU.
- 5. Tavakoly, A.A., Snow, A.D., David, C.H., Follum, M.L., Maidment, D.R. and Yang, Z.-L. (2016) Continental-Scale River Flow Modeling of the Mississippi River Basin Using High-Resolution NHDPlus Dataset. Journal of the American Water Resources Association (JAWRA), 53, 258-279.
https://doi.org/10.1111/1752-1688.12456 - 6. Ayalew, T.B., Krajewski, W.F., Mantilla, R. and Small, S.J. (2014) Exploring the Effects of Hillslope-Channel Link Dynamics and Excess Rainfall Properties on the Scaling Structure of Peak-Discharge. Advances in Water Resources, 64, 9-20.
https://doi.org/10.1016/j.advwatres.2013.11.010 - 7. Cunha, L.K., Mandapaka, P.V., Krajewski, W.F., Mantilla, R. and Bradley, A.A. (2012) Impact of Radar-Rainfall Error Structure on Estimated Flood Magnitude across Scales: An Investigation Based on a Parsimonious Distributed Hydrological Model. Water Resources Research, 48, W10515.
https://doi.org/10.1029/2012wr012138 - 8. Mantilla, R. (2007) Physical Basis of Statistical Scaling in Peak Flows and Stream Flow Hydrographs for Topologic and Spatially Embedded Random Self-Similar Channel Networks. PhD Thesis, University of Colorado, Boulder, USA.
- 9. Paik, K. and Kumar, P. (2004) Hydraulic Geometry and the Nonlinearity of the Network Instantaneous Response. Water Resources Research, 40, W03602.
https://doi.org/10.1029/2003wr002821 - 10. Ghimire, G.R., Krajewski, W.F. and Mantilla, R. (unpublished) A Power Law Model for River Water Velocity in U.S. Upper Midwestern Basins.
- 11. Snow, A.D., Scott D.C., Swain N.R., Nelson J., Ames D.P., Jones N.L., Ding D., Noman N., David C.H., Pappenberger F. (2016) A Cloud-Based High-Resolution National Hydrologic Forecast System Downscaled from a Global Ensemble Land Surface Model. Journal of the American Water Resources Association (JAWRA), 52, 950-964.
https://doi.org/10.1111/1752-1688.12434 - 12. Torrence, C. and Compo, G.P. (1998) A Practical Guide to Wavelet Analysis. Bulletin of the American Meteorological Society, 79, 61-78.
- 13. Labat, D. (2005) Recent Advances in Wavelet Analyses: Part 1. A Review of Concepts. Journal of Hydrology, 314, 275-288.
https://doi.org/10.1016/j.jhydrol.2005.04.003 - 14. Foufoula-Georgiou, E. and Kumar, P., Eds. (1995) Wavelets in Geophysics. Academic Press, New York, 337.
- 15. Gochis, D.J., Yu, W. and Yates, D.N. (2015) The WRF-Hydro Model Technical Description and User’s Guide, Version 3.0. NCAR Technical Document.
https://ral.ucar.edu/sites/default/files/public/projects/wrf_hydro/WRF_Hydro_Technical_Description_and%20User_Guide_v1.0.pdf - 16. Lin, Y. and Mitchell, K.E. (2005) The NCEP Stage II/IV Hourly Precipitation Analyses: Development and Applications. Preprints, 19th Conference on Hydrology, San Diego, CA, American Meteorological Society, 1.2.
http://ams.confex.com/ams/Annual2005/techprogram/paper_83847.htm - 17. Reed, S.M. and Maidment, D.R. (1999) Coordinate Transformations for Using NEXRAD Data in GIS-Based Hydrologic Modeling. Journal of Hydrologic Engineering, 4, 174-182.
https://doi.org/10.1061/(ASCE)1084-0699(1999)4:2(174) - 18. Xia, Y., et al. (2012) Continental-Scale Water and Energy Flux Analysis and Validation for the North American Land Data Assimilation System Project Phase 2 (NLDAS-2): 1. Intercomparison and Application of Model Products. Journal of Geophysical Research, 117, D03109.
https://doi.org/10.1029/2011jd016048 - 19. Xia, Y., et al. (2012) Continental-Scale Water and Energy Flux Analysis and Validation for the North American Land Data Assimilation System Project Phase 2 (NLDAS-2): 2. Validation of Model-Simulated Streamflow. Journal of Geophysical Research, 117, D03110.
https://doi.org/10.1029/2011jd016051 - 20. Liu, Y., Brown, J.D., Demargne, J. and Seo, D.-J. (2011) A Wavelet-Based Approach to Assessing Timing Errors in Hydrologic Predictions. Journal of Hydrology, 397, 210-224.
https://doi.org/10.1016/j.jhydrol.2010.11.040



















