Journal of Water Resource and Protection
Vol.08 No.13(2016), Article ID:72284,16 pages
10.4236/jwarp.2016.813094
Modeling for Inter-Basin Groundwater Transfer Identification: The Case of Upper Rift Valley Lakes and Awash River Basins of Ethiopia
Mebruk Mohammed1,2, Bisrat Ayalew3
1Addis Ababa Institute of Technology, Addis Ababa University, Addis Ababa, Ethiopia
2Policy Study and Research Center, Addis Ababa, Ethiopia
3Adama Science and Technology University, Adama, Ethiopia
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 24, 2016; Accepted: November 25, 2016; Published: November 28, 2016
ABSTRACT
Groundwater movement beneath watershed divide is one component of the hydrological cycle that is typically ignored due to difficulty in analysis. Numerical ground- water models, like TAGSAC, have been used extensively for predicting aquifer responses to external stresses. In this paper TAGSAC code was developed to identify the inter-basin groundwater transfer (IBGWT) between upper Awash River basin (UARB) and upper rift valley lakes basin (URVLB) of Ethiopia. For the identification three steady state groundwater models (for UARB, URVLB and for the two combined basins) were first created and calibrated for the 926 inventoried wells. The first two models are conceptualized by considering the watershed divide between the two basins as no-flow. The third model avoids the surface water divide which justifies IBGWT. The calibration of these three models was made by changing the recharge and hydrogeologic parameters of the basins. The goodness of fit indicators (GoFIs) obtained was better for the combined model than the model that describes the URVLB. Furthermore, the hydraulic head distribution obtained from the combined model clearly indicates that there is a groundwater flow that doesn’t respect the surface water divide. The most obvious effect of IBGWT observed in these two basins is that it diminishes surface water discharge from URVLB, and enhances discharge in the UARB. Moreover, the result of this study indicates potential for internal and cross contamination of the two adjacent groundwater.
Keywords:
Inter-Basin Groundwater Transfer, Numerical Groundwater Modeling, TAGSAC, Upper Awash River Basin, Upper Rift Valley Lakes Basin

1. Introduction
Understanding the hydrological relation between basins has great importance in the study of watershed hydrology, management, and groundwater and pollution assessment. Groundwater movement beneath topographic divide is one component of the hydrological cycle that is typically ignored due to difficulty in analysis. Most watershed hydrology studies attempt to avoid inter-basin groundwater transfer (IBGWT) by selecting sites that are believed to be “tight”. While IBGWT is typically not addressed; it is an important hydrological process that has been found to occur throughout the world. Identifying and understanding of this hydrological process must be adapted in basin study and management for better and accurate analysis of watershed hydrology.
Inter basin groundwater flow analysis has been an important research topic in the last few years. This is as a result of many geo-environmental engineering problems having direct or indirect impact on groundwater flow. The detection of IBGWT increases the importance of regional land use planning for areas overlying the IBGWT system.
IBGWT can at least be detected using head data. The potential for groundwater to move from basin to basin is related to the relative altitude and geological structure of the individual basin. Where the rocks that form the boundary between these adjacent basins are sufficiently permeable, there will be flow into or out of the basin. Identifying the regional head and checking the geological structure of the two basins can give full information, about the possibility of IBGWT. Thus if the geologic characters between the two adjacent basin are similar, then groundwater models could show the hydraulic head distribution across the two adjacent basins which ultimately show the possibility of IBGWT.
The main objective of this paper is then to identify the possibility of groundwater transfer between basins, Awash River and Rift Valley Lakes using numerical groundwater modeling. By identifying hydrogeological setting and the head potential along the two basins’ surface water divide, this study will show the groundwater flow direction for possible IBGWT. The connection between basins is a relatively unexplored and potentially significant factor in the further understanding of the two adjacent basins’ hydrology.
Most hydrological studies ( [1] [2] ) in Ethiopia are based on the assumption that the groundwater divide and surface water divide are coincident. Such assumption leads to wrong quantification and prediction of the groundwater flow system. The most obvious effect of IBGWT is to diminish surface water discharge from watersheds that lie in the recharge area of the basin (in which IBGWT originates), and enhance discharge in the basin where regional aquifer discharges (receiving IBGWT). This problem could be solved by incorporating the concept of IBGWT into the hydrologic study. In order to quantify, manage and plan groundwater resource efficiently, IBGWT must be studied and incorporated in basin hydrology. Its importance especially in the most developed river basins of Ethiopia (Awash River and Rift Valley lakes) is even more vital. Moreover, understanding IBGWT between basins is important to assess the potential for internal and cross contamination.
2. Materials and Method
2.1. Location of the Study Area
Both Upper Awash basin and Upper Rift valley lake basin are located in central Ethiopia at the western margin of the Main Ethiopian Rift. The capital city, Addis Ababa, is located at the northern end of the basin. The study area (aquifer) is selected so that it can basically form a groundwater basin. A groundwater basin is formed by identifying the possible discharge and recharge areas. Thus the study area is bounded by the two perennial rivers namely Upper Awash River (a few kilometers lower from its origin to Koka Lake) and Meki River from its source to Ziway Lake (see Figure 1). It covers a total area of 2200 km2. The study area is bounded by 8˚03'N and 8˚39'E latitude 38˚37'E and 39˚06'E longitude. This area is divided into two sub-basins belonging to Awash and Rift valley lakes basin:
1) The area bounded by Lake Ziway, Meki River and the water divide with the Awash River basin it represents Upper RVLB, and it covers 781.21 km2 drainage basin area.
2) The Awash sub basin with a total drainage area of 1420.39 km2 bounded by the surface water divide with RVLB basin, Lake Koka and Awash River upstream of Lake Koka.
The climate is sub-humid in the central Main Ethiopian Rift, semi-arid close to the Kenyan border and arid in the Afar. On the high plateau to the west of Addis Ababa the rainfall distribution shows a continuous increase from the spring rains to the summer peak rainfall. The distribution of rainfall over the highland areas is modified by orographic effects and is significantly correlated with altitude. In this study area there are a number of metrological stations, but ten of them are used for average rainfall estimation in the model basin. The climate of the Awash River Basin varies from humid subtropical over central Ethiopia (upper awash basin) to arid over the Afar lowlands ( [4] [5] ).

Figure 1.Location of the study area ((a) is major basins of Ethiopia adopted from [3] ; (b) is the study area showing the two sub-basins and boundaries).
2.2. Data Processing
The data processing follows the guideline given in [6] . The data process starts with planning, which focuses on collecting the available groundwater related information within a defined season, the questions at hand is to identify inter-basin groundwater transfer between two adjacent basins of Ethiopia through modeling. The next stage involves using all available data and knowledge of the region of interest to develop the conceptual model (conceptualization), which is a description of the known physical features and the groundwater flow processes related to inter-basin groundwater transfer. The next stage is design, which is the process of deciding how to best represent the conceptual model in a mathematical model. Model construction is the implementation of model design by defining the inputs for the selected modeling tool. The calibration and sensitivity analysis of the model occurs through a process of matching model outputs to a historical record of observed data.
2.3. Modeling for Inter-Basin Groundwater Transfer
Modeling the groundwater flow system in the two basins is expected to show the possible interaction between the two basin’s groundwater. The methodology adopted to analyze the IBGWT between the Upper Awash River Basin (UARB) and Upper Rift Valley Lakes Basin (URVLB) is shown in Figure 2. Three groundwater models were first created. Two separate groundwater models for each sub basin by considering the watershed divide between the two basins as Neumann boundary with zero flux. Each of these models will be calibrated for well and spring data inventoried within these basins. The calibration is made by changing the surface recharge and hydrogeologic parameters. The third groundwater model treats the two basins as one (avoiding the surface water divide) and is calibrated for all wells/springs inventoried in both sub-basins. The results of the two standalone sub-basin models are compared with the third model. For comparison the measures of goodness of fit indicators (GoFI) of the third model for the well/spring data inventoried in each sub basin is compared with the stand alone model accuracies. The accuracy of the results in predicting the inventoried data will then be interpreted for possible inter-basin groundwater transfer.
Figure 2. Flow chart for inter basin groundwater transfer identification.
The three groundwater models, hereafter referred as Model-1, Model-2 and Model-3, are:
Model 1: Groundwater model for upper part of the Awash basin bounded by the surface water divide with Rift Valley Lakes basin, Lake Koka and Awash River upstream of Lake Koka.
Model 2: Groundwater model for part of the Rift Valley Lakes Basin bounded by Lake Ziway, Meki River and the surface water divide with the Awash River basin.
Model 3: Groundwater model of the whole study area bounded by Lake Koka, Awash River upstream of Lake Koka, Lake Ziway, Meki River including the watershed divide of Awash River basin and rift valley lakes basin.
The typical modeling approach for each of the above three models is shown in Figure 3. For each model recharge and hydrogeologic parameters were adjusted to bring about satisfactory model calibration. For each model a separate recharge and hydrogeologic parameters were used during their calibration. While calibrating goodness fit indicators were obtained for well and spring data inventoried in each model’s territory.
2.4. Data Set and Data Sources
The study is to be based primarily on existing (collected by different organizations) geologic, hydro-geologic, meteorological and topographic data. Where existing data are inadequate supplemental field observation and data collection was performed. Field data collection basically include recording of latitude, longitude, elevation and static water level of the boreholes and springs. Geological map of Ethiopia, monthly rainfall
Figure 3. Groundwater modeling flow chart.
data, Digital Elevation Model (DEM), well/spring location information and surface water divide were collected from different offices viz. Ministry of Water Resources and Electricity, Water Works Design and Supervision Enterprise, National Meteorological Agency of Ethiopia. The data collected were processed for quality and consistency. For data processing and consistency checking application software like Surfer 10, Global Mapper 15, and Matlab (R2010b) programming language were used.
1) Topography
The topography of the study area is as shown in Figure 4. The topographic map was derived from 90 m DEM of the two basins. The minimum elevation is attained at 1640 m above mean sea level (amsl) and 1600 m amsl at Lake Ziway in the URVLB and at Lake Koka in UARB, respectively.
2) Well and spring inventory
In both UARB and URVLB more than 2200 wells were inventoried among them the majorities are wells (shallow hand dug wells and deep wells) and a few of them were springs. The data were collected from Federal Water works design and supervision Enterprise during the study time (September 2014 to April 2015). From these inventoried data the data quality and consistency checking has resulted in 926 wells/springs for analysis, of which 160 are in UARB and 766 are in URVLB. Consistency here is seen from the time of observation point of view. Most of the wells are shallow hand dug wells with minimum depth of 11 m and few are deep wells with maximum depth of 295 m. The range in the observed head values were, 155.5 m for wells in UARB, 740.4 m for wells in URVLB and 740.4 m, for entire well and spring inventoried in the study area. Here range is defined as the difference between the minimum and maximum observed water levels. The information from these wells used in the model are: well location (UTM coordinate of each well) and static water level. The selected wells location is shown in Figure 4.
Figure 4. Surface topography with inventoried well/spring location of the study area.
2.5. Conceptual Model
A conceptual model is a hypothetical simplified description of the groundwater system to be studied. Features often described in conceptual models include Relationship and extent of hydrogeologic units, Aquifer material properties (hydraulic conductivity), Potentiometric surfaces, Water budget, Boundary locations (depth to bedrock, impermeable layer boundaries, etc.), Boundary conditions (fluxes, heads, natural water bodies) and System stresses (withdrawal wells, infiltration trenches, etc.) [7] .
1) Recharge boundary
To deduce the recharge over the model area, the rainfall distribution across the model domain is necessary. Recharge is one of the parameters in the model calibration. During calibration a trial fraction of the total rainfall over a surface is used. In humid areas with porous soils, 25% of annual rainfall may recharge the aquifer; in contrast, in desert regions recharge is very small to 1% of rainfall or less [8] . Accordingly since the location of the study is not desert while calibrating, the recharge fraction in the model was varied between 5% and 25%.
To come up with the annual rainfall distribution, a Thiessen polygon method (as described in [9] ) of interpolation among the rainfall gauging stations within and nearby the modeling area was adopted. From National Meteorological Service Agency (NMSA) eleven metrological stations in and very close to the study area were first identified. The monthly rainfall data of these selected stations were checked for data quality and consistency. After using the Thiessen polygon method ten meteorological stations are found to contribute to the study area. The result of the Thiessen polygon analysis is as shown in Figure 5 and Table 1. From Table 1 it is possible to deduce that the average annual rainfall all over the study area is 879.95 mm.
To see the average monthly variation of the rainfall the above stations is shown in Figure 6. The graph is in the order of Alem Tena, Bui, Ejersa, Etheya, Hombol and Meki.
Table 1. Mean annual rainfall of the ten stations with their area coverage.
Figure 5. Constructed Thiessen polygon for the study area. ‘
Figure 6. Monthly rainfall distribution of the study area for some selected stations (Source: NMSA).
2) Hydrogeology: The Awash basin is located in the tectonically active East African Rift System and it has a complex geology. Groundwater recharge from the highlands is substantial and it flows in a relatively shallow depth. In the Upper and Middle Valley the groundwater levels range between 30 and 70 m. The levels drop to lower than 200 m in some areas in the southern corner of the Awash valley [10] . In the upper basin, upstream of the Koka dam, the Awash River is hydraulically linked to the aquifers [11] .
Groundwater occurs in a very wide spectrum of geological settings. According to Karimi et al., [11] and Ayenew [12] , water in the study area is supplied as a result of jointing and fracturing especially in the deeper aquifer region. The yield of water from fractured rock is dependent upon the frequency and interconnectedness of flow pathways. The more traditional notion of dealing with fractured rock aquifers is that as the scale of interest increases the more appropriate it is to employ equivalent porous media modeling approaches. This approach makes the assumption that a representative elementary volume (REV) of material characterized by equivalent hydraulic parameters can be defined. Modeling results are only valid at scales larger than the REV [13] .
3) Boundary conditions: Mathematical models of groundwater flow based on equations are classified as boundary value problems. To obtain a unique solution of such equations additional information about the physical state of the process is required. This information is supplied by boundary and initial conditions. For steady-state problems, only boundary conditions are required [14] .
The two most basic types of boundary conditions in groundwater flow analysis are constant head boundaries and no-flow boundaries. Constant head boundaries occur along the boundary of water bodies like lakes or reservoirs. No-flow boundaries occur at the interface between the aquifer and materials with markedly lower hydraulic conductivity. The finite element method can handle all types of boundary conditions, including no-flow boundaries, specified head boundaries, specified flux boundaries, and leakage boundaries [15] .
In the three models constant head boundary condition was set for the rivers (Awash and Meki) in the locations where the river is perinnial. The two lakes (Koka and Ziway) boundaries that come in contact with the model are treated as constant head boundaries.
The border of the study area extends to the watershed divide that exists between the model area and adjacent small basins. These boundaries are treated as general head boundary. The watershed divide between the two rivers (Meki and Awash) was treated as no flow boundary for Model-1 and Model-2.
The top surface of the study area is treated as recharge boundary where the recharge is taken as a fraction of the annaul rainfall over the surface. The bottom of the model is taken as a no flow boundary, where by bed rock is assumed to exist. The bottom level is fixed on the basis of its effect on the model domain. As the interest of this paper is to explore the possibility of interbasin groundwater transfer in the shallow aquifer zones, bed rock is assumed to exist at 300 m below the minimum surface elevation in the study area.
2.6. Groundwater Modeling
Among of the solution techniques assessment, numerical models were found to have more advantages over other solution techniques [16] . Unlike analytical methods numerical methods yield approximate solutions to the governing equation through the discretization of space and time. In this study TAGSAC is used for solving the groundwater flow equation. In the TAGSAC approximation procedure, the flow region is first discretized into a network of finite elements, and an interpolating trial function is used to represent the unknown dependent variable (hydraulic head) over the discretized region. An integral approximation of the flow equation is then obtained using the Galerkin weighted residual criterion. Spatial integration is performed piecewise over each element. Upon assemblage of the elements and incorporation of boundary conditions, a system of nodal equations is obtained. For a steady-state simulation, these nodal equations are algebraic equations. TAGSAC has proofed to be applicable in a number of researches done all over the globe [17] .
The most common shapes for finite elements are triangles and trapezoids for two- dimensional flow, and triangular and trapezoidal prisms for three-dimensional flow [15] . In this study triangular prism element is selected. The hydrogeologic parameters are specified for each element in the mesh. By taking into consideration the study area and the computer in use the mesh is generated by 300 meters element length. The nodes have right-handed Cartesian coordinates (x, y, z), z-axis points in the vertical upward direction (the elevation of the nodes above sea level). For the three models the numbers of nodes generated were 38,140, 21,946 and 58,400 for Model-1, Model-2 and Model-3, respectively. The numbers of elements generated with average 300 m side length were 37,084, 20,878 and 57,188 for the respective models.
3. Model Calibration and Results
To demonstrate that groundwater models are realistic, field observations of aquifer response are compared to corresponding model simulated values in model calibration, with the general objective of reducing the difference. Calibration is the process of adjusting model parameters (material properties and recharge conditions) until (l) the model is consistent with the analyst’s understanding of the groundwater flow system and with all available data, and (2) computed values of head closely match measured values at selected points in the aquifer (locations of wells and springs). The procedure is essentially an exercise in “trial and error” wherein a plausible set of model parameters are proposed, computed and measured values of head are compared, and model parameters are adjusted to improve the fit. A typical manual trial-and-error calibration process followed in this study. A flow model is considered calibrated when it can reproduce, to an acceptable degree, the hydraulic heads of the natural system being modeled.
In the model hydraulic head is computed for the three models by varying the hydraulic conductivity for the five geologic zones of the area and the surface recharge. After a number of trial hydraulic parameters for zones in Figure 7 and recharge, the parameters in Table 2 are selected as the best among other combinations.
Table 2. Geologic parameters of the study area for classified geological zones.
Figure 7. Geological classification of the area used in the model.
For the above hydraulic conductivity and recharge values the modeled and the measured values comparison can be seen in Figure 8. The best fit equation obtained between the modeled (y-axis) and measured head (x-axis) is made for the three models. In an ideal calibration, the points will fall on a straight line with a 1V:1H slope; i.e., the computed value equals the measured value. The degree of scatter about this theoretical line is a measure of overall calibration quality [18] . The slope in the best fit equations in Figure 8 being closer to one implies the acceptability of the modeling results. R2 compares estimated and measured head, and ranges in value from 0 to 1. If it is 1, there is a perfect correlation between the modeled and measured values or there is no difference between the estimated and measured values. At the other extreme, if the R2 is 0, the regression equation is not helpful in predicting.
The primary calibration target in this study is hydraulic head (water level). Accordingly, steady-state calibration was made using static water level observations of 926 wells. The effectiveness of calibration was evaluated by the following lumped quantitative performance measures:
Mean error (ME) is the mean of the differences between measured heads (hm) and simulated heads (hs):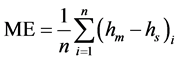 . As both positive and negative residuals could result in the calculation, ME should be close to zero for a good calibration.
. As both positive and negative residuals could result in the calculation, ME should be close to zero for a good calibration.
Mean absolute error (MAE) is the mean of the absolute value of the differences between measured and simulated heads: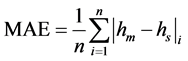 . The MAE measures the
. The MAE measures the
average magnitude of the errors in a set of predictions, without considering their direction.
The root mean square (RMS) error is the square root of the average of the squared differences between measured heads and simulated heads: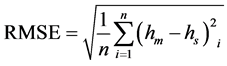 . The RMSE is used as the basic measure of calibration for heads.
. The RMSE is used as the basic measure of calibration for heads.
Uncertainty in head measurements can be the result of many factors including, measurement error, scale errors, and various types of averaging errors, and specific to this study case the accuracy of GPS in use. The maximum acceptable value of calibration criterion depends on the magnitude of the change in head over the problem domain. As a general calibration criteria RMSE equal to or less than 10% of the observed head range in the aquifer being simulated is better [18] . The ME and MAE are characterized by low values indicating that the model was well calibrated. The value of the correlation coefficient (R2) being closer to 1 indicates a good performance of the models.
From Table 3 it is evident that Model 3 represents better the wells observed in Upper Rift Valley Lakes Basin than Model-2. This clearly show that the influence of the neighbor upper awash basin on the upper rift valley lakes basin, in Model-2 this influence was blocked by the no flow boundary assumed. The presence of the no flow boundary between the URVLB and UARB in Model 2 doesn’t help in improving the model accuracy. Their interaction could be seen from Figure 8(c) which shows the result of Model-3. Figure 9(a) and Figure 9(b), respectively, show the result of the calibrated Model-1 and Model-2 for parameters shown in Table 2.


Figure 8. Simulated versus measured head comparison.
Table 3. Summary of calibration errors.



Figure 9. Computed groundwater head and flow directions (a) Model-1; (b) Model-2; (c) Model-3.
From Figure 9(a) and Figure 9(b) it is evident that the groundwater flows towards the Koka and Ziway Lakes, respectively. This is because of the no flow boundary condition set along their border. In Figure 9 the Model-3 result along with the water surface divide is depicted. From this figure it is clear that groundwater flows from Rift Valley Lakes Basin towards Awash River basin is observed.
4. Conclusions
For correct management of the existing water resources and their optimal use, ground- water potential and its flow direction and suitable plans must be developed based on objectives suitable to the region. Groundwater models have been used extensively for such analysis and are generally adequate for predicting aquifer head changes. However, the three-dimensional model described in this paper was developed to identify the inter-basin groundwater transfer between upper Awash River basin and upper Rift Valley lakes basin.
For the IBGWT identification three groundwater models (Model-1 for upper Awash River basin, Model-2 for Upper Rift Valley Lakes Basin and Model-3 for combined Upper Awash and Upper Rift Valley lakes basin) were first created. Two separate groundwater models for each sub basin (Model-1 and Model-2) by considering the watershed divide between the two basins as no-flow. The third groundwater model (Model-3) treats the two basins as one (avoiding the surface water divide). The calibration of these three models was made by changing the recharge and hydrogeologic parameters of the basins. For the calibration 926 (160 for Model-1, 766 for Model-2 and 926 for Model-3) wells and springs were inventoried whereby the modeled and measured hydraulic head at these well/spring locations is tested for measure of goodness of fit. Among the goodness of fit indicators obtained for the Model-1, Model-2 and Model-3 the RMSE were 7.605 m, 11.745 m and 11.702 m, respectively. These results are well below the recommended values for calibrated model. Model-3 RMSE values for well data in Model-1 and Model-2 were 12.582 and 10.914 m, respectively, which shows that Model-3 better describes the flow system in URVLB than Model-2. This result with the hydraulic head distribution obtained from Model-3 clearly indicates that there is a groundwater flow that doesn’t respect the surface water divide.
In groundwater modeling the assumption that the groundwater divide and surface water divide are coincident is not valid in this case. Such assumption leads wrong quantification and wrong prediction of the groundwater flow system. The most obvious effect of IBGWT is to diminish surface water discharge from URVLB (in which IBGWT originates), and enhance discharge in the UARB (receiving IBGWT). Moreover, the result of this study is important to assess the potential for internal and cross contamination of the groundwater.
Acknowledgements
The authors are grateful to Addis Ababa Institute of technology, Federal Policy study and research center for their strong support of the research publication. We would also like to acknowledge Federal water works design and supervision enterprise and Ethiopian Meteorological Agency for giving us the data related to this research. Last but not least the authors are grateful to the anonymous reviewers for their valuable comments that improve this publication.
Cite this paper
Mohammed, M. and Ayalew, B. (2016) Modeling for Inter- Basin Groundwater Transfer Identification: The Case of Upper Rift Valley Lakes and Awash River Basins of Ethiopia. Journal of Water Resource and Protection, 8, 1222- 1237. http://dx.doi.org/10.4236/jwarp.2016.813094
References
- 1. Atnafu, Y. and Mohammed, M. (2014) Characterization of Lake Water Groundwater Interaction in Hawassa Basin. Unpublished MSc. Thesis, AAU, AAiT.
- 2. Ayenew, T. (2001) Numerical Groundwater Flow Modelling of the Central Main Ethiopian Rift Lakes Basin. SINET: Ethiopian Journal of Science, 24, 167-184.
- 3. Awulachew, S.B., Yilma, A.D., Loulseged, M., Loiskandl, W., Ayana, M. and Alamirew, T. (2007) Water Resources and Irrigation Development in Ethiopia. Colombo, Sri Lanka. Working Paper 123, International Water Management Institute, 78 p.
- 4. Daniel, G. (1977) Aspects of Climate and Water Budget in Ethiopia. Technical Monograph, Addis Ababa University Press, Addis Ababa.
- 5. Lemma, G. (1996) Climate Classification of Ethiopia. Meteorological Research Report Series No. 3, National Meteorological Services Agency of Ethiopia, Addis Ababa.
- 6. Barnett, B., Townley, L.R., Post, V., Evans, R.E., Hunt, R.J., Peeters, L., Richardson, S., Werner, A.D., Knapton, A. and Boronkay, A. (2012) Australian Groundwater Modeling Guidelines. National Water Commission, Canberra.
- 7. USACE (U.S. Army Corps of Engineers) (1999) Engineering and Design Groundwater Hydrology, Washington DC.
- 8. Moore, J.E. (2002) Field Hydrogeology a Guide for Site Investigations and Report Preparation. Lewis Publishers, CRC Press LLC.
https://doi.org/10.1201/9781420032253 - 9. Ragunath, H.M. (2006) Hydrology, Principles Analysis Design. New Age International (P) Limited, New Delhi.
- 10. Ayenew, T., Kebede, S. and Alemyahu, T. (2008) Environmental Isotopes and Hydrochemical Study Applied to Surface Water and Groundwater Interaction in the Awash. Hydrological Processes, 22, 1548-1563.
https://doi.org/10.1002/hyp.6716 - 11. Karimi, P. (2014) Spatial Evapotranspiration, Rainfall and Land Use Data in Water Accounting—Part 2: Reliability of Water Accounting Results for Policy Decisions in the Awash Basin. Hydrology and Earth System Sciences Discussions, 11, 1-44.
- 12. Ayenew, T. (2007) The Distribution and Hydrogeological Controls of fluoride in the Groundwater of Central Ethiopian Rift and Adjacent Highlands. Environmental Geology, 54, 1313-1324.
https://doi.org/10.1007/s00254-007-0914-4 - 13. Long, J.C.S., Remer, J.S., Wilson, C.R. and Witherspoon, P.A. (1982) Porous-Media Equivalents for Networks of Discontinuous Fractures. Water Resources Research, 18, 645-658.
https://doi.org/10.1029/WR018i003p00645 - 14. Konikow and Reilly (1998) Groundwater Modeling. In: Dellure, J.W., Ed., The Hand Book of Groundwater Engineering, CRC press, Boca Raton, 20:1-20:40.
https://doi.org/10.1201/9781420048582.ch20 - 15. Fitts, C.R. (2002) Groundwater Science. Academic Press.
- 16. Praveena, S.M., Abdullah, M.H., Aris, A.Z. and Bidin, K. (2010) Groundwater Solution Techniques: Environmental Applications. Journal of Water Resource and Protection, 2, 8-13.
https://doi.org/10.4236/jwarp.2010.21002 - 17. Mohammed, M., Watanabe, K. and Takeuchi, S. (2010) Grey Model for Prediction of Pore Pressure Change. Environmental Earth Sciences, 60, 1523-1534.
https://doi.org/10.1007/s12665-009-0287-y - 18. Anderson, M.P. and Woessner, W.W. (1992) Applied Ground Water Modeling: Simulation of Flow and Advective Transport. Academic Press, 1-143, 295-314.









