Journal of Software Engineering and Applications
Vol.7 No.6(2014), Article
ID:46357,8
pages
DOI:10.4236/jsea.2014.76046
Resampling Simulator for the Probability of Detecting Invasive Species in Large Populations
David E. Legg1, Jeffrey G. Fidgen2, Krista L. Ryall2
1Department of Ecosystem Science and Management, University of Wyoming, Laramie, USA
2Great Lakes Forestry Centre, Sault Ste. Marie, Canada
Email: dlegg@uwyo.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 March 2014; revised 15 April 2014; accepted 22 April 2014
ABSTRACT
This paper proposes a resampling simulator that will calculate probabilities of detecting invasive species infesting hosts that occur in large numbers. Different methods were examined to determine the bias of observed cumulative distribution functions (c.d.f.s), generated from prototype resampling simulators. One involved seeing if they matched theoretical c.d.f.s, which were generated using formulae for calculating the probability of the union of many events (union formulae), which are known to be correct. Others involved assessing the bias of observed c.d.f.s, generated from using prototype resampling simulators operating on much larger simulated populations, when computation of theoretical c.d.f.s from the union formulae was not practical. Examples are given for using the proposed resampling simulator for detecting an invasive insect pest within the context of an invasive species management system.
Keywords:Resampling Simulator, Detection of Invasive Species, Invasive Species Management System, Large Populations

1. Introduction
When a species enters an area where it did not previously exist, it may be called an invasive. Detection of invasives is important to help prevent their permanence and creating unwanted outcomes.
Some invasives can have devastating impacts on economies and ecological systems [1] [2] . Ideally, we strive for early detection of invasives so that extirpation can be achieved, such as the USDA Forest Service’s early— detection, rapid response program for invasive forest pests [3] . Failing that, and after invasives have partially spread across a landscape, detection remains important for their delimitation and management [4] .
Sometimes accidental importation of an invasive species can be anticipated; we just do not know when or where it will occur. Examples include the accidental introduction of a the Asian long-horned beetle (more information on http://www.mnr.gov.on.ca/en/Business/Forests/2ColumnSubPage/STEL02_166979.html), the emerald ash borer (more information on http://emeraldashborer.info/), and the Asian carp (more information on http://asiancarp.us/).
Some detection efforts for invasive insect or plant pathogenic disease involves looking for the pest or disease on or in a host, which is an organism the invasive prefers to attack, damage, and kill. For these situations, we sample a host population to try to find the pest or disease; therefore, detection efforts are applied to identifiable groups or populations of hosts. Examples of host populations include agricultural fields, wood lots, orchards, or municipal right of ways.
When a finite population is examined to detect an invasive, it is important to determine the number of host individuals within that population. Though somewhat subjective, a small population may contain ≤ 1000 individuals; a large population may contain many millions of individuals. Detection of invasives in small populations may involve a census and, if not, may involve detection probabilities that are easily computed using formulae of the union of many independent events (union formulae) [5] .
Detection of invasives in populations with many hosts rarely involves a census and cannot be done with union formulae because of resource limitations [5] . Instead, Legg et al. [5] suggest using simulation resampling to compute the detection probabilities.
This paper puts forward a model for the design and development of a resampling simulator for computing detection probabilities of invasive species in populations that have many hosts. In Section 2, we propose a design for the resampling simulator. In Section 3, we describe a development process for that design, and in Section 4, we place the resampling simulator in the context of an invasive species management system.
2. Resampling Simulator
The proposed resampling simulator has five distinct components:
• Population simulator;
• Random resampler;
• Random resampler test;
• Relative frequency generator, and;
• Cumulative distribution function (c.d.f.) generator.
Figure 1 illustrates the proposed design for the resampling simulator.
The first component, the population simulator, creates a simulated host population of size N, such that individuals being infested by an invasive assume one numerical value (e.g., 1.0) and those that are not assume
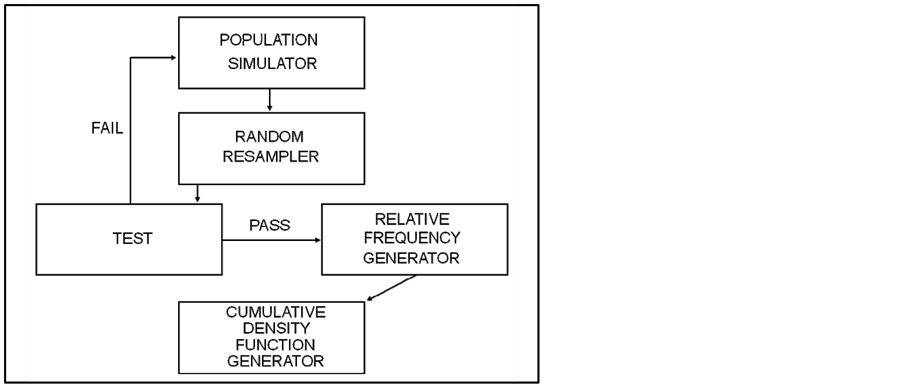
Figure 1. Proposed design for the resampling simulator.
another (e.g., 0.0). The population simulator places the simulated individuals in an array so they will have an identifiable position structure. The array may appear as a vector or as a matrix, and its spatial arrangement is inconsequential to the function of the resampling simulator.
The random resampler component creates an unbiased random permutation of the positions of individuals in an array of a simulated population, simulates an inspection of each, and counts how many have been inspected until first detection occurs. It notes the number on which the infestation was detected, then resamples the simulated population x times (x = number of iterations or resampling efforts). Value for x depends on what is being estimated and can range from 200 [6] to 10,000 [7] .
As suggested by Press et al. [8] , the random number generator or, in this case, the random permutation process (which makes use of a random number generator), should be tested to verify that it selects positions from the array without bias. Hence there is a need for the third, or test component.
The fourth component involves generating a relative frequency distribution of sample numbers on which first detection occurred, over the x resampling efforts. The final component involves generating a.c.d.f. from the outcome of the relative frequency generator; this provides the probability of detection for a simulated population for any sample number, n:n = 1, 2, ···, N.
3. Development of a Resampling Simulator
Development of a resampling simulator involved three phases: 1) selecting a random permutation algorithm, 2) testing that algorithm for bias against a known c.d.f., and 3) developing alternative methods for detecting bias. Perhaps the most important part of the random resampler was to select an algorithm to randomly permute a large set of numbers. Typically random number generators will provide, in our case, integers between specified lower and upper limits, inclusive, irrespective of whether they have been previously selected. Generating a random integer that has already been selected is redundant and inefficient and will require the resampling simulator to run much longer than is necessary. This would not be much of an issue for very small populations. However, it is a major issue for large populations.
There are several algorithms that efficiently perform random permutations. For this we used a Fisher-Yates shuffle [9] , later slightly modified by Durstenfield [10] , and popularized by Knuth [11] . Briefly this algorithm uses a random number generator to select a position number from a list of size N. The simulated host at that position is placed in a random permutation array, and then is removed from the list. Next, the algorithm generates a number from the remaining N − 1 positions, with the simulated host at that position being placed in the random permutation array, and then is removed from the list. This continues until all simulated hosts are selected. This algorithm was in turn based on the RAN2 (IDUM) portable random number generator of uniform deviates published by Press et al. [8] , which was seeded from the computer clock.
Given the variability of random number seeding methods, potential for modulo bias, language variability when handling large numbers, and register size influence on computations [8] , we tested the random resampler for bias. This was done by seeing if observed c.d.f.s generated from the random resampler, when converted to an observed c.d.f, would essentially match those produced by the union formulae, which are known to be correct. Initially this was done by matching many observed c.d.f.s with a theoretical c.d.f. for a population size of 1000. Results, which are shown in Figure 2, indicated systematic departure (bias) of the observed c.d.f. from the theoretical c.d.f. for very low levels of infestation. Investigation revealed that this occurred because, initially, the populations that were generated via the population simulator were placed in arrays that themselves were not randomly permuted. When we randomly permuted arrays of the initial, simulated populations, then applied the random resampler, and matched observed c.d.f.s with theoretical c.d.f.s, the results were unbiased (Figure 3). Therefore, the population simulator was followed by random permutation before use of the random resampler.
It is unlikely that an observed c.d.f., resulting from use of a random resampler operating on large simulated populations, can be checked for bias against a theoretical c.d.f. resulting from union formulae because the computer time needed to perform union formulae computations is too great [5] . Instead, a reasonable alternative may be to fit a function to the resampling results, then using that function to develop predicted c.d.f.s. Several such functions can be used, two being as follows:
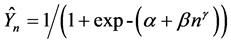 (1)
(1)
and
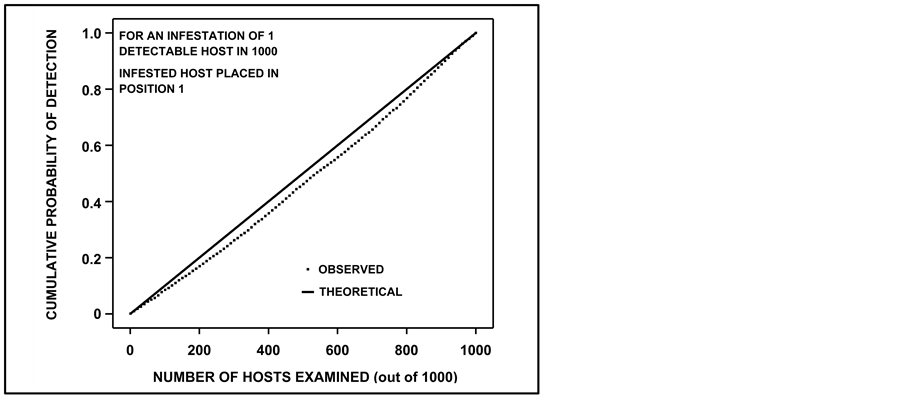
Figure 2. Observed c.d.f., produced by use of a random resampler, along with the theoretical c.d.f. that was produced by using theoretical union probability formulae. The simulated population upon which the random resampler was used was not randomly permuted; hence the biased results as the observed c.d.f. is clearly separated from the theoretical over much of the host range examined.
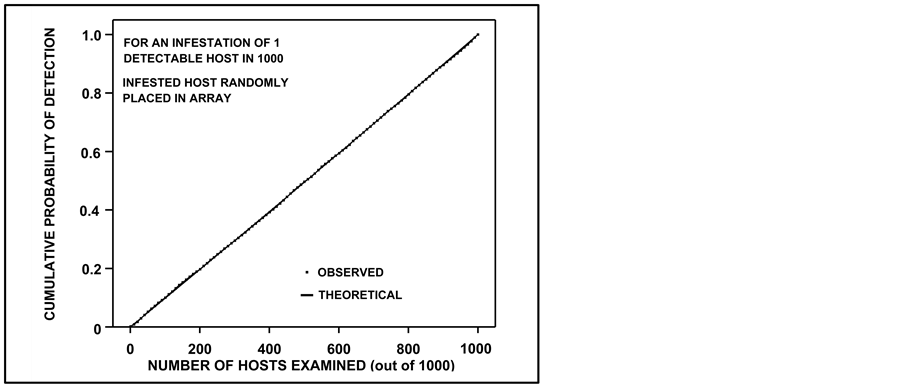
Figure 3. Observed c.d.f., produced by use of a random resampler, along with the theoretical c.d.f. that was produced by using theoretical union probability formulae. The simulated population upon which the random resampler was used was randomly permuted; hence the unbiased results as the observed c.d.f. is indistinguishable from the theoretical over the range of hosts examined.
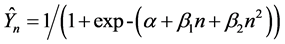 (2)
(2)
where  is the predicted proportion of x resampling trials for which first detection occurred on the nth examined individual in a simulated population, α is the y-intercept, β is the slope of a curvilinear logistic function, γ is a curve fitting exponent, and β1 and β2 are the linear and quadratic slopes of a polynomial logistic function. Intercepts and slopes should be fitted using maximum likelihood [12] . Value for γ may be iteratively derived to minimize ω in the following:
is the predicted proportion of x resampling trials for which first detection occurred on the nth examined individual in a simulated population, α is the y-intercept, β is the slope of a curvilinear logistic function, γ is a curve fitting exponent, and β1 and β2 are the linear and quadratic slopes of a polynomial logistic function. Intercepts and slopes should be fitted using maximum likelihood [12] . Value for γ may be iteratively derived to minimize ω in the following:
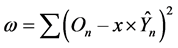 (3)
(3)
where On and  are the observed and predicted frequencies of detection for the nth individual [13] . We found c.d.f.s resulting from either Equation (1) (Figure 4) or (2) superior to those resulting from the following:
are the observed and predicted frequencies of detection for the nth individual [13] . We found c.d.f.s resulting from either Equation (1) (Figure 4) or (2) superior to those resulting from the following:
 (4)
(4)
which provided c.d.f.s of a poor fit (e.g., Figure 5); systematic departure of an observed c.d.f. from a c.d.f. produced through either (1) or (2) indicates bias.
4. Proposed Use of the Resampling Simulator in an Invasive Species Management System
The resampling simulator is meant to be used for detecting invasive species in large populations. In that context, there are recognizable steps that an entity, e.g., a farmer, municipality, or woodlot manager, should consider. These include: 1) inventory; 2) resampling heuristics; 3) resampling simulator; 4) application heuristics; 5) acceptance c.d.f.; 6) random host selection; 7) efficient host examination; and 8) extirpation/management when detection occurs; otherwise re-application of the invasive species detection and management system (Figure 6). A resampling simulator has been developed and pressed into service for detecting the invasive emerald ash borer (Agrilus planipennis Fairmaire; Coleoptera: Buprestidae). Here we relate its use with regards to the above 8 steps.
Briefly the emerald ash borer was first discovered in Detroit, Michigan, USA, and Windsor, Ontario, Canada in 2002 but likely had been present in these areas since the mid 1990s. As of 14 February, 2014, it has been detected in 21 US states and two Canadian provinces (more information on http://www.emeraldashborer.info). This insect is a non-native pest that infests and kills all species of ash native to North America and has already killed tens of millions of ash trees in the United States and Canada, resulting in significant management costs [14] . Emerald ash borer larvae feed on or “tunnel through” a narrow layer of woody tissues comprising the phloem, cambium and outer sapwood of the tree [14] ; in so doing, they disrupt the translocation of water, minerals and nutrients throughout the tree when populations are high. Oftentimes, trees may be attacked for 1 - 3 yrs before showing any signs and symptoms of infestation based on visual examination of trees from the ground. Indeed, Ryall et al. [15] found that incipient populations of emerald ash borer could be detected in trees that were not showing signs and symptoms of infestation by sampling two branches per tree and peeling the bark of the basal 50 cm of each. This method could detect trees 7 - 8 times out of 10 when they are lightly infested (i.e., infested with as few as 10 tunnels or galleries per sq. m.). Early detection of emerald ash borer provides entities (i.e., managers) the time they need to choose and then apply extirpation/management action.
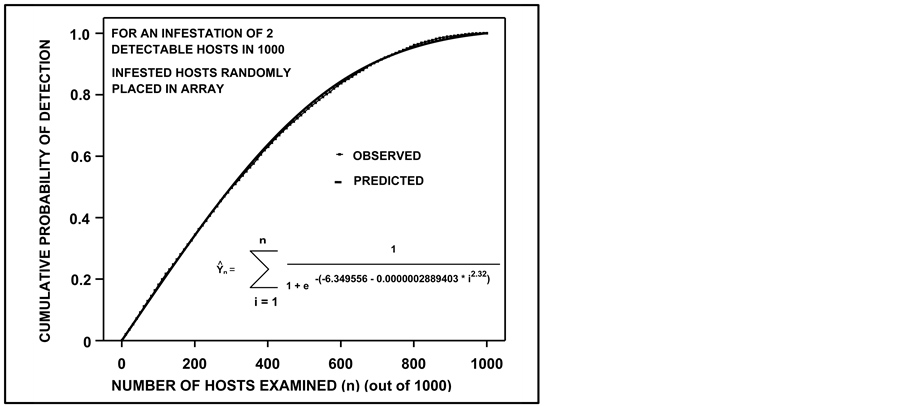
Figure 4. Observed and predicted c.d.f. from using the random resampler on a simulated population of N = 1,000 and fitting a curvilinear logistic function to the resulting detection frequencies (i.e., probabilities × x; x = number of resampling trials).
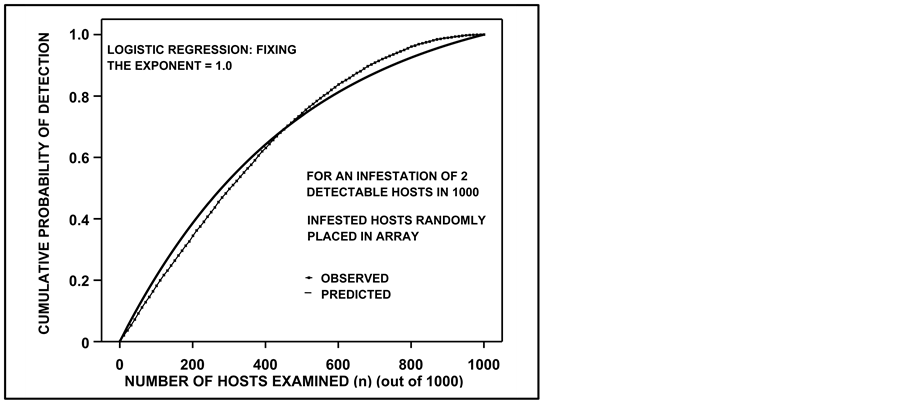
Figure 5. Resulting predicted c.d.f. from use of a logistic function , which poorly reflects the observed c.d.f. produced by the random resampler.
, which poorly reflects the observed c.d.f. produced by the random resampler.

Figure 6. Proposed use of the resampling simulator in the context of an invasive species management system.
As illustrated in Figure 6, the initial step an entity takes when detecting invasives is to conduct an inventory of the hosts. This is feasible when hosts number into the thousands, though it may take some weeks to identify each and every individual in the population. When hosts number into the millions or more, managers may consider a system of grids or random coordinates [16] .
With regards to the emerald ash borer in the municipalities of Oakville and Sault Ste. Marie, Ontario, Canada, delimitation was the objective, which was achieved by sampling of 5 - 10 trees at 1km intervals around a known infestation point. In Mississauga, Ontario, Canada, ash trees were first grouped into wards, then into populations of 5000 trees within ward; this required a c.d.f. generated from a simulated population of 5000. In the municipality of Montreal, Quebec, Canada, and Thunder Bay, Ontario, Canada, inventories were carried out in each borough, which were found to have up to 5000 ash trees so those cities also used a c.d.f. developed for 5000 simulated hosts. Resampling heuristics led the city of Montreal to determine that it had resources to survey for an infestation the size of 150 trees (3% hosts infested) in each borough. Montreal then used the resampling simulator to develop an observed c.d.f.; application heuristics led to the acceptance of that c.d.f., which is shown in Figure 7. Sampling (i.e., random host selection and efficient host examination) of ash was then conducted in several of Montreal’s boroughs both in 2012 and 2013.
After sampling, and if detection had occurred, extirpation and/or management was often done. Sometimes that involved having infested trees that were showing symptoms of emerald ash borer infestation being cut, chipped and composted, and/or having asymptomatic (but infested) trees being treated with an insecticide. For some situations, a more aggressive approach was taken to cut, chip, and compost all asymptomatic ash trees, of unknown infestation status, within a buffer zone surrounding an infested tree. An alternative but no less aggressive approach was undertaken by the municipality of Montreal, which removed all known infested trees, and then treated all other ash trees within a 400 m buffer of each with an insecticide. Sometimes a less aggressive approach to management was taken by simply removing dead trees killed by emerald ash borer so as to minimize the public safety hazard of falling limbs and dead trees.
After sampling, and if detection does not occur, then plans were made for regular re-application of part or all of the invasive species management system as the species in question continues to be a threat. This occurred in the city of Thunder Bay, Ontario, Canada, which made use of the resampling simulator to generate a c.d.f. that was used in an invasive species management system, and applied its results to ash trees beginning in 2011. At that time, no emerald ash borer population was detected after examining 200 trees of approximately 5000. Follow up re-application was then done both in 2012 and 2013.
5. Conclusion
This paper has presented methodologies and evaluation strategies for developing and testing prototype resampling simulators. These should prove useful for detecting some invasives infesting hosts that occur in large numbers. For populations of hosts that occur into the millions or more, use of the resampling simulator can be

Figure 7. An observed c.d.f. used by the municipality of Montreal, Quebec, Canada showing probabilities of 0.95 and 0.90 for detecting a 3% infestation of the emerald ash borer in a population of 5000 ash trees in each of its boroughs using branch sampling; the former probability required 194 ash trees to be examined whilst the latter required 148.
made by superimposing a system of grids or coordinates on the populations, or partitioning the populations into smaller units, each of which can be assessed by a c.d.f. generated via the proposed resampling simulator. The latter of these was done in the municipalities of Montreal and Mississauga. Other uses for the proposed resampling simulator revealed that it has been used by municipalities to clarify their options on probabilities of detecting insipient emerald ash borer infestations given their resources and the available management tactics. In the future, applications of the proposed resampling simulator, using increasingly faster processor speeds, multiple processors, and computers with very large capacities for memory, should allow for the computation of observed c.d.f.s for detecting invasives infesting hosts that number into the many millions.
Acknowledgements
We thank the municipalities of Montreal, Thunder Bay, Mississauga, Oakville, Toronto, and Sault Ste. Marie for sharing their experiences when using the resampling simulator.
References
- Morrison, W.P. and Peairs, F.B. (1994) Response Model Concept and Economic Impact. Proceedings of the Thomas Say Publications in Entomology, Entomological Society of America, Lanham, 16 December 1994, 1-11.
- Kovacs K.F., Haight, R.G., McCullough, D.G., Mercader, R.J., Siegert, N.W. and Liebhold, A.M. (2010) Cost of Potential Emerald Ash Borer Damage in US Communities, 2009-2019. Ecological Economics, 69, 569-578. http://dx.doi.org/10.1016/j.ecolecon.2009.09.004
- Rabaglia R., Duerr, D., Acciavatti, R. and Ragenovich, I. (2008) Early Detection and Rapid Response for Non-Native Bark and Ambrosia Beetles. U.S.D.A. Forest Service, Forest Health Protection Washington DC, 2 Pages.
- Legg D.E and Archer, T.L. (1994) Sampling Methods, Economic Injury Levels, and Economic Thresholds for the Russian Wheat Aphid (Homoptera: Aphididae). Proceedings of the Thomas Say Publications in Entomology, Entomological Society of America, Lanham, 16 December 1994, 313-336.
- Legg D.E, Fidgen, J.G. and Ryall, K.L. (2010) Computing Union Probabilities of Many Independent Events: With a Case Study Example on Sampling of the Invasive Emerald Ash Borer, Agrilus planipennis. http://w3.uwyo.edu/~dlegg/union2.html
- Efron B. and Tibshirani, R.J. (1993) An Introduction to the Bootstrap. Section 6.4, Chapman & Hall/CRC, Boca Raton, 50-53.
- Fidgen J.G., Legg, D.E. and Salom, S.M. (2006) Binomial Sequential Sampling Plan for Hemlock Wooly Adelgid (Hemiptera: Adelgidae) Sistens Infesting Individual Eastern Hemlock Trees. Journal of Economic Entomology, 99, 1500-1508. http://dx.doi.org/10.1603/0022-0493-99.4.1500
- Press W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. (2003) Numerical Recipes in FORTRAN 77. 2nd Edition, Vol. 1, Cambridge University Press, Cambridge, 267-276.
- Fisher R.A. and Yates, F. (1938) Statistical Tables for Biological, Agricultural, and Medical Research. Oliver and Boyd, London, 20, Example 12.
- Durstenfield R. (1964) Algorithm 235: Random Permutation. Communications of the ACM, 7, 420. http://dx.doi.org/10.1145/364520.364540
- Knuth D.E. (1969) The Art of Computer Programming. Vol. 2, 3rd Edition, Addison-Wessley, Reading, 124-125.
- Haberman S.J. (1978) Analysis of Qualitative Data. Vol. 1, Academic, New York, 292-353.
- Legg D. (2003) LINLOGIT: A Computer Program for Calculating Linear Logistic Regression Functions. http://w3.uwyo.edu/~dlegg/curve.html
- Poland, T.M. and McCullough D.G. (2006) Emerald Ash Borer: Invasion of the Urban Forest and the Threat to North America’s Ash Resource. Journal of Forestry, 104, 118-124.
- Ryall K.L., Fidgen, J.G. and Turgeon, J.J. (2011) Detectability of the Emerald Ash Borer (Coleoptera: Buprestidae) in Asymptomatic Urban Trees by Using Branch Samples. Environmental Entomology, 40, 679-688. http://dx.doi.org/10.1603/EN10310
- Legg D.E. and Yeargan, K.V. (1985) Method for Random Sampling Insect Populations. Journal of Economic Entomology, 78, 1003-1008.

