Journal of Software Engineering and Applications
Vol.07 No.07(2014), Article ID:46574,6 pages
10.4236/jsea.2014.77051
A Logical Treatment of Non-Termination and Program Behaviour
Martin Ward1*, Hussein Zedan2
1Software Technology Research Lab, De Montfort University, Leicester, UK
2Applied Science University, Al Eker, Bahrain
Email: *martin@gkc.org.uk, hussein.zedan@googlemail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 February 2014; revised 10 March 2014; accepted 18 March 2014
ABSTRACT
Can the semantics of a program be represented as a single formula? We show that one formula is insufficient to handle assertions, refinement or slicing, while two formulae are sufficient: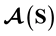 , defining non-termination, and
, defining non-termination, and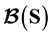 , defining behaviour. Any two formulae
, defining behaviour. Any two formulae 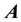 and
and 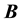 will de- fine a corresponding program. Refinement is defined as implication between these formulae.
will de- fine a corresponding program. Refinement is defined as implication between these formulae.
Keywords:
Formal Methods, Refinement, Non-Termination, Non-Determinism, Weakest Precondition, Temporal Logic, Wide-Spectrum Language

1. Introduction
The idea of using a single formula to represent the behaviour of a program is a very attractive one: proving that two programs are equivalent then reduces to the task of proving that two formula are equivalent. For the latter task, mathematicians have developed many powerful techniques over the last few thousand years of the history of mathematics.
In this paper, we show that a single formula is insufficient to represent the semantics of a program in the de- sired way, but there are two formulae which are sufficient.
2. The WSL Language
The WSL transformation theory is based in infinitary logic: an extension of first order logic which allows infi- nitely long formulae. The statements in the WSL kernel language are as follows: 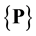 is an assertion which terminates immediately if
is an assertion which terminates immediately if 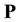 is true and aborts if
is true and aborts if 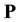 is false,
is false,  is a guard which ensures that
is a guard which ensures that 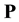 is true without changing the value of any variable,
is true without changing the value of any variable, 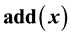 adds the variables in
adds the variables in 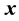 to the state space, if they are not already present, and assigns arbitrary values to the variables.
to the state space, if they are not already present, and assigns arbitrary values to the variables. 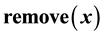 removes the variables in
removes the variables in 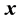 from the state space,
from the state space, 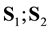 is sequential composition,
is sequential composition, 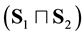 is nondeterministic choice, and
is nondeterministic choice, and 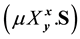 is a recursive subroutine which also adds the variables in
is a recursive subroutine which also adds the variables in ![]() to the state space and removes the variables in
to the state space and removes the variables in ![]() from the state space.
from the state space.
The semantics of a WSL program is defined as a function which maps each initial state to the set of possible final states. A state is either the special state![]() , which represents non-termination, or a proper state which is a function from a set of variables (the state space) to the set of values. The semantics of a program is always de- fined in the context of a particular initial state space and final state space.
, which represents non-termination, or a proper state which is a function from a set of variables (the state space) to the set of values. The semantics of a program is always de- fined in the context of a particular initial state space and final state space.
For any list of variables![]() , we define
, we define ![]() to be the set of variables in
to be the set of variables in![]() , and
, and ![]() and
and ![]() to be the cor- responding sequences of primed and doubly primed variables. The formula
to be the cor- responding sequences of primed and doubly primed variables. The formula ![]() is true precisely when the value of any variable in
is true precisely when the value of any variable in ![]() differs from the value of the corresponding variable in
differs from the value of the corresponding variable in![]() .
.
The interpretation function ![]() maps each statement
maps each statement ![]() and initial state space
and initial state space ![]() to the corres- ponding state transformation (under a model
to the corres- ponding state transformation (under a model ![]() for the logic in question). For a state space
for the logic in question). For a state space![]() , and set of values
, and set of values![]() , let
, let ![]() be the set of states on
be the set of states on ![]() and
and ![]() (including
(including![]() ), and for any formula
), and for any formula ![]() let
let ![]() be the set of states which satisfies the formula. See [1] for details.
be the set of states which satisfies the formula. See [1] for details.
For initial state ![]() we define
we define ![]() for every statement
for every statement![]() , i.e. if the program is started in the non-terminating state then it cannot be guaranteed to terminate. (Starting the program in a non-terminating state simply means that some previous program in the sequence has failed to terminate, so this program can never actually start. This restriction simply means that a later statement in a sequence cannot somehow “recover” from non-termination of an earlier statement in the sequence the program).
, i.e. if the program is started in the non-terminating state then it cannot be guaranteed to terminate. (Starting the program in a non-terminating state simply means that some previous program in the sequence has failed to terminate, so this program can never actually start. This restriction simply means that a later statement in a sequence cannot somehow “recover” from non-termination of an earlier statement in the sequence the program).
The semantics for the recursive program is simply the intersection of the semantics for each finite truncation. The result is the least defined statement which is a refinement of all the truncations.
If the initial state space is empty, then there are two possible initial states: ![]() and the single proper state
and the single proper state![]() . For
. For ![]() the set of final states must be
the set of final states must be![]() , by definition. So the state transformation is entirely determined by its value on the initial state
, by definition. So the state transformation is entirely determined by its value on the initial state![]() . If the final state space is also empty, then there are exactly three distinct state transformations, corresponding to the three possible sets of states.1 The three state transformations are
. If the final state space is also empty, then there are exactly three distinct state transformations, corresponding to the three possible sets of states.1 The three state transformations are![]() ,
, ![]() and
and ![]() where:
where:
![]()
These correspond to the three fundamental statements![]() ,
, ![]() and
and ![]() :
:
![]()
![]()
1Recall that if ![]() is in the set of final states, then every other state has to be included: so
is in the set of final states, then every other state has to be included: so ![]() is not a valid final set of states.
is not a valid final set of states.
Note that there are three different semantic function which use no variables, but only two semantically-dif- ferent formulae with no free variables (namely ![]() and
and![]() ). Under any interpretation of the logic, any formula with no free variables must be interpreted as either universally true or universally false. There is no way to map three different semantics onto two formulae: so this proves that a single formula is insufficient to re- present the semantics of a program.
). Under any interpretation of the logic, any formula with no free variables must be interpreted as either universally true or universally false. There is no way to map three different semantics onto two formulae: so this proves that a single formula is insufficient to re- present the semantics of a program.
3. The Abort and Behaviour Predicates
Since it is not possible to represent the semantics of a program using one formula, we will now consider how we can represent the denotational semantics of a program using two formulae from infinitary first order logic. The formulae are defining in terms of the weakest precondition.
For any program ![]() and postcondition (condition on the final state space)
and postcondition (condition on the final state space)![]() , the weakest precondition
, the weakest precondition ![]() is the weakest condition on the initial state space such that if the initial state satisfies
is the weakest condition on the initial state space such that if the initial state satisfies ![]() then
then ![]() is guaranteed to terminate in a state which satisfies
is guaranteed to terminate in a state which satisfies![]() .
.
In [1] , we show that ![]() can be defined as a formula in infinitary logic and that refinement can be characterised by the weakest precondition as follows: for any to programs
can be defined as a formula in infinitary logic and that refinement can be characterised by the weakest precondition as follows: for any to programs ![]() and
and ![]() with the same initial and final state spaces,
with the same initial and final state spaces, ![]() is a refinement of
is a refinement of![]() , written
, written![]() , if and only if for all postconditions
, if and only if for all postconditions![]() :
:
![]()
In the same paper, we also prove that it is not necessary to determine the weakest preconditions for all postconditions: two very simple postconditions are sufficient. These are the conditions ![]() and
and ![]() where
where ![]() is a list of all the variables in
is a list of all the variables in ![]() and
and ![]() is a list of new variables, not appearing in either program, which are the doubly-primed versions of the variables in
is a list of new variables, not appearing in either program, which are the doubly-primed versions of the variables in![]() . Then
. Then ![]() if and only if:
if and only if:
![]()
For any statement![]() , the formula
, the formula ![]() describes precisely those initial states on which
describes precisely those initial states on which ![]() is guaranteed to terminate. For each of these states, the formula
is guaranteed to terminate. For each of these states, the formula ![]() describes the behaviour of
describes the behaviour of ![]() in the sense that, if
in the sense that, if ![]() is an initial state for which
is an initial state for which ![]() terminates, and
terminates, and ![]() is an extension of
is an extension of ![]() which adds the variables
which adds the variables ![]() to the state with a given set of values, then
to the state with a given set of values, then ![]() satisfies
satisfies ![]() precisely when the values assigned to
precisely when the values assigned to ![]() form a possible final state for
form a possible final state for ![]() when they are assigned to the corresponding un- primed variables.
when they are assigned to the corresponding un- primed variables.
To be more precise, we will prove the following theorem:
Theorem 3.1. If ![]() is the interpretation of
is the interpretation of![]() , then for every initial state
, then for every initial state ![]() and final state
and final state![]() , the corresponding extended initial state
, the corresponding extended initial state ![]() is in
is in![]() , and conversely, every state in
, and conversely, every state in ![]() is of the form
is of the form ![]() for some initial state
for some initial state ![]() and
and![]() .
.
Proof: Suppose ![]() is the interpretation of
is the interpretation of ![]() as a state transformation from
as a state transformation from ![]() to
to![]() , and let
, and let ![]() be any initial state. Let
be any initial state. Let ![]() be any proper state in
be any proper state in ![]() (i.e. any element of
(i.e. any element of ![]() apart from
apart from![]() ). Let
). Let ![]() be the extension of
be the extension of ![]() which adds
which adds ![]() to the initial and final state spaces and preserves the values of these variables. Then
to the initial and final state spaces and preserves the values of these variables. Then ![]() is the interpretation of
is the interpretation of ![]() as a state transformation from
as a state transformation from ![]() to
to ![]() and for every varia- ble
and for every varia- ble![]() , the initial and final values of
, the initial and final values of ![]() on
on ![]() are identical. Let
are identical. Let ![]() be the state
be the state ![]() extended to state space
extended to state space ![]() which gives the variables in
which gives the variables in ![]() the same values that the corresponding unprimed variables have in
the same values that the corresponding unprimed variables have in![]() . So, for every
. So, for every![]() ,
, ![]() , and
, and ![]() for
for![]() . Let
. Let ![]() be the correspond- ing extension to
be the correspond- ing extension to![]() . Then, by the definition of
. Then, by the definition of![]() ,
,![]() .
.
Claim: ![]() is in the interpretation of
is in the interpretation of![]() . To prove the claim, assume for contradiction that
. To prove the claim, assume for contradiction that ![]() is in
is in![]() . Then
. Then ![]() is guaranteed to terminate in a state which satisfies
is guaranteed to terminate in a state which satisfies![]() , in other words, every state in
, in other words, every state in ![]() satisfies
satisfies![]() . But state
. But state ![]() is in
is in ![]() and within
and within![]() , for each
, for each![]() ,
,![]() . So
. So ![]() does not satisfy
does not satisfy![]() , which is a contradiction.
, which is a contradiction.
Conversely, any state which satisfies ![]() is of the form
is of the form ![]() for some
for some ![]() and
and![]() , since
, since ![]() cannot change the value of any variable in
cannot change the value of any variable in![]() . So, let
. So, let ![]() be any initial state which satisfies
be any initial state which satisfies![]() , where
, where ![]() is the restriction of
is the restriction of ![]() to
to ![]() and
and ![]() is the restriction of
is the restriction of ![]() to
to ![]() and where
and where ![]() is the state on
is the state on ![]() which corresponds to
which corresponds to![]() . We claim that
. We claim that![]() . Assume for contradiction that
. Assume for contradiction that![]() , then
, then ![]() is guaranteed to terminate on
is guaranteed to terminate on ![]() (since otherwise
(since otherwise ![]() contains every state) and
contains every state) and ![]() is not a possible final state for
is not a possible final state for![]() . So every final state in
. So every final state in ![]() differs from
differs from![]() . As before, let
. As before, let ![]() be the extension of
be the extension of ![]() over
over ![]() such that
such that ![]() for all
for all![]() . Then
. Then ![]() for all
for all![]() , and by definition of
, and by definition of![]() , every final state in
, every final state in ![]() differs from
differs from![]() . So,
. So, ![]() terminates on
terminates on ![]() and every final state in
and every final state in ![]() satisfies
satisfies![]() . So
. So ![]() which is a contradiction.
which is a contradiction.
As an example, for the program ![]() If the final state space is
If the final state space is![]() , then:
, then: ![]() .
.
In [1] we also prove the Representation Theorem:
Theorem 3.2. For any statement![]() , let
, let![]() . Then:
. Then:
![]()
The representation theorem seems to imply that a third formula, namely![]() , is needed to fully characterise the behaviour of a program. However, this formula can be derived from the behaviour formula:
, is needed to fully characterise the behaviour of a program. However, this formula can be derived from the behaviour formula:
Theorem 3.3. For any statement![]() ,
,![]() .
.
We define two formulae: ![]() which captures the termination properties of
which captures the termination properties of ![]() (the abort states) and
(the abort states) and ![]() which captures the behaviour of
which captures the behaviour of![]() :
:
![]()
![]() is true on precisely those initial states for which
is true on precisely those initial states for which ![]() can abort (not terminate), while
can abort (not terminate), while ![]() is true on initial states for which the values of
is true on initial states for which the values of ![]() are the values of
are the values of ![]() in one of the possible final states. Note that an initial state for which
in one of the possible final states. Note that an initial state for which ![]() could abort will include all possible values in the set of final states, so we would ex- pect that
could abort will include all possible values in the set of final states, so we would ex- pect that ![]() for all statements
for all statements![]() .
.
If ![]() is guaranteed to terminate and satisfy
is guaranteed to terminate and satisfy ![]() and if
and if![]() , then
, then ![]() is also guaranteed to terminate and satisfy
is also guaranteed to terminate and satisfy![]() . So the weakest precondition is monotonic in the postcondition, and, since
. So the weakest precondition is monotonic in the postcondition, and, since![]() , we have
, we have![]() , and therefore:
, and therefore:
![]()
With these definitions we can prove that ![]() and
and ![]() fully characterise the refinement property:
fully characterise the refinement property:
Theorem 3.4. For any statements ![]() and
and![]() , with the same initial and final state spaces,
, with the same initial and final state spaces, ![]() is a refine- ment of
is a refine- ment of![]() , written
, written![]() , if and only if:
, if and only if:
![]()
Note that the implications are in the opposite direction to the weakest precondition implications since ![]() and
and ![]() are both the negation of a weakest precondition.
are both the negation of a weakest precondition.
With these definitions we can rewrite Theorem 3.2 as:
![]()
or, equivalently:
![]()
The three statements may be interpreted informally as stating:
1. If there is no defined behaviour (terminating or otherwise) then the statement is null;
2. Otherwise, if ![]() is true, then the statement aborts;
is true, then the statement aborts;
3. Otherwise, new values ![]() are assigned to the variables
are assigned to the variables ![]() such that
such that ![]() is satisfied.
is satisfied.
For null-free programs, ![]() , this is Dijkstra’s “Law of the Excluded Miracle” [2] , and so for these programs the initial guard is always equivalent to
, this is Dijkstra’s “Law of the Excluded Miracle” [2] , and so for these programs the initial guard is always equivalent to![]() , and
, and ![]() is true.
is true.
Theorem 3.5. Let ![]() and
and ![]() be any two formula, such that (1)
be any two formula, such that (1) ![]() and (2) No variable in
and (2) No variable in ![]() ap- pears free in
ap- pears free in![]() . Let
. Let
![]()
Then ![]() and
and![]() .
.
We have proved that:
1) Given any statement![]() , we can define the corresponding
, we can define the corresponding ![]() and
and ![]() by using weakest precondi- tions;
by using weakest precondi- tions;
2) Given any two formulae, ![]() and
and![]() , where
, where ![]() and no variable in
and no variable in ![]() appears in
appears in![]() , we can de- fine a statement
, we can de- fine a statement ![]() such that
such that ![]() and
and![]() .
.
These results prove that the two formulae ![]() and
and ![]() completely capture the semantic behaviour of statement
completely capture the semantic behaviour of statement![]() .
.
Given any two formulae ![]() and
and ![]() we can define
we can define ![]() as the formula
as the formula![]() . Then
. Then ![]() is true and none of the variables in
is true and none of the variables in ![]() are free in
are free in![]() . So
. So ![]() and
and ![]() satisfy the requirements for Theorem 3.5. Note that if
satisfy the requirements for Theorem 3.5. Note that if ![]() and
and ![]() already satisfy the requirements, then
already satisfy the requirements, then![]() .
.
These comments motivate the definition of a function ![]() which maps any two formulae
which maps any two formulae ![]() and
and ![]() to a WSL statement:
to a WSL statement:
![]()
By Theorem 3.5, ![]() and
and![]() .
.
In the case where ![]() and none of the variables in
and none of the variables in ![]() appears free in
appears free in![]() , we have:
, we have: ![]() and
and![]() .
.
Four fundamental programs are![]() ,
, ![]() ,
, ![]() and
and ![]() for which the corresponding formulae are given in Table 1. From this table we see that:
for which the corresponding formulae are given in Table 1. From this table we see that:
![]()
when ![]() is non-empty, then all three refinements are strict refinements. Note that
is non-empty, then all three refinements are strict refinements. Note that ![]() and
and ![]() have the same behaviour but different termination conditions, while
have the same behaviour but different termination conditions, while ![]() and
and ![]() have the same termination conditions but different behaviour. (When
have the same termination conditions but different behaviour. (When ![]() is empty
is empty ![]() is equivalent to
is equivalent to ![]() and the formula
and the formula ![]() is equivalent to
is equivalent to![]() .)
.)
Examples
Some example programs to illustrate the formulae:
![]()
![]()
![]()
![]()
Here, ![]() is both more defined (terminating on more initial states) and more deterministic than
is both more defined (terminating on more initial states) and more deterministic than![]() , and so
, and so ![]() is a refinement of
is a refinement of![]() . A refinement of a program can define any behaviour for initial states on which the original program aborts, so
. A refinement of a program can define any behaviour for initial states on which the original program aborts, so ![]() is also a refinement of
is also a refinement of![]() . Finally,
. Finally, ![]() is more deterministic than
is more deterministic than ![]() in that it restricts the set of possible final states (for initial states with
in that it restricts the set of possible final states (for initial states with ![]() the set of final states is empty).
the set of final states is empty).
These facts are reflected in the formulae in Table 2.
Clearly, ![]() and
and ![]() which shows that
which shows that![]() . Also
. Also ![]() and
and ![]() which shows that
which shows that![]() . However, it is not the case that
. However, it is not the case that ![]() since when
since when ![]() in- itially,
in- itially, ![]() must assign
must assign ![]() the value 1, while
the value 1, while ![]() can non-deterministically choose to assign
can non-deterministically choose to assign ![]() the value 1 or 3. Conversely,
the value 1 or 3. Conversely, ![]() is not refined by
is not refined by ![]() because
because ![]() is defined on initial states for which
is defined on initial states for which ![]() is not defined: namely, those initial states in which
is not defined: namely, those initial states in which![]() .
.
Finally, ![]() is a (strict) refinement of all the other programs, and none of the other programs is a refinement of
is a (strict) refinement of all the other programs, and none of the other programs is a refinement of ![]() because
because ![]() is null on initial states with
is null on initial states with![]() .
.
Given that ![]() and
and ![]() capture the semantics of a program, it should be possible to compute the formulae for a compound statement from the formulae for the components. For the primitive statements in the first level of WSL, the formulae are given in Table 3.
capture the semantics of a program, it should be possible to compute the formulae for a compound statement from the formulae for the components. For the primitive statements in the first level of WSL, the formulae are given in Table 3.
![]()
Table 1. ![]() and
and ![]() for some fundamental programs.
for some fundamental programs.
![]()
Table 2. ![]() and
and ![]() for the example programs.
for the example programs.
![]()
Table 3. ![]() and
and ![]() for the atomic statements.
for the atomic statements.
4. Computing A and B for Compound Statements
Given the two formulae ![]() and
and![]() , which are in effect, the weakest preconditions on
, which are in effect, the weakest preconditions on ![]() for two par- ticular postconditions, we can determine the weakest precondition for any given postcondition. This means that we can compute
for two par- ticular postconditions, we can determine the weakest precondition for any given postcondition. This means that we can compute ![]() and
and ![]() for any compound statement, given the corresponding formulae for the compo- nent statements.
for any compound statement, given the corresponding formulae for the compo- nent statements.
For nondeterministic choice:
![]()
and similarly:
![]()
For deterministic choice:
![]()
and similarly:
![]()
For sequential composition:
![]()
In other words, for ![]() to abort on an initial state,
to abort on an initial state, ![]() must not be null and either
must not be null and either ![]() aborts or
aborts or ![]() ter- minates in a state in which
ter- minates in a state in which ![]() aborts.
aborts.
To compute ![]() we need to compute
we need to compute![]() , but this contains a postcondition which includes variables in
, but this contains a postcondition which includes variables in![]() . We can solve this problem by computing the formula
. We can solve this problem by computing the formula ![]() and then renaming
and then renaming ![]() to
to ![]() in the result. Note that the postcondition
in the result. Note that the postcondition ![]() is simply
is simply![]() .
.
![]()
In other words, for ![]() to be a possible final state for
to be a possible final state for ![]() on initial state
on initial state![]() , either
, either ![]() aborts or there exists some intermediate state
aborts or there exists some intermediate state ![]() which is a possible final state for
which is a possible final state for ![]() and for which
and for which ![]() gives
gives ![]() as a possible final state when started in this initial state.
as a possible final state when started in this initial state.
Recursion ![]() is defined in terms of the set of all finite truncations. Define:
is defined in terms of the set of all finite truncations. Define:
![]()
![]()
Then for any postcondition![]() :
:
![]()
So:
![]()
5. Temporal Logic
Temporal logic [3] is a class of logical theories for reasoning about propositions qualified in terms of time and can therefore be used to reason about finite and infinite sequences of states. These sequences can define an op- erational semantics for programs which maps each initial state to the set of possible histories: where a history is a possible sequence of states in the execution of a program. Since a formula can describe an infinite sequence of states: and therefore a non-terminating program, there would appear to be no need for the special state ![]() to indicate non-termination, and therefore it would appear possible to represent the operational semantics of a pro- gram using a single formula in temporal logic.
to indicate non-termination, and therefore it would appear possible to represent the operational semantics of a pro- gram using a single formula in temporal logic.
This turns out not to be the case: a single formula is not sufficient, but two formulae (the temporal equivalent of the abort and behaviour predicates defined here) are sufficient. Lack of space precludes a full discussion of these questions in this paper.
References
- Ward, M. (2004) Pigs from Sausages? Reengineering from Assembler to C via Fermat Transformations. Science of Computer Programming, Special Issue on Program Transformation, 52, 213-255. http://www.gkc.org.uk/martin/papers/migration-t.pdf
- Dijkstra, E.W. (1976) A Discipline of Programming. Prentice-Hall, Englewood Cliffs.
- Moszkowski, B. (1994) Some Very Compositional Temporal Properties. In: Olderog, E.-R., Ed., Programming Con- cepts, Methods and Calculi, IFIP Transactions, North-Holland Publishing Co., Amsterdam, 307-326.
NOTES
![]()
*Corresponding author.



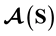 , defining non-termination, and
, defining non-termination, and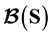 , defining behaviour. Any two formulae
, defining behaviour. Any two formulae 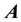 and
and 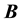 will de- fine a corresponding program. Refinement is defined as implication between these formulae.
will de- fine a corresponding program. Refinement is defined as implication between these formulae.
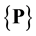 is an assertion which terminates immediately if
is an assertion which terminates immediately if 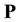 is true and aborts if
is true and aborts if 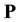 is false,
is false,  is a guard which ensures that
is a guard which ensures that 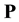 is true without changing the value of any variable,
is true without changing the value of any variable, 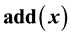 adds the variables in
adds the variables in 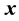 to the state space, if they are not already present, and assigns arbitrary values to the variables.
to the state space, if they are not already present, and assigns arbitrary values to the variables. 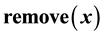 removes the variables in
removes the variables in 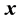 from the state space,
from the state space, 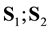 is sequential composition,
is sequential composition, 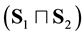 is nondeterministic choice, and
is nondeterministic choice, and 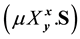 is a recursive subroutine which also adds the variables in
is a recursive subroutine which also adds the variables in 


















































































































































































































































































































































































