Journal of Software Engineering and Applications
Vol.7 No.3(2014), Article ID:44257,8 pages DOI:10.4236/jsea.2014.73016
An Autonomous Exploration Strategy for Cooperative Mobile Robots
Mohammad Al Khawaldah1, Mohammad Al-Khedher1, Ibrahim Al-Adwan1, Ayman Al Rawashdeh2
1Mechatronics Engineering Department, Al-Balqa Applied University, Amman, Jordan
2Electrical Engineering Department, Al-Balqa Applied University, Amman, Jordan
Email: moh.alkhedher@fet.edu.jo
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 2 February 2014; revised 28 February 2014; accepted 7 March 2014
ABSTRACT
Frontier-based exploration methods are efficient for multi-robot exploration systems. In this paper, enhanced frontier-based techniques are used with team of cooperating mobile robots to explore unknown environment. The aim of the exploration algorithm is to minimize the exploration time by coordinating the robots to maximize overall utility by minimizing the potential of overlapping in information gained amongst the robots. The proposed frontier-based exploration algorithm is based on a new bidding function to decrease the overlap between the robots in addition to the utility and cost parameters. A special parameter depends on the future positions of the robots is also considered. The proposed algorithm has been tested with different environments. We also compared it to A* algorithm. Comparisons demonstrated the efficiency of proposed algorithm.
Keywords:Autonomous; Intelligent; Frontier; Multi-Robot Exploration; Mapping; A-Star

1. Introduction
Most mobile robots become unable to navigate efficiently when placed in unknown environments. Therefore, several algorithms have been proposed to solve the problem of exploration and mapping of an unknown environment. Among those methods are geometric maps (grid-based maps) [1] -[3] . A grid-based map is a set of small squares (pixels); these squares are called map cells and each cell has a value reflects the probability that the corresponding area in the environment is occupied. The occupancy grid maps are constructed from stochastic estimates of the occupancy state of an object in a certain cell. For example, zero value means that we are 100% sure that the cell is free and one value means that we are 100% sure that the corresponding area is occupied. It is possible to construct and maintain these maps with relatively low computing power in small workspace. However, in large-size environments the required computational capabilities become larger to handle these maps.
This paper introduces the exploring of an unknown environment with a team of mobile robots. Robot teams can explore an unknown environment faster than a single robot; however this needs specific strategies to control these robots to create maps for the environment. This is an essential challenge in mobile robotics. For instance, the robots need to know what areas are worthwhile to explore and how to distribute themselves effectively in order to thoroughly map previously unknown areas [4] .
Most previous work in mapping dealt with single robots. There are, however, advantages in mapping with multiple robots [5] . The most obvious is that multiple robots can often do the task in less time. The key issue in coordinated multi-robot exploration is how to assign target locations to the individual robots such that the overall mission time is minimized. Generally, robots need the environment map to navigate effectively. Therefore, in many mobile robots applications, robots need to explore their environment themselves and arrange their sensory data to get an understandable representation for the environment. The applications may include, search and rescue, hazardous material handling, and devastated area exploration after a disaster.
The use of multi-robot systems has other rewards over single robot systems. Firstly, it increases the redundancy which makes teams of robots more fault-tolerant than only one robot. Moreover, Merging of overlapping information can help compensate for sensor uncertainty. For example, team of robots can localize themselves more precisely than one robot.
2. Related Works
Most of the published works in the field are based on the frontier-based technique in which robots are directed to the edges between explored and unexplored areas. In this technique, each robot is encouraged to select a free cell which has unexplored adjacent cells to be its target cell. When is gets there, it explores the adjacent unexplored cells and the process repeats.
The frontier-based exploration was initially developed by Yamauchi et al. [6] . He presented a technique to learn maps with a team of mobile robots. He introduced the concept of frontiers between known and unknown areas in a grid map. Frontier-based exploration can be used to map indoor environments where walls and obstacles may be in arbitrary orientations. In his approach, robot shared perceptual information, however, it maintain separate global maps, and make independent decisions about where to explore. This approach groups adjacent cells into frontier regions. Each robot heads for the centered of the closest frontier region, but there is no explicit coordination. As a result, the robots may end up covering the same area and may even physically interfere with one another.
Another technique was presented by Simmons et al. [4] . They presented a powerful technique for coordinating multiple, heterogeneous robots in their task of exploring and mapping large, indoor environments. They consider two coordination problems, creating a single global map from the sensor information of the individual robots, and deciding where each robot should go in order to create the map most effectively.
More developed was presented by Burgard et al. [5] . They proposed a technique in which the goal was to minimize the overall exploration time. He applied target points for the individual robots so that they simultaneously explore different regions of the environment. He presented an approach for the coordination of multiple robots, which simultaneously takes into account the cost of reaching a target point and its utility. Whenever a target point is assigned to a specific robot, the utility of the unexplored area visible from this target position is reduced. This means different target locations are assigned to the individual robots.
Alex et al. [7] [8] increased research interest in systems composed of multiple autonomous mobile robots exhibiting cooperative behavior. He Analyze different topography coverage methods for robots with limited sensing and computational capabilities.
Sheng et al. [9] provided a simple, totally distributed bidding algorithm for the coordination that not only considers the limited communication range, but also introduces a nearness measure in the exploration algorithm so that the robots tend to stay together. A 2D occupancy grid of a specified resolution is used to model the environment to be explored. Robots seek to explore the area individually with the maximum information gain with minimum cost, which is the distance from the current position to the target position.
R. Roucha et al. in [10] dealt with 3D mapping with multiple robots. They proposed a grid-based model of a 3D map, which stores for each cubic cell coverage information. The technique employs frontier-based exploration. At the beginning of the exploration process an initial map is given to the robot. After that it gets a new set of measurements, updates the map, and shares useful information with other robots. Then it might receive information from other robots and the map is updated according to this information. After getting the new map, a new viewpoint for the sensor is chosen and the robot starts moving accordingly. The robot continues updating the map whenever new data is received from other robots during their navigation. Once the robot reaches the new target position, the process is repeated.
In all of the above mentioned works, there is no serious solution for the problem of overlap amongst the robots. Moreover, the presented exploration algorithms have not been tested with different environments or with different number or configuration of obstacles. In this paper a new exploration algorithm is proposed, in which the robots work in teams and coordinate their actions. Our idea depends on selecting a frontier target cell to increase the efficiency of the exploration. The proposed technique is an extension of the algorithms described in [8] [9] [11] . The new technique tries to decrease the overlap between the robots as much as possible. The new exploration algorithm was tested with different environment sizes, different obstacle distributions and different obstacles numbers. Eventually, we compared the results of our exploration algorithm with the results of one of the known exploration algorithms in the literature. Promising results were obtained.
3. Exploration Method
All of our experiments were conducted using the simulation software—Netlogo [9] which is well known in the literature and employed in many published research works [10] [11] . Netlog enables the computer-based investtigation of the exploration process by a number of agents in an occupancy-grid-based environment. In Netlog, the environment is simulated as an m-by-n grid of square cells. Each cell has information about itself stored in variables. With Netlog, the same experiment can be repeated and results are stored in an Excel file for further analysis.
The main goal in this paper is to build a map for the unknown environment. The map is an m-by-n grid of square cells, each cell of which is allocated a number to represent its occupancy status. Zero represents that the cell is free and One to represent that the cell is occupied.
Each robot is equipped with eight infra red sensors which are mounted with physical angle of 45˚ around the robot body, with these sensors the robot can detect the occupancy of its eight neighbors. Also, it can distinguish weather a neighboring cell is occupied by another partner. Each robot knows its own position and the position of its partner and they move between the centers of cells. An equal amount of time (a single step in Netlogo) is required to perform a 360˚ scan and to move to a neighboring cell. Furthermore, robots send their new sensory data to a shared map which is updated in every step of the simulation. The communication between the robots is on, and error free. Finally, the environment edges are treated as occupied cells. During the exploration, each cell of the map is assigned one of the states as shown in Table 1, which shows the colour code used to identify each state.
At the beginning of each exploration, all of the cells in the environment map are colored with gray in which three robots (button) will explore the environment. When a robot visits a cell, all of its free neighboring cells are colored with white by scanning as shown in Figure 1. The exploration process is completed when all the cells are explored (free or occupied) as shown in Figure 2.
4. Cooperating Robots Exploration
A large number of published works in multi-robot exploration depends on the use of “frontier cells” e.g. [1] -[6] . Frontier cells are the borders between explored and unexplored areas. When a robot is directed to such a cell, it is expected that it will get information about the unexplored area when it arrives. Because a map may contain several unexplored areas, the challenge arises of how to plan the exploration mission by choosing the most
Table 1. Cells color codes.
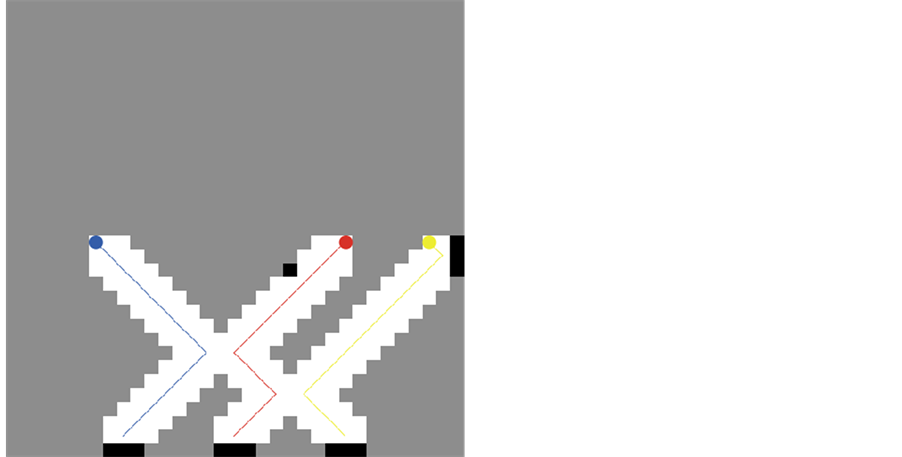
Figure 1. The map with three robots during the exploration process.
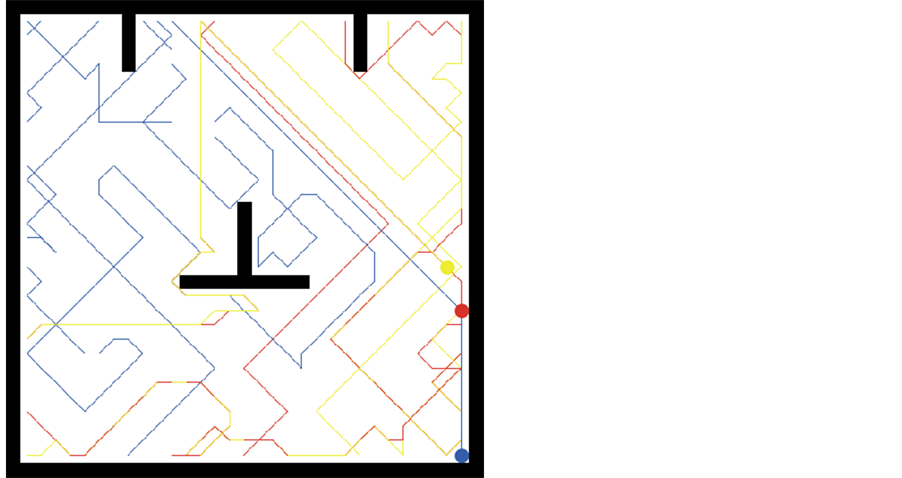
Figure 2. A completed map with three robots ant trajectories.
appropriate frontier cells. In [1] -[6] the utility of the target frontier cell is computed. The utility of a target cell is the number of unexplored cells which can be scanned from that target cell. Then the cost of reaching that target cell is computed. The cost is a function of the target cell distance. Finally, the target cell with the maximum [Utility – Cost] value wins and the robot starts moving towards its target. This is the general algorithm that guides the exploration in the above mentioned published works.
Apart from the above mentioned two factors—cost and utility, the distance of the other robot from the cell is also considered when computing the bidding value for a frontier cell. This third factor introduces potential benefit of keeping the two robots apart.
The distances in this paper (i.e. between two robots, between a robot and a frontier, or between a robot and a target cell for another robot) are calculated according to the flood fill algorithm [12] . It allows us to find the shortest path to a desired point on the map.
Each robot computes the bidding value Bi for each frontier cell in its shared map based on the bidding function represented in Equation (1). The relative importance of each term in the formula is adjusted by a weight value.
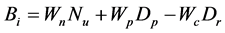 (1)
(1)
where Bi: The bidding value for the frontier cell i (the target cell);
Dr: The distance from the robot to the target cell;
Dp: The distance from the closest robot (the partner) to the target cell;
Nu: The number of unknown neighbors for the target cell;
Wn (weight neighbors), Wp (weight partner) and Wc (weight cost) are the weight factors for Nu, Dp and Dr, and respectively.
Each robot scans the eight neighbouring cells around it and adds the new information (the scan information) to the shared map which is available to both robots. Then each robot computes the bidding function according to Equation (1) for all of its frontier cells in the shared map. Each robot has its own bidding function values for the frontier cells in the shared map, computed from its own point of view. A cell can be a frontier cell to more than a robot. The same cell may yield different bidding value to different robots. Finally, each robot chooses among its frontier cells the one with the maximum bidding function value max{Bi} and starts moving towards it.
The robots explore at the same time, and make their decisions on where to go at the next step based on the same map. Equation (1) shows that we are trying to guide each robot to a cell with a large number of unexplored neighboring cells, far away from its partner, and close to its current position.
5. Experimentation and Results
The experimentation procedure is as follows:
1) We started with one robot exploration; the time spent to finish the exploration is recorded. The experiment is repeated five times and the average is taken. This process is repeated for two, three, four… eight robots. As before, each experiment is repeated five times and the average of exploration time is recorded.
2) Same procedure in 1 was repeated with the same environment but with an obstacle introduced inside the environment as shown in Figure 3.
To enhance our algorithm we adjusted the bidding function represented by Equation (1). The adjustment tries aims at further reduction of overlap among robots. Instead of considering the distance of the closest robot in the bidding function, we considered the distance of the closest target cell that has been assigned by any other robot. The new bidding function tries to spread the robots in their environment. It is represented by Equation (2).
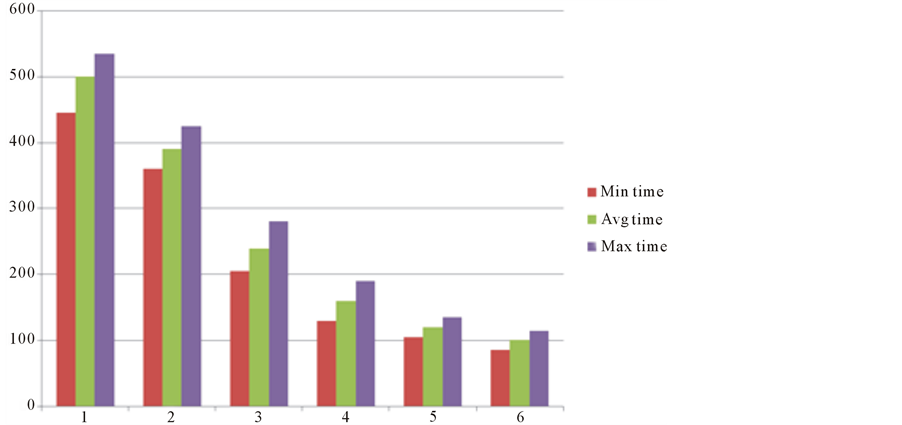
Figure 4 shows how the exploration time varies with the number of exploring robots. It is clear that as the number of robot increases the time required to finish the exploration decreases. This is due to the fact that robots explore simultaneously, and work in parallel.
 (2)
(2)
where Bi: The bidding value for the frontier cell i (the target cell);
Dr: The distance from the robot to the target cell;
Dt: The distance from the closest target (the to the target cell;
Nu: The number of unknown neighbors for the target cell;
Wn (weight neighbors), Wt (weight target) and Wc (weight cost) are the weight factors for Nu, Dp and Dr, and respectively.
The main difference between Equations (1) and (2) is that we have the term WpDp (weight and distance of the closest robot) while in Equation (2) we have WtDt (weight and distance of the target of the closest robot).
The procedure in 1 was repeated with the new bidding function in Equation (2) and with the environment shown in Figure 3. The results are shown in Figure 5.
Figure 5 shows how the exploration time varies with the number of exploring robots. As before, as the number of robot increases the time required to finish the exploration decreases. This is due to the fact that robots explore simultaneously, and work in parallel. More importantly, it is clear that considering the target cell reduced
 (a)
(a) (b)
(b)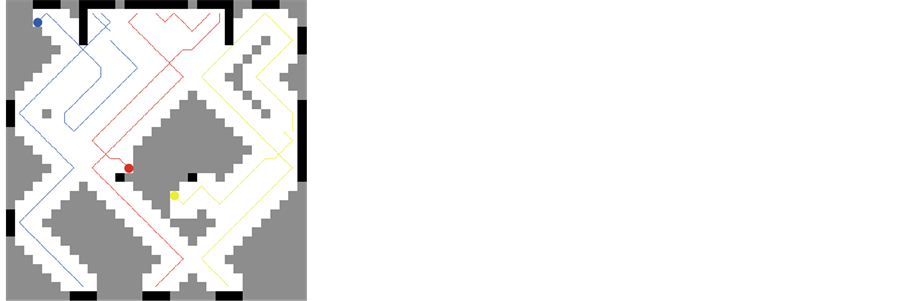 (c)
(c) (d)
(d)
Figure 3. Sequential steps of environment exploration.
the exploration time.
6. A* Exploration Algorithm
We have implemented the A* algorithm to explore the entire environment with a single robot (Figure 6). The procedure is describes as:
1) Create a search graph G, consisting solely of the startnodes. Puts on a list called OPEN.
2) Create a list called CLOSED that is initially empty.
3) LOOP: if OPEN is empty, exit with failure.
4) Select the first node on OPEN, remove it from OPEN and put it on CLOSED. Call this node n.
5) If n is a goal node, exit successfully with the solution obtained by tracing a path along the pointers from n to s in G.
6) Expand node n, generating the set, M, of its successors and install them as successors of n in G.
7) Establish a pointer to n from those members of M that were not already in G (i.e., not already on either OPEN or CLOSED). Add these members of M to OPEN. For each member of M that was already on OPEN or CLOSED, decide whether or not to redirect its pointer to n. For each member of M already on CLOSED, decide

Figure 5. Time steps vs number of robots for obstacle-free environment.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f)
Figure 6. Implementation of A* algorithm to explore the environment.
for each of its descendents in G whether or not to redirect its pointer.
8) Reorder the list OPEN, either according to some scheme or some heuristic merit.
9) Goto LOOP [13] .
The exploration results show more complicated step movement and higher computation time than our proposed algorithm.
7. Conclusion
A frontier-based new exploration algorithm is discussed to improve the exploration efficiency of unknown environments with team of cooperating mobile robots. It is shown that the time required to explore the environment has been significantly reduced. We noticed that the distance of the closest target cell of the closest robot in the bidding function leads to a better reduced exploration time. Compared to A* algorithm our proposed procedure needs less computation time and less movement step.
References
- Dave, R.N. (1991) Characterization and Detection of Noise in Clustering. Pattern Recognition Letters, 12, 657-664. http://dx.doi.org/10.1016/0167-8655(91)90002-4
- Matia, F. and Jimenez, A. (1998) Multisensor Fusion: An Autonomous Mobile Robot. Journal of Intelligent and Robotic Systems, 22, 129-141.
- Zelinsky, A. (1991) Mobile Robot Map Making Using Sonar. Journal of Robotic Systems, 8, 557-577. http://dx.doi.org/10.1002/rob.4620080502
- Simmons, R., Apfelbaum, D., Burgard, W., Fox, D., Thrun, S. and Younes, H. (2000) Coordination for Multi-Robot Exploration and Mapping. Proceedings of the 17th National Conference on Artificial Intelligence and 12th Conference on Innovative Applications of Artificial Intelligence, Austin, 30 July-3 August 2000, 852-858.
- Burgard, W., Moors, M., Stachniss, C. and Schneider, F. (2005) Coordinated Multirobot Exploration. IEEE Transactions on Robotics, 21, 376-378. http://dx.doi.org/10.1109/TRO.2004.839232
- Yamauchi, B., et al. (1998) Frontier-Based Exploration Using Multiple Robots. Proceedings of the 2nd International Conference on Autonomous Agents, Minneapolis, 10-13 May 1998, 47-53. http://dx.doi.org/10.1145/280765.280773
- Cao, Y.U., Fukunaga, A.S., Kahng, A. and Meng, F. (1997) Cooperative Mobile Robotics: Antecedents and Directions. Autonomous Robots, Pittsburgh, 5-9 August 1995, 7-27.
- Burgard, W., Fox, D., Moors, M., Simmons, R. and Thrun, S. (2000) Collaborative Multi-Robot Exploration. IEEE International Conference on Robotics and Automation, 1, 476-481.
- Sheng, W., Yang, Q., Tan, J. and Xi, N. (2006) Distributed Multi-Robot Coordination in Area Exploration. Robotics and Autonomous Systems, 54, 945-955. http://dx.doi.org/10.1016/j.robot.2006.06.003
- Rocha, R., Dias, J. and Carvalho, A. (2005) Cooperative Multi-Robot Systems: A Study of Vision-Based 3-D Mapping Using Information Theory. Robotics and Autonomous Systems, 53, 282-311. http://dx.doi.org/10.1016/j.robot.2005.09.008
- Fox, D., Ko, J., Konolige, K., Limketkai, B., Schulz, D. and Stewart, B. (2006) Distributed Multi-Robot Exploration and Mapping. Proceedings of the IEEE, 94, 1325-1339. http://dx.doi.org/10.1109/JPROC.2006.876927
- Wilensky, U., NetLogo (1999) Center for Connected Learning and Computer-Based Modeling, Northwestern University. Evanston, IL. http://ccl.northwestern.edu/netlogo/
- Russell, S.J. and Norvig, P. (2003) Artificial Intelligence: A Modern Approach. Prentice Hall, Upper Saddle River, 97-104.