Journal of Software Engineering and Applications
Vol.7 No.2(2014), Article ID:42750,9 pages DOI:10.4236/jsea.2014.72009
On Exploiting Temporal, Social, and Geographical Relationships for Data Forwarding in Delay Tolerant Networks
School of Information Technology, Deakin University, Melbourne, Australia.
Email: zhijie.li@deakin.edu.au, ming.li@deakin.edu.au, longxiang.gao@deakin.edu.au
Copyright © 2014 Zhijie Li et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Zhijie Li et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 30th, 2013; revised December 28th, 2013; accepted January 6th, 2014
KEYWORDS
Delay Tolerant Networks; Temporal-Social Relationship; Temporal-Geographical Relationship
ABSTRACT
Because of unpredictable node mobility and absence of global information in Delay Tolerant Networks (DTNs), effective data forwarding has become a significant challenge in such network. Currently, most of existing data forwarding mechanisms select nodes with high cumulative contact capability as forwarders. However, for the heterogeneity of the transient node contact patterns, these selection approaches may not be the best relay choices within a short time period. This paper proposes an appropriate data forwarding mechanism, which combines time, location, and social characteristics into one coordinate system, to improve the performance of data forwarding in DTNs. The Temporal-Social Relationship and the Temporal-Geographical Relationship reveal the implied connection information among these three factors. This mechanism is formulated and verified in the experimental studies of realistic DTN traces. The empirical results show that our proposed mechanism can achieve better performance compared to the existing schemes with similar forwarding costs (e.g. end-to-end delay and delivery success ratio).
1. Introduction
At present, mobile device, an effective and convenient communication tool without the bound of time and place, has become an essential part of human life. The proliferation of mobile devices caused increasing challenges for data forwarding in Delay Tolerant Networks (DTNs). Due to the unpredictable mobility, only intermittent connectivity among mobile nodes exists in DTNs [1]. In order to forward data to a destination within a given time constraint and mitigate the impact of mobility of mobile nodes, it is necessary to make an effective data forwarding decision for DTNs, such as optimal path selection. Recently, time-varying networks (e.g. [2,3]) and social networks (e.g. [4,5]), which utilize the influence of time factors and social characteristics in DTNs, have been attracted by some researches. This paper proposes a model to combine time, social characteristics and geographical information into one coordinate system to analyze the relationship among these three factors and to predict the data forwarding decision within the time constraint.
Due to the lack of routing, social and global information at individual nodes, most of current data forwarding mechanisms in DTNs are based on the prediction of node capability of contacting others (e.g. [6-8]). Some of these mechanisms, such as Epidemic [9] and PRoPHET [10], have introduced flooding or partial flooding methods, which may cause network congestion, interference and high resource consumption. Some other routing protocols like CAR [11] and HiBOp [12] utilized context information, including the history records, the battery status, and the connectivity rate, to select the transmission path. Meanwhile, some latest researches indicate that timevarying networks (e.g. [2,13]) and social networks (e.g. [4,5]) have played an increasing role in data transmission and optimal path selection.
However, most of latest studies analyzed the impacts of time and social characteristics respectively. We have observed that the temporal, the social and the geographical factors contribute to and influence the efficiency of data forwarding in DTNs. Figure 1 illustrates a simple relationship between them and efficiency of data forwarding. It can be analyzed from following two perspectives. Temporal-Social Relationship: An individual may have many different social properties, such as vocation, friendship, nationality etc. The influence of these social properties on communication may be highly skewed during different time periods. For instance, a student A may frequently contact his/her classmates or professors in the day-time rather than night-time. While, he/she may frequently contact his/her friends during night-time and weekend, but not in the day-time of weekday. Thus we analyze this influence to represent the skewness of contact distribution and improve the data forwarding performance in DTNs. Temporal-Geographical Relationship: the frequency and possibility of an individual appearing in different locations may also be changed with time. For instance, people may have high possibility of staying in office, company, or visiting business partners during daytime, and staying at home, or frequently visiting some places they are interested in at night-time or weekend. We analyze this phenomenon to represent its relationship with data forwarding in DTNs.
Both Temporal-Social Relationship and Temporal-Geographical Relationship are modeled as Power Law [14], which means that for every individual, the frequently contacted persons and the frequently visited places only occupy around 20% of the all persons and places he/she contacted and visited. Thus when a node gets a huge number of other nodes as forwarder candidates, only the top 20% candidates with high probability could be se-

Figure 1. A brief relationship between data forwarding and three factors.
lected as forwarders.
The contribution of this paper is to use the social contact topology to study the data forwarding problem in DTNs based on the time varying impact. The remaining sections of this paper are organized as follows. In the next section, we will introduce the related works relevant to our project. We then analyze the relationship among time, social properties, and geography in Section 3. Also once the analysis is presented; we build an efficient data forwarding model in DTNs. We then evaluate our approach and report its performance in Section 4 through simulation. Finally Section 5 concludes this paper.
2. Related Works
During last ten years, there are many studies on data forwarding in DTNs (e.g. [15-18]). Based on the different data forwarding mechanisms, there are three major different types of algorithms which are Epidemic [9], Opportunistic [17] and Probabilistic [10]. However, Epidemic introduces the method of flooding which may cause high resource consumption and network congestion. Opportunistic could reduce the loads of networks but also reduce the efficiency of data forwarding. Probabilistic exploits the probabilities to describe the mobility information of each node which is exploited in our proposed mechanism.
With the development of social networks and timevarying networks, these two topics have been attracted an increasing number of researches. Many proposals have been presented in the literature for time-varying networks. In such network, the interactions among the elements of the system are rapidly changing and are characterized by processes whose timing and duration are defined on a very short time scale. In 2011, Casteigts et al. [19] integrated the vast collection of concepts, formalisms and results of highly dynamic wireless and mobile networks into a unified coherent framework TVGs (time-varying graphs), which could introduced vast dynamical aspects, including random walks [20], topology and temporal distance, topological and temporal eccentricity, topology and temporal diameter and so on. It could be used to solve the computability and complexity of the exploration problem in a class of highly dynamic networks, which played as a central role in DTNs [13]. Thus, TVG is an efficient approach to address the data forwarding in DTNs [19].
Moreover, some recent researches have studied the time varying social networks. In 2009, Chan et al. [5] introduced a framework for detecting time-varying communities on human mobile networks. This community detection algorithm requires little user interventions/adjustments once initialized, and can adapt to the changing and evolving networks. In the same year, Tang et al. [21] designed new temporal distance metrics, which are able to capture the temporal characteristics of time-varying graphs (i.e. delay, duration and time order of contacts), to quantify and compare the speed/delay of information diffusion processes taking into account the evolution of a network from a local and global view. In 2013, Gao et al. [1] proposed effective forwarding metrics to improve the performance of data forwarding in DTNs, by exploiting the transient social contact patterns. These patterns represent the transient contact distribution, network connectivity and social community structure in DTNs, which can be uniformly represented as a Gaussian function. By using this method, the accuracy of the prediction of the mobile nodes contact capabilities could be improved; the nodes centralities could be evaluated within the given scope and time constraint; and the data delivery ratio could be improved significantly within the similar forwarding costs of existing schemes.
In order to analyze the impacts of time, social behaviors and geography on data forwarding in DTNs, we concern not only geographic information but also social and time domains factors. Our mechanism combines social, geographic and time information to calculate the overall forwarding selection probability and determine the best routes. The data forwarding in DTNs is based on the community information. The contextual information in our proposed approach consists of location attributes, social aspects, and time pattern.
3. The Relationship Between Time, Social Properties, and Geography
In this section, we analyze the relationships of temporal, social and spatial characters have relationships based on experimental observation from realistic DTN traces. These factors could influence individual human mobility patterns [22].
3.1. Traces
We study the relationships of three factors on two sets of DTN traces, MIT Reality trace [23] and UCSD dataset [24,25]. These traces record contacts among users with mobile devices on university campus. The devices are equipped with Bluetooth or WiFi interfaces, so as to detect and communicate with each other. In the MIT Reality trace [23], the devices periodically detect their peers via their Bluetooth interfaces, and a contact is recorded when two devices move close to each other. Table 1 summarizes the MIT Reality Mining dataset.
In the UCSD trace [24,25] which consists of WiFi enabled devices, the devices search for nearby WiFi Access Points (APs) and associate themselves to the APs with the best signal strength. A contact is recorded when two devices are associated to the same AP. As summarized in Table 2, the two traces differ in their scale, detection period, as well as the contact density and duration.
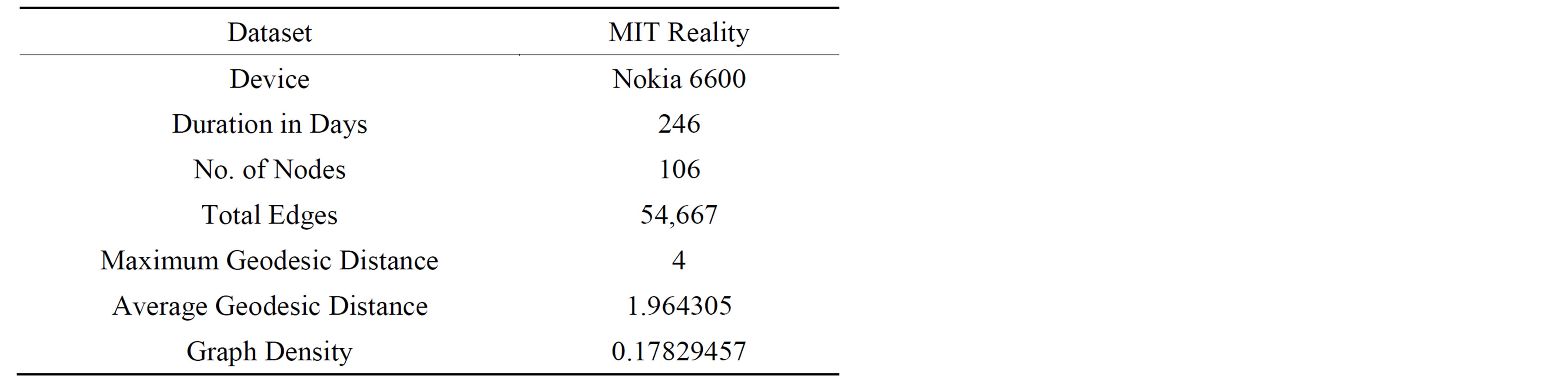
Table 1. Summarization of MIT Reality Mining dataset.

Table 2. Summarization of UCSD dataset.
3.2. Temporal-Social Relationship
It is important to notice that human social behaviors have a significant impact on social topology. Most of contacts in MIT Reality trace file have same social background. For example most people came from the MIT Media Lab with academic background. Gao et al. [1] have proved that time could determine social behaviors. For instance, the contact frequency among classmates during the daytime is much higher than the night-time, which indicates that this social contact topology is more accessible in day time rather than in night time.
In order to present this situation, the contact distribution is formulated as alternative appearances of activeperiod and break-period. Most contacts happen during the active-period, while only very few contacts happen during break-period at random. The contact frequency between each pair of nodes will be varied with time. This pattern formulation is illustrated in Figure 2, which shows the contact frequency of the MIT Reality trace file. It is obvious that the data forwarding frequency of contact varied with time. The majority of contacts among nodes/people were appeared between 14:00 and 18:00 (active-period).
Furthermore, the influence of social behaviours on contact frequency also varied with time. Different communities have different activity patterns correspond to the different time slots. For example, two main communities in MIT Reality trace file, Affiliation Community and Hangout Community, have different activity patterns in the same time period. As show in Figures 3 and 4, during the daytime from 9 am to 9 pm, the Affiliation community is more active than the Hangout community; while during the night time from 9 pm to 3 am, the Hang-

Figure 2. Two months contact frequency sample from MIT Reality Trace File with Gaussian Distribution.

Figure 3. Two months affiliation community contact frequency from MIT Reality Trace File with Gaussian Distribution.

Figure 4. Two months Hangout community contact frequency from MIT Reality Trace File with Gaussian Distribution.
out community is more active than affiliation community.
The distribution of these figures follows the Gaussian Distribution which is shown as Formula 1and their parameters are listed in Table 3.
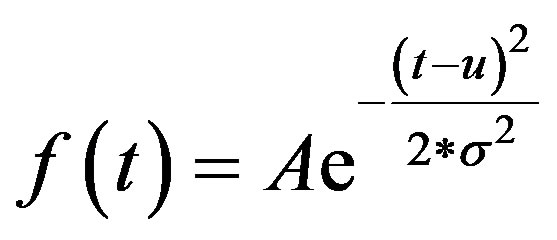 (1)
(1)
3.3. Temporal-Geographical Relationship
Besides the influence of social behaviors, human contacts have a high degree of temporal and spatial regularity, where each individual is characterized by a timeindependent characteristic travel distance and a significant probability to return to a few highly frequented locations. As Figure 5 shows, most of contacts occurred in two cellular towers’range which located close MIT campus.
Moreover, Figure 6 illustrates the number of packets operated in 5 typical Aps located in 5 different floors of UCSD (from basement to 4th floor). It is obvious that the number of operated packets in each AP is changed with time, and their fluctuation trends are similar with time varying. Thus the busy degree of a location is related to time. By using this Temporal-Geographical Relationship, the possibility of a node appeared in different locations in different time could be predicted.
3.4. Data Forwarding Model in DTNs
In MobySpace [26], the distance between two nodes i and j can be calculated and represented through Euclidean distance as below:
 (2)
(2)
Where xik and xjk is the coordinates of node i and j in dimension k. The forwarders selection is based on the nodes which can reduce Euclidean distance to the destination. However, all nodes in DTNs have to be located in advance which is unpractical in many cases. This paper develops an appropriate data forwarding mechanism, by exploiting Temporal-Social relationship and TemporalGeographical relationship, for more accurate prediction of node contact capability with the given time constraint. In this case, the data size is assumed small enough to be carried by any node and be completely transmitted dur-

Table 3. Gaussian Distribution parameters for Figures 2-4.
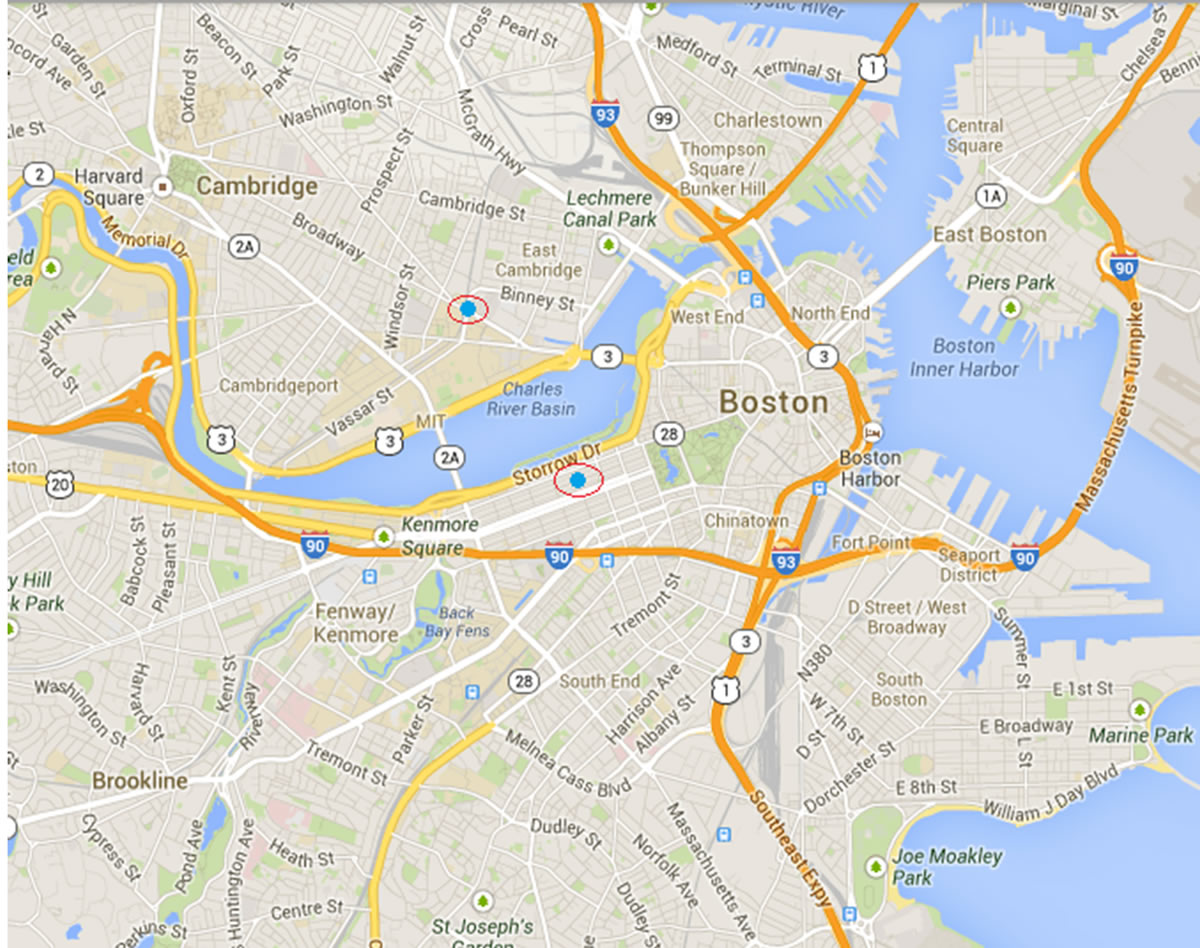
Figure 5. A two months contact topology example on MIT Reality dataset.

Figure 6. Number of packets operated in 5 different Aps on UCSD dataset in one day
ing a contact. The Temporal-Social relationship follows Gaussian Distribution and the Temporal-Geographical relationship follows Power Law. Time patterns, social contact topology, and location are combined together to generate an overall delivery probability as the forwarding selection critical.
The data forwarding decisions based on TemporalSocial relationship are more effective. Such advantage is illustrated in Figure 7, where relay A at time t carries data and needs to decide whether to forward data to node B or C.
The time constraint for data forwarding is shorter than one day. Each node in DTNs contains many different social properties. In this case we only analyze two main social properties, such as vocation and friendship. To simplify, S1i stands for the influence of first social property of node i and S2i stands for the influence of second social property of node i. Also we set a threshold H for these social properties. Only if such value is over H, the social property could influence the data forwarding in DTNs. The Temporal-Social Influence can be illustrated as Formula 3:
 (3)
(3)
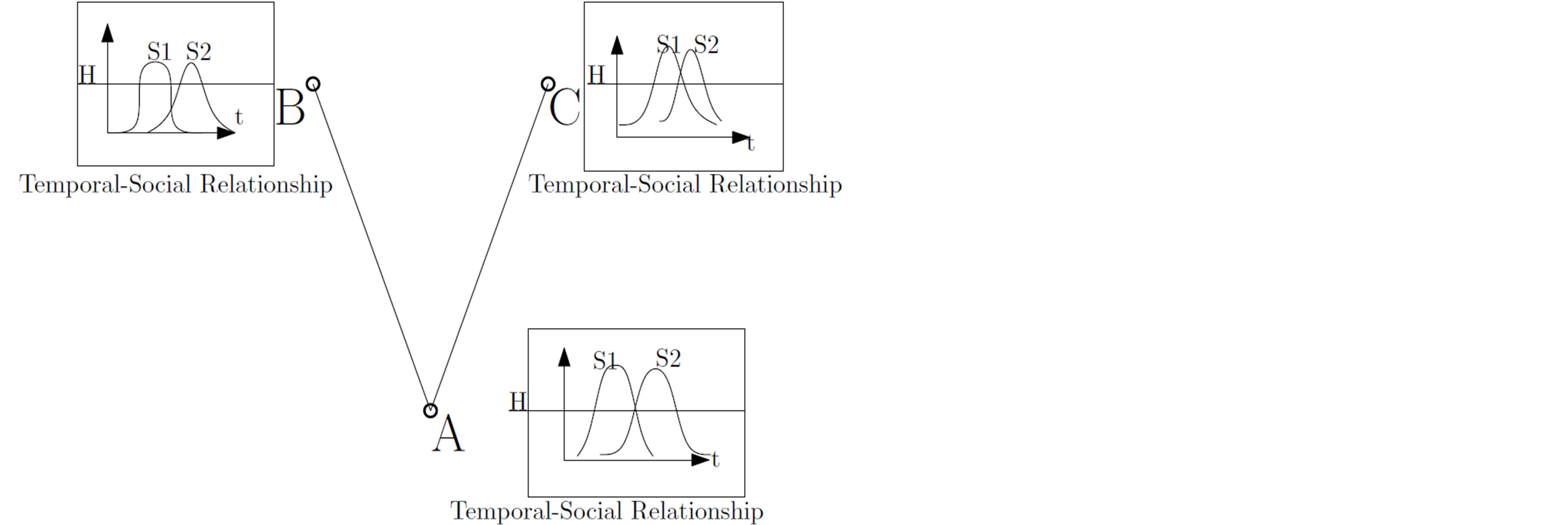
Figure 7. Overview of transient node contact pattern.
In addition, the influence of two social properties S1 and S2 are different in different time slot. Also in some time slot it is difficult to estimate whose influence is more significant on data forwarding decision. Therefore the total Temporal-Social Influence S = S1 + S2.
According to [5], the weight between node i and j related to time-varying is show as an Aging Formula:
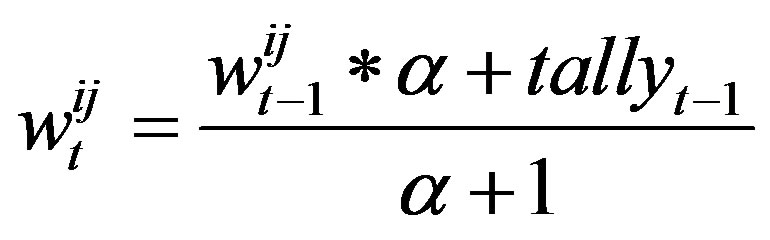 (4)
(4)
Where the contact duration of the current time interval t is tallied as tallyt, and an aging factor is set as α. 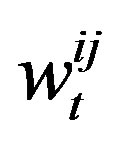 represents the history accumulator between entities i and j, which is also the weight between two nodes. In addition, we set a social related ratio for each two nodes:
represents the history accumulator between entities i and j, which is also the weight between two nodes. In addition, we set a social related ratio for each two nodes:
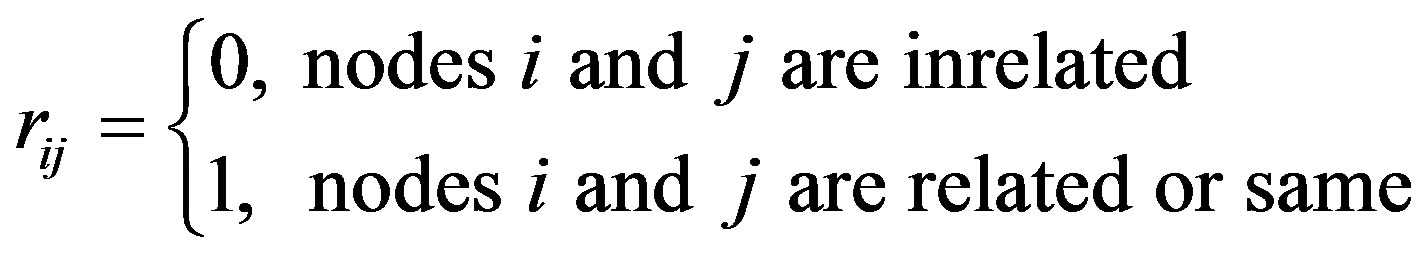 (5)
(5)
The weight between node i and j with time t could be adjusted as:
 (6)
(6)
Assuming there are N nodes in DTNs, the probability for node i communicates with node j in time t based on social property is:
 (7)
(7)
Additionally, the probability of node i visits location l can be represented as Function 8 below:
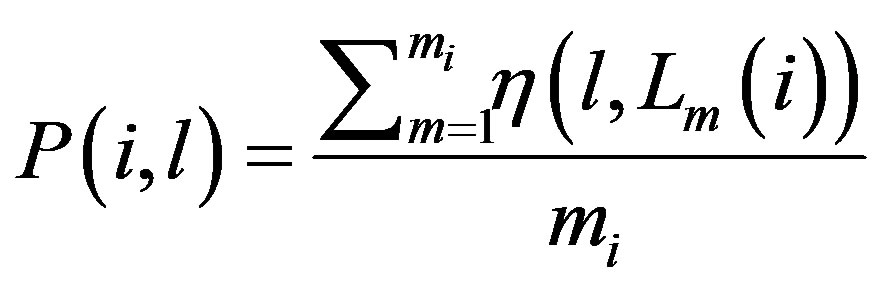 (8)
(8)
Where mi represents the number of APs user i visited and Lm(i) is a vector to store all location information of user i. Function η(x, y) is
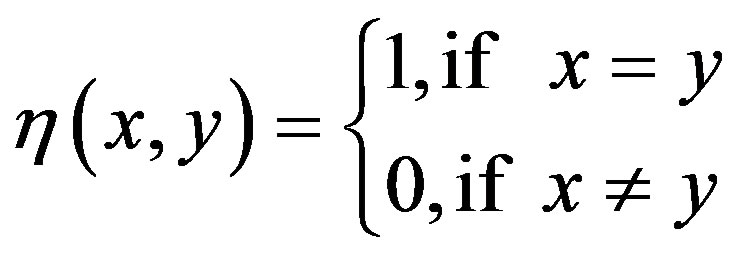 (9)
(9)
We utilize APs (Access Points) to locate the location of each node in different time. The probability for node i appeared in APm is changed with time t. Assuming during time period [tstart, tend], APm detects node i in its range. If a node i stay over a time period ΔT, it can be treated that this node appears in location l. Thus the probability of node I appear at location l in time t⋴[tstart, tend] is:
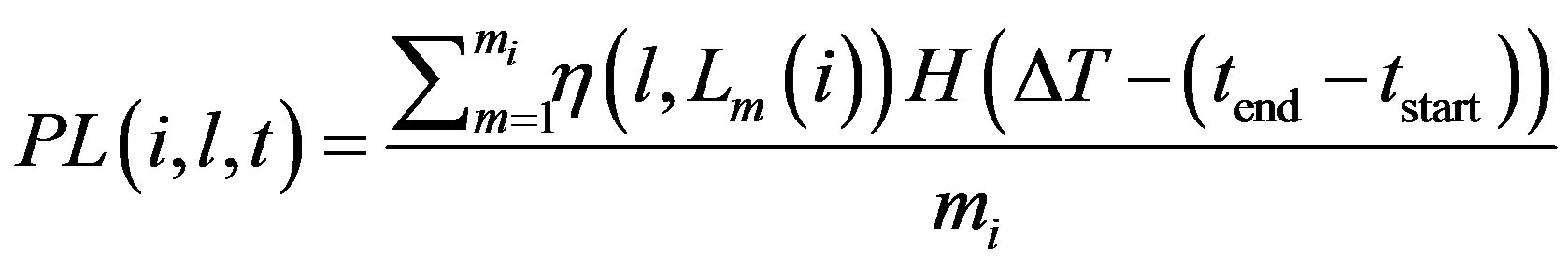 (10)
(10)
Where H(x) is the Heaviside Step Function [27] defined as:
 (11)
(11)
The probability of node i and j to appear at the same location l during the same time period is
 (12)
(12)
Every node in DTNs records a N × M matrix L which can be shown as Table 4. Here N is the total number of nodes in DTNs and M is the total number of APs. We also introduce an array named stamp [N] which represent the latest updated time on node i in matrix L. When nodes a and b meet each other, firstly they swap their matrix L and compare with the stamp [N] of themselves. If the ith row in stamp [N] of b has been outdated, b will update its stamp [i] by using node a’s matrix.
Moreover, when node i move to APm, it impacts the probability distribution of this node appeared in all APs. Matrix L and stamp [N] has to be renewed following the Functions below [10]:
 (13)
(13)
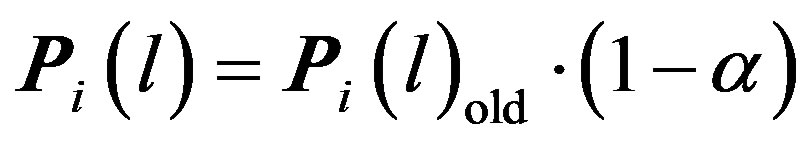 (14)
(14)
Where Ρi is the ith row vector of node i; Ρi(m) is the mth component of Ρi; Ρi(m)old is the value before renew. Function 13 increases the probability of node i appeared in APm, as well as Function 14 reduces its probability

Table 4. Probability for each node appeared in APs in different time.
appeared in other APs. α is the correction factor whose value is between 0 and 1. Thus the probability that node a select forwarder i forwarding the data to destination j in time t could be calculated as Formula (15):
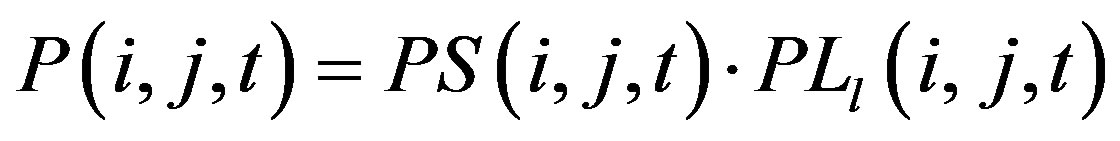 (15)
(15)
4. Experiments
Since there is no description regarding social properties of nodes in UCSD dataset, the performances of our proposed mechanism are evaluated based on MIT Reality Mining Dataset, which recorded 106 subjects in real social network from 2004 to 2005 at MIT Media Laboratory [23]. In order to reach the requirements of DTNs, our simulation mainly analyses and studies the Bluetooth trace file. Each Bluetooth scanning is treated as a contact pattern. However, in this dataset, the information of location and node movements does not be recorded. This issue has been solved by Ficek et al. in 2010 [28]. The relative location information and node movement information can be associated with cell towers’ IDs. In MIT Dataset, only 46.75% of all unique cell locations can be retrieved with the geographical coordinates. In order to remedy this deficiency, the 35 most active nodes are selected to study. Their location information can be shown in Figure 5 which is the map of MIT University. This map is divided into many 10 × 10 grids. The blue points are the most frequently visited location (we use red circle highlighting them).
We compare our mechanism with Bubble Rap, PRoPHET and Simbet from the following two perspectives.
1) Average Success Delivery Ratio: the number of packets arrived at the destination successfully comparing with the number of packets sent from the source.
2) Average End-To-End Delay: the number of hop counts taken to forward a packet from source to destination.
The data in MIT Dataset was collected during 9 month. The store-and-forward process is recorded by days. These two approaches do not conform to reality. Thus we use hop counts measuring Average End-To-End Delay.
Despite MIT Reality Mining dataset has provided the information of several social communities and locations, in order to get a general result, our experiment compares the overall social communities with single community, such as Affiliation and Hangout.
Figures 8 and 9 illustrate the performance of data forwarding in different communities under different time factors. A means the performance is evaluated without time pattern, while B takes time into evaluation. Figure 5 shows that the average success delivery ratio of multisocial communities is higher than the single one. Figure 6 shows the similar results that the end to end delay
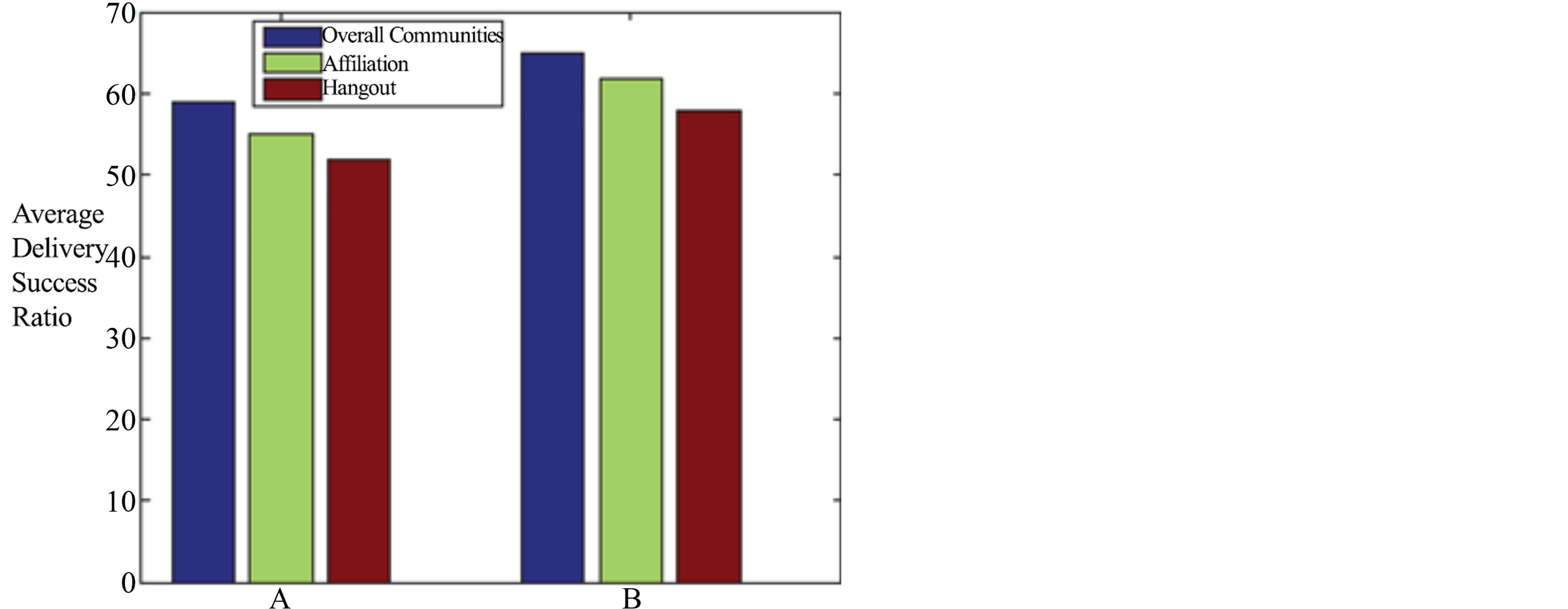
Figure 8. Average delivery success ratio of different communities affected by location information.
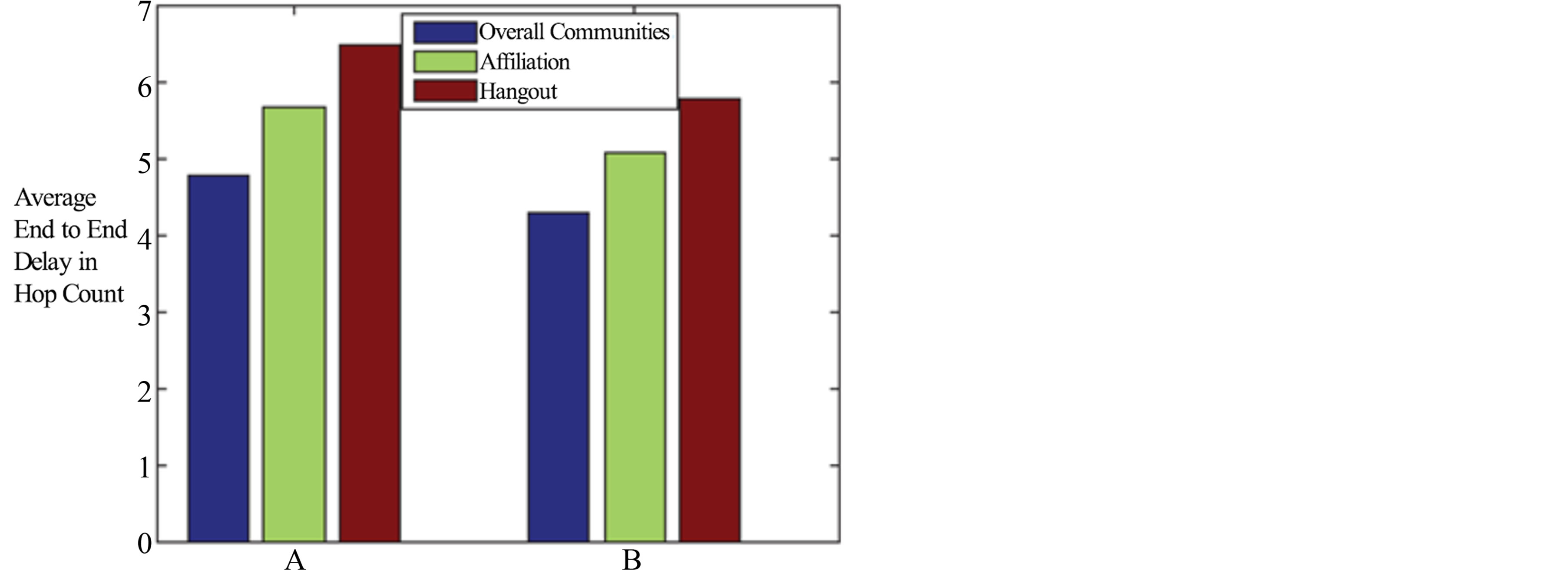
Figure 9. Average end-to-end delay of different communities affected by location information.
is much lower in multi-social communities than single one. Both of these two figures illustrate that the time pattern benefits to the routing in DTNs. Thus multi-social communities and time pattern can improve the performance of data forwarding.
Figures 10 and 11 compare the performance of our mechanism with Bubble Rap, PRoPHET and Simbet. From these two figures, it is obvious that the performance of our mechanism is better than the others. The above results show the importance of the time pattern. If time, geographic and social characteristics can work together, the performance of data forwarding in DTNs will be improved significantly.
5. Conclusion
We propose an appropriate data forwarding mechanism, which organizes time, geographic and social characteristics into one coordinate system, to improve the efficiency of data forwarding in DTNs. Temporal-Social Relationship and Temporal-Geographical Relationship have been
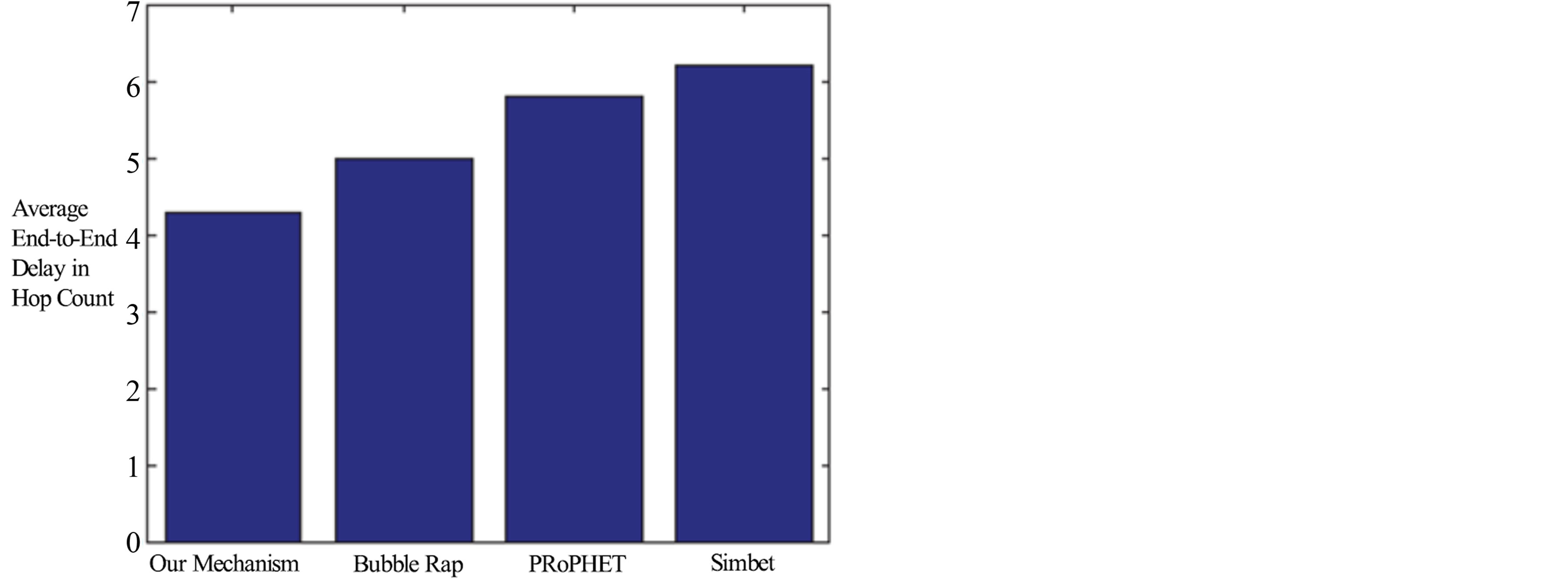
Figure 10. Average Delivery Success Ratio compared with other benchmarks.
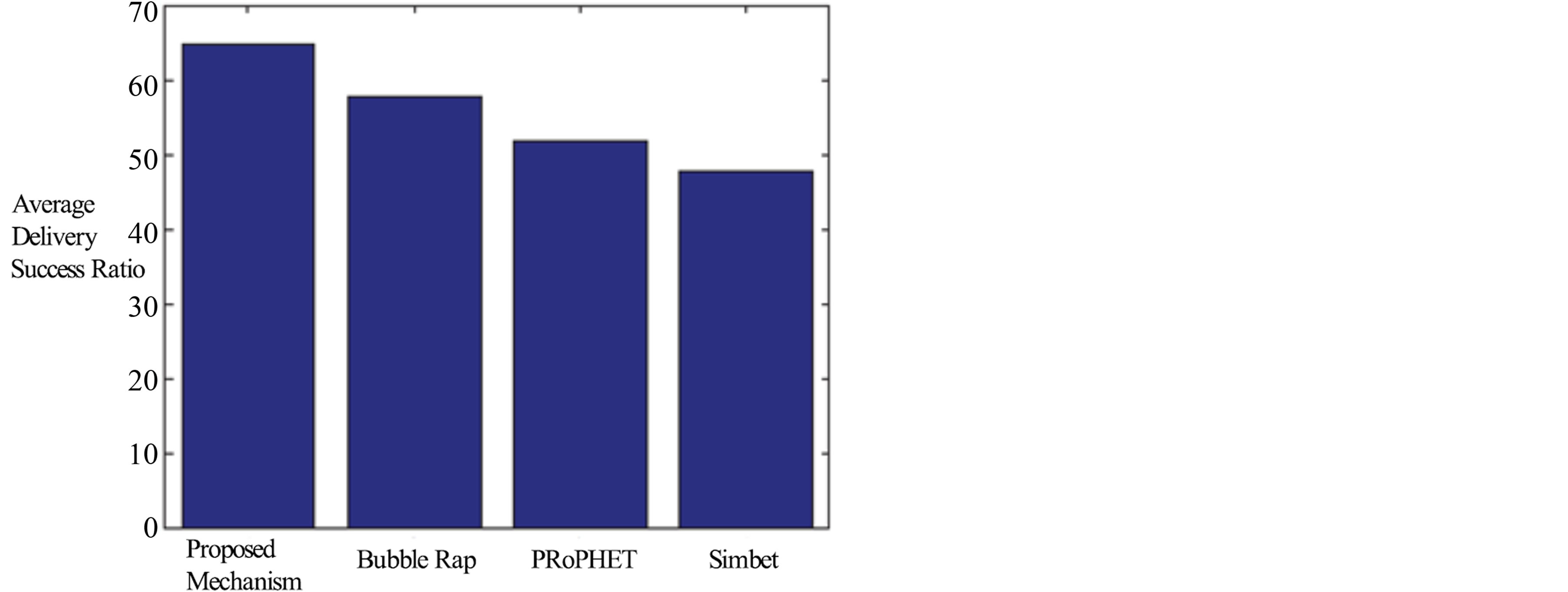
Figure 11. Average end-to-end delay compared with other benchmarks.
introduced and analyzed in our mechanism. By using this model, the overall forwarding probability of each node can be predicted. Also based on this probability, multicast routing can be done in DTNs. Experiment results verify that this routing protocol has the highest average success ratio and lowest end-to-end delay compared with other benchmark DTNs routing protocols.
REFERENCES
- W. Gao, G. Cao, T. L. Porta and J. Han, “On Exploiting Transient Social Contact Patterns for Data Forwarding in Delay Tolerant Networks,” IEEE Transactions on Mobile Computing, Vol. 12, No. 1, 2013, pp. 151-165. http://dx.doi.org/10.1109/TMC.2011.249
- N. Perra, B. Goncalves, R. Pastor-Satorras and A. Vespignani, “Activity Driven Modeling of Time Varying Net-Works,” Scientific Reports, Vol. 2, 2012.
- A. Baronchelli, S. Liu and N. Perra, “Contagion Dynamics in Time-Varying Metapopulation Networks,” Bulletin of the American Physical Society, Vol. 58, No. 1, 2013.
- M. Newman, “Networks: An Introduction,” Oxford University Press, Oxford, 2009.
- S.-Y. Chan, P. Hui and K. Xu, “Community Detection of Time-Varying Mobile Social Networks,” Complex Sciences, Springer, 2009, pp. 1154-1159.
- P. Costa, C. Mascolo, M. Musolesi and G. P. Picco, “Socially-Aware Routing for Publish-Subscribe in DelayTolerant Mobile ad hoc Networks,” IEEE Journal on Selected Areas in Communications, Vol. 26, No. 5, 2008, pp. 748-760. http://dx.doi.org/10.1109/JSAC.2008.080602
- Q. Yuan, I. Cardei and J. Wu, “Predict and Relay: An Efficient Routing in Disruption-Tolerant Networks,” Proceedings of the 10th ACM International Symposium on Mobile ad hoc Networking and Computing, ACM, 2009, pp. 95-104.
- P. Hui, J. Crowcroft and E. Yoneki, “Bubble Rap: SocialBased Forwarding in Delay-Tolerant Networks,” IEEE Transactions on Mobile Computing, Vol. 10, No. 11, 2011, pp. 1576-1589. http://dx.doi.org/10.1109/TMC.2010.246
- A. Vahdat, D. Becker, et al., “Epidemic Routing for Partially Connected ad hoc Networks,” Technical Report CS-200006, Duke University, 2000.
- A. Lindgren, A. Doria and O. Schelen, “Probabilistic Routing in Intermittently Connected Networks,” Service Assurance with Partial and Intermittent Resources, Springer, 2004, pp. 239-254. http://dx.doi.org/10.1007/978-3-540-27767-5_24
- M. Musolesi and C. Mascolo, “Car: Context-Aware Adaptive Routing for Delay-Tolerant Mobile Networks,” IEEE Transactions on Mobile Computing, Vol. 8, No. 2, 2009, pp. 246-260. http://dx.doi.org/10.1109/TMC.2008.107
- C. Boldrini, M. Conti, J. Jacopini and A. Passarella, “Hibop: A History Based Routing Protocol for Opportunistic Networks,” IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoW-MoM 2007), Espoo, 18-21 June 2007, pp. 1-12.
- P. Flocchini, B. Mans and N. Santoro, “On the Exploration of Time-Varying Networks,” Theoretical Computer Science, Vol. 469, 2013, pp. 53-68. http://dx.doi.org/10.1016/j.tcs.2012.10.029
- L. A. Adamic, R. M. Lukose, A. R. Puniyani and B. A. Huberman, “Search in Power-Law Networks,” Physical Review E, Vol. 64, No. 4, 2001, Article ID: 046135.
- S. Jain, K. Fall and R. Patra, “Routing in a Delay Tolerant Network,” Proceedings of the 2004 Conference on Applications, Technologies, Architectures and Protocols for Computer Communications, Vol. 34, No. 4, 2004, pp. 145-158. http://dx.doi.org/10.1145/1030194.1015484
- Z. Wu, H. Song, S. Jiang and X. Xu, “A Grid-Based Stable Routing Algorithm in Mobile ad hoc Networks,” 1st Asia International Conference on Modelling & Simulation (AMS’07), Phuket, 27-30 March 2007, pp. 181-186.
- L. Pelusi, A. Passarella and M. Conti, “Opportunistic Networking: Data Forwarding in Disconnected Mobile ad hoc Networks,” IEEE Communications Magazine, Vol. 44, No. 11, 2006, pp. 134-141. http://dx.doi.org/10.1109/MCOM.2006.248176
- C. Liu and J. Wu, “Scalable Routing in Delay Tolerant Networks,” Proceedings of the 8th ACM International Symposium on Mobile ad hoc Networking and Computing, ACM, 2007, pp. 51-60.
- A. Casteigts, P. Flocchini, W. Quattrociocchi and N. Santoro, “Time-Varying Graphs and Dynamic Networks,” in Ad-hoc, Mobile and Wireless Networks, Springer, 2011, pp. 346-359.
- N. Perra, A. Baronchelli, D. Mocanu, B. Goncalves, R. Pastor-Satorras and A. Vespignani, “Random Walks and Search in Time-Varying Networks,” Physical Review Letters, Vol. 109, No. 23, 2012, Article ID: 238701. http://dx.doi.org/10.1103/PhysRevLett.109.238701
- J. Tang, M. Musolesi, C. Mascolo and V. Latora, “Temporal Distance Metrics for Social Network Analysis,” Proceedings of the 2nd ACM Workshop on Online Social Networks, ACM, 2009, pp. 31-36.
- M. C. Gonzalez, C. A. Hidalgo and A.-L. Barabasi, “Understanding Individual Human Mobility Patterns,” Nature, Vol. 453, No. 7196, 2008, pp. 779-782. http://dx.doi.org/10.1038/nature06958
- N. Eagle and A. Pentland, “Reality Mining: Sensing Complex Social Systems,” Personal and Ubiquitous Computing, Vol. 10, No. 4, 2006, pp. 255-268. http://dx.doi.org/10.1007/s00779-005-0046-3
- Y.-C. Cheng, J. Bellardo, P. Benk¨o, A. C. Snoeren, G. M. Voelker and S. Savage, “Jigsaw: Solving the Puzzle of Enterprise 802.11 Analysis,” ACM, Vol. 36, No. 4, 2006.
- Y.-C. Cheng, M. Afanasyev, P. Verkaik, P. Benk¨o, J. Chiang, A. C. Snoeren, S. Savage and G. M. Voelker, “Automating Cross-Layer Diagnosis of Enterprise Wireless Networks,” ACM, Vol. 37, No. 4, 2007.
- J. Leguay, T. Friedman and V. Conan, “Mobyspace: Mobility Pattern Space Routing for DTNS,” ACM SIGCOMM, 2005.
- R.-J. Lange, “Potential Theory, Path Integrals and the Laplacian of the Indicator,” Journal of High Energy Physics, Vol. 2012, No. 11, 2012, pp. 1-46. http://dx.doi.org/10.1007/JHEP11(2012)032
- M. Ficek and L. Kencl, “Spatial Extension of the Reality Mining Dataset,” IEEE 7th International Conference on Mobile Adhoc and Sensor Systems (MASS), San Francisco, 8-12 November 2010, pp. 666-673.

