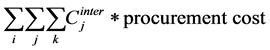Journal of Service Science and Management
Vol.09 No.04(2016), Article ID:69027,11 pages
10.4236/jssm.2016.94037
Global Production and Sales Network Planning
Qian Huang, Jiahua Weng, Jiaxin Zhou, Hisashi Onari
School of Creative Science & Engineering, Waseda University, Tokyo, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 June 2016; accepted 23 July 2016; published 26 July 2016
ABSTRACT
Due to the large changes in global market demands and production environment, redesigning of production and sales network planning is playing a key role to support the optimization of Global Production Networks (GPN). Making separate decisions regarding production capacity, and sales scale in GPN might decrease profits. Therefore, we propose an integrated method to simultaneously determine those two sub-problems. As the proposed model is a multi-product, multi-plant, multi-production-line, multi-market, multi-sales-price problem, in order to copy with the large search space of solutions, we apply the concept of a genetic algorithm and develop an efficient heuristic for better performance accuracy.
Keywords:
Production Capacity, Sales Scale, Mathematical Model, Meta Heuristic, Simultaneously

1. Introduction
The global market environment can be described as having global factors that are external to a manufacturing company’s control but can significantly affect business planning. Currently, we see that the market has been expanding globally. To continue to grow successfully, manufacturing companies should learn to address the global marketplace. Marketing studies show a growing middle class in developing countries such as China, India, and Brazil. In other words, manufacturing companies can serve these needs by targeting this large market. Traditional production planning in a Global Production Network (GPN) has focused separately on optimizing manufacturing and sales planning as different departments with different year-end objectives. The manufacturing department devotes itself to minimizing manufacturing costs, and the sales department is devoted to maximizing sales revenue. Yet, the maximization of product sales revenue does not mean that manufacturing costs are minimized. Additionally, in many cases, inappropriate decision-making related to oversized production capacity leads to increases in production investment costs. Therefore, integrating these sub-processes in a GPN is necessary to ensure a tradeoff among them.
Furthermore, coordination among sub-processes is a better method for obtaining an appropriate production plan in a GPN. Cost functions need to be properly constructed using mathematical models because improper construction causes the business model to deviate from real-life production operations and the inability to use the exact database provided by a real enterprise. Eventually, defects in a cost management system cannot provide decision-makers with persuasive advice when making business decisions.
Therefore, it is necessary to redesign the production planning of a GPN through integrated sub-processes and reconstructed cost functions to obtain a better decision support system to aid enterprise decision-makers.
2. Literature Review
2.1. Production and Distribution Problems
The literature contains numerous papers related to these issues. We categorized these papers into three dimensions on the basis of the manipulated variable: (1) production decision problem, (2) distribution decision problem, and (3) production and simultaneous distribution decision problem.
First, the production decision problem occurs when decision variables are based on production activities, such as production facility/equipment numbers, production quantities, and production sequence/batch size. Many studies integrate the sub-processes in a GPN but actually only coordinate them in the form of cost functions, not through manipulated variables between multiple processes. From the viewpoint of manipulated variables, we call these types of problems production decision problems. Single-product models, multi-product models, and single-plant models exist [1] - [3] . Moreover, studies exist on multi-product, multi-plant, and multi-market problems [4] - [6] .
Second, the distribution decision problem occurs when demand among markets and a plant are known and entail deciding on distribution activities, such as distribution facility/equipment numbers, distribution modes, distribution quantities, and routing. [7] [8] present decisions related to fleet size problems. [9] [10] discuss port selection problems. [10] [11] consider the routing problem in a global environment. [12] develops scheduling planning for logistics network problems.
Third, another problem is the production and distribution simultaneous decision problem, meaning that at least one manipulated variable exists in both production and distribution activities. With those types of studies as the background, [5] [13] [14] consider distribution activities as manipulated variables that belong to production activities. They decide on distribution activities, such as truck numbers for inland distribution. Furthermore, [15] discusses the route selection problem of whether to use a direct distribution or a multi-distribution path through other depots. These types of studies are rare but important in strategy and tactical decision support systems for real-life enterprises.
2.2. Production and Sales Problems
The core business processes in a GPN are production, distribution, and sales. Very few studies exist that discuss production and sales decision problems. Among these limited papers, [16] provides two perspectives on long- term capacity management for manufacturing and sales strategies and states the importance of simultaneously deciding on production and sales problems. However, no modeling construction exists. [17] extends the research theory based on [16] and uses construct mathematical models to describe the production network, and provides both an integrated model and a decoupling model for the production sales problem. The advantage of an integrated model has been proven through numerical experiments. However, inventory quantity is the decision variable for their model’s sales process, which is considered an operational level factor regarding the enterprise decision of the sales and operation (S & OP) planning problem. [18] also provides an integrated production net- work model at the operational level. As an objective function, the model maximizes the profits of a manufacturing company and, in particular, refers to sales prices among markets. One shortcoming of the model is that sales prices are given in advance. When redesigning a GPN’s production planning, we believe that sales price as a decision factor of the sales process is very important in today’s mid-to long-term decision-making for enterprises.
Thus, the purpose of this paper is to propose an integrated method to decide simultaneously production and sales planning in a GPN to support tactical decision-making for manufacturing enterprises.
Section 3 is devoted to a description of the integrated model with three sub-processes. Section 4 presents the solution algorithms of a Genetic Algorithm (GA) and two crossover methods. Section 5 reports on the numerical results. Finally, the summary and conclusion comprise Section 6.
3. Model Formulation
3.1. Problem Description
This work considers the optimal design and operation of multi-products, multi-production lines, multi-plants, multi-markets, and multi-sales prices of the global production, distribution, and sales network problem. In general, each product belongs to a product group, and each product group is allocated to one or several production lines in a different plant.
Plant locations are given, and each plant comprises several production lines. Each production line has a fixed assets cost and a fixed labor cost. If the allocation of market demand is within the standard production capacity of a production line, then the manufacturing cost of this line is constant. However, the unit manufacturing cost of this line is decreasing, production quantity is increasing, and overtime labor costs increase if market demand allocation is higher than the standard production capacity but not higher than the maximum production capacity. Another situation is allocation of market demand that is higher than the maximum production capacity; in this case, capacity expansion in the form of a new production line for the related plant should occur.
Market zone locations are also given. Each market zone has multi-product demand but in an unidentified quantity. In other words, the demand for product types and the quantity for each region are not given. We can obtain a sales price and demand quantity trend from the Price-Quantity (PQ) curve in each market, and each product has several sales prices associated with the corresponding specific quantity. For instance, in some developing economic regions, demand quantity is very sensitive to sales prices. Therefore, as sales prices decline, demand quantity increases in rhythm. However, as constraints, there are absolute minimum sales prices and maximum demand quantities for each product in each region.
The links between plants and markets are distribution channels that use maritime transportation. In practice, several distribution types can be selected, such as industrial shipping, tramp shipping, and liner shipping. Because of the complexity and long lead-time related to global transportation, we consider outsourcing our distribution process. We are able to obtain shipping cost sheets from an outsourcing transportation company that could indicate the unit shipping costs from plant to market for each product.
In this mathematical model, we determine the production quantity for each product from plants to markets and the sales prices of each product in each market as our manipulated variable. The objective function is to maximum the total annualized profit of the production network, taking into account both fixed and variable costs. This paper considers a steady-state form of this problem according to which sales price, production, and distribution flows are determined through optimization.
3.2. Production-Distribution-Sales Model
Following the previously described problem, we formulate the production-distribution-sales model using Mixed Integer Programming (MIP). We aim to obtain optimal planning for this GPN.
Assumptions:
(1) Each production line has the capability to produce correlative product groups;
(2) Each production line has a production standard and maximum capacity but can be expanded through variable or fixed costs;
(3) There is a variable distribution cost between each plant and market;
(4) Demand in each market comes from end users of that region;
(5) Several candidate prices exist for each product in each market;
(6) Several candidate demand quantities exist for each product in each market;
(7) There are no inventory quantity limits in the markets; and,
(8) Inventory capacity can change by increasing the rental warehouse area.
Index and set
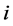 plants
plants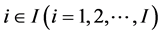 .
.
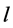 manufacturing lines
manufacturing lines .
.
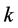 products
products .
.
 product groups
product groups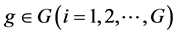 .
.
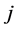 market zones
market zones .
.
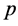 sales prices
sales prices .
.
 manufacturing lines in plant i.
manufacturing lines in plant i.
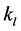 products that can be produced on line l.
products that can be produced on line l.
Parameters
Production:
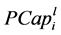 standard production capacity of plant i for line l (time) .
standard production capacity of plant i for line l (time) .

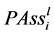






Distribution:
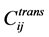
Sales:






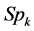




Manipulated variables.
Production:
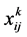
Sales:

3.3. Cost Functions
The problem is formulated using MIP with an objective function of total profit maximization:
Max

Subject to:



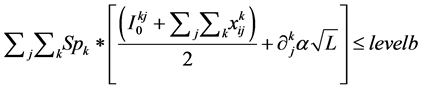
The maximization of total profit in the objective function includes total sales revenue and total production cost. Total production cost includes manufacturing cost, distribution cost and sales cost. In detail, manufacturing cost of standard production, overtime production, and capacity expansion cost of production line. Distribution cost of vessel sailing cost from plants to sales market. Sales cost of import duty, stock cost, and sunk cost.
The objective (1) is to maximize total profits associated with production cost, distribution cost, and sales cost. Constraint (2) is production capacity constraints that guarantee that production quantity should not be less than the demand quantity allocated to plant i. Constraint (3) enforces the minimum production at each selected line l. Constraint (4) is the demand constraints for market j, which indicates that demand for product k should not exceed the production quantity in each plant. Constraint (5) is the warehouse constraints for market j, which indicate that the inventory in each market should not exceed warehouse capacity.
Manufacturing cost
Case1: Annualized fixed costs + material costs
If
Case2: Annualized fixed costs + material costs + overtime work costs
If
Case 3: Annualized fixed costs + material costs + capacity expansion costs
If
Distribution cost
Sales cost
Sales cost = Duty cost + Stock cost + Sunk cost
(1) Duty cost
(2) Stock cost
If
Stock cost =
Average stock quantity + safety stock quantity
the market floor space
(3) Sunk cost
Procurement cost
4. Heuristic Solution
The model proposed in Part 3 is based on MIP, which has been certified to be much more difficult to solve using mathematical techniques when the scale of the problem increases. Numerous studies consider solutions to production-distribution optimization models using Genetic Algorithms (GA). GAs are proven to be highly effective and efficient at solving complex SCM problems because directed and stochastic search methods can find good solutions easily and in a shorter period [1] - [3] [19] - [24] . Therefore, in this study, we use the concept of a GA to develop our global production planning system.
4.1. Chromosome Representation
The chromosome representation of the proposed genetic algorithm can be divided into two parts. The first part is a price choice chromosome that selects the sales price (P) among candidate prices in each market for each product. After a product’s sales price is chosen, the corresponding demand quantity (Q) is also known. Each gene in the price choice chromosome is represented as a 0 or a 1, as shown in Figure 1(a). The second part is a production allocation chromosome that determines the production plant number for each product k in market j. Each gene of the production allocation chromosome is represented in the form of a plant number, as shown in Figure 1(b1).
In the production allocation chromosome, we attempted two methods to allocate market demand. One method is to not divide the demand quantity for one product from one market. In other words, the demand quantity of each product in each market can only be allocated to one plant. The other method involves the opportunity to divide the demand quantity of each product in each market to multiple plants, as shown in Figure 1(b2).
4.2. Chromosome Evaluation
The fitness of chromosomes in every generation is calculated using the total profit of the GPN. Which we have discussed in 3.3. The total profit is equal total sales revenue minus total production costs. Total production costs construct with manufacturing, distribution and sales costs. As manipulated variables are both exist in sales revenue and production costs, there is not easy to find good fitness value except many generations calculation.
4.3. Crossover Operator
We propose a cost-based multi-segments crossover operator: (1) two parents are randomly selected among excellent individual groups that are within high ranks in a population; a judgment condition exists that indicates that the two parents are not same; (2) the higher unit production cost genes (worse segments) are found through a cost-based calculation of one parent chromosome; (3) these worse segments are changed with the same position of the other parent chromosome (both in price choice and population allocation chromosome); (4) the newly generated chromosome is then copied into the new population.
4.4. Mutation Operator
We use a mutation method to obtain a better global solution through half-random mutation. A single chromosome



Figure 1. Chromosomes representation. (a) The price choice chromosome; (b1) The production allocation chromosome (no division); (b2) The production allocation chromosome (with division).
is randomly selected from the remaining chromosomes, a gene locus is found using probability, and a judgment condition exists to find the market demand group through that gene locus; then let the group genes change from 1 to 0 or 0 to 1. Moreover, the plant number is randomly selected from plant i0 to iI−1.
5. Performance Evaluation
The GA procedure was coded in Python2.0.
An integrated approach for the optimization of sub-problems was proposed to increase the total profit by approximately 18% compared with the discoupling method. However, investment in the production capacity of our method is only approximately 70% of that of the discoupling method. Simply, the integrated method may achieve higher profits but also less capacity investment compared with the discoupling method (Figure 2).
The integrated method is more effective in highly price sensitive markets. When the degree of price sensitivity is low and approximately1, nearly no improvement occurs relative to the decoupling method. However, along with price sensitivity increasing, profits from the integrated method increase (Figure 3).
Two crossover operator methods were proposed. The top 1 method is to find the worst segment and exchange it for another; the top 3 method engages in a larger search to find other worse segments to exchange with, except for the worst one, thus proving its effectiveness relative to the top 1 method. The top 3 method achieved better total profit performance when minimal changes in fitness value are observed in consecutive generations. The results implied that the solution space is very large and GA is a proper metaheuristic algorithm for our research (Figure 4).
Figure 2. Numerical results for two methods.
Figure 3. Profit rate in different price sensitive markets.
Figure 4. Numerical results for two crossover operator methods.
Figure 5. Market demand with and without division allocation.
From the experimental data, we see that the production allocation method of each product with division is better than that without division in both top1 and top3 crossover methods, as shown in Figure 4. Therefore, in practice, we advise manufacturing companies to allocate each product’s demand to multiple plants when adequate conditions exist to engage in multi-plant manufacturing. From another viewpoint of algorithm effectiveness, as the division allocation method could also be considered an upper limit condition of the proposed production planning system, the result highlights the effectiveness of the top3 crossover method proposed (Figure 5).
6. Conclusions
This paper proposed an integrated production capacity and sales scale planning method using both manipulated variables and cost functions. To more simply construct the model to be as close to real-world enterprise operations, we designed the manufacturing process cost functions using an operation time base, including equipment fixed costs and labor variable costs. We constructed the sales process cost functions by varying tariffs with routing, by varying stock cost through sales scale, and by varying sunk cost through stock cost. Using our model, the numerical experimental results proved the advantage of the integrated method over the decoupling method for the economic growth environment of a GPN. Also emphasized was a market that became more sensitive, which made the effectiveness of the proposed method more obvious.
From a business viewpoint, the proposed MIP integrated model aims to assist decision-makers to simultaneously coordinate manufacturing and sales departments when they prepare optimized production planning for a GPN. This integrated approach considers sales price as a decision factor of the sales process, which is very important in today’s mid-to long-term enterprise decision-making. Moreover, because production capacity is determined simultaneously with sales scale, surplus production capacity investments can be avoided to provide an opportunity to increase a GPN’s profits through proper production planning.
Our model presented is developed using the concept of GA, which has been proven to be an effective method to address GPN problems. We represented the chromosomes in a simple and flexible manner in two parts―the price chromosome and the production allocation chromosome―and developed two crossover methods for evolutionary processes. The top 3 crossover method indicated better performance than the top 1 method. Then, we changed the chromosome representation from no division formal to division formal for production allocation. The latter, division allocation chromosome representation and top 3 crossover method, showed the best performance in the numerical experimental results. The results implied that the solution space is very large and GA is a proper meta heuristic algorithm for our research.
Production capacity and sales scale decision problems are very important for global manufacturing firms when making mid- to long-term decisions. Effective production planning can increase firm profits. Future studies should extend the analysis to integrate other major horizontal or vertical factors of a GPN that reflect the different tendencies of enterprises when making decisions.
Cite this paper
Qian Huang,Jiahua Weng,Jiaxin Zhou,Hisashi Onari, (2016) Global Production and Sales Network Planning. Journal of Service Science and Management,09,320-330. doi: 10.4236/jssm.2016.94037
References
- 1. Garavelli, A.C., Okogbaa, O.G. and Violante, N. (1996) Global Manufacturing Systems: A Model Supported by Genetic Algorithms to Optimize Production Planning. Computers & Industrial Engineering, 31, 193-196.
http://dx.doi.org/10.1016/0360-8352(96)00109-X - 2. Hou, Y.C. and Chang, Y.H. (2002) The New Efficient Hierarchy Combination Encoding Method of Evolution Strategies for Production Allocation Problems. Computers & Industrial Engineering, 43, 577-589.
http://dx.doi.org/10.1016/S0360-8352(02)00126-2 - 3. Chang, Y.H. and Hou, Y.C. (2008) Dynamic Programming Decision Path Encoding of Genetic Algorithms for Production Allocation Problems. Computers & Industrial Engineering, 54, 53-65.
http://dx.doi.org/10.1016/j.cie.2007.06.034 - 4. Cunha, C.B. and Mutarelli, F. (2007) A Spreadsheet-Based Optimization Model for the Integrated Problem of Producing and Distributing a Major Weekly Newsmagazine. European Journal of Operational Research, 176, 925-940.
http://dx.doi.org/10.1016/j.ejor.2005.06.065 - 5. Aydinel, M., Sowlati, T., Cerda, X., Cope, E. and Gerschman, M. (2008) Optimization of Production Allocation and Transportation of Customer Orders for a Leading Forest Products Company. Mathematical and Computer Modelling, 48, 1158-1169.
http://dx.doi.org/10.1016/j.mcm.2007.12.025 - 6. Tsiakis, P. and Papageorgiou, L.G. (2008) Optimal Production Allocation and Distribution Supply Chain Networks. International Journal of Production Economics, 111, 468-483.
http://dx.doi.org/10.1016/j.ijpe.2007.02.035 - 7. Fagerholt, K. (1999) Optimal Fleet Design in a Ship Routing Problem. International Transactions in Operational Research, 6, 453-464.
http://dx.doi.org/10.1111/j.1475-3995.1999.tb00167.x - 8. Bendall, H.B. and Stent, A.F. (2001) A Scheduling Model for a High Speed Containership Service: A Hub and Spoke Short-Sea Application. International Journal of Maritime Economics, 3, 262-277.
http://dx.doi.org/10.1057/palgrave.ijme.9100018 - 9. Lirn, T.C., Thanopoulou, H.A., Beynon, M.J. and Beresford, A.K.C. (2004) An Application of AHP on Trans-Shipment Port Selection: A Global Perspective. Maritime Economics & Logistics, 6, 70-91.
http://dx.doi.org/10.1057/palgrave.mel.9100093 - 10. Guy, E. and Urli, B. (2006) Port Selection and Multicriteria Analysis: An Application to the Montreal-New York Alternative. Maritime Economics & Logistics, 8, 169-186.
http://dx.doi.org/10.1057/palgrave.mel.9100152 - 11. Fagerholt, K. (2004) Designing Optimal Routes in a Liner Shipping Problem. Maritime Policy & Management, 31, 259-268.
http://dx.doi.org/10.1080/0308883042000259819 - 12. Agarwal, R. and Ergun, Ö. (2008) Ship Scheduling and Network Design for Cargo Routing in Liner Shipping. Transportation Science, 42, 175-196.
http://dx.doi.org/10.1287/trsc.1070.0205 - 13. Sakawa, M., Nishizaki, I. and Uemura, Y. (2001) Fuzzy Programming and Profit and Cost Allocation for a Production and Transportation Problem. European Journal of Operational Research, 131, 1-15.
http://dx.doi.org/10.1016/S0377-2217(00)00104-1 - 14. Tang, J., Yung, K.L., Ip, A.W. and Liu, S. (2007) Synchronized Production and Transportation Planning Using Subcontracted Vehicles in a Production-Distribution Network. Transportation Planning and Technology, 30, 113-146.
http://dx.doi.org/10.1080/03081060701390528 - 15. Bilgen, B. (2010) Application of Fuzzy Mathematical Programming Approach to the Production Allocation and Distribution Supply Chain Network Problem. Expert Systems with Applications, 37, 4488-4495.
http://dx.doi.org/10.1016/j.eswa.2009.12.062 - 16. Olhager, J., Rudberg, M. and Wikner, J. (2001) Long-Term Capacity Management: Linking the Perspectives from Manufacturing Strategy and Sales and Operations Planning. International Journal of Production Economics, 69, 215-225.
http://dx.doi.org/10.1016/S0925-5273(99)00098-5 - 17. Feng, Y., D’Amours, S. and Beauregard, R. (2008) The Value of Sales and Operations Planning in Oriented Strand Board Industry with Make-to-Order Manufacturing System: Cross Functional Integration under Deterministic Demand and Spot Market Recourse. International Journal of Production Economics, 115, 189-209.
http://dx.doi.org/10.1016/j.ijpe.2008.06.002 - 18. Park, Y.B. (2005) An Integrated Approach for Production and Distribution Planning in Supply Chain Management. International Journal of Production Research, 43, 1205-1224.
http://dx.doi.org/10.1080/00207540412331327718 - 19. Chan, F.T., Chung, S.H. and Wadhwa, S. (2005) A Hybrid Genetic Algorithm for Production and Distribution. Omega, 33, 345-355.
http://dx.doi.org/10.1016/j.omega.2004.05.004 - 20. Farahani, R.Z. and Elahipanah, M. (2008) A Genetic Algorithm to Optimize the Total Cost and Service Level for Just- in-Time Distribution in a Supply Chain. International Journal of Production Economics, 111, 229-243.
http://dx.doi.org/10.1016/j.ijpe.2006.11.028 - 21. Gen, M. and Syarif, A. (2005) Hybrid Genetic Algorithm for Multi-Time Period Production/Distribution Planning. Computers & Industrial Engineering, 48, 799-809.
http://dx.doi.org/10.1016/j.cie.2004.12.012 - 22. Tasan, A. (2006) A Two Step Approach for the Integrated Production and Distribution Planning of a Supply Chain. In: Huang, D.-S., Li, K. and Irwin, G.W., Eds., Intelligent Computing, Springer, Berlin, 883-888.
- 23. Aliev, R.A., Fazlollahi, B., Guirimov, B.G. and Aliev, R.R. (2007) Fuzzy-Genetic Approach to Aggregate Production-Distribution Planning in Supply Chain Management. Information Sciences, 177, 4241-4255.
http://dx.doi.org/10.1016/j.ins.2007.04.012 - 24. Kazemi, A., Zarandi, M.F. and Husseini, S.M. (2009) A Multi-Agent System to Solve the Production-Distribution Planning Problem for a Supply Chain: A Genetic Algorithm Approach. The International Journal of Advanced Manufacturing Technology, 44, 180-193.
http://dx.doi.org/10.1007/s00170-008-1826-5