Journal of Service Science and Management
Vol.5 No.3(2012), Article ID:22446,11 pages DOI:10.4236/jssm.2012.53028
Risk Evaluation of Dynamic Alliance Based on Fuzzy Analytic Network Process and Fuzzy TOPSIS
![]()
1Dongling School of Economics and Management, University of Science and Technology Beijing, Beijing, China; 2Department of Electrical and Computer Engineering, Texas A&M University, College Station, USA.
Email: xiaoguang@ustb.edu.cn, mlu@ece.tamu.edu
Received May 25th, 2012; revised June 23rd, 2012; accepted July 4th, 2012
Keywords: Fuzzy Analytic Network Process; TOPSIS; Dynamic Alliance; Risk Evaluation
ABSTRACT
Dynamic alliance formations have increased dramatically over the past decade for its adaptation to environmental change and market competition. However, many fail, while an even greater proportion perform poorly. The risk analysis of dynamic alliance will help enterprises to choose a coalition partner and make a reasonable benefit allocation plan. It’s also good for reducing the risk and keeping the stability of the alliance. Based on the interaction and feedback relationships between criteria and/or indices, an index system for evaluating the risk of dynamic alliance is developed. With the information uncertainty and inaccuracy being considered, a new hybrid model based on fuzzy analytic network process (FANP) and fuzzy technique for order performance by similarity to ideal solution (TOPSIS) is proposed. The local weights of criteria and indices are obtained by fuzzy preference programming (FPP), and the comprehensive weights are derived by FANP. According to fuzzy TOPSIS, an optimal alternative is chosen by the closeness coefficient based on the shortest distance from the positive and the farthest distance from the negative ideal solutions. Finally, a numerical case is given by the proposed method.
1. Introduction
With the rapidly increasing competitiveness in global, enterprise cooperation is necessary in order to meet the market’s requirements for quality, responsiveness, and customer satisfaction. As a result, dynamic alliance, defined as voluntary interfirm cooperative arrangements, has become a noteworthy trend in recent years. However, despite the growing numbers and increasing significance of dynamic alliance, many fail, while an even greater proportion perform poorly. Recent estimates put the failure rate of alliances between 60% and 70%, suggesting firms that pursue alliances are more likely than not to fail [1]. Although such failures may be for many interrelated reasons—and may be defined in various ways—two common causes are poor partner selection and poor alliance management [2]. Li and Liao [3] pointed out that despite many problems on dynamic alliance, such as partner selection, operation management, information exchanges and their standards, etc. have been investigated, and the risk management of dynamic alliance has not received deserved attention until now. This article focuses on risk evaluation, which is the most important phase of risk management for dynamic alliance.
Venkatesh et al. [4] investigated the dynamic aspects of a co-marketing alliance and offered guidelines to establish profitable and self-sustaining alliances. They examined two questions. First, under what market-driven characteristics should either brand manufacturer forge or sustain the alliance. Second, what product market characteristics should the alliance promoter seek or alter to increase its payoffs from the alliance. Das and Teng [5] proposed a model of dynamic alliance that has managerial risk perception as its core. The model consists of the following parts: the antecedents of risk perception, relational risk and performance risk, risk perception and structural preference, and the resolution of preferences. Rosenkranz and Schmitz [6] explored the dynamic evolution of property rights regimes in R&D alliances using the incomplete contract approach, and characterized different scenarios in which the optimal ownership structure may change over time due to a trade-off between inducing know-how disclosure and ensuring maximum effort. Ip et al. [7] pointed out that minimizing risk in partner selection and ensuring the due date of a project were the key problems to overcome in dynamic alliance. They developed a risk-based partner selection method and a rule-based genetic algorithm with embedded project scheduling to solve the problem. Das and Kumar [8]
discussed three kinds of learning in alliances—namely, content, partner-specific, and alliance management—and the saliencies and implications of particular types of learning in different alliance stages. Huang et al. [9] proposed a fuzzy synthetic evaluation embedded nonlinear integer programming model of risk programming for dynamic alliance and presented a tabu search algorithm for the model. Delerue and Simon [10] pointed out that cross-cultural interactions were growing at an exponential pace. Consequently, it was becoming important to be aware of the existence and precise nature of cultural differences in risk perceptions. Huang et al. [11] introduced a Distributed Decision Making (DDM) model for the risk management of dynamic alliance. The model has two levels, which describe the decision processes of the owner and the partners of the dynamic alliance, respectively. It can be regarded as a combination of both the top-down and bottom-up approaches for risk management of the dynamic alliance. Lee et al. [12] demonstrated the locus of dynamic knowledge articulation and dynamic capabilities development by investigating drivers of dynamic learning in service alliance firms, etc.
However, the interaction and feedback relationships between criteria and/or indices are not completely considered in the existing research literatures. What’s more, during the risk evaluation process of dynamic alliance, there are lots of uncertainty and fuzzy information, the crisp pairwise comparison seems to be insufficient and imprecise to capture the right judgments of decisionmakers. Therefore, Zhou and Song proposed a FANPbased method to make up for the deficiency in the conventional risk assessment process [13].
The objective of this paper is to present a new hybrid model based on FANP and fuzzy TOPSIS for risk evaluation of dynamic alliance. According to FANP, the weights of criteria/indices are derived. The candidates can be ranked based on their relative closeness according to fuzzy TOPSIS. TOPSIS compromise solution is quite similar to what happens during the decision making process in risk evaluation: most of the time, the best solution is not reached since the criteria are not in agreement, some must be maximized and others minimized. Such an ANP/AHP-based TOPSIS driven by a set of weighting factors associated with the selected criteria has been proven effective for final ranking via an iterative procedure [14].
2. Preliminary Knowledge
2.1. Triangular Fuzzy Number
A fuzzy set is a class of objects with a continuum of grades of membership. Such a set is characterized by a membership function, which assigns to each object a grade of membership ranging between zero and one. A triangular fuzzy number (TFN) is denoted simply as (l, m, u). The parameters l, m and u, respectively, denote the smallest possible value, the most promising value, and the largest possible value that describe a fuzzy event. Each TFN has linear representations on its left and right side such that its membership function can be defined as
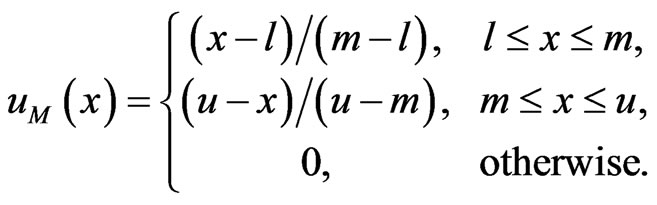 (1)
(1)
2.2. Fuzzy Analytic Network Process
The Analytic Network Process (ANP), introduced by Saaty [15], is a generalization of the Analytic Hierarchy Process (AHP). The basic assumption of the AHP is that the decision-making problem can be decomposed in a linear top-to-bottom form as a hierarchy, where the upper levels are functionally independent from all lower levels, and the elements in each level are also independent. However, many decision-making problems cannot be structured hierarchically, or there would have strong interactions and dependencies between criteria and/or indices. The resulting analytic network process provides a framework for dealing with decision-making problems within which assumptions about dependencies between criteria and alternatives are unnecessary.
AHP/ANP has been proposed as a suitable multi-criteria decision analysis tool [16,17]. However, the AHP/ ANP-based decision model seems to be ineffective in dealing with the inherent fuzziness or uncertainty for judgment during the pairwise comparison process. Although the use of the discrete scale of 1 - 9 to represent the verbal judgment in pairwise comparisons has the advantage of simplicity, it does not take into account the uncertainty associated with the mapping of one’s perception or judgment to a number. In real-life decision-making situation, the decision makers or stakeholders could be uncertain about their own level of preference, due to incomplete information or knowledge, complexity and uncertainty within the decision environment. Such conditions will occur when evaluating the risk of dynamic alliance. Therefore, it’s more appropriate to make risk management plan under fuzzy condition.
A number of methods have been developed to handle fuzzy comparison matrices. For example, Laarhoven and Pedrycz [18] suggested a fuzzy logarithmic least squares method (LLSM) to obtain triangular fuzzy weights from a triangular fuzzy comparison matrix. Buckley [19] utilized the geometric mean method to calculate fuzzy weights. Chang [20] proposed an extent analysis method, which derives crisp weights for fuzzy comparison matrices. Xu [21] brought forward a fuzzy least squares priority method (LSM). Csutora and Buckley [22] came up with a Lambda-Max method, which is the direct fuzzification of the well-known kmax method. Mikhailov [23] developed a fuzzy preference programming method, which also derives crisp weights from fuzzy comparison matrices. Srdjevic [24] proposed a multi-criteria approach for combining prioritization methods within the AHP, including additive normalization, eigenvector, weighted leastsquares, logarithmic least-squares, logarithmic goal programming and fuzzy preference programming. Wang et al. [25] presented a modified fuzzy logarithmic least square method. Yu and Cheng [26] developed a multiple objective programming approach for the ANP to obtain all local priorities for crisp or interval judgments at one time. Huo et al. [27] proposed new parametric prioritization methods (PPMs) to determine a family of priority vectors in AHP, etc.
2.3. Fuzzy Preference Programming Method
FPP method, as a reasonable and effective means, is adopted in this study. This method can acquire the consistency ratios of fuzzy pairwise comparison matrices without conducting an additional study, and the local weights can be easily solved with the help of a Matlab program. The stages of Mikhailov’s fuzzy prioritization approach are as follows [23].
Consider a prioritization problem with n elements, where the pairwise comparison judgments are represented by normal fuzzy sets or fuzzy numbers. Suppose the decision-maker can provide a set 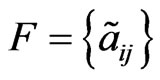 of
of  fuzzy comparison judgments, i = 1, 2, ∙∙∙, n − 1; j = 2, 3, ∙∙∙, n; j > i, represented as triangular fuzzy numbers
fuzzy comparison judgments, i = 1, 2, ∙∙∙, n − 1; j = 2, 3, ∙∙∙, n; j > i, represented as triangular fuzzy numbers . The problem is to derive a crisp priority vector
. The problem is to derive a crisp priority vector , such that the priority ratios wi/wj are approximately within the scopes of the initial fuzzy judgments, or
, such that the priority ratios wi/wj are approximately within the scopes of the initial fuzzy judgments, or
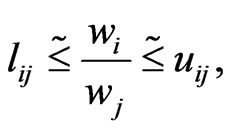 (2)
(2)
where the symbol “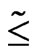 ” denotes the statement “fuzzy less or equal to”.
” denotes the statement “fuzzy less or equal to”.
Each crisp priority vector w satisfies the double-side inequality (2) with some degree, which can be measured by a membership function, linear with respect to the unknown ratio wi/wj,
 (3)
(3)
Taking into consideration the specific form of the membership functions (3), the prioritization problem can be further transformed into a bilinear program of the type
 (4)
(4)
The optimal solution to the non-linear problem (w*, l*) might be obtained by employing some appropriate numerical method for non-linear optimization. The optimal value l*, if it is positive, indicates that all solution ratios completely satisfy the fuzzy judgment, which means that the initial set of fuzzy judgments is rather consistent. A negative value of l* shows that the solutions ratios approximately satisfy all double-side inequalities (2). Therefore, the optimal value l* can be used for measuring the consistency of the initial set of fuzzy judgments.
3. Proposed Risk Evaluation of Dynamic Alliance Framework
This study proposes a novel hybrid analytic approach based on the FANP and fuzzy TOPSIS methodologies to assist in risk evaluation of dynamic alliance. We first identify the evaluation criteria, and present the evaluation model in the following subsections.
3.1. Index system of Risk Evaluation
With the risk sources of dynamic alliance being considered, an index system of risk evaluation for dynamic alliance is presented. The index system is made up of five parts: technique risk, market risk, cooperation risk, risk of natural environmental and risk of social environmental, as shown in Figure 1.
Technique risk and cooperation risk belong to inner risk. On the contrary, market risk, risk of natural environment and social environment belong to outer risk. Technique risk is caused by the technique of partners, including complication of technique, maturity of technique and relationships of technique. Cooperation risk is due to the differences in management, communication and partner’s business reputation in an alliance. Market risk is caused by the situation of market competition, new product development or the appearance of substitute and environmental change of target market. The risk of natural environment is due to the earthquakes, droughts, and other natural risk, including frequency of disasters, disaster losses per year and harm degree of single disaster. The risk of social environment is caused by war, policy and legal system, and so on, including domestic political environment, foreign political environment, policy and legal system and capacity of solving emergency.
In Figure 1, the interaction and feedback relationships
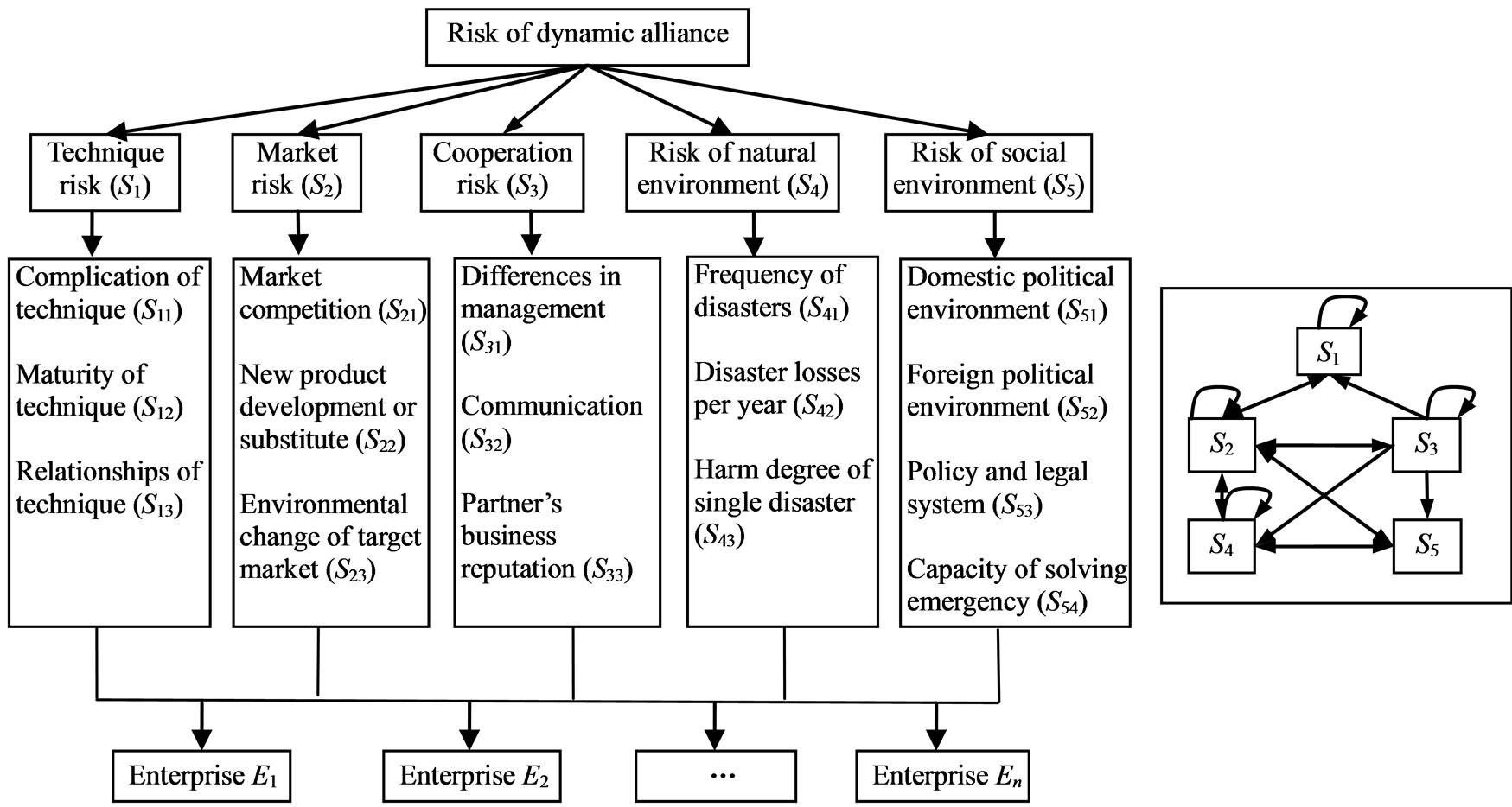
Figure 1. Index system of risk evaluation of dynamic alliance.
between criteria and/or indices are being considered. Generally, if market risk (S2) has an effect on technique risk (S1), then a line with arrow from S1 to S2 is added. If the sub-criteria of market risk (S2) have interaction itself, then S2 is inner dependence, and an arc with arrow is added to S2.
3.2. Fuzzy Linguistic Variables
During the process of risk evaluation, experts tend to specify their preferences in the form of natural language expressions. The fuzzy linguistic variables are variables reflect different aspects of human language. Their values represent the range from natural to artificial language.
When the values of a linguistic factor are being reflected, the resulting variable must also reflect appropriate modes of change. Moreover, variables describing a human word or sentence can be divided into numerous linguistic criteria, such as equally important, moderately important, important, very important and absolutely important. For the purposes of the present study, two 9- point scales are proposed for relative importance of pairwise comparison and rating the candidates, as shown in Tables 1 and 2.
3.3. FANP-Based Approach
The weights of criteria and sub-criteria are obtained based on FANP. The FANP-based approach is proposed stepby-step as follows.
Step 1. Build a network structure and list the interaction and feedback relationships among the components, as shown in Figure 1. A four-level evaluation index system is presented: the first level is the comprehensive risk
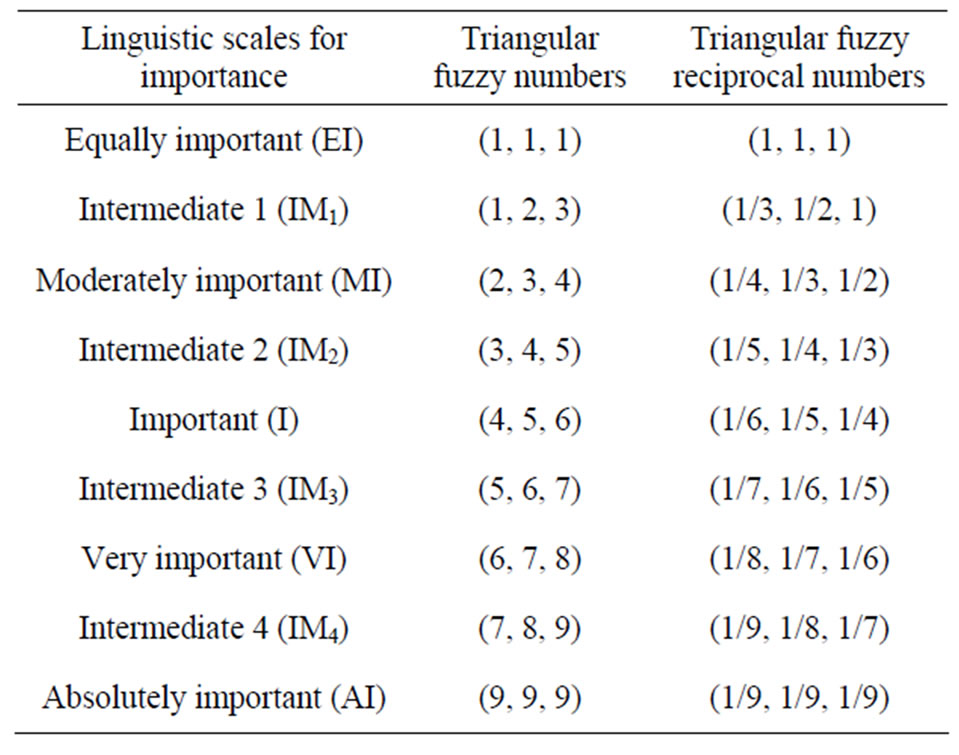
Table 1. Linguistic scales for relative importance of pairwise comparison.
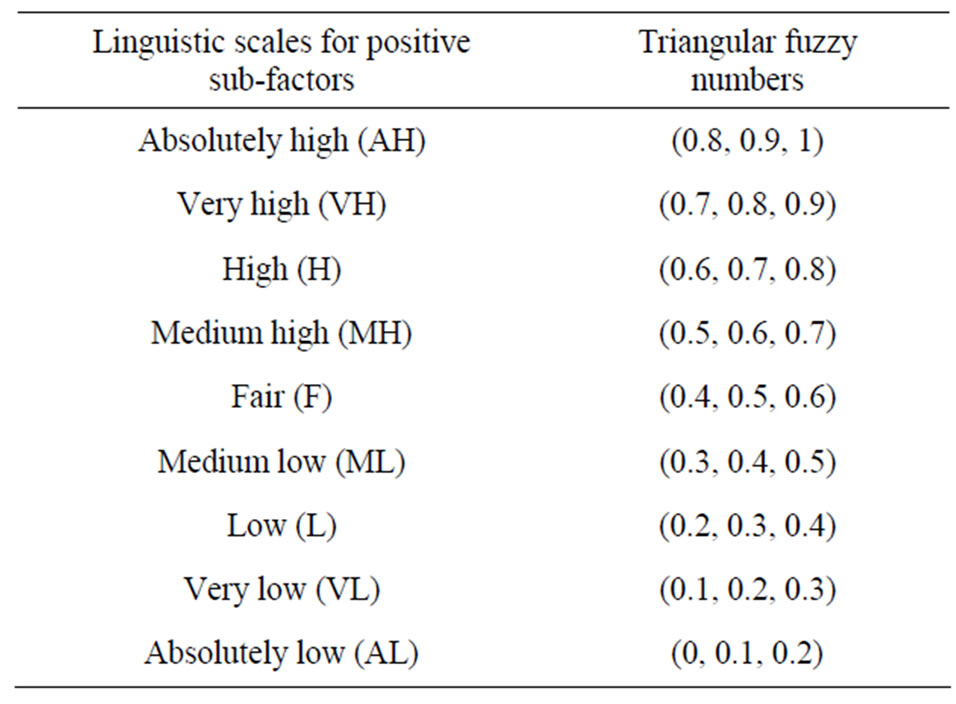
Table 2. Linguistic scales for rating the candidates.
of dynamic alliance; the second level is criteria, including technique risk, market risk, cooperation risk, risk of natural environment and risk of social environment; the third level is sub-criteria, including 16 indicators; the lowest one is candidates.
Step 2. Establish pairwise comparison matrices by the decision committee using the linguistic scales given in Table 1. The decision makers are asked to respond to a series of pairwise comparison with respect to the dimensions/attributes-enablers levels in Figure 1. For example, the market competition (S21) and the new product development or substitute (S22) are compared using the question “How important is the market competition when it is compared with the new product development or substitute at the dimension of market risk?” and the answer is “intermediate important (IM1)”, so this linguistic scale is placed in the relevant cell against the triangular fuzzy numbers (1, 2, 3). All the fuzzy evaluation matrices are produced in the same way.
Step 3. Calculate the local weights and consistency ratios. According to formulation (4), local weights and consistency ratios of the criteria and sub-criteria are calculated by FPP method with the help of Matlab.
Step 4. Construct an unweighted supermatrix on the basis of the interdependencies in the network. The supermatrix is a partitioned matrix, where each submatrix is composed of a set of relationships between criteria and indices. Three types of relationships may be encountered in this model: independence from succeeding components, interdependence among components and interdependence between levels of components.
Step 5. Derive a weighted supermatrix. Because in each column it consists of several eigenvectors each of them sums to one and hence the entire column of the matrix may sum to an integer greater than one, the unweighted supermatrix needs to be stochastic to derive the weighted supermatrix.
Step 6. Generate a limit supermatrix by raising the weighted supermatrix to powers until it converges.
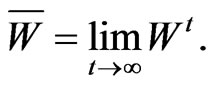 (5)
(5)
Step 7. Obtain the global weight. A global weight of each index can be computed by multiplying the local weight of the criterion level indicator, the weight of independent sub-criterion and the weight of interdependent subcriterion.
 (6)
(6)
where wij is the comprehensive weight, Pi is relative importance weight of dimension i on final goal;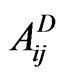 , relative importance weight for attribute-enabler j of dimension i, and for the dependency (D) relationships within attribute-enabler’s component level;
, relative importance weight for attribute-enabler j of dimension i, and for the dependency (D) relationships within attribute-enabler’s component level;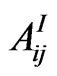 , stabilized relative importance weight for attribute-enabler j of dimension i, and for the independency (I) relationships within attribute-enabler’s component level.
, stabilized relative importance weight for attribute-enabler j of dimension i, and for the independency (I) relationships within attribute-enabler’s component level.
3.4. Fuzzy TOPSIS Approach
TOPSIS method is a classical approach to multi-attribute or multi-criteria decision making problems, which was first proposed by Hwang and Yoon [28] and expanded by Chen and his cooperators [29]. It is a practical and useful technique for ranking and selection of a number of externally determined alternatives through distance measures. The foundational principle is that the chosen alternative should have the shortest distance from the positive ideal solution and the farthest distance from the negative ideal solution.
In the traditional TOPSIS, the performance ratings and the weights of the criteria are given as crisp values. Under many conditions, crisp values are inadequate to model real world situations because human judgment and preference are often ambiguous and cannot be estimated with exact numerical values. To resolve the ambiguity frequently existing in the process of judgment and evaluation, fuzzy sets were applied to establish a prototype fuzzy TOPSIS [30,31].
According to fuzzy TOPSIS, the candidates can be ranked based on their relative closeness. The process is proposed step-by-step as follows.
Step 8. Evaluate the ratings of candidates by the decision committee using the linguistic variables given in Table 2. Assume that a decision group has K persons, and then the ratings of candidates with respect to each criterion can be calculated as
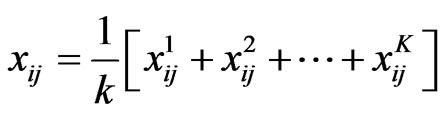 , (7)
, (7)
where 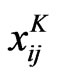 is the rating of the kth decision maker, and xij can be described by triangular fuzzy numbers, such as xij = (aij, bij, cij).
is the rating of the kth decision maker, and xij can be described by triangular fuzzy numbers, such as xij = (aij, bij, cij).
Step 9. Construct a fuzzy decision matrix by converting the linguistic scales into triangular fuzzy numbers according to Table 2.
Step 10. Normalize the fuzzy decision matrix. As there are benefit criteria and cost criteria, the fuzzy decision matrices need to be normalized. Given a TFN  , in reference to the fuzzy TOPSIS method developed by Chen [28], the normalized performance rating can be calculated by
, in reference to the fuzzy TOPSIS method developed by Chen [28], the normalized performance rating can be calculated by
 (8)
(8)
and
 (9)
(9)
where
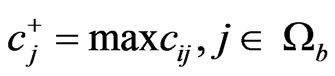 ,
,
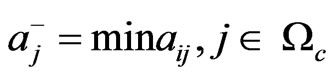 with B being the benefit criteria set (the larger
with B being the benefit criteria set (the larger , the greater preference), and C being the cost criteria set (the smaller
, the greater preference), and C being the cost criteria set (the smaller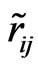 , the greater preference).
, the greater preference).
Hence, the normalized matrix 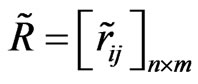 can be obtained.
can be obtained.
Step 11. Obtain the deal and negative ideal solutions. The ideal solutions can be defined as:

Step 12. Determine the distances between each candidate and the positive or negative ideal candidate.
By considering the different importance of each criterion obtained from FANP method, the weighted distance can be calculated as:
 (10)
(10)
 (11)
(11)
where  and
and  are the primary and secondary distant measure, respectively. The distance of each candidate from the ideal alternative can be thereby calculated by
are the primary and secondary distant measure, respectively. The distance of each candidate from the ideal alternative can be thereby calculated by
 (12)
(12)
Similarly, the separation from the negative ideal solution is given by
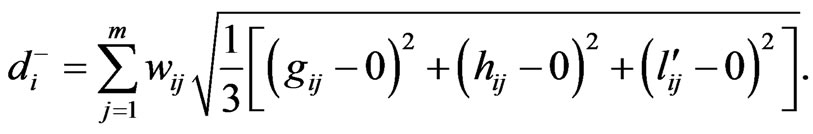 (13)
(13)
Step 13. Calculate the relative closeness .
.
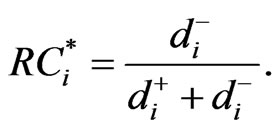 (14)
(14)
According to the values of , the candidates can be ranked.
, the candidates can be ranked.
4. Case Study
Suppose four spinning mills will form a dynamic alliance through pre-test. The four candidates are recorded as E1, E2, E3 and E4. In order to make a reasonable benefit allocation plan and attain a stability of the alliance, a crossfunctional decision committee consisting of various departments works to evaluate the risk of the four enterprises, named as D1, D2 and D3. The results will assist in making benefit allocation plan and risk management as well. The risk evaluating process based on FANP and fuzzy TOPSIS is as follows.
Step 1. With the interaction and feedback relationships between dimensions and/or attribute-enablers being considered, a four-level evaluation index system is presented, as shown in Figure 1.
Step 2. Pairwise comparison matrices among dimensions and/or attributes are formed by the decision committee using the linguistic scales given in Table 1. For example, Table 3 is the pairwise comparison matrix for market competition (S21), new product development or substitute (S22) and environmental change of target market (S23) at the dimension of market risk.
Expert opinions will be converted into the corresponding triangular fuzzy numbers, as shown in Table 4. All the fuzzy evaluation matrices are produced in the same manner.
Step 3. Local weights of the factors and sub-factors which take part in the second and third levels of the ANP model, provided in Figure 1, are calculated by FPP method. For instance, according to equation (4), the local weights of Table 4 can be obtained by solving the following non-linear programming.

Table 3. The comparison matrix at the dimension of market risk using linguistic variables.
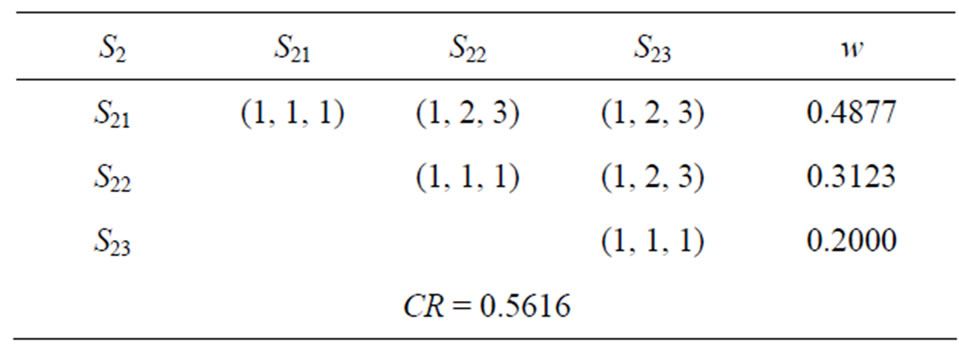
Table 4. The comparison matrix at the dimension of market risk using TFNs.
It can be solved by Matlab, and the optimal solutions are w1 = 0.4877, w2 = 0.3123, w3 = 0.2000, as shown in Table 4. Consistency index CR is 0.5616, which shows that the experts’ opinions have a good consistency, and the local weights are acceptable. All the local weights of comparison matrices are calculated in the same way.
Step 4. According to the interdependencies among dimensions and attribute-enablers of the ANP model, an unweighted supermatrix is built, as shown in Table 5.
Step 5. The unweighted supermatrix is being randomized to derive the weighted supermatrix.
Step 6. According to equation (5), multiplying the weighted supermatrix by itself until the supermatrix’s row values converge to the same value for each column of the matrix, then we choose any column from the steady limit supermatrix as the local weights of the interdependency indicators, as shown in Table 6.
Step 7. According to equation (6), the comprehensive weight wij of each index can be calculated, as shown in Table 7, and 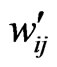 is the normalized weight of wij.
is the normalized weight of wij.
Step 8. The ratings of the enterprises with respect to each indicator are determined by Table 2.
Step 9. To construct fuzzy decision matrix, the linguistic scales are converted into triangular fuzzy numbers. According to the formulation (7), the ratings of the candidates with respect to each criterion can be calculated Step 10. According to equations (8) and (9), the normalized fuzzy decision matrix can be acquired, as shown in Table 8.
Step 11. Positive and negative ideal solutions are defined as

Step 12. According to equations (12) and (13), the weighted distances of each candidate from FPIS and FNIS can be calculated, as shown in Table 9.
Step 13. According to equation (14), the relative closeness of the four enterprises can be calculated by RC1 = 0.8199, RC2 = 0.8221, RC3 = 0.830 and RC4 = 0.7861, as shown in Table 9. Therefore, the risk profile of the four enterprises can be ranked as E3 > E2 > E1 > E4, and enterprise E3 is the best one.
The same ranking of the alternatives is drawn as reference [13], but this time the weights are obtained by FANP, and the ranking is determined by the closeness coefficient based on the distances to the positive and negative ideal solutions. It provides a new approach for evaluating the risk of dynamic alliance. As mentioned before, it is more adaptive to the final ranking of the alternatives as well.
5. Conclusion
With the interaction and feedback relationships between criteria and/or indicators being considered, an index system for evaluating the risk of dynamic alliance is
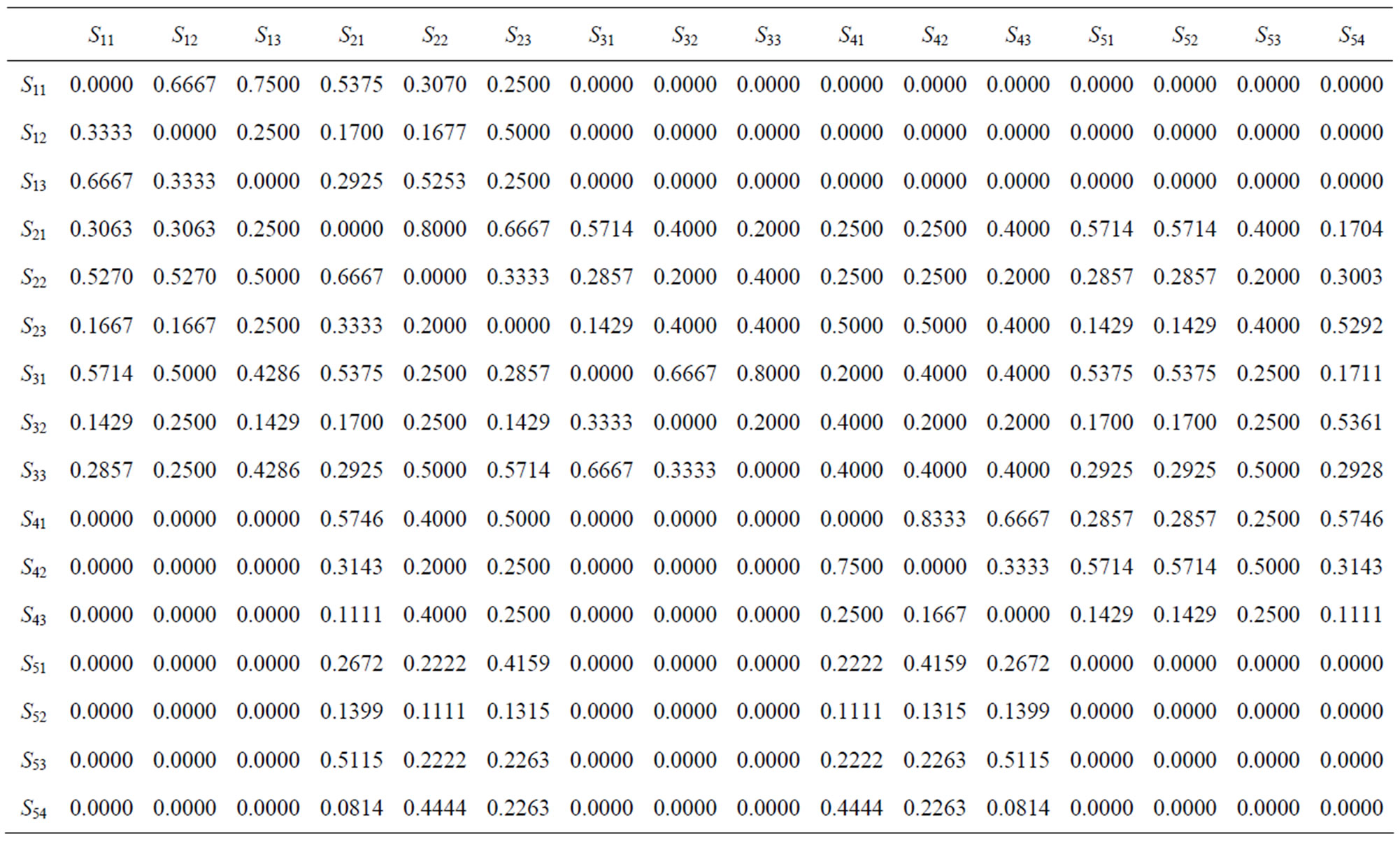
Table 5. The unweighted supermatrix.

Table 6. The limit supermatrix.
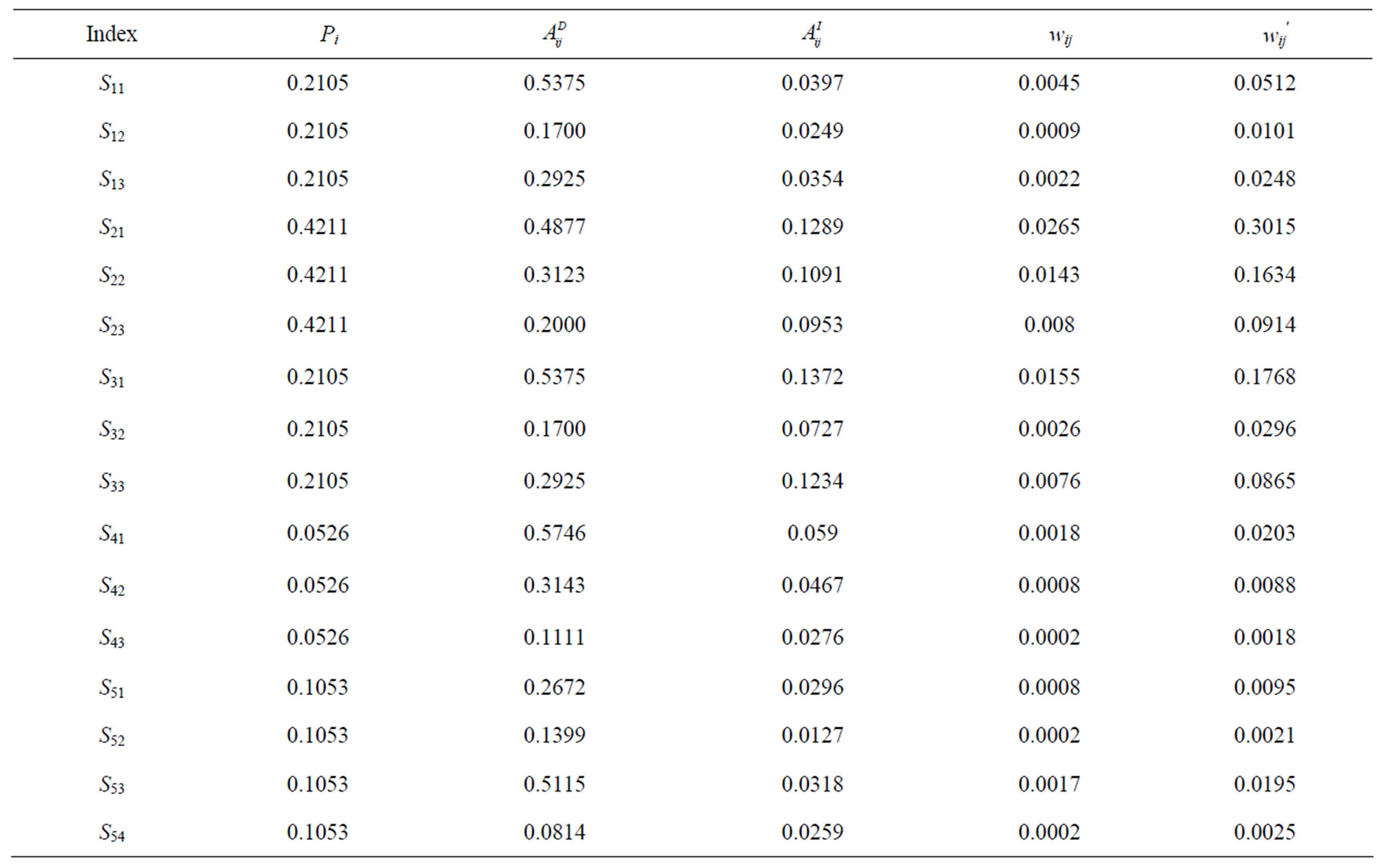
Table 7. Comprehensive weights of the indicators.

Table 8. The fuzzy normalized decision matrix.
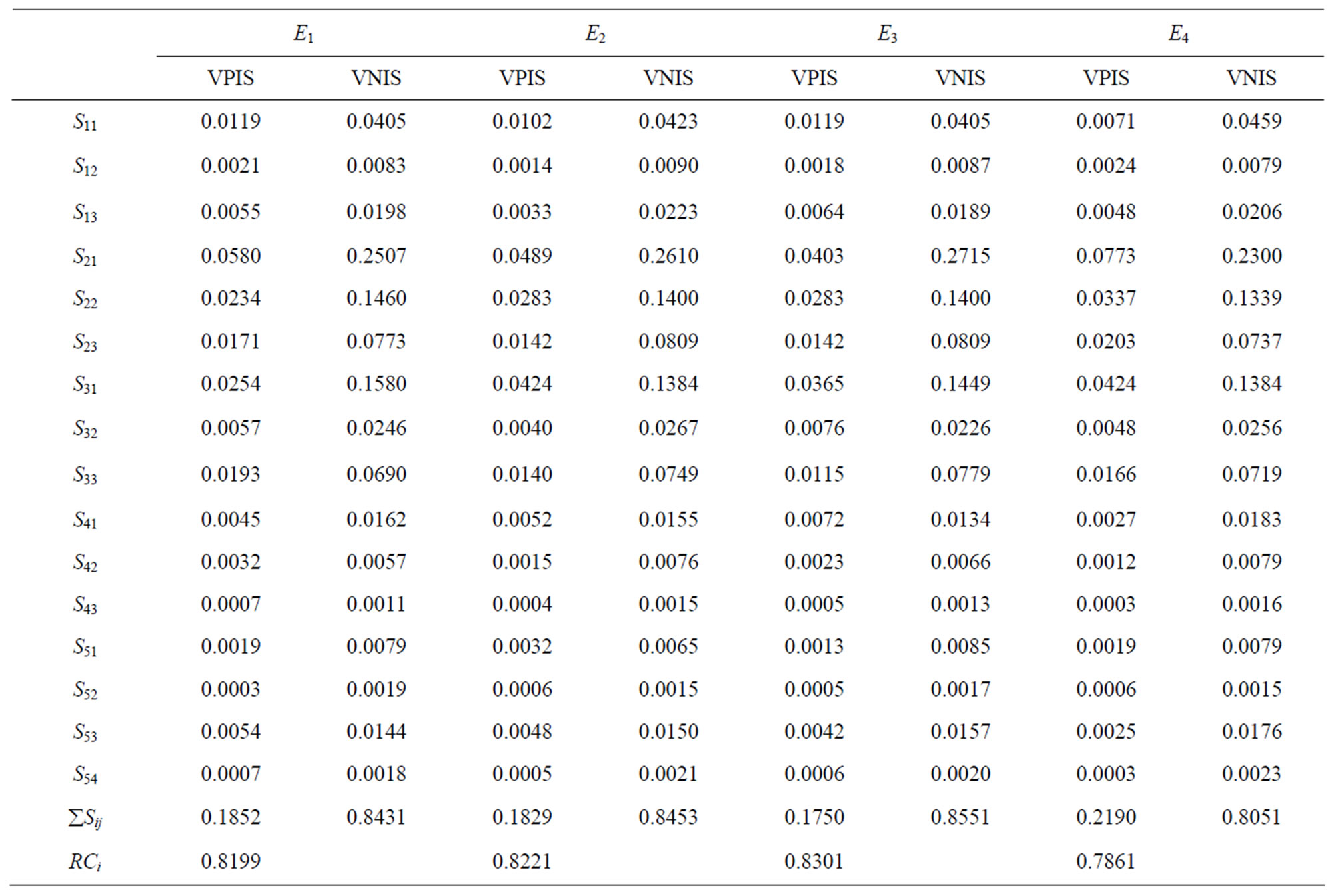
Table 9. Distances to FPIS and FNIS.
presented. With the uncertainty and the inaccuracy information during the evaluation process being considered, a model combining FANP and fuzzy TOPSIS is proposed. The local weights of criteria and indices are calculated by FPP, and the global weights are determined by FANP method. The distances between the candidates and positive ideal solutions or negative ones can be calculated by fuzzy TOPSIS. The rank of the candidates is derived by their relative closeness. A numerical case is given by the proposed method. The risk analysis of dynamic alliance will help enterprises to choose a coalition partner and make a reasonable benefit allocation plan, and it is advantageous in acquiring the stability of the union as well.
6. Acknowledgements
This work was supported by “the Fundamental Research Funds for Chinese Central Universities (No. FRF-BR-11- 009A)”.
REFERENCES
- T. P. Munyon, A. A. Perryman, J. P. Morgante and G. R. Ferris, “Firm Relationships—The Dynamics of Effective Organization Alliances,” Organizational Dynamics, Vol. 40, No. 2, 2011, pp. 96-103. doi:10.1016/j.orgdyn.2011.01.003
- S. R. Holmberg and L. J. Cummings, “Building Successful Strategic Alliances-Strategic Process and Analytical Tool for Selecting Partner Industries and Firms,” Long Range Planning, Vol. 42, No. 2, 2009, pp. 164-193. doi:10.1016/j.lrp.2009.01.004
- Y. Li and X. W. Liao, “Decision Support for Risk Analysis on Dynamic Alliance,” Decision Support Systems, Vol. 42, No. 4, 2007, pp. 2043-2059. doi:10.1016/j.dss.2004.11.008
- R. Venkatesh, V. Mahajan and E. Muller, “Dynamic CoMarketing Alliances—When and Why Do They Succeed or Fail?” International Journal of Research in Marketing, Vol. 17, No. 1, 2000, pp. 3-31. doi:10.1016/S0167-8116(00)00004-5
- T. K. Das and B. S. Teng, “A Risk Perception Model of Alliance Structuring,” Journal of International Management, Vol. 7, No. 1, 2001, pp. 1-29. doi:10.1016/S1075-4253(00)00037-5
- S. Rosenkranz and P. W. Schmitz, “Optimal Allocation of Ownership Rights in Dynamic R&D Alliances,” Games and Economic Behavior, Vol. 43, No. 1, 2003, pp. 153-173. doi:10.1016/S0899-8256(02)00553-5
- W. H. Ip, M. Huang, K. L. Yung and D. W. Wang, “Genetic Algorithm Solution for a Risk-Based Partner Selection Problem in a Virtual Enterprise,” Computers & Operations Research, Vol. 30, No. 2, 2003, pp. 213-231. doi:10.1016/S0305-0548(01)00092-2
- T. K. Das and R. Kumar, “Learning Dynamics in the Alliance Development Process,” Management Decision, Vol. 45, No. 4, 2007, pp. 684-707. doi:10.1108/00251740710745980
- M. Huang, W. H. Ip, H. M. Yang, X. W. Wang and H. C. W. Lau, “A Fuzzy Synthetic Evaluation Embedded Tabu Search for Risk Programming of Virtual Enterprises,” International Journal of Production Economics, Vol. 116, No. 1, 2008, pp. 104-114. doi:10.1016/j.ijpe.2008.06.008
- H. Delerue and E. Simon, “National Cultural Values and the Perceived Relational Risks in Biotechnology Alliance Relationships,” International Business Review, Vol. 18, No. 1, 2009, pp. 14-25. doi:10.1016/j.ibusrev.2008.11.003
- M. Huang, F. Q. Lu, W. K. Ching and T. K. Siu, “A Distributed Decision Making Model for Risk Management of Virtual Enterprise,” Expert Systems with Applications, Vol. 38, No. 10, 2011, pp. 13208-13215. doi:10.1016/j.eswa.2011.04.135
- P. Y. Lee, H. H. Chen and Y. H. Shyr, “Driving Dynamic Knowledge Articulation and Dynamic Capabilities Development of Service Alliance Firms,” The Service Industries Journal, Vol. 31, No. 13, 2011, pp. 2223-2242. doi:10.1080/02642069.2010.504820
- X. G. Zhou and Y. T. Song, “The Application of Fuzzy Analytic Network Process in Risk Evaluation of Dynamic Alliance,” Proceedings of IEEE International Conference on Supernetworks and System Management, Shanghai, 29-30 May 2011, pp. 157-162
- A. Pires, N. B. Chang and G. Martinbo, “An AHP-Based Fuzzy Interval TOPSIS Assessment for Sustainable Expansion of the Solid Waste Management System in Setúbal Peninsula, Portugal,” Resources, Conservation and Recycling, Vol. 56, No. 1, 2011, pp. 7-21. doi:10.1016/j.resconrec.2011.08.004
- T. L. Saaty, “Decision Making with Dependence and Feedback: The Analytic Network Process,” RWS Publications, Pittsburgh, 1996.
- Y. P. Ou Yang, H. M. Shieh and G. H. Tzeng, “A VIKOR Technique Based on DEMATEL and ANP for Information Security Risk Control Assessment,” Information Science, 2011, in Press. doi:10.1016/j.ins.2011.09.012
- N. S. Arunraj and J. Maiti, “Risk-Based Maintenance Policy Selection Using AHP and Goal Programming,” Safety Science, Vol. 48, No. 2, 2010, pp. 238-247. doi:10.1016/j.resconrec.2011.08.004
- P. J. M. Van Laarhoven and W. Pedrycz, “A Fuzzy Extension of Saaty’s Priority Theory,” Fuzzy Sets and Systems, Vol. 11, No. 1-3, 1983, pp. 229-241.
- J. J. Buckley, “Fuzzy Hierarchical Analysis,” Fuzzy Sets and Systems, Vol. 17, No. 3, 1985, pp. 233-247. doi:10.1016/0165-0114(85)90090-9
- D. Y. Chang, “Applications of the Extent Analysis Method on Fuzzy AHP,” European Journal of Operational Research, Vol. 95, No. 3, 1996, pp. 649-655. doi:10.1016/0377-2217(95)00300-2
- R. Xu, “Fuzzy Least-Squares Priority Method in the Analytic Hierarchy Process,” Fuzzy Sets and Systems, Vol. 112, No. 3, 2000, pp. 359-404. doi:10.1016/S0165-0114(97)00376-X
- R. Csutora and J. J. Buckley, “Fuzzy Hierarchical Analysis: The Lamda-Max Method,” Fuzzy Sets and Systems, Vol. 120, No. 2, 2001, pp. 181-195. doi:10.1016/S0165-0114(99)00155-4
- L. Mikhailov, “Deriving Priorities from Fuzzy Pairwise Comparison Judgements,” Fuzzy Sets and Systems, Vol. 134, No. 3, 2003, pp. 365-385. doi:10.1016/S0165-0114(02)00383-4
- B. Srdjevic. “Combining Different Prioritization Methods in the Analytic Hierarchy Process Synthesis,” Computers & Operations Research, Vol. 32, No. 7, 2005, pp. 1897- 1919. doi:10.1016/j.cor.2003.12.005
- Y. M. Wang, T. M. S. Elhag and Z. S. Hua, “A Modified Fuzzy Logarithmic Least Squares Method for Fuzzy Analytic Hierarchy Process,” Fuzzy Sets and Systems, Vol. 157, No. 23, 2006, pp. 3055-3071. doi:10.1016/j.fss.2006.08.010
- J. R. Yu and S. J. Cheng, “An Integrated Approach for Deriving Priorities in Analytic Network Process,” European Journal of Operational Research, Vol. 180, No. 3, 2007, pp. 1427-1432. doi:10.1016/j.ejor.2006.06.005
- L. A. Huo, J. B. Lan and Z. X. Wang, “New Parametric Prioritization Methods for an Analytical Hierarchy Process Based on a Pairwise Comparison Matrix,” Mathematical and Computer Modelling, Vol. 54, No. 11-12, 2011, pp. 2736-2749. doi:10.1016/j.mcm.2011.06.062
- C. L. Hwang and K. Yoon, “Multiple Attributes Decision Making Methods and Applications,” Springer, Berlin, 1981. doi:10.1007/978-3-642-48318-9
- S. J. Chen, C. L. Hwang and F. P. Hwang, “Fuzzy Multiple Attribute Decision Making,” Lecture Notes in Economics and Mathematical System, Vol. 375, 1992, pp. 1- 531.
- C. T. Chen, “Extensions of the TOPSIS for Group Decision-Making under Fuzzy Environment,” Fuzzy Sets and Systems, Vol. 114, No. 1, 2000, pp. 1-9. doi:10.1016/S0165-0114(97)00377-1
- I. Mahdavi, N. Mahdavi-Amiri, A. Heidarzade and R. Nourifar, “Designing a Model of Fuzzy TOPSIS in Multiple Criteria Decision Making,” Applied Mathematics and Computation, Vol. 206, No. 2, 2008, pp. 607-617. doi:10.1016/j.amc.2008.05.047

