Journal of Biomedical Science and Engineering
Vol.08 No.08(2015), Article ID:58700,10 pages
10.4236/jbise.2015.88045
Theoretical Evaluation of Both Unknown Substrate Concentrations and Enzyme Kinetic Constants of Metabolic Cycles
Antonio Sillero*, Víctor García-Herrero
Departamento de Bioquímica, Facultad de Medicina, Instituto de Investigaciones Biomédicas Alberto Sols UAM/CSIC, Madrid, Spain
Email: *antonio.sillero@uam.es
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 June 2015; accepted 7 August 2015; published 10 August 2015
ABSTRACT
A formula has been deduced, and named as 2ESKV, relating the concentration of two consecutive substrates of a metabolic cycle with the kinetic constants of the two enzymes involved in their synthesis and degradation. After application of formula 2ESKV to consecutive pairs of substrates and enzymes, a system of interrelated equations was obtained allowing a great variety of theoretical postulates to calculate, back and forth: bunches of unknown enzyme kinetic constants and substrate concentrations, from complementary sets of known data. This vision of a metabolic cycle is of partial application to irreversible pathways and can be useful for modeling and understanding of metabolomics data. To our knowledge, the formula 2ESKV is here described for the first time.
Keywords:
Metabolic Cycles, Evaluation Substrates, Evaluation Enzymes Constants, Differential Equations, Mathematica

1. Introduction
The study of enzyme kinetics and modeling is experimenting a revival with both the access to web databases and the increasing computer power [1] -[4] . Complex biological problems can now be investigated with experimental and theoretical approaches, both presenting their own limitations: experimental data are sometimes difficult, costly and lengthy to be implemented; theoretical alternatives offer many survey possibilities but must be in harmony with the experimental findings. The joining of both complementary alternatives is part of the modern System Biology [5] -[7] .
In this sense, part of the previous experimental work on ubiquitin activating enzyme [8] was modeled and amplified with a theoretical approach [9] . The advantages resulted from this double approach directed our efforts to focus previous results from our laboratory with this double vision [10] .
The work presented here amplified previous studies from this laboratory [10] [11] and started from the simulation of an irreversible pathway (composed of 6 substrates and 5 enzymes), using a system of differential equations (see below). When the pathway is initiated with the first substrate, it is successively transformed into the consecutive substrates, ending with its total transformation onto the final substrate. The time course of the concentration of the different substrates in a linear irreversible pathway is here named as their “profiles” (Figure 1(A) and Figure 1(B)); the theoretical transformation of a linear into a cyclic pathway is performed by adding a new enzyme (E6) which catalyzes the inter-conversion between the first (a) and the last (f) substrate of the primitive linear pathway. This transformation is visualized in Figure 1, where panels (A) and (D) represent schemes of linear and cyclic pathways, respectively. The novelty of this work starts with an apparently minor observation: during a transitory time, the rate of synthesis and degradation of two consecutive substrates of an irreversible pathway is equal, i.e., they are in a transitory steady state; from the mathematical expression of that instant, a formula is obtained (named as 2ESKV), applicable to all the consecutive pairs of substrates and enzymes of any cycle. In our view, this is a new finding correlating all the substrates and enzyme kinetic of any metabolic cycle.
2. Nomenclature
The linear pathway considered here as a model contains 5 enzymes (E1 to E5) and 6 substrates named from (a) to (f); the cyclic pathway contains 6 enzymes (E1 to E6) and 6 substrates (Figure 1, panels (A), (D)).
The Mathematica Program 9.0 [12] was used throughout this work to solve the differential equations describing those pathways (see Table 1), with the following main commands: derivatives, D[f(x), x]; plot representations, Plot [f(x), x, xmin, xmax]; solution of a system of differential equations, NDSolve [eqns, vars] and Solve [eqns, vars]; a', b', etc., correspond to da/dt, db/dt, etc.; on occasions the term “box”, in the context of a cycle, refers to the (potential) location of a substrate; a box can be empty or ready to accommodate its substrate. The commands used for the solution of differential equations (see Table 1) are assembled in five parts: 1) Equations of the actual velocities of the enzymes (named from v1 to v6); for an appropriate recognition by Mathematica, Vmax and Km have been named as V and K, followed by a subscript with the letter of the corresponding substrate. For example Va and Ka refer, unequivocally, to the Vmax and Km values of enzyme E1 towards its substrate (a), etc.; the sequence of the reactions is indicated in Figure 1, panels (A), (D); 2) The actual values of the kinetic constants for each enzyme and the values assigned to all the constants in the control pathway are equal to unity; these values can be changed by the operator at will (Table 1); 3) Differential equations used to calculate the substrate concentrations along the reaction time; these equations are followed by the initial conditions, unknowns be solved and reaction time; 4) The statements required for the Mathematica Program to solve the differential equations shown in 3), and to represent the profiles of the substrates (Figure 1, panels (B) and (E)); 5) The statements required for the Mathematica Program to solve the differential equations shown in 3), and to present the graphs with the derivatives of the profiles (Table 1); (Figure 1, panels (C) and (F)).The Mathematica Program in Table 1 has been arranged in such a way that may serve to represent: the substrate profiles of the cycle, (parts 1 + 2 + 3 + 4) (panel (E), Figure 1); the derivative of those profiles, (parts 1 + 2 + 3 + 5) (panel (F), Figure 1); the panels (B) and (C) corresponding to a linear pathway were obtained following the same instructions as above with the unique, but important modification, of making Vf = 0 in part 2 of Table 1.
3. Results and Discussion
3.1. Linear Pathway
From the profiles of a metabolic irreversible pathway it can be inferred that at their apexes the concentration value of each metabolite (Sn) is constant (Figure 1(B)), because the rate of its synthesis equals that of its degradation; in mathematical terms the value of the derivative of its profile (dSn/d t) is zero at this time point, as indicated by the vertical line for substrate (c) (Figure 1(B) and Figure 1(C)). Substrate (c) is synthesized from substrate (b) (dotted line) by enzyme E2 (Equation (1)), and transformed to the following substrate (d) by E3 (Equation (2)).Although other consecutive substrates of the pathway could be considered, the following calculations refer exclusively to substrates (b)-(d).
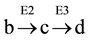
Accordingly, the rate of synthesis and degradation of substrate (c) by enzymes with Michaelis-Menten kinetics is shown in Equation (1) and Equation (2), respectively
Figure 1. Representation of an irreversible linear metabolic pathway (panels (A)-(C) and of a cyclic pathway (panels (D)- (F)). Panels (A) and (D) are schematic drawings of both types of pathways, composed by the same number of substrates (6), but different number of enzymes five or six, respectively. In panels (B) and (E), are the substrate profiles of the linear and cyclic pathways, respectively, obtained as described in the Table 1 (parts 1 + 2 + 3 + 4). In panels (C) and (F) are the derivatives of both profiles obtained as described in Table 1 (parts 1 + 2 + 3 + 5). In one case, as indicated in panel (D), the reaction between (c) and (d) was also considered catalyzed by a reversible enzyme (E3N). This particular case will be considered in Figure 2 (see also Table 4 and Table 7. The vertical line in panel (B) indicates exclusively its intersection with the profiles of substrates (c) and (b) (coincident full circle) and (d) (empty circle); the intersections in panel (C) are marked with full, empty circles, and an x sign for substrates (c), (d) and (b), respectively.
Table 1. Mathematica protocol for drawing of Figure 1.
 (1)
(1)
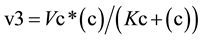 (2)
(2)
as
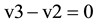 at the indicated time point (Figure 1(B))
at the indicated time point (Figure 1(B))
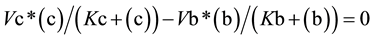 (3)
(3)
From Equation (3), the value for (c) as a function of (b) (Equation (4a)) or the value of (b) as function of (c) (Equation (4b)) can be easily deduced,
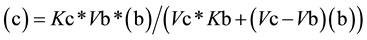 (4a)
(4a)
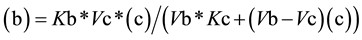 (4b)
(4b)
In general, the relationship between the concentrations of any substrate intermediate (named as Sn) and the preceding one (Sn − 1), at the apex of substrate Sn, is according to Equation (5),
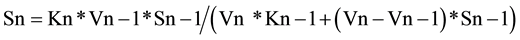 (5)
(5)
Formula (5) (named also as 2ESKV, due to the participation of 2 substrates and 2 enzymes, with their kinetics constants), of an apparently limited interest, simply reflects the relative value of two consecutive substrates at steady state and at a specific time in a linear metabolic irreversible pathway.
3.2. Comparative Aspects of Linear and Cyclic Pathways
Unless some regulatory mechanisms operate [11] , the initial substrate of a linear (irreversible) pathway is totally converted into a final product through the sequential appearance and disappearance of the intermediate metabolites of the pathway. The steady state condition is reached only with both the total synthesis of the final product and the consumption of the intermediates metabolites. At this end stage, the derivatives of all the profiles of a linear pathway are zero (Figure 1(C)).
By contrast, in a cyclic pathway, continuous transformation among the substrates/metabolites takes place during a certain time (Figure 1(E), 0 to 4 min) and, thereafter, a dynamic steady state is reached as a consequence of a mutual and unique relationship (Formula (5) or 2ESKV) among a pair of substrate concentration and their corresponding enzyme kinetic constants (see below), as an orchestra performing a symphony in the absence of a director. The initial substrate (in this example (a), 1 mM) is transformed/distributed in the boxes of the cycle Figure 1, panels (D)-(F)). At the early initial steps of the reaction, the time course for substrate concentrations of linear or cyclic pathways (their profiles) are very similar (compare panels (B) and (E) in Figure 1, from 0 to 4 min). Afterwards, the intermediate metabolites of the linear irreversible pathway tend to zero, whereas those of the cyclic pathway tend to reach a fixed concentration. As a consequence, for an obvious different reason, the derivatives of the cyclic and irreversible profiles tend to zero (Figure 1, panels (C) and (F)). As shown below, the interdependence among all substrates, each one with the preceding or with the next one (two by two) of a metabolic cycle, converts Formula (5) (or 2ESKV) in a very useful tool to quantify metabolite concentrations and enzyme kinetic constants of metabolic cycles, as shown below.
3.3. A General Procedure to Calculate the Concentration of the Substrates and Enzyme Kinetic Constants of a Metabolic Cycle, with Significant Examples
Formula (5) (or 2ESKV) was deduced initially through application of a system of differential equations to elucidate the time course of substrate levels in an irreversible metabolic pathway (see 3.1); it could be considered as a kind of photography of an instant metabolic situation where the concentration of two consecutive substrates are in steady state.
By its own nature, a metabolic cycle can be viewed as a system tending to reach a steady state situation between two consecutive substrates and, therefore, among all the substrates of the cycle; against expectation, application of Formula (5) generates a new relationship among substrates and enzyme kinetic constants of any cycle; this relationship can be translated into a series of equations, allowing deduction of unknown fragments from other known components of the cycle. In our view, and based on the plethora of data accumulated in multiple data banks, this methodology could be of general and multiple applications to cycles operating under physiological conditions, and to analyze the consequences that changes in both, the concentration of some substrates or in the values of some enzyme kinetic constants, may produce on the functional status of the cycle. The above general considerations on the usefulness of formula 2ESKV will be implemented with the selected 4 examples of model cycles composed of 6 substrates and 6 enzymes (Figure 1(D); Table 2), representatives of a variety of metabolic situations.
Table 2. Evaluation of Substrate concentrations from enzyme kinetic constants and vice versa, using formula 2ESKV and the general protocol described in Table 1. The specific applications for each of the 4 Examples are in Table 4.
3.3.1. Example 1
From the known values of 12 kinetic constants and the total sum of substrate concentration, the concentration of each substrate can be calculated.
This first example will be also taken as a general procedure for these calculations as detailed in Table 3. This Table contains the Mathematica protocol to analyze a model cycle composed of 6 enzymes (E1 to E6), their 12 kinetic constants, and assuming as known a value of 120 mM for the total concentration of the 6 substrates (a to f); however, the particular concentration of each one is unknown, and it is to be calculated. The column on the left (Table 3) shows the two consecutive pair of substrates to be considered (from a <--->f). Any substrate can be taken as the first or as the last one of the cycle, although substrates (a) and (f) were selected as such. The column at the right displays the formula 2ESKV applied to the indicated consecutive pair of substrates. At the bottom of Table 3 are the instructions given to Mathematica to solve the equations using the command NSolve. These instructions may differ depending on the cycle to be approached. Nevertheless, some general rules apply: 1) the number of equations must be equal to the number of unknowns; 2) the program automatically offers a set of solutions/possibilities (4)-(6) for the unknowns, some of them with unrealistic negative values. To avoid this possibility, the program is instructed to return only values >0. Finally the unknowns to be solved are stated. Note as in Example 1, the formula corresponding to the step f- > a was not used (for unnecessary or redundant) in the command NSolve. Another different step (but only one) can be eliminated with the same result. As expected, the sum of the calculated values for each substrate was (indeed) 120 mM (exactly, 120,000,059) (see Table 2 and Table 4).
The standard procedure outlined in Table 3, could be taken as a model example. Many other possibilities can be contemplated; in each case the operator should modify the NSolve instructions according to the objectives. To simplify the procedure, significant application possibilities were collected in these four examples, with the initial conditions and solutions shown in Table 2, and with the specific mathematical instructions in Table 4. The first column of Table 2 contains the parameters to be considered: substrates ((a) to (f)) and kinetic constants of enzymes E1 to E6, named as Ka, Va, to Kf, Vf). There are two columns for each one of the four examples, one for the fixed values (or known values) and another one for the unknown values (Table 2). Table 4 contains the necessary instructions for the Mathematica solutions of examples 1 to 4 (Table 2). Note as in Table 4, the calculated results are in bold characters in the four examples.
3.3.2. Example 2
From the prefixed concentration values for each one of the substrates (as calculated in Example 1) and from 7 known kinetic constants (Kb, Kd, Kf, Va, Vc, Ve, Vf), the 5 unknown kinetic constants (Ka, Kc, Ke, Vb, Vc) were calculated (Table 2 and Table 4). The line (a + b + c + d + e + f = 120) of the command Solve (Table 3) was elim-
Table 3. A general procedure to calculate the concentration of the substrates of a metabolic cycle. The method was applied to a cycle composed by 6 substrates and 6 enzymes (Figure 1(D). From the known kinetic constants values and the total sum of the substrates concentration, the concentration of each particular substrate was calculated. See also Table 4, Example 1 and Table 2, Example 1.
Table 4. Protocol followed to apply Equation (5) for the solution of the problems specified in Table 2.
inated in this example (for unnecessary). Note as in this, and in other examples, substrate concentrations and the Kn and/or Vn constant values used were those obtained in previous Examples, what could be taken as an inner control of the mathematical procedure.
3.3.3. Example 3
From the prefixed concentration values for each one of the substrates ((a) to (f)) and from a particular set of known kinetic constants, the rest of the kinetic constants were calculated (Table 2 and Table 4); a treatment similar to the above Example 2 was applied.
3.3.4. Example 4
From the prefixed values for the 12 kinetic constants and the concentration value of only one substrate (c), the concentrations of the other 5 substrates were calculated (Table 2 and Table 4). This example can be taken as a kind of instructive and very useful approach: the concentration of all the substrates of a cycle can be predicted from the kinetic constants and from the concentration of only one substrate. This example (Table 2) was also useful to test whether the differential equations system used in Table 1 to plot Figure 1 render identical results as those obtained by application of formula 2ESKV; the substrate concentration reached at steady state was the same in both cases (results not shown, see also Figure 2, displaying a similar approach).
3.4. Application of Formula 2ESKV to a Cycle Including One Reversible Step
A reversible step of the cycle, involving three substrates (b), (c) and (d) and 3 enzymes (E2, E3N and E4) (see Figure 1, panel (D)), was simulated considering reversible, the reaction between (c) and (d), catalyzed by enzyme E3N,
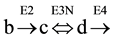
Two different, but complementary approaches were followed to analyze the concentration of the substrates of the cycle, at steady state: 1) the use of differential equations; 2) application of variants of formula 2ESKV. In both cases, the initial conditions of the cycle are specified in Table 1 and in Table 5.
A) For the first purpose, and to facilitate the handling of Mathematica, Table 5 was created containing 6 enzymes with the shown kinetic constants, and only one initial fixed substrate (a) (1 mM) to be distributed among
Figure 2. Substrate profiles representation of a cyclic pathway with one reversible step between c<===>d catalyzed by E3N. A scheme of this pathway is shown in Figure 1.The protocol given to Mathematica to plot this figure is as outlined in the text, Table 4 and in Table 5. The concentrations reached at equilibrium (between brackets) for each substrate, and calculated with the 2ESKV formula, described also in Table 5, agree quite well with those visualized in this representation obtained with the differential equations and when the reaction time was expanded until the substrates reached equilibrium.
Table 5. Mathematical protocol used to obtain the substrate profile of a cycle with a reversible step (E3N) with all the kinetic constants fixed (known) and with only one fixed (known) substrate concentration (a. 1 mM). The resulting plot is represented in Figure 2.
the boxes of the cycle. One of the enzymes (E3N) catalyzed the unique reversible reaction with the indicated initial equation velocity usually considered in this type of reactions (v3N) and with indicated Km and Vmax values in the forward (Kcfw, Vcfw) and in the reverse directions (Kcr, Vcr). The profile courses of the 6 substrates were followed until the steady states were reached (Figure 2).
B) Following similar reasoning as in 3.1, variants of formula 2ESKV were elaborated considering that all substrates (particularly (b), (c) and (d)) reached the steady state concentration (Figure 1, panel (D); Table 6, Figure 2). Table 6 is apparently more complicated than Table 3, although in both cases Formula 2ESKV was applied. Table 6 contains 3 panels (A)-(C). The left upper part of panel (A) indicates the transformation between consecutive substrates a<---->f, including the reverse reaction between substrates (c) and (d); in the upper right side of panel (A) are the formulas for substrates (a) to (f); at the bottom of panel (A) are the instructions given to the command NSolve for the solutions of the indicated equations.
The equation for substrate (d) was obtained as indicated in panel (B) of Table 6;
The equation for substrate (c) was obtained as indicated in panel (C) of Table 6.
The calculated concentration values (mM) obtained for the 6 substrates were a- > 0.137249, b- > 0.126577, c- > 0.0337561,d- > 0.228748, e- > 0.383544, f- > 0.090125 (Table 7).
These exact values, obtained by application of formula 2ESKV as indicated in Table 6, agree quite well with those visualized with the differential equations approach (Table 1; Figure 2, between brackets: a (0.13), b (0.12), c (0.03), d (0.22), e (0.38), f (0.09)).
Table 6. The case of a metabolic cycle with one reversible step (Figure 1(A)).
Table 7. Use of the formula 2ESKV to calculate the substrate concentration of a cycle with a reversible step, knowing the value of the kinetic constant and the concentration of only one substrate (a, 1 mM). The values of the parameters are in Table 5.
4. Discussion
Mathematical simulations of linear pathways have been preferentially approached in most of the reactions involved in metabolic and regulatory networks of the cell. In this work, the formula 2ESKV was deduced starting from the unique time point where the concentration of a substrate reached a steady-state situation in an irreversible linear pathway. This formula is readily applicable to a metabolic cycle where, by its own nature, tends to reach a situation of quasi equilibrium among all the substrates. The metabolic pathways of a cell are composed of interconnected cycles and linear pathways, with multiple regulatory points, with activators, inhibitors, reversible and irreversible steps, and with a continuous entry and exit of metabolites at many levels, etc. Probably because linear pathways are present in most of those reactions, mathematical simulations of these pathways have been preferentially approached [1] [2] [5] [6] [13] -[15] . Cyclic pathways, of similar pivotal importance, have attracted a minor number of these studies with the exception of the classical Krebs/glyoxylate [16] -[21] and urea cycles [22] -[24] . Superimposed to this complex machinery is the fact that most of the metabolite pairs must be in a quasi equilibrium status. As a consequence, formula 2ESKV can be of potential application, if the kinetics constants of the enzyme(s) acting on two consecutive substrates are known.
Finally, it can be speculated whether formula 2ESKV can be applied, with the proper conceptual modifications to other cyclic systems, such as ecological or economical cycles, tending also to reach equilibrium among their constituents. In these cases, the concept of Vmax and Km can be viewed as the maximal capacity to execute an action and under which circumstances half of this action is performed, respectively.
Acknowledgements
We thank Javier Pérez for very helpful drawing assistance and Drs. María Antonia Günther Sillero and José González Castaño for helpful comments on the manuscript. This investigation was supported by Grant BFU2009-08977.
Cite this paper
AntonioSillero,VíctorGarcía-Herrero, (2015) Theoretical Evaluation of Both Unknown Substrate Concentrations and Enzyme Kinetic Constants of Metabolic Cycles. Journal of Biomedical Science and Engineering,08,479-489. doi: 10.4236/jbise.2015.88045
References
- 1. Alberty, R.A. (2011) Enzyme Kinetics: Rapid-Equilibrium Enzyme Kinetics. John Wiley & Sons, Hoboken.
http://dx.doi.org/10.1002/9780470940020 - 2. Goldbeter, A. (2013) Oscillatory Enzyme Reactions and Michaelis-Menten Kinetics. FEBS Letters, 587, 2778-2784. http://dx.doi.org/10.1016/j.febslet.2013.07.031
- 3. Chen, W.W., Niepel, M. and Sorger, P.K. (2010) Classic and Contemporary Approaches to Modeling Biochemical Reactions. Genes & development, 24, 1861-1875.
http://dx.doi.org/10.1101/gad.1945410 - 4. Milanowski, P., Carter, T.J. and Weber, G.F. (2013) Enzyme Catalysis and the Outcome of Biochemical Reactions. Journal of Proteomics Bioinform, 6, 132-141.
http://dx.doi.org/10.4172/jpb.1000271 - 5. Fell, D. (1997) Understanding the Control of Metabolism. Portland Press, Portland. Distributed by Ashgate Pub. Co. in North America, London; MiamiBrookfild, VT.
- 6. Klipp, R., Herwig, R., Kowald, A., Wierling, C. and Lehrach, H. (2005) System Biology in Practice. Wiley-VCH Verlag GmbH &Co, Winheim (FRG).
http://dx.doi.org/10.1002/3527603603 - 7. Alon, U. (2006) An Introduction to System Biology. Design Principles of Biological Circuits. CRC Pres, Taylor & Francis Group, London.
- 8. Günther Sillero, M.A., de Diego, A., Perez-Zuniga, F.J. and Sillero, A. (2008) Synthesis of Bisphosphonate Derivatives of ATP by T4 DNA Ligase, Ubiquitin Activating Enzyme (E1) and Other Ligases. Biochemical Pharmacology, 75, 1959-1965.
http://dx.doi.org/10.1016/j.bcp.2008.02.017 - 9. López-Cánovas, F.J., Cánovas, F., Günther Sillero, M.A. and Sillero, A. (2010) Mathematical Model for the Ubiquitin Activating Enzyme E1. Journal of Biomedical Science and Engineering, 3, 274-284.
http://dx.doi.org/10.4236/jbise.2010.33037 - 10. López-Cánovas, F.J., Gomes, P.J. and Sillero, A. (2013) Mathematica Program: Its Use to Simulate Metabolic Irreversible Pathways and Inhibition of the First Enzyme of a Metabolic Pathway as Visuaized with the Reservoir Model. Computers in Biology and Medicine, 42, 853-864.
http://dx.doi.org/10.1016/j.compbiomed.2013.04.003 - 11. García-Herrero, V., López-Cánovas, F.J. and Sillero, A. (2014) A Model Metabolic Cycle Simulated with the Mathematica Program. Journal of Biomedical Science and Engineering, 7, 286-295.
http://dx.doi.org/10.4236/jbise.2014.75031 - 12. Wolfram, S. (2013) Wolfram Mathematica Tutorial Collection.
http://www.wolfram.com/learningcenter/tutorialcolection - 13. Voet, D. and Voet, J.G. (2004) Biochemistry. John Wiley & Sons, Hoboken, 1482-1493.
- 14. Segel, I.H. (1975) Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady State Enzyme Systems. Wiley, New York
- 15. Bisswanger, H. (2004) Enzyme Kinetics: Principle and Methods. Wiley-VCH, Weinheim.
- 16. Albe, K.R. and Wright, B.E. (1992) Systems Analysis of the Tricarboxylic Acid Cycle in Dictyostelium discoideum. II. Control Analysis. The Journal of Biological Chemistry, 267, 3106-3114.
- 17. Oliveira, J.S., Bailey, C.G., Jones-Oliveira, J.B., Dixon, D.A., Gull, D.W. and Chandler, M.L. (2003) A Computational Model for the Identification of Biochemical Pathways in the krebs Cycle. Journal of Computational Biology: A Journal of Computational Molecular Cell Biology, 10, 57-82.
http://dx.doi.org/10.1089/106652703763255679 - 18. Wu, F., Yang, F., Vinnakota, K.C. and Beard, D.A. (2007) Computer Modeling of Mitochondrial Tricarboxylic Acid Cycle, Oxidative Phosphorylation, Metabolite Transport, and Electrophysiology. The Journal of Biological Chemistry, 282, 24525-24537.
http://dx.doi.org/10.1074/jbc.M701024200 - 19. Nazaret, C., Heiske, M., Thurley, K. and Mazat, J.P. (2009) Mitochondrial Energetic Metabolism: A Simplified Model of TCA Cycle with ATP Production. Journal of Theoretical Biology, 258, 455-464.
http://dx.doi.org/10.1016/j.jtbi.2008.09.037 - 20. Amador-Noguez, D., Feng, X.J., Fan, J., Roquet, N., Rabitz, H. and Rabinowitz, J.D. (2010) Systems-Level Metabolic Flux Profiling Elucidates a Complete, Bifurcated Tricarboxylic Acid Cycle in Clostridium acetobutylicum. Journal of Bacteriology, 192, 4452-4461.
http://dx.doi.org/10.1128/JB.00490-10 - 21. Smith, A.C. and Robinson, A.J. (2011) A Metabolic Model of the Mitochondrion and Its Use in Modelling Diseases of the Tricarboxylic Acid Cycle. BMC Systems Biology, 5, 102.
http://dx.doi.org/10.1186/1752-0509-5-102 - 22. Bachmann, C. and Colombo, J.P. (1981) Computer Simulation of the Urea Cycle: Trials for an Appropriate Model. Enzyme, 26, 259-264.
- 23. Morris Jr., S.M. (2002) Regulation of Enzymes of the Urea Cycle and Arginine Metabolism. Annual Review of Nutrition, 22, 87-105.
http://dx.doi.org/10.1146/annurev.nutr.22.110801.140547 - 24. Maher, A.D., Kuchel, P.W., Ortega, F., de Atauri, P., Centelles, J. and Cascante, M. (2003) Mathematical Modelling of the Urea Cycle. A Numerical Investigation into Substrate Channelling. European Journal of Biochemistry, 270, 3953-3961.
http://dx.doi.org/10.1046/j.1432-1033.2003.03783.x
NOTES
*Corresponding author.






