Journal of Biomedical Science and Engineering
Vol.08 No.03(2015), Article ID:54709,10 pages
10.4236/jbise.2015.83013
Computational Analysis of Anastomotic Angles by Blood Flow Conditions in Side-to-End Radio-Cephalic Fistulae Used in Hemodialysis
Janaína de Andrade Silva1, José Karam-Filho2, Carlos Cristiano H. Borges3*
1Graduate Program of Computational Modeling, Federal University of Juiz de Fora, Juiz de Fora, Brazil
2CMC/National Laboratory for Scientific Computing, Petrópolis, Brazil
3PPGMC/Federal University of Juiz de Fora, Juiz de Fora, Brazil
Email: nainasjdr@hotmail.com, jkfi@lncc.br, *cchborges@ice.ufjf.br
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 January 2015; accepted 12 March 2015; published 17 March 2015
ABSTRACT
Chronic renal failure is a disease that affects a considerable population percentage that requires the hemodialysis procedure which is a blood filtration. This process is extremely stressful in many cases for the patient, because there is a continuous degradation of vessels and fistulae susceptible to this process due to the alterations of the stress at the blood vessel walls and flow patterns, leading to diseases such as intimal hyperplasia and consequent stenosis. Experimental in vivo researches in this area are very difficult to perform. In this sense computational models become interesting non invasive options to understand what happens to the blood in non viscometric geometries. In this work, we analyse blood flow, through computational modeling, in arteriovenous fistulae used in hemodialysis, using geometries with dimensions close to real ones. Discretization of the governing equations was made through a finite volume technique with the PISO―Pressure Implicit with Splitting of Operators―algorithm, using as a basis the OpenFOAM software platform. Large vessel Newtonian fluid model was used to analyze six possible anastomotic angles (20˚, 25˚, 30˚, 35˚, 40˚, 45˚). To analyze the possibility of stenosis formation caused by hyperplasia, results for wall shear stress, oscillatory shear index (OSI), velocity and local circulation fields were obtained, showing that higher angles presented more secondary flows and larger extensions of stagnation regions near the critical areas of the junctions. Moreover, a range around 25˚ was identified to be the most suitable choice for clinical applications, minimizing possibility of diseases.
Keywords:
Hemodialysis, Wall Shear Stress, Stagnation Flow, Finite Volume Method, Blood Flow, Large Vessels

1. Introduction
Chronic renal failure is a disease in which partial loss of the kidney function occur in a slow, progressive and irreversible way. As a leading alternative treatment for this deficiency, the blood filtering process called hemodialysis is used. This is a process which consists in filtering blood and removing impurities from this fluid, similar to the process executed by the kidney. The blood is first transported through a venous access connected to an artificial arterial fistula and subsequently the blood passes through the dialysis process being filtered [1] . In this case, the chronic renal failure patient may undergo various disorders such as nausea and loss of venous access, among others.
The problems related to fistulae are believed to be caused due to friction generated by the shear forces of blood on the vessel walls, causing diseases like intimal hyperplasia and thrombosis [2] [3] .
Intimal hyperplasia is a process in which cells proliferate on the vessel walls in response to injury. This can reduce the diameter of the vessels, obstructing the passage of blood, and can lead to blood clotting [4] [5] forming stenoses. The main region of stenosis formation generated by hyperplasia is near the junction of the vein or graft and the main vessel, generally an artery, causing failure in the maturation of vascular grafts for hemodialysis [6] . One of the most widely used vascular access is the junction between the radial artery and the cephalic vein known as radio-cephalic fistula, arranged mostly in two different configurations known as end-to-end and side-to-end anastomoses. These junctions suffer constantly with the development of stenoses [7] .
Endothelial cells are sensitive to wall shear stress and in oscillatory flows these cells and those within the flowing blood are subjected to a wide range of varying shear stress. Both high and low shear influence the ways these cells respond to local hemodynamic conditions. There is a propensity to develop stenoses at specific sites, suggesting that the geometry of the fistula and the resulting local hemodynamic conditions have their role in the development of that disease [8] .
In vascular vessels, shear stress acts mainly on the inner surface of the vessels wall (endothelium) and has an indirect function to regulate vessel diameter. Following [9] , high levels of shear increases wall thickness and expand vessel diameters, and low shear stresses induces reduction in vessel diameters leading to intimal hyperplasia and other pathologies [10] [11] . Studies relating shear stress and endothelium responses suggest that normal, relative high, levels of shear stress also stimulates endothelium to release antithrombotic biochemical agents [12] - [17] . [18] performed in vitro investigations of cell responses from cultured endothelium cells subjected to simple shear flows and, among many other enlightening conclusions, the authors reported the bad association between oscillating and low levels of shear stress, and regions with disturbed flows were associated with local accumulation of LDL cholesterol.
According to several researches, low shear stresses are accompanied by unstable fluid conditions like turbulence, stagnation regions, recirculation and are related to several pathologies [19] [20] . Atherogenesis in arteries has been identified in association with low shear stresses by [3] [19] - [23] . Low shear stress levels have been associated to anastomosis, thrombosis and intimal hyperplasia in grafts [6] , and to in-stent restenosis [24] . Progressive plaques and vascular remodeling have been related to low shearing regions in an in vivo study of coronary artery by [25] , and to oscillating shear stress by [26] .
[27] investigated flow conditions in end-to-end fistulae accesses used in hemodyalisis, considering Carreau model for blood. In [2] analyses of radial-cephalic fistulae have been carried out for three configurations: end- to-end, side-to-end with antegrade and retrogate flow for a fixed anastomotic angle.
Aiming the suitability of minimally invasive techniques, computational models capable of simulating blood behavior are being widely required. Considering computational fluid dynamics, [28] performed simulations analyzing and indicating disturbed flow conditions in association with shear stress in carotid bifurcation for large vessel Newtonian blood model. Wall shear-stress and flow distribution have been computationally investigated by [29] in cerebral aneurisms. In [2] , radial-cephalic fistulae for three conformations were analyzed: end- to-end, side-to-end with antegrade and retrogate flow for a fixed anastomotic angle. In [30] they were simulated anastomotic angles of 30˚, 40˚, 60˚ and 90˚ using Carreau model and, from the results for velocity and relative residence time, conclusions have been reported in favor of the smaller angle.
In this work, aiming to contribute to the investigation of better anatomical configurations that could generate more favorable hemodynamic conditions, to minimize the problems related with fistulae failures, computational analyses are performed considering six medium to small anastomotic angles: 20˚, 25˚, 30˚, 35˚, 40˚ and 45˚, before any stenosis or other pathologies have started. In this case, the vessel diameters are big enough (>0.1 mm) to consider large vessel Newtonian blood flow model [31] -[35] . A finite volume computational method is used to solve the equations for the pulsating flow problems, using as a basis the OpenFoam free software platform. To analyze the possibility of stenosis formation, results are obtained here for wall shear stress, oscillatory index, velocity contour fill and local circulation fields. From the results, a narrow range around 25˚ is suggested as the most suitable choice for clinical applications, minimizing possibilities of diseases.
2. Methodology
2.1. Geometrical Model
3-D arteriouvenous radial-cephalic side-to-end fistulae with antegrade blood flow are considered here. Straight arteries of length 15.0 cm and 3.1 mm diameter; vein of length 10.0 cm and 4.01 mm of diameter, with anastomotic angles of 20˚, 25˚, 30˚, 35˚, 40˚ and 45˚ will be studied. In Figure 1, inlet and outlets are identified by i and o, respectively, and arrows indicate the directions of the flow at those locations.
At the artery inlet section, a pulsating velocity condition will be prescribed and at the outlets a developed flow condition will be considered.
2.2. Mathematical Model for the Flow
Blood is very well known to be a suspension of several components, large and small ones, in almost Newtonian liquid called plasma, and is, in essence, a non-Newtonian fluid in the sense that it is able to alter its structure and adapt itself behaving differently depending on where it is flowing in. These differences come out depending on several factors, being very evident if blood is flowing in large or in small vessels. In normal large vessels (without stenosis, etc.), (diameters > 0.1 mm) Reynolds numbers are high enough to preclude aggregation of red cells (RBC) and Womersley numbers (Wo) are high, characterizing the pulsating effects to be considerable, [31] [32] [35] [36] , but viscosity independent of the shear rate for a fixed hematocrit, characterizing Newtonian behavior. Differently, in small vessels Reynolds numbers are smaller than 1, pulsation is negligible (Wo < 1) and diverse non-Newtonian behaviors come out with viscosity being a function of the shear rate due to the key cell aggregation process which involves protein content, platelets action, varying particle concentration, and other factors [32] [33] [36] - [39] . Several constitutive equations have been proposed in order to describe non-Newtonian behavior of blood, none of them being the general one and experiments supply the constitutive parameters from viscometric flows. In the classical biomechanics of fluids, accounting for large and small vessel diameters (d), hemodynamic is divided into macro (d > 0.1 mm) and micro circulation (d < 0.1 mm), respectively. From the non-Newtonian fluid mechanics point of view [34] suggested an intermediate range called mesocirculation (50 μm < d < 300 μm).
Taking into account the geometries of the arterial-cephalic fistulae studied here, with dimensions greater than 1 mm, blood is being considered as a Newtonian fluid.
Consider a 3-D domain, 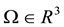 , with boundary
, with boundary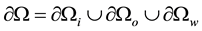 , where i stands for inlet, o for outlet and w for wall, and time t:
, where i stands for inlet, o for outlet and w for wall, and time t: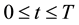 , with T being the pulse period. Then, Newtonian incompressible transient blood flow can be modeled by the following conservation of mass and momentum equations
, with T being the pulse period. Then, Newtonian incompressible transient blood flow can be modeled by the following conservation of mass and momentum equations
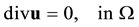 (1)
(1)
Figure 1. Scheme for arteriovenous fistulae.
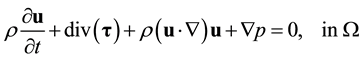 (2)
(2)
 (3)
(3)
subject to the boundary conditions
 (4)
(4)
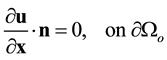 (5)
(5)
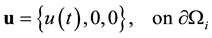 (6)
(6)
where 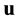 is the velocity vector,
is the velocity vector, 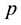 is the hydrostatic pressure,
is the hydrostatic pressure, 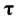 is the deviatoric part of the stress tensor,
is the deviatoric part of the stress tensor, 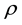 is the blood density (here set as 1045 kg/m3),
is the blood density (here set as 1045 kg/m3), 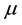 is the blood viscosity (considered 4.0 mPa.s), div is the divergence operator,
is the blood viscosity (considered 4.0 mPa.s), div is the divergence operator, 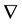 is the gradient operator and
is the gradient operator and 


Once determined the velocity field, 




This is an important variable indicating the friction level at the wall. However, to analyze the WSS at each instant of time is unfeasible and it does not directly supply a measure of the oscillations of the shear stress field for the pulse period. Then, it will be used here the idea, first introduced by [40] , of an oscillatory shear index, OSI, through the form proposed by [7] , which is determined for each point of the vessel walls:
Figure 2. Pulsating flow entrance used in the simulations.

Equation (9) quantify the degree of deviation of WSS from its medium direction during the whole cardiac period, 
2.3. Computational Model
To solve the equation system of the flow (Section 2.2) in the arteriovenuos geometric models for the six angles, a finite volume method, [42] , was used through the OpenFoam free platform [43] , adopting the well known PISO algorithm (Pressure Implicit with Splitting of Operators), [44] which is a modification of the classical SIMPLE (Semi-Implicit Method for Pressure Linked Equations) scheme [42] , by introducing an additional pres- sure correction step. This makes PISO to converge faster than SIMPLE and to better accommodate irregular cells. The process starts by solving the discretized pressure equation [45] by using the GAMG solver (Geometric Agglomerated Algebraic Multigrid Solver) from which a fast solution is obtained to generate a starting solution for the final finer mesh. For the solution of dicretized velocity equation [45] , the PBiCG solver was used. This is a preconditioner bi-conjugate gradient solver to asymmetric matrices. Additionally, a simple incomplete LU diagonal-based preconditioner, adequate to linear multigrid methods, was used [43] . In the computational experiments the meshes varied from 9000 for the 20˚ to 13,000 for the 45˚ angle hexahedral cells with time step of 10−5 s in all cases. Figure 3 depicts the final mesh for the 45˚ angle case, and illustrates the general aspect for the other angles. To change the anastomotic angles, but allowing sufficient hydraulic lengths to fully developed flow at the inlet and at the outlets, for all the angle cases the fistulae were placed at the mean length point of the artery. This is the rotation point for the half size of the vein, starting from the alignment of both longitudinal axes until reached the desired anastomotic angle (measured clockwise), with the remaining part maintained pa- rallel to the artery direction.
3. Computational Results and Discussions
Simulations have been performed for side-to-end radial-cephalic arteriovenous fistulae with pulsating antegrade flow, testing six anastomotic angles: 20˚, 25˚, 30˚, 35˚, 40˚ and 45˚. Results are presented for velocity contour fill, stream lines, WSS for the peak systole and the minimum diastole instants and OSI for the during time period


Figures 6(a)-6(f) present the results for WSS in the systolic peak. They are very non-homogenous, with the higher values occurring along the proximal artery branches and smaller ones at the veins. Long extents of higher values than the normal ones (2.0 - 7.0 Pa) are present in this peak for all configurations, but the angles of 35˚ to
Figure 3. Arteriovenous fistula 3D model―general mesh used.


Figure 4. Results of simulation to velocity in peak systolic 


Figure 5. Results of simulation to velocity in minimum diastolic 
45˚ present these values even at the ceiling of the distal artery branch. The most homogeneous distribution of WSS is presented by the angle of 25˚, considering the normal range (light blue to orange colors in the graphic scale). The same can be observed when looking the minimum diastolic results of Figures 7(a)-7(f). But in these critical cases, at the regions of the junctions, the most favorable (higher values of WSS in longer extents and bounded by the normal values) are the angles of 25˚, 20˚, and 30˚, in this order. Angles of 35˚ to 45˚ present unfavorable very low WSS values along the veins and at the junction.



Figure 6. Results of simulation to wall shear stress in peak systolic 
Systolic peak and minimum diastolic are only two instants of the whole pulse period. Although that wall shear stress levels are very important to cause intimal pathologies, their variations and oscillations are reported as being of major importance for stenosis formation, especially at the junction region. Then, results for the oscillation shear index have been obtained here by Equation (9), previously defined, which takes into account a mean variation of the shear stress along the whole period at each point of the walls. Figures 8(a)-8(f) illustrate these results at the junctions. Dark blue color contours indicate very low or null oscillation levels, OSI < 0.01, while OSI > 0.01 indicate higher oscillation degrees. Two views for each angle case are presented to better locate the regions with higher OSI. It can be observed that the areas with higher oscillations are placed near the junctions, with the angles of 35˚ to 45˚ presenting greater extents of high OSI. The angle of 25˚ presented smaller areas of high OSI followed by the angles of 20˚ and 30˚.
4. Conclusions
In this work, 3-D arteriovenous radial-cephalic side-to-end fistulae with antegrade blood flow have been computationally modelled for anastomotic angles of 20˚, 25˚, 30˚, 35˚, 40˚ and 45˚, to investigate anatomical configurations that could generate more favorable hemodynamic conditions, to minimize the problems related with fistulae failures. Large vessel blood flow model has been considered and a Finite Volume computational method was used to solve the equations for the pulsating flow problems in the OpenFoam free software platform. To analyze the possibility of stenosis formation, results were obtained here for wall shear stress, oscillatory index, velocity contour fill and local circulation fields. From the results, it is possible to conclude:
・ From the velocity fields and, especially, from the stream lines, higher angles presented more secondary flows and larger extensions of stagnation regions near the critical areas of the junctions;



Figure 7. Results of simulation to wall shear stress in minimum diastolic 



Figure 8. Results of simulation to oscilatory shear stress. (a) 20˚; (b) 25˚; (c) 30˚; (d) 35˚; (e) 40˚; (f) 45˚.
・ From the WSS results, higher stresses have been detected along the artery walls than along the veins, and smaller angles being more favorable since they presented higher shear stress levels along the areas close to the junctions as well as a more homogeneous distribution;
・ From the OSI, it was possible to better analyze the effects of oscillating shear at the walls, from which the higher it is, the higher is the possibility of pathologies to come up. The 25˚ angle presented less extension areas of high OSI, followed by 20˚ and 30˚;
・ As a consequence it is suggested here that the range 25˚ ± 5˚ is the most favorable for clinical applications.
・ The results here predict larger areas of oscillation shear at the fistulae as in [30] , however, they spread out along the veins.
・ There is an evident correspondence between the sites of stagnation areas and those of higher OSI.
Acknowledgements
J. A. Silva acknowledges the financial support of CAPES, J. Karam-Filho acknowledges CNPq/FAPERJ and C. C. H. Borges is thankful to CNPq, FAPEMIG and CAPES.
References
- Ministry of Health (Brazil), Virtual Health Library of the Ministry of Health (2011) Kidney Disease (Chronic Kidney Disease). (In Portuguese) http://bvsms.saude.gov.br/bvs/dicas/228_insuf_renal2.html
- Ene-Iordache, B. and Remuzzi, A. (2012) Disturbed Flow in Radial-Cephalic Arteriovenous Fistulae for Haemodialysis: Low and Oscillating Shear Stress Locates the Sites of Stenosis. Nephrology Dialysis Transplantation, 27, 358-368. http://dx.doi.org/10.1093/ndt/gfr342
- Nordgaard, H., Swillens, A., Nordhaug, D., Kirkeby-Garstad, I., Van Loo, D., Vitale, N., Patrick, S., Haaverstad, R. and Lovstakken, L. (2010) Impact of Competitive Flow on Wall Shear Stress in Coronary Surgery: Computational Fluid Dynamics of a LIMA-LAD Model. Cardiovascular Research, 88, 512-519. http://dx.doi.org/10.1093/cvr/cvq210
- Subbotin, V.M. (2007) Analysis of Arterial Intimal Hyperplasia: Review and Hypothesis. Theoretical Biology and Medical Modelling, 4, 1-20. http://dx.doi.org/10.1186/1742-4682-4-41
- Costa, R.F.B. and Fagundes, D.J. (2002) Experimental Models of Intimal Hyperplasia: Effects of Ionizing Radiation. Acta Cirurgica Brasileira, 17, 189-193. http://dx.doi.org/10.1590/S0102-86502002000300007 (in Portuguese).
- Haruguchi, H. and Teraoka, S. (2003) Intimal Hyperplasia and Hemodynamic Factors in Arterial Bypass and Arteriovenous Grafts: A Review. Journal of Artificial Organs, 6, 227-235. http://dx.doi.org/10.1007/s10047-003-0232-x
- Sivanesan, S., How, T.V., Black, R.A. and Bakran, A. (1999) Flow Patterns in the Radiocephalic Arteriovenous Fistula: An in Vitro Study. Journal of Biomechanics, 32, 915-925. http://dx.doi.org/10.1016/S0021-9290(99)00088-3
- Roy-Chaudhury, P., Spergel, L.M., Besarab, A., Asif, A. and Ravani, P. (2007) Biology of Arteriovenous Fistula Failure. Journal of Nephrology, 20, 150-163.
- Irace, C., Gnasso, A., Cirillo, F., Leonardo, G., Ciamei, M., Crivaro, A., Renzulli, A. and Cotrufo, M. (2002) Arterial Remodeling of the Common Carotid Artery after Aortic Valve Replacement in Patients with Aortic Stenosis. Stroke, 33, 2446-2450. http://dx.doi.org/10.1161/01.STR.0000032103.59213.BC
- Glagov, S., Zarins, C.K., Giddens, D.P. and Ku, D.N. (1988) Hemodynamics and Atherosclerosis―Insights and Perspectives Gained from Studies of Human Arteries. Archives of Pathology & Laboratory Medicine, 112, 1018-1031.
- Zarins, C.K., Weisenberg, E., Kolettis, G., Stankunavicius, R. and Glagov, S. (1988) Differential Enlargement of Artery Segments in Response to Enlarging Atherosclerotic Plaques. Journal of Vascular Surgery, 7, 386-394. http://dx.doi.org/10.1016/0741-5214(88)90433-8
- Frangos, J.A., Eskin, S.G., McIntire, L.V. and Ives, C.L. (1985) Flow Effects of Prostacyclin Production by Cultured Human Endothelial Cells. Science, 227, 1477-1479. http://dx.doi.org/10.1126/science.3883488
- Rubanyi, G.M., Romero, J.C. and Vanhoutte P.M. (1986) Flow-Induced Release of Endothelium-Derived Relaxing Factor. American Journal of Physiology, 250, H1145-H1149.
- Helmlinger, G., Berk, B.C. and Nerem, R.M. (1985) Calcium Responses of Endothelial Cell Monolayers Subjected to Pulsatile and Steady Laminar Flow Differ. American Journal of Physiology, 269, C367-C375.
- Malek, A.M., Jackman, R., Rosenberg, R.D. and Izumo, S. (1994) Endothelial Expression of Thrombomodulin Is Reversibly Regulated by Fluid Shear Stress. Circulation Research, 74, 852-860. http://dx.doi.org/10.1161/01.RES.74.5.852
- Malek, A.M., Alper, S.L. and Izumo, S. (1999) Hemodynamic Shear Stress and Its Role in Atherosclerosis. JAMA, 282, 2035-2042. http://dx.doi.org/10.1001/jama.282.21.2035
- Resnick, N., Yahav, H., Shay-Salit, A., Shushy, M., Schubert, S., Zilberman, L.C.M. and Wofovitz, E. (2003) Fluid Shear Stress and the Vascular Endothelium: For Better and for Worse. Progress in Biophysics and Molecular Biology, 81, 177-199. http://dx.doi.org/10.1016/S0079-6107(02)00052-4
- Li, Y.S.J., Haga, J.H. and Chien, S. (2005) Molecular Basis of the Effects of Shear Stress on Vascular Endothelial Cells. Journal of Biomechanics, 38, 1949-1971. http://dx.doi.org/10.1016/j.jbiomech.2004.09.030
- Cybulsky, M.I. and Gimbrone, M.A. (1991) Endothelial Expression of a Mononuclear Leukocyte Adhesion Molecule during Atherogenesis. Science, 251,788-791. http://dx.doi.org/10.1126/science.1990440
- Ku, D.N., Giddens, D.P., Zarins, C.K. and Glagov, S. (1985) Pulsatile Flow and Atherosclerosis in the Human Carotid Bifurcation. Positive Correlation between Plaque Location and Low Oscillating Shear Stress. Arteriosclerosis, Thrombosis, and Vascular Biology, 5, 293-302. http://dx.doi.org/10.1161/01.ATV.5.3.293
- Cunningham, K.S. and Gotlieb, A.I. (2005) The Role of Shear Stress in the Pathogenesis of Atherosclerosis. Laboratory Investigation, 85, 9-23. http://dx.doi.org/10.1038/labinvest.3700215
- Zarins, C.K., Giddens, D.P., Bharadvaj, B.K., Sottiurai, V.S., Mabon, R.F. and Glagov, S. (1983) Carotid Bifurcation Atherosclerosis: Quantitative Correlation of Plaque Localization with Flow Velocity Profiles and Wall Shear Stress. Circulation Research, 53, 502-514. http://dx.doi.org/10.1161/01.RES.53.4.502
- Moore Jr., J.E., Xu, C., Glagov, S., Zarins, C.K. and Ku, D.N. (1994) Fluid Wall Shear Stress Measurements in a Model of the Human Abdominal Aorta: Oscillatory Behavior and Relationship to Atherosclerosis. Atherosclerosis, 110, 225-240. http://dx.doi.org/10.1016/0021-9150(94)90207-0
- Murphy, J. and Boyle, F. (2010) Predicting Neointimal Hyperplasia in Stented Arteries Using Time-Dependant Computational Fluid Dynamics: A Review. Computers in Biology and Medicine, 40, 408-418. http://dx.doi.org/10.1016/j.compbiomed.2010.02.005
- Stone, P.H., Coskun, A.U., Kinlay, S., Popma, J.J., Sonka, M., Wahle, A., Yeghiazarians, Y., Maynard, C., Kuntz, R. and Feldman, C.L. (2007) Regions of Low Endothelial Shear Stress Are the Sites Where Coronary Plaque Progresses and Vascular Remodelling Occurs in Humans: An in Vivo Serial Study. European Heart Journal, 28, 705-710. http://dx.doi.org/10.1093/eurheartj/ehl575
- Cheng, C., Tempel, D., van Haperen, R., van der Baan, A., Grosveld, F., Daemen, M.J. and de Crom, R. (2006) Atherosclerotic Lesion Size and Vulnerability Are Determined by Patterns of Fluid Shear Stress. Circulation, 113, 2744- 2753. http://dx.doi.org/10.1161/CIRCULATIONAHA.105.590018
- Ene-Iordache, B., Mosconi, L., Remuzzio, G. and Remuzzi, A. (2001) Computational Fluid Dynamics of a Vascular Access Case for Hemodialysis. Journal of Biomechanical Engineering, 123, 284-292. http://dx.doi.org/10.1115/1.1372702
- Lee, S.-W., Antiga, L. and Steinman, D.A. (2009) Correlations among Indicators of Disturbed Flow at the Normal Carotid Bifurcation. Journal of Biomechanical Engineering, 131, Article ID: 061013. http://dx.doi.org/10.1115/1.3127252
- Naughton, N.M., Plourde, B.D., John, R., Stark, J.R., Hodis, S. and Abraham, J.P. (2014) Impacts of Waveforms on the Fluid Flow, Wall Shear Stress, and Flow Distribution in Cerebral Aneurysms and the Development of a Universal Reduced Pressure. Journal of Biomedical Science and Engineering, 7, 7-14. http://dx.doi.org/10.4236/jbise.2014.71002
- Ene-Iordache, B., Cattaneo, L., Dubini, G. and Remuzzi, A. (2013) Effect of Anastomosis Angle on the Localization of Disturbed Flow in “Side-to-End” Fistulae for Haemodialysis Access. Nephrology Dialysis Transplantation, 28, 997- 1005. http://dx.doi.org/10.1093/ndt/gfs298
- Pedley, T.J. (1980) The Fluid Mechanics of Large Blood Vessels. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511896996
- Lighthill, J. (1989) Mathematical Biofluiddynamics. SIAM Regional Conference Series in Applied Mathematics, 3rd Edition, Philadelphia.
- Fung, Y.C. (1997) Biomechanics: Circulation. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4757-2696-1
- Bortoloti, M.A.A. (2006) A Finite Element Formulation for Pseudoplastic Flows. Ph.D. Thesis, LNCC, Petrópolis. (In Portuguese)
- Sharma, M.K., Singh, K. and Bansal, S. (2014) Pulsatile MHD Flow in an Inclined Catheterized Stenosed Artery with Slip on the Wall. Journal of Biomedical Science and Engineering, 7, 194-207. http://dx.doi.org/10.4236/jbise.2014.74023
- Karam, F.J. (2001) Introduction to Human Cardiovascular System: Part I―Blood Rheology and Newtonian and Non-Newtonian Models. In Prints from II-Summer School on Computational Methods in Biology, LNCC/MCT, Petrópolis, 1-36. (In Portuguese)
- Stoltz, J.-F., Singh, M. and Riha, P. (1999) Hemorheology in Practice. IOS Press, Amsterdam.
- Popel, A.S. and Johnson, P.C. (2005) Microcirculation and Hemorheology. Annual Review of Fluid Mechanics, 37, 43- 69.
- Sequeira, A. (2010) Hemorheology and Mathematical Models. Bulletin of the Portuguese Society of Hemorheology and Microcirculation-SPHM, 25, 5-17.
- Ku, D.N., Giddens, D.P., Zarins, C.K. and Glagov, S. (1985) Pulsatile Flow and Atherosclerosis in the Human Carotid Bifurcation. Positive Correlation between Plaque Location and Low Oscillating Shear Stress. Arteriosclerosis, Thrombosis, and Vascular Biology, 5, 293-302. http://dx.doi.org/10.1161/01.ATV.5.3.293
- He, X. and Ku, D.N. (1996) Pulsatile Flow in the Human Left Coronary Artery Bifurcation: Average Conditions. Journal of Biomechanical Engineering, 118, 74-82. http://dx.doi.org/10.1115/1.2795948
- Patankar, S. (1980) Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing Corporation, Washington DC.
- Open CFD (2009) The Open Source CFD Toolbox. User Guide, Open CFD Ltd.
- Versteeg, H.K. and Malalasekera, W. (2007) An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Pearson Education, Harlow.
- Behrens, T. (2009) OpenFOAM’s Basic Solvers for Linear Systems of Equations: Solvers, Preconditioners, Smoothers. Technical Report, Technical University of Denmark, Lingby.
NOTES
*Corresponding author.




























