Journal of Biomedical Science and Engineering
Vol.7 No.7(2014), Article
ID:46586,8
pages
DOI:10.4236/jbise.2014.77042
Heterogeneity of Viscoelastic Properties of Myocardial Muscle Fiber: Mathematical Model
Alexey Timofeevich Smoluk, Leonid Timofeevich Smoluk*, Yuri Leonidovich Protsenko
Institute of Immunology and Physiology Ural Branch of the RAS, Ekaterinburg, Russia
Email: *fusion_lab@pisem.net
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2014; revised 21 May 2014; accepted 28 May 2014
ABSTRACT
Mathematical model describing the processes of mechanical stress development in response to strain of heterogeneous muscle fiber is created. The numerical algorithm to calculate viscoelastic properties of muscle fiber of arbitrary length is developed. In numerical experiments by the model it is shown that the local heterogeneity of geometrical and mechanical parameters of structural units of the model significantly influences in resulting mechanical response of whole fiber. Also it is established the close connection between parameters of mechanical and geometrical heterogeneity compensating each other. It is supposed that the mechanism may modulate the myocardial remodeling under changing load.
Keywords:Modelling of Heterogeneity, Viscoelastic Properties, Muscle Fiber, Myocardium

1. Introduction
Viscoelastic properties of the myocardium play an important role in the mechanisms ensuring heart function by modulating mechanical parameters of heart wall during diastole. The modulation substantially defines the stroke volume [1] [2] . Passive tension provided by various morphological myocardial structures is one of the factors defining the rate of cardiomyocyte contraction [3] . The heterogeneity of functional parameters including viscoelastic properties was established to be observed at different levels of myocardial tissue organization from cell to organ in health and especially in pathology [4] -[7] . For example during myocardial infarction the ventricular wall stiffness firstly increases in consequence of hypoxia and then it considerably decreases and finally increases (postinfarction scar) [8] . This local process significantly changes mechanical properties of the whole myocardial tissue. Moreover the influence of local heterogeneity of viscoelastic properties of ventricular wall segments to the forming of myocardial mechanical response is poorly understood today. It is largely conditional on complexity of experimental study of the interaction of heterogeneous segments in myocardium. Previously to solve such problems a method of muscle duplex was developed. It is an experimental approach to studying biomechanical and bioelectrical properties of heterogeneous system consisting of two different units [9] . By the muscle duplex method it obtained some important features of the contractile function of interacting segments in heterogeneous myocardium [10] -[12] . Though the experimental study of heterogeneous systems consists of greater number of units, it is an awkward task to date. Thus to analyze influence spatial-temporal heterogeneity of the same systems, the using mathematical models become virtually the only possible solution. The aim of this study is to present the development of a model approach describing the viscoelastic behavior of the myocardial tissue as a heterogeneous biological system. Previously we have developed three-dimensional structural model describing viscoelastic behavior of myocardial morphological unit [13] . It has been shown that the model could be applied at different organization levels of myocardial tissue [14] . Also we have obtained new data about influence of heterogeneity of local geometrical and mechanical properties of model structural units to the mechanical response of the simple heterogeneous system consisting of two structural three-dimensional units to the stretching [15] . In present work the model approach has been developed to describe more complex systems consisting of an arbitrary number of units.
2. Materials and Methods
The simple block model of heterogeneous system consisting of two series connected models of myocardial morphological unit is in detail described in our previous work [15] . Behavior of this heterogeneous system is described by the following system of nonlinear differential equations (1):
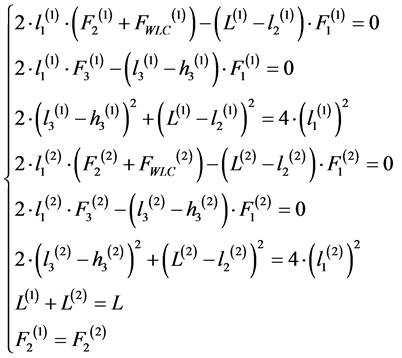 ,
, 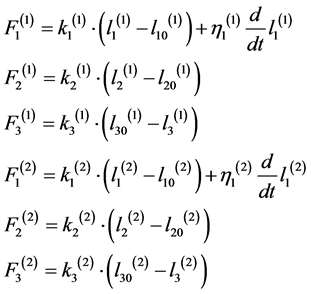 , (1)
, (1)
where: 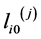 are initial lengths of (j)-block the model elements;
are initial lengths of (j)-block the model elements;
 are current lengths of (j)-block the model elements;
are current lengths of (j)-block the model elements;
 are spatial sizes of (j)-inextensible block of the model;
are spatial sizes of (j)-inextensible block of the model;
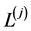 are length of entire (j)-block of the model;
are length of entire (j)-block of the model;
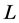 is length of entire model;
is length of entire model;
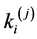 are elastic coefficients of corresponding elements;
are elastic coefficients of corresponding elements;
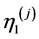 are viscous coefficients of (j)-block;
are viscous coefficients of (j)-block;
 are forces developing by corresponding elements;
are forces developing by corresponding elements;
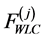 are forces developed by (j)-block in accordance with Worm-like chain model of titin.
are forces developed by (j)-block in accordance with Worm-like chain model of titin.
The first three equations describe the viscoelastic behavior of the first unit. The following three equations describe the viscoelastic behavior of the second unit. The last two equations are the coupling equations. They show that sum of the lengths of the first and second units is equal to the length of the entire model and forces applied to the first and second blocks are the same in the case series connection. Generally the system (1) can not be solved analytically. The numerical solution of the system (1) is rather dependent on the choice of initial approximation of the parameter values of structural elements. Four nonlinear differential equations are added to the system (1) when increasing unit count to each unit. It is practically impossible to solve the system of equation without precise selection of initial approximation for the three-unit model. That makes the approach not usable to describe the systems consisting of more than two elements. Therefore to solve the problem the algorithm of model equation linearization is developed. It is used the following difference scheme:
 , (2)
, (2)
where  is unknown value of variable x at time moment t;
is unknown value of variable x at time moment t;
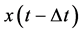 is established value of variable x at time moment
is established value of variable x at time moment , where
, where ![]() is a time step of the difference scheme;
is a time step of the difference scheme;
![]() is unknown increment of variable x;
is unknown increment of variable x;
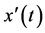 is unknown value of derivative of the function
is unknown value of derivative of the function  at time moment t.
at time moment t.
In this approach, dynamic state of the model, consisted of N-series connected units, is described by the following system of linear equations at various time moments:
 , (3)
, (3)
where  is a column vector of variables, with
is a column vector of variables, with
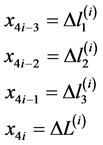 , (4)
, (4)
where ,
, 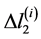 ,
,  ,
,  are increments of values
are increments of values ,
, 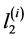 ,
, 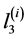 ,
, 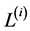 respectively with
respectively with![]() .
.
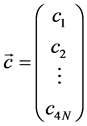 is a column vector of the constant terms, with
is a column vector of the constant terms, with
 (5)
(5)
with![]() ,
, 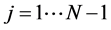
 is a coefficient matrix, with
is a coefficient matrix, with
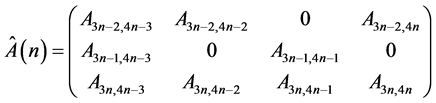 (6)
(6)
 is a submatrix describing the isolated unit of the model, where
is a submatrix describing the isolated unit of the model, where
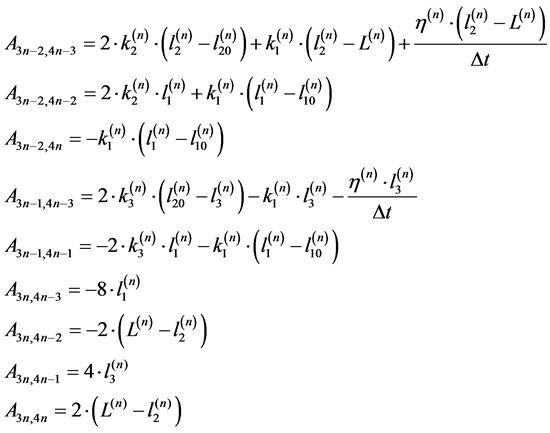 (7)
(7)
with ![]()
 (8)
(8)
is a zero submatrix;
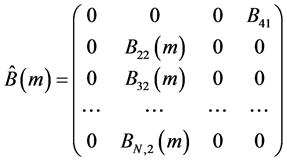 (9)
(9)
is a submatrix describing the relationships between units, where
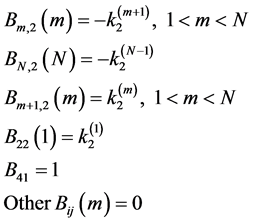 (10)
(10)
with![]() ,
, 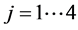 ,
, ![]()
According to the Rouché-Capelli theorem solution of this linear system at each time step of the iterative process exists and is unique. This approach has a significant advantage over the numeric solution of non-linearized system of equations, in which convergence of this method to a particular solution is determined by the accuracy of the initial conditions, thus complicating the algorithm for finding the correct decision. To analyze the system behavior the following task has been solved. Is it possible to compensate geometrical or mechanical heterogeneity by the change of local mechanical or geometrical model parameters respectively? To answer this question we carried out the series of numerical experiments. The results are described in the next section.
3. Results
To verify developed algorithm of equation linearization, the system describing heterogeneous model consisted of 2 units, was considered. Solutions obtained using the initial and linearized equations were shown to be similar. The approximation accuracy was R2 = 0.9999. Figure 1 shows the step deformation response of the two-unit heterogeneous model for both approaches. On this chart one can see a good agreement between different numerical algorithms. Thus, the proposed algorithm for solving system of equations in N-units model is suitable to solve assigned task.
To study the features of heterogeneity of viscoelastic characteristics in extended muscle fiber, the system of 5 series connected units was considered (Figure 2). At first, the length of longitudinal element of the first unit was decreased by 2% and the effect of the first unit geometrical heterogeneity on the total response due to step deformation (with constant increment of 2% of initial entire model length) of whole fiber was investigated (marked by an arrow on Figure 2).
Then this heterogeneity was compensated by changing the local mechanical parameters (such as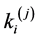 ,
,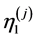 ) of the units (changed parameters are marked with blue color in Table 1). As a result the mechanical response of heterogeneous system almost completely coincided with mechanical response of the initial system (Figure 3). The approximation accuracy was R2 = 0.9997. The detail information about values of each structural parameters of the model is presented in Table 1 (the first block of the model contains the information about initial model; the second —about geometrically heterogeneous model and third—about compensated heterogeneous model).
) of the units (changed parameters are marked with blue color in Table 1). As a result the mechanical response of heterogeneous system almost completely coincided with mechanical response of the initial system (Figure 3). The approximation accuracy was R2 = 0.9997. The detail information about values of each structural parameters of the model is presented in Table 1 (the first block of the model contains the information about initial model; the second —about geometrically heterogeneous model and third—about compensated heterogeneous model).
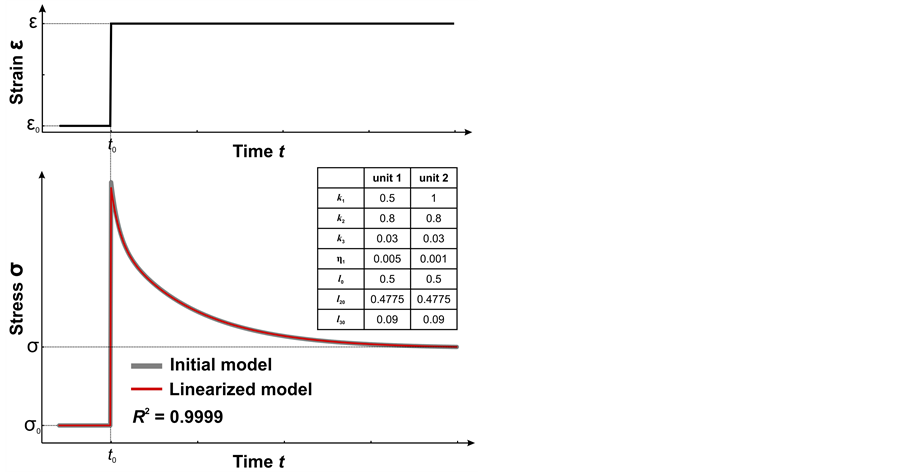
Figure 1. Example stress relaxation curve (bottom) in response to stepwise stretching (above). Application of the linearized algorithm for model composed of two heterogeneous structural units: response of the model, obtained by solving the system of equations (1)—grey curve; response of the model, obtained by solving the system of equations (3)—red curve. The panel on the right shows the geometrical and mechanical parameters of the two-unit model.

Figure 2. Scheme of the model heterogeneity system, composed of 5 units. Heterogeneity is introduced by unit 1 (marked by an arrow).
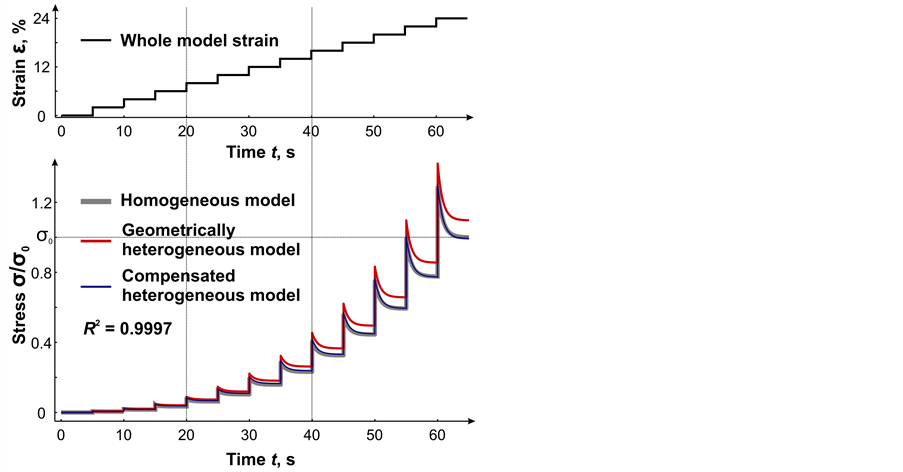
Figure 3. Stress relaxation curves (below) in heterogeneous system, composed of 5 units during stepwise stretching (above) with constant increment of 2% of initial entire model length. Homogeneous model—grey curve; geometrically heterogeneous model—red curve; compensated heterogeneous model— blue curve.
Table 1. Values of the structural and mechanical parameters of the model. Changed parameters are marked by cyan color.
4. Discussion
On the basis of model of myocardial morphofunctional unit, numeric algorithm for calculating the system composed of arbitrary number of structural units was developed. This algorithm allows describing nonlinear viscoelastic properties of heterogeneous (geometrically and mechanically) muscle fiber of arbitrary length in stationary and dynamic modes. Universality of the method is that it can be applied to describe viscoelastic behavior of various biological tissues. Numerical experiments have shown significant effect of local heterogeneity of geometrical and mechanical parameters of distinct structural units on the total mechanical response. The stress relaxation in the response to stepwise stretching was used as one of the main characteristics of the response of the system. We have previously shown that such a generalized characteristic gives integrated information about the elasticity and viscosity of the object of biological tissue under investigation [13] .
When analyzing the data obtained in the developed model, it was found that the local geometric heterogeneity has a significant impact on the global viscoelastic properties of the entire system.
In addition, geometrical or mechanical local heterogeneity in the model can be compensated by introducing heterogeneity into mechanical or geometrical parameters of structural model units respectively. After the compensation the mechanical response of the entire model is almost identical in comparison with the response of the model prior to the introduction of heterogeneity (approximation accuracy is more than 99.9%). This confirms the viability of the developed algorithm. Besides it should be noted that proposed approach shows the influence of compensated geometrical and mechanical heterogeneity to active mechanical properties of myocardial fiber via Frank-Starling mechanism.
It is also known that the myocardial fibers of ventricular wall consist of chain-like connected cardiomyocytes either sequentially or in parallel (via intercalary discs) [16] . In turn, the fibers connected in parallel are combined into bundles that form segments of the ventricular wall. Therefore, further elaboration of the represented approach supposes the development of a spatial model to take into account not only longitudinal but transverse deformations and interaction each other unit. In the future, that will allow investigating the effect of local defects on the total mechanical properties in various biological tissues.
Conflict of Interest Statement
The authors have no conflict of interest.
Acknowledgements
This work is supported by RFBR Grant 13-04-00367-A, Project 12-Y-4-1009 of the Presidium of the Ural branch of the RAS, OPTEC Grant 2013 year
References
- Allen, D.G. and Kentish, J.C. (1985) The Cellular Basis of the Length-Tension Relation in Cardiac Muscle. Journal of Molecular and Cellular Cardiology, 17, 821-840. http://dx.doi.org/10.1016/S0022-2828(85)80097-3
- Brady, A.J. (1991) Mechanical Properties of Isolated Cardiac Myocytes. Physiological Reviews, 71, 413-428.
- Sweitzer, N.K. and Moss, R.L. (1993) Determinants of Loaded Shortening Velocity in Single Cardiac Myocytes Permeabilized with Alpha-Hemolysin. Circulation Research, 73, 1150-1162. http://dx.doi.org/10.1161/01.RES.73.6.1150
- Brutsaert, D.L. (1985) Nonuniformity: An Important Physiological Modulator of the Contractile Performance of the Normal Heart. Verhandelingen—KoninklijkeAcademievoorGeneeskunde van België, 47, 257-286.
- Antzelevitch, C. and Fish, J. (2001) Electrical Heterogeneity within the Ventricular Wall. Basic Research in Cardiology, 96, 517-527. http://dx.doi.org/10.1007/s003950170002
- Bogaert, J. and Rademakers, F.E. (2001) Regional Nonuniformity of Normal Adult Human Left Ventricle. American Journal of Physiology—Heart and Circulatory Physiology, 280, H610-620.
- Litten, R.Z., Martin, B.J., Buchthal, R.H., Nagai, R., Low, R.B. and Alpert, N.R. (1985) Heterogeneity of Myosin Isozyme Content of Rabbit Heart. Circulation Research, 57, 406-414. http://dx.doi.org/10.1161/01.RES.57.3.406
- Raya, T.E., Gay, R.G., Lancaster, L., Aguirre, M., Moffett, C. and Goldman, S. (1988) Serial Changes in Left Ventricular Relaxation and Chamber Stiffness after Large Myocardial Infarction in Rats. Circulation, 77, 1424-1431. http://dx.doi.org/10.1161/01.CIR.77.6.1424
- Protsenko, Y.L., Routkevitch, S.M., Gur’ev, V.Y., Katsnelson, L.B., Solovyova, O., Lookin, O.N., Balakin, A.A., Kohl, P. and Markhasin, V.S. (2005) Hybrid Duplex: A Novel Method to Study the Contractile Function of Heterogeneous Myocardium. American Journal of Physiology—Heart and Circulatory Physiology, 289, H2733-2746. http://dx.doi.org/10.1152/ajpheart.00306.2005
- Solovyova, O., Katsnelson, L.B., Konovalov, P., Lookin, O., Moskvin, A.S., Protsenko, Y.L., Vikulova, N., Kohl, P. and Markhasin, V.S. (2006) Activation Sequence as a Key Factor in Spatio-Temporal Optimization of Myocardial Function. Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences, 364, 1367-1383.
- Markhasin, V.S., Balakin, A.A., Katsnelson, L.B., Konovalov, P., Lookin, O.N., Protsenko, Y. and Solovyova, O. (2012) Slow Force Response and Auto-Regulation of Contractility in Heterogeneous Myocardium. Progress in Biophysics and Molecular Biology, 110, 305-318. http://dx.doi.org/10.1016/j.pbiomolbio.2012.08.011
- Markhasin, V.S., Solovyova, O., Katsnelson, L.B., Protsenko, Y., Kohl, P. and Noble, D. (2003) Mechano-Electric Interactions in Heterogeneous Myocardium: Development of Fundamental Experimental and Theoretical Models. Progress in Biophysics and Molecular Biology, 82, 207-220. http://dx.doi.org/10.1016/S0079-6107(03)00017-8
- Smoluk, L. and Protsenko, Y. (2012) Viscoelastic Properties of the Papillary Muscle: Experimental and Theoretical Study. Acta of Bioengineering and Biomechanics, 14, 37-44.
- Smoluk, L. and Protsenko, Y. (2010) Modeling of Viscoelastic Properties of Isolated Myocardial Tissue Samples at Different Levels: Cardiomyocytes and Trabeculae. Biophysical Journal, 98, 555a. http://dx.doi.org/10.1016/j.bpj.2009.12.3006
- Smoluk, A.T., Smoluk, L.T. and Protsenko, Y.L. (2012) Stress Relaxation of Heterogeneous Myocardial Tissue. Numerical Experiments with 3D Model. Biophysics, 57, 804-807. http://dx.doi.org/10.1134/S0006350912060176
- Smerup, M., Nielsen, E., Agger, P., Frandsen, J., Vestergaard-Poulsen, P., Andersen, J., Nyengaard, J., Pedersen, M., Ringgaard, S., Hjortdal, V., Lunkenheimer, P.P. and Anderson, R.H. (2009) The Three-Dimensional Arrangement of the Myocytes Aggregated Together within the Mammalian Ventricular Myocardium. Anatomical Record, 292, 1-11. http://dx.doi.org/10.1002/ar.20798
NOTES

*Corresponding author.


