Journal of Biomedical Science and Engineering
Vol.6 No.9(2013), Article ID:36410,8 pages DOI:10.4236/jbise.2013.69106
A new method of lung sounds filtering using modulated least mean square—Adaptive noise cancellation
![]()
Department of Biomedical Engineering, Faculty of Engineering, University of Science and Technology, Sana’a, Yemen
Email: noman_qaed@yahoo.com
Copyright © 2013 Noman Qaid Al-Naggar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 6 July 2013; revised 5 August 2013; accepted 12 August 2013
Keywords: Lung Sound; Filtering of Lung Sound; Least Mean Squares Algorithm; Adaptive Noise Cancelling
ABSTRACT
Advanced processing of lung sound (LS) recording is a significant means to separate heart sounds (HS) and combined low frequency noise from instruments (NI), with saving its characteristics. This paper proposes a new method of LS filtering which separates HS and NI simultaneously. It focuses on the application of least mean squares (LMS) algorithm with adaptive noise cancelling (ANC) technique. The second step of the new method is to modulate the reference input r1(n) of LMS-ANC to acquiesce combining HS and NI signals. The obtained signal is removed from primary signal (original lung sound recording-LS). The original signal is recorded from subjects and derived HS from it and it is modified by a band pass filter. NI is simulated by generating approximately periodic white gaussian noise (WGN) signal. The LMS-ANC designed algorithm is controlled in order to determine the optimum values of the order L and the coefficient convergence μ. The output results are measured using power special density (PSD), which has shown the effectiveness of our suggested method. The result also has shown visual difference PSD (to) normal and abnormal LS recording. The results show that the method is a good technique for heart sound and noise reduction from lung sounds recordings simultaneously with saving LS characteristics.
1. INTRODUCTION
Biological signals are often noisy and non stationary. These factors tremendously complicate analysis of biosignals [1]. Respiratory sounds present noninvasive measures of lung airway conditions [2]. However, features of lung sounds (LS) may be contaminated by heart sounds (HS) because lung and heart sounds overlap in terms of time domain and spectral content [3]. Generally, all LSs originate from airways during inspiration-expiration-cycles [4]. The LS propagating through lung tissues in the parenchyma can be heard over the chest wall using a sound-transducer. The tissue acts as a frequency filterlike structure whose characteristics vary according to pathological and indeed physiological changes [5].
Auscultation is one of the most important non-invasive and simple diagnostic tools for detecting disorders in the respiratory tract like lung diseases. However, despite their effectiveness, these instruments only provide a limited and subjective perception of the respiratory sounds. The drawbacks of using stethoscopes and listening to the sounds are using the human ear area, and their inability to provide an objective study of the detected respiratory sounds. They lack sufficient sensitivity and the existence of imperfect system of nomenclature.
Besides the fact that normal and abnormal lung sounds are mixed in the airways and therefore pose a problem of classification of respiratory diseases, semi-periodic HS from heartbeat activity invariably interferes with the LS and therefore masks or inhibits clinical interpretation of LS particularly over low frequency components. The main frequency components of HS are in the range 20 - 100 Hz. This is the range in which LS has major components [6]. Therefore, since HS and LS overlap in frequency and are somewhat non-stationary, the major problem being faced in separating HS from LS is doing so without tempering with the main characteristic features of the LS.
Generally, LSs are produced during inspiration and expiration cycles, and are found in the frequency range 20 - 1200 Hz. There are two types of lung sound, namely, normal and abnormal lung sounds. Normal breath sounds can be categorized into three classes: bronchial, bronchovesicular, and vesicular sounds. Each class of sounds is detected during auscultation according to the characteristics described in [7]. HSs are clearly audible in lung sounds recorded on the anterior chest and may be heard to a lesser extent in lung sounds recorded over posterior lung lobes.
High-pass filtering of lung-sound recordings to reduce heart sounds would remove significant components of lung sounds. Filtering techniques are categorized as linear adaptive filters and filters employing time-frequency based methods. Several filtering schemes are outlined within these two categories. In [8], a recursive least squares (RLS) based adaptive noise cancellation (ANC) filtering technique is proposed to separate or reduce the HS from LS. Here, a band pass filtered version of the recorded HS was used as the reference signal. Time frequency (TF) filtering techniques have also been proposed for HS reduction in LS [9,10].
Methods of heart sound localization are indicated in conjunction with the studies of heart-sound cancellation. Same researchers [11-13] confirm that the adaptive filter is more effective in reducing noise from time series data than linear filters, wavelet shrinkage, and chaosbased noise reduction schemes. The simplest method to reduce HS effects is to apply a high pass filter with cutoff frequency varying from 50 - 150 Hz [3]. More complex methods to reduce HS from breath sound recordings have been described in the literature as adaptive filtering techniques [14], wavelet denoising [15], and combination of HS localization-and-removal and LS prediction [16,17].
This paper proposes a novel LS filtering method which combines:
• Separating heart sounds (HS) and combined low frequency noise from instruments (NI) simultaneously, while saving LS characteristics.
• Modulating the reference input r1(n) of LMS-ANC to acquiesce combining HS and NI signals.
To achieve the objectives of the algorithm the following tools are used:
• Accruing HS derived from LS original signal by suitable band pass filter with controlled cutoff frequency and order.
• Simulating NI by generating approximately periodic white gaussian noise (WGN).
• Combining HS and simulated WGN.
• Designing a suitable controlled algorithm LMS-ANC in order to determine the optimum values of L order and the coefficient convergence μ.
• Estimating the output results (obtained LS signal) and comparing it with combining signal used power special density (PSD).
PSD has been shown the effectiveness of the LMSANC filtering with suggested method.
The rest of this paper is organized as follows: Section 2 introduces the methodology, which describes the experimental procedure and the proposed modulation method of LMS-ANC. Section 3 presents results and discussion of output signals of ANC, and compares its PSD to normal and abnormal LS. Finally, conclusions are presented in Section 4.
2. METHODOLOGY
2.1. Experimental Procedure
The lung sound has recorded by Computerized Recording Channel of Lung Sound (CRCLS) on the chest and back, right and left [18]. LS signals have been recorded from five healthy (17 - 27 years old) and three unhealthy subjects at the laboratory of BME Deptartment at the University of Science and Technology, under the control of a professional physician. The signals have been recorded at a 44,100 Hz sampling rate, 16 bits and pre filtered at band pass 7.5 - 2500 Hz. Recordings have been monitored and processed by LS recorder program created with Graphical User Interface (GUI), which provides real-time displaying for lung sound (LS) and downsample it to 11,025 Hz sampling rate for easier analysis.
Each subject has been instructed to breathe so that one breathing cycle occurred every approximately three seconds, (one cycle per ~3 s.). At every flow rate and had at least five breathing cycles at each target flow. Same recordings have been repeated for each subject and each recording consisted of approximately 20 s. For each target flow and concluded with an approximately 5 sec of breath hold (total of ~25 s).
In [4,7], researchers have used adaptive filtering with a pre-processing stage comprising a variable amplifier gain. Other groups used an adaptive filter based on the least mean square (LMS) algorithm to remove HS interferences. In both cases, researchers used HS recorded from close to the patient’s heart location as the reference signal for the adaptive system, which of course are not completely free of LS. The sounds signals have been pre-filtered to remove DC and to prevent aliasing, using CRCLS custom-built 8th order Butter worth band pass filters with pass band 7.5 to 2500 Hz, and amplified by a gain of 200. HS, in our case, has been derived from the original signal recorded from chest at different frequentcies range 20 to 100 Hz, 20 to 150 Hz and to 300 Hz. Other important parameter is the L order of band pass filters, which is applied in the range 2 ≤ L ≤ 120. The frequency range and L are applied depending on the properties of recoding signal and normal or abnormal. The obtained HS signal is used as a reference signal input of adaptive filter.
2.2. Adaptive Noise Canceller (ANC)
The main types of linear adaptive filters are the adaptive noise cancellation and linear prediction. Many researchers have applied ANC to lung sound recordings to reduce heart sounds [14].
The linear adaptive filter with finite memory (finiteduration impulse response—FIR) has been applied for heart sound reduction and noise, which means that the internal structure of the adaptive filter contains only forward feed capability [7,14]. The most common form of a finite memory, or FIR filter is the FIR transversal filter and it adapts algorithm, which updates the tap weights ωk of the transversal filter. So the mean square error (MSE) is minimized and an estimate of the desired output results consists of unit-delay elements that delay each of the M-samples of the input (L is the filter order); elements that multiply weights by input samples; and adders. Each sample, k, of the L-samples of an input reference vector, r1(n), that is multiplied by the conjugate of a weight value, ωk, and these products are summed to form the filter output y(n).
Figure 1 shows the main components of ANC filter as follows:
a) Input of the primary signal x(n)b) Input of reference signal r1(n)c) Filter output y(n)d) Finally the estimation error e(n).
The primary input signal consists of the desirable signal L(n) and the noise signal r0(n) as shown in Equation (1),
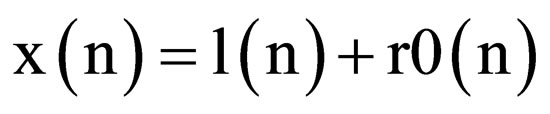 (1)
(1)
The reference input r1(n) is modulated to a complex signal, which contains HS and generated signal NI simulated by WGN. Therefore, the generated signal NI accompanied with recording process of LS, which is created from instruments and surrounding environment of LS recording.
The generated NI is based on the methods presented in [19,20]. The methods proposed temporally to generate WGN on real quasi period. It is added to the synthetic HS in various magnitude scales in order to acquire synthetic biosignals corrupted by WGN at a wide range

Figure 1. Schema of adaptive noise cancellation.
of signal to noise ratios (SNR). Only SNR higher than 0 dB is considered, because significant noise level distorts ECG in such a degree that low magnitude complexes are not identifiable. However, this method is evaluated on both synthetic periodic signals of the known HS period combined with WGN on real quasi period. Equation (2) is the reference modulated HS signal, h(n), and generated WGN, d(n).
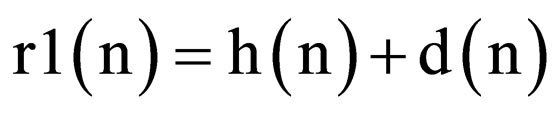 . (2)
. (2)
The output of the Adaptive filter, e(n), is the minimum MSE (MMSE) estimate of the component of the primary signal as shown in Equation (3).
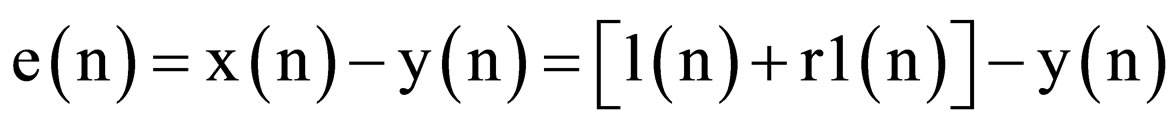 , (3)
, (3)
where y(n) is the structure of the FIR, which can be represented in Equation (4),
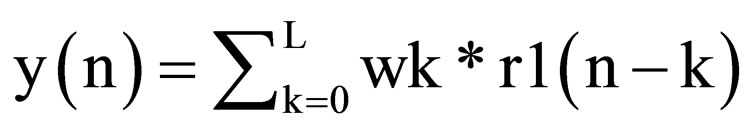 . (4)
. (4)
The weights are updated with each iteration, n, based on feedback of the estimation error to the adaptive filter unit.
2.3. LMS Algorithm
The LMS algorithm choice is based on its simplicity and it does not require measurements of the pertinent correlation function. It also requires matrix inversion.
It uses Equation (3) to get square error e2(n), which is the square error (MSE) between the output y(n) (equal to wx(n)) and the reference signal r1(n), as given Equation (5)
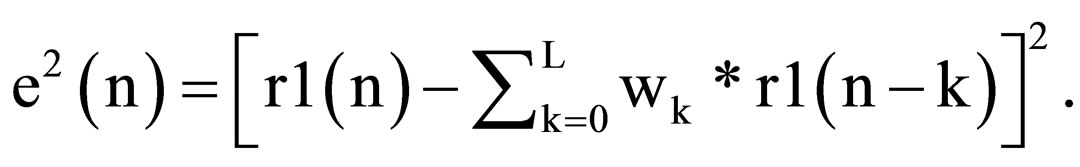 (5)
(5)
Shortly, it is possible to calculate the filter coefficient vector for each iteration k having information about the previous coefficients  and gradient µ, multiplied by a constant, as shown in Equation (6)
and gradient µ, multiplied by a constant, as shown in Equation (6)
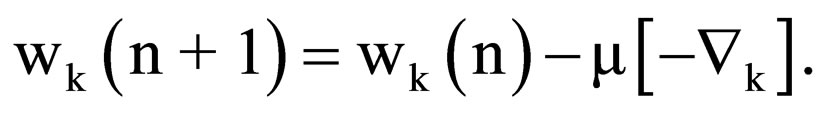 (6)
(6)
The gradient vector is defined by Equation (7)
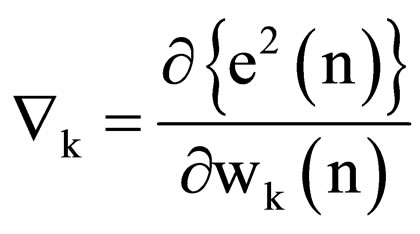 . (7)
. (7)
This equation with equation 6 Lead to get Equation (8)
 . (8)
. (8)
The coefficient µ is constant, which must be chosen for quick adaptation without losing stability. The filter is stable if µ satisfies the following condition,
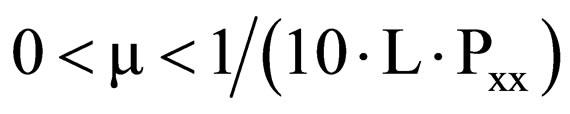 (9)
(9)
where L is the filter order and Pxx is the power of the input signal [21].
The LMS algorithm is initiated with an arbitrary value w(0) for the weight vector at n = 0. The successive corrections of the weight vector eventually leads to the minimum value of the mean squared error.
3. RESULTS
The results demonstrate the ability of the proposed method, where the modified signal r1(n) filtered in Matlab from LS (primary) as stated in the experimental procedure. The obtained results have been controlled by the following parameters:
• The length of signal or segment 25,000 to 32,000 samples at 11,025 Hz frequency sampling rate. This length should include 3 R peaks of ECG waveform as minimum in this segment.
• The convergence factor µ, which controlled using Equation (9).
• The order L of LMS-ANC is chosen in the range 4 ≤ L ≤ 64. The middle value of this range is the optimum value that worked with normal and abnormal LS signals.
The effect of changing the above parameters is monitored by PSD spectrum of LMS-ANC output signal e(n) and the graphic view of output signal e(n).
Figure 2 shows HS, h(n), that are derived from the original signal, which was recorded from subject with abnormal diagnose. This recoding has been recorded from front and slightly right position of chest. Chosen recording shows clarifying result after filtering and ECG waveform. Figure 3 shows HS and generated WGN, d(n).The combination of these signals is the modulated reference signal r1(n) of LMS-ANC input. WGN is based on Matlab command “randn function”, which is a standard Gaussian distribution which has mean = 0 and variance = 1, so when calculate the overall variance of n it will be 1.
Figures 4 and 5 show the primary signal of an abnormal LS recording before and after applying method. In comparison, there is a significant difference between the views of both graphics, where frequency components of recording in Figure 5 are less than in Figure 4. These results are controlled and modulated by two parameters of LMS-ANC; order L and the convergence factor µ.

Figure 2. HS derived from original LS recording.

Figure 3. HS combined with WGN-Reference signal r1(n).

Figure 4. The primary signal LS/ original LS recording before LMS-ANC.

Figure 5. The primary signal LS/original LS recording after LMS-ANC.
These parameters are very important; because it lead to appropriate filtering and to get adequate adaptation of designed filter.
Figure 6 demonstrates more clearly the difference in PSD of LS before and after LMS-ANC. The PSD of filtered signal shows different frequencies in different intervals, whereas PSD before filtering doesn’t.
This interprets that PSD of LS before filtering contains more frequencies which can’t be differentiated as illustrated PSD. PSD after filtering demonstrate different components of frequency. This explains that the HS frequency and NI have been removed successfully from LS. Calculated PSD, which is used in this work depends on FFT, explains that the frequency components before filtering are more in spectrum, which is blind and solid. On the other hand, when the signal contains less frequencies, spectrum shows distinguishable frequency values and bands after applying the method as shown in Figure 6. The obtained results indicate that the method of modified input reference with LMS-ANC has been effectively worked and successfully reduced HS and NI from LS.
Furthermore, the method has been applied to normal LS recording using the same steps stated previously. Figure 7 shows the normal LS recording, which recorded from healthy adult. Position of recording is the right of chest to upper. In this figure R peaks of ECG waveform have been monitored, shown in circle, the effect of proposed method beginning from derived HS to output signal e(n) of LMS-ANC.
Figure 8 shows PSD of normal LS before and after applying our method. Spectrum shows clearly better frequency components of the LS after filtering than beforefiltering
4. DISCUSSION
The proposed method of composited signals (HS + noise), is applied to the reference input of LMS-ANC, and it is appropriate to separate HS and brewed noise of instrument from LS. Segmentation signal has been applied to inputs of LMS-ANC upon getting stationary segment signal [8]. To modify the ANC, based on two-channel input, a reference signal was generated from the primary input signal by the proposed reference generation system. By experiment, it was confirmed that controlled algorithm has been required to choose suitable segment or period of primary signal as well as reference signal. The main controlled steps are order L and the convergence factor µ. These values were chosen based on same arguments like frequency response of LMS-ANC, observed PSD spectrum, comparison frequency bands of LS before and after LMS ANC filter.
The length of segment begins from 25,000 to 32,000 samples.
The idea of using LMS-ANC is the confirmed results; that the single Input ANC can effectively reduce a heart sound in an auscultation sound [22]. This is a key point used to extract a periodic signal component as HS in small segment as well as WGN adding to HS. These has been experimented by designed algorithm.
The reference input receive a noise r1(n) uncorrelated with the x(n) signal but correlated in some way with the noise r0(n). The reference r1(n) passes through a filter to produce an output y(n) that is a close estimate for primary input noise as stated in Equation (3). This estimated noise is subtracted from the corrupted signal to produce an estimated error e(n) (filtered LS signal) at the ANC system output. Therefore, the method has used in our case to obtain the reference signal derived from the original signal is optimally an appropriate band pass filter.
RLS-ANC algorithm has used with HS reference signal derived from LS at 20 - 300 Hz band pass filter [8]. Experiment has approved that such method is not suitable for all LS types at same cutoff frequency, and because of recording positions. This approach ignored other types of noise including in LS (e.g. instrumentation and surrounded environmental noises), moreover experimentally LMS-ANC more suitable for LS property than RLS-ANC.
Another method in [13] is used ECG as a reference signal to reduce HS from lung sound. This method is unsuitable because both inputs of adaptive filter must be sounds using, other words the primary signal is auscultation record whereas, the reference signal is ECG waveform recording.
The reference HS in [14] has been recorded from a healthy subject using a stethoscope microphone with the sampling rate of 44,100 Hz. This method depends on HS

Figure 6. The PSD The primary signal before LMS-ANC and after it.

Figure 7. The steps of applied method on normal LS recoding before and after LMS-ANC.
 (a) (b)
(a) (b)
Figure 8. The PSD of the primary signal (normal LS recoding): (a) PCD before LMS-ANC; (b) PSD after LMS-ANC.
as standard that is subtracted from primary input signal (LS) of an adaptive filter. It uses the LMS adaptive equalizer for detecting the HS segments from coefficients of the original signals which is required for comparison with reference HS in order to remove the HS segment from the contaminated signal. The stated method has not considered the different heart beat rate and its degree of regularity and time delay of each recording and obtained undesirable results due to different characteristics and mismatched frequency components in both signals.
Finally, filtering heart sounds (HS) and combined low frequency noise from instruments simultaneously, has not been used yet by other researchers in this field. Filtering combining noise in the same time with saving LS characteristics is differentiated from other methods. Moreover, combining signal (HS and NI) has applied on reference input and controlled parameters of LMS-ANC, all together, are considered as a new method of LS filtering. The proposed method has shown effective result in terms of PSD.
5. CONCLUSIONS AND FUTURE WORK
The proposed method has been used for LS filtering effectively and to remove HS and combined low frequency noise from instruments. Derived HS from the original signal and simulated low frequency noise has been applied to the reference input r1(n) of LMS-ANC with controlled parameters, used all to gather and considered as a new method in LS filtering. PSD has demonstrated significant performance after the proposed method is used with LMS ANC algorithm controlled by order and the convergence factor.
Future work can apply method in hardware. Recording LS and HS simultaneously from chest uses two sensors, one for LS and another for HS. The two recording signals will be applied to inputs of LMS-ANC. This trend can be applied in clinical diagnoses for HS and LS. It requires the development of instruments and data analysis.
REFERENCES
- Gao, J., Hu, J. and Tung, W.-W. (2011) Facilitating joint chaos and fractal analysis of biosignals through nonlinear adaptive filtering. PLoS One, 1, e24331.
- Sathesh, K. and Muniraj, N.J.R. (2012) Survey on separation of heart sounds from lung sounds by adaptive filtering. International Journal of Microsystems Technology and its Applications (IJMTA), 1, 1-10.
- Pradeep, K.J. and Anant, K.G. (2011) Heart sound separating from lung sound using Lab VIE. IJCST, 2, 418- 425.
- Thato, T. and Saeid, S. (2007) Separation of heart sound signal from lung sound signal by adaptive line enhancement. Proceedings of 15th European Signal Processing Conference (EUSIPCO), Poznan, 3-7 September 2007, 1231-1235.
- Schuttler, F., Penzel, T. and Wichert, P.V. (1997) Digital recording and computer-based analysis of lung sounds. Proceedings of the 18th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Amsterdam, 31 October-3 November 1996, 2301-2302.
- Thato, T. (2008) Digital signal processing algorithms and techniques for the enhancement of lung sound measurements. Ph.D. Thesis, Loughborough University, Loughborough.
- Potdar, R.M., Anup, M., Vinni, S. and Tripti, R. (2012) Performance evaluation of different adaptive filtering algorithms for reduction of heart sound from lung sound. International Journal of Engineering and Advanced Technology (IJEAT), 1, 61-67.
- Gnitecki, J., Moussavi, Z. and Pasterkamp, H. (2003) Recursive least squares adaptive noise cancellation filtering for heart sound reduction in lung sounds recordings. Proceedings of the 25th Annual International Conference of the IEEE, Engineering in Medicine and Biology, 3, 2416-2419.
- Hadjileontiadis, L.J. and Panas, S.M. (1998) A waveletbased reduction of heart sound noise from lung sounds. International Journal of Medical Informatics, 52, 183- 190. doi:10.1016/S1386-5056(98)00137-3
- Pourazad, M.T., Moussavi, Z. and Thomas, G. (2009) Heart sound cancellation from lung sound recordings using time-frequency filtering. IEEE Transactions on Biomedical Engineering, 44, 216-225.
- Gao, J.B., Sultan, H., Hu, J. and Tung, W.W. (2010) Denoising nonlinear time series by adaptive filtering and wavelet shrinkage: A comparison. IEEE Signal Processing Letters, 17, 237-240. doi:10.1109/LSP.2009.2037773
- Tung, W.W., Gao, J.B., Hu, J. and Yang, L. (2011) Recovering chaotic signals in heavy noise environments. Physical Review E, 83, 171-182.
- Yip, L. and Zhang, Y.T. (2001) Reduction of heart sounds from lung sounds recording by automated gain control and adaptive filtering techniques. Proceedings of the 23rd Annual International Conference of the IEEE, Engineering in Medicine and Biology Society, 3, 2154- 2156.
- Sathesh, K. and Muniraj, N.J.R. (2012) Separation of heart sounds from lung sounds using LMS adaptive equalizer implementation in cadence tools. International Journal of Mechanic Systems Engineering (IJMSE), 2, 48-52.
- Abhishek, M. and Sinha, G.R. (2012) Denoising of PCG signal by using wavelet transforms. Advances in Computational Research, 4, 46-49.
- Flores-Tapia, D., Moussavi, Z. and Thomas, G. (2007) Heart sound cancellation based on multiscale products and linear prediction. IEEE Transactions on Biomedical Engineering, 54, 234-243. doi:10.1109/TBME.2006.886935
- Ahlstrom, C., Liljefeldt, O., Hult, P. and Ask, P. (2005) Heart sound cancellation from lung sound recordings using recurrence time statistics and nonlinear prediction. IEEE Signal Processing Letters, 12, 812-815. doi:10.1109/LSP.2005.859528
- Noman Al, N. (2012) Development of computerized recording channel of lung sound. Journal of Medical and Bioengineering (JOMB), 1, 52-55. doi:10.12720/jomb.1.1.52-55
- Tsalaile, T., Naqvi, S., Nazarpour, K., Sanei, S. and Chambers, J. (2008) Blind source extraction of heart sound signals from lung sound recordings exploiting periodicity of the heart sound. IEEE ICASSP, 2008, 461-464.
- Karagiannis, A. and Constantinou, Ph. (2010) On the processing of white gaussiannoise biomedical signals with the empirical mode decomposition. Analysis of Biomedical Signals and Images, 20, 439-446.
- Garcés, L.E. (2007) Artifact removal from EEG signals using adaptive filters in cascade 1. Journal of Physics: Conference Series, 90, 012081.
- Lee, Y.J., Kim, P.U., Lee, G., Cho, J.H. and Kim, M.N. (2010) Single input ANC for suppression of breath sound. World Academy of Science, Engineering and Technology, 44, 1160-1162.

