Chinese Medicine
Vol.10 No.02(2019), Article ID:93451,67 pages
10.4236/cm.2019.102005
Acupuncture Treating Dystrophy Based on pH
—Mathematical Reasoning of Treatment Principle Based on Yin Yang Wu Xing Theory in Traditional Chinese Medicine (III)
Yingshan Zhang1*, Bibo Zhang2
1School of Statistics, Faculty of Economics and Management, East China Normal University, Shanghai, China
2Henan Province Zhang Bibo Institute of Traditional Chinese Medicine Acupuncture and Moxibustion, Henan, China

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 4, 2018; Accepted: June 27, 2019; Published: June 30, 2019
ABSTRACT
Theory of both Zangxiang (藏象) and Jingluo (经络) is useful in understanding disease. By using mathematical reasoning based on Yin Yang Wu Xing Theory in Traditional Chinese Medicine (TCM), this paper demonstrates the treatment principle: “Searching for a root cause of disease in cure, treatment of both the root-cause and symptoms at the same time” (治病求本, 标本兼治). It means that for a human body, there is the mathematical structure of both Zangxiang and Jingluo as her/his second physiological system. It can be used to determine both the root-cause and symptoms of the sick organ by using both Zangxiang and Jingluo. In general, for the human blood pH value, the normal range of theory is [7.34539, 7.45461] nearly to [7.35, 7.45], and the center is 7.4. The first or second transfer law of a human body’s energies changes according to the different blood pH values whether in the normal range or not. Human disease treatment should protect and maintain the balance of two incompatibility relations: the loving relationship and the killing relationship. As an application, acupuncture is used to treat limb-girdle muscular dystrophy.
Keywords:
Traditional Chinese Medicine (TCM), Yin Yang Wu Xing Theory, Steady Multilateral Systems, Incompatibility Relations, Side Effects, Medical and Drug Resistance Problem

1. Introduction
Theory of both Zangxiang (藏象) and Jingluo (经络) is useful in understanding disease. Zangxiang and Jingluo are two general mathematical structures. Human body blood pH value of both Zangxiang and Jingluo is a general parameter linking together the complexity of relations between organ pairs, the organ itself, the capabilities for intervention reaction and self-protection of the body and mind as a whole, related to the environment, food, health and personal history, air, water, earth, climate, season, etc. Human body blood pH value is as useful in understanding disease as the average is in statistics, or as the expected value is in probability calculation.
The studies of Prof. Macro Pianesi, President of the International Association UN PUNTO MACROBIOTICO, began as a pioneer work continuing the work of Japanese Nyoiti Sakurazawa, known in the West as Georges Ohsawa, the founding father of Macrobiotics. For example, thanks to these studies and macrobiotic cooking, over 25,000 disease patients have been cured in the last 8 years in the state of Africa alone, even with understandable and interesting economic implications.
Macrobiotic diet therapy trials have started in other parts of the world as well, including China: Prof. Wang Bin (Director of the Department of Medical Matters, Tibetan and Ethnic Medicine Hospital, University of Traditional Chinese Medicine, Beijing), Dr. Weiguo Ma and Dr. Bing Xu (also from the University of Traditional Chinese Medicine, Beijing), and Dr. Yujing Quian (Doctor in Traditional Chinese Medicine at Capital Normal University), who reported their experiences in a conference held in Italy on October 18, 2010.
Mario Pianesi never ceases to thank the Ancient Chinese for the depth of their thinking, and for the value they give to food in their reflections and observations. Among others, Prof. Mario Pianesi identifies an important indicator for human health: the value of blood pH, which, under normal conditions, ranges from 7.35 to 7.45, and the center is 7.4. Outside this range (acid: Yin condition; alkaline: Yang condition), disease appears. Almost always, when there is a disease, the condition of blood is a Yin condition, little is a Yang condition.
There are a lot of evidences (e.g., experimental identification for probability and real applications) to support this viewpoint, such as, Shirakabe et al. [1] , Kaur et al. [2] , Aly et al. [3] , Intven et al. [4] , Patel et al. [5] , Handman et al. [6] , Natalia et al. [7] , Barfod et al. [8] , Zhu et al. [9] , Zhu et al. [10] , Robert et al. [11] , Mona et al. [12] , Saritas et al. [13] , Stevens et al. [14] , and so on.
The body begins to activate the necessary mechanisms to restore this parameter to its appropriate range. If the body is unable to restore optimal pH levels, the disease may become chronic and lead to dire consequences.
Zhang et al. [15] - [23] have started a great interest and admired works for Traditional Chinese Medicine (TCM), where, through mathematical reasoning, they demonstrate the presence of incompatibility relations, which are predominant in daily life, yet absent in traditional Aristotelian Western logic.
Many people as Western person are beyond all doubt, the Yin Yang Wu Xing theory is superior to the traditional true-false logic, which does not contemplate incompatibility relations, which Zhang [19] has expertly explained from a mathematical standpoint.
The work Zhang [15] [16] has started, allows many people like Western person to think of a true re-foundation of mathematical language, to make it a better suited tool for the needs of mankind and the environment. Although so doing, Zhang [19] also brings to light the difficulty of establishing the values of both the intervention reaction coefficients and the self-protection coefficient as parameters with due accuracy.
In this paper, the introduction of a parameter such as a blood pH value will be suggested, in order to facilitate the understanding and the calculation of these values. This paper ventures to suggest this with all due to respect, because it be believed that the path Zhang [15] [16] has started, in such an understandable way from the mathematical point of view, will be very useful for all mankind searching for tools to understand the mechanisms of life.
The article proceeds as follows. Section 2 contains a parameter model and basic theorems, in order to explain the intervention reaction coefficients and the self-protection coefficient through the introduction of a parameter model to study the normal range of a human blood pH value, while the first or second transfer law of a human body’s energies is demonstrated in Section 3, proved through the concept of both relation costs and the relationship analysis of steady multilateral systems. Furthermore, if the range of a human blood pH value is divided into four parts from small to large, for the body in every part, the prevention or treatment method of a human body’s diseases as the treatment principle of TCM is given respectively in Section 4. As an application, acupuncture is used to treat limb-girdle muscular dystrophy in Section 5 and conclusions are drawn in Section 6.
2. Parameter Model and Basic Theorems
The concepts and notations in Zhang [18] are start and still used.
Let be the gold number. Denoted , namely healthy number. It is because the healthy number can make the healthy balance conditions and hold if and . Assuming , namely unhealthy number. It is because under a poor self-protection ability, the unhealthy number can make the following unhealthy balance conditions hold:
if and . Thus .
A parameter model of a human blood pH value in a mathematical sense based on Yin Yang Wu Xing Theory of TCM is reintroduced by using the functions and of the human blood pH value x described as follows.
Let be a human blood pH value, where the values 7 and 7.8 are the minimum and maximum acceptable the blood pH value. Denoted the center value 7.4 is the target as the expectation of the human blood pH value. Define a function of the blood pH value x in below:
(1)
A parameter model is considered as
(2)
Theorem 2.1 Under model (2), the following statements hold.
1) The one that is equivalent to the other that , where is a monotone decreasing function of x if or a monotone increasing function of x if ; and is a monotone decreasing function of if ; and is a monotone decreasing function of if .
(2) If , then
and
3) If , then
and
4) Taking and where , there are
and
where
5) Taking and where , there are
firstly, and if ;
secondly, and where if in which ;
thirdly, and where if in which ;
finally, and where
if in which .
In particular, when c is nearly to 1/2, there are
and the following statements hold.
a) The absolute value is nearly to 0 if in which .
b) The value is included in the interval respectively if in which .
c) The value is included in the interval respectively if in which . #
Corollary 2.1 Under model (2), the following statements hold.
1) For any , there is a unique solution and there is also a unique solution , such that
2) The condition is equivalent to each of the following conditions:
3) The condition is equivalent to each of the following conditions:
4) The condition is equivalent to each of the following conditions:
5) The condition is equivalent to each of the following conditions:
Theorem 2.1 and Corollary 2.1 can be found in Zhang [23] .
Remark 1. In west, through experiment or through practice observation, many researchers [1] - [14] have obtained the normal range of human blood pH value as . But in TCM, from Yin Yang Wu Xing Theory, Zhang [17] has already determined: for the normal range of a healthy body. Taking and where for a human body which has the capabilities of both intervention reaction and self-protection. From Corollary 2.1, the condition is equivalent to . In other words, in Theory of TCM, the normal range of human blood pH value is considered as , nearly to . Of course, little difference of the two intervals which makes the diagnosis of disease as a result, there may be no much difference as a suspect. In fact, TCM uses the rule from the Yin Yang Wu Xing Theory instead of the normal range of human blood pH value. The equivalence of Corollary 2.1 shows that TCM is The scientific.
Zhang [17] has already determined: a body is said healthy when the intervention reaction coefficient satisfies . In logic and practice, it’s reasonable that is near to 1 if the input and output in a human body are balanced, since an output organ is absolutely necessary other organs of all consumption. In case: , all the energy for intervening organ can transmit to other organs which have neighboring relations or alternate relations with the intervening organ. The condition can be satisfied when and for an organ since implies . In this case, . If this assumption is set up, then the intervening principle: “Real disease with a healthy body is to rush down its son and virtual disease with a healthy body is to fill its mother” based on the Yin Yang Wu Xing theory in image mathematics by Zhang et al. [20] , is quite reasonable. But, in general, the ability of self-protection is often insufficient for a usual human body, i.e., is small. A common standard is which comes from the balance condition of the loving relationship if . In other words, there is a principle which all losses are bear in a human body. Thus the general condition is often . Interestingly, they are all near to the golden numbers. It is the idea to consider the unhealthy number since the poor condition of self-protection ability can make the unhealthy balance conditions hold
if and .
By Theorem 2.1 and Corollary 2.1, implies .
And implies
.
And implies
where
since .
And implies
where
since .
The last one is the healthy interval in a person’s self-protection ability poor conditions. The interval range than the normal human body’s health requirements too strict, only the first three interval ranges are considered as a normal human body’s health. If keep two decimal places, then the first three intervals are the same as . This shows that range is stable. The interval as the normal range of human blood pH value may be also appropriate. To conservative estimates, the interval of the largest length of the first three range intervals is used, i.e., , as the theoretical analysis of the normal range. In fact, the range is better than the range . It is because the range satisfies the healthy balance conditions and if and . In other words, the parameter or the range is the healthy running condition of both the killing relationship and the loving relation at the same time. But neither are the others. The human blood pH value must be precise calculation to keep at least 5 decimal places can ensure correct because of its sensitivity to the diagnosis of disease.#
Remark 2. Western Medicine is different from TCM because the TCM has a concept of Chi or Qi (气) as a form of energy. From the energy concept, that one organ or subsystem of the human body is not running properly (or disease, abnormal), is that the energy deviation from the average of the organ is too large, the high (real disease) or the low (virtual disease). But there do not exist these concepts of both real diseases and virtual diseases in Western medicine. For the normal range of blood pH value of some human body as , in TCM, if , the body is considered as a real disease since the human blood pH value is too high; if , the body is considered as a virtual disease since the human blood pH value is too low. Thus TCM identifies an important indicator for a human body’s health: the human blood pH value, which, under normal conditions, ranges from 7.34539 to 7.45461. Outside this range (acid: Yin condition; alkaline: Yang condition), disease appears. Almost always absolutely, when there is virtual disease, the condition of human blood pH value is a Yin condition; when there is real disease, the condition of human blood pH value is a Yang condition.#
Remark 3. Obviously, when applying the hypothesis of Theorem 2.1 and Corollary 2.1 to other fields than a human body’s health, it is necessary to identify a global parameter in each field that is able to yield a general Yin or Yang condition in relation to the average behavior of the studied phenomenon, and that maintains the equations at a sufficiently simple level of writing and application. In fact, let where the values min and max are the minimum and maximum acceptable the index x. Denoted the value is the target as the expectation of the index x such that . In Equations (1) and (2), replace by , respectively. The equivalent condition of a healthy body is considered as , where
3. Relationship of the Steady Multilateral Systems
3.1. Energy Changes of a Steady Multilateral System
In order to apply the reasoning to other fields rather than a human body’s health, Zhang [17] has started a steady multilateral system imitating a human body. A most basic steady multilateral system is as follows.
Theorem 3.1 [20] For each element x in a steady multilateral system V with two incompatibility relations, there exist five equivalence classes below:
which the five equivalence classes have relations in Figure 1.#
The Yin Yang Wu Xing model can be written as follows. Define
corresponding to wood, fire, earth, metal, water, respectively, and assume where (hereinafter the same).
And take satisfying
where is the Descartes product in set theory and
Figure 1. Finding Yin Yang Wu Xing Model.
is the multiplication relation operation. The relation multiplication of is isomorphic to the addition of module 5. Then is a steady multilateral system with one equivalent relation and two incompatibility relations and where is the inverse relation operation. The Yin and Yang mean the two incompatibility relations and the Wu Xing means the collection of five disjoint classifications of . The model is called Yin Yang Wu Xing model, denoted simply by .
It can be proved by Theorem 3.2 in Zhang [23] that the steady multilateral system in Theorem 3.1 is the reasoning model of Yin Yang Wu Xing in TCM if there is an energy function satisfying
The parameter is called the coefficient of the vital or righteousness energy. The parameter is called the coefficient of the evil energy. A human body is called healthy if the vital or righteousness coefficient is greater than or equal to the evil coefficient . Otherwise, the human body is called unhealthy. For a healthy human body, the transfer law of the Yang vital or righteousness energy in the Yin Yang Wu Xing Model is
Figure 1 in Theorem 3.1 is the figure of Yin Yang Wu Xing theory in Ancient China. The steady multilateral system V with two incompatibility relations is equivalent to the logic architecture of reasoning model of Yin Yang Wu Xing theory in Ancient China. What describes the general method of human bodies can be used in the human body.
By non-authigenic logic of TCM, i.e., a logic which is similar to a group has nothing to do with the research object [20] , in order to ensure the reproducibility such that the analysis conclusion can be applicable to any a human body, a logical analysis model can be chosen which has nothing to do with the object of study. The Tao model of Yin and Yang is a generalized one which means that two is basic. But the Tao model of Yin Yang is simple in which there is not incompatibility relation. The analysis conclusion of Tao model of Yin Yang cannot be applied to an incompatibility relation model. Thus the Yin Yang Wu Xing model with two incompatibility relations of Theorem 3.1 will be selected as the logic analysis model in this paper.
On the other hand, the steady multilateral system is called the Tao model, denoted simply by , if it satisfies the following conditions:
The relation multiplication of is isomorphic to the addition of module 2. The element 1, or 0 is called a Yang force or a Yin force respectively. For a healthy human body, the transfer law of the Tao force in the Tao model is from Yang to Yin.
In TCM, any material can be found, not Yang is Yin. No matter of Yin and Yang are unable to see, known as dark matter, or nonphysical. Therefore, the Tao force often exists in the physical world. Any steady multilateral system only force under the action of the Tao, may be to perceive.
Furthermore, the steady multilateral system
is called the Telluric effluvium model, denoted simply by , if it satisfies the following conditions:
The number 1, or 2, or 3 is called the tengen (天元), the earth material (地元), the people ability (人元), respectively. The set of is called three types of talent or material. It is with elements, . The each of elements, , is called the primordial energy (元气), essence derived from food (谷气), defensive energy (卫气), essential substance circulating in the channels and blood vessels (营气), genuine energy (真气), pectoral energy (宗气), respectively. Another name is respectively
Generally positive or Yang material, they are able to be perceived, but few can see the material itself, can only use signs. Therefore, the Yang energy symptoms of the set calls the marrow energy (髓); The Yin energy of the set calls the blood energy (血); The Yin energy of the set calls the saliva energy (津); The Yin energy of the set calls the essence of water and grain (水谷精微).
Growth and conveyance in the six energies known as the six roots (根); As the fruit of these six energies known as the six fruits (结); Storage of these four energies known as the four seas(四海); Energy exchange of the four kinds of known as the four streets(四街). Of course, for a healthy human body, the transfer law of each of the six energies is from its root (root-causes) (根) to its fruit (symptoms) (结).
Western Medicine is different from TCM because the TCM has a concept of Chi or Qi (气) as a form of energy of steady multilateral systems. It is believed that this energy exists in all things of steady multilateral systems (living and non-living) including air, water, food and sunlight. Chi is said to be the unseen vital force that nourishes the human body and sustains the human body’s life. It is also believed that an individual is born with an original amount of Chi at the beginning of human body’s life and as a human body grows and lives, the human body acquires or attains Chi or energy from “eating” and “drinking”, from “breathing” the surrounding “air” and also from living in its environment. The steady multilateral system having an energy is called the anatomy system or the first physiological system. And the first physiological system also affords Chi or energy for the steady multilateral system’s meridian system (Zang Xiang (藏象) and Jing-Luo (经络)) which forms a parasitic system of the steady multilateral system, called the second physiological system of the steady multilateral system. The second physiological system of the steady multilateral system controls the first physiological system of the steady multilateral system. A steady multilateral system would become ill or dies if the Chi or energy in the steady multilateral system is imbalanced or exhausted, which means that and .
For example, in TCM, a human body as the first physiological system following the Yin Yang Wu Xing theory was classified into five equivalence classes as follows:
wood (X) = {liver, bravery, soul, ribs, sour, east, spring, birth};
xiang-fire ( ) = {pericardium, the triple energizer, nerve, the blood, bitter taste, the south, summer, growth};
earth( ) = {spleen, stomach, willing, meat, sweetness, center, long summer, combined};
metal ( ) = {lung, large intestine, boldness, fur, spicy, west, autumn, accept};
water ( ) = {kidney, bladder, ambition, bone, salty, the north, winter, hiding};
jun-fire ( ) = {heart, small intestine, nerve, the blood, bitter taste, whole body, whole direction, throughout the year, overall growth}.
Fire ( ) = xiang-fire ( ) jun-fire( ).
There is only one of both loving and killing relations between every two classes. General close is loving, alternate is killing.
In every category of internal, think that they are with an equivalent relationship, between each two of their elements there is a force of similar material accumulation of each other. It is because their pursuit of the goal is the same, i.e., follows the same “Axiom system”. It can increase the energy of the class at low cost near to zero if they accumulate together. Any nature material activity follows the principle of maximizing so energy or minimizing so cost. In general, the size of the force of similar material accumulation of each other is smaller than the size of the loving force or the killing force in a stable human body. The stability of any human body first needs to maintain the equilibrium of the killing force and the loving force. The key is the killing force. For a stable human body, if the killing force is large, i.e., becomes larger by Theorems 3.4 and 3.5 below, which needs positive exercise, then the loving force is also large such that the force of similar material accumulation of each other is also large. They can make the human body more stable. If the killing force is small, i.e., becomes smaller by Theorems 3.4 and 3.5 below, which means little exercise, then the loving force is also small such that the force of similar material accumulation of each other is also small. They can make the human body becoming unstable. The Chi or energy is also called the food hereafter for simply. In order to get the food, by Attaining Rule in Zhang [23] , the second physiological system must make the first physiological system intervened, namely exercise. It is because only by intervention on the first physiological system, the second physiological system can be to get food.
The second physiological system of the steady multilateral system controls the first physiological system of the steady multilateral system, abiding by the following rules.
Definition 3.1 (Zangxiang (藏象)) Assume the Yin Yang Wu Xing model is implemented by the Tao force of the Tao model . Then the steady multilateral system is called the Zangxiang or the Five Zang-organs model of the steady multilateral system.
The Zangxiang model satisfies as follows:
Each of the elements,
is called respectively
corresponding to the Chinese words respectively:
also corresponding to the notations in Theorem 3.1 respectively:
Here, each of the elements: is called wood, fire, earth, metal, water, respectively, and this is Yang, is Yin.
In TCM, another name of the Zangxiang system is the ten Heavenly Stems (天干). It means in the changes of energy transmission, plays a major role, is under the power of positive (Yang), although it is invisible, the reason of behind the sign.
In the ten heavenly stems, Yang is respectively:
Yin is respectively:
Yin is in the inside (里), Yang is in the outside (表). The relationship between the inside and the outside is the liking relationship.
The laws of the Zangxiang system or the ten Heavenly Stems model are summarized in Figure 2.#
Definition 3.2 (Jingluo) Assume the Telluric effluvium model is implemented by the Tao force of the Tao model . Then the steady multilateral system is called the Jingluo or the Six Fu-organs model of the steady multilateral system.
The Jingluo model satisfies as follows:
Each of the elements,
is called respectively
Figure 2. Relations of ten Heavenly Stems.
Corresponding to the Chinese words respectively:
Also corresponding to the notations in Theorem 3.1 as the five viscera and six entrails respectively:
Here, each of the elements: is called wood, xiang-fire (相火), earth, metal, water, jun-fire (君火) respectively, and this is Yang, is Yin.
In TCM, another name of the Jingluo system is the twelve Earthly Branches (地支). It means in the changes of energy transmission, plays a second role, is under the power of negative (Yin), although it is tangible, a sign of strength can be observed directly.
In the twelve earthly branches, Yang is respectively
Yin is respectively
Yin is in the inside (里), Yang is in the outside (表). The relationship between the inside and the outside is the liking relationship.
In the twelve earthly branches, other names of them are corresponding to the human body’s organs respectively:
Or, respectively,
The laws of the Jingluo system or the twelve Earthly Branches model are summarized in Figure 3.#
In TCM, the Zangxiang and Jingluo models are not the anatomy systems as
Figure 3. Relations of twelve Earthly Branches.
the first physiological system corresponding to their steady multilateral systems, are only them the mathematical logic models. If there are the Yin Yang Wu Xing model , the Telluric effluvium model and the Tao model , then the Zangxiang model and the Jingluo model must be existed in logic. So they form a parasitic system of the Yin Yang Wu Xing system , namely the second physiological system of the steady multilateral systems and .
In TCM, the Zangxiang model cannot be observed directly, so it is hidden behind the Jingluo system, namely the Zangxiang (藏象) model. Chinese word “藏” is the meaning of the hidden behind. Therefore, only the twelve meridians can be observed. Began to grow the 12 kinds of energies of each place, referred to as the basic root-causes (本). To generate the results of the 12 kinds of energies, referred to as the symptoms (标). Management of the 12 kinds of energies of each system, known as meridians or the Jingluo systems. Of course, for a healthy human body, the transfer law of each of the 12 kinds of energies is from its basic root-causes (本) to its symptoms (标).
In spite of the ten heavenly systems cannot be observed, but it can be observed according to the reasoning of the twelve earthly branches system. So the logic relation of both the ten heavenly stems system and the twelve earthly branches system must be known.
Definition 3.3 (Logic Relation of Ten Heavenly Stems Hidden behind Twelve Earthly Branches) Logic Relation of Ten Heavenly Stems Hidden behind Twelve Earthly Branches must follow the relationship between the growth of the ten heavenly elements.
For the ten heavenly stems, although they are hidden in the 12 earthly branches, the existing way is not completely the same. They each have 12 kinds of growth status:
According to the names of Yin and Yang attribute is different, their growth way also each are not identical. Yang heavenly stems energy transmission is energy transmitted along the twelve earthly branches, and Yin heavenly stems energy transfer is against the twelve earthly branches transmission of energy transmitted sequence.
The following ten heavenly stems are hidden behind the twelve earthly branches as follows:
All Logic Relations of Ten Heavenly Stems Hidden behind Twelve Earthly Branches are summarized in Figure 4.
See Figure 4. and Table 1 and Table 2, all pure Yang: Jia, Bing, Geng, Ren of Ten Heavenly Stems are hidden behind Palms corners, clockwise for growth and officer. Only Yang earth: Wu of Ten Heavenly Stems is hidden behind Palms on both sides, clockwise for the growth, crowned, officer, disease and cemeteries.
All pure Yin: Yi, Ding, Xin, Gui of Ten Heavenly Stems are hidden behind the sides of the palms, counterclockwise to raise, crowned and officer. Only Yin
Figure 4. Ten Heavenly Stems Hidden behind Twelve Earthly Branches.
Table 1. Ten Heavenly stems grow-strong-die-extinction (I).
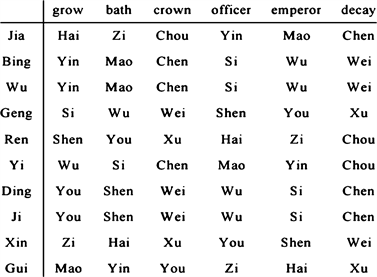
Table 2. Ten Heavenly stems grow-strong-die-extinction (II).
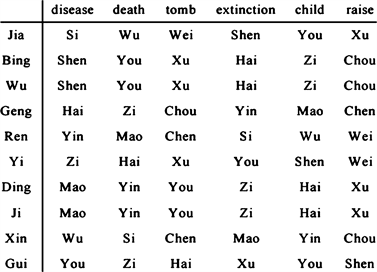
earth: Ji of Ten Heavenly Stems is hidden behind Palms up and down, counterclockwise for the tomb, crowned and officer. #
Property 3.1 (Ten Heavenly Stems Grow-Strong -Die -Extinction Hidden behind Twelve Earthly Branches) Ten heavenly stems under a number of laws, the ten heavenly stems inside the twelve earthly branches transmission rule can be gotten as follows. The five Yang heavenly stems: Jia, Bing, Wu, Geng, Ren was born by Hai, Yin, Yin, Si, Shen clockwise respectively; The five Yin heavenly stems: Yi, Ding, Ji, Xin, Gui was born by Wu, You, You, Zi, Mao counterclockwise respectively. Using mathematical language, all of these laws are summarized in Table 1 and Table 2.#
Property 3.2 (The rationality of the name of Twelve Earthly Branches) The following notations in Definition 3.2 is reasonable.
It is with the correct meaning of the Yin Yang Wu Xing Model in Theorem 3.1.#
Energy concept is an important concept in Physics. Zhang etc [21] introduce this concept to the steady multilateral systems or image mathematics [20] and uses these concepts to deal with the steady multilateral system diseases (mathematical index too high or too low). In mathematics, a steady multilateral system is said to have Energy (or Dynamic) if there is a non-negative function which makes every subsystem meaningful of the steady multilateral system. Similarly to Zhang etc [21] , unless stated otherwise, any equivalence relation is the liking relation, any neighboring relation is the loving relation, and any alternate relation is the killing relationship.
Suppose that V is a steady multilateral system having an energy, then V in the steady multilateral system during a normal operation, its energy function for any subsystem of the steady multilateral system has an average (or expected value in Statistics), this state is called as normal when the energy function is nearly to the average. Normal state is the better state.
That a subsystem of the steady multilateral system is not running properly (or disease, abnormal) is that the energy deviation from the average of the subsystems is too large, the high (real disease) or the low (virtual disease).
In addition to study these real or virtual diseases, TCM is often not only considered the energy change (Attaining or Affording) of each element in the corresponding group, but also studied a kind of relation costs. There are three kinds of relationship between each two elements of the Zangxiang system or the Jingluo system, namely the merged, synthesized and combined.
The merged relationship between two the same elements x and y is the joining operation in a set, i.e., . The element z is the result of two the same elements x and y merging. The purpose of merging is in order to get the large result energy of element z through inputting two the same elements x and y.
The synthesized relationship between two elements x and y is the multiply operation in the corresponding group system with a multiplication *, i.e., . The element z is the result of two elements x and y synthesized. The purpose of synthesized is in order to get the result energy of element z through inputting two elements x and y.
The combined relationship between two elements x and y is the division operation in the corresponding group system with a multiplication *, i.e., . The element z is the cost of two elements x and y combined. The purpose of combined is in order to maintain or strengthen the relation between x and y through inputting the cost element z.
In general, a relationship cost is low if the cost element in the corresponding group is easy to get. A relationship cost is high, on the other hand, if the cost element in the corresponding is hard to come by.
In this case, in general, the human body pH value or . This relation cost is low because this relation cost element is easy to get. The low relation cost can make the intervention increasing the sizes of both the intervention reaction coefficients and the self-protection coefficient .
But in general, the human body blood pH value or . This relation cost is high because the relation cost element is hard to come by. The high relation cost can make the sizes of both the intervention reaction coefficients and the self-protection coefficient decreasing response to intervention.
The purpose of intervention is to make a human body return to normal state. The method of intervention is to increase or decrease the energy of an organ.
What kind of intervening should follow the principle to treat it? Western medicine emphasizes directly treatments on the sick organ after the sick of organ has occurred, but the indirect intervening of oriental medicine is required before the sick of organ will occur. Which is more reasonable?
Based on this idea, many issues are worth further discussion. For example, if an intervening has been implemented to a sick organ before the sick of organ will occur, what relation disease will be low cost which does not need to be intervened? what relation disease will be high cost which needs to be intervened?
3.2. Kinds of Relationship Costs of Steady Multilateral Systems
For a steady multilateral system V with two incompatibility relations, suppose that the subsystems are the same as those defined in Theorem 3.1. Then the relation diseases can be decomposed into the following classes:
Definition 3.4 (merged(合并), synthesized(合成) and combined (化合)) Suppose that both x and y are two elements of system of Zangxiang or Jingluo.
The merged relationship between two the same elements x and y is the joining operation in a set, i.e., . The element z is the result of two the same elements x and y merging. The purpose of merging is in order to get the large result energy of element z through inputting two the same elements x and y.
The synthesized relationship between two elements x and y is the multiply operation in the corresponding group system with a multiplication *, i.e., . The element z is the result of two elements x and y synthesized. The purpose of synthesized is in order to get the result energy of element z through inputting two elements x and y.
The combined relationship between two elements x and y is the division operation in the corresponding group system with a multiplication *, i.e., . The element z is the cost of two elements x and y combined. The purpose of combined is in order to maintain or strengthen the relation between x and y through inputting the cost element z.
The synthesized and combined operations in system of Zangxiang or Jingluo are the same since .#
Property 3.3 Suppose that both x and y are two elements of the Zangxiang system. Then the following statements are true.
1) The lowest cost element is
.
The second low cost is
.
The third low cost is
The fourth low cost is
2) The highest cost element
The second high cost is
3) The synthesized relationships of the ten Heavenly Stems at zero costs are as follows:
4) The combined relationships of the ten Heavenly Stems at low costs are as follows:
5) The combined relationships of the ten Heavenly Stems are at highest costs as follows:
All relation laws of the Zangxiang system or the ten Heavenly Stems model are summarized in Figure 2. It means that both the liking relation and the loving relation have the low cost, but the killing relation has high cost.#
Property 3.4 Suppose that both x and y are two elements of the Jingluo system. Then the following statements are true.
1) The lowest cost elements are as follows:
The second low cost elements are as follows:
2) The highest relation cost elements are as follows
The second high cost elements are as follows
3) The merged relationships of the twelve Earthly Branches at zero costs are as follows:
4) The synthesized relationships of the twelve Earthly Branches at zero costs are as follows:
5) The combined relationships of the twelve Earthly Branches at low costs are as follows:
(6)The combined relationships of the twelve Earthly Branches at high costs are as follows:
All relation laws of the Jingluo system or the twelve Earthly Branches model are summarized in Figure 3. It means that the hand phase in Figure 3, all transverse relationship with low cost, but all vertical relationship with high cost. On the other hand, in the three types {Yin, Mao}, {Wu, Wei}, {Xu, Hai} or the three types {Chen, Si},{Shen, You},{Zi, Shou} for the vertices of the triangle respectively, the relationship between the cost is low. Otherwise, the relationship between the cost is high.#
3.3. First Transfer Laws of a Human Body’s Energies of Steady Multilateral Systems with a Healthy Body
Suppose that a steady multilateral system V having energy function is normal or healthy. Let x be the human blood pH value of V. Taking , and where and is defined in Equations (1) and (2). The healthy body means that the conditions and hold. By Corollary 2.1, it is equivalent to the normal range or the healthy condition . That implies that the body is without the ability of self-protection, i.e., . Of course, the body cannot be healthy. It is because for any , when , there are
such that the healthy condition cannot hold.
By using Corollary 2.1 and Theorems 2.1 and 3.1, the following Theorems 3.2 and 3.3 can be obtained as the transfer law of occurrence and change of a human body’s energies with a healthy body.
Theorem 3.2 (The first transfer law of the ten Heavenly Stems with a healthy body) Let the human blood pH value which is equivalent to the conditions and .
The transfer law of each of the 10 kinds of energy in the the Zangxiang system or the ten Heavenly Stems model is from its root-causes to its symptoms. Furthermore, for the healthy body, the transfer law of the Yang vital or righteousness energies of the ten heavenly stems is transferring along the loving or liking order of the ten heavenly stems as follows:
And the transfer law of the Yin vital or righteousness energies of the ten heavenly stems is transferring against the loving or liking order of the ten heavenly stems as follows:
All transfer laws of the Zangxiang system or the ten Heavenly Stems model for a healthy body are summarized in Figure 2. It means that only both the liking relation and the loving relation have the transfer law of the Yang or Yin vital or righteousness energies of the ten heavenly stems. Yang is transferring along the loving or liking order of the ten heavenly stems. Yin is transferring against the loving or liking order of the ten heavenly stems.#
Theorem 3.3 (The first transfer law of the twelve Earthly Branches with a healthy body)Let the human blood pH value which is equivalent to the conditions and .
The transfer law of each of the 12 kinds of energy in the Jingluo system or the twelve Earthly Branches model is from its root-causes to its symptoms. Furthermore, for the healthy body, the transfer law of the Yang vital energies of the twelve earthly branches is transferring along the loving or liking order of the twelve earthly branches as follows:
The transfer law of the Yin vital energies of the twelve earthly branches is transferring against the loving or liking order of the ten heavenly stems as follows:
All transfer laws of the Jingluo system or the twelve Earthly Branches model for a healthy body are summarized in Figure 3. It means that only both the liking relation and the adjacent relation have the transfer law of the Yang or Yin vital or righteousness energies of the twelve earthly branches. Yang is transferring along the loving or liking order of the twelve earthly branches. Yin is transferring against the loving or liking order of the twelve earthly branches.#
Remark 4. Theorems 3.2 and 3.3 are called the transfer law of occurrence and change of a human body’s energies with a healthy body, simply, the first transfer law.
For a Yang energy of X and the Zangxiang system or the ten Heavenly Stems model for a healthy body, the first transfer law is transferring along the loving or liking order of the ten heavenly stems as follows:
For a Yin energy of X and the Zangxiang system or the ten Heavenly Stems model for a healthy body, the first transfer law is transferring against the loving or liking order of the ten heavenly stems as follows:
For a Yang energy of X and the Jingluo system or the twelve Earthly Branches model for a healthy body, the first transfer law is transferring along the loving or liking order of the twelve earthly branches as follows:
For a Yin energy of X and the Jingluo system or the twelve Earthly Branches model for a healthy body, the first transfer law is transferring against the loving or liking order of the twelve earthly branches as follows
Because the energy change between and needs to be adjusted by the energy of , so generally believe that the Yin energy of X begins with the Yang energy of . This is in Zi to Yin (11 PM at night to the next day at half past five) need to have a rest.
The transfer relation of the first transfer law running is the loving or liking relationship, denoted by or . The running condition of the first transfer law is both and .
By Theorem 2.1 and Corollary 2.1, the running condition is nearly equivalent to both and . The best-state condition of the first transfer law is where which is the best state of for a healthy body. To follow or utilize the running of the first transfer law is equivalent to the following method. For dong so, it is in order to protect or maintain the loving relationship. The method can strengthen both the value tending to be large and the value tending to be small at the same time. In other words, the way can make all of both and c tending to be large. It is because the running condition of the loving or liking relationship is the stronger the use, which dues to the greater the use. In other words again, if the treatment principle of the loving relationship disease is to use continuously abiding by the first transfer law, then all of both the intervention reaction coefficients and the coefficient of self-protection where will tend to be the best state, i.e., and .
Side effects of medical problems were the question: in the medical process, destroyed the balance of the normal systems which are not sick or intervened subsystems. The energy change of the intervened system is not the true side effects issue. The energy change is called the pseudo or non-true side effects issue since it is just the food of the second physiological system of the steady multilateral system for a healthy body by Attaining Rule. The best state of the self-protection coefficient, i.e., , where , implies the non-existence of any side effects issue if the treatment principle of TCM is used. Therefore any disease that causes side effects issue occurrence in the first place dues to the non-best state of self-protection ability, i.e., . To follow or utilize the running of the first transfer law can make both and . At this point, the paper advocates to follow or utilize the first transfer law. It is in order to avoid the side effects issue occurrence for a healthy body.#
3.4. Second Transfer Laws of a Human Body’s Energies of Steady Multilateral Systems with an unhealthy Body
Suppose that a steady multilateral system V having energy function is abnormal or unhealthy. Let x be the human blood pH value of V. Taking and where , and is defined in Equations (1) and (2). The unhealthy body means that the conditions and hold, which is equivalent to the abnormal range .
From [20] and by using Corollary 2.1 and Theorems 2.1 and 3.1, the following Theorems 3.4 and 3.5 can be obtained as the transfer law of occurrence and change of a human body’s energies with an unhealthy body.
Theorem 3.4 (The transfer law of the ten Heavenly Stems with an unhealthy body) Let the human blood pH value which is equivalent to the conditions and .
The transfer law of each of the 10 kinds of energy in the Zangxiang system or the ten Heavenly Stems model for an unhealthy body is from its root-causes to its symptoms.
Furthermore, for the unhealthy body, if a subsystem X of a steady multilateral system V falls a real disease, then the disease comes from the mother SX of X. The transfer law of the Yang vital or righteousness energies of the ten heavenly stems is transferring against the killing or liking order of the ten heavenly stems as follows:
And if a subsystem X of a steady multilateral system V falls a virtual disease, then the disease comes from the son XS of X. The transfer law of the Yin vital or righteousness energies of the ten heavenly stems is transferring along the killing or liking order of the ten heavenly stems as follows:
All transfer laws of the Zangxiang system or the ten Heavenly Stems model for an unhealthy body are summarized in Figure 2. It means that only both the liking relation and the killing relation have the transfer law of the Yang or Yin vital or righteousness energies of the ten heavenly stems. Yang is transferring against the killing or liking order of the ten heavenly stems. Yin is transferring along the killing or liking order of the ten heavenly stems.#
Theorem 3.5 (The transfer law of the twelve Earthly Branches with an unhealthy) Let the human blood pH value which is equivalent to the conditions and .
The transfer law of each of the 12 kinds of energy in the Jingluo system or the twelve Earthly Branches model for an unhealthy body is from its root-causes to its symptoms.
Furthermore, for the unhealthy body, if a subsystem X of a steady multilateral system V falls a real disease, then the disease comes from the mother SX of X. The transfer law of the Yang vital energies of the twelve earthly branches is transferring against the killing or liking order of the twelve earthly branches as follows:
For the unhealthy body, if a subsystem X of a steady multilateral system V falls a virtual disease, then the disease comes from the son XS of X. The transfer law of the Yin vital energies of the twelve earthly branches is transferring along the killing or liking order of the twelve earthly branches as follows:
All transfer laws of the Jingluo system or the twelve Earthly Branches model for an unhealthy body are summarized in Figure 3. It means that only both the liking relation and the alternate relation have the transfer law of the Yang or Yin vital or righteousness energies of the twelve earthly branches. Yang is transferring against the killing or liking order of the twelve earthly branches. Yin is transferring along the killing or liking order of the twelve earthly branches.#
Remark 5. Theorems 3.4 and 4.5 are called the transfer law of occurrence and change of energies with an unhealthy body, simply, the second transfer law.
For a Yin energy of X and the Zangxiang system or the ten Heavenly Stems model for an unhealthy body, the second transfer law is transferring along the killing or liking order of the ten heavenly stems as follows:
For a Yang energy of X and the Zangxiang system or the ten Heavenly Stems model for an unhealthy body, the second transfer law is transferring against the killing or liking order of the ten heavenly stems as follows:
For a Yin energy of X and the Jingluo system or the twelve Earthly Branches model for an unhealthy body, the second transfer law is transferring along the killing or liking order of the twelve earthly branches as follows:
For a Yang energy of X and the Jingluo system or the twelve Earthly Branches model for an unhealthy body, the second transfer law is transferring against the killing or liking order of the twelve earthly branches as follows:
The transfer relationship of the second transfer law running is the killing or liking relationship, denoted by or . The running condition of the second transfer law is both and .
By Theorem 2.1 and Corollary 2.1, the running condition is equivalent to both and . That means the lack of capability of self-protection. Of course, it is the basis condition of running the second transfer law.
The stopping condition of the second transfer law is both
and , which is the running condition of the first transfer law, or, the existence condition of capabilities of both intervention reaction and self-protection. To follow or utilize the running of the second transfer law is equivalent to the following method. For dong so, it is to protect and maintain the killing or liking relationship of the steady multilateral system. The method can strengthen all of both and tending to be small at the same time. In other words, using the method can make c tends to be large for a fixed . It is because the transferring condition of the killing or liking relation disease is the weaker the use, which dues to is the greater the use. The transferring way can make both and at the same time such that the killing or liking relation disease cannot be transferred. In other words again, if the treatment principle of the killing relationship diseases is to use continuously abiding by the second transfer law, then the coefficient of self-protection will tend to be the occurrence state, i.e., where , and the coefficients of intervention reaction also will tend to the healthy state, i.e., , such that .#
Medical and drug resistance problem is that such a question, beginning more appropriate medical treatment, but is no longer valid after a period. In the state
by Theorem 3.4 and 3.5, any medical and drug resistance problem is non-existence if the treatment principle of TCM is used. But in the state
by Theorems 3.4 and 3.5, the medical and drug resistance problem is always existence, even if the treatment principle of TCM has been used. It is because virtual XK cannot kill real SX if X is intervened by increasing its energy. In other words, the lack of capability of self-protection, i.e., , implies the possible existence of a medical and drug resistance problem, although the treatment principle of TCM has been used. At this point, the paper advocates to follow or utilize the second transfer law in order to prevent and avoid the medical and drug resistance issue occurrence for the unhealthy body.#
4. Treatment Principle of TCM
In order to explain treatment principle of TCM, the changes in the blood pH value range is divided into four parts. From [20] , Theorems 2.1 and 3.1-3.5, Properties 3.1-3.4 and Corollary 2.1, it can be easily proved that the following theorem is true.
Theorem 4.1 Suppose that the subsystem X of a steady multilateral system falls ill. Let x be the human body blood pH value of the steady multilateral system. Denoted the parameters of the normal range as follows
Then the following statements are true.
1) Suppose that as virtual, in which X or XK falls a virtual disease with an unhealthy body. The subsystem X or XK itself is the root-cause of a happened virtual disease. And the son XS of X is the symptoms of an expected or a happened virtual disease. The primary treatment is to increase the energy of the subsystem X or XK directly. And the secondary treatment is to increase the energy of the son XS of X, and at the same time, to decrease the energy of the prisoner KX of XS.
2) Suppose that as virtual-normal, in which X or SX will fall a virtual disease with a healthy body. The mother SX of X is the root-cause of an expected virtual disease. And the subsystem X or SX is the symptoms of an expected virtual disease. The primary treatment is to increase the energy of the mother subsystem SX of X which is an indirect treating for X. And the secondary treatment is to increase the energy of X itself, and at the same time, to decrease the energy of the prisoner XK of X.
3) Suppose that as real-normal, in which X or XS will encounter a real disease with a healthy body. The son XS of X is the root-cause of an expected real disease. And the subsystem X itself is the symptoms of an expected real disease. The primary treatment is to decrease the energy of the son subsystem XS of X which is an indirect treating for X. And the secondary treatment is to decrease the energy of X itself, and at the same time, to increase the energy of the bane KX of X.
(4) Suppose that as real, in which X or KX encounters a real disease with an unhealthy body. The subsystem X or KX itself is the root-cause of an expected or a happened real disease. And the mother SX of X is the symptoms of an expected real disease. The primary treatment is to decrease the energy of the subsystem X or KX directly. And the secondary treatment is to decrease the energy of the mother SX of X, and at the same time, to increase the energy of the bane XK of SX.#
Remark 6. Treatment principle of Theorem 4.1 based on ranges of the human body blood pH value is called the treatment principle of TCM, since it is in order to protect and maintain the balance of two incompatibility relations: the loving or liking relationship and the killing or liking relationship.
For the unhealthy body where or , the treatment principle is the method for doing so in the following:
The primary treatment is to increase or decrease the energy of X directly corresponding to or respectively, and the secondary treatment is to increase the energy of XS or XK while to decrease the energy of KX or SX, respectively.
The primary treatment is in order to protect and maintain the loving or liking relationship, abiding by TCM’s ideas “Virtual disease with an unhealthy body is to fill itself” and “Real disease with an unhealthy body is to rush down itself”. It is because the method for dong so is not only greatly medical diseases of their own, but also provides the pseudo side effects as the food for the second physiological system. The method is to promote the first physiological system running since the second physiological system controls the first physiological system. And it is also to improve the loving or liking relationship to develop since the loving or liking relationship mainly comes from the first physiological system. The loving or liking relationship to develop can strengthen both that tends to be large and that tends to be small at the same time. In other words, the way can make all of both and c tend to be large, at least, c greater than zero for an unhealthy body and , such that the body from unhealthy to healthy, or the first physiological system works, or, the occurrence of capability of self-protection, or, the running of the first transfer law, or, the stopping of the second transfer law.
The secondary treatment is in order to protect or maintain the killing or liking relationship, abiding by TCM’s ideas “Don’t have disease cure cure non-ill” and “Strong inhibition of the same time, support the weak”. By the second transfer law in Theorems 3.4 and 3.5, the more serious relation disease is the relation disease between virtual XS and real KX, or between real SX and virtual XK respectively.
Abiding by TCM’s idea “Don’t have disease cure cure non-ill”, it must be done to prevent or avoid the more serious relation disease between virtual XS and real KX, or between real SX and virtual XK occurrence respectively.
Abiding by TCM’s idea ‘Strong inhibition of the same time, support the weak”, it must be done to increase the energy of XS or XK while decrease the energy of KX or SX respectively.
The method for doing so can improve the killing or liking relationship to develop since real XS or XK can kill virtual KX or SX respectively. The killing or liking relationship to develop means that both and tend to be small at the same time. In other words, the way can make, for fixed , c tending to be large, at least, greater than zero for an unhealthy body, such that the body from unhealthy to healthy, or the first physiological system works, or, the occurrence of capability of self-protection, or, the running of the first transfer law, or, the stopping of the second transfer law.
For the healthy body where or , the treatment principle is the method for doing so in the following:
The primary treatment is to increase or decrease the energy of SX or XS corresponding to or respectively, and the secondary treatment to increase the energy of KX or X while to decrease the energy of X or XK, respectively.
The primary treatment is in order to protect and maintain the loving or liking relationship, abiding by TCM’s ideas “Virtual disease with a healthy body is to fill mother” and “Real disease with a healthy body is to rush down its son”. It is because the method for dong so is not only greatly medical diseases of their own, but also provides the pseudo side effects as the food for the second physiological system. The method is to promote the first physiological system running since the second physiological system controls the first physiological system. And it is also to improve the loving or liking relationship developing since the loving or liking relationship mainly comes from the first physiological system. The loving or liking relationship developing can strengthen both that tends to be large and that tends to be small at the same time. In other words, using the way can make all of both and tending to be large, the best, all equal to 1 for a healthy body, such that the capability of self-protection is in the best state, or, the non-existence of side effects issue, or, the non-existence of medical and drug resistance problem.
The secondary treatment is in order to protect or maintain the killing or liking relationship, abiding by TCM’s ideas “Don’t have disease cure cure non-ill” and “Strong inhibition of the same time, support the weak”. By the first transfer law, the more serious relation disease is the relation disease between real X and virtual KX or between virtual X and real XK corresponding to real X or virtual X, respectively.
Abiding by TCM’s idea “Don’t have disease cure cure non-ill”, it must be done to prevent and avoid the more serious relation disease between real X and virtual KX or between virtual X and real XK occurrence corresponding to real X or virtual X respectively.
Abiding by TCM’s idea “Strong inhibition of the same time, support the weak”, it must be done to increase the energy of KX or X while decrease the energy of X or XK respectively.
The method for doing so can improve the killing or liking relationship developing since real KX or real X can kill virtual X or virtual XK respectively. The killing or liking relationship developing also means that both and tend to be small at the same time. In other words, using the way can make, for fixed , tending to be large, the best, equal to 1 for a healthy body, such that the capability of self-protection is in the best state, or, the non-existence of side effects, or, the non-existence of medical and drug resistance issue.#
5. Acupucture Is Used to Treat Limb-Girdle Muscular Dystrophy
The patient, female, 3 years old. Four months ago complained of fatigue, abdominal pain. She is more likely to be tired and restless than her peers, and cry after waking up at night. To Zhengzhou city a hospital check ecg showed: extended PR value. By checking the myocardial enzyme: the index of creatine kinase was high (500.5 U/L, normal range (26, 200)), the body’s blood pH value was low (7.24409, virtual, normal range [7.34539, 7.45461] and the center 7.4), preliminary determination of myocarditis. By myocarditis was discharged on hospital treatment after 9 days, 20 days after the review of myocardial enzyme: the index of creatine kinase higher, (1573 U/L, normal range (26, 200)), the body’s blood pH value lower (7.23682, virtual, normal range [7.34539, 7.45461] and the center 7.4). Hence to a Beijing hospital for emg and its genetic testing. Genetic testing results show that a clear diagnosis of limb girdle muscular dystrophy. This disease in western medicine, there is no treatment and effective drugs. On July 3, 2017 children to Henan province Zhang Bibo institute of TCM acupuncture treatment.
Children are suffering from the disease is a genetic disease, is relatively rare. Should adhere to the TCM thinking. According to the clinical symptoms, muscular dystrophy in TCM “expression paralysis syndrome” category. Need to regulate spleen and stomach, benefit Chi and blood. The age of children is small, her capability of self-protection is poor. Her pathogenesis is lack of innate endowment, acquired taste disorder, need to regulate spleen and stomach, tonic is deficient.
Because the body pH blood value is or , by (1) of Theorem 4.1, the subsystem earth(XK) (the spleen and stomach) falls a virtual disease with an unhealthy body. The subsystem earth(XK) (the spleen and stomach) itself is the root-cause of a happened virtual disease. And the son xiang-fire ( ) (the pericardium and the triple energizer) of wood(X) (the liver and gallbladder) is the symptoms of an expected virtual disease. The primary treatment is to increase the energy of the subsystem earth(XK) (the pleen and stomach) directly. And the secondary treatment is to increase the energy of the son xiang-fire ( ) (the pericardium and the triple energizer) of wood(X) (the liver and gallbladder), and at the same time, to decrease the energy of the prisoner metal (KX) (the lung and large intestine) of xiang-fire ( ) (the pericardium and the triple energizer).
Therefore, the primary treatment in to find out holes: SanYinJiao (三阴交, to increase the energy of the subsystem earth ( ) (the spleen) directly), ZuSanLi (足三里, to increase the energy of the subsystem earth ( ) (the stomach) directly), the TianShu (天枢, to increase the energy of the subsystem earth ( ) (the stomach) directly), ZhongWan (中脘, to increase the energy of the subsystem earth ( ) (the stomach) directly).
Secondary treatment is to find out holes: NeiGuan (内关,to increase the energy of the son xiang-fire ( ) (the pericardium) of wood(X) (the liver and gallbladder)), HeGu (合谷, to decrease the energy of the prisoner metal ( ) (the large intestine) of xiang-fire ( ) (the pericardium and the triple energizer)).
Methods: mild reinforcing and attenuating, prick .Once a day.
After 40 days of acupuncture therapy, the children lack of power and fatigue symptoms improved significantly, not to cause abdominal pain, sleep smoothly at night. Review of myocardial enzymes: the index of creatine kinase is lower, (192 U/L, normal range (26, 200)), the body’s blood pH value is virtual-normal (7.34929, normal range [7.34539, 7.45461] and the center 7.4). Children with symptoms improved obviously, and myocardial enzyme decline in more than half. Return no recurrence.
Muscular dystrophy in TCM belongs to “expression paralysis syndrome” category. The paper of the emperor neijing (“皇帝内经”) discusses the pathogenesis “limbs are adhered to in the stomach ..., spleen disease cannot make the stomach fluid, limb may not be the great water spirit, bones and muscles are not born to chi, reason need not how”, “the energy (Chi) of the foot TaiYin spleen meridian is off, pulse will not honor muscle”, “so the lung hot leaf scorch, fur muscles weak thin, the born is an expression paralysis syndrome”. Think its pathogenesis is: the spleen and stomach are deficient, Chi and blood not free.
The paper of the emperor neijing (“皇帝内经”) treatment method is put forward as follows: “treating expression paralysis syndrome alone takes the YangMing meridian”, “fill their honor (荣穴) and smooth their shu (俞穴), adjust its virtual and real condition, harmony with its inverse and smooth. Channels of the same flesh and blood, with its time by month”. Points out that the treatment should take its YangMing meridian, fill their honor (荣穴) and smooth their shu (俞穴).
SanYinJiao hole (三阴交穴, three vaginal intercourse hole) belongs to the foot TaiYin spleen meridian or the subsystem earth ( ). It is one of the famous Yang back nine needle holes (回阳九针穴, clinical first aid commonly used nine effective acupuncture point, for the treatment of syncope, cold limbs vein lies, Yang would like to take off, the operation can be back to Yang to save lives. Due to the “acupuncture poly examples”(“针灸聚英”),that is, YaMen (哑门), LaoGong (劳宫), SanYinJiao (三阴交), YongQuan (涌泉), DaXi (大溪), ChungWan (中脘), HuanTiao (环跳), ZuSanLi (足三里), HeGu (合谷)). Acupuncture three vaginal intercourse hole advocates the and blood of the whole body, fills the energies of spleen and stomach, helps the transport of the energies, clears and activates the channels and collaterals, and harmonies with the effect of Chi and blood.
ZuSanLi hole (足三里穴, foot three mile hole) belongs to the foot YangMing stomach meridian or the subsystem earth ( ). It is one of the famous four total holes (四总穴, Ancient acupuncture doctor summed up four holes commonly used in clinical practice effect. The holes are ZuSanLi (足三里), WeiZhong (委中), LieQue (列缺), or HeGu (合谷). “Acupuncture dacheng” (“针灸大成”) carrying “four total hole song”: “both belly and abdominal stay at ZuSanLi, both waist and back find in Weizhong, the head looks for LieQue, both surface and mouth are closed by HeGu.” Briefly summarizes the way the attending of the four points. Future generations on this basis, and gain “both chest and threats response in NeiGuan (内关), first aid looking for ShuiGou (水沟)” two words, said six total holes). It is also one of the famous twelve sky-star holes (天星十二穴, one of the most important and commonly used acupuncture points in a human body’s twelve meridians, the treatment of diseases is widespread, curative effect is obvious. The holes are ZuSanLi (足三里), NeiTing (内庭), QvChi (曲池), HeGu (合谷), WeiZhong (委中), ChengShan (承山), TaiChong (太冲), KunLun (昆仑), HuanTiao (环跳), YangLing (阳陵), TongLi (通里), LieQue (列缺)). Of course, it is also one of the famous Yang back nine needle holes (回阳九针穴). “The peaceful holy benevolence formulae” (“太平圣惠方”) said “the five labors won over and thin, seven injured empty spent, all adjustments by the foot three mile”. Needle foot three mile, make up and down with blood Chi lines, YangMing meridian Chi can be better run in channels and collaterals, to charge the insides or five-zang and six-fu organs.
Acupuncture SanYinJiao and ZuSanLi, a spleen and a stomach, a surface and an inside, health the spleen and harmony the stomach, is good for Chi and produces blood, and finally increases the energy of earth (XK).
TianShu hole (天枢穴, pivot hole) also belongs to the foot YangMing stomach meridian (足阳明胃经) or the subsystem earth ( ). It is also the tomb of hand YangMing large intestine meridian (手阳明大肠经). It is the hub of the stomach. Acupuncture TianShu hole can dredge relieving Chi, regulate the hardness of middle and lower energizers. Has the energy function of two-way regulate spleen and stomach, can increase the energy of the subsystem earth ( ).
ZhongWan hole (中脘穴, ChungWan hole) belongs to the Ren vein (任脉) or the foot YangMing stomach meridian (足阳明胃经) or the subsystem earth ( ). It is one of the famous Yang back nine needle holes (回阳九针穴). It is also the tomb of foot YangMing stomach meridian (足阳明胃经). It is also the gather hole of fu-organs of eight gather holes. It is also the gather hole of the hand TaiYang bladder meridian (手太阳膀胱经), the hand ShaoYang triple energizer meridian (手少阳三焦经) and Ren vein (任脉). Acupuncture ZhongWan can regulate spleen and stomach, regulate Chi activity of six-fu-organs, can increase the energy of the subsystem earth ( ).
NeiGuan hole (内关穴, Shut hole) belongs to the hand JueYin pericardium meridian (手厥阴心包经) or the subsystem xiang-fire ( ). It is one of the famous six total holes (六总穴). This hole for collaterals acupuncture point, secondly, one of the gather holes of eight veins. The hand JueYin pericardium meridian presided over the network to its heart. Acupuncture NeiGuan can promote the heart Yang, leader of the sanjiao (triple energizer), and finally can increase the energy of xiang-fire ( ).
HeGu hole (合谷穴, valley hole) belongs to the hand YangMing large intestine meridian (手阳明大肠经) or the subsystem metal ( ). It is one of the famous Yang back nine needle holes (回阳九针穴). It is one of the famous four total holes (四总穴) or six total holes (六总穴). It is also one of the famous twelve sky-star holes (天星十二穴). It is the original point of the hand YangMing large intestine meridian. The original holes flow in the SanJiao (triple energizer), originated from the kidney under the navel of motion energy (Chi). Acupuncture HeGu can stimulate the function of movement of the whole body energy (Chi), to decrease the energy of the subsystem metal ( ).
The above points are suitable, can adjust the energy function of spleen and stomach, tonic dredge Chi and blood, promote the viscera energy function recovery.
This example with the type of limb with muscular dystrophy, at present, in the world is a medical problem, no effective drugs and methods of treatment. The author USES “regulate spleen and stomach, Chi and blood tonic” thinking of traditional Chinese medicine treatment of 40 days, does have effect and obvious effect. Consulting relevant literature, the writer has not been found by acupuncture treatment of this kind of disease related information, so the topic.
The analysis of this paper focus on the mathematical structure of both Zangxiang and Jingluo. How about the real cases? In the real cases, there are a lot of kinds of diseases. In mathematics, first, you must determine the scope of the illness. That is to say: must determine which Zangxiang and meridian disease belongs to. For example, for the purpose of this case, must first determine the disease belongs to the spleen Zang and the foot YangMing stomach meridian.
How to fit the Zangxiang (藏象) and Jingluo (经络)into a mathematical model. Regards the Zangxiang and Jingluo as a mathematical model, which can be mathematically proved that deal with the method of the disease. For example, for the purpose of this case, dealing with the first method is to deal directly with the spleen Zang of the disease as the root-cause, i.e., to increase the energy of the spleen Zang. Auxiliary treatment method is to increase the energy of the pericardium meridian as symptoms, at the same time, reduce the energy of the lung meridian as symptoms. This method of healing must pass the mathematics to prove.
The effect of Zangxiang and Jingluo on the blood pH value should be evaluated. Measurement of the blood pH value objective is to determine whether the body health, disease of real or virtual illness, and mathematically sure cure method. For example, for the purpose of this case, the blood pH range, is the situation of the (1) of Theorem 4.1 as virtual, natural the cure method is determined. So, measuring the blood pH value in the range is a very important work. Because for different people in different time, the treatment methods are not the same. Must by measuring the blood pH value in the range at any time, to determine the cure method should be used at any time.
For the purpose of this case, it may be not necessary to show the hand ShaoYin heart meridian (手少阴心经). But from the perspective of mathematical analysis, the hand ShaoYin heart meridian is must considered. Because the hand ShaoYin heart meridian and the hand JueYin pericardium meridian although belong to the heart Zang, but the hand JueYin pericardium meridian can substitute for the hand ShaoYin heart meridian under fault. So to increase the energy of the heart Zang must be the hand JueYin pericardium meridian, can’t be the hand ShaoYin heart meridian.#
6. Conclusions
This work shows how to treat the diseases of a human body by using the human blood pH value x. For the human blood pH value, the range of theory is nearly to . By both the Zangxiang system or the ten Heavenly Stems model and the Jingluo system or the twelve Earthly Branches model, there is the first or second transfer law of human energies corresponding to a healthy body or an unhealthy body respectively. The first or second transfer law of human energies changes according to the different human body’s blood pH values whether in the normal range or not. For the normal range, the first transfer law of human energies in Theorems 3.2 and 3.3 runs; for the abnormal range, the second transfer law of human energies in Theorems 3.4 and 3.5 runs.
We assume that the range of a human body’s blood pH value x is divided into four parts from small to large. Both second and third are for a healthy body with a virtual or real disease respectively. In this case, the root-cause of a virtual or real disease is the mother or son of the falling-ill subsystem X respectively, and the symptoms are the subsystem X itself. Abiding by TCM’s idea: “Searching for a root cause of disease in cure, treatment of both the root-cause and symptoms at the same time” (治病求本, 标本兼治), the works are first the prevention or the treatment for the mother or son of a virtual or real disease respectively, the second the prevention or the treatment for a more serious relation disease between virtual X and real XK or between real X and virtual KX, respectively. Both the root-cause and the symptoms come from the first transfer law of human energies in Theorems 3.2 and 3.3.
And both first and fourth are for an unhealthy body with a virtual or real disease respectively. In this case, the root-cause of a virtual or real disease is the subsystem X itself and the symptoms of the son or mother of the falling-ill subsystem X respectively. Abiding by TCM’s idea: “Searching for the primary cause of disease in treatment, treat both symptoms and root-cause” (治病求本, 标本兼治), the works are first the prevention or the treatment for itself of a virtual or real disease respectively, the second is the prevention or the treatment for a more serious relation disease between virtual XS and real KX or between real SX and virtual XK, respectively. Both the root-cause and the symptoms come from the second transfer law in Theorems 3.4 and 3.5.
Human disease treatment should protect and maintain the balance or order of two incompatibility relations: the loving or liking relationship and the killing or liking relationship. The method for doing so can make the tend to be large, i.e., all of both and c tend to be large, at least, greater than zero for an unhealthy body; or, the best, equal to 1 for a healthy body.
The following way can make the capabilities of both intervention reaction and self-protection become in the best state, the non-existence of side effects issue, the non-existence of medical and drug resistance problem, and so on.
1) Suppose that , as virtual, in which X or XK falls a virtual disease with an unhealthy body. The subsystem X or XK itself is the root-cause of a happened virtual disease. And the son XS of X is the symptoms of an expected or a happened virtual disease. Abiding by TCM’s idea: “Searching for the primary cause of disease in treatment, treat both symptoms and root-cause” (治病求本,标本兼治), it should be done to do in the following.
In order to protect or maintain the loving relationship, abiding by TCM’s idea “Virtual disease with an unhealthy body is to fill itself” (虚则补之), increase the energy of X or XK directly.
In order to protect or maintain the killing relationship, abiding by TCM’s idea “Don’t have disease cured, cure non-ill” (不治已病治未病), do a preventive treatment for the more serious relation disease between virtual XS and real KX.
Through the intervening principle of “Strong inhibition of the same time, support the weak” (抑强扶弱), increase the energy of the son XS of X while decrease the energy of the prisoner KX of XS.
2) Suppose that , as virtual-normal, in which X or SX falls a virtual disease with a healthy body. The mother SX of the subsystem X is the root-cause of an expected virtual disease. And the subsystem X itself is the symptoms of an expected virtual disease. Abiding by TCM’s idea: “Searching for a root cause of disease in cure, treatment of both the root-cause and symptoms at the same time” (治病求本, 标本兼治), it should be done to do in the following.
In order to protect or maintain the loving relationship, abiding by TCM’s idea “Virtual disease with a healthy body is to fill its mother” (虚则补其母), increase the energy of the mother SX of X. The treating way is an indirect treating for X.
In order to protect or maintain the killing relationship, abiding by TCM’s idea “Don’t have disease cured, cure non-ill” (不治已病治未病), do a preventive treatment for the more serious relation disease between virtual X and real XK.
Through the intervening principle of “Strong inhibition of the same time, support the weak” (抑强扶弱), increase the energy of X itself while decreasing the energy of the prisoner XK of X.
3) Suppose that , as real-normal, in which X or SX falls a real disease with a healthy body. The son SX of the subsyste X is the root-cause of an expected real disease. And the subsystem X itself is the symptoms of an expected real disease. Abiding by TCM’s idea: “Searching for a root cause of disease in cure, treatment of both the root-cause and symptoms at the same time” (治病求本, 标本兼治), it should be done to do in the following.
In order to protect or maintain the loving relationship, abiding by TCM’s idea “Real disease with a healthy body is to rush down its son” (实则泄其子), decrease the energy of the son SX of X. The treating way is an indirect treating for X.
In order to protect or maintain the killing relationship, abiding by TCM’s idea “Don’t have disease cured, cure non-ill” (不治已病治未病), do a preventive treatment for the more serious relation is ease between real X and virtual KX.
Through the intervening principle of “Strong inhibition of the same time, support the weak” (抑强扶弱), decrease the energy of X itself while increasing the energy of the bane KX of X.
4) Suppose that , as real, in which X or KX falls a real disease with an unhealthy body. The subsystem X or KX itself is the root-cause of a happened real disease. And the mother SX of X is the symptoms of an expected or a happened real disease. Abiding by TCM’s idea: “Searching for a root cause of disease in cure, treatment of both the root-cause and symptoms at the same time” (治病求本, 标本兼治), it should be done to do in the following.
In order to protect or maintain the loving relationship, abiding by TCM’s idea “Real disease with an unhealthy body is to rush down itself” (实则泄之), decrease the energy of X or KX directly.
In order to protect or maintain the killing relationship, abiding by TCM’s idea “Don’t have disease cured, cure non-ill” (不治已病治未病), do a preventive treatment for the more serious relation disease between real SX and virtual XK.
Through the intervening principle of “Strong inhibition of the same time, support the weak” (抑强扶弱), decrease the energy of the mother SX of X while increase the energy of the bane XK of SX.#
Acknowledgements
Sincerely thanks Prof. Francesco Marchetti (Teacher at the Torelli High School, Fano, Italy; Member of the International Association UN PUNTO MACROBIOTICO, Founded by Prof. Mario Pianesi, Email: francescomarchetti56@gmail.com) for its valuable advice.
This article has been repeatedly invited as reports, such as People’s University of China in medical meetings, Shanxi University, Liaocheng University, Xuchang College, and so on. The work was supported by Specialized Research Fund for the Doctoral Program of Higher Education of Ministry of Education of China (Grant No. 200802691021).
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Zhang, Y.S. and Zhang, B.B. (2019) Acupuncture Treating Dystrophy Based on pH. Chinese Medicine, 10, 39-105. https://doi.org/10.4236/cm.2019.102005
References
- 1. Shirakabe, A., Hata, N., Kobayashi, N., Shinada, T., Tomita, K., Tsurumi, K., Matsushita, M., Okazaki, H., Yamamoto, Y., Yokoyama, S., Asai, K. and Mizuno, K. (2012) Clinical Significance of Acid-Base Balance in an Emergency Setting in Patients with Acute Heart Failure. Journal of Cardiology, 60, 288-294. https://doi.org/10.1016/j.jjcc.2012.06.004
- 2. Sharandeep, K., Praveen, K., Virendra, K., Kumar, S.S. and Arun, K. (2013) Etiology and Prognostic Factors of Acute Liver Failure in Children. Indian Pediatrics, 50, 677-679. https://doi.org/10.1007/s13312-013-0189-7
- 3. Hany, A., Meno, L., Jonathan, W., Elvira, P., Alan, D. and Charles, S. (1997) Partial Liquid Ventilation (PLV) and Lung Injury: Is PLV Able to Modify Pulmonary Vascular Resistance? Journal of Pediatric Surgery, 32, 197-202. https://doi.org/10.1016/S0022-3468(97)90178-0
- 4. Intven, F., Boogaard, M.V.D., Pickkers, P., Moviat, M., Voort, P.V.D. and Hoeven, H.V.D. (2013) Stewart Analysis of Apparently Normal Acid-Base State in the Critically Ill. Journal of Critical Care, 28, 1048-1054. https://doi.org/10.1016/j.jcrc.2013.06.005
- 5. Kumar, P.S., Singh, Y.S., Singh, H.P. and Bajaj, N. (2014) To Study PH Disorders in Severe Acute Malnutrition. Journal of Evolution of Medical and Dental Sciences, 3, 12132-12139. https://doi.org/10.14260/jemds/2014/3602
- 6. Handman, H., Rais Bahrami, K., Rivera, O., Seale, W.R. and Short, B.L. (1997) Use of Intratracheal Pulmonary Ventilation versus Conventional Ventilation in Meconium Aspiration Syndrome in a Newborn Pig Model. Critical Care Medicine, 25, 2025-2030. https://doi.org/10.1097/00003246-199712000-00020
- 7. Natalia, B.M. and Steven, W.D. (2015) Amphetamine-Like Analogues in Diabetes: Speeding towards Ketogenesis. Case Reports in Endocrinology, 2015, Article ID: 917869. https://doi.org/10.1155/2015/917869
- 8. Barfod, C., Lauritzen, M.M.P., Danker, K., Soletormos, G., Berlac, P.A., Lippert, F., Lundstrom, L.H., Antonsen, K. and Lange, K.H.W. (2012) The Formation and Design of the ‘Acute Admission Database’-a Database Including a Prospective, Observational Cohort of 6279 Patients Triaged in the Emergency Department in a Larger Danish Hospital. Scandinavian Journal of Trauma, Resuscitation and Emergency Medicine, 20, 1-8.
- 9. Zhu, L.L., Tee, K.L., Roccatano, D., Sonmez, B., Ni, Y., Sun, Z.H. and Schwaneberg, U. (2010) Directed Evolution of an Antitumor Drug (Arginine Deiminase PpADI) for Increased Activity at Physiological pH. ChemBioChem, 11, 691-697. https://doi.org/10.1002/cbic.200900717
- 10. Zhu, L.L., Verma, R., Roccatano, D., Ni, Y., Sun, Z.H. and Schwaneberg, U. (2010) A Potential Antitumor Drug (Arginine Deiminase) Reengineered for Efficient Operation under Physiological Conditions. ChemBioChem, 11, 2294-2301. https://doi.org/10.1002/cbic.201000458
- 11. Kalb, R., Kram, R., Morgera, S., Slowinski, T. and Kindgen-Milles, D. (2013) Regional Citrate Anticoagulation for High Volume Continuous Venovenous Hemodialysis in Surgical Patients With High Bleeding Risk. Therapeutic Apheresis and Dialysis, 17, 202-212. https://doi.org/10.1111/j.1744-9987.2012.01101.x
- 12. Boaz, M., Iskhakov, A., Tsivian, A., Shimonov, M., Berkenstadt, H., et al. (2011) Perioperative Metabolic Alkalemia Is More Frequent Than Metabolic Acidemia in Major Elective Abdominal Surgery. Journal of Clinical Monitoring and Computing, 25, 223-230. https://doi.org/10.1007/s10877-011-9299-8
- 13. Saritas, Z.K., Korkmaz, M., Saritas, T.B. and Sivaci, R.G. (2014) Comparison of the Depth of Anesthesia Produced with Dexmedetomidine-Sevoflurane or Medetomidine-Sevoflurane by Using Bispectral Index Monitoring. Acta Scientiae Veterinariae, 42, 1-7.
- 14. Stevens, D.C., Campbell, J.P., Carter, J.E. and Watson, W.A. (1994) Acid-Base Abnormalities Associated With Cocaine Toxicity In Emergency Department Patients. Journal of Toxicology-Clinical Toxicology, 32, 31-39. https://doi.org/10.3109/15563659409000428
- 15. Zhang, Y.S. (1993) Multilateral Matrix Theory. Chinese Statistics Press, Beijing.
- 16. Zhang, Y.S. (2007) Multilateral System Theory. http://www.mlmatrix.com
- 17. Zhang, Y.S. (2011) Mathematical Reasoning of Treatment Principle Based on Yin Yang Wu Xing Theory in Traditional Chinese Medicine. Chinese Medicine, 2, 6-15. https://doi.org/10.4236/cm.2011.21002
- 18. Zhang, Y.S. (2011) Mathematical Reasoning of Treatment Principle Based on Yin Yang Wu Xing Theory in Traditional Chinese Medicine (II). Chinese Medicine, 2, 158-170. https://doi.org/10.4236/cm.2011.24026
- 19. Zhang, Y.S. (2012) Mathematical Reasoning of Treatment Principle Based on the Stable Logic Analysis Model of Complex Systems. Intelligent Control and Automation, 3, 1-15. https://doi.org/10.4236/ica.2012.31001
- 20. Zhang, Y.S. and Shao, W.L. (2012) Image Mathematics-Mathematical Intervening Principle Based on Yin Yang Wu Xing Theory in Traditional Chinese Mathematics (I). Applied Mathematics, 3, 617-636. https://doi.org/10.4236/am.2012.36096
- 21. Zhang, Z.Q. and Zhang, Y.S. (2013) Mathematical Reasoning of Economic Intervening Principle Based on Yin Yang Wu Xing Theory in Traditional Chinese Economics (I). Modern Economics, 4, 130-144. https://doi.org/10.4236/me.2013.42016
- 22. Feng, N.Q., Qiu, Y.H., Wang, F., Zhang, Y.S. and Yin, S.Q. (2005) A Logic Analysis Model about Complex System’s Stability: Enlightenment from Nature. In: Huang, D.S., Zhang, X.P. and Huang, G.B., Eds., Advances in Intelligent Computing. ICIC 2005. Lecture Notes in Computer Science, vol. 3644, Springer, Berlin, Heidelberg, 828-838. https://doi.org/10.1007/11538059_86
- 23. Zhang, Y.S. (2017) pH 7.35 to 7.45-Mathematical Reasoning of Treatment Principle Based on Yin Yang Wu Xing Theory in Traditional Chinese Medicine (II). International Journal of Chinese Medicine.
Appendix
Proof of Property 3.1. See Figure 3., since the emperor prosperous place of Jia Yang wood of the ten heavenly stems is in Mao of the twelve earthly branches, so the rowing place is in Hai. It is because by Definition 3.3, counterclockwise to arrange, emperor as Mao, officer as Yin, crowned as Chou, bathing as Zi, rowing as Hai.
Similarly, the emperor prosperous place of Bing, Wu, Geng, Ren Yang fire, earth, metal, water of the ten heavenly stems is in Wu, Wu, You, Zi of the twelve earthly branches, so the rowing place is in Yin, Yin, Si Shen of the twelve earthly branches respectively.
See Figure 3. Again, since the emperor prosperous place of Yi Yin wood of the ten heavenly stems is in Yin of the twelve earthly branches, so the rowing place is in Wu. It is because by Definition 3.3, clockwise to arrange, emperor as Yin, officer as Mao, crowned as Chen, bathing as Si, rowing as Wu.
Similarly, the emperor prosperous place of Ding, Ji, Xin, Gui Yin fire, earth, metal, water of the ten heavenly stems is in Si, Si, Chen, Hai of the twelve earthly branches, so the rowing place is in You, You, Zi, Mao of the twelve earthly branches respectively.
Therefore, the five Yang heavenly stems: Jia, Bing, Wu, Geng, Ren was born Hai, Yin, Yin, Si, Shen respectively; The five Yin heavenly stems: Yi, Ding, Ji, Xin, Gui was born Wu, You, You, Zi, Mao respectively. It completes the proof.#
Proof of Property 3.2. By Definition 3.3 and Properties 3.3 and 3.4, there are
Therefore, the synthesized and synthesized or combined relationship between two elements
and
is as wood (X) in Theorem 3.1.
Similarly, the synthesized and combined relationship between two elements
and
is as metal (KX) in Theorem 3.1 since
The synthesized and synthesized relationship between two elements
and
is as earth (XK) in Theorem 3.1 since
The synthesized and synthesized relationship between two elements
and
is as xiang-fire ( ) (相火) in Theorem 3.1 since
The synthesized relationship between between the comprehensive energy of two elements
and
is as water (SX) in Theorem 3.1 since
The synthesized relationship between two elements
and
is as jun-fire ( ) (君火) in Theorem 3.1 since
Therefore, the following notations in Definition 3.2 is reasonable.
It is with the correct meaning of the Yin Yang Wu Xing Model in Theorem 3.1.#
Proof of Property 3.3. Consider the Zangxiang system or the ten Heavenly Stems model . Its all relations are as follows:
Use of these relations, to calculate the cost of all the specified relationship, can be found: the loving or liking relationship with low cost, and the killing relationship with the high cost. It completes the proof.#
Proof of Property 3.4. Consider the Jingluo system or the twelve Earthly Branches model . Its all relations are as follows:
Use of these relations, to calculate the cost of all the specified relationship, can be found: the hand phase in Figure 3, all transverse relationship with low cost, but all vertical relationship with high cost.
On the other hand, in {Yin, Mao}, {Wu, Wei}, {Xu, Hai} type or {Chen, Si}, {Shen, You}, {Zi, Shou} type for the vertices of the triangle respectively, the relationship between the cost is low. Otherwise, the relationship between the cost is high. It completes the proof.#
Proof of Theorem 3.2. See Figure 2., in the Zangxiang system or the ten Heavenly Stems model for a healthy human body, only both the liking relation and the loving relation have the transfer law of the Yang or Yin vital or righteousness energies. By Theorem 3.2 of Zhang [23] , Yang is transferring along the order of the loving relationship. Yin is transferring against the order of the loving relationship.
By Property 3.3, the following relation cost (0, (23)) is low.
It is because the element (1, 0) of the ten Heavenly Stems is a Tao force, which is a low cost if the Yin Yang Wu Xing model is implemented by the Tao force of the Tao model . Their relations are called the liking relation.
Because the liking relationship cannot change the transfer law of the order of the loving relation, so, by Theorem 3.2 in Zhang [23] , Yang is transferring along the order of the ten heavenly stems. Yin is transferring against the order of the ten heavenly stems. It completes the proof.#
Proof of Theorem 3.3. See Figure 3., in the Jingluo system or the twelve Earthly Branches model for a healthy human body, only both the liking relation and the adjacent relation have the transfer law of the Yang or Yin vital or righteousness energies.
By Definition 3.3, the elements of the twelve earthly branches have properties: Zi as the Yang water, Chou as the Yin earth, Yin as the Yang wood, Mao as the Yin wood, Chen as the Yang earth, Si as the Yin fire, Wu as the Yang fire, Wei as the Yin earth, Shen as the Yang metal; You as the Yin metal, Xu as the Yang earth, Hai as the Yang water. Here, earth element exists everywhere, so the energy transport order is mainly composed of wood, fire, metal and water elements.
About wood, fire, metal and water element to determine a natural transmission law of wood to fire, to metal by soil, then reach the water. That is to say: a natural Yin energy transmission rule is as follows:
Its main content is still follow the intergeneration transmission sequence of Yin Yang Wu Xing.
By Property 3.4, the following relation cost (0, (23))
It is because the element (0, (23)) of the twelve Earthly Branches is an essential substance circulating in the channels and blood vessels (营气). It is a low cost element if a human body “eats”. Their relations are called the liking relation for a healthy human body, denoted by .
Because the liking relationship cannot change the transfer law of the order of the loving relation, so,the above elements replacing transmission rule of the twelve earthly branches element, get the transmission law of the twelve earthly branches:
The relationship
can be abbreviated as
.
Thus
Because the order
is transferring against the loving order of the twelve earthly branches, of course, by Theorem 3.2 in Zhang [23] , it is the transfer law of the Yin vital or righteousness energies of the twelve earthly branches.
By Theorem 3.2 in Zhang [23] , Yang is transferring along the order of the loving relationship. Yin is transferring against the order of the loving relationship. So, the transfer law of the Yin vital or righteousness energies of the twelve earthly branches is transferring against the order of the loving or liking relationship. It is because the liking relationship cannot change the transfer law of the order of the loving relation.
Thus, the transfer law of the Yang vital or righteousness energies of the twelve earthly branches is as follows:
The relationship
can be abbreviated as
.
Thus
Because the order
is transferring along the loving order of the twelve earthly branches, of course, by Theorem 3.2 in Zhang [23] , it is the transfer law of the Yang vital or righteousness energies of the twelve earthly branches.
Therefore, the transfer law of the Yang or Yin vital or righteousness energies of the twelve earthly branches is obtained as follows: Yang is transferring along the liking or loving order of the twelve earthly branches. And Yin is transferring against the liking or loving order of the twelve earthly branches. It completes the proof.#
Proof of Theorem 3.4. See Figure 2., in the Zangxiang system or the ten Heavenly Stems model for an unhealthy human body, only both the liking relation and the killing relation have the transfer law of the Yang or Yin vital or righteousness energies. By Theorem 3.3 of Zhang [23] , Yang is transferring against the order of the killing relationship. Yin is transferring along the order of the killing relationship.
By Property 3.3, the following relation cost (1, 0) is low.
It is because the element (1, 0) of the ten Heavenly Stems is a Tao force, which is a low cost if the Yin Yang Wu Xing model is implemented by the Tao force of the Tao model . Their relations are called the liking relation.
Because the liking relationship cannot change the transfer law of the order of the killing relation, so, by Theorem 3.3 in Zhang [23] , Yang is transferring along the order of the killing or liking relation of the ten heavenly stems. Yin is transferring along the order of the killing or liking relation of the ten heavenly stems. It completes the proof.#
Proof of Theorem 3.5. See Figure 3., in the Jingluo system or the twelve Earthly Branches model for an unhealthy human body, only both the liking relation and the alternate relation have the transfer law of the Yang or Yin vital or righteousness energies.
By Property 3.4, the following relation cost (0, (23)) is low.
It is because the element (0, (23)) of the twelve Earthly Branches is an essential substance circulating in the channels and blood vessels (营气). It is a low cost element if the economic society “eats”. Their relations are called the liking relation for a healthy human body, denoted by .
By Theorem 3.3 in Zhang [23] , Yang is transferring against the order of the killing relationship. Yin is transferring along the order of the killing relationship. So, the transfer law of the Yin vital or righteousness energies of the twelve earthly branches is transferring along the order of the killing or liking relationship. It is because the liking relationship cannot change the transfer law of the order of the killing or liking relation.
In mathematics, by Theorem 3.3 in Zhang [23] , for the unhealthy human body, the transfer law of the Yin vital energies of the twelve earthly branches is as follows:
It is because the order
is transferring along the killing order of the twelve earthly branches.
Similarly, Yang is transferring against the order of the killing or liking relationship. So, the transfer law of the Yang vital or righteousness energies of the twelve earthly branches is transferring against the order of the killing or liking relationship. It is because the liking relationship cannot change the transfer law of the order of the killing or liking relation.
In mathematics, by Theorem 3.3 in Zhang [23] , for the unhealthy human body, the transfer law of the Yang vital energies of the twelve earthly branches is as follows:
It is because the order
is transferring against the killing order of the twelve earthly branches. It completes the proof.#
Proof of Theorem 4.1. Let
1) By the (1) of Theorem 4.1 in Zhang [23] , X and XK as continuous subsystems of occurring disease, it only need to be proved that the subsystem X itself is the root-cause of a virtual disease and that the son subsystem XS of X is the symptoms of disease at this time.
In this case, the human body is unhealthy. The first physiological system is running hardly. The loving relationship is running hardly. Only the killing relationship run normally.
By Theorems 3.2 and 3.3, the first transfer law of a human body’s energies is not to work. By Theorems 3.4 and 3.5, the second transfer law of a human body’s energies is beginning to work.
By the theory of Zangxiang and Jingluo in Definition 3.1 and 3.2, the virtual disease of the subsystem X is transferring from the virtual disease of its son XS for a good self-protection ability. Consider whether the subsystem X virtual disease, the cause of its root-cause will be able to direct the subsystem X treatment. In the following, consider the result of the subsystem X direct intervention.
From Theorem 3.2 and Corollary 3.2 in [20] , the subsystem X was considered as virtual. When the capability of self-protection is nearly to the best state, i.e., where , if you increase the energy of the subsystem X directly, then its capabilities of both intervention reaction and self-protection can make the subsystems SX, KX and XK restored at the same time, but the subsystems X and XS will increase their energies, i.e., changed by the increments
respectively.
Since the human body blood pH value makes such that , therefore the subsystem X can obtain the large increment and the subsystem XS will get the small increment . The later is the pseudo side effects issue, by Attaining Rule in Zhang [23] , which is just the food of the second physiological system of the steady multilateral system since that the human body is unhealthy, virtual and X intervened makes that the second physiological system will attain the Chi or energy (Yang energy) from the son XS of the intervened subsystem X The attaining way is an indirect treating for X as an unhealthy human body with a virtual disease. That means for the intervened subsystem X direct treatment effect is in accordance with the working principle of system and meridian system. So say: the subsystem X deficiency disease is why disease at this time. Thus, the subsystem X itself is the root-cause of a virtual disease. Of course, the son subsystem XS of X is the symptoms of disease at this time. Need to use the method of the intervening principle of “Strong inhibition of the same time, support the weak” (抑强扶弱) action to treat.
2) By the (2) of Theorem 4.1 in Zhang [23] , X and SX as continuous subsystems of occurring disease, it only need to be proved that the mother SX of subsystem X is the root-cause of a virtual disease and the subsystem X itself is the symptoms of a virtual disease at this time.
In this case, the human body is healthy. The first physiological system is running normally. The loving relationship is running normally. The liking relationship is also running normally. By Theorems 3.2 and 3.3, the first transfer law of a human body’s energies is doing to work. By Theorems 3.4 and 3.5, the second transfer law of a human body’s energies is not to work.
By the theory of Zangxiang and Jingluo in Definition 3.1 and 3.2, the virtual disease of the subsystem X is transferring from the virtual disease of its mother SX for a good self-protection ability. Consider whether the mother SX of the subsystem X virtual disease, the cause of its root-cause will be able to direct the mother SX of the subsystem X treatment. In the following, consider the result of the mother SX of the subsystem X treatment direct intervention.
From Theorem 3.2 and Corollary 3.2 in [20] , the subsystem X will be considered as virtual. First the case is studied that the capability of self-protection is in the best state, i.e., where . If the energy of the subsystem SX is intervened to increase its energy, then its capabilities of intervention reaction and self-protection can make the subsystems KX, XK and XS restored at the same time, but the subsystems SX and X will increase their energies, i.e., changed by the increments
respectively.
Since the human body blood pH value makes such that mainly , therefore the subsystem X can obtain the large increment and the subsystem SX will get the small increment . The later is the pseudo side effects issue, by Attaining Rule in Zhang [23] , which is just the food of the second physiological system of the steady multilateral system since that the human body is healthy, virtual and SX intervened makes that the second physiological system will attain the Chi or energy from the intervened subsystem SX directly for a healthy with a virtual disease. That means for the intervened subsystem SX direct treatment effect is in accordance with the working principle of system and meridian system. So say: the subsystem SX deficiency disease is why disease at this time. Thus, the mother subsystem SX of X is the root-cause of a virtual disease. Of course, the subsystem X itself is the symptoms of a virtual disease at this time. Need to use the method of the intervening principle of “Strong inhibition of the same time, support the weak” (抑强扶弱) action to treat.
3) By the (3) of Theorem 4.1 in Zhang [23] , X and XS as continuous subsystems of occurring disease, it only need to be proved that the son XS of X the root-cause of a real disease and the subsystem X itself is the symptoms of a real disease at this time.
In this case, the human body is healthy. The first physiological system is running normally. The loving relationship is running normally. The liking relationship is also running normally. By Theorems 3.2 and 3.3, the first transfer law of a human body’s energies is doing to work.By Theorems 3.4 and 3.5, the second transfer law of a human body’s energies is not to work.
By the theory of Zangxiang and Jingluo in Definitions 3.1 and 3.2, the virtual disease of the subsystem X is transferring from the virtual disease of its son XS for a good self-protection ability. Consider whether the son XS of the subsystem X virtual disease, the cause of its root-cause will be able to direct the son XS of the subsystem X treatment. In the following, consider the result of the son XS of the subsystem X treatment direct intervention.
From Theorem 3.2 and Corollary 3.2 in [20] , the subsystem X will be considered as real. First the case is studied that the capability of self-protection is in the best state, i.e., where . If the energy of the subsystem XS is intervened to decrease its energy, then its capabilities of intervention reaction and self-protection can make the subsystems XK, KX and SX restored at the same time, but the subsystems X and XS will decrease their energies, i.e., changed by the increment
respectively. Since the human body blood pH value makes such that mainly , therefore the subsystem X can obtain the substantial reduction
and the subsystem XS will get a modest reduction . The later is the pseudo side effects issue, by Attaining Rule in Zhang [23] , which is just the food of the second physiological system of the steady multilateral system since that the human body is healthy, real and XS intervened makes that the second physiological system will attain the Chi or energy from the intervened subsystem XS directly for a healthy with a real disease. That means for the intervened subsystem XS direct treatment effect is in accordance with the working principle of system and meridian system. So say: the subsystem XS real disease is why disease at this time. Thus, the son subsystem XS of X is the root-cause of a real disease. Of course, the subsystem X itself is the symptoms of a real disease at this time. Need to use the method of the intervening principle of “Strong inhibition of the same time, support the weak” (抑强扶弱) action to treat.
4) By the (4) of Theorem 4.1 in Zhang [23] , X and KX as continuous subsystems of occurring disease, it only need to be proved that the subsystem X itself is the root-cause of a real disease and that the mother SX of X is the symptoms of a real disease at this time.
In this case, the human body is unhealthy. The first physiological system is running hardly. The loving relationship is running hardly. Only the killing relationship is running normally. By Theorems 3.2 and 3.3, the first transfer law of a human body’s energies is not to work. By Theorems 3.4 and 3.5, the second transfer law of a human body’s energies is beginning to work.
By the theory of Zangxiang and Jingluo in Definitions 3.1 and 3.2, the virtual disease of the subsystem X is transferring from the real disease of its mother SX for a good self-protection ability. Consider whether the subsystem X virtual disease, the cause of its root-cause will be able to direct the subsystem X treatment. In the following, consider the result of the subsystem X treatment direct intervention.
From Theorems 3.2 and Corollary 3.2 in [20] , the subsystem X was considered as real. When the capability of self-protection is in the best state, i.e., where , if the energy of the subsystem X is intervened to decrease its energy directly, then its capabilities of intervention reaction and self-protection can make the subsystems XK, KX and XS restored at the same time, but the subsystems X and SX will decrease their energies, i.e., changed by the increments
respectively.
Since the human body blood pH value makes such that , therefore the subsystem X can obtain the substantial reduction and the subsystem SX will get a modest reduction . The later is the pseudo side effects, by Attaining Rule in Zhang [23] , which is just the food of the second physiological system of the steady multilateral system since that the human body is unhealthy, real and X intervened makes that the second physiological system will attain the Chi or energy from the mother SX of the intervened subsystem X. The attaining way is an indirect treating for X as an unhealthy human body with a real disease. That means for the intervened subsystem X direct treatment effect is in accordance with the working principle of system and meridian system. So say: the subsystem X real disease is why disease at this time. Thus the subsystem X is the root-cause of a real disease. Of course, the mother SX of X is the symptoms of a real disease at this time. Need to use the method of the intervening principle of “Strong inhibition of the same time, support the weak” (抑强扶弱) action to treat. It completes the proof.#





