Received 9 April 2014; revised 8 May 2014; accepted 7 June 2014

ABSTRACT

This paper is the first in a two-part series that introduces an easy-to-implement central command architecture for high-order autonomous unmanned aerial systems. This paper discusses the de- velopment and the second paper presents the flight test results. As shown in this paper, the cen- tral command architecture consists of a central command block, an autonomous planning block, and an autonomous flight controls block. The central command block includes a staging process that converts an objective into tasks independent of the vehicle (agent). The autonomous planning block contains a non-iterative sequence of algorithms that govern routing, vehicle assignment, and deconfliction. The autonomous flight controls block employs modern controls principles, dividing the control input into a guidance part and a regulation part. A novel feature of high-order central command, as this paper shows, is the elimination of operator-directed vehicle tasking and the manner in which deconfliction is treated. A detailed example illustrates different features of the architecture.

Keywords:

Unmanned Aerial Vehicles, Autonomy, Central Command, High-Order Systems, Deconfliction

1. Introduction

Unmanned aerial vehicles (UAV) are gaining interest with relaxing restrictions in civilian airspaces. Looking ahead, a systematic approach is needed for autonomous unmanned aerial systems (AUAS) consisting of a large number of vehicles (agents). This paper, which is the first in a series of two papers, presents an easy-to-imple- ment architecture for high-order AUAS; the second paper presents flight test results. The different AUAS ap- proaches are referred to in this paper as command approaches with central command at one extreme and indi- vidual command at the other. In central command, the AUAS authority lies in one entity, and the vehicle re- quires only limited information about its environment. Central command is naturally suited to problems dictated by global objectives, such as search and surveillance in precision agriculture, border security, law enforcement, and wildlife and forestry services, to name a few. In individual command, the authority lies in the individual ve- hicle. The vehicle requires local situational awareness, communication with other vehicles, and understanding of system objectives. Individual command is naturally suited to problems dictated by local objectives that require coordination, like those found in air traffic control problems and in coordinated pick and place problems.

When an AUAS operates multiple vehicles in close proximity some method of preventing collisions becomes necessary. Collision avoidance, or the real-time act of recognizing and maneuvering to avoid an impending con- flict, also called “see and avoid”, is a fundamental principle of current flight operations and will be a require- ment of future operations that share manned airspace. In contrast, deconfliction, or the act of planning paths in advance that do not conflict, is a central command level method of preventing conflicts as events are planned. Collision avoidance and deconfliction are not mutually exclusive; deconfliction prevents collisions between planned or known events whereas collision avoidance prevents collisions between unplanned events. Future sys- tems will incorporate both methods. This paper develops a robust method of deconfliction based on an assign- ment method that produces non-crossing paths. This method is presented within an easy-to-implement architec- ture that is scalable to high-order AUAS. The method section introduces the basic architecture and the results section provides a detailed example.

The requirements of an architecture under which high-order AUAS become feasible is the subject of ongoing research. Bellingham, Tillerson, et al., 2003 [1] separated their architecture into 1) routing, 2) vehicle assign- ment of tasks, and 3) deconfliction, after which the vehicles receive their directions. Cummings, Bruni, et al., 2007 [2] separated their architecture into 1) central mission and payload management, 2) navigation, 3) vehicle autopilots, and 4) flight controls. Shima and Rassmussen [3] describe a pantheon of architectures across the three axes of command, information availability and performance. Concerning user load, Adams, Humphrey, et al., 2009 [4] studied the problems that arise with human attention when one or more users give commands and monitor data. Donmez, Nehme, et al., 2010 [5] showed that wait time increases with the number of vehicles in AUAS that do not have full autonomous planning. These studies suggest that full autonomy is a necessary re- quirement in high-order central command. About computational requirements, routing and task assignment are combinatorial problems that have prohibitive computational requirements for high-order AUAS, necessitating heuristics. Gardiner, Ahmed, et al., 2001 [6] reviewed real-time collision avoidance algorithms for multiple UAVs and illustrated the computational complexities that limit the number of vehicles and flight time. How, King, et al., 2004 [7] demonstrated a simultaneous task assignment and deconfliction approach with 8 vehicles. These studies suggest the use of heuristics and non-iterative algorithms to reduce computational complexity. Pertaining to the question of the division of labor between remote and on-board processing, it is natural to per- form the flight controls on-board to reduce communication throughput requirements to remote transmission of off-board command decisions at perhaps 1 Hz or less. Edwards and Silverberg, 2010 [8] exploited this division of labor in an autonomous soaring flight demonstration. Concerning the choice between acquiring on-board states from synthesized relative measurements (using situational awareness) or from inertial measurements (like IMU and GPS), Levedahl and Silverberg, 2005 [9] showed that acquiring on-board states from inertial mea- surements is particularly well-suited to the central command problem because of the sensitivity issues that arise in synthesized relative measurements in high-order AUAS.

2. Method

2.1. The High-Order Central Command (HOCC) Architecture

The HOCC architecture is described by the block diagram shown in Figure 1. Drawing from the work of Bel- lingham, Tillerson, Richards, and Howe [1] , the HOCC architecture is divided into central command, autonom- ous planning, and autonomous flight controls. The central command block directs the execution of objectives. It contains a staging process that converts the high-level objective into assignable tasks. The autonomous planning block is an efficient, non-iterative sequence of three processes called Routing (R), Vehicle Assignment (V), and Deconfliction (D). A unique feature of the architecture introduced in this paper, as shown below, is that while the processes have internal iterations, they never require going back to a previous process (external iterations).

The complexity of the individual processes used, namely the Visibility Graph method, the A* method, the Hun- garian method, are well known. For example, the number of calculations in A* is on the order of nmE log(V) where n is number of vehicles, m is number of tasks, E is number of obstacle edges, and V is number of obstacle vertices and the number of calculations in the Hungarian method is on the order of n⁴. The elimination of exter- nal iterations, as described below, leads to a robust, computationally efficient algorithm. Throughout this paper, we only consider vehicles that are assignable to every task (homogeneity).

2.2. Staging

As shown in Figure 1, a user is provided information from an operational area and other field parameters, and data C_j (j = 1, 2, …) generated by AUAV payload P_j (j = 1, 2, …). Using this and other information, the user commands an objective. In absence of fully autonomous planning algorithms that remove the vehicle from the calculus, user load would be, at the very least, proportional to the number of vehicles, which is prohibitive in high-order systems. Thus a critical feature of the HOCC architecture introduced in this paper is the decoupling of the objective from the vehicles and, instead, the expression of the commands in terms of a relatively small number of parameters. Operator commanded dynamic re-tasking of individual vehicles no longer applies.

The staging process converts an objective into a set of tasks. This paper considers spatial staging, such as passing over a point (for imagery or delivery), a line scan (following a line segment) which could be part of covering a wider region, and loitering (orbiting a point) which could arise when a vehicle is waiting for further instructions or to monitor a point of interest. The spatial tasks have starting points, so the conversion of an ob- jective into a set of tasks determines a set of spatial points that vehicles need to reach. During the staging process the candidate routes are unknown and the assignment of vehicles to tasks is unknown.

2.3. Routing

Autonomous planning is the second block of the HOCC architecture and routing is its first process. Support tasks, such as launching or recovering and refueling, are conducted by the administrator (A) who operates in the background. The routing process itself is performed in two parts, mapping the environment and choosing a path [10] . The first part produces a graph of a vehicle-task route segment. In this paper, the Visibility Graph method [11] is employed. Briefly, this method produces a graph of possible connections between vehicles and obstacle vertices, tasks and vertices, and between the vertices themselves, representing a graph of possible routes through the environment. Note that search areas are regarded as obstacles to prevent routes from passing through them, which can otherwise lead to conflicts. After determining the graph between a vehicle point and a task, the second part is to find the shortest route between them. This part is performed by the A* method [12] . This me- thod does not first find the different paths from which the shortest path could be found. Instead, it searches in the direction of the task, and can leave portions of the graph unsearched. The shortest vehicle-task routes are col- lected into a matrix of vehicle-task route lengths used in vehicle assignment. New routing is calculated each time a vehicle completes a task and when a new objective is initiated.

2.4. Vehicle Assignment

A frequent goal in AUAS path planning, because of limited fuel and flight duration requirements, is to deter- mine vehicle routes by minimizing distance of travel of individual vehicles. An important variation on this goal, which is introduced in this paper, is the minimization of total distance of travel of all of the vehicles (a min-sum assignment). The minimization of total distance of travel leads to an importing routing principle: The routes de- termined by minimizing total distance of travel do not cross. The mathematical proof of this routing principle is presented in the Appendix. Although non-crossing is guaranteed, the paths can still touch obstacles. Indeed, ve- hicle-task segments can share vertices of obstacles, as shown in Figure 2 below.

As shown, two vehicle task routes share vertex C. The vehicle at A travels to C and then to A*. The vehicle at B travels to C and then to B*. Notice that the total distance of travel after the shared vertex, CA* + CB*, is the same whether A travels to A* or to B*. Indeed, the solution to the minimization problem is indeterminate when two routes share a vertex. The presence of this indeterminacy, however, presents an opportunity. It allows the algorithm to ensure that the vehicles do not conflict after passing the shared vertex C, such as a task at A* re- quiring a vehicle to loiter for a short time, thereby staying very near the path of the vehicle proceeding to B*. Assume that the vehicles begin at the same time and that vehicle B reaches C before vehicle A. The algorithm selects the vehicle that first reaches vertex C to travel to the farthest point, in this case, the vehicle at B travels to B*. The inspection of a potential conflict associated with a separation distance falling below a minimal level is thus reduced to checking separation distances while the vehicles are traveling along the two segments AC and BC before the shared vertex. The desire to ensure that vehicle separation distances exceed required minimums makes total distance of travel an important cost function in AUAS path planning. Thus, the min-sum assignment enables rapid deconfliction of planned paths by checking only shared vertices.

The assignments that minimize the total distance of travel are determined in this paper by the Hungarian me- thod [13] . It is likely that an objective will have more tasks than the system has vehicles, or that a new objective might be added. This leads to repeated application of the assignment method. The assignments are updated each time a task is completed or when a new objective arrives. Therefore, the number of assignments is equal to the total number of tasks plus the number of objectives. The computational cost of the Hungarian method is smaller than the computational cost of the Visibility method and the A* method when obstacle vertices outnumber tasks

or vehicles.

2.5. Deconfliction

As described above and proven in the Appendix, potential conflicts in this HOCC architecture are treated mainly by avoiding them in the first place (in contrast with collision avoidance). As stated earlier, this was accom- plished by utilizing the non-crossing property of a min-sum assignment. Non-crossing is a more powerful state- ment than deconfliction. A deconflicted route means two vehicles must not occupy the same space at the same time, but the non-crossing property shows that the entire length of the paths do not cross at any time. This de- couples vehicle speed from the path planning and is useful in solving the potential conflicts in the vicinity of ob- stacle vertices. By loosening any initial assumptions about vehicle speed, shared vertices can be deconflicted by small speed adjustments without changing the path of the vehicle. Because the assigned path is known not to in- tersect with other paths, this small speed adjustment cannot cause other routing conflicts, eliminating the need to re-check the final solution for conflicts The elimination of route intersections leaves potential conflicts only in the neighborhood of boundaries of obstacles that are shared by more than one vehicle. When a potential conflict is identified, the first step is to determine whether or not a conflict arises. The simplest action is to eliminate a conflict by adjusting the speed of one or more vehicles without changing any routes. Minor speed adjustments around the cruise speed are almost always feasible. In extreme cases timing can be corrected by placing vehicles in holding patterns, and is scalable to high-order AUAS when route segments are sufficiently long. Other reme- dies, like route adjustment [9] , become a last resort.

2.6. Autonomous Flight Controls

The autonomous planning block leads to vehicle assignments. The vehicle assignments represent low frequency and bandwidth information that can be performed off-board. The autonomous flight controls, in contrast, re- present higher frequency and bandwidth processes that are ideally suited for on-board implementation. Best practices in autonomous flight controls are reviewed below. The first step is to convert assigned routes to guid- ance paths (G). At this stage routes are refined to account for turning radii and other properties to enable ve- hicles to follow the routes precisely. Indeed, slopes and curvatures of connected line segments are discontinuous at route vertices and can’t be followed precisely. Circular arcs between line segments [14] produce paths whose directions of travel (first derivatives) are continuous. Further refinement produces paths whose turning radii (second derivatives) are continuous, which allows time for the AUAV to change its flight direction through roll. The next step is to regulate the guidance paths. The k-th vehicle regulates its guidance path r_k independent and without awareness of other vehicles. An external disturbance u_Dk, like a wind load, causes deviations from the actual flight path x_k. The control surfaces are adjusted by a guidance input u_Nk and a regulation input u_Rk. The guidance input serves to fly the vehicle along its guidance path in the absence of external disturbances and the regulation part compensates for errors. The primary errors are caused by external disturbances but others errors originate from prescribing non-smooth guidance paths, transducer error, and model errors in the plant L_k. The

guidance state 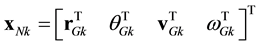is received while following the actual state

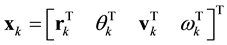. Let u_k represent the control input vector. The equations governing the motion of the

vehicle, the autonomous navigator, the autonomous regulator and the form of the control input are

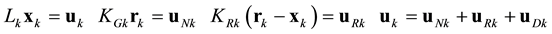
where K_Gk is the guidance operator, K_Rk is the regulator operator, and where the control input is the sum of a guidance input u_Gk, a regulator input u_Rk, and a disturbance input u_Dk. This is called the modern control form [15] . Note that the operator notation above does not specify the realization, that is, whether the system is represented by differential equations, difference equations, algebraic equations, or a hybrid. Under ideal condi- tions (K_Gk = L_k and the guidance input is smooth), the guidance input causes the vehicle to follow the guidance state vector exactly. It follows that the input-output relationship for the vehicle, the error, and the characteristic equation are:

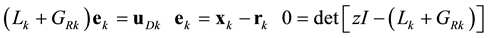
where I is the identity operator and e_k is the state error vector. The characteristic equation is independent of the guidance state vector. Therefore, the regulator gain matrix G_Rk determines the vehicle’s stability characteristics (settling time, peak-overshoot, and steady-state error) independent of the guidance state vector r_k. These best practices pertaining to autonomous flight controls are summarized as an AUAS Flight Controls Principle: Assume that a realizable guidance path has been produced and that a vehicle has the control authority capable of maintaining the guidance path within certain limits placed on settling time, peak overshoot, and steady-state error. Then autonomous guidance and autonomous regulation can be designed by separate and distinct methods. Following best practices in autonomous flight controls lead to vehicle paths that more closely follow their gui- dance paths, which is of particular interest in autonomous systems that are not instrumented with on-board collision avoidance systems.

3. Results

3.1. Problem Statement

Four vehicles loiter in an air space that contains a no-fly zone (obstacle), as shown in Figure 3. At time t = 0, an AUAS user commands the AUAS to search area A. At time t = T, while the vehicles are searching area A, the user gives a second command to search area B. The AUAS, once completing its two objectives, is commanded to return to the original loiter points.

3.2. HOCC Solution

The scenario begins with the AUAS user commanding the first objective to survey area A. The command to survey area B is made later. The staging process converts the objective to search area A into 5 line segment tasks after which the vehicles are tasked to return to their original loiter points (see Figure 4). Each line segment is regarded as a task and a vehicle can follow any line segment from the left or from the right.

Figure 4 shows the first step in determining the shortest route between any one vehicle point and the end points associated with a task. There are two end points associated with each task since the vehicle is allowed here to follow a line segment from the left or the right. Consider the vehicle point and the pair of end points as- sociated with the bottom line segment, as shown. The graph connects solid dots that designate allowable points and the squares that designate obstacle vertices (points designated by circles are not allowed). This figure only shows some of the possible connections in the graph. The first step in determining the best route, when employ- ing the visibility graph method, is to produce a graph that connects the vehicle point to the two end points. The number of different routes along the segments, as shown, is a combinatorial problem, and even enumerating all of the possibilities is computationally expensive in high-order AUAS. As an alternative, the visibility graph me- thod is used, recognizing that it does not consider all of the possibilities.

After determining the possible graphs between a vehicle point and a task, the next step is to find the shortest route between them. The shortest vehicle-task routes between one of the vehicles and each of the five tasks are shown in Figure 5. There are comparable shortest vehicle-task routes between each of the other vehicles and the five tasks, as well (not shown). It happens that the best end points are each on the right side of the search area for the vehicle shown. You will see in Figure 6 that there is a different vehicle for which its shortest vehicle- task route is to an end point located on the left side of the search area.

Once the shortest vehicle-task routes are determined, vehicles need to be assigned to tasks. This is done by minimizing the total distance of travel of the vehicles (see Figure 6).

In Figure 7, the vehicles are shown on their way to their first task when a second objective arrives. The stag- ing process turns the second search area into 5 new line segment tasks. The vehicles are shown at the instant that the new objective arrives. As shown, two tasks are currently being executed, and their end-points are no longer available to be assigned. The points that are available are shown as solid dots. When no longer available, the end-points are indicated by circles. Also, notice that past routes are indicated by thin lines and that the proposed routes are indicated by thick lines. As shown, there will be a total of ten tasks and two objectives so the total number of time intervals will be twelve.

Figure 8 is shown at the same instant as Figure 7 but the newly calculated routes are now shown. As shown, only the assignment of the green vehicle changes and heads to the new search area. Note that vehicles in the

process of executing a task are assigned to new tasks from the end point of the task currently being executed. When the new objective arrived, the blue and yellow vehicles were performing tasks, so their proposed paths beyond their current tasks were also included in the calculation. The proposed route of the yellow vehicle is to the left end point of the task just below its current task and the proposed route of the blue vehicle is to the right end of the task just above its current task. The red vehicle, after the new calculation, is assigned to the same end point as in the previous time interval.

The yellow vehicle is the first vehicle to complete a task. The completion of its task triggers the start of the third time interval. Figure 9 shows the vehicles at this instant, the past routes (thin lines), and the routes pro- posed over this time interval (thick lines). Notice that, because the red vehicle is executing its task, its next as- signment is being considered. As the remaining tasks in the original search area are assigned, it is easy to see that the blue vehicle has a shorter route to the new area than the red or yellow vehicles. Thus the red vehicle is assigned the task previously allotted to blue, and blue’s assignment changes to the new search area. The assign- ments given to the green and the yellow vehicles are the same as in the previous time interval.

In Figure 10, the yellow vehicle has just completed its 2^nd task. The red and blue vehicles completed their first tasks, so a total of 4 tasks have been completed at this instant. Indeed, Figure 10 shows the start of the 6^th time interval. As stated earlier, routes never cross but they can share obstacle vertices (squares). Indeed, the blue, red, and yellow vehicles are approaching the top right vertex. The presence of shared vertices prompts actions in the deconfliction block. The first action is to check whether there is a conflict in the neighborhood of the shared vertex. The checking of this potential conflict reveals that the blue vehicle reaches the vertex first, then the yel- low vehicle and finally the red vehicle. Moreover, the separation distances were all determined to be larger than the required minimum. Recall to avoid potential conflicts, that the vehicle that first reaches the shared vertex is assigned the route to the farthest end point. Thus, the proposed route of the blue vehicle is to the right-most task, the proposed route of the yellow vehicle is to the next right-most task, and the proposed route of the red vehicle is to the third right-most task.

In Figure 11, the green vehicle has just completed its task, triggering the 9^th time interval. The green vehicle has been assigned the task of following the middle task in search area B, completing the available tasks and leaving the red vehicle unassigned. This unassigned vehicle is assigned to a loiter point to await further tasks.

In Figure 12, the green vehicle has just completed a task, triggering the 10^th time interval. During this time interval, the bottom left vertex of the 2^nd search area is a shared vertex. The green vehicle arrives at the vertex before the blue vehicle so the green vehicle returns to the loiter point that is farther from the vertex.

In Figure 13, the yellow vehicle completes the last task, triggering the 12^th time interval. The red vehicle is already at a loiter point, the green vehicle is on route to a loiter point leaving the yellow and blue vehicles that happen to be tasked to pass the bottom left vertex in search area B. The blue vehicle reaches the vertex first, so it

is routed to the farthest remaining vertex.

Figure 14 shows the complete routes of all four vehicles, with the vehicles having returned to the loiter points.

4. Summary and Conclusions

This paper presented an easy-to-implement central command architecture that is well suited to a large number of unmanned aerial vehicles―overcoming present limitations pertaining to operator task load, computational com- plexity and vehicle deconfliction. The architecture consists of a central command block, an autonomous plan- ning block, and an autonomous flight controls block. Building on results found in the literature pertaining to

AUAS, the central command block is fully autonomous thereby overcoming user load limitations associated with a large number of vehicles. The autonomous planning part is a non-iterative sequence of algorithms that govern routing, vehicle assignment, and deconfliction. The non-iterative nature of the algorithms overcomes computational limitations. The routing exploits a new routing principle that naturally prevents vehicle routes from crossing. An example illustrates the different features of the architecture. This paper is the first in a series of two papers; the second will report on flight test results.

References

Appendix: The Shortest Lines between Two Point Sets Do Not Cross

Definition: Let two curved line segments intersect. The intersection point is a crossing point if the correspond- ing tangent lines are not parallel and the point is located in the interior of the line segments (is not an end point of a line segment).

Definition: A planar domain D in R² refers to a subset of R² that can be bounded externally by a closed curve and internally by closed curves.

Definition: Refer to the set of points as point set A(n), and to the set of points as point set

B(m), in which points Q_i and q_i are contained in a planar domain D and The curved line segments in D that connect each point in A(n) to a unique point in B(m) compose the connecting set C(n, m) of A(n) and B(m). Each curved line segment is called a connecting line segment.

Definition: The connecting line segments in a connecting set C(n, m) of A(n) and B(m) of the shortest total

length are called minimal connecting line segments.

Lemma: Line Segments

Consider the following three well-known results:

1) The shortest length L of a curved line segment is produced by the straight line segment between the two end points (see Figure A1(a)). This is more simply stated as “The shortest distance between two points is a straight line.”

2) The length of any one side of a triangle is smaller than the total length of the other two sides (see Figure A1(b)). This result follows from the Pythagorean Theorem.

3) Any point inside a triangle can be connected to any two of its vertices to form a pair of connected line segments. The length of these line segments is larger than the length of the side that connects the two vertices and is smaller than the length of the other two sides (see Figure A1(c)). This result follows from the second re- sult.

Theorem: The Shortest Lines between Two Point Sets Do Not Cross

Minimal connecting line segments in any connecting set C(n, m) do not cross. This is more simply stated as “The shortest lines between two point sets do not cross.”

Proof: Figure A2 illustrates the theorem for a planar domain that is bounded internally by rectangular-shaped closed curves. The connecting line segments are colored and the minimizing line segments are black. The actual proof begins next.

Begin the proof by ordering the points in A(n) and B(m) so that the minimal connecting line segments in C(n,

m) are. The shortest total length is Next, remove connecting line segment

Q₁q₁ from C(n, m), remove Q₁ from A(n), and remove q₁ from B(m) to produce the connecting set C(n ? 1, m ? 1)

of A(n ? 1) and B(m ? 1). It is now shown that are minimal connecting line segments in C(n ? 1, m ?1).

In other words, let’s show that the following key equation holds:

To show this, assume that are not minimal connecting line segments in C(n ? 1, m ? 1), in which

case there exists a total length L* that is smaller than L_min(n ? 1, m ? 1). This leads to the contradictory result:

L_min(n, m) = |Q₁q₁| + L* < |Q₁q₁| + L_min(n ? 1, m ? 1) = L_min(n, m). Indeed, are minimal connecting

line segments in.

The key equation can be invoked in a sequence that begins with n connecting line segments, and ends with any two. Furthermore, n line segments do not cross if any combination of two does not cross. Thus, it remains to prove the theorem for n = 2 connecting line segments. The case of n = 1 line segment should be proven, too; in this case the crossing of the curved line is with itself. Now, consider the case of n = 2.

Two crossing line segments are shown in Figure A3(a) and a view of the infinitesimal region surrounding the crossing point is shown in Figure A3(b) along with two new short-circuiting line segments. Say that the two straight line segments Aa and Bb shown in Figure A3(b) contribute to the total length L by an infinitesimal amount dL. As shown, by result (1) in the Lemma, the total length of the short-circuiting line segments can be used to eliminate the crossing point and switch the assignment from Aa and Bb to the assignment of Ab and Ba while shortening dL and therefore shortening L. But L was the smallest total length, which is contradictory. It follows that the two line segments could not have crossed. The two line segments in Figure A3(a) can be re- garded as one line segment, so one line segment could not have crossed on itself, either.