Intelligent Information Management
Vol. 4 No. 4 (2012) , Article ID: 21405 , 9 pages DOI:10.4236/iim.2012.44016
A New Metric for Measuring Relatedness of Scientific Papers Based on Non-Textual Features
Computer Engineering Department, Ferdowsi University of Mashhad, Mashhad, Iran
Email: zarrinkalam.fattane@stu-mail.um.ac.ir, kahani@um.ac.ir
Received May 12, 2012; revised June 27, 2012; accepted July 10, 2012
Keywords: Relatedness Measure; Citation Recommendation; Digital Library
ABSTRACT
Measuring relatedness of two papers is an issue which arises in many applications, e.g., recommendation, clustering and classification of papers. In this paper, a digital library is modeled as a directed graph; each node representing three different types of entities: papers, authors, and venues, and each edge representing relationships between these entities. Based on this graph model, six different types of relations are considered between two papers, and a new metric is proposed for evaluating relatedness of the papers. This metric only focuses on the relational features, and does not consider textual features. We have used it in combination with a textual similarity measure in the context of citation recommendation systems. Experimental results show that using this metric can successfully improve the quality of the recommendations.
1. Introduction
Due to the fast pace of papers on the web, a main challenge of a researcher is to acquire appropriate knowledge about current state of his research area. Surveying all related papers in a field can be complex and time consuming. One approach is to start with an important related work and trace its citing and cited papers. Another approach is using traditional keyword-based search engines like Google. Both approaches provide a long list of papers to be studied, and they need manual filtering which is tedious and inefficient [1,2].
As a result, a recent approach, utilized by most digital libraries, is to provide a facility that automatically recommends papers related to a given paper (e.g. Google Scholar1), and more recently for a given input text (e.g. refseer2). A major issue of these facilities is finding papers that are related to a specific paper. Therefore, a measure of relatedness is required. Different features of papers can be used to define such a measure.
Relying only on the textual features, like title and abstract, has the disadvantage that it suffers from the complexities and ambiguities known in the natural language processing domain [3]. For example, it is possible that two pieces of texts written by different authors are describing a similar issue but with different words. Therefore, their textual similarity might be low while they are semantically similar and related. Further, a paper P1 that discusses a fuzzy congestion control algorithm for computer networks may have low textual similarity with the original paper P2 that introduces the idea of fuzzy logic; though P1 is related to P2.
Using non-textual features like references can discover more implicitly related papers in comparison with text based methods. However, they have coverage problems, for instance, a recently published paper might not yet be cited by any other paper [1,4].
In this paper, a new measure is proposed which computes the relatedness of two papers using six different types of relations between them. These relations are based on the non-textual features of the papers. The textual features are not used in the proposed measure, since the goal has been to have a measure that is application independent, and in different applications it can be combined with textual features in different ways. In the ex perimental evaluations discussed in this paper, the measure is used in the context of the citation recommendation systems, and the results show that it improves the quality of the recommendations.
The rest of the paper is organized as follows. Section 2 gives a briefly review of related work on relatedness measures used in different applications. The proposed measure is described in Section 3. Section 4 discusses and evaluated the application of this metric in a citation recommender system. Finally, Section 5 concludes the paper by presenting some directions for future works.
2. Related Work
There are some works in the literature which propose measures for relatedness of two papers. Such measures can be used in applications like recommending, clustering and classification of papers. Based on the features which are used in the definition of measures, these works can be divided into three categories.
The first category contains works that utilize only textual features like title, abstract and citation context of papers. Traditional textual similarity measures [5] model documents as a vector of words, and use for instance cosine similarity, for evaluating the relevance of documents. Lakkaraju et al. [6] represent documents as trees of concepts and compute their similarity by a tree-edit distance algorithm. They use this measure to develop a document recommendation system for CiteSeer authors [7]. Using concepts results in better performance since a concept encompass more semantic information in comparison with a single word. Similarly, [8] uses LDA to extract latent topics from the documents and uses these topics in measuring the relatedness of documents.
Citation context is another textual feature which has been used in some researches. The underlying idea is that the citation contexts of a paper provide an explicit description of that paper from the point of view of the author of the citing paper and it can be seen as the abstract of the cited work which highlights its main concepts [9]. Therefore, the citation context can be used in combination with other textual features for measuring the similarity of two papers. This approach is used by Huang et al. [4] for finding related papers, by He et al. [10] to recommend citations for an input text and also by Aljaber et al. [11] to clustering documents.
It must be noted that despite these improvements, due to the inherent complexities and ambiguities of the natural language such as synonymy and polysemy, relying only on the textual similarity is not successful in covering all the features that contribute to the relevance of two papers. This is evidenced for instance by the limitations from which most keyword-based search engines and document-retrieval systems suffer [12].
The second category of papers focuses on non-textual features, e.g. attributes which are extracted from the citation graph of papers. Co-citation [13] and bibliographic coupling [14], are two well-known metrics for measuring relatedness of papers. In co-citation, two papers are considered highly related if there are a large number of papers that cite both of them. From the point of view of bibliographic coupling, two papers that have a large number of common references are considered as highly relevant.
McNee et al. [15] use the citation graph attributes like co-citation for finding similar papers in their proposed collaborative filtering algorithm to recommend citations for an input text and Couto et al. [16] use these bibliometrics measures to classify documents.
Using non-textual features, in comparison with textbased methods, have the benefit that they have the potential to discover more implicitly related papers [4]. However, not considering textual features has also its own disadvantages, since it ignores the main element that is used by the author of the paper to expresses his idea, i.e. the text of the paper. Additionally, it must be noted that methods based on citation graph have coverage problems, for instance, a recently published paper yet to be cited by any other paper [1]. Also issues like invalid self-citations might reduce precision of the relevance measurements.
The works of the third category use a combination of both the textual and non-textual features. In CiteSeer [17], similarity of papers is measured using a combination of three basic metrics: textual similarity of the paper body, header similarity, and citation similarity which is based on co-citation.
Torres et al. [18] present a hybrid recommender system that uses different similarity measures for its algorithm. They conclude that using a hybrid measure which employs both textual and non-textual features improves quality of recommendations.
Bethard et al. [19] propose a new relatedness measure which employs new features like topic similarity and author behavioral patterns, in addition to features like citation count and paper year. The underlying measure of [1] is also a linear combination of text features and citation graph attributes like, citation count, and Katz distance [20].
In this paper a new metric is proposed for measuring the relatedness of two papers. It belongs to the second category, since it considers only relational features of the papers. It can be combined with different textual similarity measures to provide a customized measure for different applications.
3. The Proposed Metric
In this section, first the underlying conceptual model of a digital library is described and then the proposed measure for computing relatedness of two papers from the digital library is introduced.
3.1. Conceptual Model
Here, a digital library is considered to be composed of three types of entities: papers, authors, and venues (the conference/journal where a paper is presented). There are different kinds of relations between these entities, for instance a relation from a paper to an author who has written that paper, or from a paper to the venue where it has been presented in. Based on these relations, four relational features are defined for each paper Pi (1 ≤ i ≤ N):
refListi: {Pj | Pi references Pj};
citListi: {Pj | Pi is cited by Pj};
authListi: list of the authors of Pi;
venuei: venue of Pi.
As a result, a digital library can be modeled by a directed graph G = (V, E) in which the set of vertices V has a vertex for each distinct entity, and the set of edges E contains an edge for each distinct relation between those entities.
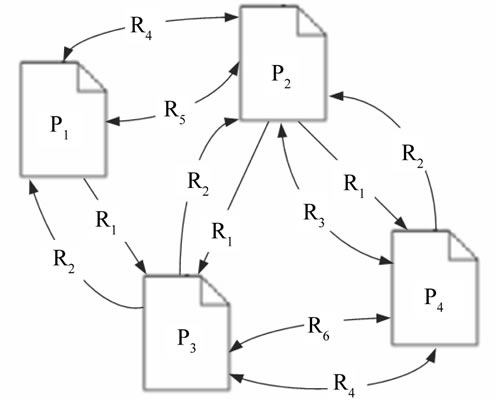
Figure 1 shows the graph representation of a sample digital library. For example, relational features of the paper P2 are:
refList2: {P3, P4};
citList2:O;
authList2: {A2, A3};
venue2: V1.
Based on these four relational features, six different relations, Ri (1 ≤ i ≤ 6), are defined from a paper Pi to another paper Pj:
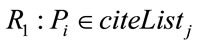 ;
;
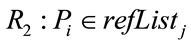 ;
;
 ;
;
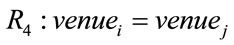 ;
;
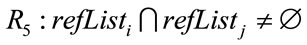 ;
;
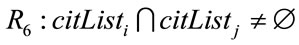 .
.
Using these six types of relations, it is possible to create another directed graph from the original graph of the digital library. The goal of this graph, which is called paper graph, is to represent the papers and their relationships. Therefore, its vertex set includes only the papers, and its edge set contains instances of the six relation types. For example, the corresponding paper graph of Figure 1 is illustrated in Figure 2.
The relations R1 to R6 are based on the following ideas. When a paper references, or is cited by, another paper, the two papers are explicitly stated (by the author of the referencing paper) to be related to each other. This is reflected in relations R1 and R2. Further, since papers of a specific author or venue are usually focused on a specific subject or domain, they can be considered as related. This is the idea behind R3 and R4. Relations R5 and R6, correspondingly, reflect the notions of bibliographic coupling and co-citation which are two core concepts in the citation analysis field.
Two papers that have at least one common reference are said to be bibliographically coupled [14]. The common reference can be seen as an evidence of the relatedness of the two papers. The greater is the number of common references between two papers, the stronger is
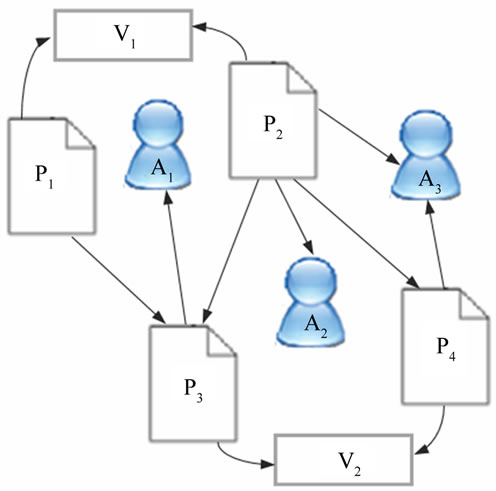
Figure 1. The graph representation of a digital library.
their bibliographic coupling, and hence their relatedness.
Two papers are said to be co-cited if there is a third papers that cites both of them [13]. Again, this common citing paper can be considered as a sign of relatedness of the two papers. The greater is the number of the common citing papers, the greater is the degree of co-citation, and therefore the relatedness of the two papers.
3.2. Relatedness Measure
Using the six relation types introduced above, the relatedness of two papers Pi and Pj is defined as shown in Formula (1):
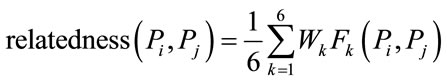 (1)
(1)
where Fk (1 ≤ k ≤ 6) is a function that returns the relatedness value of papers Pi and Pj based on the corresponding relation Rk in the interval [0,1]. Further, Wk (1 ≤ k ≤ 6) is the weight assigned to value of Fk.
The six functions F1 to F6 are defined as:


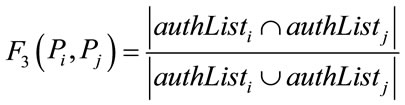

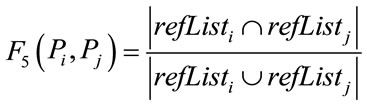
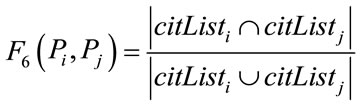
In these functions, a return value of 0 means no relatedness, while a return value of 1 indicates a strong relatedness between the two papers.
The return value of 1 for functions F1 and F2 is based on the idea that if there is a relation of R1 or R2 between two papers Pi and Pj, it evidences a strong relation between them, since the authors of one paper (Pi in the case of R1, and Pj in the case of R2) have explicitly confirmed the relationship by giving reference to another paper. In the case of F4, if two papers have an identical venue, their relatedness from the point of view of R4 is 1, otherwise it is 0.
Functions F3, F5, and F6 are respectively associated with relations R3, R5, and R6, and there is a similar idea behind them. In the case of F3, the more common authors two papers have, the more related they can be considered. However, the ratio of common authors to all authors of the two papers is also important. For instance, 2 common authors out of 3 authors indicates a stronger relatedness in comparison with 2 common authors out of 6. Therefore, the return value of F3 is directly related to the number of common authors between them, and also inversely related to the total number of their distinct authors.
The value of the weight Wk (1 ≤ k ≤ 6) indicates importance of the relation Rk in measuring the relatedness of the two papers. Our point of view is that this is an application-dependent issue, and these weights must be calculated with regard to the specific application which uses the proposed measure. This weight assignment task is usually an issue in defining new multi-factor measures. Two possible ways to do this is 1) to ask experts for assigning weights, and 2) to use evolutionary algorithms like Genetic Algorithm to determine the weights.
4. Use Case: Citation Recommendation System
A sample use case where the proposed measure can be used is in the context of paper recommendation systems. A major issue in these systems is finding papers which are related to a specific paper. Therefore a measure of relatedness is required.
In this paper, the application of the proposed metric is evaluated in a citation recommendation system. This system as a paper recommendation system gets a text as input, and recommends a list of papers which should be cited in different places of the input text. If such a system is available, the researcher can write an essay about his idea and then use the system to find recommended citations, which are papers related to his essay.
In the next sections, first, a citation recommendation algorithm is described which uses the proposed relatedness measure. Then this algorithm is evaluated.
4.1. A Citation Recommendation Algorithm
The proposed citation recommendation algorithm gets a piece of text as input and uses a local digital library to generate a list of recommended papers that should be cited by the input text.
Since the input of the algorithm is only raw text that does not have features like authors, references, and venue, the proposed measure cannot be directly applied. Therefore for each paper Pi (1 ≤ i ≤ N) in the local digital library, its textual similarity to input text is computed by calculating cosine similarity of the TF/IDF vectors of Pi and input. Then the top C papers with the most textual similarity to the input are selected as its CandSet.
The CandSet now includes C papers that each of them, in addition to the textual features, has features like venue and list of authors and references. Therefore, the proposed measure can be applied to calculate the relatedness of each paper of the CandSet to other papers of the digital library. The algorithm performs this calculation to find top K papers from the digital library, which have the most total relatedness to all papers of the CandSet.
4.2. Evaluation
The citation recommendation algorithm described above has been implemented in Java, and the role of the proposed relatedness measure has been evaluated through experiments. In this section these experiments are discussed.
4.2.1. Experiment Setup
a) Sample Digital Library
In order to provide a sample digital library for the experiments, data of about 30,000 papers has been collected from CiteSeerX3. Then a filtering was performed and papers with many missing values (e.g. papers that their abstract, title and venue were missing) were removed. Additionally, papers published after 2007 (about 550 papers) were removed and used as the input data in the experiments.
For each of these papers, its text (without its reference list) has been given to the algorithm as input text, and its reference list has been considered as the expected output of the recommendation algorithm. The filtering process led to a sample digital library with about 12,000 papers, which were stored in a MySQL database.
b) Evaluation MetricsFor evaluating the above citation recommendation algorithm, an automatic evaluation approach is used. In this approach, for every input paper, its text is given to the recommender system as input, and its list of references is considered as the excepted output.
Different metrics can be used to measure quality of recommendations. In this paper three metrics Recall, Cocited probability and NDCG4 are used.
Recall is defined as the percentage of input references that appear in the top K recommended citations. Recommendations that are not in the reference list of the input paper cannot be considered totally unrelated to it. Therefore, Co-cited probability is used as a metric for measuring quality of such recommendations. NDCG is used for evaluating the order of recommendations in the output. More details about these metrics can be found in [10].
c) Experimental ParametersIn order to determine the appropriate value of C, i.e. the size of the CandSet, a simple experiment was conducted. A set of 100 papers were randomly chosen from the input data, and they were used for executing the recommendation algorithm with different values of C from {5, 10, 15, 20, 25, 30, 35, 40, 45, 50}. For each value of C, the execution time, and three evaluation metrics recall, cocited_probability, and NDCG were calculated for top-k recommendations. Analysis of the results has shown that a value of C = 25 is a good choice since it provides a tradeoff between the execution time and other evaluation metrics.
As mentioned in Section 3.2, the proposed measure uses different weights for each of the six relation types. In order to set these weights in the experiments, a genetic algorithm is developed as described below.
In the developed genetic algorithm, each chromosome has six genes, each for indicating one of the six weights. The first generation includes 50 chromosomes with random values in the interval [0,1]. To calculate fitness of each chromosome, the value of its genes used as the weights of the relations and the recommendation algorithm is executed on a small set (about 50 inputs) of input data. Then, the output of the algorithm is evaluated in terms of the three metrics and the sum of the normalized values of these metrics is used as the fitness value of the corresponding chromosome.
After running the genetic algorithm for 20 generations, the best chromosome has been used as the weights of the six relation types. Table 1 shows this result.
4.2.2. Experiments
In order to evaluate different features of the proposed algorithm, three different experiments have been executed. In this section these experiments are discussed.
EXP1. The goal of the first experiment is to evaluate the effectiveness of the proposed measure in the context of citation recommendation systems. In this experiment the citation recommendation algorithm described in Section 4.1 is compared with two baselines: the first baseline uses only textual similarity, this allows us to see the effect of using relational features in addition to the textual features, and the second one is based on the Katz measure [20], which is a measure for computing distance of two nodes in a graph. In our experiment, we have used the specific version of the Katz measure which is customized for the context of citation recommendation [1]. The reason why we have selected the Katz measure is that it is also based on the relational features of the papers, and it is shown that this measure considerably improves the quality of recommendations in [1].
EXP2. The second experiment seeks to evaluate the effect of assigning weights to different relation types in the proposed measure. To do so, the proposed citation recommendation algorithm is executed in two versions: in simple version the proposed algorithm executed with the entire six weights equal to 1 and in GA-based weighted version with weights assigned by the genetic algorithm shown in Table 1.
EXP3. The third experiment is conducted to identify the importance of each of the six relation types in the proposed citation recommendation algorithm. More specifically it is intended to understand:
a) The positive influence of each of the relation types in the absence of other relation types. To do so, each of the six relation types has been used in isolation.
b) The negative influence of ignoring each of the relation types. To do so, each time one of the relation types is ignored and the recommendation algorithm is executed with using other relation types.
4.2.3. Result Analysis
In this section results of the three experiments are analyzed.
EXP1. Figures 3 to 5 illustrate the results of EXP1 and EXP2. As it is shown, the proposed relatedness measure has considerably improved the results in terms of all the three metrics in comparison with the baseline

Table 1. The weights of the six relation types.
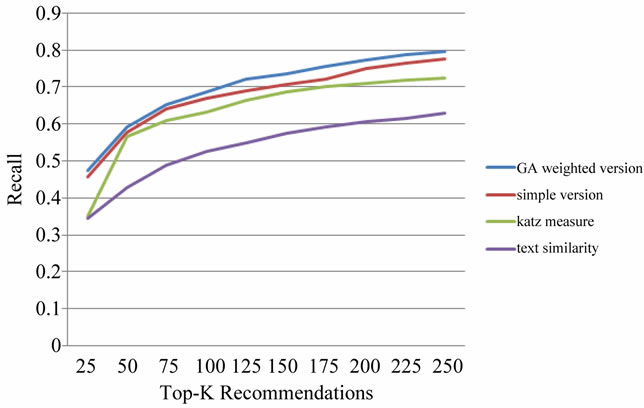
Figure 3. Results of EXP1 and EXP2 in terms of recall.
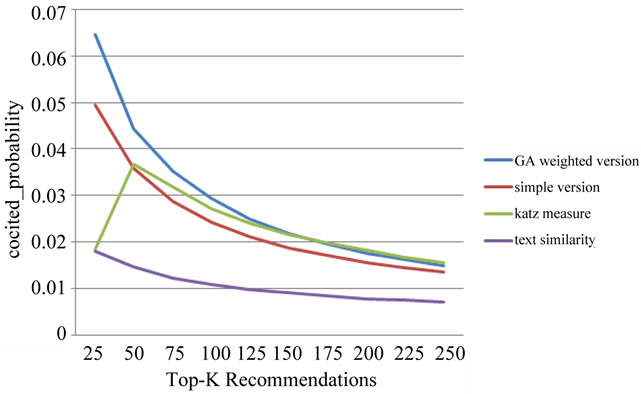
Figure 4. Results of EXP1 and EXP2 in terms of cocited_ probability.
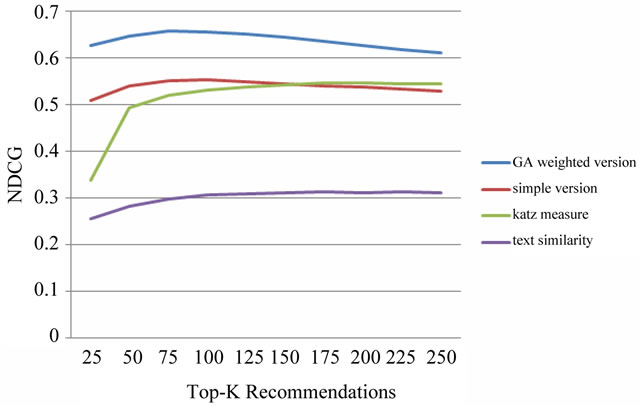
Figure 5. Results of EXP1 and EXP2 in terms of NDCG.
which uses only textual similarity. Therefore, the idea of using relational features in measuring relatedness of two papers has been effective.
Further, the Katz measure similarly outperforms the text-only baseline, but its result is not better than the results of our measure. It must be noted that generally it is more important to have quality top-k results in smaller values of k. As it is shown in Figures 4 and 5 an advantage of our measure is that in the smaller values of k, its results are much better than those of the Katz.
EXP2. As it is illustrated in Figures 3 to 5 the GAbased weighted version of the proposed measure has resulted in better recommendations in comparison with the simple version. The difference is considerable in the case of the NDCG and cocited_probability metrics, especially for small values of k. As a result, it can be concluded that assigning weights to the six relation types is important, and the proposed genetic algorithm is successful in this task.
EXP3.a As it can be understood from Figures 6 to 8, when using each relation in isolation, the relation R1 has
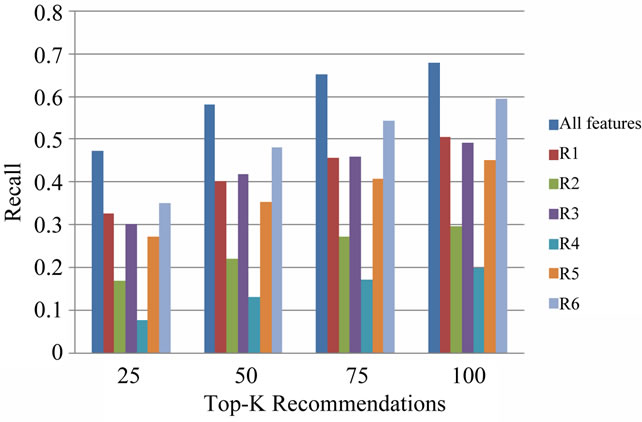
Figure 6. Results of EXP3.a in terms of recall.
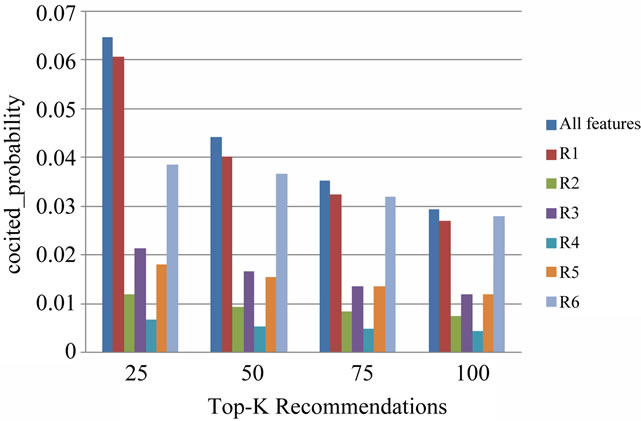
Figure 7. Results of EXP3.a in terms of cocited_probability.
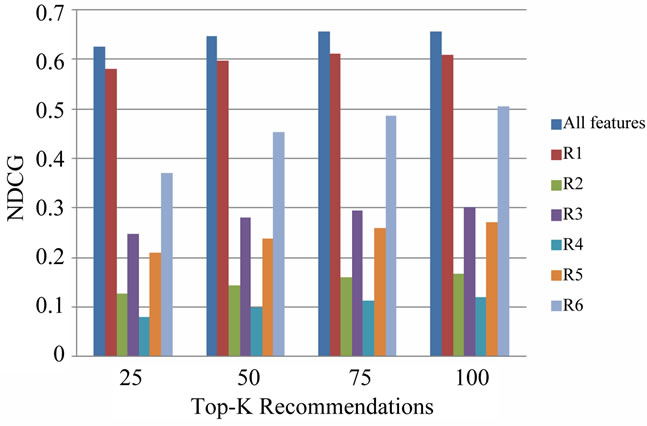
Figure 8. Results of EXP3.a in terms of NDCG.
the most positive impact on NDCG and cocited_probability, and the relation R6 on recall of the recommendation algorithm. Further, the relations R3, R5, R2, and R4 come after R1 and R6.
Another important point concluded from these figures is that although the relations R1 and R6 are the most effective relations, but their results still is not as good as when they are combined with other relations. This means that the aggregation of these six relation types in the proposed measure has been a good choice.
EXP3.b As it is shown in Figures 9 to 11; absence of each of the six relation types reduces the quality of results. In other words none of them is ignorable. Further, among the six relation types, absence of the relation R1 has the most negative effect, and this is considerable in comparison with other relations. After R1 comes R6.
The results of EXP3 support the weight values assigned by the proposed GA. The relations R1 and R6 which turned out by EXP3 to be the most effective relations, have received greater weights from the GA.
In the following, a discussion is presented on the justification of the importance of each of the six relations.
The goal of a citation recommendation algorithm is to recommend papers that should be cited by the input text.
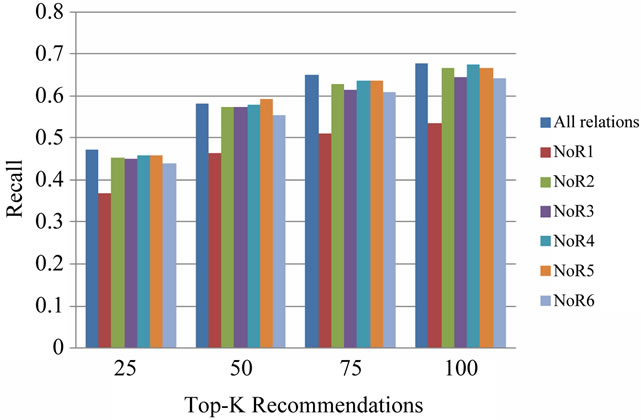
Figure 9. Results of EXP3.b in terms of recall.
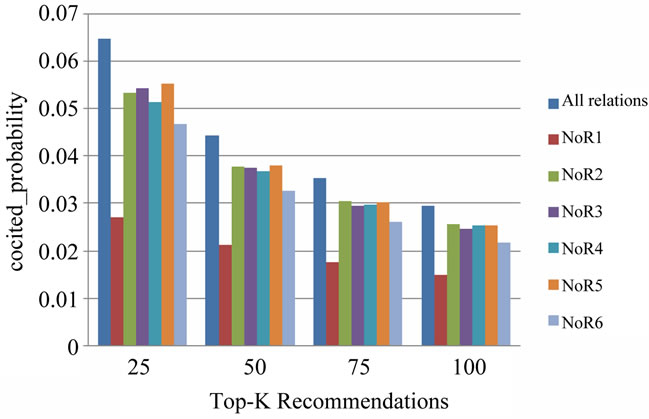
Figure 10. Results of EXP3.b in terms of cocited_probability.
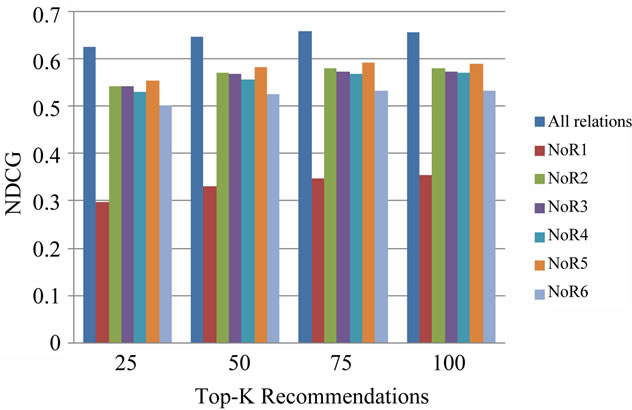
Figure 11. Results of EXP3.b in terms of NDCG.
In the proposed algorithm, CandSet includes papers that have the most textual similarity with the input text. Therefore if there is a paper Pi that most of the CandSet papers have a relation R1 with it, i.e. they cite it, then it is reasonable to say that the input text should also cite Pi. Therefore, a relation R1 has great contribution in determining papers that should be recommended.
On the other hand, the relation R2 does not have such a contribution in the context of citation recommendation. Since if there is a paper Pi that has a relation R2 with most of the CandSet papers, i.e. cites most of them, then it does not provide enough evidence to say that the input text should cite Pi. Therefore, in comparison with R1, R2 has a lower weight in this context.
The relation R4 has had little effect on the performance of the citation recommendation algorithm. This can be justified as knowing that there is a relation R4 from a paper Pi to another paper Pj does not say anything about whether Pi should cite Pj or vice versa, because usually papers of a venue (i.e. conference or journal) cover multiple subjects. Therefore R4 does not have much contribution in the citation recommendation context.
In case of the relation R3, if there is a relation R3 from Pi to Pj, i.e. they have common authors, it can be said, to some extent, that Pi must cite Pj. The reason is that papers of an author usually focus on a similar subject. Authors continue their previous works and do self-citation in their new papers. On the other hand, it is probable that an author publishes papers on different domains. Therefore existence of an R3 relation has more effect in citation recommendation than R4, and less effect than R1.
If there is a paper Pi that has a relation R6 with most of the CandSet papers, it means that for most of the CandSet papers like Pj there is a paper Pk that cites both Pi and Pj. Therefore, since CandSet papers are candidate to be cited by the input text, Pi can be considered as related to CandSet papers, and a candidate for being cited by the input text. As the experiments have shown, R6 is effective in the context of citation recommendation.
If there is a paper Pi that has a relation R5 with most of the CandSet papers, it means that for most of the CandSet papers like Pj there is a paper Pk that is cited by both Pi and Pj. Therefore, Pi can be considered as related to CandSet papers, but the qualification of Pi for being cited by the input text is not as strong as the case with R6. Therefore R5 must have a lower weight compared to R6, and this is evidenced by the experiments.
5. Conclusions
In this paper a new metric is proposed for computing the relatedness of two papers in a digital library, which is based on the relational features of papers. Each feature has a corresponding weight which shows its importance in the context where the measure is used.
To evaluate this measure, we have employed it in combination with a textual similarity measure in a citation recommendation algorithm. In order to determine required weights, a genetic algorithm is used. The experiments have shown that this measure improves the quality of the recommendations. Further experiments support that the GA has been successful in assigning appropriate weights.
Our future work includes evaluating the proposed related-ness measure in other contexts (e.g. plagiarism detection, and reviewer recommendation for journal submissions), and assessing other relational features for inclusion in the relatedness measure (e.g. number of the times that a paper is cited in another paper).
REFERENCES
- T. Strohman, W. B. Croft and D. Jensen, “Recommending Citations for Academic Papers,” Proceedings of the 30th Annual ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), Amsterdam, 23-27 July 2007, pp. 705-706.
- S. Bethard and D. Jurafsky, “Who Should I Cite? Learning Literature Search Models from Citation Behavior,” Proceedings of ACM Conference on Information and Knowledge Management, New York, 2010, pp. 609-618.
- M. Vallez and R. Pedraza-Jimenez, “Natural Language Processing in Textual Information Retrieval and Related Topics,” 2007. http://www.hipertext.net
- S. Huang, G. Xue, B. Zhang, Z. Chen, Y. Yu and W. Ma, “TSSP: A Reinforcement Algorithm to Find Related Papers,” IEEE/WIC/ ACM International Conference on Proceedings of the Web Intelligence (WI’04), Shanghai, 20-24 September 2004, pp. 117-123.
- G. Salton and C. Buckley, “Term Weighting Approaches in Automatic Text Retrieval,” Information Processing and Management, Vol. 24, No. 5, 1988, pp. 513-523. dio:10.1016/0306-4573(88)90021-0
- P. Lakkaraju, S. Gauch and M. Speretta, “Document Similarity Based on Concept Tree Distance,” Proceedings of the Nineteenth ACM Conference on Hypertext and Hypermedia, Pittsburgh, June 2008, pp. 19-21. doi:10.1145/1379092.1379118
- K. Chandrasekan, S. Gauch, P. Lakkaraju and H. P. Luong, “Concept-Based Document Recommendations for CiteSeer Authors,” Proceedings of the 5th International Conference on Adaptive Hypermedia and Adaptive Web- Based Systems, Hannover, 29 July-1 August 2008, pp. 83- 92.
- G. H. Martín, S. Schockaert, C. Cornelis and H. Naessens, “Finding Similar Research Papers Using Language Models,” Proceedings of the 2nd Workshop on Semantic Personalized Information Management: Retrieval and Recommendation (SPIM’11), 2011, pp. 106-113.
- A. Ritchie, “Citation Context Analysis for Information Retrieval,” Ph.D. Thesis, University of Cambridge, Cambridge, 2008.
- Q. He, J. Pei, D. Kifer, P. Mitra and C. L. Giles, “Context-Aware Citation Recommendation,” Proceedings of the 19th International World Wide Web Conference (WWW), Raleigh, 26-30 April 2010, pp. 421-430. doi:10.1145/1772690.1772734
- B. Aljaber, N. Stokes, J. Bailey and J. Pei, “Document Clustering of Scientific Texts Using Citation Contexts,” Information Retrieval, Vol. 13, No. 2, 2010, pp. 101-131. doi:10.1007/s10791-009-9108-x
- M. R. Henzinger, R. Motwani and C. Silverstein, “Challenges in Web Search Engines,” Proceedings of the 18th International Joint Conference on Artificial Intelligence, Acapulco, 2003, pp. 1573-1579.
- H. Small, “Co-Citation in the Scientific Literature: A New Measurement of the Relationship between Two Documents,” The American Society of Information Science, Vol. 24, No. 4, 1973, pp. 265-269. doi:10.1002/asi.4630240406
- M. Kessler, “Bibliographic Coupling between Scientific Papers,” American Documentation, Vol. 14, No. 1, 1963, pp. 10-25. doi:10.1002/asi.5090140103
- S. McNee, I. Albert, D. Cosley, P. Gopalkrishnan, S. Lam, A. Rashid, J. Konstan and J. Ried, “On the Recommending of Citations for Research Papers,” Proceedings of the 2002 ACM Conference on Computer Supported Cooperative Work, New Orleans, 16-20 November 2002, pp. 116-125.
- T. Couto, N. Ziviani, P. Calado, M. Cristo, M. Gonçalves, E. S. D. Moura and W. C. Brandão, “Classifying Documents with Link-Based Bibliometric Measures,” Information Retrieval, Vol. 13, No. 4, 2010, pp. 315-345. doi:10.1007/s10791-009-9119-7
- C. L. Giles, K. D. Bollacker and S. Lawrence, “CiteSeer: An Automatic Citation Indexing System,” Proceedings of Third ACM Conference on Digital Libraries, Pittsburgh, 23-26 June 1998, pp. 89-98. doi:10.1145/276675.276685
- R. Torres, S. M. McNee, M. Abel, J. A. Konstan and J. Riedl, “Enhancing Digital Libraries with TechLens,” Proceeding of IEEE/ACM Joint Conference on Digital Libraries (ACM/IEEE JCDL’2004), Washington DC, 2004, pp. 228-236.
- S. Bethard and D. D. Jurafsky, “Who Should I Cite? Learning Literature Search Models from Citation Behavior,” Proceedings of ACM Conference on Information and Knowledge Management, Toronto, 26-30 October 2010, pp. 609-618.
- D. Liben-Nowell and J. Kleinberg, “The Link Prediction Problem for Social Networks,” Proceeding of the 12th International Conference on Information and Knowledge Management, New Orleans, 2-8 November 2003, pp. 556-559.
NOTES
1http://scholar.google.com.
2http://citeseerx.ksu.edu.sa.
3http://citeseerx.ist.psu.edu.
4Normalized discounted cumulative gain.