Intelligent Information Management
Vol.6 No.1(2014), Article ID:41653,4 pages DOI:10.4236/iim.2014.61002
New Adaptive Compensator Robust to Memoryless Nonlinear Distortion
Oh Sang Kwon
Division of Information Technology, The Cyber University of Korea, Seoul, South Korea
Email: narcis@cyberkorea.ac.kr
Copyright © 2014 Oh Sang Kwon. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Oh Sang Kwon. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received May 4, 2012; revised June 3, 2012; accepted July 2, 2012
ABSTRACT
In this paper, the new hybrid adaptive Volterra filter was proposed to be applied for compensating the nonlinear distortion of memoryless nonlinear systems with saturation characteristics. Through computer simulations as well as the analytical analysis, it could be shown that it is possible for both conventional Volterra filter and proposed Volterra filter, to be applied for linearizing the memoryless nonlinear system with nonlinear distortion. Also, the simulation results demonstrated that the proposed Volterra filter may have faster convergence speed and better capability of compensating the nonlinear distortion than the conventional Volterra filter.
Keywords: Adaptive; Nonlinear; Volterra; Compensator; Convergence
1. Introduction
The linear filters have played a very popular role in the development of various signal processing techniques. The obvious advantage of linear filters is their inherent simplicity. Design, analysis, and implementation of such filters are relatively straightforward tasks in many applications. However, for systems with high performances, the distortion problem exists due to nonlinearities of the system and decreases the performance of conventional signal processing system. For example, there are several situations in which the performance of linear filters is unacceptable. A simple but highly pervasive type of nonlinearity is the saturation-type nonlinearity. Trying to identify these types of systems using linear models can often give misleading results. Another situation where nonlinear models will do well when linear models will fail miserably is that of trying to relate to two signals with non-overlapping spectral components. Therefore, a variety of workers have recognized the need for the nonlinear control system and in practicality, it may be studied in many applications [1-3]. Fortunately, with the development of high-speed processor in recent days, it is possible to implement the signal processing algorithms for the nonlinear system, which has not been impossible due to its complexities and computation problem.
In general, the nonlinear filter to represent the nonlinear system, may be based on the functional series. And the characteristics of the nonlinear filter are similar to those of linear systems because the filter output is composed of linear combination of filter coefficients. Also, the adaptive algorithms in linear systems to adapt the filter coefficients, can be applied to the nonlinear system directly, and the analysis is similar to that of the linear system. As the adaptive algorithms to adapt the filter coefficients in the nonlinear system, the least mean square (LMS) and least square (LS) algorithms etc. can be used. However, the nonlinear filter may have more computation complexities and slower convergence speed than those of the linear system because it may use more coefficients than the nonlinear system. Therefore, a variety of workers have recognized the need for the nonlinear control system with less computation complexities and faster convergence speed and it may be developed in many applications [4-7].
In this paper, the new adaptive Volterra filter was proposed to be applied for compensating the nonlinear distortion of memoryless nonlinear systems with saturation characteristics. Through computer simulations as well as the analytical analysis, it could be shown that it is possible for the proposed hybrid Volterra filter to be applied for linearizing the memoryless nonlinear system with non-linear distortion. Also, the simulation results demonstrated that the proposed hybrid filter may have faster convergence speed and better capability of compensating the nonlinear distortion than the conventional Volterra filter.
2. Proposed Adaptive Nonlinear Compensator
In this paper, the new adaptive compensator was proposed to be applied for compensating the nonlinear distortion of memoryless nonlinear systems. A block diagram of the proposed adaptive nonlinear compensator is shown in Figure 1. The memoryless adaptive compensator, or pre-processor 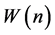 is located in front of a nonlinear system H. Here,
is located in front of a nonlinear system H. Here,
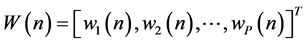 and H is assumed to be the linear combination of the nonlinear functions. In Figure 1, the adaptive compensator is composed of linear combination of the nonlinear functions, and the relations between inputs and outputs are as follows
and H is assumed to be the linear combination of the nonlinear functions. In Figure 1, the adaptive compensator is composed of linear combination of the nonlinear functions, and the relations between inputs and outputs are as follows
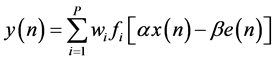 (1)
(1)
Here P is the number of the used functions and fi represents the nonlinear functions. The output of the adaptive compensator and the output of the nonlinear function can be represented as follows, respectively.
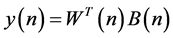 (2)
(2)
 (3)
(3)
where 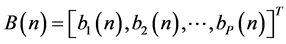 with
with
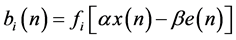
Also, the distortion 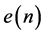 included in
included in 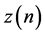 can be defined as the difference between the output
can be defined as the difference between the output 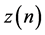 and the input
and the input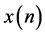 .
.
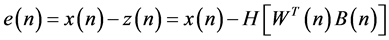 (4)
(4)
The optimum coefficient value of the compensator is given by minimizing the variance of the distortion. So, the following equation can be produced.
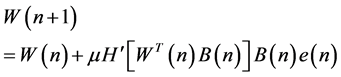 (5)
(5)
Also, the above equation can be reduced as follows [8]
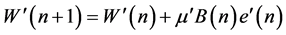 (6)
(6)
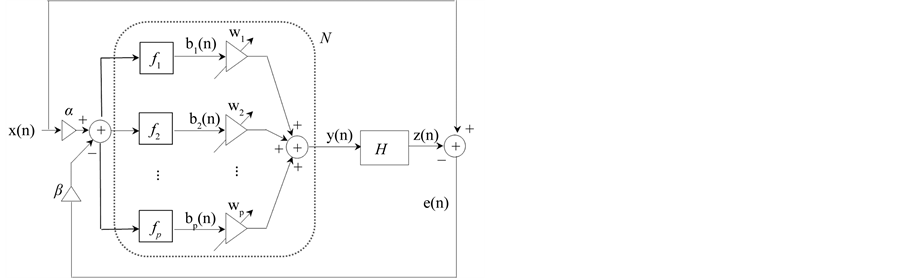
Figure 1. The linearization scheme of the proposed adaptive Volterra compensator.
where 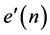 is the error due to
is the error due to  and
and 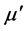 is a constant that determines the convergence and stability. In the above Equation (6), the compensation mechanism of filter coefficients is similar to that of the convention all LMS algorithm, and only one addition and one multiply are increases.
is a constant that determines the convergence and stability. In the above Equation (6), the compensation mechanism of filter coefficients is similar to that of the convention all LMS algorithm, and only one addition and one multiply are increases.
3. Simulation Results
For the computer simulations, a traveling wave tube (TWT) is selected as the nonlinear object model, which may be used in a satellite communication as a power amplifier [9]. In the TWT model, the relationship between an input and an output is as follows and it represents the saturation characteristics, illustrated as Figure 2,
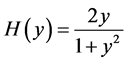 (7)
(7)
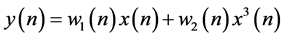 (8)
(8)
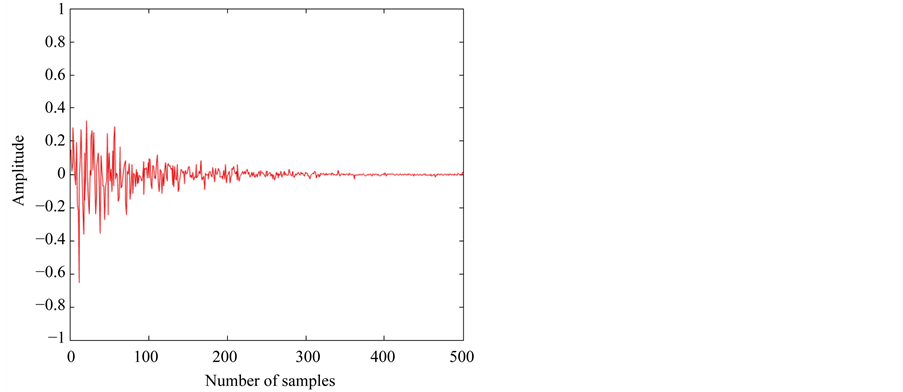
Because the TWT characteristic function is an odd function, the Taylor’s series composed of odd functions, can be used as a function of the compensator for estimation of the inverse function. Random signals are used as input signals, which are distributed uniformly between −1 and +1. For the computer simulations, the conventional Volterra compensator and the proposed compensator are used to be compared with each other, and the results are expressed as average of the independent simulations. Figure 3 represents results of the nonlinear distortion attenuation in the nonlinear system H. In the figure, (a) and (b) represent the results of both the conventional Volterra compensator and the proposed compensator respectively, and it is verified that the latter converges faster than the former. Figure 4 represents the trajectories of filter coefficients for both filters, in which the conventional Volterra filter may adapt more slowly than the proposed hybrid filter. Both algorithms converge to the coefficients value of about 0.5075 and 0.1018, and

Figure 2. The input-output characteristics of TWT.
 (a)
(a)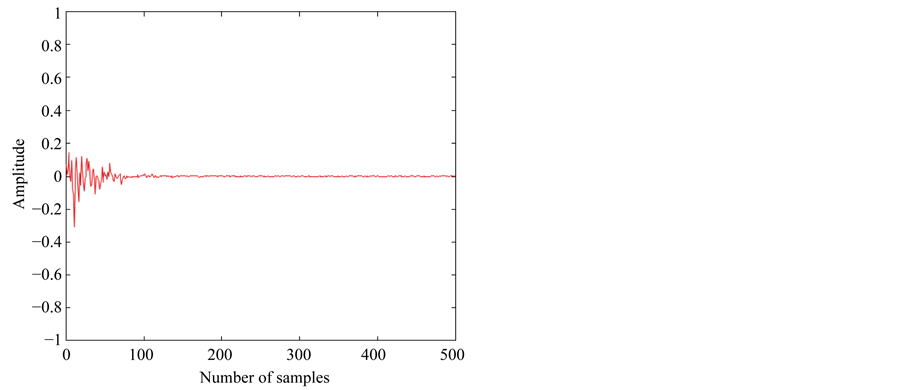 (b)
(b)
Figure 3. The mean sample error signal of nonlinear distortion attenuation using (a) the conventional Volterra compensator and (b) the proposed adaptive compensator.
 (a)
(a) (b)
(b)
Figure 4. The mean trajectories of the filter coefficients using (a) the conventional Volterra compensator and (b) the proposed adaptive compensator.
0.5040 and 0.0267, for the first-order and the third-order coefficients, respectively.
Figure 5 represents the results of the linearization, in which the filter coefficients of the steady state are used when both algorithms converge to the optimum solution sufficiently. In the figure, (a) represents the characteristics of H before compensation, and (b) and (c) represents the characteristics after compensation by the conventional Volterra compensator and the proposed compensator respectively. Especially, the complexity of computation of the proposed compensator is nearly equal to that of the conventional Volterra compensator.
4. Conclusion
In this paper, the new adaptive Volterra compensator was proposed to be applied for compensating the nonlinear distortion of memoryless nonlinear systems. The simulation results demonstrated that the proposed adaptive
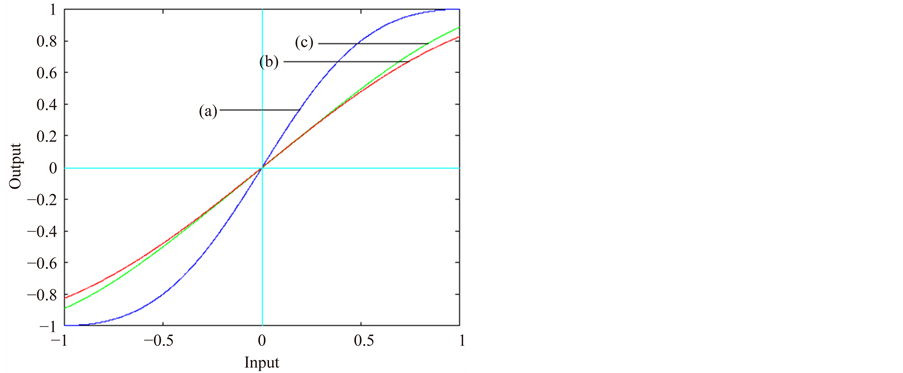
Figure 5. The performance of linearized TWT distortion. (a) no compensation (b) after the conventional Volterra compensation (c) after the proposed adaptive compensation.
Volterra compensator could have faster convergence speed and better capability of compensating the nonlinear distortion than the conventional Volterra compensator, with nearly equal complexity of computation.
[1] REFERENCES
[2] M. Schetzen, “The Volterra and Wiener Theories of Nonlinear Systems,” Wiley, New York, 1980.
[3] J. B. Bendat, “Nonlinear System Analysis and Identification from Random Data,” John Wiley, New York, 1990.
[4] T. Ogunfunmi, “Adaptive Nonlinear System Identification: Volterra and Wiener Model Approaches,” Springer, London, 2007. http://dx.doi.org/10.1007/978-0-387-68630-1
[5] Z. J. Cai and E.-W. Bai, “How Nonlinear Parametric Wiener System Identification is Under Gaussian Inputs?” IEEE Transactions on Automatic Control, Vol. 57, No. 3, 2012, pp. 738-742. http://dx.doi.org/10.1109/TAC.2011.2166318
[6] E. W. Bai and J. Reyland, “Towards Identification of Wiener Systems with the Least Amount of a Priori Information on the Nonlinearity: IIR Cases,” Automatica, Vol. 45, 2009, pp. 956-965. http://dx.doi.org/10.1016/j.automatica.2008.11.020
[7] W. A. Frank, “An Efficient Approximation to the Quadratic Volterra Filter and its Application in Real-Time Loudspeaker Linearization,” Signal Processing, Vol. 45 No. 1, 1995, p. 97. http://dx.doi.org/10.1016/0165-1684(95)00044-E
[8] W. Ji and W.-S. Gan, “Identification of a Parametric Loudspeaker System Using an Adaptive Volterra Filter,” Applied Acoustics, Vol. 73, No. 12, 2012, pp. 1251-1262. http://dx.doi.org/10.1016/j.apacoust.2012.03.007
[9] B. Widrow and S. D. Stearns, “Adaptive Signal Processing,” Prentice-Hall, Englewood Cliffs, 1985.
[10] A. A. M. Saleh, “Frequency-Independent and FrequemcyDependent Nonlinear Models of TWT Amplifiers,” IEEE Transactions on Communications, Vol. COM-29, No. 11, 1981, pp. 1715-1720. http://dx.doi.org/10.1109/TCOM.1981.1094911

