Received 6 May 2016; accepted 19 June 2016; published 22 June 2016

ABSTRACT

To deal with the problem of uncertain type of multiple-attribute electronic commerce investment decision whose attribute weights can’t be fully known, a index which measures the decision- making plan-close degree was Introduced, and a decision-making model based on the scheme close degree was established. The article analyses the application of the model used in investment decisions.

Keywords:

Multiple-Attribute Decisions, Scheme Close Degree, Decisions

1. Introduction

In essence, after determining the comprehensive attribute values of each scheme, multiple-attribute decision making ranks and optimizes the schemes according to their comprehensive attribute values. At presents, the decision making theory and method about the multi-attribute decisions whose attribute weights information is completely known is complete. But in order to deal with the problem of electronic commerce investment decision, decisions made by managers according to their experiences are too subjective, because the weights of factors in the decision making process are difficult to be determined accurately due to the complexity of the economic system and the fluidity of the market situation [1] . The article solves the uncertain type of multiple attribute decision making problems part of whose attribute weights information is completely unknown. In the first place, a key indicator-scheme close degree was introduced, and then, a decision making model based on the scheme close degree was given which was one of methods to solve the problem.

2. Basic Theory

Hypotheses: 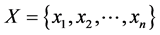is the scheme aggregate of the decision making problem;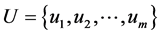

is the attribute aggregate; 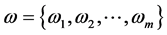is the weight vector of the attribute;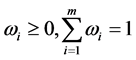. H is the

attribute weight vector according to the known weight information, 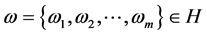[2] . Especially, if H is null set, attribute weight is completely unknown. Scheme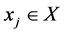, attribute i is measured, and attribute value of 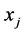is got, so decision matrix 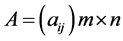is made up. Common attribute types are benefit-type, cost-type, fixed-type, interval-type and deviation-type. To eliminate the influence of different physical dimensions to investment decisions, standardize the decision matrix 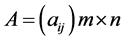and get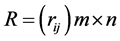. The relation of comprehensive attribute value and weight of Scheme is

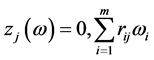(1)

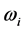is the weight of attribute.

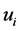When weight is certain, the strengths and weaknesses of each scheme can be known by their comprehensive attribute value. When is unknown, comprehensively attribute value cannot be got by equation (1) [3] . The situation when attribute weight cannot be completely known will be discussed.

In certain, comprehensive attribute values are expected to be big. The problem of multi-target decision is thought about.

(MOP) Target function:

Restraint:

If, this is the optimal solution to the following single-target optimized model:

(SOP1) Target function:

Restraint:

is the comprehensive attribute ideal value of scheme

is the minus comprehensive attribute ideal value of scheme

If is the optimal solution to the following single-target optimized model:

(SOP2) Target function:

Restraint:

and are the ideal point and minus ideal point of multi-objective decision problem (MOP) respectively.

The included angle cosine of Scheme comprehensive attribute value vector and ideal point is:

The included angle cosine of Scheme comprehensive attribute value vector and minus ideal point:

To consider the comprehensive attribute value of each scheme as one unit, scheme close degree is used. Scheme close degree function is:

(2)

(3)

For random, the scheme comprehensive attribute value vector as gets larger, otherwise, the scheme comprehensive attribute value vector will be more similar to minus ideal points when schemes are far away from their optimal condition [4] . So we can consider scheme close degree as a reasonal indicator to measure decision schemes. We maximise this indicator and establish the following single-objective optimised model:

(SOP3) Target function:

Restraint:, (H is already known)

The optimal attribute weight vector can be gotten, and then the corresponding scheme comprehensive attribute value vector can also be gotten. Schemes are ranked and sorted by their comprehensive attribute value.

According to the above-mentioned theory, an uncertain type multi-objective decision method based on scheme close degree is given. The following are specific

Steps:

1) Decision matrix based on investment decision problem is fomed;

2) Regulate to be;

3) Use model (SOP1) and (SOP2) to get ideal point and minus ideal point ;

4) Use equation (2) to calculate a, b;

5) Solve single-objective decision model (SOP3) and get optimal solution, close degree and relevant scheme comprehensive attribute value vector;

6) Rank and sort schemes by their comprehensive attribute value.

3. Application Exemples

There are four e-commerce investment schemes x₁, x₂, x₃, x₄ to be measured. Attributes are company strategy u₁, market scale u₂, risk u₃, capital u₄, strengths of rivals u₅ and scope u₆ [5] . Attribute values of each schemes are shown in Table 1.

u₃ and u₅ are cost-type attributes; u₁, u₂, u₄ and u₆ are benefit-type attributes. The weight of attribute u_i is unknown. Certain weight information is:

Pick over schemes.

Specific Steps are:

1) Form decision matrix using figures in Table 1,

2) Use the following formula to regulate matrix A,

T₁, T₂ are sets of benefit-type and cost-type respectively. Standardization matrix is gotten:

3) Use model (SOP1) and (SOP2) to get ideal point and minus ideal point, ,

4) Use equation (2) to calculate a = 1.4906, b = 1.7083;

5) Use model (SOP3) to get the following single-objective decision model:

Target function:

Restraints:

Ideal solution is. Close degree is. The relevant comprehensive attribute value vector is. So schemes ranks are. The optimal scheme is.

4. Conclusion

Decision-making model based on the scheme close degree can determine what is the optimal plan in the lack of weight information and thus provides scientific basis for decision makers to draw up electronic business investment programmes under uncertain conditions. From the example analysis, this model not only determines what is the optimal plan but also ascertains weights for each attribute influencing decisions. Decision makers can know the importance of each attribute according to the size of their weights and give greater attention to big-weight attributes based on the actual situation, so they can adopt pointed countermeasures in order to get more benefit.

Cite this paper

Fengna Ge,Xinxin Ding, (2016) Uncertain Type of Multiple-Attribute Electronic Commerce Investment Decision Model Based on the Close Degree of the Scheme and Its Applications. iBusiness,08,31-35. doi: 10.4236/ib.2016.82004

References

NOTES

^*Corresponding author.