Positioning
Vol.06 No.04(2015), Article ID:60888,15 pages
10.4236/pos.2015.64009
Integration of Multi-Constellation GNSS Precise Point Positioning and MEMS-Based Inertial Systems Using Tightly Coupled Mechanization
Mahmoud Abd Rabbou, Ahmed El-Rabbany
Department of Civil Engineering, Ryerson University, Toronto, Canada

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 21 September 2015; accepted 1 November 2015; published 4 November 2015

ABSTRACT
We develop a new integrated navigation system, which integrates multi-constellations GNSS precise point positioning (PPP), including GPS, GLONASS and Galileo, with low-cost micro-electro- mechanical sensor (MEMS) inertial system, for precise positioning applications. To integrate GNSS and the MEMS-based inertial system, the process and measurement models are developed. Tightly coupled mechanism is adopted, which is carried out in the GNSS raw measurements domain. Both un-differenced and between-satellite single-difference (BSSD) ionosphere-free linear combinations of pseudorange and carrier phase GNSS measurements are processed. Rigorous models are employed to correct GNSS errors and biases. The GNSS inter-system biases are considered as additional unknowns in the integrated error state vector. The developed stochastic model for inertial sensors errors and biases are defined based on first order Gaussian Markov process. Extended Kalman filter is developed to integrate GNSS and inertial measurements and estimate inertial measurements biases and errors. Two field experiments are executed, which represent different real-world scenarios in land-based navigation. The data are processed by using our developed Ryerson PPP GNSS/MEMS software. The results indicate that the proposed integrated system achieves decimeter to centimeter level positioning accuracy when the measurement updates from GNSS are available. During complete GNSS outages the developed integrated system continues to achieve decimeter level accuracy for up to 30 seconds while it achieves meter-level accuracy when a 60-second outage is introduced.
Keywords:
GNSS, GPS, Galileo, GLONASS, MEMS, PPP, Tightly Coupled

1. Introduction
Global navigation satellite systems (GNSS) provide worldwide positioning, velocity and time synchronization. Traditionally, highly accurate GNSS positioning solution is obtained through carrier-phase observables in differential mode involving two or more receivers. However, the requirement of a base station is usually problematic for some applications. Comparable positioning accuracy, without requiring extra infrastructure, can be achieved through precise point positioning (PPP) technique [1] . PPP uses either un-differenced or between-satellite single difference carrier-frequency and pseudorange observations from a single receiver, in addition to precise orbit and clock products. PPP commonly employs un-differenced ionosphere-free linear combination of GPS observations. Unfortunately, GPS often experiences poor satellite visibility or weak constellation geometry in urban areas. This limitation can be overcome through combining multi-constellation GNSS, which is not simply achieved by adding the additional measurements to existing GPS observation models. Inter-system biases exist, which must be taken into account in order to make effective use of the additional GNSS observation.
Employing multi-GNSS systems, in contrast to GPS only, decreases the probability of partial GNSS outages due to the availability of a large number of satellites observations. However, GNSS positioning solution may not always be available due to complete GNSS outages in urban canyons. These limitations can be overcome through integrating the GNSS observations with a relatively environment-independent system, the inertial navigation system (INS). Differential GPS are traditionally used for precise positioning applications with different grade levels of inertial sensors such as a navigation grade inertial system (e.g. [2] [3] ), and a tactical grade INS (e.g. [4] [5] ). Typically, previous research employed high-end INS to enhance the GPS solution. Petovello et al. (2003) [4] used high-end INS to shorten the ambiguity search time following brief GPS data outages by feeding the estimation filter with position and position variance-covariance matrix. As well, inertial sensor measurements were used to identify the GPS cycle slip, which in turn improved GPS reliability [6] . Unfortunately, high- end inertial sensors are expensive and may not provide a cost effective solution. Advances in micro-electro- mechanical sensors (MEMS) provide the development of a generation of low-cost inertial sensors, which make them attractive to many users. However, in general, MEMS sensors have poorer performance and stability compared with high-end INS due to the high noise level and severe biases and drifts affecting the MEMS-based inertial sensors. A number of researchers have investigated the integration of GPS system with MEMS-based inertial sensors (e.g. [7] -[9] ). Most of the previous research either employed the differential or classical single point positioning GPS. As such, severe positioning errors were introduced during the GPS outages, which restricted the applications of those systems. More recently, the PPP is presented in the integration system in a number of studies [10] -[18] . However, these studies were based on the pseudoorange and carrier phase observations of a single GNSS constellation, namely GPS.
Considering the recent advances in MEMS-based accelerometers, the up to date GNSS constellations and the advances in PPP techniques, this research aims to develop a new integrated navigation system for precise positioning and navigation applications. MEMS-based accelerometers equipped with fiber optic gyros, which limit the orientation errors, are used. GNSS-based PPP including GPS, GLONASS and Galileo systems observations are used to update the system through a tightly coupled mechanism. The developed integrated system shows decimetre to centimetre level accuracy when GNSS observations are available. It is shown that the additional GNSS observations enhance the positioning accuracy in comparison with the traditional GPS kinematic positioning solution. Better positioning accuracy is obtained with BSSD ionosphere-free model, in comparison with the traditional un-differenced ionosphere-free model. In addition, the developed integrated system continues to achieve decimeter level accuracy for up to 30 seconds while it achieves meter-level accuracy when a 60-second outage is introduced.
2. Multi-Constellation GNSS-PPP Measurement Models
In this study, both un-differenced and between-satellite single differenced ionosphere-free models are considered. Pseudorange and carrier phase observations of three GNSS systems are processed, namely GPS, GLONASS and Galileo. The general un-differenced ionosphere-free linear combinations of GNSS observations can be written as [19] :
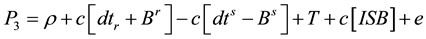 (1)
(1)
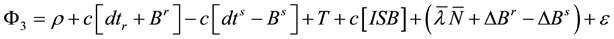 (2)
(2)
where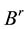 ,
, 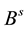 are ionosphere-free differential code biases for receiver and satellites, respectively; ISB is the inter-system bias which is the difference between receiver differential code bias of the GPS and the other GNSS systems. The inter-system bias for GPS is equal zero;
are ionosphere-free differential code biases for receiver and satellites, respectively; ISB is the inter-system bias which is the difference between receiver differential code bias of the GPS and the other GNSS systems. The inter-system bias for GPS is equal zero;  is the difference between receiver differential code and phase biases;
is the difference between receiver differential code and phase biases; 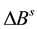 is the difference between satellite differential code and phase biases. As can be seen from Equation (1) to Equation (2), the un-calibrated biases such as
is the difference between satellite differential code and phase biases. As can be seen from Equation (1) to Equation (2), the un-calibrated biases such as 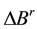 and
and 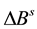 are lumped with the GNSS ambiguity parameters.
are lumped with the GNSS ambiguity parameters.
The IGS-MGEX precise orbital and clock products are used to mitigate the satellite orbit and clock errors [20] . The UNB3 tropospheric model, consisting of the Saastamoinen vertical propagation delay model and Niell mapping function, is used to account for the dry tropospheric component [21] . The effects of ocean loading, Earth tide, carrier-phase windup, sagnac, relativity, and satellite antenna phase-center variations are rigorously modeled as detailed in [22] . As a result, the mathematical model for the un-differenced GNSS ionosphere-free observations can be simplified to
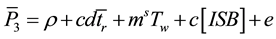 (3)
(3)
 (4)
(4)
where 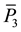 and
and  are the corrected pseudorange and carrier phase measurements, respectively
are the corrected pseudorange and carrier phase measurements, respectively 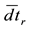 is receiver clock error lumped with GNSS receiver differential code bias;
is receiver clock error lumped with GNSS receiver differential code bias; 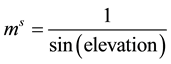 is the mapping
is the mapping
function for the troposphere wet delay component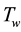 ; B is the float ambiguity in meters as described in Equation (2). To develop the mathematical equations for BSSD, we refer to the GNSS satellite by k. GPS satellite l is taken as the reference satellite to form tight BSSD ionosphere-free linear combination.
; B is the float ambiguity in meters as described in Equation (2). To develop the mathematical equations for BSSD, we refer to the GNSS satellite by k. GPS satellite l is taken as the reference satellite to form tight BSSD ionosphere-free linear combination.


It can be seen that the receiver clock offset is cancelled out when forming our BSSD mathematical equations. Additionally, the receiver differential code and phase biases are cancelled out for the GPS system observations while these receiver biases are reduced significantly for GLONASS and Galileo observations. However, forming BSSD leads to mathematical correlations among the observations, which must be taken into account when the covariance matrix of the observations is formed. Equations (3)-(6) are used to develop the measurement models of the proposed GNSS/INS integrated system for both un-differenced and between satellites single differences modes, respectively. However, due to the nonlinearity of GNSS observation models, the GNSS mathematical model should be expanded through Tylor Expansion to be employed in updating the tight PPP/INS integration as follows
For undifferenced GNSS ionsphere-free model;


And for BSSD GNSS ionosphere-free model:


where 


2.1. Inertial Navigation Motion Model
Inertial navigation is a method where the current position, velocity and attitude of a moving object are determined from a history of acceleration and angular velocity measurements. Acceleration and angular velocity are measured using accelerometers and gyros. Unlike GNSS systems, the INS performance is not affected in environments as urban canyons; it is independent of external electro-magnetic signals. However, the main drawback of an INS is the degradation of its performance with time. In order to control the errors to an acceptable level continues updates from, for example, GNSS are necessary.
The mathematical model of the inertial navigation system is commonly described in the framework of linear dynamic systems. The dynamic behavior of such systems can be described by using a state-space representation. For this purpose, a system of non-linear first-order differential equations can be described as [23] :

where 








The matrix 

The matrix 






2.2. GNSS-PPP/MEMS-Based IMU Implementation
To build the proposed GNSS/INS integrated navigation system, tightly coupled architecture is implemented adopting extended Kalman filter (EKF). GNSS pseudorange, carrier phase and Doppler measurements as well as INS-derived observations are processed to produce estimates of the state vector including position, velocity and attitude. The precise GNSS ephemerides as well as the outputs of position 

tial sensors mechanization are used to predict the INS pseudorange





differenced with the INS-predicted measurements. The residuals 















To implement the mechanization of the developed integrated system, the EKF is used as an estimator to merge the GNSS observations and INS records. The estimated state vector δx consists of 26 + n states describing the basic state vector including the nine navigation parameter errors, the inertial sensors errors including the bias drift and scale factor, and errors unique to the GNSS measurements, which are mainly the receiver clock offset and drift, the troposphere wet delay component, the GPS/GLONASS ISB and GPS/Galileo ISB with additional n states related to the float ambiguity parameters Bi. The complete state vector for un-differenced ionosphere-free technique can be written as.

where 









Figure 1. GNSS PPP/MEMS based IMU integration mechanism.
meters, respectively. Both 

EKF includes two parts the system model and the observation model. The system model is obtained from the INS dynamic errors augmented with the additional GNSS errors as follows.

where 



δZ is the measurement vector consisting of the differences between the corrected GNSS and the predicted INS measurements. When un-differenced ionosphere-free model is used δZ can be defined as:

H is the design matrix containing geometry factors defined according to the GNSS mathematical model used. The design matrix is arranged with columns corresponding to the states unique to inertial sensors errors such as




where d are the direction cosine matrix D elements for pseudorange and phase; s is the direction cosine matrix S elements for Doppler measurements. The Element of D and S can be computed as follows


where X, Y and Z are are the satellite coordinates computed using the final IGS-MEGX orbital products and corrected for the effect of earth rotation during signal transit; φ, λ and h are the INS positioning coordinates; N is the prime vertical radius of curvature. To form the BSSD measurement model, between-satellite single difference matrix 



where 


where 

2.3. Tests and Results Analysis
Two real vehicular tests were conducted to evaluate the performance of the developed integrated GNSS-PPP/ MEMS-based INS system (Figure 2). The vehicular tests were carried out through downtown Kingston, Ontario, Canada, which was designed to represent challenging situations for real GNSS satellite navigation availability including turns, straight portions, high speed, and slow speeds. The NovAtel SPAN-CPT system and the GNSS Trimble R10 receiver were used to collect the navigation data. The SPAN-CPT system consists of the NovAtel OEM4 receiver and a MEMS-based IMU, which contains three MEMS-based accelerometers and three fiber optic gyros. Carrier phase-based differential GNSS (DGNSS) solution is used as a reference solution. In order to create this reference solution, a GNSS Trimble R7 receiver was setup at a nearby station with precisely known coordinates. The raw dual-frequency GNSS pseudorange, carrier phase and Doppler measurements were collected at a 1 Hz rate, while the IMU raw data was logged at a rate of 100 Hz. The duration of the first trajectory test was set for about 55 minutes while the duration of the second test was 34 minutes. Four scenarios are considered in this research. The traditional GPS-based integrated system and the developed GNSS-based integrated system including GPS, GLONASS and Galileo, are studied to investigate the contribution of the additional GNSS systems to the positioning accuracy of the integrated system. Both un-differenced and BSSD ionosphere-free PPP techniques are adopted for GPS-based and GNSS-based integrated systems. To investigate the positioning accuracy of the integrated system during complete GNSS outages, a number of simulated outages is introduced for each trajectory test. The data were processed using our Ryerson PPP GNSS/MEMS software in un-difference and BSSD modes. The program is implemented in MATLAB R2013a using the Intel® Core i7-3517U CPU and 6 GB RAM. The computational burden of the whole process is 39.41 s including reading both INS and GNSS observations, Kalman filtering process with GNSS updating every second and results writing.
2.3.1. First Trajectory
The first trajectory test area is shown in Figure 3 with the locations of simulated outages. Figure 4 shows the GNSS satellite availability during the observation time.
Figure 2. Equipment setup.
Figure 3. Test area and simulated complete GNSS outages for the first trajectory.
Figure 5 shows the positioning accuracy of the developed integrated system when the observations of all GNSS satellites are included in the solution, i.e., no outages are inserted. It can be seen that the addition of GLONASS and Galileo observations enhances the positioning accuracy and convergence time in comparison with the GPS-only positioning solution. Further improvement is attained in the positioning solution through BSSD ionosphere-free linear combination model, in comparison with the traditional un-differenced counterpart.
Table 1 summarizes the statistical characteristics, mainly the root mean square error (RMSE) and the maximum error after the convergence time, for the four PPP integrated system scenarios mentioned above. Comparing the RMSE values for each scenario, it can be seen that the positioning precision is improved by 40%, 41% and 41% for latitude, longitude and altitude in the multi-constellation GNSS PPP solution compared with the GPS-only PPP solution. In addition, using BSSD ionosphere-free PPP technique improves the positioning precision case by 23%, 15% and 13% for latitude, longitude and altitude, in comparison with the traditional un-dif- ferenced ionosphere-free PPP technique.
To mimic challenging positioning conditions in urban areas, including complete blockage of the GNSS satellites, twelve simulated complete satellite outages of 60 s, 30 s and 10 s were introduced in the first trajectory.
Figure 4. GNSS satellites availability during the first trajectory test.
Figure 5. Positioning accuracy for the first trajectory, with no outages inserted.
Figure 6 shows the positioning errors during the various outages, referenced to carrier-based DGPS solution with full satellite availability. As can be seen, both of the un-difference and BSSD models produce similar positioning accuracy during the outages. In addition the contribution of the additional GNSS systems observation can be considered marginal, as the positioning error during a complete GNSS outage depends on the accuracy of the positioning solution just before the occurrence of outage. As well, the additional GNSS observations can only slightly improve the inertial sensor bias estimation, compared with that of GPS-only. In the 60-second GNSS outage the maximum positioning error reached meter level in most cases, while it reached a decimeter level in 10-seccond outage. Table 2 shows the average maximum positioning errors in latitude, longitude and
Figure 6. Positioning accuracy for the first trajectory, with simulated complete GNSS outages inserted.
Table 1. Statistical analysis of GNSS positioning precision for the first trajectory, with no outages inserted.
Table 2. Average maximum positioning errors during GNSS simulated outages for the first trajectory.
altitude, respectively, during the three simulated GNSS outages for both BSSD and un-differenced ionosphere- free models for the first trajectory.
2.3.2. Second Trajectory
The second trajectory test area is shown in Figure 7 with the locations of simulated outages. Similar to the first trajectory, the locations of the simulated outages were selected to present different driving conditions. The second trajectory is featured with higher vehicle velocities compared with the first trajectory. Figure 8 shows the satellite availability during the observation time.
Figure 9 shows the positioning accuracy for the developed integrated system when the observations of all GNSS satellites are included in the solution, i.e., no outages are inserted. Table 3 summaries the statistical analysis for the results of the four scenarios, as described earlier. It can be seen that the solution characteristics of the second trajectory are similar to those of the first trajectory, which confirms the consistency of the positioning solution.
Figure 7. Test area and simulated complete GNSS outages for the second trajectory.
Figure 8. GNSS satellite availability during the second trajectory test.
Figure 9. Positioning accuracy for the second trajectory, with no outages inserted.
Table 3. Statistical analysis of GNSS positioning precision for the second trajectory, with no outages inserted.
Eight simulated GNSS outages, each with duration of 60 s, 30 s and 10 s, respectively, were introduced such that they encompass all conditions of the trajectory, including straight portions and turns. Figure 10 shows the positioning errors during the GNSS simulated outages, which presents comparable positioning accuracy with the results of the first trajectory.
Table 4 shows the average maximum positioning errors in latitude, longitude and altitude, respectively during the three simulated GNSS outages for both BSSD and un-differenced ionosphere-free models for the second trajectory. Similar to those of the first trajectory, the average maximum positioning error reached meter level during the 60-second GNSS outage, while it reached a decimeter level in 10-seccond outage.
3. Conclusion
We developed new algorithms for the integration of multi-constellation GNSS PPP, including GPS, GLONASS and Galileo systems, and MEMS-based inertial system. Both un-differenced and between-satellite single difference ionosphere-free linear combinations of carrier phase and code GNSS measurements were considered. Tightly coupled mechanism was implemented and extended Kalman filter (EKF) technique was developed to merge the GNSS and inertial measurements. The performance of the newly developed models was analyzed by using two real trajectory tests. The positioning results of the integrated system showed that centimeter to
Figure 10. Positioning accuracy for the second trajectory, with simulated complete GNSS outages inserted.
Table 4. Average maximum positioning errors during GNSS simulated outages for the second trajectory.
decimeter-level accuracy was achievable when the GNSS satellite were available. The addition of GLONASS and Galileo observations enhanced the positioning accuracy in comparison with standalone GPS-based solution. Better positioning accuracy was obtained with BSSD IF model in comparison with the un-differenced IF model for both GPS- and GNSS-based models. During the GNSS outages, the integrated system showed meter-level accuracy in most cases when a 60-second outage was introduced. However, the positioning accuracy was improved to a few decimeter and decimeter-level accuracy when 30- and 10-second GPS outages were introduced. Comparable results were obtained from both BSSD and un-differenced models under GNSS outages.
Cite this paper
Mahmoud AbdRabbou,AhmedEl-Rabbany, (2015) Integration of Multi-Constellation GNSS Precise Point Positioning and MEMS-Based Inertial Systems Using Tightly Coupled Mechanization. Positioning,06,81-95. doi: 10.4236/pos.2015.64009
References
- 1. Zumberge, J.F., Heflin, M.B., Jefferson, D.C., Watkins, M.M. and Webb, F.H. (1997) Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. Journal of Geophysical Research, 102, 5005-5017. http://dx.doi.org/10.1029/96JB03860
- 2. El-Sheimy, N., Schwarz, K.P., Wei, M. and Lavigne, M. (1995) VISAT: A Mobile City Survey System of High Accuracy. Proceedings of The 8th International Technical Meeting of the Satellite Division of the Institute of Navigation, ION 1995, Institute of Navigation, Palm Springs, 12-15 September 1995, 1307-1315
- 3. Grejner-Brzezinska, D.A., Da, R. and Toth, C. (1998) GPS Error Modeling and OTF Ambiguity Resolution for High- Accuracy GPS/INS Integrated System. Journal of Geodesy, 72, 626-638.
http://dx.doi.org/10.1007/s001900050202 - 4. Petovello, M.G., Cannon, M.E. and Lachapelle, G. (2003) Benefits of Using a Tactical Grade INS for High Accuracy Positioning. Navigation, 51, 1-12.
http://dx.doi.org/10.1002/j.2161-4296.2004.tb00337.x - 5. Nassar, S. and El-Sheimy, N. (2005) Wavelet Analysis for Improving INS and INS/DGPS Navigation Accuracy. Journal of Navigation, 58, 119-134. http://dx.doi.org/10.1017/S0373463304003005
- 6. Cannon, M.E. (1992) Integrated GPS-INS for High-Accuracy Road Positioning. Journal of Surveying Engineering, 118, 103-117. http://dx.doi.org/10.1061/(ASCE)0733-9453(1992)118:4(103)
- 7. Shin, E.H., Niu, X.J. and El-Sheimy, N. (2005) Performance Comparison of the Extended and the Unscented Kalman Filter for Integrated GPS and MEMS-Based Inertial Systems. Proceedings of the 2005 National Technical Meeting of The Institute of Navigation, San Diego, 24-26 January 2005, 961-969.
- 8. Mezentsev, O. (2005) Sensor Aiding of HSGPS Pedestrian Navigation. Dissertation, University of Calgary, Calgary.
- 9. Abdel-Hamid, W., Abdelazim, T., El-Sheimy, N. and Lachapelle, G. (2006) Improvement of MEMS-IMU/GPS Performance Using Fuzzy Modeling. GPS Solutions, 10, 1-11.
http://dx.doi.org/10.1007/s10291-005-0146-6 - 10. Zhang, Y.F. and Gao, Y. (2008) Integration of INS and Un-Differenced GPS Measurements for Precise Position and Attitude Determination. Journal of Navigation, 61, 87-97.
http://dx.doi.org/10.1017/s0373463307004432 - 11. Shin, E.H. and Scherzinger, B. (2009) Inertially Aided Precise Point Positioning. Proceedings of ION GNSS 2009, Institute of Navigation, Savannah, 22-25 September 2009, 1892-1897.
- 12. Rabbou, M.A. and El-Rabbany, A. (2014) Tightly Coupled Integration of GPS Precise Point Positioning and MEMS- Based Inertial Systems. GPS Solutions, 19, 601-609.
http://dx.doi.org/10.1007/s10291-014-0415-3 - 13. Du, S. and Gao, Y. (2010) Integration of PPP GPS and Low Cost IMU. The 2010 Canadian Geomatics Conference and Symposium of Commission I, ISPRS, Calgary, 15-18 June 2010.
http://www.isprs.org/proceedings/XXXVIII/part1/09/09_04_Paper_19.pdf - 14. Rabbou, M.A. and El-Rabbany, A. (2015) Integration of GPS Precise Point Positioning and MEMS-Based INS Using Unscented Particle Filter. Sensors, 15, 7228-7245.
http://dx.doi.org/10.3390/s150407228 - 15. Kjørsvik, N.S., Gjevestad, J.G.O., Brøste, E., Gade, K. and Hagen, O.K. (2010) Tightly Coupled Precise Point Positioning and Inertial Navigation Systems. International Calibration and Orientation Workshop EuroCOW 2010, Castelldefels, 10-12 February 2010.
- 16. Rabbou, M.A. and El-Rabbany, A. (2014) Non-Linear Filtering for Precise Point Positioning GPS/INS Integration. International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences, XL-2, 127-132. http://dx.doi.org/10.5194/isprsarchives-XL-2-127-2014
- 17. Roesler, G. and Martell, H. (2009) Tightly Coupled Processing of Precise Point Position (PPP) and INS Data. Proceedings of ION GNSS 2009, Institute of Navigation, Savannah, 22-25 September 2009, 1898-1905.
- 18. Rabbou, M. and El-Rabbany, A. (2014) Tightly Coupled Integration of GPS-PPP and MEMS-Based Inertial System Using EKF and UKF. Proceedings of FIG Congress 2014, Engaging the Challenges, Enhancing the Relevance, Kuala Lumpur, 16-21 June 2014, 1-11.
- 19. Rabbou, M.A. and El-Rabbany, A. (2015) Precise Point Positioning Using Multi-Constellation GNSS Observations for Kinematic Applications. Journal of Applied Geodesy, 9, 15-26.
http://dx.doi.org/10.1515/jag-2014-0021 - 20. Montenbruck, O., Steigenberger, P., Khachikyan, R., Weber, G., Langley, R.B., Mervart, L. and Hugentobler, U. (2014) IGS-MGEX: Preparing the Ground for Multi-Constellation GNSS Science. Inside GNSS, 9, 42-49.
- 21. Leandro, R.F., Langley, R.B. and Santos, M.C. (2008) UNB3m_pack: A Neutral Atmosphere Delay Package for Radiometric Space Techniques. GPS Solutions, 12, 65-70.
http://dx.doi.org/10.1007/s10291-007-0077-5 - 22. Kouba, J. (2009) A Guide to Using International GNSS Service (IGS) Products. International GNSS.
- 23. Jekeli, C. (2001) Inertial Navigation Systems with Geodetic Applications. Walter de Gruyter, Berlin.
http://dx.doi.org/10.1515/9783110800234


























