Received 5 May 2015; accepted 14 July 2015; published 20 July 2015

ABSTRACT

Precise Point Positioning (PPP) is traditionally based on dual-frequency observations of GPS or GPS/GLONASS satellite navigation systems. Recently, new GNSS constellations, such as the European Galileo and the Chinese BeiDou are developing rapidly. With the new IGS project known as IGS MGEX which produces highly accurate GNSS orbital and clock products, multi-constellations PPP becomes feasible. On the other hand, the un-differenced ionosphere-free is commonly used as standard precise point positioning technique. However, the existence of receiver and satellite biases, which are absorbed by the ambiguities, significantly affected the convergence time. Be- tween-satellite-single-difference (BSSD) ionosphere free PPP technique is traditionally used to cancel out the receiver related biases from both code and phase measurements. This paper introduces multiple ambiguity datum (MAD) PPP technique which can be applied to separate the code and phase measurements removing the receiver and satellite code biases affecting the GNSS receiver phase clock and ambiguities parameters. The mathematical model for the three GNSS PPP techniques is developed by considering the current full GNSS constellations. In addition, the current limitations of the GNSS PPP techniques are discussed. Static post-processing results for a number of IGS MGEX GNSS stations are presented to investigate the contribution of the newly GNSS system observations and the newly developed GNSS PPP techniques and its limitations. The results indicate that the additional Galileo and BeiDou observations have a marginal effect on the positioning accuracy and convergence time compared with the existence combined GPS/GLONASS PPP. However, reference to GPS PPP, the contribution of BeiDou observations can be considered geographically dependent. In addition, the results show that the BSSD PPP models slightly enhance the convergence time compared with other PPP techniques. However, both the standard un-differenced and the developed multiple ambiguity datum techniques present comparable positioning accuracy and convergence time due to the lack of code and phase-based satellite clock products and the mathematical correlation between the positioning and ambiguity parameters.

Keywords:

GNSS, PPP, GPS, GLONASS, Galileo, BeiDou, BSSD, Multiple Ambiguity Datum

1. Introduction

Precise Point Positioning has been studied by a number of research groups in the last two decades (e.g. [1] and [2] ). To speed up the PPP solution convergence time, a number of PPP ambiguity resolution techniques have been developed [3] - [5] . PPP has been used in a number of applications, including precise surveying, disaster monitoring, offshore exploration, and others [6] - [8] . Commonly, in precise point positioning (PPP), the un-dif- ferenced ionosphere free linear combination of GPS and GLONASS code and phase measurements are used to cancel out the first order ionospheric effect [9] - [11] . The satellite orbits and clock errors can be accounted for using IGS precise orbital and clock products. The GPS/GLONASS inter-system bias can be considered as additional unknown in addition to the receiver clock bias. The tropospheric error component can be modeled sufficiently by using number of empirical models such as Saastamoinen and Hopfield models or can be accounted for by using regional tropospheric correction models such as the NOAATrop model [12] . The effects of ocean loading, earth tide, carrier-phase windup, sagnac, relativity, and satellite antenna phase-centre variations can be rigorously modeled [13] . However, the major drawback of the standard technique is the long convergence time to reach to centimeter positioning accuracy due to the satellite geometry in addition to the improper modeling of errors and biases, such as the satellite and receiver code biases. The satellite geometry can be enhanced by adding the newly constellation satellites system namely the European navigation satellite system (Galileo) and the Chinese navigation satellite system (BeiDou). The additional observations can enhance the satellite geometry and reduce the convergence time of the PPP [11] [14] [15] .

On the other hand, the satellite code bias is lumped to the phase ambiguity parameters and as one receiver clock unknown is used in both code and phase measurements, the receiver code bias is also absorbed by the ambiguity parameters. To completely cancel out the receiver related biases from both code and phase GNSS observations, between-satellite-single-difference (BSSD) ionosphere-free PPP technique can be used [16] . In GNSS constellations level, multiple GNSS satellites are used as references. However, in BSSD technique, the satellite differential code biases are still affecting the phase ambiguities due to the dissimilarities of satellites code biases which are produced from the signals spectrum dissimilarities in the filtering and correlation processes [17] . One of the major drawbacks of this technique is minimum two satellites should be available in each GNSS system which is still not guaranteed especially for Galileo and BeiDou systems.

Collins et al. (2010) developed a new PPP technique known as the decoupled clock (DC) PPP technique. This technique used fixed ambiguity datum technique to separate the code and phase receiver clocks with introducing new phase receiver clock. Additional satellite fixed ambiguity datum technique is used in network analysis to produce phase clock corrections which allows for the satellite hardware delays and satellite initial carrier-phase bias to be lumped to the GPS satellite clock phase corrections [3] . In addition code based clock corrections are also produced combined by time-varying satellite code biases. With the decoupled clock corrections, the un- differenced ambiguity resolution becomes feasible [18] . However, in multi-constellations PPP level, multiple ambiguity datum (MAD) are needed considering the multiple GNSS receiver clocks differences. Unfortunately, up to date, there no code and phase based clock corrections available for the GNSS constellations. As a result, this research will develop the mathematical equations for this technique in the scale of GNSS and investigate only the impact of separating the receiver biases from the phase measurements on the PPP convergence time. The mathematical model for the standard undifferenced, BSSD and MAD PPP techniques are developed in the scale of the full GNSS constellations, including GPS, GLONASS, Galileo and BeiDou. Also, this research will discuss the current limitations of the current GNSS PPP techniques based on their mathematical models and the current availability of GNSS products. Data collected from a number of MGEX GNSS stations are processed. The developed GNSS PPP techniques are assessed based on the convergence time and the positioning accuracy results.

2. GNSS Observations Equations

The general ionosphere-free equations for pseudorange and carrier-phase can be written as ( [19] and [20] )

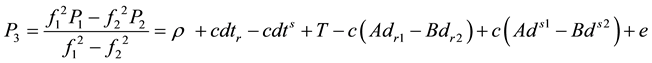(1)

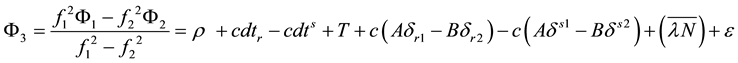(2)

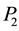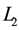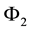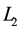where and are GNSS pseudorange measurements on and, respectively; and are the GNSS carrier phase measurements on and, respectively; and 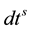are the clock errors for receiver and satellite, respectively; 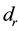and 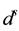are frequency-dependent code hardware delay for receiver and satellite, respectively; and 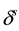are frequency-dependent carrier phase hardware delay for receiver and satellite, respectively; e, ε are relevant system noise and un-modeled residual errors; and is the ambiguity term for phase measurements. For the un-differenced ionosphere free linear combination, this term is not integer due to

the non-integer nature of the combination coefficients, , where and are the

and non-integer ambiguity parameters, including the initial phase biases at the satellite and the receiver, respectively; and are the wavelengths of the and carrier frequencies, respectively; c is the speed of light in vacuum; T is the tropospheric delay component; ρ is the true geometric range from the antenna phase center of the receiver at reception time to the antenna phase center of the satellite at transmission time. A

and B are frequency dependent factors and.

2.1. Standard Un-Differenced GNSS PPP Technique

Using Equations (1) and (2) and considering GPS time as a reference time system, the un-differenced ionosphere-free linear combinations of GPS, GLONASS, Galileo and BeiDou observations can be written as [11]

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

where G, R, E and C refer to GPS, GLONASS, Galileo and BeiDou systems observations, respectively; ISB is the inter-system bias;, are ionosphere-free differential code biases for receiver and satellites, respectively; is the difference between receiver differential code and phase biases; is the difference between satellite differential code and phase biases. As can be seen from Equations (7) to (10), the un-calibrated biases such as and are lumped with the ambiguity parameters. Table 1 shows the mathematical equations for the different GNSS biases.

2.2. Between Satellites Single Difference GNSS PPP Technique

To completely remove the receiver related biases from both the code and phase GNSS observations, between

satellite-single-difference (BSSD) ionosphere-free PPP technique can be used for combined GNSS observations model. For each system, a reference satellite is selected while the other GNSS satellites observations are subtracted from it. To develop the mathematical equations of BSSD technique, four GNSS satellites are selected mainly GPS l, GLONASS m, Galileo n and BeiDou o, to be reference satellites to the four constellation systems observations. Following [11] , GNSS-BSSD model can be written as.

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

As can be seen from Equations (19) to (26) that the receiver related code and phase biases, receiver clocks and inter-system biases are completely removed. However, the mathematical correlation between the observations should be taken into account when forming the observation weighted matrix for this model [16] .

2.3. Multiple Ambiguity Datum (MAD) GNSS PPP Technique

To remove the effect of the receiver and satellite code biases from GNSS phase measurements, ambiguity-fixed datum technique can be used to separate the code and phase receiver clocks. This can be done by fixed one of the satellite ambiguity by arbitrary number [3] . In this case, the receiver clock combined with the fixed satellite ambiguity will be considered as a receiver clock reference for other phase observations receiver clocks. The undifferenced mathematical model can be reformatted by lumping the ambiguity of a reference satellite to the phase receiver clock assuming the ambiguity parameter of the reference satellite is zero. In multi-constellation GNSS combination, the difference between the GNSS receiver code biases is also lumped to the inter-system biases as clarified in Table 1. As a result, multiple reference satellites are needed to separate the ISBs of code and phase measurements. In this model, the phase receiver clock model will be shifted by the ambiguity parameter of the selected GPS reference satellite leading to code biases free. Also the phase inter-system biases ISPB will be lumped by the differences between the ambiguities of the GPS reference satellite and the other GNSS reference satellites and it will be also code biases free. The mathematical model for MAD PPP technique can be written as follows.

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

where and are the code and phase receiver clocks respectively, and are the code and phase satellite clocks respectively, ISPB and ISCB are the code and phase inter-system biases respectively, 1 and 2 refers to the satellite number from each GNSS system. The new phase receiver clock unknown will be

which in role makes the ambiguities for the remaining GPS satellite phase observations are the

difference between the GPS satellite ambiguity and the GPS reference satellite ambiguity,. As can been seen, only one phase receiver clock unknown is considered for all GNSS constellations, as a result, for other GNSS observations the GPS reference satellite ambiguity will be com

bined with the phase inter-system bias ISPB. To avoid system singularity, other ambiguity-datum is needed for each system. For each system, the ambiguity of the GNSS reference satellite will be combined with the ISPB as a result the phase inter-system bias for a GNSS system will be shifted by the difference between the

GPS and the GNSS system reference satellites,. The ambiguities for the remaining GNSS satellites will be the difference between the GNSS satellite ambiguity and the GNSS reference satellite ambiguity where j refers to the GNSS system,.

It can be seen that from the MAD PPP phase observation equations that the receiver and satellite code biases are eliminated. However, some limitations should be clarified in the current GNSS PPP techniques.

3. Current limitations of GNSS PPP Techniques

Based on the mathematical equations presented in the traditional un-differenced PPP technique, it can be noticed that there is a coupling between the positioning parameters in the code and phase measurements due to the underdetermined nature of the phase observations. In other words, as we cannot estimate the positioning parameters from the phase measurements only due to the existence of the ambiguity parameters, the code measurements are needed to aid in estimating the positioning parameters till reaching to correct resolved ambiguity parameters. Up till reaching to correct ambiguity parameters with continuous decreasing of the ambiguity uncertainty (reducing ambiguity variances with time), the estimation filter is converting with time to estimate precise positioning parameters from the precise phase measurements. During this period, which is called as the convergence time, the receiver and satellite code biases and their stochastic nature highly contribute on the estimated positioning parameters. Due to the mathematical correlation between the ambiguities and the positioning parameters, the ambiguities are highly affected by these code biases in addition to the phase biases as can be seen in Equations (7) to (10). Combining code and phase biases to the ambiguities is leading to increasing the time to reach to correct resolved ambiguity parameters.

To enhance the convergence time of the current PPP positioning solution which as mentioned above is highly affected by the quality of the code observations, the code measurements should be improved by eliminating or modeling the receiver and satellite code biases. The receiver code and phase biases can be completely eliminated by applying BSSD technique as can be seen in Equations (11) to (18). Theoretically, both the un-differenced and BSSD techniques are statistically identical, assuming that the stochastic characteristics of the time-varying nature of the receiver code biases are modelled perfectly or the receiver code bias and the positioning parameters are mathematically uncorrelated. Due to the imperfection of the stochastic modelling of the receiver biases, its time-varying nature is affecting the positioning parameters (and the ambiguities) which is leading to a poorer precision solution (longer convergence time) for the un-differenced technique than the BSSD solution. However, the enhancement in convergence time of the BSSD is limited due to the time-varying nature of the satellite code biases. In addition, the differencing process applied to the GNSS observations will increase the noise ration of the difference observations. As the satellite code biases cannot be eliminated similar to the receiver code biases, it should be modeled or combined to the satellite clock corrections.

The IGS and MGEX-IGS clock products are already combined with the satellite code biases. However, these products are only combined with constant satellite code biases due to the combined code-phase measurement estimation and the smoothing process applied. Figure 1 shows a comparison between the phase-based clock corrections obtained from Natural Resources Canada (NRCan), and the IGS clock corrections for August 3, 2008. It can be noticed that the IGS clock correction is phase-based smooth clock version. As a result, the current IGS clock products cannot simulate the time-varying satellite code biases affect the pseudorange measurements in the user model. To overcome this limitation, satellite code based clock corrections combined with time-varying satellite code biases should be estimated and used as a satellite clock corrections for only the pseudorange measurements in the MAD PPP technique. On the other hand, to preserve the integrity nature of the ambiguity

parameters, phase based satellite clock corrections should be estimated and employed as a satellite clock correction for the phase measurements only. Similar to the traditional IGS clock products, the phase based clock corrections will be combined with a constant bias which is the ambiguity of the reference satellite used in the network analysis. However, in contrast to the IGS clock products, this bias can be kept to be integer value (combination of integer values on L1 and L2) to preserve the integrity nature of the ambiguity parameters for the used model (Collins et al. 2010).

Based on the discussion above, combining the BSSD technique which removes the receiver code biases with multiple ambiguity datum considering code, and phase based clock corrections will significantly reduce the convergence time and enhance the ambiguity resolution. However, currently, these clock products are not available for the GNSS constellations. As the traditional IGS MGEX clock products are employed in MAD technique, the code observations used in both the standard technique and the MAD technique will be statistically the same. As a result, the convergence time in both techniques should be comparable. In contrast, at present, the BSSD technique may provide shorter convergence time compared with the un-differenced and MAD techniques based on the balance between the eliminations of the time-varying receiver code biases and the higher noise ration expected of the difference observations. Due to the lack of phase and code based products, currently combining the MAD and BSSD techniques will not present also shorter convergence time. To clarify the theoretical mathematical models introduced in this research analytically, a comparison between the three PPP techniques is presented in the next section.

4. Analysis and Results

To investigate the contribution of the newly GNSS observations, GNSS data from four IGS MGEX stations are processed namely, CUT0, BRST, DLF1 and UNB at DOY 305, 2013. The input data are the un-differenced first- order ionosphere-free linear combination of GNSS code and carrier-phase measurements. The IGS MGEX precise orbit and clock products are employed to account for orbital and clock errors [21] . Tropospheric errors are accounted for using the UNB3 model [22] . All remaining errors, including carrier-phase windup, relativity, Sagnac, earth tides, and ocean loading are corrected for with sufficient accuracy by using existing models [13] .

Figure 2 and Figure 3 show the positioning error results and the GNSS satellite availability for CUT0 and UNB stations, respectively, as examples. As can be seen that compared with the existence combined GPS/ GLONASS PPP positioning solution, the additional Galileo and BeiDou observations have a marginal effect on the positioning accuracy and convergence time. The insignificant effect is due to the sufficient number of GNSS satellite observations originally available from both GPS and GLONASS. To assess the contribution of the new GNSS observations compared to the GPS PPP positioning accuracy, both GPS/Galileo and GPS/BeiDou are shown in comparison with the GPS only PPP. Due to the limited number of Galileo satellites, the contribution of Galileo observations can be considered insignificant on enhancing the GPS PPP positioning accuracy and convergence time. However, the contribution of BeiDou observations can be considered significant in some station such as CUT0 when sufficient number of satellites is available in contrast with the UNB station with maximum three BeiDou satellites available. As a result, the contribution of BeiDou can be considered geographically dependent. Figure 4 summarizes the positioning accuracy after two hours of GNSS observation processing for the different GNSS combinations. It can be noticed that two to four centimeters enhancement in multi-constellation GNSS positioning accuracy is detected compared with the GPS positioning accuracy.

To test the developed GNSS PPP techniques, namely the standard un-differenced, multiple ambiguity datum (MAD) and BSSD ionosphere-free techniques, further GNSS data from four MGEX IGS stations are processed namely BRST, BRUX, FAA1 and GMSD at DOY 1, 2014. Figure 5 and Figure 6 show the positioning accuracy with time and a comparison among the un-differenced, code and phase receiver clock estimation biases for stations BRST and BRUX, respectively, as examples.

Although the MAD technique theoretically separates the receiver code and phase clock estimations as clarified in Section 2.3, both the standard un-differenced and MAD ionosphere-free techniques show comparable positioning accuracy and convergence time. This is due to the mathematical correlations between the positioning and clocks-ambiguities parameters as clarified in Section 3. These correlations can be clearly noticed when comparing the phase and un-differenced clocks estimations in Figure 5 and Figure 6. It can be clearly seen that during the convergence time the phase clock estimation is affected by the fluctuations in code measurements as

a result, the phase clock behavior during this period is comparable to the code and un-differenced clock behavior. On the other hand, the BSSD model shows slight improvements in convergence time compared with other GNSS PPP techniques. The advantage of using the BSSD model is that the BSSD model completely removes the receiver biases from both code and phase measurements. As a result, the code contributions on positioning estimations are enhanced due to elimination of receiver code biases, which in role enhance the ambiguities estimations

as clarified in Section 3. In addition, further enhancements on ambiguities come from removing the receiver phase biases. However, as can be seen in Figure 7, the positioning accuracy after one hour of processing GNSS observations for the three techniques are comparable due to the statistical similarity between the BSSD and un-differenced techniques after the convergence time as clarified in Section 3.

5. Conclusion

In this paper, three GNSS PPP techniques, namely the un-differenced, between satellite single difference (BSSD) Multiple Ambiguity Datum (MAD) ionosphere-free PPP techniques were developed to process the multi-con- stellations GNSS observations. In multiple ambiguity datum technique, the phase and code clocks were theoretically separated by introducing phase clock parameter biased by the reference satellite ambiguity. The BSSD model cancelled out the receiver related biases and errors from both GNSS code and phase measurements. The IGS MGEX clock and orbital products were used to correct for the satellite clock and orbital errors. GNSS data produced from a number of MGEX stations was used to investigate the accuracy and convergence time for the different PPP techniques. Also, the contribution of the additional Galileo and BeiDou systems observations on the traditional GPS/GLONASS PPP positioning accuracy and convergence time was investigated. The results showed that the contribution of Galileo observations could be considered marginal on enhancing both the GPS and GPS/GLONASS PPP positioning accuracy and convergence time due to the limited Galileo observations. However, the contribution of BeiDou observations can be considered geographically dependent based on the BeiDou satellite availability in each station. The multiple ambiguity datum (MAD) GNSS PPP technique presented comparable convergence time compared with the standard un-differenced technique due to the lack of code and phase-based satellite clock products and the mathematical correlation between the positioning and clock-ambiguity parameters. However, the BSSD model was slightly improved the convergence time compared with other techniques. Moreover, the three GNSS PPP techniques showed comparable positioning accuracy after one hour of GNSS observations processing.

Cite this paper

Mahmoud AbdRabbou, (2015) Multiple Ambiguity Datum Precise Point Positioning Technique Using Multi-Constellation GNSS: GPS, GLONASS, Galileo and BeiDou. Positioning,06,32-43. doi: 10.4236/pos.2015.63004

References