Positioning
Vol.4 No.3(2013), Article ID:36346,13 pages DOI:10.4236/pos.2013.43023
Map Aided Pedestrian Dead Reckoning Using Buildings Information for Indoor Navigation Applications
![]()
Mobile Multi-Sensor Systems Research Group, Department of Geomatics Engineering, University of Calgary, Calgary, Canada.
Email: maaattia@ucalgary.ca
Copyright © 2013 Mohamed Attia et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 23rd, 2013; revised July 18th, 2013; accepted July 31st, 2013
Keywords: Indoor Navigation; Map Matching; Geospatial Data Model; Pedestrian Dead Reckoning (PDR)
ABSTRACT
Navigation systems play an important role in many vital disciplines. Determining the location of a user relative to its physical environment is an important part of many indoor-based navigation services such as user navigation, enhanced 911 (E911), law enforcement, location-based and marketing services. Indoor navigation applications require a reliable, trustful and continuous navigation solution that overcomes the challenge of Global Navigation Satellite System (GNSS) signal unavailability. To compensate for this issue, other navigation systems such as Inertial Navigation System (INS) are introduced, however, over time there is a significant amount of drift especially in common with low-cost commercial sensors. In this paper, a map aided navigation solution is developed. This research develops an aiding system that utilizes geospatial data to assist the navigation solution by providing virtual boundaries for the navigation trajectories and limits its possibilities only when it is logical to locate the user on a map. The algorithm develops a Pedestrian Dead Reckoning (PDR) based on smart-phone accelerometer and magnetometer sensors to provide the navigation solution. Geospatial model for two indoor environments with a developed map matching algorithm was used to match and project navigation position estimates on the geospatial map. The developed algorithms were field tested in indoor environments and yielded accurate matching results as well as a significant enhancement to positional accuracy. The achieved results demonstrate that the contribution of the developed map aided system enhances the reliability, usability, and accuracy of navigation trajectories in indoor environments.
1. Introduction
Maps have been used for centuries to transit users from one place to another. In the last decade, navigation devices have used digital maps to locate the position of the user and assist in providing navigational directions. Recently, maps have become more than just a visualization tool in navigation systems; they are now an aiding tool for enhancing the reliability of the obtained navigation solutions.
Many navigation tools now, rely on digital maps as the primary media for displaying navigation information to the user. These applications usually use a navigation system consisting of a GPS receiver, a map and a geospatial database. Although these systems usually provide accurate positioning information, they can only do so in GPSfriendly environments. Navigation in GPS-denied environments, such as indoor facilities, usually has difficulty maintaining accurate positioning information due to GPS signal blockage and multipath. The performance of these systems can be improved by integrating other navigation sensors such as INS. Although useful in some cases, the drift in position errors over time due to errors in inertial sensors significantly reduces the reliability of this solution in some applications.
In this paper, map aiding navigation techniques are designed to assist navigation applications in indoor environments. The developed techniques are based on the integration of PDR navigation algorithm and geospatial data models which depend on the working environment of the user. Improving the performance of navigation systems through the implementation of additional sensors or the application of certain constraints has proven helpful in enhancing the navigation solution. In this paper, the geospatial data models for the navigated environments will be used to provide the navigation system with additional updates and boundaries. The model uses geometrical and topological information such as connectivity and proximity to help the navigation system locate the user by map matching techniques. Map matching in this case has the advantage of assisting the navigation solution by providing a logical threshold of where the user could be, forcing the navigation solution to be in certain regions. This map matching algorithm will fuse several measurements and constraints such as user position and direction to produce a better estimation for the correctly navigated passageway link. One of the main concepts in map aiding systems is that the objective of the navigation system shifts from obtaining high position accuracy information to obtaining positions with enough accuracy to allow the system to select the correct link.
The accuracy of map aiding navigation systems depends on the navigation systems used. The errors from any navigation system can produce an incorrect link selection, which could lead to a complete failure in locating the user on the appropriate link. As a result, it is not just the purpose of good algorithm, but the requirement of a reliable and accurate position solution, to assist the algorithm in selecting the appropriate link. Different navigation systems are available for pedestrian navigation applications. GPS is still the most commonly used sensor in navigation systems. It provides accurate and reliable position and velocity estimates depending on the availability of a GPS signal. Unfortunately, GPS performance in low signal environments such as indoor facilities is not reliable enough for many navigation applications. Advances in Micro-Electro Mechanical System (MEMS) technology, combined with the miniaturization of electronics, have made it possible to produce chip-based inertial sensors for use in measuring angular velocity and acceleration [1]. These chips are small, lightweight and consume very little power. As a result, they have been used in a wide range of applications in the automotive, indoor navigation and other industrial applications. MEMS technology, therefore, can be used to develop navigation systems (for outdoor or indoor environments) that are inexpensive, small, and consume very little power [2]. Today’s smart-phones contain MEMS accelerometers, magnetometers and gyroscopes, and although they are included for other purposes such as screen orientation or as a pedometer, they can be used for navigation application. In this paper, a PDR algorithm utilizing the smart-phone sensors is developed. Since MEMSbased INS systems typically exhibit very high positional drift when working in the stand-alone mode, in this paper, a map aiding system using map matching algorithm with the geospatial data model for the indoor facility is used to aid the PDR navigation solution.
The paper is outlined in the following format: Section 2 introduces the developed geospatial model for the indoor facilities; Section 3 describes the developed map matching algorithm; Section 4 discusses the PDR algorithm; Section 5 describes the integration of the three previous sections to build the map aided PDR system; Section 6 describes the field tests performed to evaluate the developed map aided system and presents the obtained results.
2. Geospatial Data Model
The geospatial data models are simply GIS maps with specific attributes required for a particular application. In navigation applications, maps and their attributes have several roles in the different stages of a navigation process. The main role and the most commonly used, is the visualization role. The map is used to present the user location and direction, as well as any other required navigation states such as velocity and orientation. In addition, and since the map can include many relevant attributes for roads and passageways, it can be used for aiding the navigation solution by implementing a logical threshold based on the geospatial model. Other attributes for other features, such as buildings, rooms, stores, and utilities are essential for many other location-based service applications. The map used for navigation should include several layers based on the region and the exact application. Selection of the specific required layer and its associated attributes is a critical issue in designing the geospatial model.
The developed map aided navigation system will use two geospatial models to evaluate the performance of the system. The geospatial model for indoor application will represent the links as polylines connecting nodes. The links will represent the possible passageways (corridors) where the user could be located in. According to the indoor navigation applications, linking the location of the user to the nearest passageway can achieve the accuracy of most of the required application such as E911, personal navigation, law-enforcement and handicapped. The attached attributes include a height change factor which plays an important role in indoor applications. Height change by stairs and elevation will lead to changing the navigated floor map; therefore the system must provide all information about both height values and places where height change can occur. Other relevant attributes such as link nodes, nodes coordinates, and all possible links diverged from each link in the straight, right and left directions, stairs, and elevators are created.
The next two sections present the geospatial model for two different locations. Both locations are located at the University of Calgary Campus. The input for both datasets is GIS shape files of the ESRI ArcGIS GIS software (provided by the University of Calgary Maps Library (UCMAPS). The used geographical coordinate datum is GCS (Geographic Coordinate system) North American 1983. The projected coordinate system used is NAD (North American datum) 1983 UTM (Universal Transverse Mercator) Zone 11N with Transverse Mercator Projection.
2.1. Geospatial Model for the Engineering Building at University of Calgary
In order to assist the map aided navigation systems for indoor applications, a modeling for the building floor information was developed. The first study area, where field tests will be performed, is the Engineering building at the University of Calgary campus. Both geometrical and topological characteristics for the building were implemented in the geospatial model [3]. The model considered main characteristics such as the passageways length, location, alignment, and the connectivity. The geospatial model itself is implemented through the three main modeling phases; conceptual, logical and physical modeling. Conceptually, the model assumes that users would be located at any time through a passageway (the corridors located in building floors), which would be geometrically modeled as polylines locates at the centerline of each corridor. The passageways cover all possible corridors and stairways. If the user enters any room, the system will locate the user on the corresponding nearest corridor. The passageways polylines (would be called as links) are connecting two points of known coordinates (would be called as nodes). Figure 1 presents the geo-
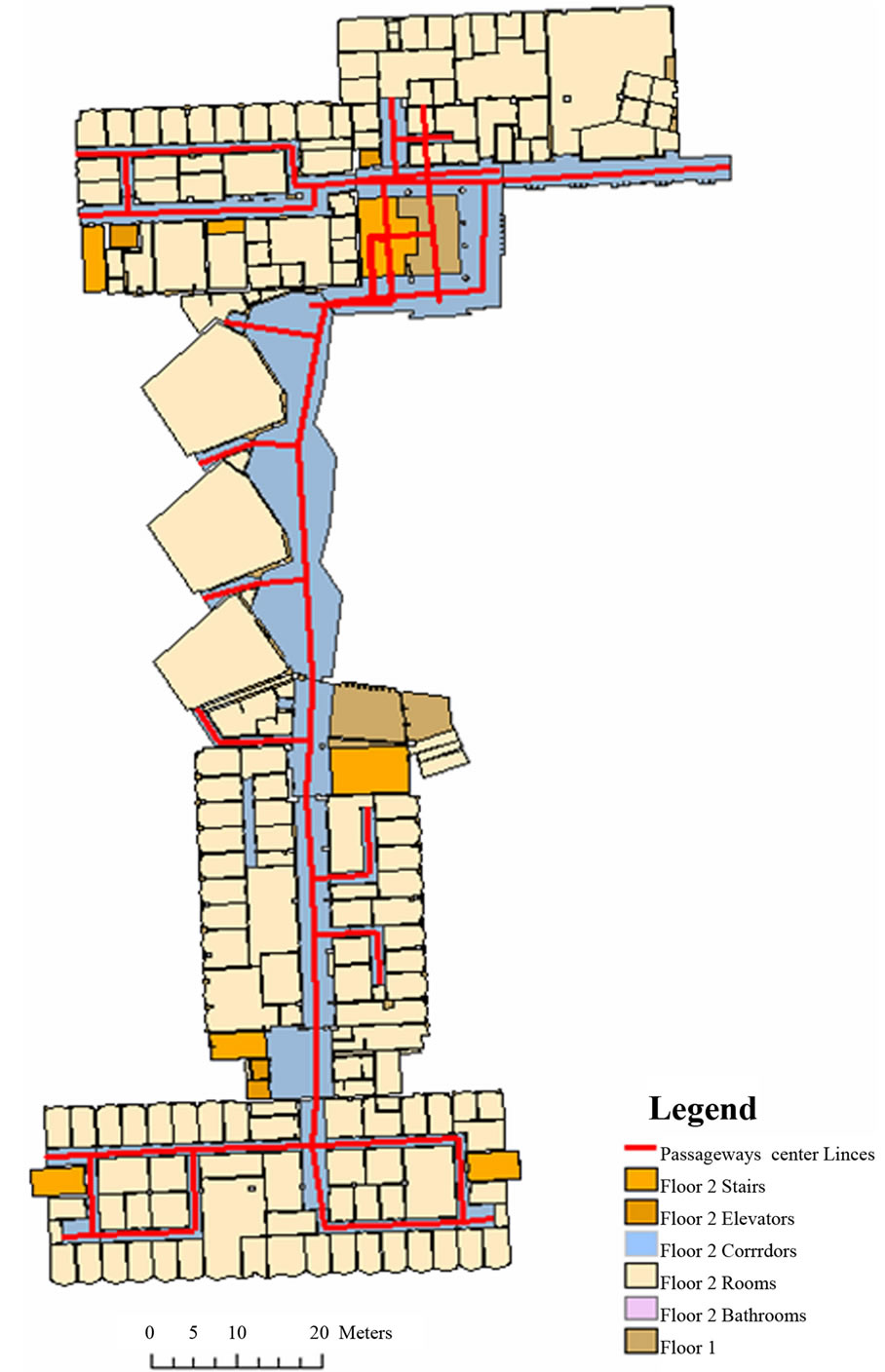
Figure 1. Geospatial model for the engineering building at university of calgary.
metrical layout for the geospatial model for the building.
The logical model, deals with the relational database, where each passageway is defined through several attributes. Table 1 presents a sample for the links database table for the engineering building. As shown in the table, each passageway should be defined by a unique identification number (ID), both its start and end (destination) nodes UTM coordinates, passageway length, floor number, and if there is a stairs on any of its sides. In addition, and to enable the turn detection algorithm inside the map aiding system, each passageway is provided by the identification number for all possible diverged passageways from both its start and end nodes.
Diverged passageways are divided to the three directions right turn, left turn, and straight direction. The physical model, which deals with internal structure of data objects by transferring the logical model into implementation, was performed using the GeoDatabase of ArcGIS software. The geospatial model was created using ArcGIS feature classes for each layer, i.e. corridors, rooms, stairs, .etc, where all are categorized under a georeferenced GeoDatabase with UTM projected northing and easting.
2.2. Geospatial Model for MacEwan Hall and Kinesiology Buildings at University of Calgary
The second study area, where field tests are performed, is the MacEwan Hall and Kinesiology building at the University of Calgary campus. Similar to the Engineering building both geometrical and topological characteristics were implemented in the geospatial model. The model considered main characteristics such as the passageways length, location, alignment, and the connectivity. The geospatial model itself is done through the three main modeling phases; conceptual, logical and physical modeling. Figures 2 and 3 present the geometrical layout for the geospatial model for MacEwan Hall and Kinesiology Building floors (1) and (2) respectively.
3. Map Matching Algorithm
There are several applicable map matching algorithms which can be classified according to their accuracy and concept [4]. Generally, there are three types for map matching; geometrical and topological algorithms, probability algorithms and advanced algorithms such as using fuzzy logic, belief theory and Bayesian networks [5-8] . The main difference between these categories is the methodology in selecting the matching link where the position will be projected on. Each algorithm uses certain inputs (position fix, velocity, heading, etc.) and performs certain logic (minimum distance, weighting between inputs, historical user’s location information, etc) in order
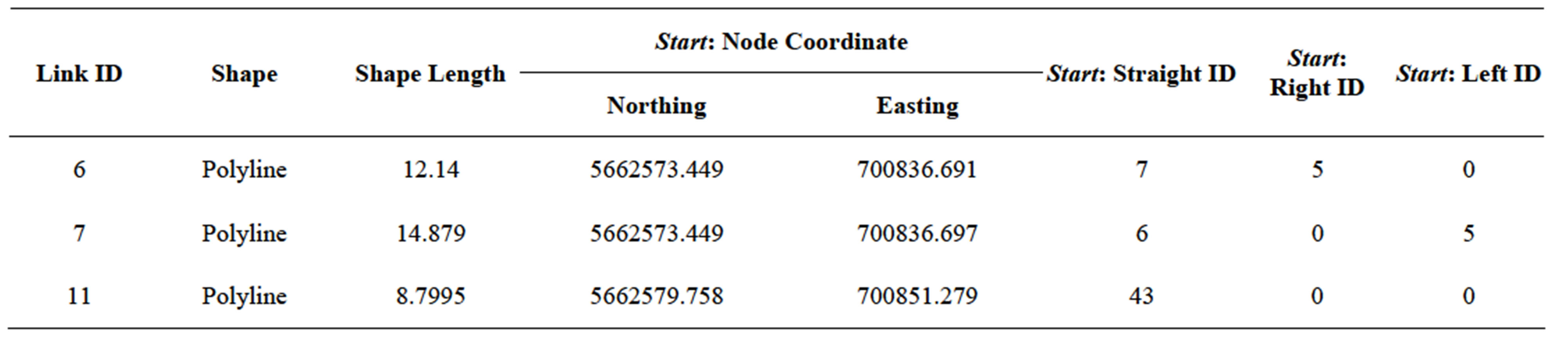
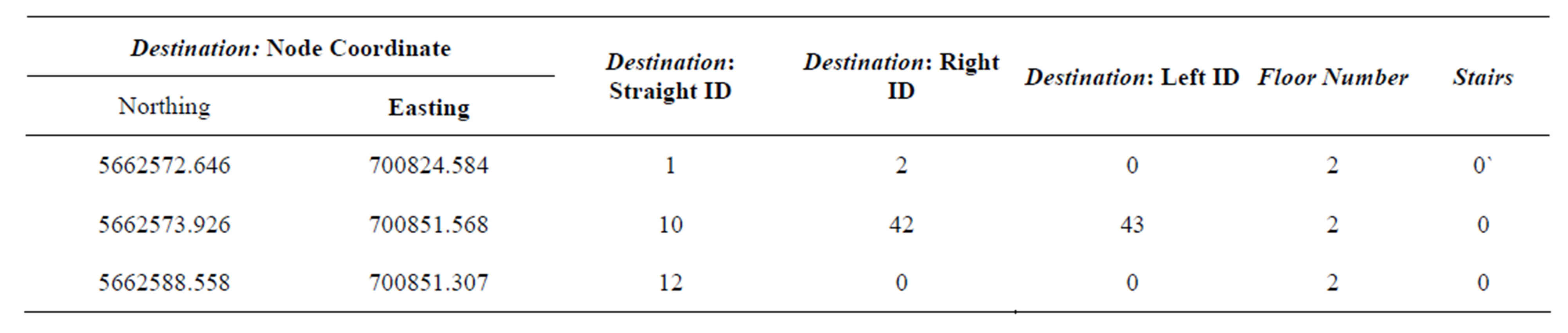
Table 1. Sample for the links database table (engineering building).

Figure 2. The geospatial model for the MacEwan and kinesiology building floor one at university of Calgary.
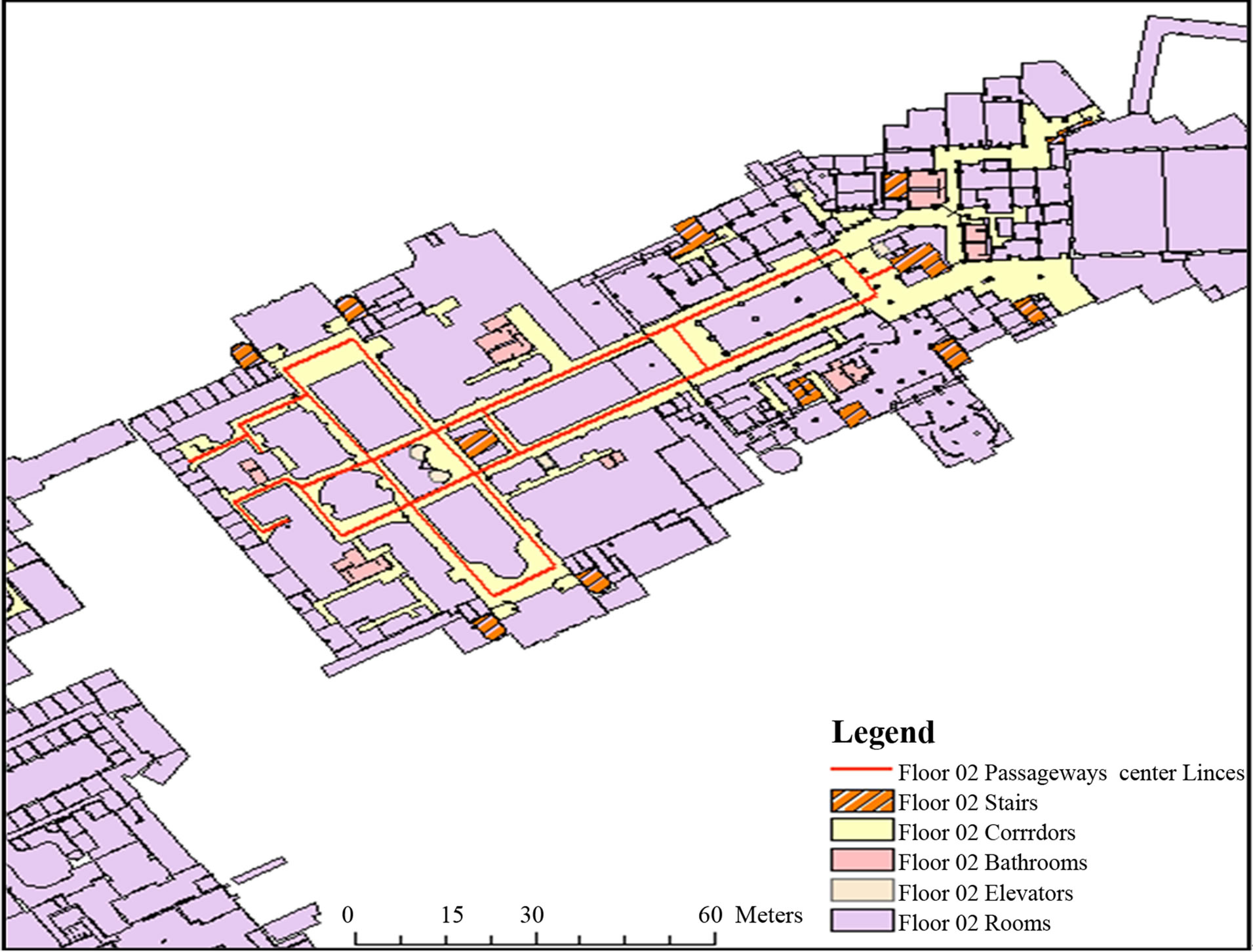
Figure 3. The geospatial model for the MacEwan and kinesiology building floor two at university of Calgary.
to select the appropriate link where the user is most probably located. The third aspect is choosing the appropriate geospatial information model which would has the required properties to support navigation application [9]. Building floor maps for indoor applications should model all possible passageways and height change access (stairs, elevators), and also consider the topological characteristics, for example connectivity between passageways [10, 11] . Some research on navigation systems for indoor applications with the assist of the building information is developed [12,13] . The main idea is to use the building information to create virtual boundaries for the navigation solution, which lead to bounding the solution in the most probable region, therefore increasing the reliability of the solution [3]
The map matching algorithm logic was developed based on point-to-curve matching [3]. The theory behind point-to-curve map matching is based on projecting the position estimated from the navigation algorithm (XS, YS) to the nearest link, which in this case is the nearest passageway. Each passageway link has started and end nodes, [(X1, Y1), (X2, Y2)]. Using the position estimate coordinates (XS, YS), a dot product between the position and the start and end nodes [(X1,Y1), (X2,Y2)] is done as shown in Equation (1) to calculate the minimum distance between the position estimate and all the links, provided that the projection lies within the extent of the link. Equation (1) is based on the concept that the minimum distance between any point and a line is the perpendicular distance which is obtained using the dot product. Once Equation (1) is applied to all the links and a link is selected, the algorithm will project the position estimate on the passageways links. The projected coordinates (XP, YP) can be obtained using Equation (2) and Equation (3) [3].
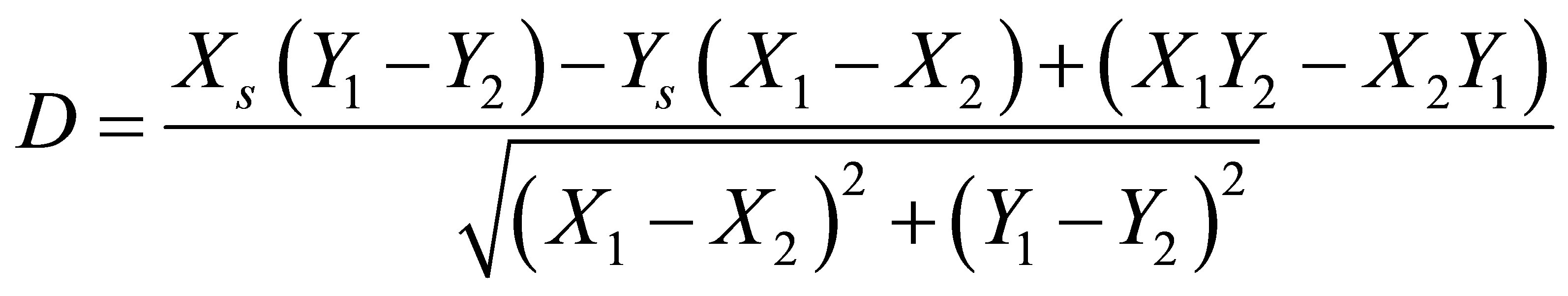 (1)
(1)
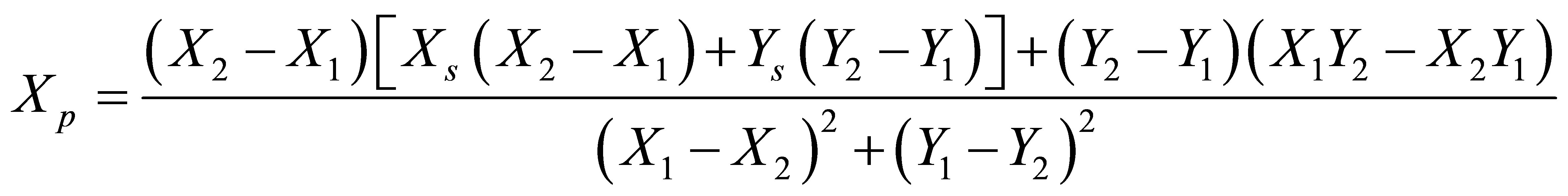 (2)
(2)
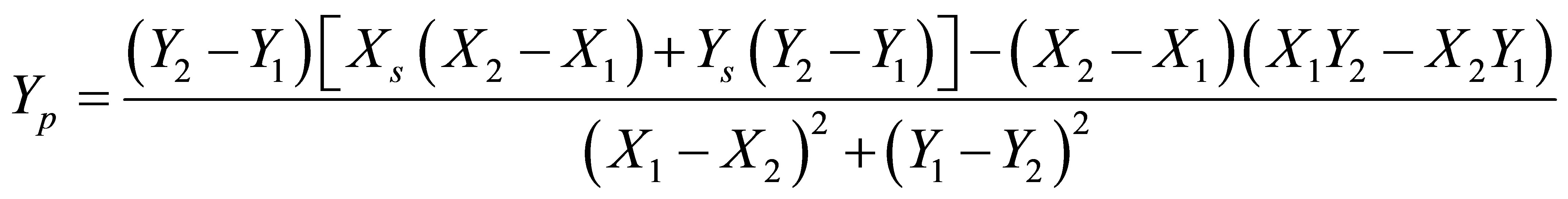 (3)
(3)
3.1. Automatic Turn Detection Algorithm
The implementation of the map matching algorithm begins with a reading of the first epoch position and projecting it onto the nearest link using the techniques described in the previous section. Upon reaching a new link, the turn detection algorithm is utilized to select the successive link. Selection of the correct link at intersections is more challenging since there could be more links achieving the small distance and it is not guaranteed that the minimum distance could lead to the correct link. In a typical four-corridor intersection or even a “T” intersection, the user could have a similar distance to all the links. However, waiting until the distance coincides on a certain link would fail the real-time processing concept.
The developed map matching algorithm includes a turn detection algorithm based on the raw gyro data for the heading direction sensor. Observing the gyro raw data for heading, and depending on the angular rate magnitude and direction, the algorithm detects whether a change in direction occurred. Real-tests datasets were used to develop the threshold in turning detection using the gyro measurements, subsequently creating a library for all the sudden changes in the angular rate magnitude and their correlation to the direction (heading) of the user. Data from the MEMS based ADI ADXRS150, ADIS16405 MEMS Gyros and Samsung Galaxy SII phone sensors were used to build a library for all the sudden changes in the angular rate magnitude and relate them to the direction (heading) of the user.
Figure 4 presents a flowchart diagram describing the
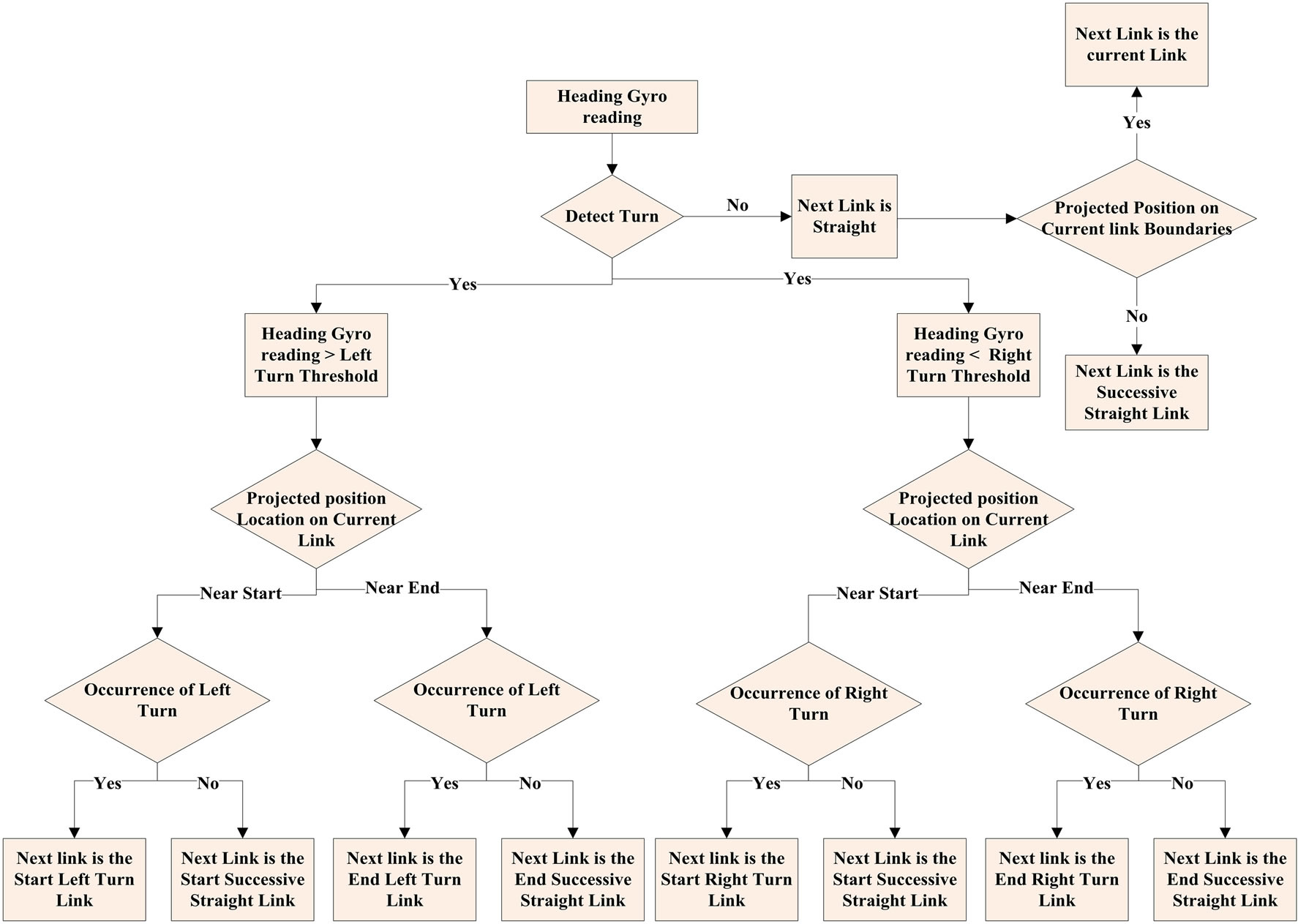
Figure 4. The logical sequence for the turn detection algorithm.
logical steps for the turn detection algorithm. Once a turn is detected, and based on the threshold sign, the algorithm then detects whether the turn is a right or left turn. The final decision for the appropriate link is then made based on the occurrence of a turn link in the associated geospatial model. For example if a right turn is detected using the gyro measurements, there must also be a right diverged link from the current link in the geospatial database to indicate that this is the correct link, otherwise the algorithm will choose the successive straight link. When the projection length exceeds any of the link two nodes, link change is decided to see if the user crossed to the straight link forward or backward
3.2. Geometrical and Topological Map Matching Algorithm
The geometrical and topological algorithm is a combination of the geometrical and turn-detection algorithm. Figure 5 illustrates the logical sequence for the developed geometrical and topological algorithm. Selection of the appropriate road segment is based on geometrical and topological properties for the network segments (links) using point-to-curve matching [5]. Once the initial position estimate is available, a query for all possible passageways segments is initiated based on the minimum perpendicular distance. A threshold is then chosen to filter any illogical returns, and the value is assumed similarly by using half the minimum distance between two parallel corridors. Therefore, to select a certain net-
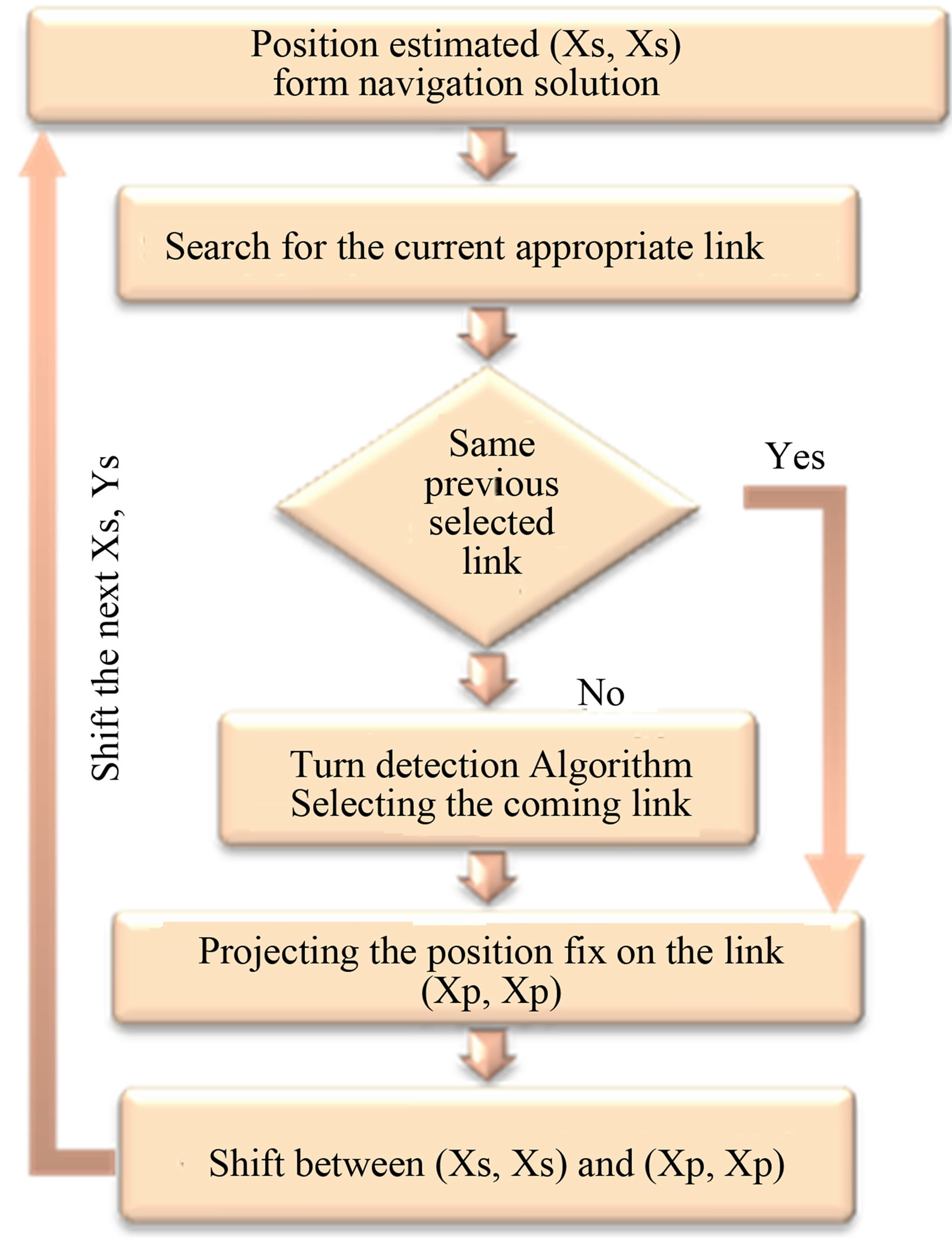
Figure 5. Geometrical and topological map matching algorithm.
work segment, the initial position estimate should have a minimum distance (less than the threshold) to this arc. Its projection should also be located between its nodes. The algorithm will then continue to match the following position estimates until the user approaches an intersection. For the appropriate segment to be selected at an intersection, further information is required in addition to the minimum distance since several links can give a minimum distance for several epochs but not necessarily the right one. The turn detection algorithm is activated in this situation.
After applying the turn-detection algorithm, the successive link is selected and the position is projected on its boundaries depending on whether the user’s direction is straight, right or left. The shift between the position fix and the projected position is computed and fed back as a transitional shift towards the next epoch’s position fix. The algorithm will shift the whole navigation solution with this value before projecting the position of the second epoch. In other words, for every epoch, the algorithm will first shift the solution using the previous epoch shift value and then project its position on the nearest link. For each epoch, the map matching algorithm uses a verification tool based on the heading value. The algorithm calculates the heading for the current selected link based on its start and end coordinates, and this value is then compared to the estimated heading state from the navigation filter. The tolerance for the difference between both headings to be accepted or rejected as a candidate link is based on the quality of the navigation sensor and the uncertainty of the heading state.
4. Navigation Solution: Pedestrian Dead Reckoning Using Smart-Phones Sensors
Pedestrian dead reckoning (PDR) is a relative positioning technique to estimate the position of on-foot users, either in outdoor or indoor environment, based on the user’s previous position and the travelled distance and orientation calculated from inertial sensors measurements. The typical inertial sensors used for PDR are tri-axial accelerometers and gyroscopes. The use of magnetometer is an assist where it is used to enhance heading estimation. The PDR process typically include three phases; Step Detection, Stride (Step) Length, and Heading Estimation (user direction) estimation. Figure 6 illustrates the main architecture for the PDR algorithm.
Equations (4) and (5) show the common PDR equations for computing the coordinates of successive navigated points 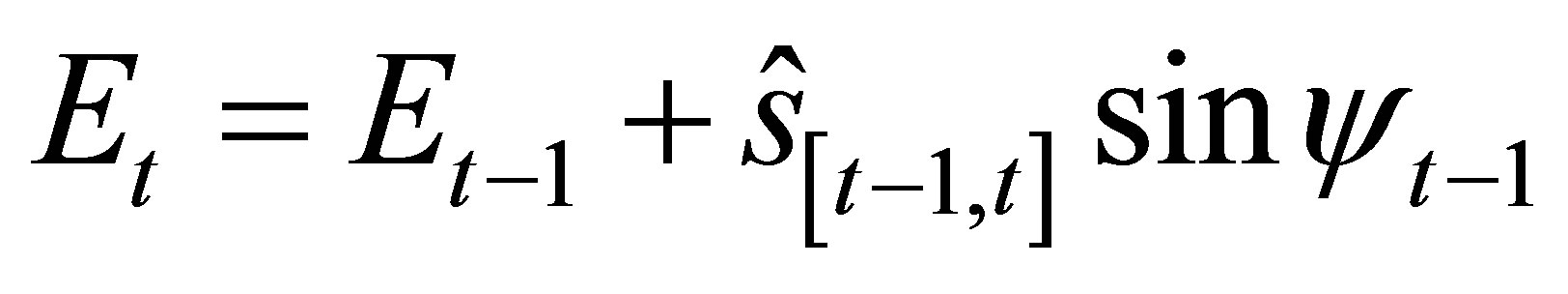 (4)
(4)
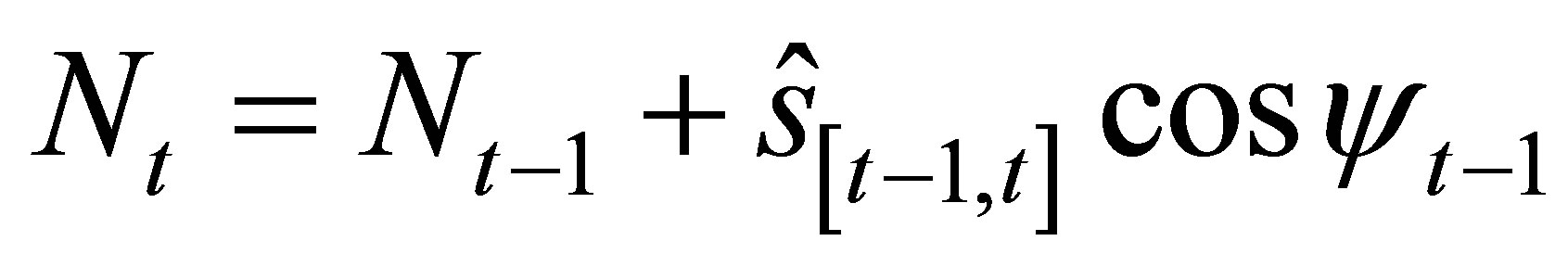 (5)
(5)
Equations (4) and (5) compute the coordinates 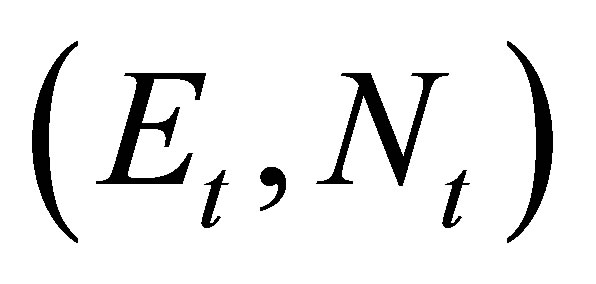 of the new position at time (t) with respect to a previously known position
of the new position at time (t) with respect to a previously known position 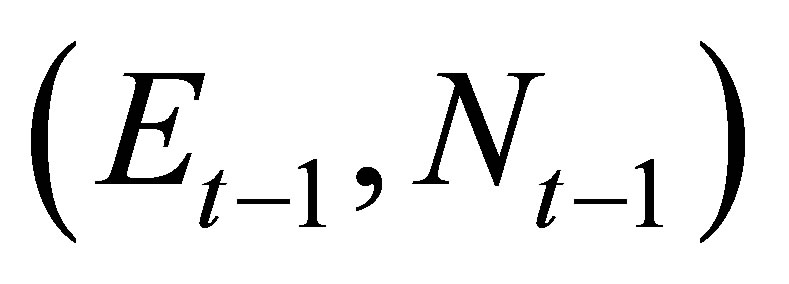 at time (t‒1), where
at time (t‒1), where 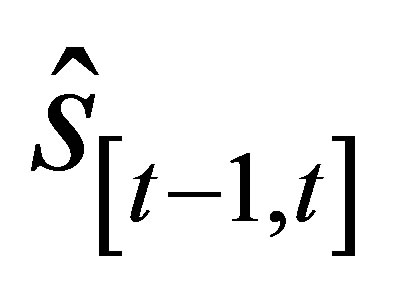 is the distance travelled by the user since time ( t‒1), and
is the distance travelled by the user since time ( t‒1), and 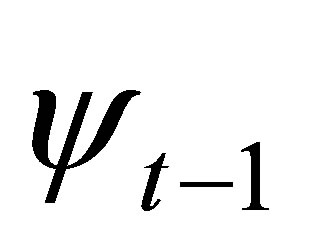 is the user heading at time (t‒1). The
is the user heading at time (t‒1). The 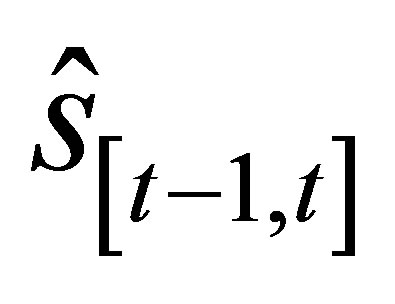 is estimated based on the Step Detection and Step length algorithms, and the
is estimated based on the Step Detection and Step length algorithms, and the 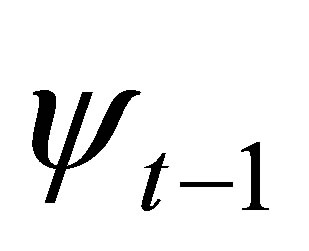 is estimated based on the Heading Estimation algorithm.
is estimated based on the Heading Estimation algorithm.
Step Detection: The step detection is the first step in any PDR algorithm. Several algorithm were developed to detect the steps in an on-foot trajectories, the main two methods are peak detection of the accelerometer data [14], and the zero crossing method [15]. The peak detection is usually performed on the forward accelerometer sensor, however sometimes it can be performed on the norm of the three axial accelerometers, which is used in this paper, where the step is detected when a local maximum of the acceleration is found within an acceptable time period. “Equation (6)” calculates the norm for the three axial accelerometers.
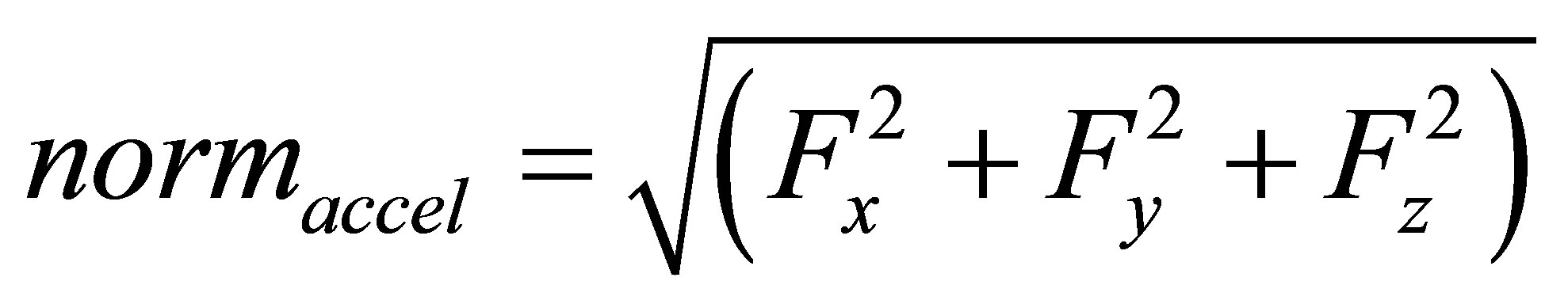 (6)
(6)
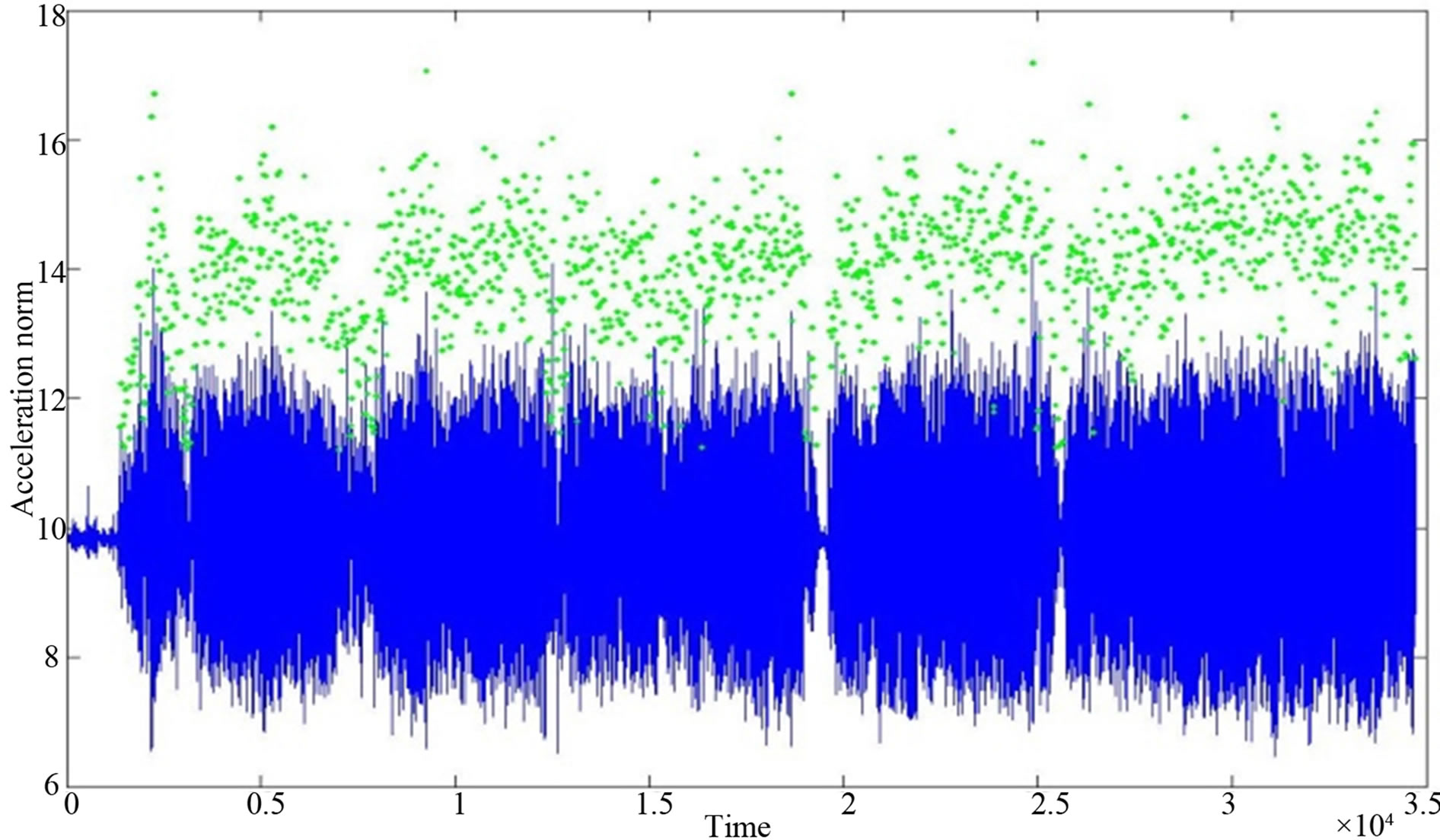
Steps can be detected based on gait cycle [14]. The gait cycle is the time consumed by the foot from leaving the ground till it hits the ground again. The accelerometer signal would sense a change in the amplitude corresponding to this movement, which leads to easy detection of the user steps. In some cases, using the accelerometer variance over a certain number of samples using a sliding window, would be better than the accelerometer signals since it removes the bias shift [16]. The developed steps detection is simply to detect the steps based on the waveform of the overall acceleration vector. A step is detected for each complete cycle around the mean value. Figure 7(a) shows the steps detected based on the waveform of the overall acceleration vector for a dataset of accelerometer from the Samsung Galaxy smart-phone. Figure 7(b) shows a zoomed view on the walking start
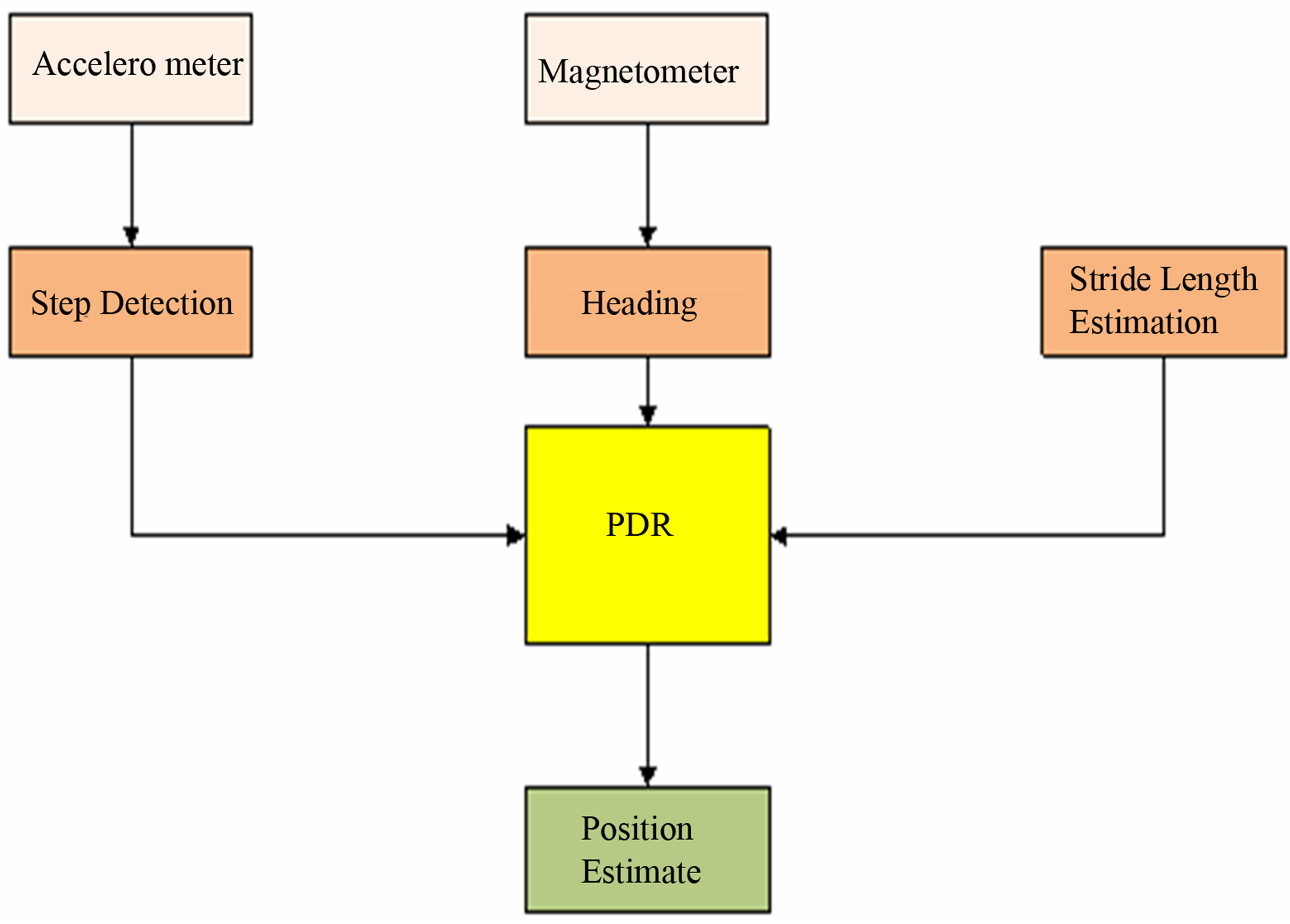
Figure 6. Pedestrian dead reckoning architecture.
 (a)
(a) 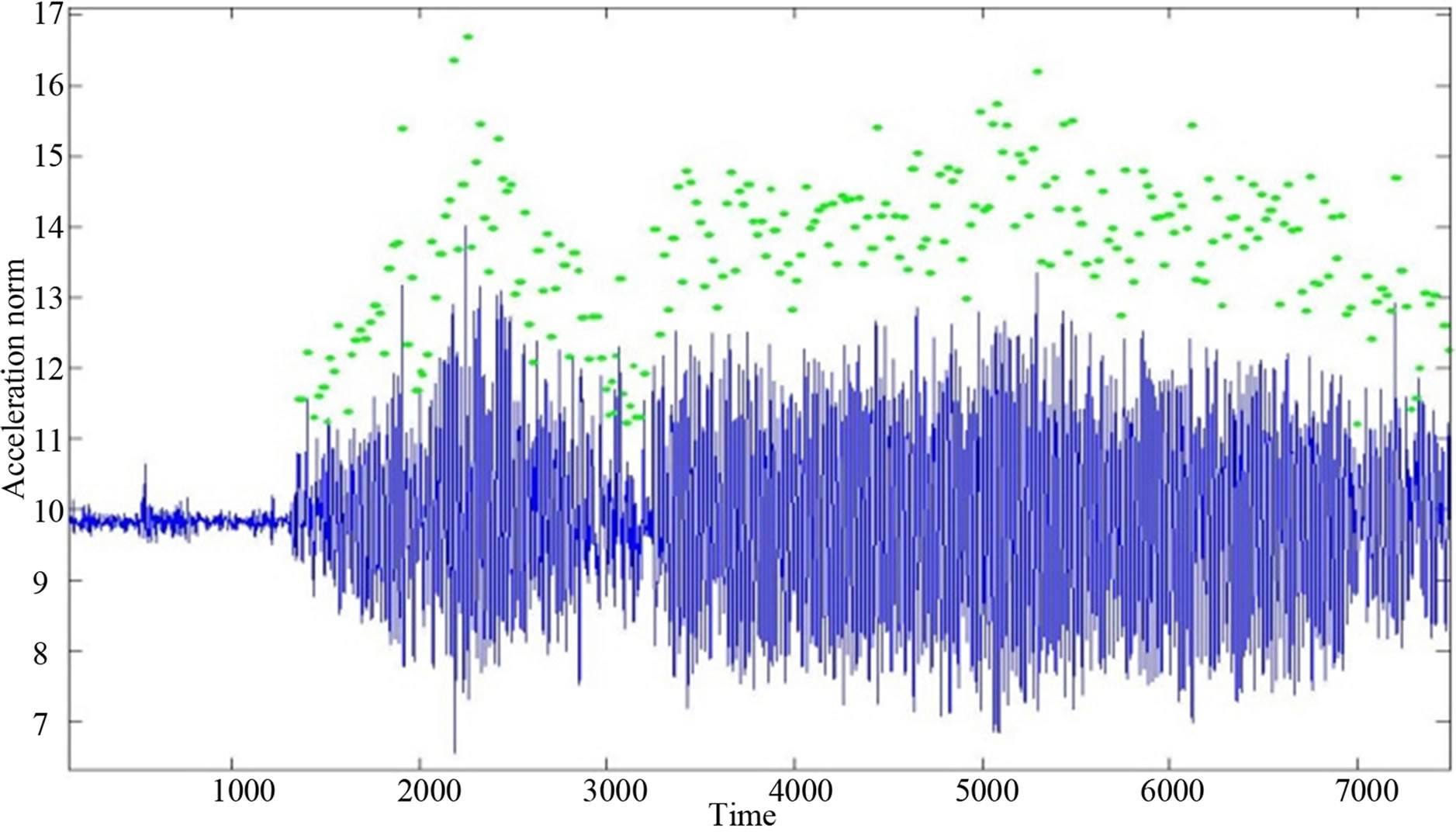 (b)
(b)
Figure 7 . (a) Acceleration norm (blue) with the detected steps (green); (b) Zoom in for the walking start with the detected steps.
region. The step length could be approximately estimated based on the cycle width and peak-to-peak values of the detected step.
Step length Estimation: Step length is defined as the corresponding travelled distance during a complete step. The step length is strongly correlated to the linear pattern of the walking frequency and the variance of the acceleration [15]. Hence, Step length can be estimated based on the linear combination of both the walking frequency and the variance of the acceleration.
The walking frequency can be calculated using Equation (7)
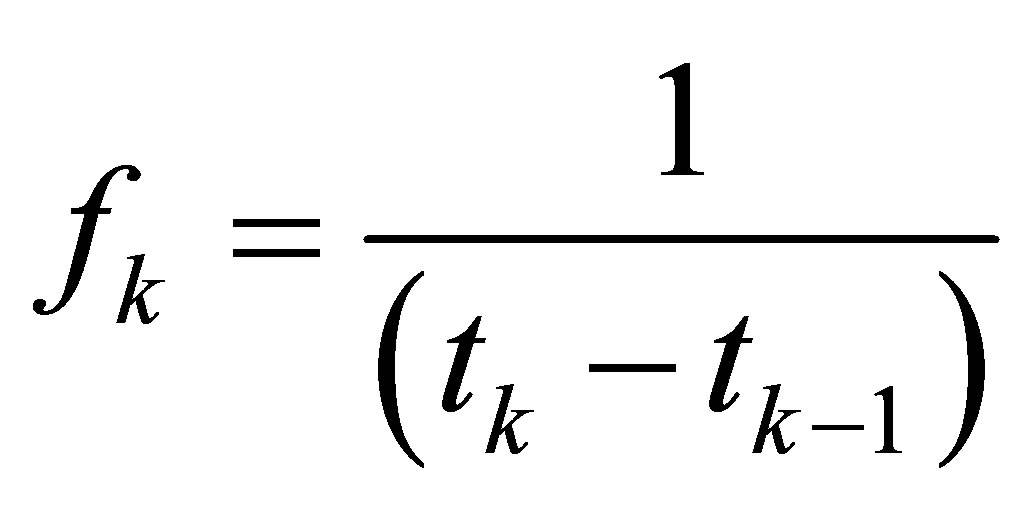 (7)
(7)
where 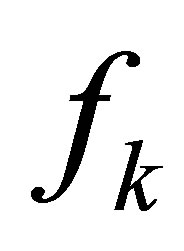 is the walking frequency from time
is the walking frequency from time 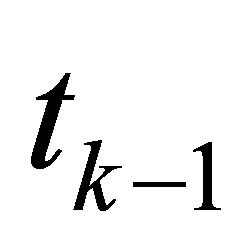 to time
to time 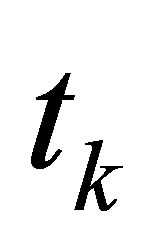 for a certain step.
for a certain step.
And the variance of the acceleration signal can be calculated using Equation (8)
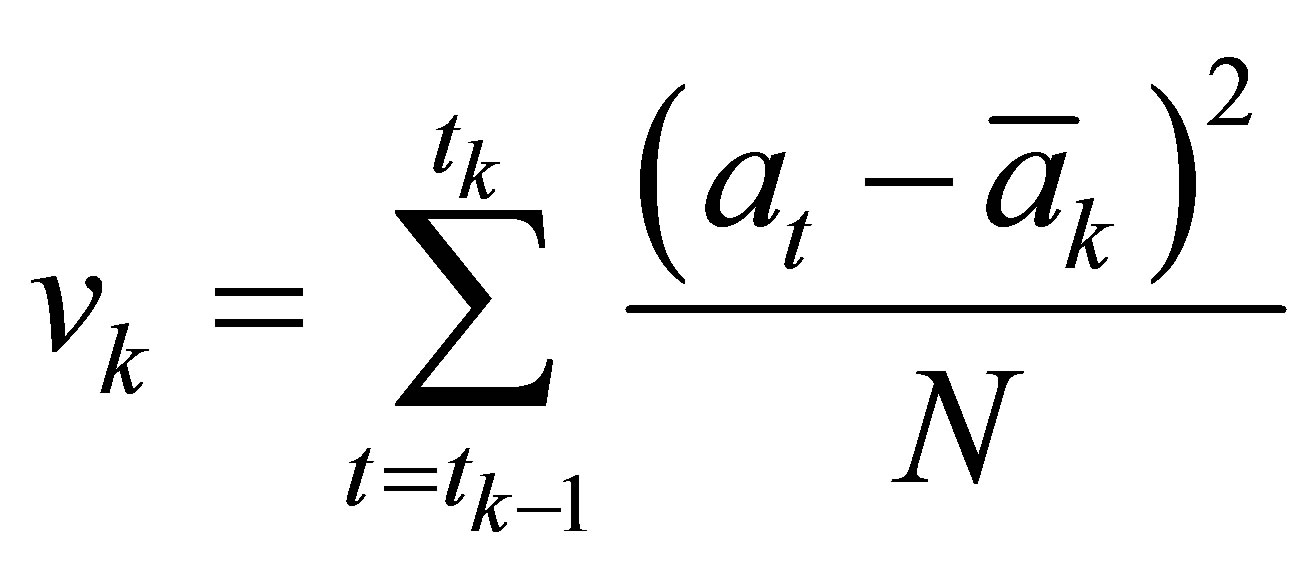 (8)
(8)
where 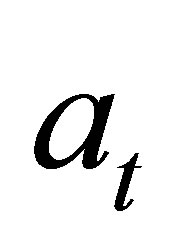 the accelerometer signal at time t is,
the accelerometer signal at time t is, 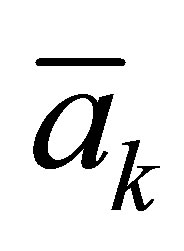 is the average of accelerometer signals during one step and N is the number of sensor outputs during one step.
is the average of accelerometer signals during one step and N is the number of sensor outputs during one step.
The inputs from the walking frequency and the variance of the acceleration, in addition to the learned parameters that are estimated based on calibration for different conditions and different grounds, is then used to estimate the stride length.
Heading Estimation: The user heading is estimated using either the gyroscope signals, the magnetometer signals or using a fusion algorithm based on both. The gyroscope measurement is not affected by the magnetic anomalies that occur in indoor environment; however it drifts with time due to its bias drift. The magnetometer measurement faces the effect of the magnetic disturbances but it provides an absolute heading that can be useful for updating the gyroscope. In this paper, the magnetometer was used to calculate the heading to avoid the huge drift from the gyroscope sensor and the requirement for its leveling. Equation (9) shows the heading calculation using the magnetometer signal (before considering the magnetic declination angle e.g. ~15˚ for Calgary, Alberta, Canada)
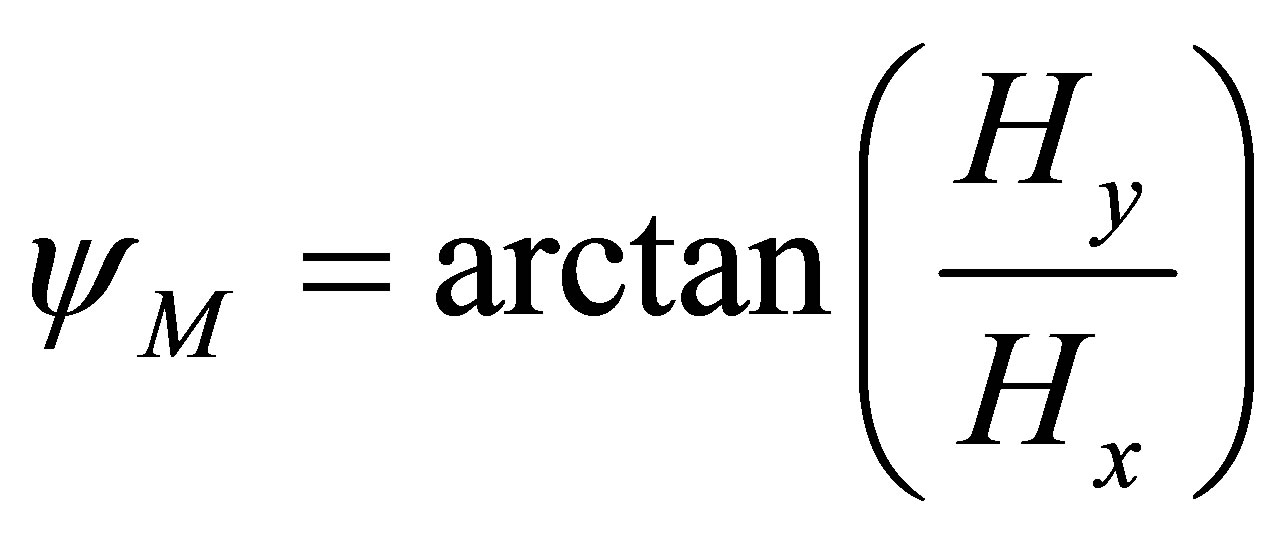 (9)
(9)
where 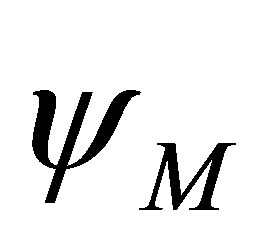 is the heading computed using the magnetometer measurements,
is the heading computed using the magnetometer measurements, 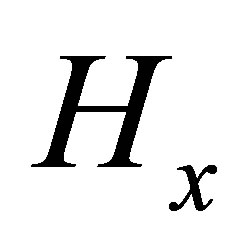 and
and 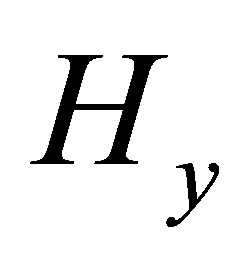 are the magnetometer measurements in the x and y axis respectively.
are the magnetometer measurements in the x and y axis respectively.
5. Map Aided PDR System
The map aided navigation system architecture is presented in Figure 8" target="_self"> Figure 8. The system main components and behavior is similar to the previously discussed direct map matching system, however it only uses the PDR estimation technique. The initial inputs for the system are the inertial measurements from the smart-phone inertial sensors, which are processed using PDR algorithm to estimate the position fixes. The PDR uses the accelerometer signals to perform the step detection process. The detected peak locations with the time between them are used to estimate the stride length. The magnetometer sensor is used to determine the heading information.
The position fixes outputs of the PDR solution are inputted into the geometrical and topological map matching algorithm, and with the help of the developed geospatial model, the position fixes are projected on the passageways links. The automatic turn detection algorithm is used to detect the user’s coming link whether to be the straight, the left turned, or the right turned diverged link. This algorithm uses the two geospatial models for the Engineering building and the Kinesiology complex and MacEwan at University of Calgary.
6. Field Test Description
6.1. Sensor Used for Field Test
The field tests were carried out using the Samsung Galaxy Smart-Phone sensors, logging the data using a commercial application called “Data logger” and transferring the logged data offline. Table 2 summarizes the Sam-
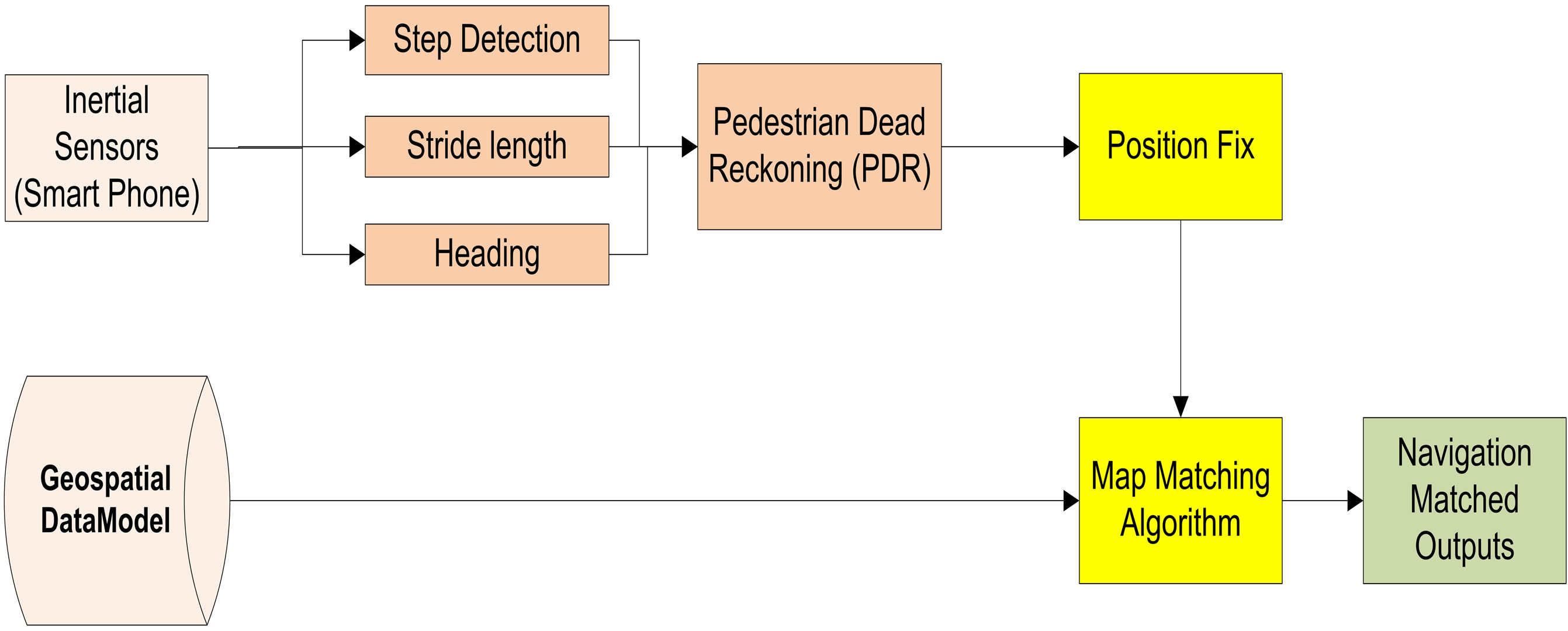
Figure 8. Map aided pdr for smart-phones architecture.
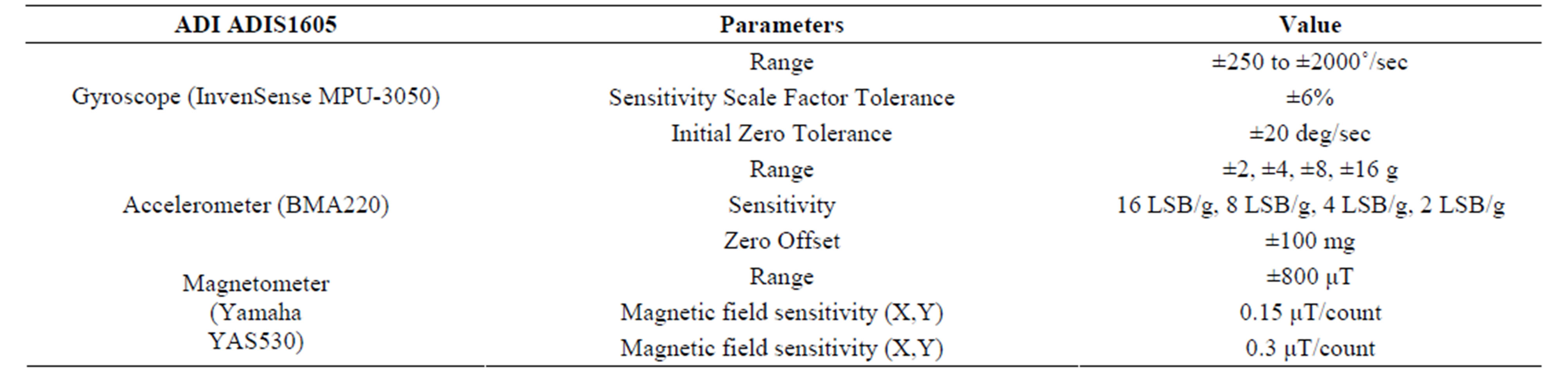
Table 2. Samsung galaxy smart-phone sensor types and specification.
sung Galaxy Smart-Phone sensor types and specification. The logged raw data for all sensors are characterized with time stamp which was utilized in synchronizing the measurements with sufficient accuracy.
6.2. Field Test Scenario Engineering Block
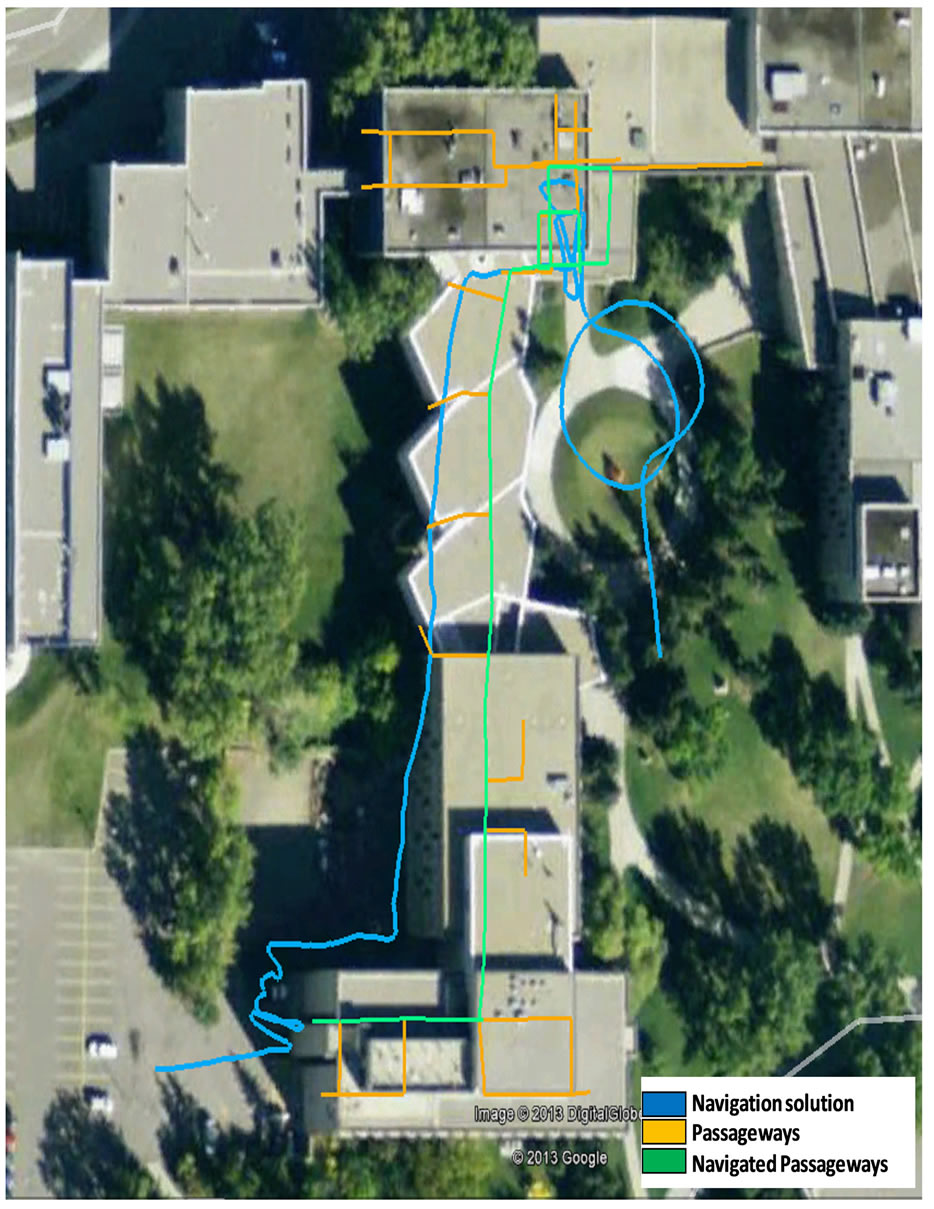
In order to verify the performance of the developed PDR map aided navigation algorithms, two indoor field tests were performed. The field tests took place in the main campus of the University of Calgary. The field test is an eleven minutes walking starting from outdoors to maintain a GPS initial solution and then indoor the School of engineering building of the University of Calgary. The tester walked double loops outdoor, and then enters the building the first floor of the building’s north gate, then climbs the stairs to the second floor, walks around the stairs, and walks inside the building to the south direction in the main corridor until reaching the end of Engineering block. The user then used the stairs located in the southwest of the building to get down to the parking outside the building in the west side. The field test was ended outdoors. In Figure 9(a) and Figure 9(b) the field trajectory is presented both in google earth view and on the floor plans view. In google earth, the PDR navigation solution is shown in blue, the building passageways in orange, and the navigated passageways in green. On the floor plans, the PDR navigation solution is shown in blue, the building passageways in red.
6.3. Field Test Scenario Kinesiology and MacEwan
The second field test is a twelve minutes walking starting from outdoors to maintain a GPS initial solution and then indoor the Kinesiology building of the University of Calgary. The test trajectory continues indoor reaching to the MacEwan student centre and getting back to the Kinesiology building. The tester stayed static outside and then started walking outdoors for around a minute, and then enters the Kinesiology building on the first floor at the south gate, the then turn right and continues to walk on the first floor heading east entering the MacEwan building until reaching the main east side stairs, climbs the stairs to the second floor, walks around the stairs, and walks inside the MacEwan building to the west direction in the main corridor until reaching the main west side stairs of MacEwan building. The user then used the stairs to head west to the Kinesiology building again and getting out of the building and walking outdoor for around a minute. The field test was ended outdoors. In Figure 10, the field trajectory is presented both in google earth view where the PDR navigation solution is shown in green, the first floor building passageways in blue, and the second floor building passageways in red. Figure 11(a) presents
 (a)
(a)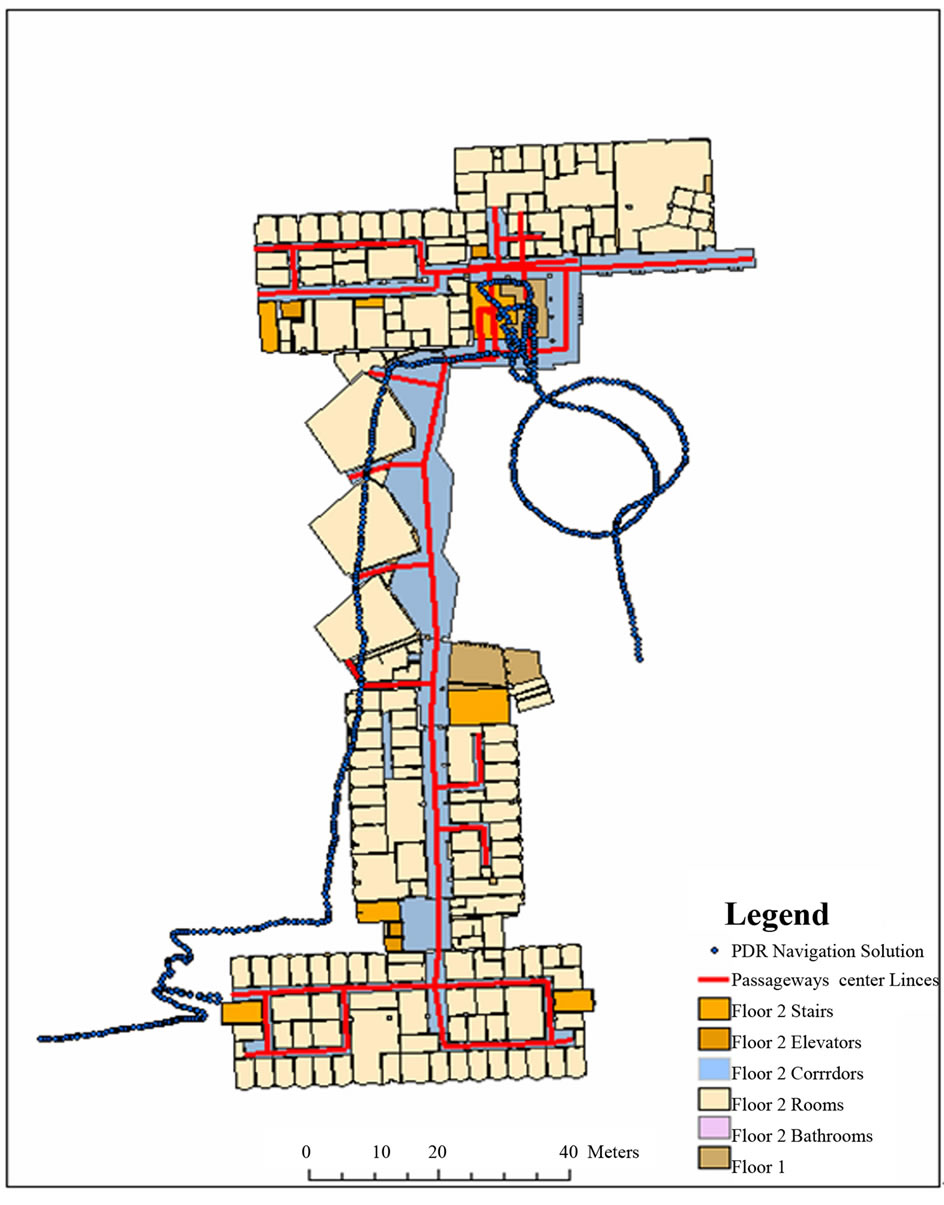 (b)
(b)
Figure 9. (a) Field test trajectory for engineering block (Google Earth (©2013 Google); (b) Field test trajectory for engineering block on floor plans.
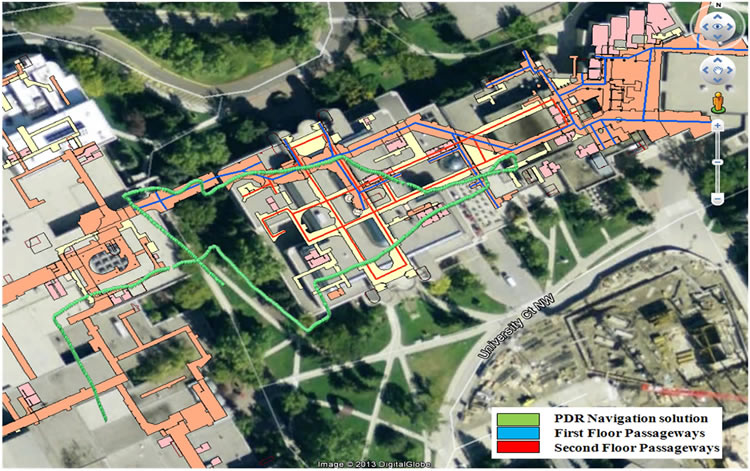
Figure 10. Field test trajectory for macewan and kinesiology (Google Earth) (©2013 Google/Image ©2013 Digital Globe).
the first floor trajectory from entering the building until reaching the stairs for the second floor on the floor maps, and Figure 11(b) presents the second floor trajectory from getting off the stairs until getting out from the building. The navigated passageways are presented in light green.
7. Results, Analysis, and Discussions
7.1. Engineering Block
The map aiding results for the map aided PDR for Smart-Phones sensors using building information algorithm for the Engineering Block field test is presented in Figure 12, the results trajectories are presented both in google earth view and on the floor plans view. In google earth, the PDR navigation solution is shown in blue, the building passageways in green, and the matched passageways in red. On the floor plans, the PDR navigation solution is shown in blue, the building passageways in black and the matched passageways in red. It can be noticed from the results, that the developed map aided PDR algorithm achieved an almost complete map matched trajectory.
Table 4 illustrates the percentage of the correct matched links, which can be seen to be 83.1% for the developed algorithm. The percentage of matched trajectory is calculated by measuring the length of the correct matched links to the all navigated passageways. The algorithm mismatched links are at the end of the trajectory upon reaching the west side stairs, where the stairs-way was very narrow and goes for three levels downstairs. These results confirm the significant contribution for the developed map aided PDR algorithm in reaching a logi-
 (a)
(a)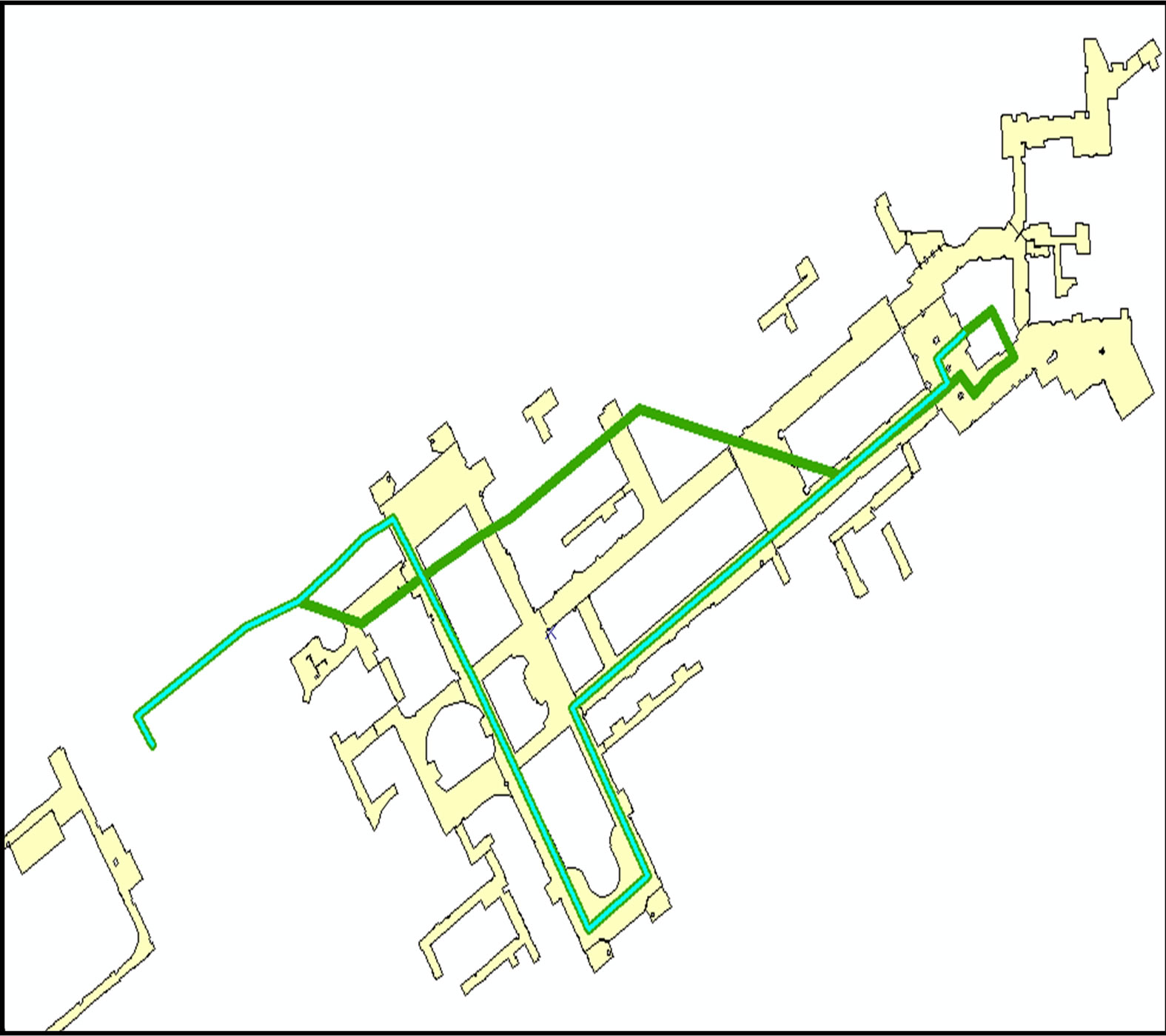 (b)
(b)
Figure 11. (a) First floor navigated passageways; (b) Second floor navigated passageways.
 (a)
(a)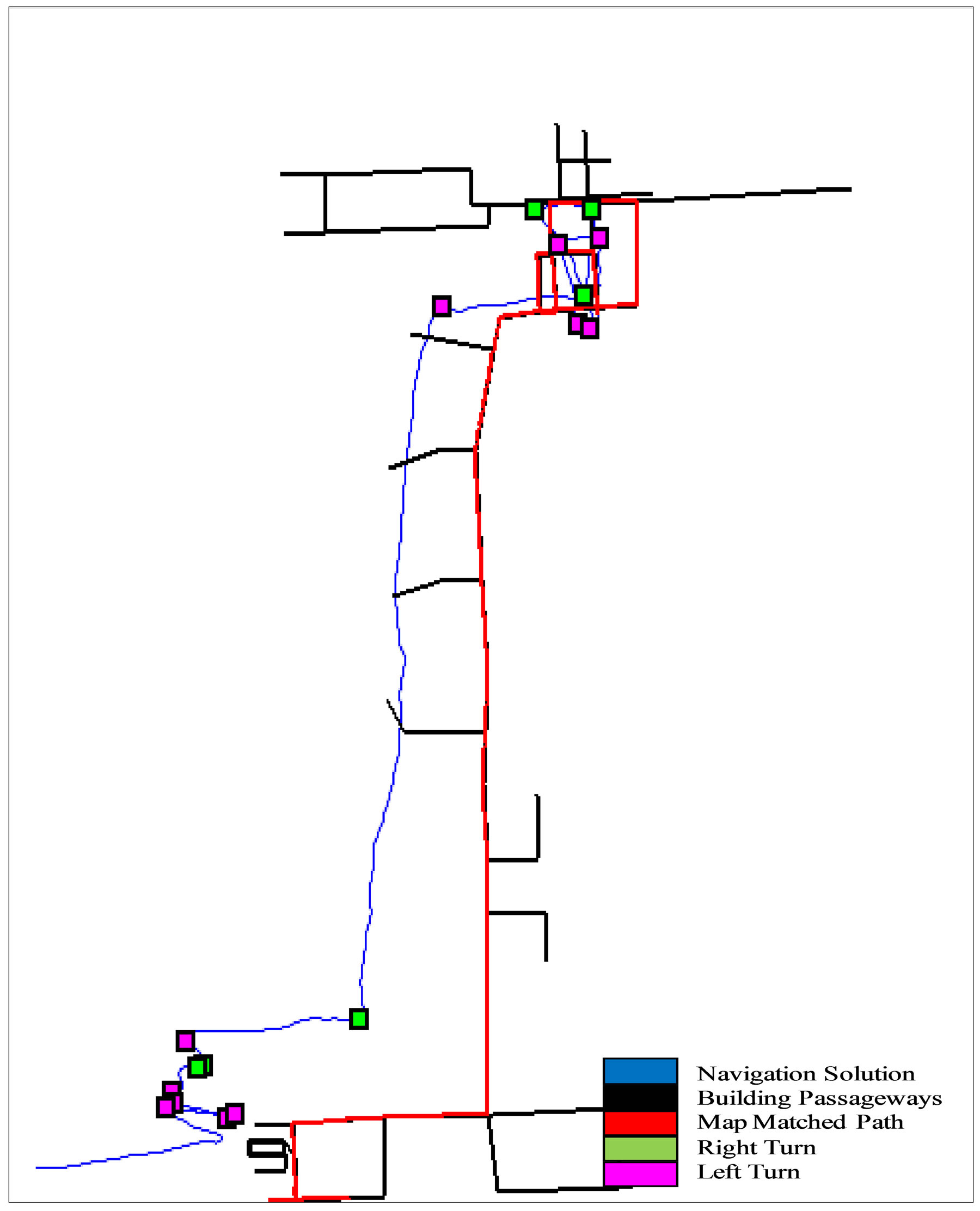 (b)
(b)
Figure 12. (a) Results for the map aided pdr navigation (Engineering Block); (b) Results for the map aided pdr navigation (Engineering Block).
cal matching sequence to successfully match all different types of passageways. In order to evaluate the improvement in positional errors, the map itself is assumed as the reference trajectory—assuming that the reference for the navigated trajectory is the centerlines for the passageways. The positional error using the PDR navigation solution achieved a maximum position error of 20.54 m and a mean position error of 12.27 m. Using the developed map aided PDR algorithm, and with the fact of having only the final stairs mismatched links, the maximum positional error is reduced to 13.45 meter, and a mean position error of 7.86, as shown in Table 3" target="_self"> Table 3.
7.2. Kinesiology and MacEwan
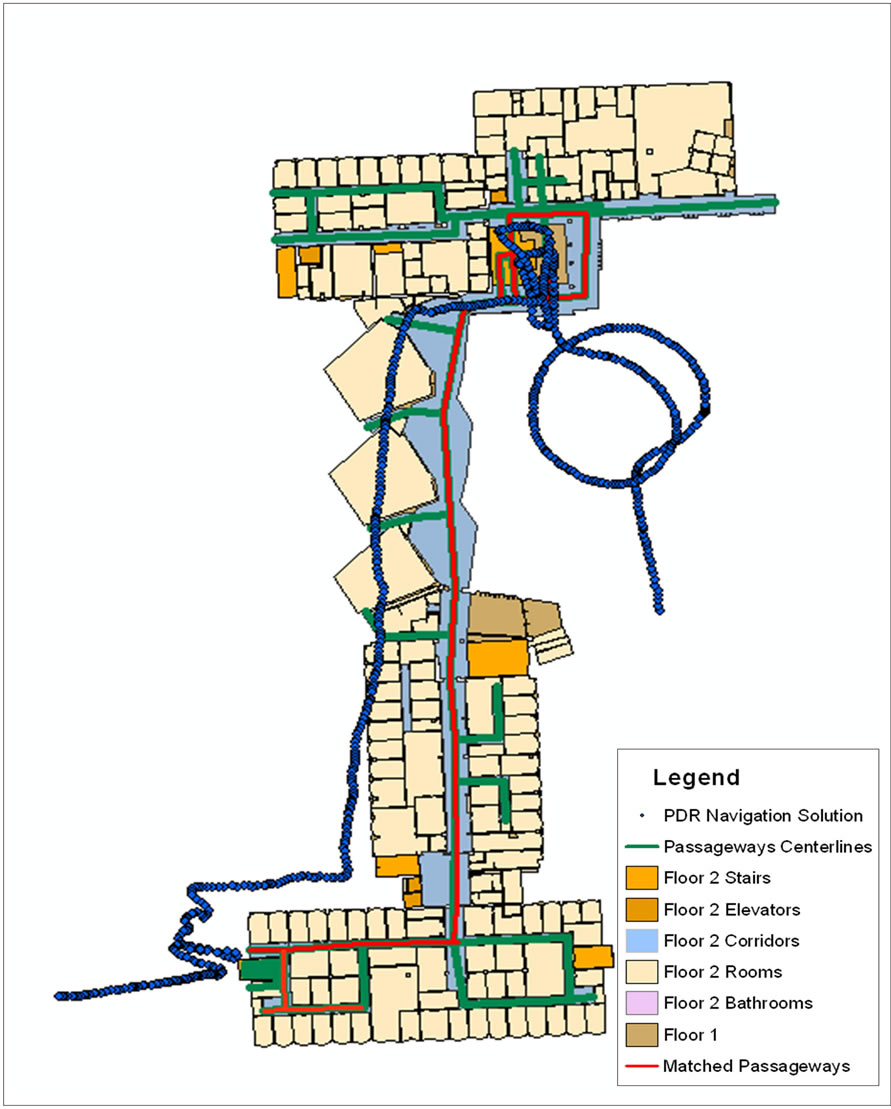
The map aiding results for the map aided PDR for Smart-Phones sensors using building information algorithm for the Kinesiology and MacEwan field test is presented in Figure 13. Figure 13 shows a simplified floor plan showing only the centrelines for the passageways and trajectories. The PDR navigation solution is shown in blue, the building passageways in black and the matched passageways in red. It can be noticed from the results, that the developed map aided PDR algorithm achieved a complete map matched trajectory, just missing a horizontal link at the end of the matched trajectory due to the length difference between the PDR navigation solution and the links database reference length, which is due to estimating the user stride length is not completely achieving the actual trajectory length. However and upon detecting the final left turn, the final link was correctly detected. Table 4 lists the percentage of the correct matched links, which can be seen to be 97.3% for the developed algorithm. The percentage of matched trajectory is calculated by measuring the length of the correct matched links to the all navigated passageways.
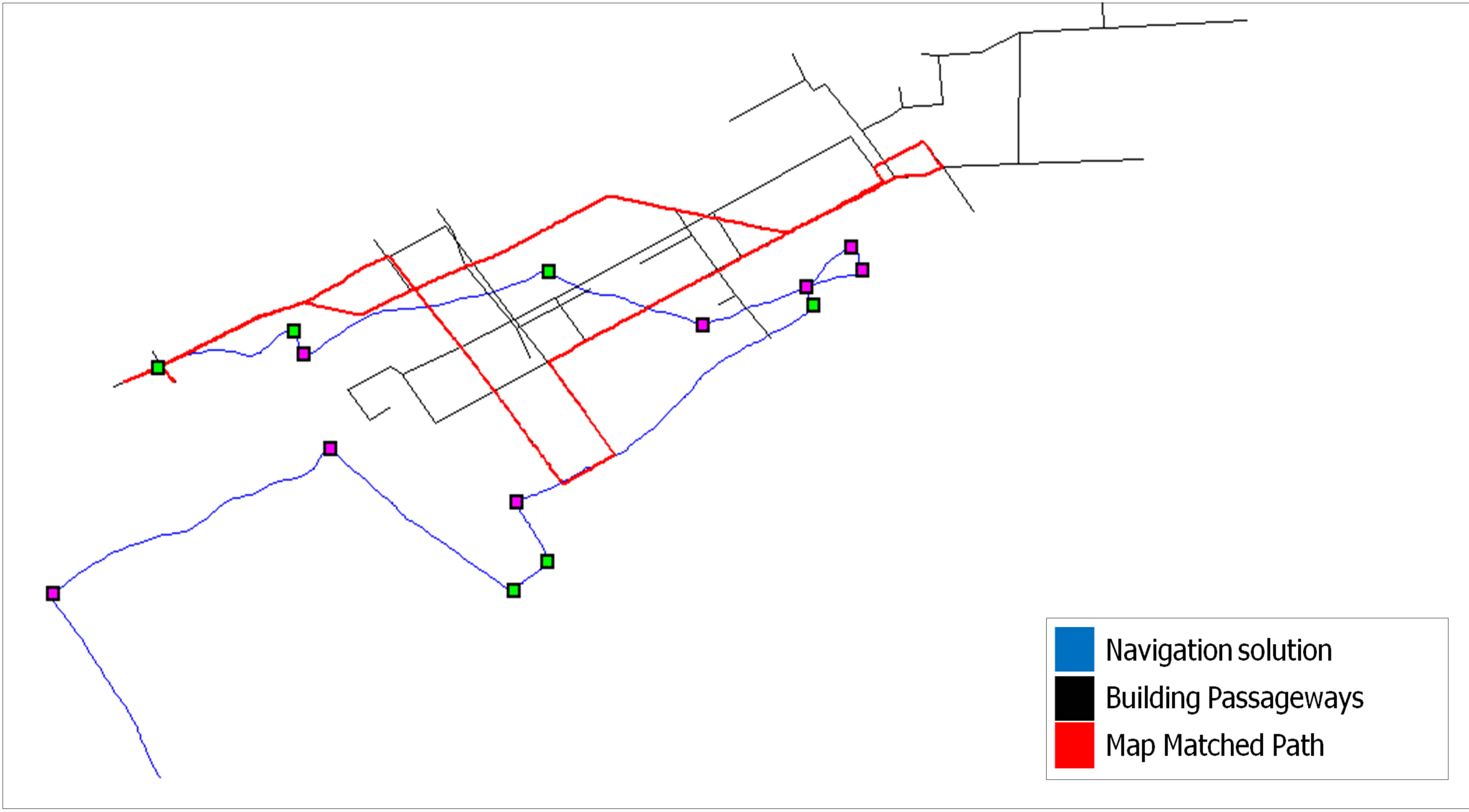
Figure 13. Results for the map aided PDR navigation (Kinesiology and MacEwan).
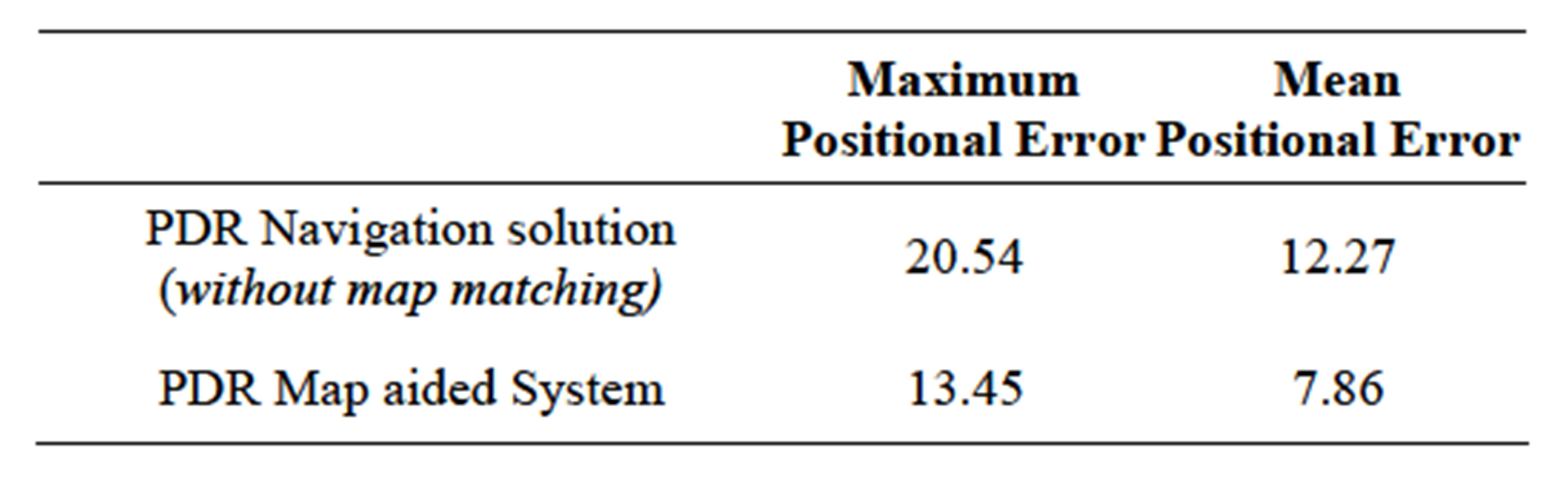
Table 3. Positional errors using the map as a reference (Engineering Block).
These results continues to confirm the significant contribution of the developed map aided PDR algorithm in reaching a logical matching sequence to successfully match all different types of passageways. The positional error using the PDR navigation solution achieved a maximum position error of 64.01 m and a mean position error of 38.49 m. Using the developed map aided PDR algorithm, and with the fact of having only the final stairs mismatched links, the maximum positional error is reduced to 7.12 meter, which is also representing the mean position error, as shown in Table 5.
8. Conclusions
The navigation applications are considered essential and vital for many areas of use: daily activities, industrial, commercial, law enforcement, and emergency applications. Navigation challenges in GPS-denied environments are currently one of the most active areas of research and as such, can produce significantly beneficial navigational aid solutions for either urban canyons or inside buildings. In this paper, indoor aided navigation solution was developed using mapping information. Map aiding system was developed based on geospatial models and map matching algorithm. The geospatial data models were built according to navigation applications requirements and characteristics. Two models were created for indoor environments to be used in implementing the map aided algorithms, and for evaluating the performance and testing of the systems in real-life trajectories. Geometrical and topological map matching algorithms based on automatic turn detection techniques were developed to project the obtained navigation solution position fix into the created geospatial data model.
A map aided PDR navigation solution was developed using the Samsung Galaxy smart-phone sensors. The PDR solution used the inertial measurements from the smart-phone to estimate a navigation solution with sufficient accuracy to be entered in the map aided algorithm.
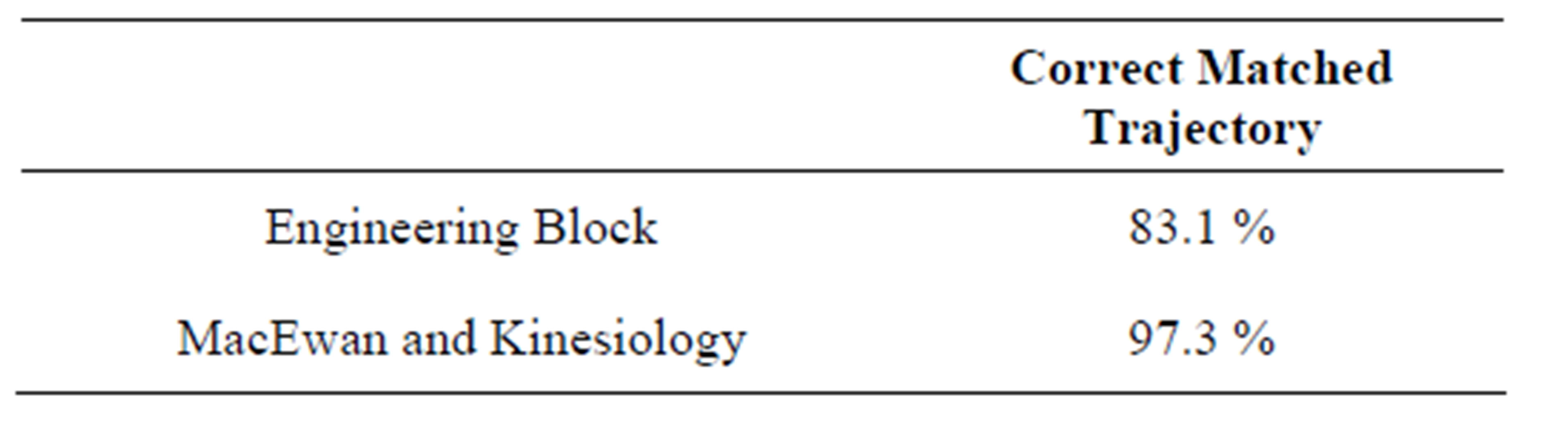
Table 4. Matching results for the pdr map aided algorithm.
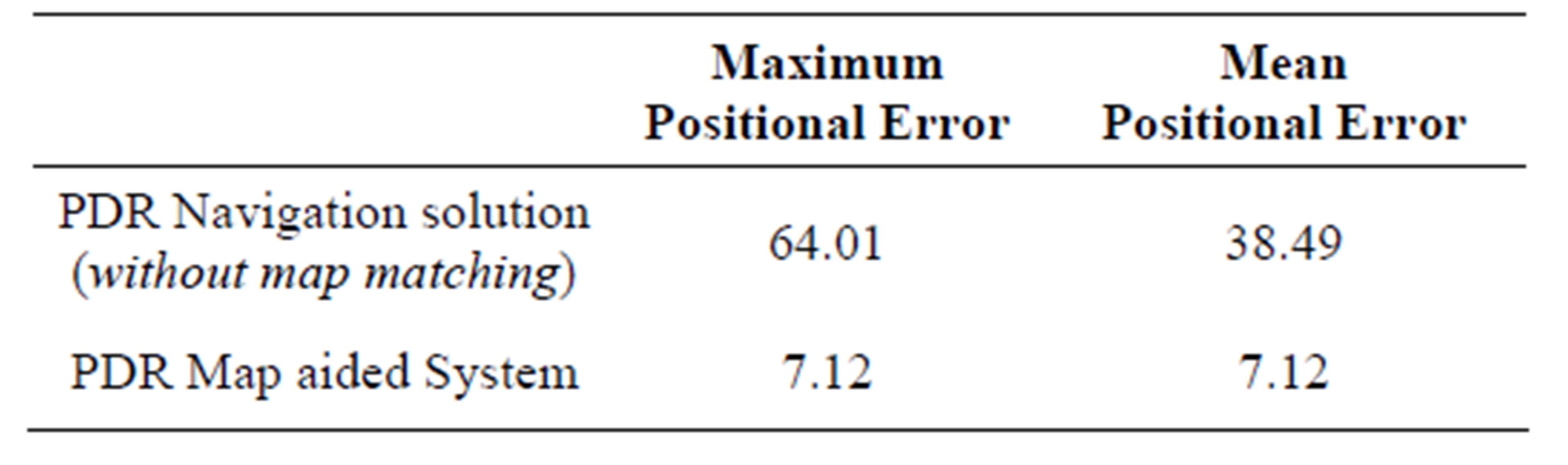
Table 5. Positional errors using the map as a reference (MacEwan and Kinesiology).
The map aided algorithm utilized the obtained PDR solution, the developed geometrical and topological map matching with turn detection technique and the geospatial data modeled for navigation applications. The algorithm provides a reliable, accurate and continuous matched navigation solution. The developed system was field-tested twice on different trajectories in different buildings and achieved a significantly reliable matched navigation solution each time based on the matching links percentage and the positional errors improvement.
9. Acknowledgements
This work was supported in part by research funds from TECTERRA Commercialization and the Natural Science and Engineering Research Council of Canada (NSERC) to Dr. Naser El-Sheimy. Also, Members of the Mobile Multi-Sensor research group, the University of Calgary are acknowledged for their efforts in field testing.
REFERENCES
- N. El-Sheimy and X. Niu, “The Promise of MEMS to the Navigation Community,” Inside GNSS, Vol. 2, 2007, pp. 46-56.
- W. Abdel-Hamid, “Accuracy Enhancement of Integrated MEMS-IMU/GPS Systems for Land Vehicular Navigation Applications,” University of Calgary, Calgary, 2004.
- M. Attia, A. Moussa, X, Zhao and N. El-Sheimy, “Assisting Personal Positioning in Indoor Environments Using Map Matching,” Archives of Photogrammetry, Cartography and Remote Sensing, Vol. 22, 2011, pp. 39-49.
- M. A. Quddus, et al., “Current Map-Matching Algorithms for Transport Applications: State of the Art and Future Research Directions,” Transportation Research Part C: Emerging Technologies, Vol. 15, No. 5, 2007, pp. 312- 328. doi:10.1016/j.trc.2007.05.002
- C. E. White, et al., “Some Map Matching Algorithms for Personal Navigation Assistants,” Transportation Research Part C: Emerging Technologies, Vol. 8, No. 1-6, 2000, pp. 91-108. doi:10.1016/S0968-090X(00)00026-7
- J. S. Greenfeld, “Matching GPS Observations to Locations on a Digital Map,” Transportation Research Board. Meeting, National Research Council (US), Washington DC, 2002.
- M. Quddus, et al., “A General Map Matching Algorithm for Transport Telematics Applications,” GPS Solutions, Vol. 7, No. 3, 2003, pp. 157-167. doi:10.1007/s10291-003-0069-z
- C. Basnayake, et al., “An HSGPS, Inertial and MapMatching Integrated Portable Vehicular Navigation System for Uninterrupted Real-Time Vehicular Navigation,” International Journal of Vehicle Information and Communication Systems, Vol. 1, 2005, pp. 131-151. doi:10.1504/IJVICS.2005.007589
- J. B. Bullock, “A Prototype Portable Vehicle Navigation System Utilizing Map Aided GPS,” University of Calgary, Calgary, 1995.
- K. Miesenberger, et al., “A Smart Indoor Navigation Solution Based on Building Information Model and Google Android,” In: Computers Helping People with Special Needs, Vol. 5105, Springer, Berlin/Heidelberg, 2008, pp. 1050-1056.
- P. Arto, et al., “Towards Designing Better Maps for Indoor Navigation: Experiences from a Case Study,” Proceedings of the 8th International Conference on Mobile and Ubiquitous Multimedia, Cambridge, 22-25 November 2009.
- G. Glanzer, et al., “Semi-Autonomous Indoor Positioning Using MEMS-Based Inertial Measurement Units and Building Information,” 6th Workshop on Positioning, Navigation and Communication, Hannover, 19 March 2009, pp. 135- 139.
- M. Khider, et al., “The Effect of Maps-Enhanced Novel Movement Models on Pedestrian Navigation Performance,” Proceedings of the 12th Annual European Navigation Conference (ENC 2008), Toulouse, 2008,pp. 22-28.
- X. Zhao, et al., “An Economical and Effective MultiSensor Integration for Portable Navigation System,” Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, September 2009, pp. 2088-2095.
- S. Shin, et al., “Adaptive Step Length Estimation Algorithm Using Low-Cost MEMS Inertial Sensors,” IEEE Sensors Applications Symposium, San Diego, 6-8 February 2007, pp. 1-5.
- A. Ali, et al., “An Improved Personal Dead-Reckoning Algorithm for Dynamically Changing Smartphone User Modes,” Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, 17-21 September 2012, pp. 2432-2439.

