Positioning
Vol.4 No.1(2013), Article ID:28353,3 pages DOI:10.4236/pos.2013.41002
Effect of Height and Geographic Latitude of Location of GPS Station on Ratio of Total Amount of Water Vapors on Wet Delay of GPS Signals
![]()
1State Committee on Land and Mapping, Baku, Azerbaijan; 2Azerbaijan State Oil Academy, Baku, Azerbaijan; 3State Aero Geodesy Enterprise of the State Committee on Land and Mapping, Baku, Azerbaijan; 4Research Institute of Aerospace Informatics, Baku, Azerbaijan.
Email: hasadzade2001@yahoo.com
Received November 22nd, 2012; revised December 23rd, 2012; accepted December 31st, 2012
Keywords: Wet Delay; GPS; Water Vapors; Measurements; Optimization
ABSTRACT
The averaged integrated parameter representing the mean value of ratio of total water vapors on wet delay 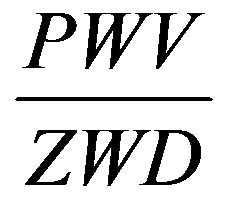 at the chosen distance of latitude
at the chosen distance of latitude 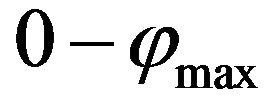 is suggested. The function of interrelation of such parameters as height of location site and latitude is suggested. It is shown, that the optimal function
is suggested. The function of interrelation of such parameters as height of location site and latitude is suggested. It is shown, that the optimal function  does exist which bring the averaged integrated parameter to its minimal value.
does exist which bring the averaged integrated parameter to its minimal value.
1. Introduction
It is well known, that in meteorology all information concerning the processes taken place at the Earth’s surface is obtained using ground measuring instruments, installed in the observation stations and satellites. It should be taken into account, that density of location of observation stations is not so high and in order to calculate the required meteorological parameter for any geographical point located among the observation stations the mathematical methods of interpretation should be applied. This question is studied in the work [1], where the necessity of integrated accounting of such factors as orography, presence of water vapors, and latitude effects arising in determining the effective values of distances upon interpolation of meteorological fields is discussed. The calculated effective values of distances can be used by purposes of interpolation of such meteorological parameters as mean monthly values of daily sums of duration of solar irradiation, daily extremal values of air temperature, atmospheric pressure of water vapors etc.
2. Brief Review of Background of Research Task
In the work [1], it was shown that the taking into account of latitude effects on estimate of interpolated values of distances increases the accuracy of interpolation. In this case the orography effects can be corrected by the way of weighted accounting of difference of location heights of studied objects. In the work [1] the following formulae is suggested to determine in effective value of distance 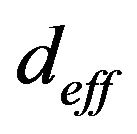 between point P and points where the measurements
between point P and points where the measurements 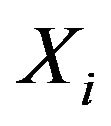 are carried out
are carried out
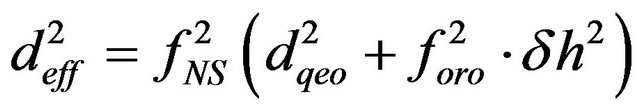 , (1)
, (1)
where
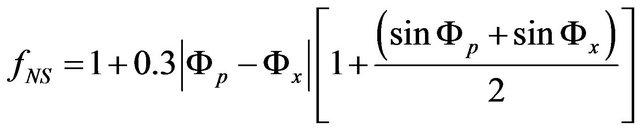 , (2)
, (2)
where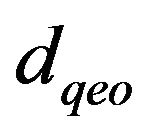 —the geographic distance;
—the geographic distance; 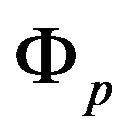 and
and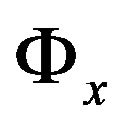 — latitudes of points P and X;
— latitudes of points P and X;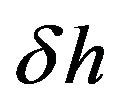 —difference of heights of points P and X;
—difference of heights of points P and X; .
.
As it is seen from Formulas (1) and (2), upon carrying out the interpolation calculations for such important parameters GPS systems as mean temperature and total amount of precipitable water vapor, the geographical latitude and height of location of relevant sites should be taken into account. The similar question is also discussed in detail in the work [2].
As it is noted in the work [2], measurements of total amount of water vapors in atmosphere using ground GPS systems began in 1992 with publications of works of Bevis et al. [3,4]. Suggested in these works methods and techniques of GPS measurements were modified in followed works of many authors, due to high importance of accurate evaluation of total amount of water vapors in atmosphere for development of meteorological prognosis, organization of climatic monitoring, for atmospheric researches and also for accurate positioning of objects. As it was shown in work [2], in order to calculate the total amount of precipitable water vapor on the basis of GPS signals delay data it is necessary to possess the data of air pressure and mean temperature at the surface of the Earth.
As it was shown in the work [4] the following simple ratio may be considered
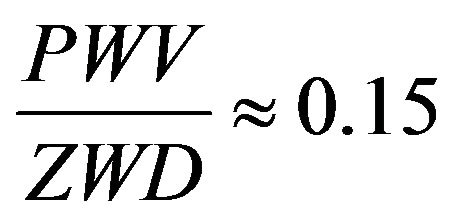 , (3)
, (3)
where PWV—total amount of precipitable water vapors; ZWD—zenith wet delay of GPS signals.
In the following works the estimate (3) was corrected and the major factors effecting on above ratio were determined.
It should be noted, that in general, the zenith wet delay may be determined as follows
 , (4)
, (4)
where ZTD—total zenith delay; ZHD—zenith hydrostatic delay.
In Formula (4), ZHD is to be calculated using wellknown empirical formulas [5,6], and PWV is determined as
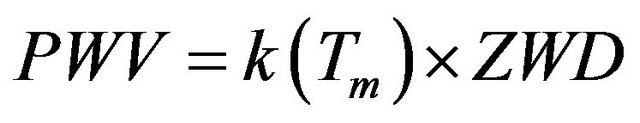 , (5)
, (5)
where —dimensionless value, depending on mean weighted value of temperature of atmosphere.
—dimensionless value, depending on mean weighted value of temperature of atmosphere.
The question on variability of the ratio  is of special importance for carrying out of practical work on GPS measurements.
is of special importance for carrying out of practical work on GPS measurements.
As it is noted in the work [2], as a result of four years experimental researches held in GPS objects of India it was determined that
 . (6)
. (6)
In this case the ratio 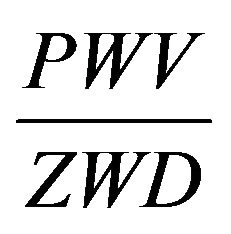 depends on geographical latitude and height of location [2].
depends on geographical latitude and height of location [2].
In the work [2] the following empirical model of dependence of ratio 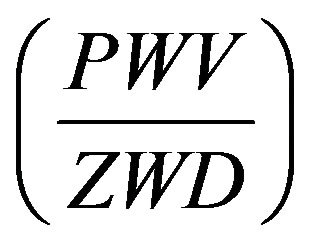 on mean height
on mean height 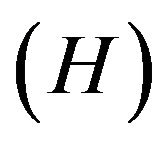 and the geographical latitude
and the geographical latitude ![]() is suggested
is suggested
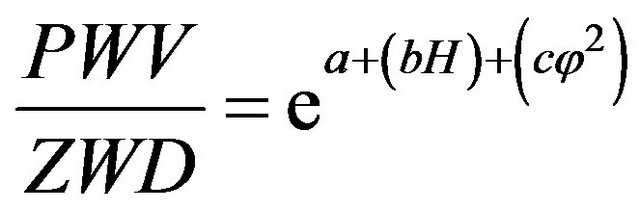 , (7)
, (7)
where
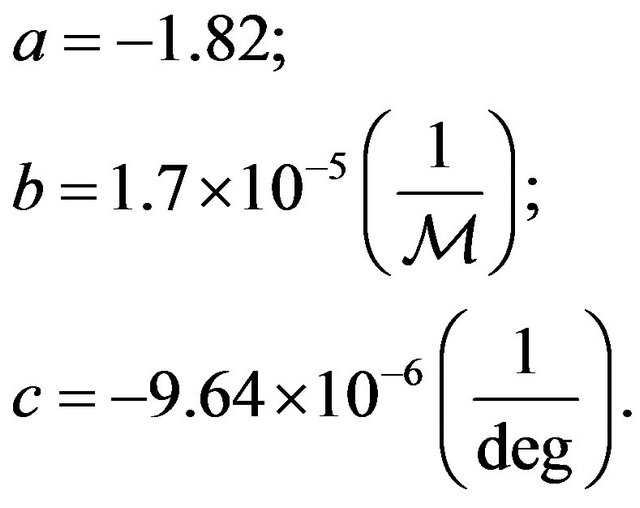
3. Formulation and Solution of the Problem
Taking into account the above brief review of modern condition of studied question and the empirical model (7) the task of research in the present paper can by formulated as follows:
1) The develop the mean integrated parameter, representing the ratio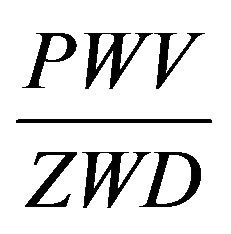 .
.
2) To bring into consideration the function of interrelation of such major parameters as H and![]() , i.e.
, i.e.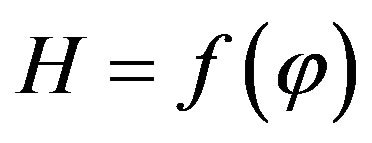 .
.
3) To find out the optimum function 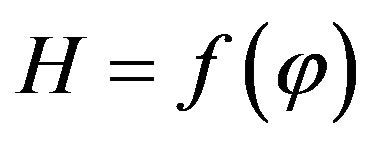 which guarantees the extremum of mean value of ratio
which guarantees the extremum of mean value of ratio
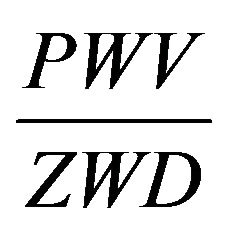 .
.
Taking into consideration the Formula (7) the mean integrated value of ratio (3) may be determined as
 . (8)
. (8)
Taking into account the suggested here function 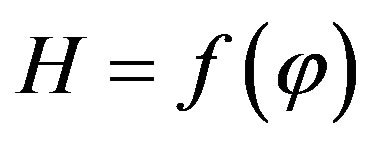 and the Equation (8) the latter can be written as
and the Equation (8) the latter can be written as
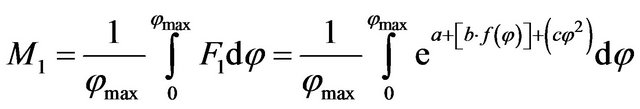 . (9)
. (9)
The limitation condition, necessary for carrying out of variation optimization can be formulated as
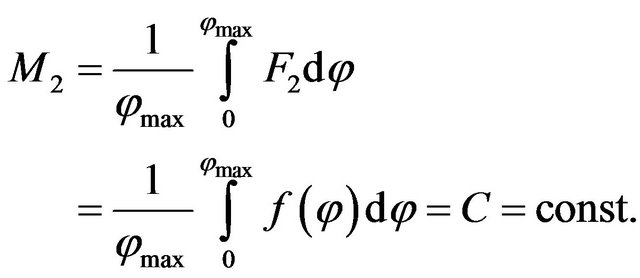 (10)
(10)
The meaning of limitation condition (10) is that the function 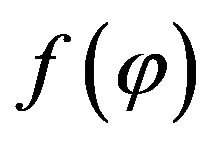 may be in arbitrary form, but its mean integrated value should be equal to apriori given constant C.
may be in arbitrary form, but its mean integrated value should be equal to apriori given constant C.
This condition makes it possible to limit the class of functions within which the optimal function 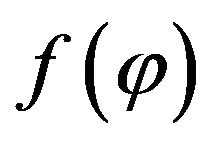 should be searched.
should be searched.
Taking into account the Formulas (9) and (10) the functional of unconditioned variation optimization can be formed as follows
 (11)
(11)
In order to find out the optimal function  we use the method of Euler, according which to calculate the optimum function
we use the method of Euler, according which to calculate the optimum function 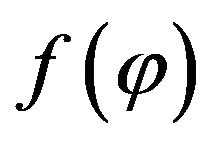 the following equation should be computed
the following equation should be computed
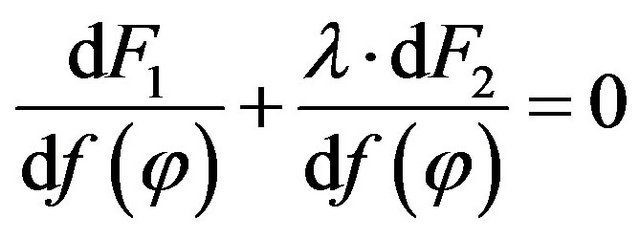 . (12)
. (12)
Taking into account Formulas (11) and (12) we get
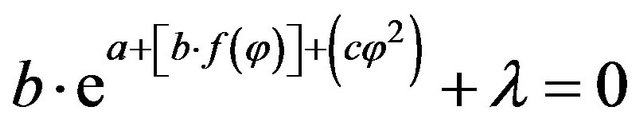 . (13)
. (13)
From Equation (13) we have
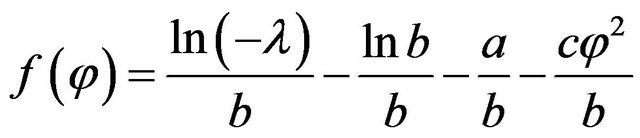 . (14)
. (14)
Taking into account Formulas (10) and (14) we can find out that
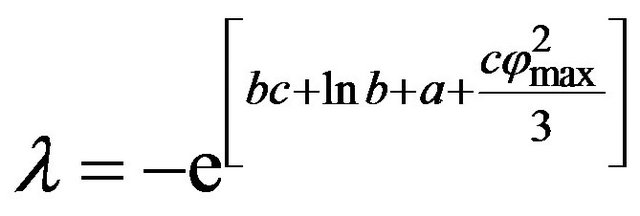 . (15)
. (15)
Taking into account the Equations (13) and (15) we have
 , (16)
, (16)
where
 .
.
The second derivative of (11) calculated in Euler method may be presented as
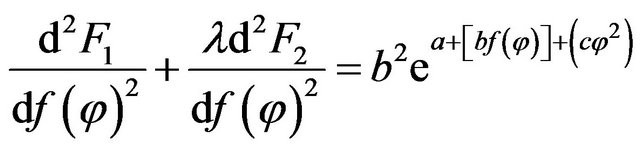 . (17)
. (17)
Thus the functional (8) riches its maximal value upon realization of function (16). It does mean, that most worse variant of dependence of H on![]() , which leads the ratio
, which leads the ratio 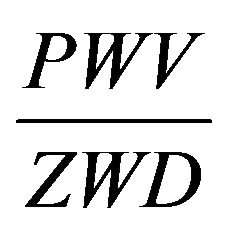 to its maximum value is the function (16).
to its maximum value is the function (16).
It should be noted, that despite the model (7) was suggested for condition of India, we can suppose, that due to general nature of question of effect of orography and geometric latitude on value of parameter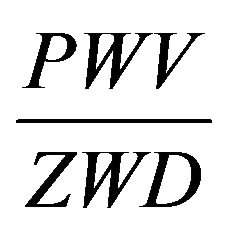 , the model (7) is true also for other countries while the coefficients a, b, c will be different for them.
, the model (7) is true also for other countries while the coefficients a, b, c will be different for them.
4. Conclusions
In conclusion we can formulate all major results of the held research:
1) The mean integrated parameter 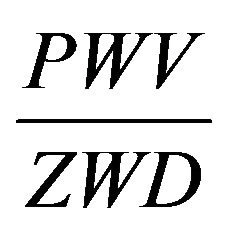 representing the averaged value of ratio of total water vapors on wet delay at the chosen distance of geographical latitude is suggested.
representing the averaged value of ratio of total water vapors on wet delay at the chosen distance of geographical latitude is suggested.
2) The function of interrelation between parameters H and![]() ,
,  is suggested and researched.
is suggested and researched.
3) The presence of optimal function 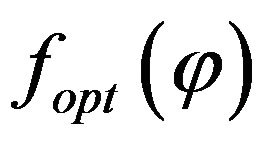 is shown, upon which the suggested mean integrated parameter can reach its minimal value.
is shown, upon which the suggested mean integrated parameter can reach its minimal value.
REFERENCES
- M. Lefevre, J. Remund, M. Albuisson and L. Wald, “Study of Effective Distances for Interpolation Schemes in Meteorology,” 27th Annual Assembly, European Geophysical Society, Nice, 21-26 April 2002.
- S. Jade and M. S. M. Vijayan, “GPS-Based Atmospheric Precipitable Water Vapour Estimation Using Meteorological Parameters Interpolated from NCEP Global Reanalysis Data,” Journal of Geophysical Research, Vol. 113, No. D03, 2008. doi:10.1029/2007JD008758
- M. Bevis, S. Businger, T. A. Herring, C. Rocken, R. A. Anthes and R. Ware, “GPS Meteoology: Remote Sensing of Atmospheric Water Vapour Using the Global Positioning System,” Journal of Geophysical Research: Atmospheres, Vol. 97, No. D14, 1992, pp. 15787-15801. doi:10.1029/92JD01517
- M. Bevis, S. Businger and S. Chiswell, “GPS Meteorology: Mapping Zenith Wet Delays on to Precipitable Water,” Journal of Applied Meteorology, Vol. 33, No. 3, 1994, pp. 379-386. doi:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
- G. Elgered, J. L. Davis, T. A. Hering and I. I. Shapiro, “Geodesy by Radio Interferometry: Water Vapour Radiometry for Estimation of the Wet Delay,” Journal of Geophysical Research, Vol. 96, No. B4, 1991, pp. 6541- 6555. doi:10.1029/90JB00834
- J. Foster, M. Bevis and W. Raymond, “Precipitable Water and the Lognormal Distribution,” Journal of Geophysical Research, Vol. 111, No. D15, 2006. doi:10.1029/2005JD006731

