Positioning
Vol.2 No.3(2011), Article ID:6959,22 pages DOI:10.4236/pos.2011.23012
Unmanned Airborne Magnetic and VLF Investigations: Effective Geophysical Methodology for the Near Future
![]()
1Department of Geophysics and Planetary Sciences, Tel Aviv University, Tel Aviv, Israel; 2NESS Company, Tel Aviv, Israel.
Email: levap@post.tau.ac.il
Received July 10th, 2011; revised August 8th, 2011; accepted August 22nd, 2011.
Keywords: ROV, Magnetics, VLF, Kalman Filtering, Multimodel Approach, Integrated Analysis
ABSTRACT
Airborne geophysical investigations are now recognized as a powerful tool for geological-geophysical mapping, mineral prospecting, environmental assessments, ecological monitoring, etc. Currently, however, there are two main drawbacks to effective application of these investigations: 1) the difficulty of conducting geophysical surveys at low altitudes, 2) heightened danger for the aircraft crew, especially in regions with a rugged topography. Unmanned or socalled Remote Operated Vehicles (ROV) surveys are not bound by these limitations. The new unmanned generation of small and maneuvering vehicles can fly at levels of a few (even one) meters above the Earth’s surface, and thus follow the relief, while simultaneously making geophysical measurements. In addition, ROV geophysical investigations have extremely low exploitation costs. Finally, measurements of geophysical fields at different observation levels can provide new, unique geological-geophysical information. This chapter discusses future geophysical integration into ROV of measurements of magnetic and VLF electromagnetic fields. The use of GPS with improved wide-band Kalman filtering will be able to provide exact geodetic coordinates. A novel interpreting system for complex environments is presented that includes non-conventional methods for localizing targets in noisy backgrounds, filtering temporary variations from magnetic and VLF fields, eliminating terrain relief influence, quantitative analysis of the observed anomalies and their integrated examination. This system can be successfully applied at various scales for analysis of geophysical data obtained by ROVs to search for useful minerals, geological mapping, the resolution of many environmental problems, and geophysical monitoring of dangerous geological phenomena.
1. Introduction
The first airborne geophysical survey was carried out by Logachev in the former Soviet Union in 1936 [1]. He used an inductor magnetometer to measure the magnetic field from an aircraft. This first air-magnetometer had a sensitivity of about 100 nT. By contrast, current aeromagnetic surveys in conventional vehicles can provide an accuracy of 5 nT and higher [2]. Salem et al. [3] described an equivalent source approach that removes small environmental noise from the airborne measurements. Tezkan et al. [4] reported a recent pilot project that tested the feasibility of unmanned aircraft systems to carry out aeromagnetic surveys. Advances in reduced size and maneuverability of Remote Operated Vehicles (ROV) have led to an accuracy of 0.5 - 1 nT (and higher) in surveys at low altitudes. The main advantages of ROVs are the absence of an aircraft crew (GPS controlled unmanned surveys can be carried out even at very low altitudes and in risky conditions) and comparatively low expenditures for geophysical observation projects. In addition, most methods of geophysical field analysis require knowledge of the field distribution at different levels over the Earth’s surface. The ROV facilitates the collection of these data without having to use transformation methods. Finally, unmanned air geophysical surveys are extremely cheap (many tens of times less than conventional aircraft surveys).
A magnetic field is natural, and a Very Low Frequency (VLF) field can be considered to be quasi-natural [5] (given that perhaps several dozen VLF transmitters in the world radiate electromagnetic waves almost continuously). Combined aircraft magnetic/VLF measurements are potentially highly effective (e.g., [6-11]), but the highflying altitudes of conventional aircraft have limited the possibilities of using VLF. The ROV application can substantially reduce the distance between the airborne vehicle and the target while preserving the main advantages of conventional surveys. Thus the two main advantages of ROVs are their low cost and the fact that they are unmanned and hence do not put crew at risk.
ROV geophysical surveys at low altitudes can make important contributions to the search for minerals, geological mapping, various environmental (including archeological-geophysical) investigations, and military monitoring [4,12-17]. To increase the amount of data retrieved on such missions, new algorithms for the processing and interpretation of magnetic/VLF fields have been developed, especially for complex physical-geological conditions (mainly presented in [18]) including inclined magnetization (polarization), rugged terrain relief, unknown level of the normal field and a variety of anomalous sources.
Despite the progress in geophysical inertial navigation systems [19-21], etc., small ROVs flying at low altitudes are not sufficiently precise. The improved Kalman filtering with wide-band noise model presented here is designed to eliminate some of the obstacles to precise navigation.
2. Improved Kalman Filtering for Precise Vehicle Navigation
Kalman filtering (KF) is one of the most widely used methods for optimal estimation of random processes. The KF algorithm is the best linear real-time recursive filtering algorithm and is used to solve optimal filtration problems for non-stationary and multidimensional systems [22-24]. However, the conventional Kalman filter is limited by the fact that KF uses white noise and that the useful signal and noise are independent. However, these limitations are a mathematical idealization that gives an approximate description of real noise. In fact, the actual noise is marked by a property that ensures the correlation of its values within a small time interval; i.e. if we denote this noise by j, then
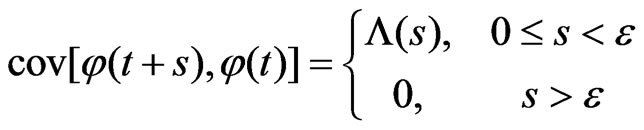 , (1)
, (1)
where 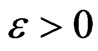 is a small value.
is a small value.
The first attempts to introduce wide-band noise into the KF model to solve navigation problems in geophysics were carried out by Eppelbaum et al. [25].
The basic idea behind the method consists of modeling physical wide-band noise in the form of a distributed delay of the mathematical noise, i.e.
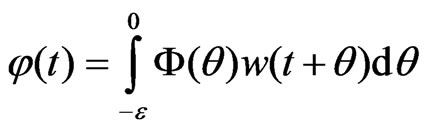 ,
, 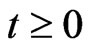 , (2)
, (2)
where w is the white noise, 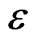 = const > 0, and F is the deterministic function. If cov[w(t), w(s)] =
= const > 0, and F is the deterministic function. If cov[w(t), w(s)] = 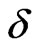 (t – s), then cov[
(t – s), then cov[ ,
, ] = 0 with s ³
] = 0 with s ³ 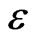 and
and
 (3)
(3)
with 0 £ s < , i.e.
, i.e. 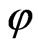 is the stationary wide-band noise.
is the stationary wide-band noise.
In geophysical practice, forms of wideband noise can be expressed by autocovariance functions. Therefore, the problem involves modeling wideband noise in the form of (2), when the autocovariance function is given.
Let the wideband noise  have the autocovariance function (1), i.e., the function
have the autocovariance function (1), i.e., the function  is known. Then from Equation (3) it follows that for
is known. Then from Equation (3) it follows that for 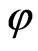 to be modeled in the form of Equation (2)
to be modeled in the form of Equation (2) 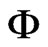 must satisfy the equation [26]:
must satisfy the equation [26]:
 =
=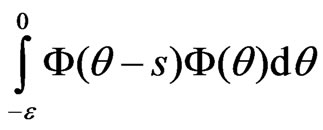 , 0 £ s £
, 0 £ s £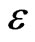 . (4)
. (4)
Equation (4) is a convolution equation. It can be solved by direct and inverse Fourier or Laplace transforms. Application of the abovementioned approach can thus enhance the precision of GPS navigation in ROVs.
3. Airborne Magnetic Data Analysis in Complex Environments
3.1. Elimination of Temporary Magnetic Variations
The accuracy of a high-precision ROV magnetic survey should not exceed the value of 1 nT. At the same time, the presence of both natural (basalts, diabases, gabbro, etc.) and artificial (iron and iron-containing) objects that have high magnetization may cause secondary variation effects which can be seen above this value. Conventional procedures for eliminating temporary (primary) magnetic variations are based on the trivial additive expression (e.g., [27]):
 , (5)
, (5)
where t is the time, x, y are the spatial coordinates, DT (x, y, t) is the magnetic field recorded along a profile, 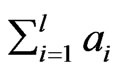 is the sum of “useful” anomalies and
is the sum of “useful” anomalies and 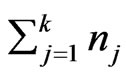 is the sum of the noise component caused by temporary variations. This formula only allows for simple subtracttion of the noise component from the observed magnetic field and cannot be used to calculate the effect of seconddary variations.
is the sum of the noise component caused by temporary variations. This formula only allows for simple subtracttion of the noise component from the observed magnetic field and cannot be used to calculate the effect of seconddary variations.
Since the secondary variation effect depends linearly on the intensity of the primary variations [28], the typical model of magnetic observations may be described in the following way [29]:
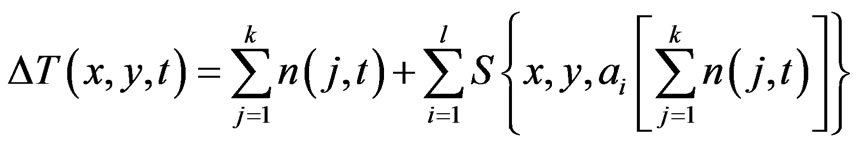 (6)
(6)
where 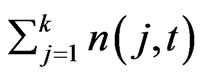 are the field variations in time,
are the field variations in time,  is the sum of the effects from the anomalous objects and geological inhomogeneities of the medium with regard to their dependence on the field variations.
is the sum of the effects from the anomalous objects and geological inhomogeneities of the medium with regard to their dependence on the field variations.
Measurements at the points of the profile made at different times t (³2) make it possible to obtain a solvable set of algebraic equations so that the signal DT can be extracted with sufficient accuracy.
3.2. Calculation of Terrain Relief Influence and Estimation of Magnetization of the Medium
Another disturbance factor is the influence of inclined relief on the magnetic measurements (the illustration here is limited to the case where the ROV follows the relief forms). Interestingly, this disturbance can help estimate the average magnetization of the medium.
It is well known that in the case of direct magnetization, the field maxima correspond to ridges of the “magnetic” relief, while the minima correspond to its valleys [27,30]. At the same time, the terrain relief effect is generally two-fold and can be attributed to the effect of the form and physical properties of the topographic bodies making up the relief and secondly to the effect of the slope of the observation line (profile), which causes variations in the distance from the field recording point to the target of excitation [18]. The correlation technique below (see Equations (7)-(9)) eliminates the effect of the first component. The second effect can be eliminated by using special expressions during the quantitative interpretation of magnetic anomalies [18].
An analytical approach [18] shows the possibility of obtaining the linear relation between the magnetic field and the height of observation to a typical element of rugged relief—a slope (an inclined ledge, or step). All the main relief forms can be approximated with the use of one or another combination of slopes (for each of these slopes, the correlation field can be constructed). Hence, as rough as it may be, there is a simple and effective method for eliminating the effect of magnetized rock relief. To apply this method, a correlation field is constructed between DT (total magnetic field) and h (height of observation) values. For typical cases the correlation field is used to determine the terrain correction:
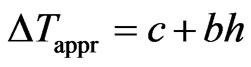 , (7)
, (7)
where DT is the magnetic field, and b and c are the factors of a linear equation computed using the least-square method (LSM).
It was shown that a b factor could be utilized to estimate the magnetization of the upper part of a geological section [18]:
 , (8)
, (8)
where I is the magnetization of the upper part of geological section, a is the acute angle between the slope face and horizon, R is the slope length across the strike.
Given that a and R are known from the field observations and coefficient b is calculated using the LSM, the I value is easy to determine. Consequently, magnetic lowaltitude measurements along the inclined slopes may be used for quick estimation of the magnetization of the target medium. Eppelbaum [31] concluded that integrated ROV horizontal and inclined observations can serve to obtain the parameters of the medium magnetization even over a flat relief.
The corrected field DTcorr may be formulated as:
 , (9)
, (9)
where DTobser is the observed field.
Elimination of the topographic effect by the correlation technique allows practically complete smoothing out of the anomalies caused by the influence of uneven relief.
Along with the linear approximation of the relationship between the field and the height, approximations in the form of the square trinomial (parabolic equation) are appropriate here. This method can be used to improve the choice of the level for reducing the field to one plane. When computing a correlation field, the areas with the largest dispersion (compared to the averaging line), correspond to the profile intervals under which the disturbing bodies are situated. The presence of dispersion in itself is indicative of a hidden inhomogeneity in the section.
3.3. Initial Analysis of Magnetic Data
Visual analysis of magnetic anomalies is one of the most important steps in an investigation and all further stages may depend on the results of this initial decision-making. The standard principles of magnetic map analysis are presented in Table 1. However, for oblique magnetization (polarization), principles 3 - 7 are not applicable. The shape of the anomalies is complicated by the horizontal component effect. This is why in the northern hemisphere, anomalies become asymmetric when the body’s magnetization is parallel to the Earth’s field. Thus, anomaly maxima of sublatitudinal-oriented bodies are

Table 1. Common principles of magnetic map analysis (developed for vertical positive redundant magnetization) (after [18], with modifications).
shifted southward, whereas the minimum is located in the northern periphery of the anomaly. If the magnetization inclination with respect to the horizon is not large (in southern latitudes), the maximum is shifted more to the south, and the intensity of the minimum increases. Inflection points (maximum gradients) in the anomaly plots are displaced southward from the projections of lateral sides of the anomalous body on the plane. In the case of a depth-limited body, one of the minima (the southern one) may disappear along the maximum periphery. In the case of three-dimensional bodies of approximately isometric section, magnetic anomaly distortions occur not only due the inclination of the magnetization vector to the horizon plane, but also due to the difference in orientation of the horizontal magnetization projection with respect to the body’s axes [32]. Therefore, the analysis of graphs is not sufficient, and generally maps need to be analyzed as well.
3.4. Advanced Quantitative Interpretation of Magnetic Anomalies
One of the main interpretation problems is the quantitative determination of magnetic anomalies (inverse problem solution). The interpretation problem consists of a detailed description of the anomalous source using the measured magnetic field. However, the major principles of quantitative interpretation that were formalized for vertical magnetization do not work under conditions of oblique magnetization in low and central latitudes. Besides the influence of oblique magnetization, additional DT anomaly distortions occur due to rugged (inclined) relief and unknown level of the normal magnetic field.
This stage involves the application of rapid methods for quantitative interpretation of magnetic anomalies to construct an initial model of the geological section. Unlike certain conventional techniques [27,33-37], the methods presented below are applicable in conditions of rugged terrain topography and arbitrary magnetization of objects where the normal field level is unknown [18].
In conditions of oblique magnetization, the “reduction to pole” calculation of “pseudogravimetric” anomalies [38] is often used. However, this procedure is only suitable when all the anomalous bodies in the area under study are magnetized parallel to the geomagnetic field, and simultaneously when the bodies have subvertical dipping. The magnetic fields can only be recalculated correctly when these restrictions are adhered to; this yields graphs that are symmetrical, and further interpretation using conventional methods can be carried out. Similar approaches based on the transformation of the observed magnetic field (for instance, analytic signal [39]), have the same limitations.
The methodology developed for complex environments [18] employs further modifications of the characteristic point method, the tangent method and the areal method, and utilizes the most commonly applied geometric models such as thin inclined bed (TIB), horizontal circular cylinder (HCC) and thick bed (TB) (a comprihensive explanation of these methods is given in [18]). These three geometric models, with different modifications, may be used for approximation and the corresponding quantitative interpretation of anomalies generated by various geological and environmental objects.
The procedures for interpreting anomalies generating the abovementioned models are presented in Tables 2-4.
The modern interpreting system developed for magnetic field analysis [18,40,41] includes the following components (besides the conventional ones): 1) Elimination of the secondary effect of time variations, 2) Calculation of the terrain relief influence and estimation of magnetization of the medium, 3) Application of an information-heuristic approach to geophysical field quailtative interpretation, 4) Inverse problem solution for complex environments (inclined relief, oblique magnetization and unknown level of the normal magnetic field), 5) 3-D modeling of magnetic (and gravity, if necessary) field. In the last 6) stage all kinds of information obtained in the previous stages (1-5) and conventional steps are integrated, and a final physical-geological model is developed.
The first stage of a ROV magnetic survey must include a priori investigation (generalization) of all available


Table 2. Formulae for quantitative interpretation of magnetic anomalies over anomalous bodies approximated by thin seam and a horizontal circular cylinder using the improved characteristic point method (after [18], with modifications).
magnetic properties of the targets and the surrounding medium. Figure 1 depicts a typical flow chart for aeromagnetic field analysis.
The following parameters are taken from the anomaly plot in the characteristic point method (Figure 2): d1 = difference of semiamplitude point abscissae, d2 = difference of extremum abscissae, d5 = difference of inflection point abscissae.
In the tangent method four tangents are employed: two horizontal lines with respect to the anomaly extrema and two inclined lines passing through the points of the bend on the leftand right-hand branches of the anomaly plot. The following terms are taken from the plot (Figure 2): d3 = difference in abscissae of the points of intersection

Table 3. Formulae for quantitative interpretation of magnetic anomalies over anomalous bodies approximated by thin seam and horizontal circular cylinder using the improved tangent method (after [18], with modifications).

Table 4. Formulae for quantitative interpretation of magnetic anomalies over anomalous bodies approximated by a thin bed and horizontal circular cylinder using the improved characteristic areal method [42].
of an inclined tangent with horizontal tangents on one branch; d4 = the same on the other branch (d3 is selected from the plot branch with conjugated extrema), d6 = interval between d3 and d4, d8 = difference in abscissae between point of intersection of left inclined tangent with lower horizontal tangent and inflection point on left branch (d6 and d8 are used for the model of thick bed only). A detailed description of magnetic field examination of a thick bed model is given in [18].
The areal method is based on calculation of separate areas limited by the anomalous curve, horizontal line and two vertical lines crossing some singular points at the anomalous curve.
When anomalies are observed on an inclined profile, the obtained parameters characterize a fictitious body. The transition from fictitious body parameters to those of
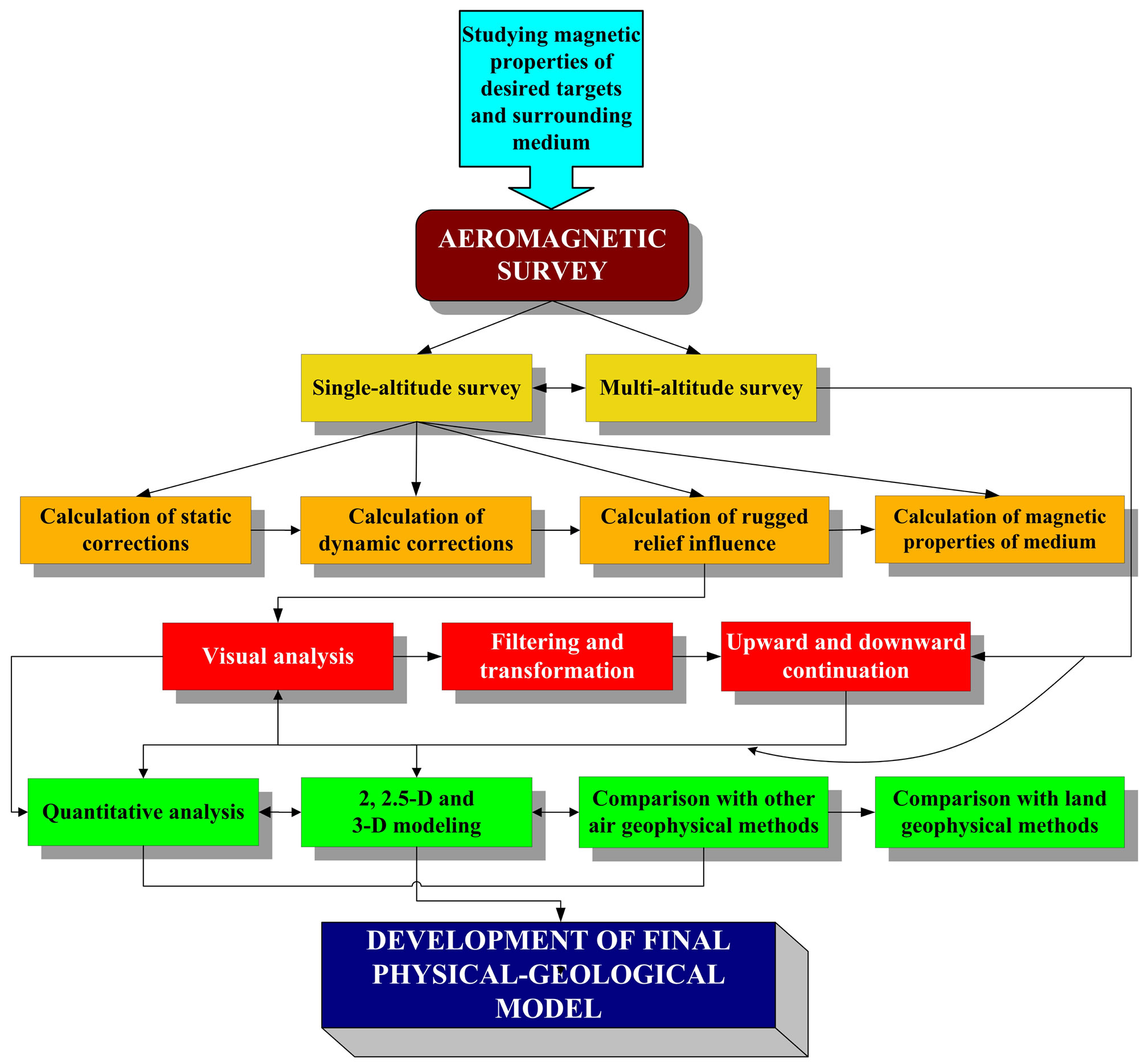
Figure 1. A generalized flow chart for airborne magnetic field analysis.
the real body is done by applying the following expressions (the subscript “r” stands for a parameter of the real body):
 , (10)
, (10)
where h is the depth of the body upper edge occurrence (or HCC center), xo is the shifting of the anomaly maximum from the projection of the center of the disturbing body to the Earth’s surface (caused by oblique magnetization), and wo is the angle of the terrain relief inclination (wo > 0 when the inclination is toward the positive direction of the x-axis).
Figure 3 illustrates the application of these methods— improved tangents and characteristic points (Figure 3(a)) and characteristic areal method (Figure 3(b))—for the airborne magnetic field analysis in the Big Somalit (southern slope of the Greater Caucasus).
4. A Scheme for VLF Data Examination
The most effective scheme for VLF data observations is when the magnetic and electric components of the electromagnetic VLF field are measured. The VLF equipment developed in the former USSR and Russia e.g., [43, 44] can be used to obtain the values of magnetic compo-
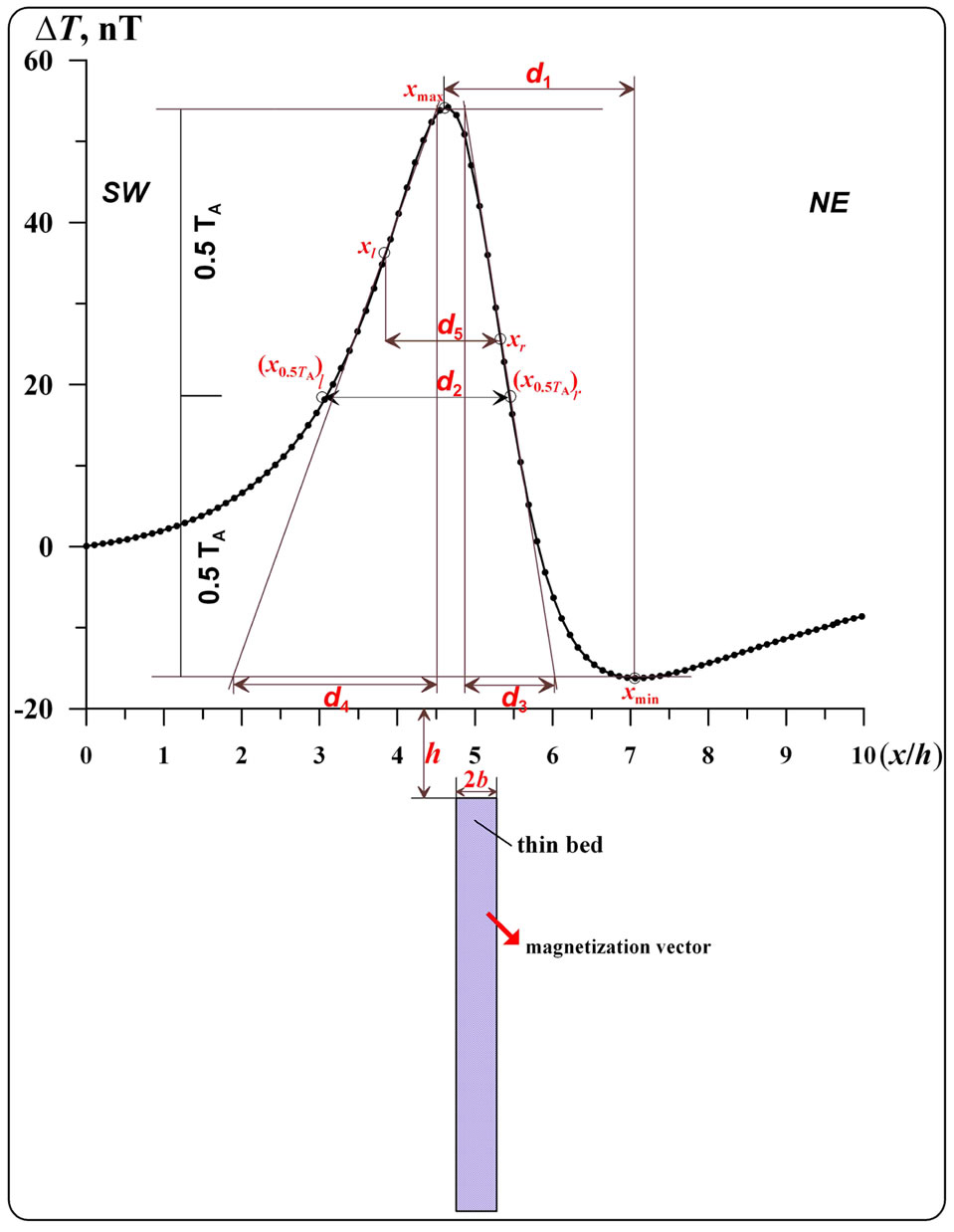
Figure 2. Position of characteristic points and tangents at DT anomaly due to an obliquely magnetized thin bed.
nents on coordinate axes: Hx, Hy and Hz, as well as changes of radio-bearing Y to the VLF transmitter (as well as other parameters). The use of magnetic VLF components in many cases is more efficient because of the comparatively low level of the various kinds of noise [45]. Observation parameters such as tilt angle and ellipticity are not discussed in this article.
An important peculiarity of a VLF ROV survey at low altitudes is the slow decrease in the VLF signal with increasing observation height over the Earth’s surface [43, 46].
4.1. Elimination of Temporary VLF Variations
The problem of eliminating time variations in the VLF method is crucially important since the intensity of these variations is often compatible with the intensity of the averaged VLF signal during the time of the field survey. The following approaches have been used to overcome this problem.
In early VLF methodology, an approximate technique was used based on field intensity measurements at a control point (CP) before and after fieldwork [47]. The corresponding corrections were introduced by interpolation assuming that the field intensity change was linear. However, practical application of this method led to con-
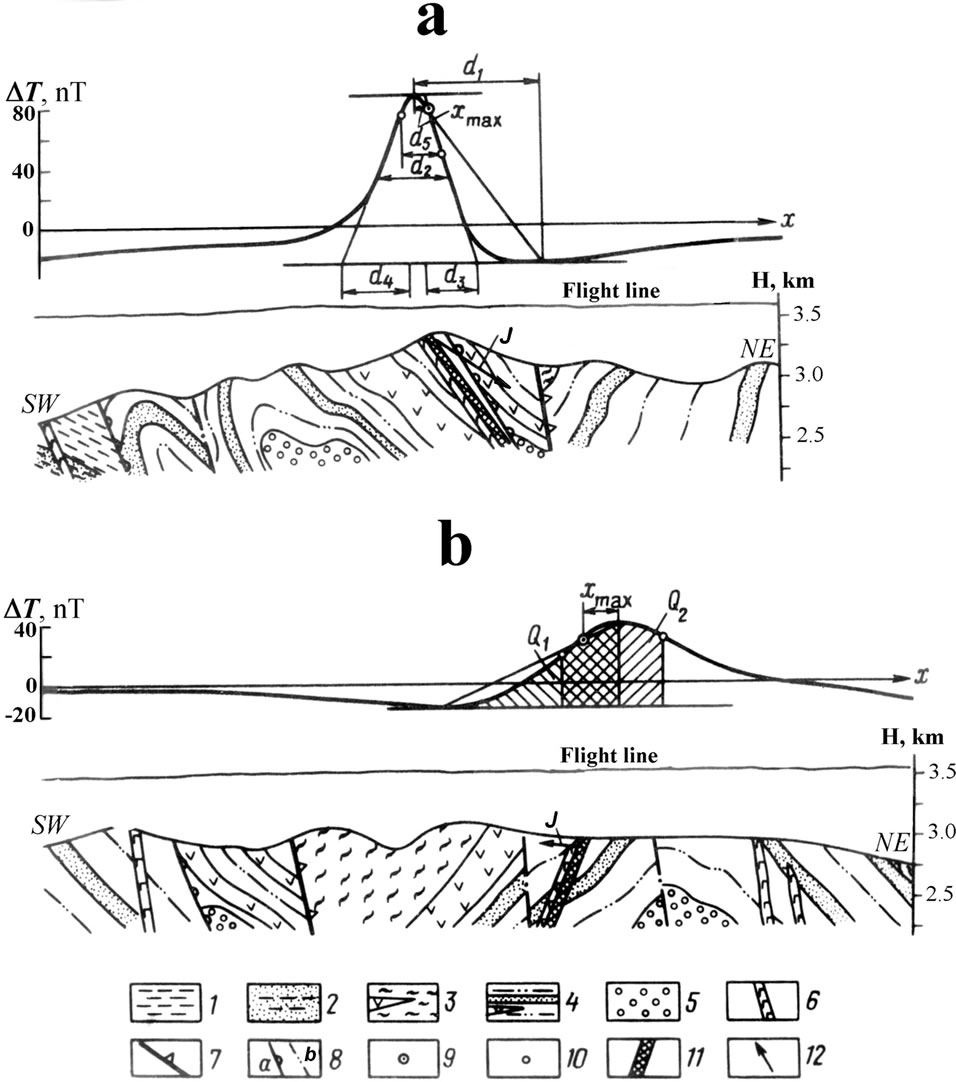
Figure 3. Examples of the quantitative interpretation of DT plots along the profiles 171 (a) and 181 (b) in the Big Somalit (southern part of the Greater Caucasus) (after [42], with modifications). 1) Yalakhkam suite J2aal2, 2) Zainkam suite J2aal1, 3) Nagab suite J1toa3, 4) Tseilakhan suite J1toa3, 5) the Lower and Middle Toarcian suite J1toa1-2, 6) dikes of the gabbro-diabasic association, 7) the Major Caucasian upthrust-overthrust, 8) ore controlling (a) and ore distributing (b) upthrust-overthrusts, 9) Reford’s point [33], 10) inflection points, 11) anomalous body according to the interpretation results, 12) obtained direction of the magnetization vector.
siderable error.
A modification of this method is described in [48]. The difference is that the time period of supposedly linear variations is assumed to be 1 hour. The area is rejected if the level of variation for 1 hour exceeds 20%. This method, however, suffers from following disadvantages. Experience in field explorations in various regions indicates that the intensity changes of the VLF fields under study (even over the course of one hour) often cannot be approximated by a straight line with sufficient accuracy. In addition, the amount of variation during this period may exceed 20%. It is also worth noting that this method neglects the effect of variation noise intensities on useful anomalies. It is obvious, however, that time variations in VLF field intensity affect the radiowave energy passing from the air into the ground. The intensity of the secondary field tends to increase or decrease, respectively (especially in the presence of anomalous objects of increased or decreased conductivity), and the variations are non-uniform. When disregarded, this fact can distort the interpretation of the results.
The Scintrex Company developed an automatic attachment to a VLF receiver. Variations are eliminated by obtaining a synchronous ratio of the vertical component Hz of the VLF magnetic field to the total horizontal component Hj. However, it was found by experimental field exploration that the Hz/Hj ratio may vary even for observations at the same point. Quantitative interpretation of the Hz/Hj curve presents certain difficulties. Another approach described by Scintrex in a recent guide for using the VLF equipment, consists of the selection of the frequency and time interval that is the most stable temporally for the target region. Vallee et al. [49] suggest a similar method. However, this approach would benefit from improvement.
The wavefront is thus assumed to be a plane whereas the primary field intensity is taken to be constant within the area of the detailed geophysical investigation (25 - 100 km2). The large distance from the utilized VLF transmitters (2,000 to 10,000 km) accounts for the uniformity of the primary field [46,50] both at CP and in the investigated area.
The following additive model of a geophysical field is applicable in practice for investigation by the VLF method:
 , (11)
, (11)
where Fj is the field observed along the profile, 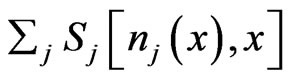 is the sum of effects from the anomaly-forming objects and geological inhomogeneities of the section (taking the dependence on field variation into account),
is the sum of effects from the anomaly-forming objects and geological inhomogeneities of the section (taking the dependence on field variation into account),  represents the noise of field variations in time (time dependence is omitted in Equation (11) for simplicity).
represents the noise of field variations in time (time dependence is omitted in Equation (11) for simplicity).
It is known that for the VLF field the conduction currents dominate the displacement currents [43,51], which is the major condition for quasi-stationarity [52]. The proportionality of the secondary electromagnetic fields (both magnetic and electric) to the primary fields has been confirmed in a number of publications e.g. [53,54]. Hence given the physical effect of the subvertical radiowave propagation in the ground [43,55] and taking into account Equation (11), the following simplified model of VLF observations can be used in practice [56]:
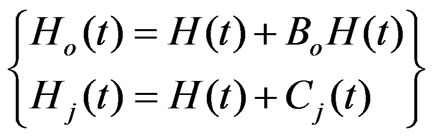 , (12)
, (12)
where Ho(t) is the observation at the control point; Hj(t) is the observation on the profile, H(t) is the primary field intensity, B and C are coefficients reflecting electromagnetic properties of the medium; indices “j” and “o” mark the observation point on the profile and CP, respectively.
Considering that Bo = const, this parameter, which is a basic value for the given area, can be assumed for convenience to be equal to zero. Solving Equations (12) in the parametric form, we obtain the values Hclear cleared from the variations for each profile point:
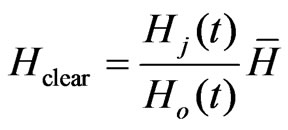 , (13)
, (13)
where  is the certain averaged value of the field.
is the certain averaged value of the field.
Thus, the proposed scheme of eliminating variations in the VLF method is based on synchronous recording of the observations along the profile and variations at CP. Automatic variation recordings present no difficulties and can be carried out with a discretization interval of 3 - 5 seconds. This method substantially eliminates observation distortions caused by field variations with time (both over the course of a day and at different days in a survey) by reducing observation results to a common level [57].
It should be noted that Bozzo et al. [58] later noted the necessity of normalization of field VLF measurements to the primary field observations.
4.2. VLF: Calculation of Rugged Relief Influence
Attempts have been made by many investigators to reduce the terrain relief effect. An analytical approach was suggested by Tarkhov [47]; however, the analytical calculations proved to be too cumbersome even for a model of a uniform slope made up of homogeneous rocks and, above all, were at variance with the experimental results. Sedelnikov [59] analyzed in detail the theoretical problem of electric field distortions caused by a single mountain and a mountain range but suggested no method for eliminating topographic effects.
Karous’s [60] publication about topographic influences on the vertical component of the VLF magnetic field (Hz) is clearly of interest, but no numerical results were reported. Eberle [61] proposed simplified formulas to calculate relief corrections for the observed electromagnetic fields; their application is however limited by a number of conditions, e.g., the requirement that the disturbing object and the observation profile should be in the most favorable position for excitation by the primary VLF magnetic field. This requirement is seldom obtained or difficult to meet.
The second approach is based on a physical (analog) simulation of electromagnetic fields. Gordeyev et al. [43] constructed models which describe quantitatively the distribution of the VLF electromagnetic field over different terrain relief forms. Baker and Myers [62] suggested an electromagnetic field “reduction” method based on their model investigations. This method, however, has the same 1imitations as found in [61].
Gordeyev [63] proposed a third approach. It is based on using a graticule (chart) method to reduce the topographic effect on the total horizontal magnetic field component of remote transmitters. It is difficult to apply at greater relief dips and can, in some cases, impair the interpretation. This limitation is traceable to the “build-up effect” of a rectangular graticule in a complicated (relative to the observation profile) topography, which in addition is often characterized by different electric properties.
It should be noted that the effect of the Earth’s surface topography on radiowave propagation is a fairly important problem in radiophysics and has been investigated by quite a number of researchers. An overview of the literature suggests that this problem has yet to be adequately resolved. A numerical calculation of radiowave scattering is a complicated electrodynamic problem even for the simple case of diffraction by a homogeneous wedge displaying finite conductivity [64,65]. The difficulties increase progressively for statistically inhomogeneous (i.e. real) surfaces. Bass and Fuks [66] emphasized that under natural conditions there is no need to find the detailed structure of a scattered field and that it is sufficient to ascertain some reflected-signal parameters averaged for the whole class of surfaces and targets. In general, researchers have apparently come to the conclusion that wave scattering is determined largely by coordinate functions and represents a combination of wave diffraction on an arbitrary surface and an application of the theory of probability and mathematical statistics.
A review of the literature and results of VLF surveys lead to the following general rules:
1) The plots of Hx (the x-axis is aligned with the observation profile) and the total horizontal magnetic field component Hj substantially copy the surface topography. There is a direct correlation between the increase or decrease in the recorded field intensities and positive or negative landforms, respectively.
2) The intensity of the recorded VLF magnetic field is directly proportional to the relative elevation of observation points. The topographic anomalies caused by local relief forms are similar to those from conductive bodies but have a smoother appearance.
3) When the angle between the radiowave arrival direction and that of a relief element is close to 0˚, the relief effect is relatively large and when this angle is close to 90˚, it is relatively small, but in any case the relief effect is always present. Since all observations are made in the “distant” (“wave”) zone, the bearing changes negligibly along the profile and the topographic anomaly is quasi-independent of the bearing change.
4) VLF field intensity is mainly dependent on the resistivity of the rocks in the upper portion of a geological section.
All the abovementioned points make it possible to apply the correlation method developed in magnetic prospecting (see section “Calculation of terrain relief influence and estimation of magnetization of medium”) to the VLF method [45]. An example of the correlation approach is presented in Figure 4. This example illustrates the application of the correlation technique on a portion of the Katekh pyrite-polymetallic deposit in the southern slope of the Greater Caucasus. A frequency of 16.0 kHz was used in the investigation (the transmitter was in Rugby, Great Britain), and the profile azimuth was 60˚. The ribbon-like band of the pyrite-polymetallic ore was located at a depth of about 60 - 80 m in the sandy argillaceous series of the Upper Aalenian. The average resistivity of the nearly uniform surrounding medium was in the range of 700 to 900 Ohm×m; the resistivity of the massive ore body was a fraction of 1 Ohm×m. The skin depth in the surrounding medium was about 110 m. Since a topographic anomaly was superimposed on a small signal from a relatively deep-seated anomalous object, it was difficult to detect the latter.
Two different correlations were made for the southwestern and the northeastern slope, yielding correlation coefficients (between the relief heights and VLF intensity) of r1 = 0.988 and r2 = 0.85. The results for the southwestern slope are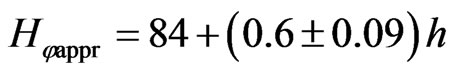 , and the northeastern slope
, and the northeastern slope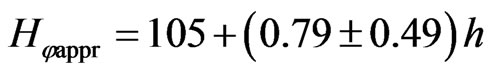 . After removing the relief effect, a positive anomaly can clearly be seen on the northeastern slope in the
. After removing the relief effect, a positive anomaly can clearly be seen on the northeastern slope in the  plot. This anomaly may be due to the edge effect of a deep ore body, whereas the minimum on the southwestern slope may correspond to the opposite edge of the subhorizontal tabular ore body, since the anomaly is not very large in this case [45].
plot. This anomaly may be due to the edge effect of a deep ore body, whereas the minimum on the southwestern slope may correspond to the opposite edge of the subhorizontal tabular ore body, since the anomaly is not very large in this case [45].
4.3. VLF: A Brief Review of Available Methods of Quantitative Analysis
An overview of the literature indicates that there are practically no reliable or rapid techniques of quantitative interpretation in the VLF method.
The methods suggested by Tarkhov [47] are semiquantitative. The procedure developed by Fraser [67] is useful primarily for revealing anomalous objects.
The techniques presented by Gordeyev and Sedelnikov [68], based on calculating the anomaly extrema ratio, require knowing the zero line (or a normal field). The wrong choice of the zero line entails substantial errors in determining the anomalous object’s quantitative parameters. Moreover, these techniques are not intended for interpretation in conditions of rugged terrain relief.
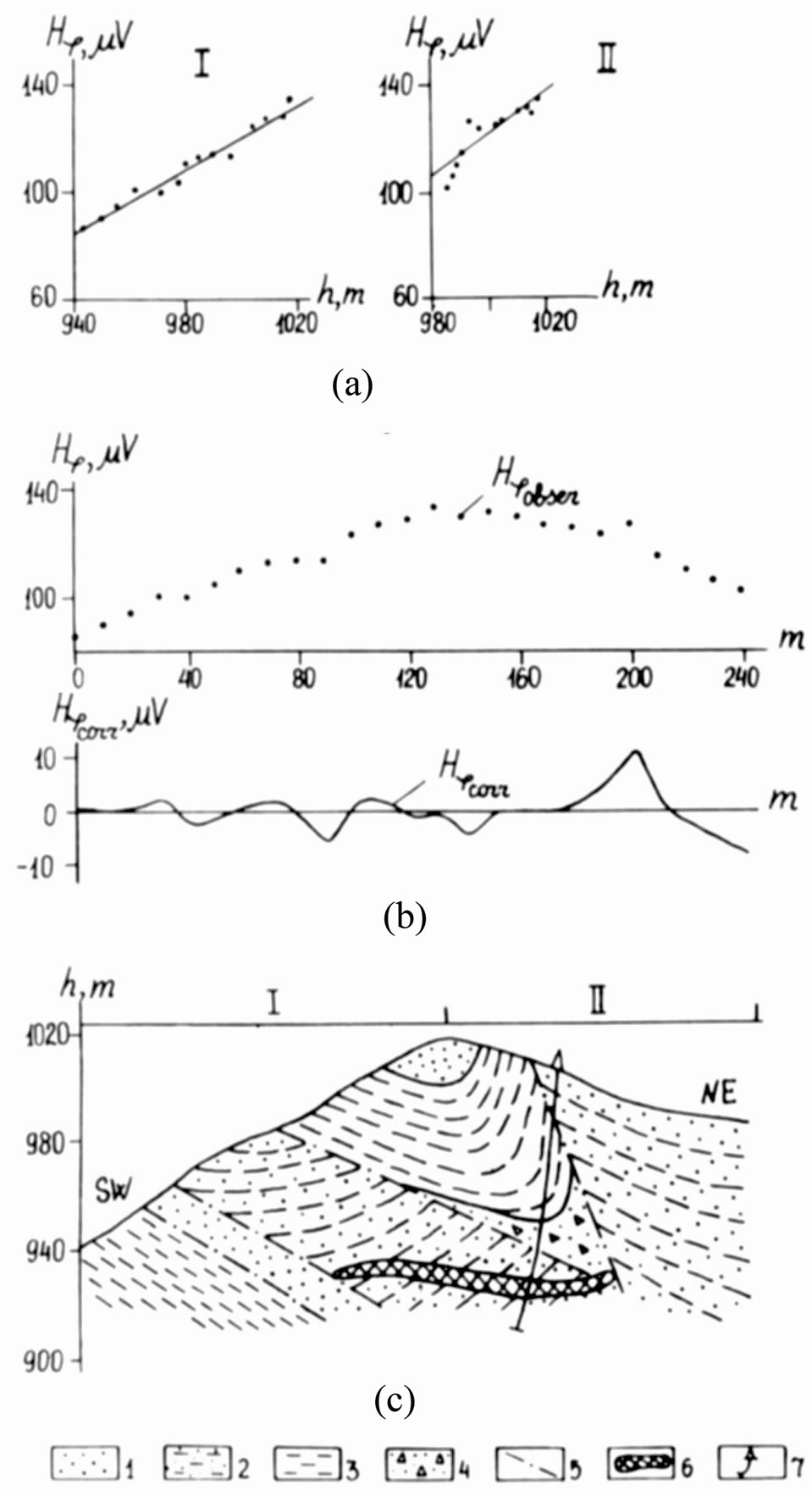
Figure 4. Correlation technique for reducing the terrain relief effect on a portion of the Katekh pyrite-polymetallic deposit (northern Azerbaijan). (a) Correlation, (b) Plots of observed and corrected Hj values, (c) Geological section. 1) fine and medium-grained sandstone, 2) alternating sandstone and clay shale strata, 3) clay shales, 4) brecciated zone, 5) fractures, 6) ore body, 7) prospecting borehole.
Dmitriyev et al. [53] solved the direct problem for a number of electromagnetic methods (including the VLF method). They provide a numerical analysis of the anomalies due to bed-like bodies as a function of their electric properties, dimensions and position with respect to the Earth’s surface and the observation profile. However, computational difficulties restrict the range of models to simple ones.
Zhdanov and Keller [69] noted that the finite differences method is the most effective method of electromagnetic field mathematical simulation. However, the expediency of its application depends on the size of the design area and the desired accuracy of the computations. For a large area of calculations or when the simulation problem needs higher accuracy, the computations exceed all possible limits even for high-performance modern computers.
Khesin et al. [18] pointed out that some approaches developed for magnetotelluric sounding [69,70] could be employed in the VLF method. Basokur and Candansayar [71] suggested using the same methodology (however, these authors concluded that this interpretation could only be qualitative). However, the application of these procedures is usually limited by the extreme variations in electric properties in the (upper) part of geological section.
Gordeyev and Sedelnikov [68] and Gordeyev et al. [43] characterized the physical (analog) simulation of VLF curves by models of a vertical inclined thin bed. The accuracy of the physical simulation and that of the numerical computations (for simple models) is at present approximately the same, and is roughly 8% - 10%.
Numerous other works, in many respects similar to those mentioned above, have dealt with the anomaly interpretation in the VLF method. For instance, Karous and Hjelt [72] and Olsson [73] reported the calculation of plots for vertical and horizontal components of the magnetic field of VLF using a model of an inclined thin bed with different dip angles. The depth of occurrence of the upper edge of the bed varies as well. Olsson [73], Tesmull and Crossley [74] and Poddar [75] computed components of the VLF fields for different types of geoelectric sections. Miecznik [76] calculated the magnetic components of the VLF field caused by another model of an anomalous object—that of a conductive cylinder placed in a homogeneous medium (the cases of both E-polarization and H-polarization are discussed).
The characteristic VLF diagrams developed by Sinha [77] can provide useful information about vertical and inclined conductive beds in simple geological-geophysical conditions. The VLF first derivative method proposed by Djeddi et al. [78] is based on perspective (the authors suggest eliminating the topographic effect of peculiarities in the interpretation process).
Olsson [55] solved the direct problem for an ideal conductive half-plane with different dip angles, when the half-plane is covered by variable-depth loose deposits. In addition, he proposed techniques for a simplified interpretation of VLF data based on the utilization of the extremum points in the anomaly plot. The synthetic models presented Pedersen and Oskooi [79] provide a better understanding of the resolving power of the VLF data. The same authors propose employing a tensor variant of VLF measurements. Monteiro et al. [80] described a quantitative interpretation of VLF-EM data using 2-D models (the authors developed a 2-D regularized modeling of VLF-EM data based on a forward solution using the finite-element method) that yields practical results about the Earth’s average resistivity in the survey area. Kaikkonen and Sharma [81] performed a 2-D simulation of noise-free and noisy media with single-body and complex models. The authors highlight the need to use reliable a priori information before running such a simulation.
4.4. VLF Field: Possible Application of Procedures Developed for Potential Field Analysis
The main equations used in the theory of alternating electromagnetic field are Maxwell’s Equations:
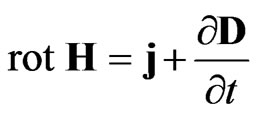 , (14a)
, (14a)
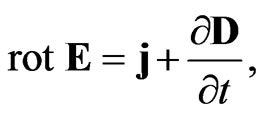 (14b)
(14b)
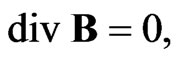 (14c)
(14c)
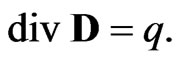 (14d)
(14d)
Here H and B are the magnetic field vectors (H stands for intensity and B for induction); E and D are the electric field vectors (E stands for intensity and D for induction); q is the charge density; j is the conduction current density.
Equation (14a) can be written as [52]:
rot H = C = jcond + jdisp,(15)
where C is the total current density; jcond and jdisp are the conduction and displacement current densities, respectively.
It has been found that at frequencies of 10 to 30 kHz, jdisp » 0 [51]. Therefore
rot H = jcond (16)
or H = n E,(17)
wheren is the electric conductivity.
An EM field can be considered quasi-stationary if it satisfies the three conditions of quasi-stationarity. Landau and Lifshitz [82] described the physical meaning of these conditions. Alpin et al. [52] formulated these conditions as applied to geophysics. These requirements are as follows:
1) Slow field variation.
2) Closed currents.
3) To avoid an appreciable lag in the magnetic field variation, the region including magnetic field generating currents and observation points must not be too large.
Let us consider these conditions in more detail.
1) The study of time variations of the VLF fields has shown that sharp changes in intensity are not characteristic of these fields. Nonetheless, variations that use a special procedure in fieldwork should be eliminated (see section “Elimination of temporary VLF variations”).
2) This condition follows from Equation (16), since div rot H = 0 and, therefore, div j = 0. Almost closed currents do not violate this condition.
3) This condition can be formulated in the following way: the length of an electromagnetic wave in the ground should essentially exceed the length of the investigated objects. This condition, as a rule, is fulfilled in the prospecting of mineral deposits, geological mapping and object analysis in engineering and military geophysics.
It is known that the fundamental solution of the Laplace Equation in the 2-D case is the following function:
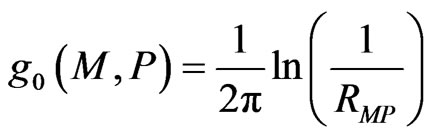 , (18)
, (18)
where RMP is the distance between points M and P (M is the observation point and P is the point of the body).
The fundamental solution of the Helmholtz wave equation is a Hankel function of the first kind with zero order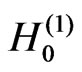 :
:
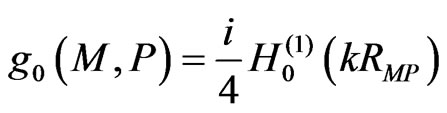 , (19)
, (19)
where k is the wave number and i is the imaginary unit.
The function (19) is the analog of the function (18) for a Laplace equation.
Using the above correspondence, Hänl et al. [83] and Dmitriyev [54] proved the relationship between Green’s solutions of the Laplace and Helmholtz equations. This allowed them to show how the results obtained in potential theory could be extended to the Helmholtz equation.
Dmitriyev et al. [53] indicated that the association of the singular points resulting from the VLF field anomaly plots with geometrical parameters of the bed is analogous to the well-known behavior of singular points in potential field anomalies. Zhdanov [84] carried out a theoretical investigation of the application of a set of Cauchy-type integral analogs to the problems of electromagnetism. It was suggested that the methods developed in potential theory for analytical continuation, separation and quantitative interpretation could be applied to quasi-stationary electromagnetic anomalies.
The quasi-stationarity of the electromagnetic field follows from condition 1).
An overview of publications [43,75,85-87] indicates that a conductive thin inclined bed (TIB) is the most common model for the VLF technique. The analytical expressions of the fields for this model (the 2D case) are presented in Table 5.
In this table Zv and Xv are the vertical and horizontal magnetic field components for vertical magnetization, respectively; Hx and Hz are the horizontal and vertical VLF magnetic field components, respectively; Ho is the VLF primary field intensity; k is the coefficient reflecting geometry and conductivity of the bed.
Evidently, Zv is proportional to Hx, whereas Xv is proportional to Hz. Similar results were obtained for a HCC model [44].
Thus, the plots of magnetic fields of VLF transmitters can be interpreted by special methods elaborated in potential field theory (in particular, in magnetic prospecting, for conditions of rugged terrain relief, oblique magnetization (polarization) and an unknown level of the normal field). The E-polarization vector, in the first approximation, is the analog of the magnetization vector [44].
In this context, the special techniques presented in Tables 2-4 are of practical interest. In the VLF method can be applied the interpretation techniques developed in magnetic prospecting for inclined thin bed and horizontal circular cylinder models. It should be noted that the total horizontal component of the VLF magnetic field 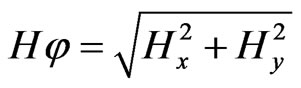 can be interpreted as the Hx component, since the contribution of the Hy component is usually relatively small.
can be interpreted as the Hx component, since the contribution of the Hy component is usually relatively small.
The essential distinctions reflecting the quasi-potential nature of the VLF electromagnetic field are as follows. In magnetic prospecting the induced magnetization vector of an inclined bed is approximately parallel to the geomagnetic field vector, irrespective of the bed dip direction, where the magnetic susceptibility does not exceed 0.1 SI unit. In electric prospecting by the VLF method under E-polarization for highly conductive objects, the equivalent vector of polarization that causes the anomalies of Hx and Hz, approaches the body axis, with a slight deviation toward the vertical for gently sloping bodies [43,88]. This makes it possible to utilize the generalized angle θ derived from these methods and to represent the difference in the inclination angles for the bed and the

Table 5. Comparison of analytical expressions for TIB in magnetic prospecting and the VLF method.
polarization vector to estimate the bed dip angle by the following empirical formulas [44]:
1) for the Hx anomaly
 , (20a)
, (20a)
2) for the Hz anomaly
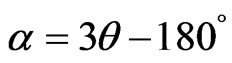 , (20b)
, (20b)
where a is the bed inclination.
For the case of observations on a sloping relief, the angle a is calculated as follows:
1) for the Hx anomaly
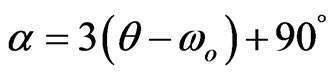 (21a)
(21a)
2) for the Hz anomaly
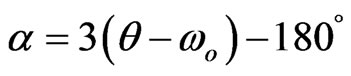 (21b)
(21b)
(wo is derived in Equation (10)).
It should be noted that the position of the upper edge could be slightly shifted from the real upper edge downward along the bed dip. This is because the linear currents are concentrated in the upper portion of the conductive object. This portion may be situated below this object’s upper edge.
An actual example of VLF data analysis (land survey) is presented in Figure 5. It should be noted that the anomalous magnetic X-component computed for the same model is very similar to the observed VLF Hz curve (their similarity follows from Table 5). The figure clearly shows that the results fit well with the geological data.
5. Revealing Buried Ring (Circular) Structures
One of key problems of airborne magnetic and VLF prospecting is the delineation of typical buried objects of various size and origin. Ways of revealing such buried objects with an a-priori shape are illustrated below through examples of identification of ring (circular) buried targets.
Ring structures (RS) are omnipresent in the Earth’s environment (Figure 6). RS are generally classified as Terrestrial and Extraterrestrial (natural RS) and Archaeological and Military/Engineering (artificial RS). It should be noted that the dimensions of natural RS are often compatible with the size of artificial RS (excluding well-studied RS measuring tens or hundreds of km in diameter) [42]. Thus problems sometimes arise not only of RS identification, but also of correct classification. Greater accuracy can be achieved by collecting more comprehensive geological (geochemical), geophysical, archaeological and engineering (military) data. In the flow chart below (Figure 6) natural RS are classified using Khain’s [89] scheme and the author’s supplements
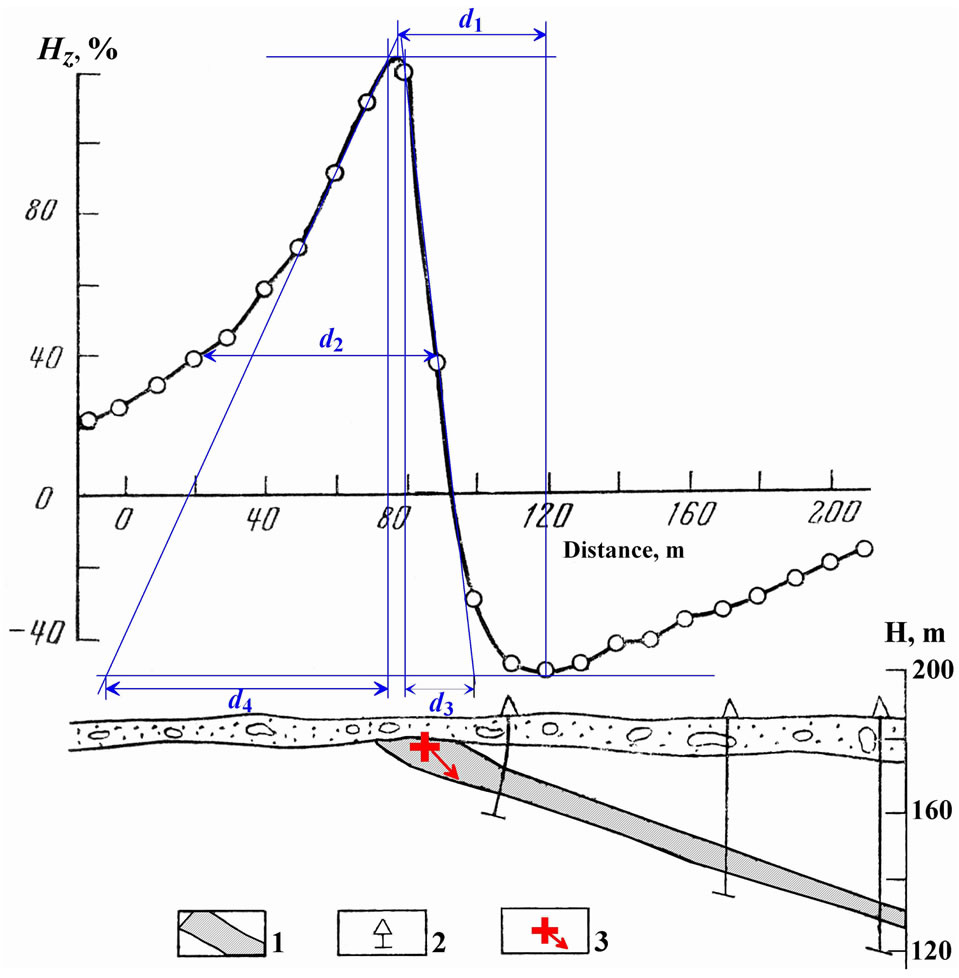
Figure 5. Quantitative analysis of the vertical magnetic component Hz of the electromagnetic VLF field in the copper-nickel deposit (Kola Peninsula, Russia) using the improved tangent and characteristic point methods (observed curve and geological section after [43]). 1) copper-nickel ore body, 2) location of drilled boreholes, 3) results of quantitative analysis: cross indicates position of the upper edge of the ore body and arrow shows its dip direction.
and extensions [90]. Archaeological RS are presented as buried caves, roads and circus rings, remains of fortresses and towers, tailings of detritus and religious edifices. Detection should be coordinated with conventional land geophysics. Military RS are displayed as rocket shafts, command posts and defensive installations (obviously, classes of these RS may be significantly extended). In the latter case the ROV application has clear cut advantages over other identification methods.
5.1. Methodology of RS Delineation
The first problem in RS analysis is to differentiate the targets from background noise. Very frequently it is difficult to single out RS in complex geological-geophysical environments, especially when the typical rectangular network of geophysical observations is used. In addition, anomalies caused by RS can be distinguished from geophysical field features by their location on the periphery of anomalous bodies. For this purpose a special method has been devised to distinguish concentric structures by computing the sums of the horizontal gradients of geophysical fields and their differences [18]. It should be noted that ROV applications make it possible to observe geophysical fields at different levels and compute the difference in horizontal gradients between them, which might be employed as additional searching indicator.
The apparent graticule radii drawn at an interval of 45˚ determine the horizontal gradients (Figure 7(c)). The sum of the gradients should be higher in the presence of circular features and other signals should remain constant. Here the correlation of the sum of the gradients (or the average gradient) for a circle with a radius Rn and a ring external to this circle limited by Rn and Rn+1 radii makes it possible to determine whether the circular feature reflects a centric or ring structure (Figure 7(d)). The sum of gradients inside the circle tends to zero in the absence of a centric texture [18]. An application of this method is depicted on a model of an inclined circular cylinder magnetized along its dip (Figures 7(a) and (b)).
6. Multimodel Approach to Geophysical Data Analysis
The multimodel approach to geophysical data analysis is described in the example below of detailed magnetic prospecting. A quantitative interpretation of magnetic anomalies (and many other geophysical methods) was traditionally oriented to a single model for buried object identification. When several hypotheses relating to the parameters of the body causing the disturbance (i.e., the buried object) were made, usually only one model was selected that roughly presented the object in the domain Wx of k-dimensional space of the physical-environmental factors. As a rule however, human, industrial and geodynamic activity as well as various geological/environmental processes affect many environmental features.
Additional sources of noise that affect interpretation include rugged terrain relief, oblique polarization of geological objects and a heterogeneous host medium. Thus the response function Gi—the geophysical field—may ambiguously represent an archaeological target. To overcome this issue, domain Wx can be divided into several subdomains W1, W2, ..., Wm and in each a single model will dominate [92]. In such a way m physical-environmental models of the same target can be developed, where each is corrected for separate subdomains W1, W2, ..., Wm.
For instance, remains of an ancient wall in specific geological conditions can be defined as a thick bed (magnetic field), a sphere (gravity field) and a horizontal plate (VLF or resistivity). The multimodel approach can also be applied at varying levels of geophysical field recording. As a result, different explanatory models contribute to the process of quantitative interpretation. Integrating several response functions GI, leads to a more accurate and reliable physical-environmental model of the buried target.
The simple model presented in Figure 8 shows how two different interpretations of the same ancient ruin can
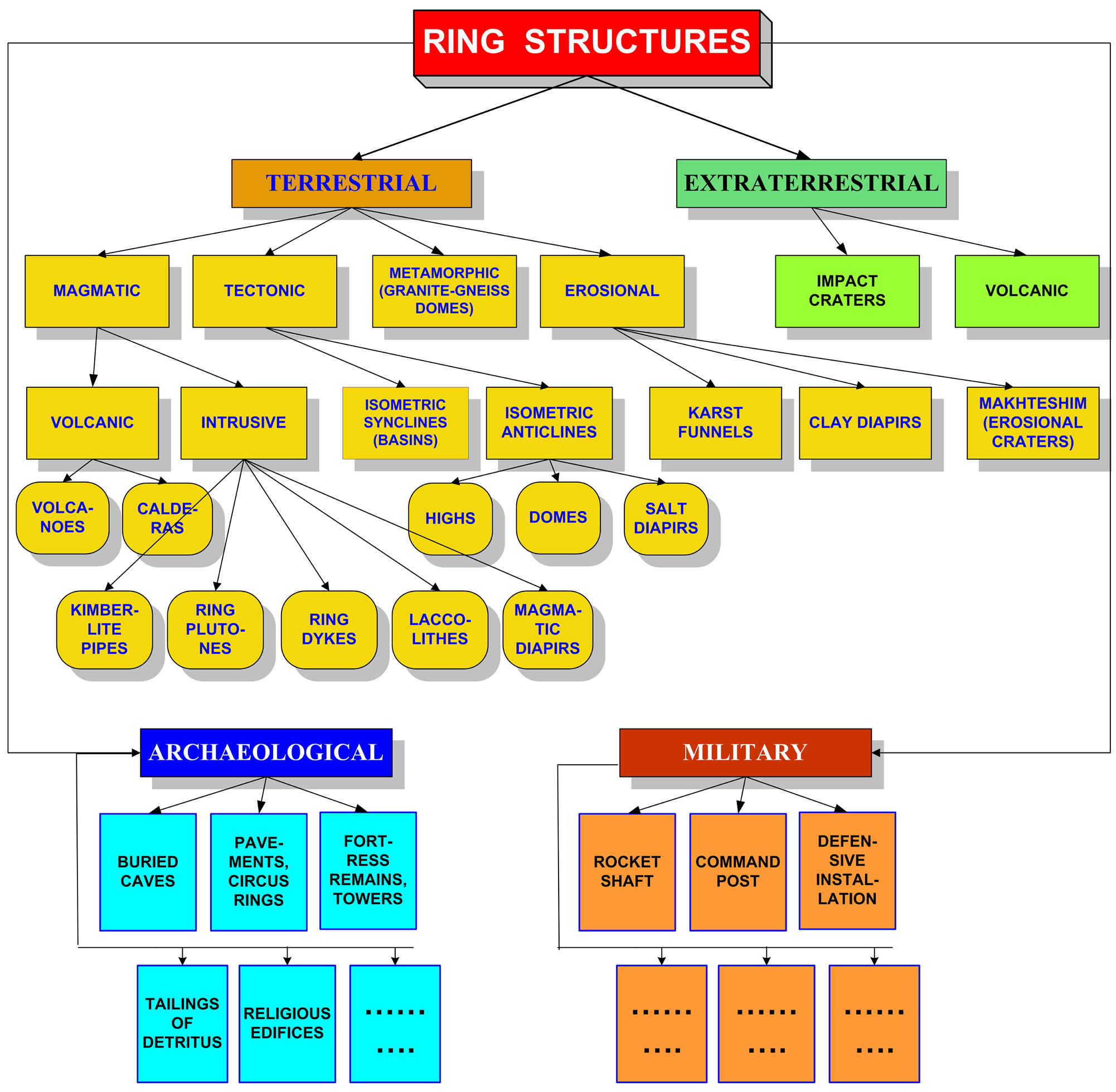
Figure 6. Classification of ring structures in the Earth’s environment (after [90,91], revised and supplemented).
be obtained by conducting a magnetic survey at two different levels (0.1 and 3.0 m, respectively). The survey at the 0.1 m level generates a typical thick bed (TKB) model (Figure 8(a)) and at the 3.0 m level, observations of the anomalous body may be interpreted as a horizontal circular cylinder HCC (Figure 8(b)). The results of the TKB model interpretation were used to determine the center of the upper edge of the anomalous body (Figure 8(a)) and the HCC model for localization of the center of HCC (Figure 8(b)). Combining these two models (we have two response functions G1 and G2 from the subdomains W1 and W2) yields a combined generalized model of the anomalous body [17]. Similar models could be developed for various scales and different geophysical methods.
In general combining different geophysical methods with their multilevel (including different depths of electrodes or geophone grounding) observations [16,17] produces a large number of combinations, which may be used for extracting additional useful information from the data.
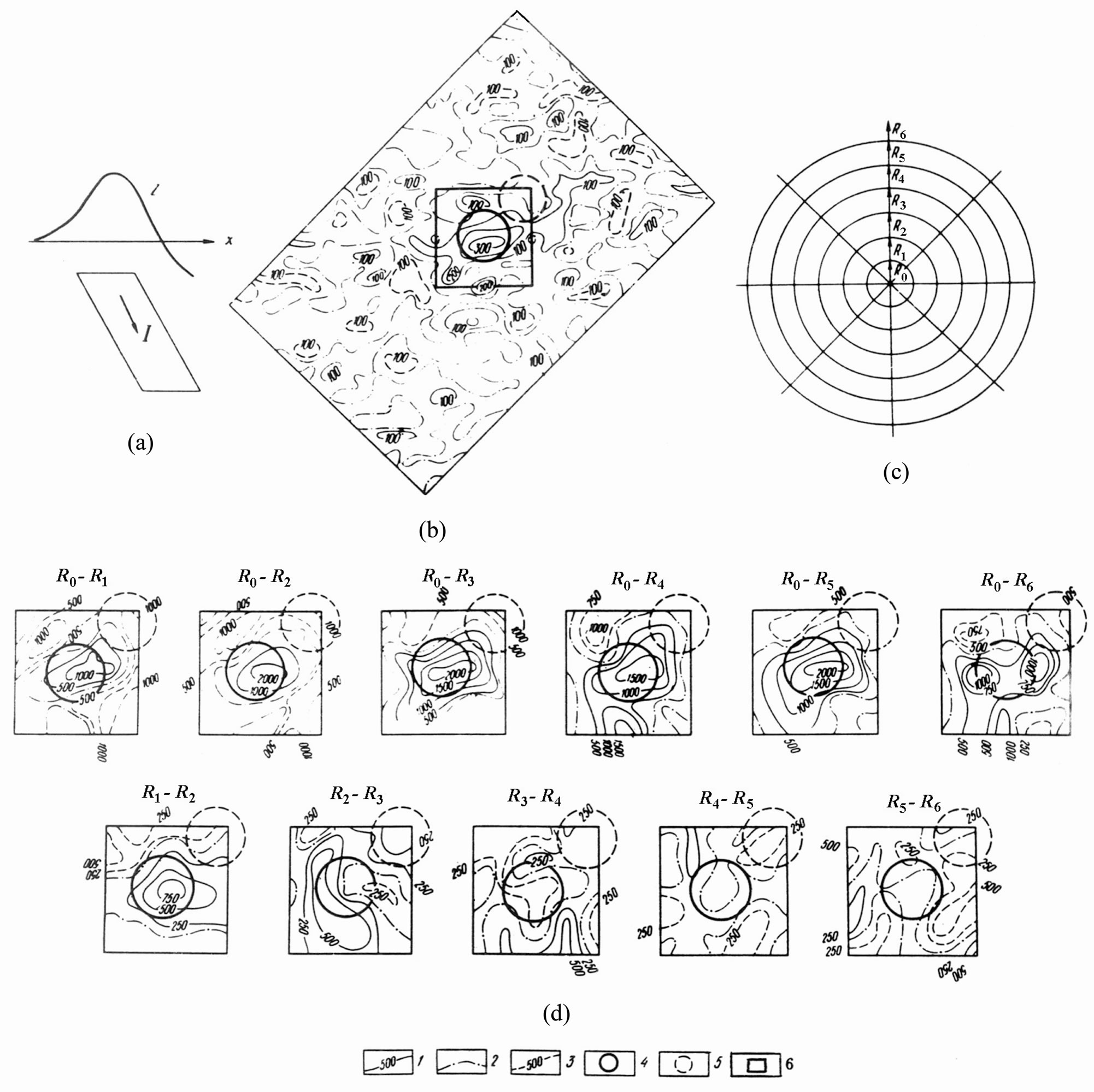
Figure 7. Singling out a concentric structure (after [18]): (a) model field of an inclined circular cylinder calculated along a profile, (b) model field complicated by random noise (in plane), (c) apparent graticule for concentric structure selection, (d) singling out a model body by summing horizontal gradients of the field within apparent circular graticule zones. Isogams of a model field (b) and the sum of its gradients (d) in conventional units: 1) positive, 2) zero, 3) negative; cylinder edge projection: 4) upper, 5) lower; 6) contour of the portion shown in (b).
7. Integrated Analysis of Magnetic and VLF Fields
Integrated analysis of magnetic and VLF fields can be carried out using both informational and wavelet approaches
7.1. Informational Approach
Since the solution of geological problems calls for integration of different geophysical methods, the abovementioned features (geophysical observations, petrophysicalmorphological characteristics and interpretation process) should be expressed in the same terms. Only then can specific concrete problems for each method be formulated.
At a specified level of accuracy of geophysical meth-
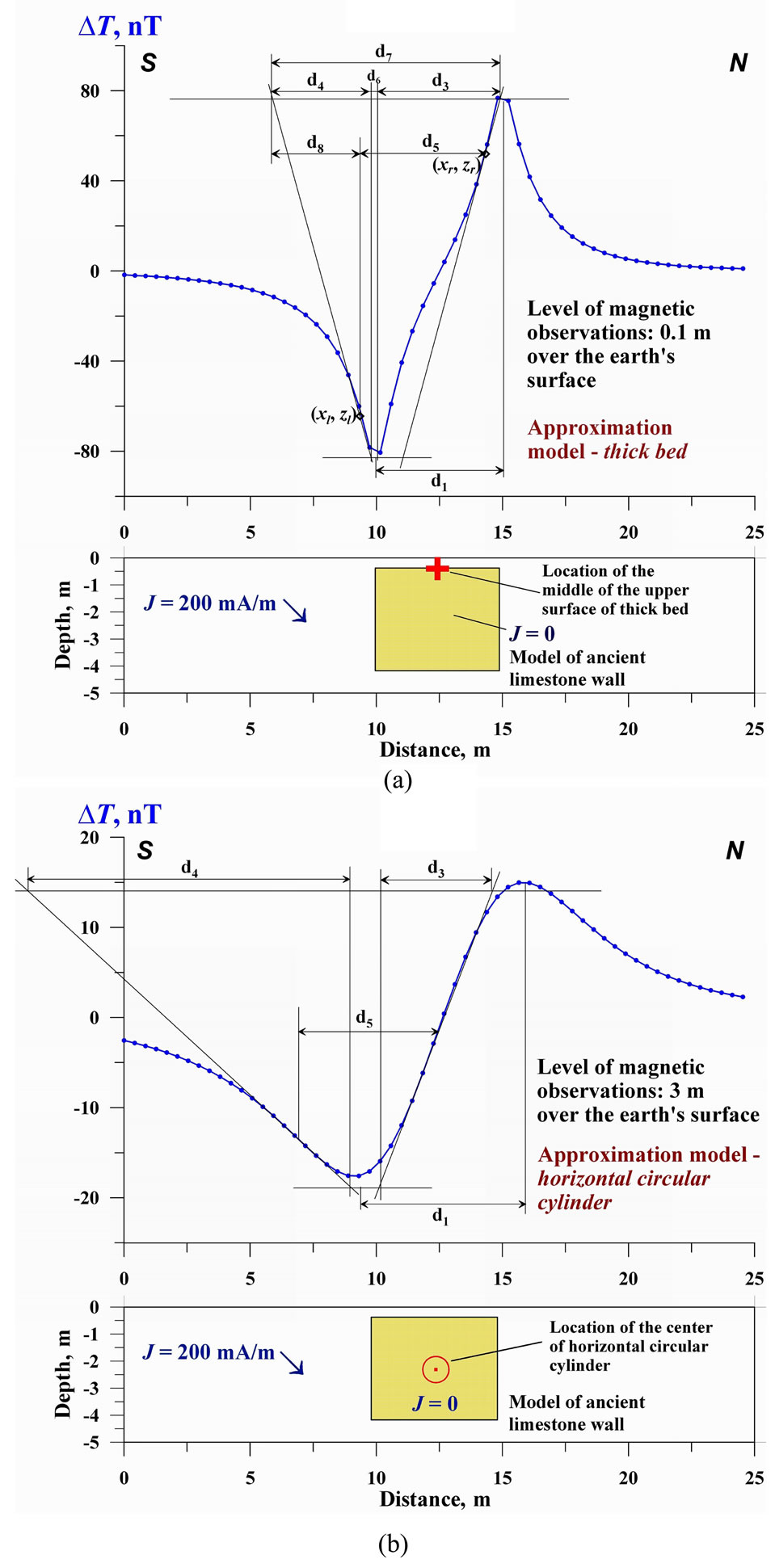
Figure 8. Realization of two-level observations with two different interpretation models: (a) model of a thick bed, (b) model of the horizontal circular cylinder (HCC). Magnetization is denoted as J.
ods and object characteristics, the integrated interpretation technique is of primary importance for integrating geophysical methods. The same is true when defining requirements and preconditions for data collection and the assessment of the findings from each method. This information can be obtained from physical sources corresponding to various classes of geological (environmental or technical) objects. The integrated interpretation, which leads to class intersection, makes it possible to single out one or several geological targets, which form a solution to the geological objective. In some cases only the comparison of fields measured by various geophysical methods leads to an “informational leap” [93], which can then single out the target objects.
In some cases, only an estimate of the amount of corresponding information contained in observations can substantiate the presence of an object in a given class. These estimates are especially valuable for integrated interpretation, as they provide a means to operate on data obtained through various methods which are now expressed in a common (informational) unit. The target is determined in terms of the maximum information obtained from the geophysical methods set.
The language of information theory [94] is the most suitable to express the essence of geological and geophysical investigations, i.e. the steps in the acquisition and processing of information. Therefore, in spite of the probabilistic calculus of the amount of information, the informational approach to this problem introduces deterministic features. Here, the advantage of the logical nature of a number of interpretation methods based on information-statistical (logical-statistical) approach becomes evident. Furthermore, this approach includes such probabilistic methods as correlation, filtering and statistical decision-making, which are widely accepted for data processing and interpretation.
Geophysical data processing is mainly intended to reduce and eliminate different kinds of noise. The main task of qualitative interpretation is to single out an object of the desired class, while that of the quantitative interpretation is to determine and refine parameters of the object. The solutions of these problems are closely interwoven and based on the model conceptions of the interpreter.
At each point the amount of information Ji due to the application of the i-th geophysical method may be expressed as [93]:
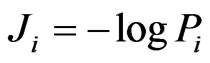 [bit] (22)
[bit] (22)
or
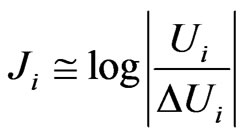 , (23)
, (23)
where Pj is the relative frequency of the j-th interval of the i-th indicator on the histogram of its distribution, Ui and DUi are the amplitude and the error of this indicator’s determination, respectively.
Even such a simple calculation of the amount of information may be effective one when operating with fields that differ physically.
After summing up the information elements, which can indicate a priori that the object of the desired class is present, random noise and components caused by different geological features are eliminated. To avoid singling out false positives the plot of , can be computed. When a large amount of information is contained in the data of only one or two methods, an integrated criterion Jint can be computed (it is only one of several types of information integration). This choice depends on the number of significant indicators and whether their relative influence is reduced [93]:
, can be computed. When a large amount of information is contained in the data of only one or two methods, an integrated criterion Jint can be computed (it is only one of several types of information integration). This choice depends on the number of significant indicators and whether their relative influence is reduced [93]:
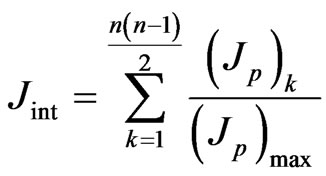 , [arbitrary units] (24)
, [arbitrary units] (24)
where Jp is determined using pairwise combinations of the results of n methods used (I1 and I2 are pairwise geophysical observations from the total number n of applied geophysical methods):
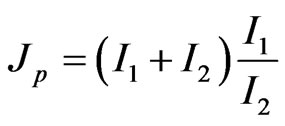 ,
, .
.
To avoid missing the detection of deeply buried objects, it is worthwhile in some cases to use the relative frequencies of average values or average field estimates on a sliding averaging interval instead of the Pj and Ui values, respectively.
Along with a simplified version based on summing up informants obtained from Equation (23), the method also exists as an “Integration” program. The latter can compute the sums of informants by Equation (22) and the corresponding parameter Jintegr (Equation (24)). Unlike other methods, this index is capable of revealing the objects characterized by the maximum number of indicators of different intensities and, at the same time, avoids missing an object which for some reason did not manifest itself by any indicator. The combination of indices serves to make interpretative conclusions.
In practice Ji is usually replaced by the relative amount of information, which is also known as the coefficient of informativity
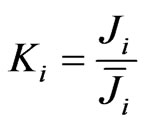 . (25)
. (25)
The value of 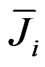 determines the information obtained when the result of Uj falls into the xj interval of the histogram with an equal probability of falling into any of the R intervals. According to [95], this is equal to average (complete) information, contained in the results achieved by measuring with a single method,
determines the information obtained when the result of Uj falls into the xj interval of the histogram with an equal probability of falling into any of the R intervals. According to [95], this is equal to average (complete) information, contained in the results achieved by measuring with a single method,
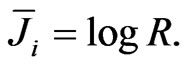 (26)
(26)
Application of Ki takes into account differences in the ranges of different fields. However, the application of expressions (22) and (24)-(26) may be not effective when there are an insufficient number of geophysical observations.
7.2. Wavelet Approach
About 20 years ago a new branch of computational mathematics—Wavelet Analysis (WA)—was developed. WA has had a significant impact on the cardinal problems of signal processing such as denoising of signals, enhancement of signals and differentiating signals with closely related characteristics [96-101].
Researchers typically need to deal with the problem of extraction of essential features from available data contaminated by random noise and a non-relevant background. If the essential structure of a signal consists of several sine waves, it can be represented trigonometrically (Fourier analysis). In this case the signal can be compared with a set of sinusoids and the consistent ones can be extracted. An indicator of the presence of a wave in a signal 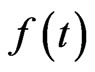 is the Fourier coefficient
is the Fourier coefficient
 .
.
Wavelet analysis provides a rich library of available and rapid, computationally efficient procedures to represent signals and select relevant waveforms. The basic assumption behind wavelet analysis is that the essential structure of a signal consists of a small number of various waveforms. The best way to determine this structure is to represent the signal by a set of basic elements containing waveforms coherent with the signal. For structures of the signal coherent with the basis function, large coefficients are attributed to a few basic waveforms, whereas small coefficients are expected for the noise and structures unrelated to the basic waveforms.
Wavelets are a family of functions ranging from functions of arbitrary smoothness to fractals.
The wavelet procedure takes place in two steps. Step 1 is decomposition, i.e. breaking up the signal to obtain the wavelet coefficients, and the second is a reconstruction, which consists of re-assembling the signal from coefficients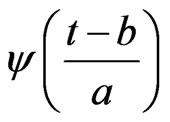 . There are many variants of WA. In the so-called continuous WA the signal f(t) is tested for the presence of waveforms.
. There are many variants of WA. In the so-called continuous WA the signal f(t) is tested for the presence of waveforms.
Here, a is a scaling parameter (dilation), and b determines the location of the wavelet  in a signal
in a signal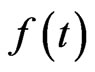 . The integral
. The integral
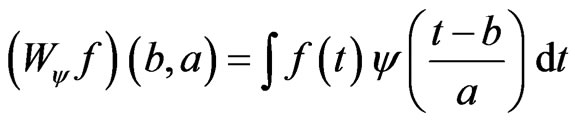 (27)
(27)
is the continuous wavelet transform.
The wavelet approach has been successfully tested on numerous models of karst terrains for which gravity and magnetic fields as well as GPR images were computed [101,102]. We chose to characterize the geometric events in the merged data curves by a representation of the curves in the Fourier domain. The assumption is that each of the A (absence of object) and P (presence of object) datasets is characterized by a number of dominating frequency bands. A perfect tool to reveal these characteristic frequency bands is provided by wavelet packet (WP) analysis [99]. Once implemented, the wavelet packet transform of a signal yields highly redundant partitions of the frequency domain. As a result, geophysicists can automatically detect the karst occupied areas and areas not containing this dangerous geological phenomenon on the basis of self-testing wavelet methodology.
8. Conclusions
Geophysical surveys using the latest generation of remote operated vehicles (ROV) have provided the impetus for mobile and detailed geophysical mapping of large territories including mountainous regions, swampy areas, areas of dense natural growth, military surveillance zones, and even archaeological sites. ROV lanes may be projected to levels previously inaccessible to geophysical aircraft survey—up to a meter above the Earth’s surface. Utilization of wide-band noise in the improved Kalman filtering model can significantly increase the accuracy of ROV navigation through the use of GPS. The advanced magnetic data methodology under complex environments (oblique magnetization, rugged relief and unknown level of the normal magnetic field) presented here can be effectively applied not only to unmanned airborne magnetic survey data, but also, with some modifications, to ROV-derived VLF measurements. In addition, a new approach to removing time variations in the VLF method was suggested. A design for the delineation of buried ring structures (as one of the possible search targets), and the application of a multimodel approach (on the example of multilevel measurements) was discussed. An integrated analysis of magnetic and VLF data can be carried out by applying both informational and wavelet approaches. Thus multilevel integrated ROV magnetic — VLF surveys will doubtless become a powerful geophysical tool in the very near future.
9. Acknowledgements
The authors would like to thank the anonymous reviewers who thoroughly reviewed the manuscript, and whose critical comments and valuable suggestions were so helpful in preparing this paper. This study was partially funded by the European Community’s FP7 Program under Grant No. 225663 Joint Call FP7-ICT-SEC-2007-1.
REFERENCES
- A. A. Logachev, “The Development and Application of Airborne Magnetometers in the U.S.S.R.,” Geophysics, Vol. 11, No. 2, 1946, pp. 135-147. doi:10.1190/1.1437230
- P. Hood, “History of Aeromagnetic Survey in Canada,” The Leading Edge, Vol. 26, No. 11, 2007, pp. 1384-1392. doi:10.1190/1.2805759
- A. Salem, K. Lei, C. Green, J. D. Fairhead and G. Stanley, “Removal of Cultural Noise from High-Resolution Aeromagnetic Data Using a Two Stage Equivalent Source Approach,” Exploration Geophysics, Vol. 41, No. 2, 2010, pp. 163-169. doi:10.1071/EG09047
- B. Tezkan, J. B. Stoll, R. Bergers and H. Crofbach, “Unmanned Aircraft System Proves Itself as a Geophysical Measuring Platform for Aeromagnetic Surveys,” First Break, Vol. 29, No. 4, 2011, pp. 103-105.
- L. V. Eppelbaum and B. E. Khesin, “VLF-Method: A New Interpretation Scheme and Feasibility of Its Application in Israel,” Transactions of the Conference of Israel Geological Society. Annual Meeting, Zikharon Yakov, 1995, p. 24.
- M. K. Seguin, “Quantitative Interpretation of a Combined Electromagnetic and Magnetic Heliported Survey for the Search of Economic Magnetic Taconite,” Geophysical Prospecting, Vol. 23, No. 3, 1976, pp. 471-491. doi:10.1111/j.1365-2478.1975.tb01543.x
- J. Bromley, B. Manhstrom, D. Nisca and A. Jamtlid, “Airborne Geophysics: Application to a Ground-Water Study in Botswana,” Ground Water, Vol. 32, No. 1, 1994, pp. 79-90. doi:10.1111/j.1745-6584.1994.tb00614.x
- R. B. K. Shives and K. L. Ford, “Applications of Multiparameter Surveys (Gamma-Ray Spectrometry, Magnetic, VLF-EM),” Geological Survey of Canada, Notes for Workshop at Whitehorse, Yukon, 1994.
- M. Bastani and L. B. Pedersen, “The Reliability of Aeroplane Attitude Determination Using the Main Geomagnetic Field with Application to Tensor VLF Data Analysis,” Geophysical Prospecting, Vol. 45, No. 5, 1997, pp. 831-841. doi:10.1046/j.1365-2478.1997.480294.x
- A. Sandrin and S. A. Elming, “Geophysical and Petrophysical Study of an Iron Oxide Copper Gold Deposit in Northern Sweden,” Ore Geology Reviews, Vol. 29, No. 1, 2006, pp. 1-18. doi:10.1016/j.oregeorev.2005.06.001
- L. Persson, A. A. Lundin, L. B. Pedersen and D. Claeson, “Combined Magnetic, EM and Resistivity Study over a High Conductive Rock Formation in Orrivaara, Northern Sweden,” Proceedings of the EGM 2010 International Workshop, Capri, 11-14 April 2011, pp. 1-4.
- L. V. Eppelbaum, Z. Ben-Avraham and A. Mishne, “Remote Pilot Vehicle Survey and Modern Geophysical Data Interpretation,” Transactions of the Conference of the Israel Geological Society. Annual Meeting, Ma’alot, 3-5 April 2000, p. 36.
- Air Force Scientific Advisory Board, “Report on Unmanned Aerial Vehicles in Perspective: Effects, Capabilities, and Technologies,” SAB-TR-03-01, 2003.
- M. DeGarmo and G. M. Nelson, “Prospective Unmanned Aerial Vehicle Operations in the Future National Airspace System,” American Institute of Aeronautics and Astronautics, 2004, Case 04-0936.
- M. de Sousa, “Unmanned Aerial Vehicles for Rapid Environmental Assessment and Mine Countermeasures,” Department of Defense, Australian Government, 2005, pp. 1-11.
- L. V. Eppelbaum, “Remote Operated Vehicle Geophysical Survey Using Magnetic and VLF Methods: Proposed Schemes for Data Processing and Interpretation,” Proceedings of the SAGEEP Conference, Philadelphia, Vol. 21, 2008, pp. 938-963.
- L. V. Eppelbaum, “Archaeological Geophysics in Israel: Past, Present and Future,” Advances of Geosciences, Vol. 24, 2010, pp. 45-68. doi:10.5194/adgeo-24-45-2010
- B. E. Khesin, V. V. Alexeyev and L. V. Eppelbaum, “Interpretation of Geophysical Fields in Complicated Environments,” Kluwer Academic Publisher, Ser.: Advanced Approaches in Geophysics, Dordrecht-LondonBoston, 1996.
- S. K. Kiselev, “Airborne Magnetometric Navigation Systems and the Prospects for Their Practical Use,” Automation and Remote Control, Vol. 62, No. 7, 2001, pp. 1138-1145. doi:10.1023/A:1010266028714
- A. A. Burns, “Geophysical Inertial Navigation System,” United States Patent No. 6493631, 30 May 2002.
- H. Hautaniemi, M. Kurimo, J. Multala, H. Leväniemi and J. Vironmäki, “The ‘Three in One’ Aerogeophysical Concept of GTK in 2004,” Geological Survey of Finland, Espoo, 2004.
- R. S. Liptser and A. N. Shiryayev, “Statistics of Random Processes: General Theory,” Springer, Berlin, 2001.
- R. G. Brown and P. Y. Hwang, “Introduction to Random Signals and Applied Kalman Filtering with MATLAB Exercises and Solutions,” John Wiley & Sons, New York, 2005.
- Y. Yang and W. Gao, “Comparison of Adaptive Factors in Kalman Filters on Navigation Results,” Journal of Navigation, Vol. 58, 2005, pp. 471-478. doi:10.1017/S0373463305003292
- L. V. Eppelbaum, A. E. Bashirov and L. R. Mishne, “On the Possibility of Precision of Eötvös Correction in the Marine Gravity Investigations,” Transactions of the 1st All-Union Conference on Marine Geophysics, Baku, in Russian, Vol. 1, 1987, pp. 89-90.
- A. E. Bashirov, L. V. Eppelbaum and L. R. Mishne, “Improving Eötvös Corrections by Wide-Band Noise Kalman Filtering,” Geophysical Journal International, Vol. 108, No. 1, 1992, pp. 193-197. doi:10.1111/j.1365-246x
- W. M. Telford, L. R. Geldart and R. E. Sheriff, “Applied Geophysics,” Cambridge University Press, Cambridge, 1991.
- P. G. Dyadkov, “On the Linearity of the Geomagnetic Variation Secondary Effects in Anomalous Fields by Modulus Measurements,” Geology and Geophysics, in Russian, No.4, 1985, pp. 129-136.
- L. V. Eppelbaum and A. R. Mishne, “High-Precision Magnetic Survey: Elimination of Secondary Time Variations,” Transactions of the Conference of the Geological Society of America, Rocky Mountain, Vol. 27, No. 4, 1995, p. 10.
- D. S. Parasnis, “Principles of Applied Geophysics,” Chapman & Hall, London, 1997.
- L. V. Eppelbaum, “An Advanced Methodology for Remote Operation Vehicle Magnetic Survey to Delineate Buried Targets,” Transactions of the 20th General Meeting of the Internernational Mineralogical Association, CH30G: Archaeometry (General Session): Composition, Technology and Provenance of Archaeological Artifacts, Budapest, 2010, p. 103.
- L. V. Eppelbaum, Z. Ben-Avraham and Y. I. Katz, “Structure of the Sea of Galilee and Kinarot Valley Derived from Combined Geological-Geophysical Analysis,” First Break, Vol. 25, No. 1, 2007, pp. 21-28. doi:10.3997/1365-2397.2007001
- M. S. Reford and J. S. Sumner, “Aeromagnetics,” Geophysics, Vol. 29, No. 1-2, 1970, pp. 482-516. doi:10.1190/1.1439384
- H. Naudy, “Une Methode d’analyse Fine des Profiles Aeromagnetiques,” Geophysical Prospecting, Vol. 18, No. 1, 1970, pp. 56-63. doi:10.1111/j.1365-2478.1970.tb02095.x
- M. B. Dobrin, “Introduction to Geophysical Prospecting,” McGraw-Hill, New York, 1976.
- D. A. Rao and H. V. Babu, “On the Half-Slope and Straight-Slope Methods of Basement Depth Determination,” Geophysics, Vol. 49, No. 8, 1984, pp. 1365-1368. doi:10.1190/1.1441763
- G. Desvignes, A. Tabbagh and C. Benech, “About the Determination of Magnetic Anomaly Sources,” Archaeological Prospection, Vol. 6, No. 2, 1999, pp. 85-105. doi:10.1002/(SICI)1099-0763
- R. J. Blakely, “Potential Theory in Gravity and Magnetic Applications,” Cambridge University Press, Cambridge, 1995. doi:10.1017/CBO9780511549816
- W. R. Roest, J. Verhoef and M. Pilkington, “Magnetic Interpretation Using the 3-D Analytic Signal,” Geophysics, Vol. 57, No. 1, 1992, pp. 116-125. doi:10.1190/1.1443174
- L. V. Eppelbaum, B. E. Khesin and S. E. Itkis, “Prompt Magnetic Investigations of Archaeological Remains in Areas of Infrastructure Development: Israeli Experience,” Archaeological Prospection, Vol. 8, No. 3, 2001, pp. 163- 185. doi:10.1002/arp.167
- L. V. Eppelbaum, “Study of Magnetic Anomalies over Archaeological Targets in Urban Conditions, Physics and Chemistry of the Earth,” Physics and Chemistry of the Earth, 2011, in press. doi:10.1016/j.pce.2011.02.005
- B. E. Khesin and L. V. Eppelbaum, “Geophysical Studies in the Caucasus,” Springer, Berlin, 2011, in press.
- S. G. Gordeyev, E. S. Sedelnikov and A. G. Tarkhov, “Electric Prospecting by the Radio Comparing and Bearing Method (VLF),” Nedra, Moscow, 1981, in Russian.
- L. V. Eppelbaum and B. E. Khesin, “VLF-Method: Elimination of Noises and Quantitative Interpretation, Coll. of Selected Papers,” Proceedings of the Symp. on Electromagnetic Compatibility “1992—From a Unified Region to a Unified World”, Section “LF to ULF” Electromagnetics and the Earth, Tel Aviv, 2-5 November 1992, pp. 1-6. doi:10.1109/ISEMC.1992.257585
- L. V. Eppelbaum, “Examples of Terrain Corrections in the VLF-method in the Caucasian Region, USSR,” Geoexploration, Vol. 28, No. 1, 1991, pp. 67-75. doi:10.1016/0016-7142(91)90028-B
- J. R. Wait, “Introduction to the Theory of VLF Propagation,” Proceedings of the IRE, Vol. 50, 1962, pp. 1624- 1647.
- A. G. Tarkhov, “Principles of Geophysical Prospecting by Radio Comparing and Bearing Method (VLF),” Gosgeoltekhizdat, Leningrad, 1961.
- USSR Ministry of Geology, “Electrical Prospecting Instruction,” Nedra, Moscow, 1984.
- M. A. Vallee, M. Chouteatu and G. J. Palacky, “Effect of Temporal and Spatial Variations of the Primary Signal on VLF Total-Field Surveys,” Geophysics, Vol. 57, No. 1, 1992, pp. 97-105. doi:10.1190/1.1443192
- R. Barra, D. L. Jones and C. J. Rodger, “ELF and VLF Radio Waves,” Journal of Atmospheric and Solar-Terrestrial Physics, Vol. 62, No. 17-18, 2000, pp. 1689-1718. doi:10.1016/S1364-6826(00)00121-8
- A. I. Zaborovsky, “Electric Prospecting,” Gostoptekhizdat, Moscow, 1963.
- L. M. Alpin, D. S. Dayev and A. D. Karinsky, “Theory of Fields Employed in Geophysical Prospecting,” Nedra, Moscow, 1985.
- V. I. Dmitriyev, I. A. Baryshnikova and K. V. Zakharov, “Anomalous Electromagnetic Fields of Geological Bodies,” Nedra, Leningrad, 1977.
- V. I. Dmitriyev, “Computer Methods in Exploration Geophysics,” Geophysicist’s Manual, Nedra, Moscow, 1982.
- O. Olsson, “Computation of VLF Response over HalfPlane and Wedge Models,” Geophysical Prospecting, Vol. 31, 1983, pp. 171-191. doi:10.1111/j.1365-2478.1983.tb01048.x
- L. V. Eppelbaum and L. R. Mishne, “Some Theoretical Aspects of Optimal Filtration of Geophysical Signals with Dependent Noises,” Deposited in VINITI, USSR Academy of Sciences, No. 6034-B88, 1988, pp. 1-10.
- L. V. Eppelbaum and M. I. Finkelstein, “Radon Emanation, Magnetic and VLF Temporary Variations: Removing Components not Associated with Dynamic Processes,” Collection of Selected Papers of the XXVI General Assembly of the European Seismological Commission, Tel Aviv, 1998, pp. 122-126.
- E. Bozzo, S. Lombardo and F. Merlanti, “VLF Prospecting: Observations about Field Experiments,” Annali di Geofisica, Vol. 37, No. 5, 1994, pp. 1215-1227.
- E. S. Sedelnikov, “The Effect of Topography on the Field of a Distant Source of Alternating Electromagnetic Field,” Izvestiya of the USSR Acad. of Sci., Ser: Physics of the Solid Earth, No. 7, 1983, pp. 102-106.
- M. Karous, “Effect of Relief in EM-Data Methods with Very Distant Source,” Geoexploration, Vol. 17, 1979, pp. 33-42. doi:10.1016/0016-7142(79)90005-X
- D. Eberle, “A Method of Reducing Terrain Relief Effects from VLF-EM Data,” Geoexploration, Vol. 19, 1981, pp. 103-114. doi:10.1016/0016-7142(81)90023-5
- H. A. Baker and S. O. Myers, “A Topographic Correction for VLF-EM Profiles Based on Model Studies,” Geoexploration, Vol. 18, 1980, pp. 135-144. doi:10.1016/0016-7142(80)90025-3
- S. G. Gordeyev, “Terrain Relief Considerations in Magnetic Fields of Remote Transmitters,” Proceedings of TSNIGRI, Vol. 179, 1983, pp. 56-60.
- L. Felsen and N. Markuvitz, “Radiation and Scattering of Waves,” Prentice-Hall, Englewood Cliffs, New York, 1973.
- E. V. Zakharov and Y. Y. Pimenov, “Numerical Analysis of Radiowave Diffraction,” Radio & Communication, Moscow, 1982.
- F. G. Bass and I. M. Fuks, “Wave Scattering from Statistically Rough Surfaces,” Pergamon, Oxford, 1978.
- D. C. Fraser, “Contouring of VLF-EM Data,” Geophysics, Vol. 34, No. 6, 1969, pp. 958-967. doi:10.1190/1.1440065
- S. G. Gordeyev and E. S. Sedelnikov, “On the Interpretation of the VLF Method Results on the Basis of the Conductive Bed Modeling,” Proceedings of TSNIGRI, No. 116, 1974, pp. 88-99.
- M. S. Zhdanov and G. V. Keller, “The Geoelectrical Methods in Geophysical Exploration,” Elsevier, Amsterdam, 1994.
- A. A. Kaufman and G. V. Keller, “The Magnetotelluric Method,” Elsevier, Amsterdam, 1981.
- A. T. Basokur and M. E. Candansayar, “Enhancing VLF Data for Qualitative Interpretation: An Example of Massive Chalcopyrite Exploration,” The Leading Edge, Vol. 22, No. 6, 2003, pp. 568-570. doi:10.1190/1.1587680
- M. Karous and S. E. Hjelt, “Determination of Apparent Current Density from VLF Measurements,” Department of Geophysics, University of Oulu, No. 89, 1979, pp. 1-9.
- O. Olsson, “VLF-Anomalies from a Perfectly Conducting Half-Plane below an Overburden,” Geophysical Prospecting, Vol. 28, No. 3, 1980, pp. 415-434.
- F. A. Tesmull and D. I. Crossley, “Inversion of VLF-Data for Simple Lateral Inhomogeneities,” Geological Survey of Canada, No. 81-15, 1981, pp. 79-86.
- M. Poddar, “Very Low-Frequency Electromagnetic Response of a Perfectly Conducting Half-Plane in a Layered Half-Space,” Geophysics, Vol. 41, 1982, pp. 1059-1067. doi:10.1190/1.1441369
- S. Miecznik, “Ciala Cylindryezne w Polo Plaskey Fali Electromagnetycznei,” Techn. Poszuk. Geol., Vol. 25, No. 3, 1986, pp. 16-22.
- A. K. Sinha, “Recent Developments in Quantitative Interpretation of VLF-EM Data,” In: K. K. Roy, et al., Eds., Deep Electromagnetic Exploration, Narosa Publishing House, New Delhi, 1998, pp. 599-606
- M. Djeddi, H. A. Baker and A. Tabbagh, “Interpretation of VLF-EM Anomalies of 3D Structures by Using Linear Filtering Techniques,” Annali Di Geofisica, Vol. 41, No. 2, 1998, pp. 151-163.
- L. B. Pedersen and B. Oskooi, “Airborne VLF Measurements and Variations of Ground Conductivity,” Surveys in Geophysics, Vol. 25, No. 2, 2004, pp. 151-181. doi:10.1023/B:GEOP.0000028161.90659.4b
- S. F. A. Monteiro, A. Mateus, J. Figueiras and M. A. Concalves, “Mapping Groundwater Contamination Around a Landfill Facility Using the VLF-EM Method— A Case Study,” Journal of Applied Geophysics, Vol. 60, No. 2, 2006, pp. 115-125.
- P. Kaikkonen and S. P. Sharma, “A Comparison of Performances of Linearized and Global Nonlinear 2-D Inversion of VLF and VLF-R Electromagnetic Data,” Geophysics, Vol. 66, No. 2, 2001, pp. 462-475. doi:10.1190/1.1444937
- L. D. Landau and E. M. Lifshitz, “Electrodynamics of Continuous Media,” Pergamon Press, Oxford, 1960.
- H. Hänl, A. W. Maue and K. Westpfahl, “Theorie Der Beugung,” Springer-Verlag, Berlin, 1961.
- M. S. Zhdanov, “The Analogues of the Cauchy Type Integral for the Theory of Geophysical Fields,” Nauka, Moscow, 1984.
- S. P. Sharma and P. Kaikkonen, “Two-Dimensional Nonlinear Inversion of VLF-R Data Using Simulated Annealing,” Geophysical Journal International, Vol. 133, No. 3, 1998, pp. 649-668. doi:10.1046/j.1365-246X.1998.00523.x
- D. Beamish, “Quantitative 2D VLF Data Interpretation,” Journal of Applied Geophysics, Vol. 45, No. 1, 2000, pp. 33-47. doi:10.1016/S0926-9851(00)00017-3
- B. Oskooi and L. B. Pedersen, “Resolution of Airborne VLF Data,” Journal of Applied Geophysics, Vol. 58, No. 2, 2006, pp. 158-175. doi:10.1016/j.jappgeo.2005.06.002
- A. Poikonen and I. Suppala, “On Modeling Airborne very Low-Frequency Measurements,” Geophysics, Vol. 54, No. 12, 1989, pp. 1596-1606. doi:10.1190/1.1442627
- V. E. Khain, “Main Problems of the Modern Geology,” Nauka, Moscow, 1995.
- L. V. Eppelbaum, Ya. Livshits, A. Flexer and Z. BenAvraham, “Integrated Geological-Geophysical Analysis of Ring Structures Phenomenon in the Eastern Mediterranean,” Transactions of the Conference of Israel Geological Society, Annual Meeting, Mizpe-Ramon, 23-24 March 1998, p. 25.
- L. V. Eppelbaum, “Localization of Ring Structures in Earth’s Environments,” Journal of the Archaeological Society of the Slovakian Academy of Science, Special Issue: Arch Prospect, Vol. 66, 2007, pp. 145-148.
- L. V. Eppelbaum, “Multilevel Observations of Magnetic Field at Archaeological Sites as Additional Interpreting Tool,” Proceedings of the 6th Conference of Archaeological Prospection, Roma, 14-17 September 2005, pp. 1- 4.
- B. E. Khesin and L. V. Eppelbaum, “The Number of Geophysical Methods Required for Target Classification: Quantitative Estimation,” Geoinformatics, Vol. 8, No. 1, 1997, pp. 31-39.
- C. E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, Vol. 27, No. 3-4, 1948, pp. 379-432, 623-656.
- E. S. Ventsel, “The Probability Theory,” 5th ed., Nauka, Moscow, 1983.
- L. Alperovich and V. Zheludev, “Long-Period Geomagnetic Precursors of the Loma-Prieta Earthquake Discovered by Wavelet Method,” In: M. Hayakawa, Ed., Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes, TERRAPUB, Tokyo, 1999, pp. 123-135.
- V. Zheludev and L. Alperovich, “Wavelet Analysis as a Tool for Revealing Geomagnetic Precursors of an Earthquake,” Seismo-Electromagnetics, TERRAPUB, Vol. 255, Tokyo, 1999.
- K. Wapenaar, R. Ghose, G. Toxopeus and J. Fokkema, “The Wavelet Transform as a Tool for Geophysical Data Integration,” Integrated Computer-Aided Engineering, Vol. 12, No. 1, 2005, pp. 5-23.
- A. Averbuch, V. Zheludev, P. Neittaanm and J. Koren, “Block Based Deconvolution Algorithm Using Spline Wavelet Packets,” Journal of Mathematical Imaging and Vision, Vol. 38, No 3, 2010, pp. 197-225. doi:10.1016/j.acha.2010.10.004
- A. Averbuch, K. Hochman, N. Rabin, A. Schclar and V. Zheludev, “A Diffusion Frame-Work for Detection of Moving Vehicles,” Digital Signal Processing, Vol. 20, No. 1, 2010, pp. 111-122. doi:10.1016/j.dsp.2009.02.002
- L. V. Eppelbaum, L. S. Alperovich, V. Zheludev and A. Pechersky, “Application of Informational and Wavelet Approaches for Integrated Processing of Geophysical Data in Complex Environments,” Proceedings of the 2011 SAGEEP Conference, Charleston, Vol. 24, 10-14 April 2011, pp. 24-60.
- L. V. Eppelbaum, L. S. Alperovich and V. Zheludev, “Informational and Wavelet Methodologies for Combined Analysis of Geophysical Data within the ISTIMES project”, Transactions of the 7th EUG Meetings, Geophysical Research Abstracts, EGU2011-1742, Vienna, Vol. 13, 2-7 May 2011, pp. 1-2.

