Journal of Geographic Information System
Vol.10 No.02(2018), Article ID:83614,18 pages
10.4236/jgis.2018.102009
An Integrated Framework for Road Detection in Dense Urban Area from High-Resolution Satellite Imagery and Lidar Data
Asghar Milan
Surveying Department, National Cartographic Center, Tehran, Iran
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 14, 2018; Accepted: April 6, 2018; Published: April 9, 2018
ABSTRACT
Automatic road detection, in dense urban areas, is a challenging application in the remote sensing community. This is mainly because of physical and geometrical variations of road pixels, their spectral similarity to other features such as buildings, parking lots and sidewalks, and the obstruction by vehicles and trees. These problems are real obstacles in precise detection and identification of urban roads from high-resolution satellite imagery. One of the promising strategies to deal with this problem is using multi-sensors data to reduce the uncertainties of detection. In this paper, an integrated object-based analysis framework was developed for detecting and extracting various types of urban roads from high-resolution optical images and Lidar data. The proposed method is designed and implemented using a rule-oriented approach based on a masking strategy. The overall accuracy (OA) of the final road map was 89.2%, and the kappa coefficient of agreement was 0.83, which show the efficiency and performance of the method in different conditions and interclass noises. The results also demonstrate the high capability of this object-based method in simultaneous identification of a wide variety of road elements in complex urban areas using both high-resolution satellite images and Lidar data.
Keywords:
High-Resolution Satellite Images, Lidar Data, Object-Based Analysis, Feature Extraction

1. Introduction
Due to the importance of geospatial information of road networks in urban and suburban areas, during the last decades, a large number of prominent research works have been performed on automatic road detection [1] [2] [3] . This detection procedure, especially in dense urban areas, is a real challenging problem in remote sensing community. This is mainly because of spectral and spatial variations of road pixels, the spectral similarity of roads to other features such as buildings, parking lots and sidewalks, and the obstruction by vehicles and trees. These problems are real obstacles for precise detection and identification of urban roads from high-resolution satellite imagery. Disha and Saroha [4] proposed two automatic and semi-automatic methods for detecting urban roads from high-resolution satellite images. In the semi-automatic method, a few seed points, describing the roads coarsely, are needed to be provided. Then, Snake model is applied for road network extraction. In the automatic method, Fuzzy C-Means (FCM), as an unsupervised clustering algorithm, is used to classify the satellite image. Hough Transform is, then, applied in a window to get segment candidates, which increases the robustness of the method. A fitness function is also used to group the segments. The membership values of the connection lines are used for connecting the grouped segments. Finally, the misclassified road pixels are removed, and the central axes of roads are extracted. Bhirud and Mangala [5] presented a road detection method based on the composition of gradient operator and skeletonization. They used sub-operators, such as filtering and thresholding, to preprocess the data, and then, ultimately created a color scheme through the use of morphological operators for detecting and mapping the roads in rural areas. Maurya et al. [6] performed a two steps road detection framework from imagery. First, using k-means unsupervised classification to cluster the image into the road and non-road pixels. This may misclassify some irrelevant pixels, such as those of buildings or parking areas, in road class. Therefore, in the next step, morphological functions were applied to eliminate these misclassified pixels.
In research by Ying et al. [7] , a hierarchical algorithm was used for road detection from digital elevation models. Various factors such as height, intensity, morphological attributes and other local features have been used for this goal. Then, local morphological filtering methods detected boundaries and details of the road profiles. You and Zhao [8] detected roads from Lidar data. First, the Lidar point cloud was divided into ground points and above-ground classes. Then, buildings and trees were distinguished by minimizing the energy. Next, structural frames were designed and implemented to search for roads among the intensity data. Then, road width and direction was scored using a map. This local search process only determines candidate roads. A Markovian network was, then, used to find undiscovered roads. The combination of frame-local fitness and Markov random field (MRF), in overall, leads to more precise and complete road detection. Peng [9] used both intensity and elevation from Lidar data for urban road detection. First, Lidar data were filtered and classified as either ground or above-ground points using a triangulated irregular network (TIN). Then, Lidar point clouds that belong to the ground class were classified into two categories: road and non-road. This classification was performed based on brightness information. The TIN model thus improved the precision of road point detection. Silva et al. [10] introduced a method based on Radon transform for road detection from Lidar data and high-resolution aerial images. This method iteratively finds the line segments and produces roads centerlines starting from these segments. A framework based on the use of multiple features was proposed and evaluated by Xiangyun et al. [11] . This method detects the road centerlines from the remaining ground points after filtering. The main idea of this method is to detect the smooth geometric primitives of potential road centerlines efficiently and to separate non-road features such as parking lots and bare ground, from roads. The method consists of three major steps: 1) Spatial clustering based on multiple features using an adaptive mean shift for detecting the center points of roads, 2) Stick tensor voting for enhancing the salient linear features, and 3) a weighted Hough transform for extracting the arc primitives of the road centerlines. They obtained relatively high completeness and correctness for the two ISPRS benchmark datasets of Vaihingen and Toronto. Also, they stated that this method could yield better performance than template matching and phase-coded disk methods. Jinliang et al. [12] used a semantic model based on the object-attribute-relation (OAR) concept of human cognition to perform an experimental study on extracting road information from Quick Bird multispectral images. The results showed relatively accurate detection of the lengths and widths of roads.
For road detection, panchromatic or multi-spectral images, especially in urban areas, will yield ambiguous results, due to the additional complexities. For example, in an aerial photo or a high-resolution satellite image, both roads and buildings will appear similar, because their construction materials are usually the same. As a result, they cannot be readily distinguished [13] . This becomes worse when they are in shadow or covered by roofs or walls of tall buildings. Accordingly, neither automatic nor semi-automatic methods will be entirely reliable in these dense urban areas [14] . Moreover, the outputs of methods that use 2D images are more ambiguous than those with 3D inputs. Lidar point data have the potential to distinguish 3D features from one another, to distinguish 3D from 2D, and to distinguish 2D features from one another. However, Lidar intensity data are affected by a high amount of noise, and therefore are unable to distinguish roads from features with similar return signal power. Consequently, the full potential of the Lidar data cannot be exploited from raw data [15] [16] . Combining these two kinds of complementary data sources seem to be reasonably promising for road extraction, 3D urban modeling, etc. [17] . The main idea behind the integration of Lidar and optical imagery is that the strengths of one data type can compensate for the weaknesses of others. For example, being short of spectral information, Lidar data have high classification confusion between human-made and natural objects, whereas multispectral data have increasing classification confusion between spectrally identical objects in complex urban landscapes. In the light of these findings, this paper presents a method for detecting a wide variety of roads, including highways, bridges, main and side street and even alleys, at an acceptable level from high-resolution images and Lidar data. Our proposed method uses a hierarchical rule-based strategy and can benefit from many spectral, geometrical, conceptual and textural features in a multi-step hierarchical procedure. In this method, step by step, other objects have been separated from the roads, and finally, the type of roads will be identified and mapped.
2. Materials and Methods
2.1. Materials
Two data sets from a region in the city of San Francisco were used in this research. One dataset contains Quick Bird’s four bands of R, G, B, and NIR with a ground pixel size of 2.4 m (Figure 1(b)) and its panchromatic image with a 60-cm pixel size (Figure 1(a)). The other dataset contains Lidar points cloud with a density of 9 points per square meter (Figure 1(c)). The Lidar dataset contains information such as the intensity of the return wave and multiple returns in addition to 3D coordinates of points.
2.2. Proposed Method
The major steps of the proposed method are demonstrated in Figure 2. These steps are: Pre-processing of both spectral and Lidar data, Segmentation, Hierarchal classification, Object-based feature analysis, Object-based post processing and finally Road mapping. In the following sections, the details about each step are presented.
2.2.1. Preprocessing of Lidar Data
To prepare Lidar data, three preprocessing operations have been applied as follows:
1) Filtering: this step is mainly designed and applied to eliminate the noise from the raw data, and to enhance the quality of the Lidar data. Octree filter was used for noise reduction, which also minimizes the required storage space for these data. By this filtering, a cube is initially fitted to an overall 3D space. This cube is, then, divided into eight smaller cubes until a predefined threshold is
Figure 1. Research data set. (a) Panchromatic image; (b) Multispectral (NIR, R, and G) image; (c) Lidar height points cloud.
Figure 2. Overview of different steps of the proposed method.
reached. Afterward, all points in the smallest cube are removed and replaced by a new point in the centroid of these previous points [18] . This leads to a reduction of data volume along the cubes’ dimensions. If there is only one point in a cube, it is considered as noise and is thus removed from the points cloud.
2) Triangulation: After filtering the Lidar points cloud; these data are entered into a triangulation process. Lidar data can be triangulated into two forms of [x, y, z] or [x, y, intensity], using Delaunay method [19] .
3) Interpolation: In this process, an interpolation technique, such as bilinear interpolation, was applied to the elevation and the intensity data to produce raster images containing this information.
2.2.2. Optical Satellite Data Processing
Optical imaging systems have both high resolution and multispectral capabilities for various earth observation applications. To benefice from these advantages for the objective of road detection, data fusion can be an efficient way to produce the data with both high spatial and multispectral characteristics. In this paper, Gram-Schmidt spectral sharpening was used [20] .
2.2.3. Image Segmentation
Segmentation is the process of dividing the image into several homogeneous regions which consist of similar pixels. For segmentation, the values of scale, the weight of spectral heterogeneity (
), shape (
), smoothness (
), compactness (
) and the weight of the spectral bands should be determined. Moreover, other parameters of spectral heterogeneity (
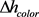
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Urban areas contain objects with a large variety of spectral heterogeneity in each class. Accordingly, the weight of spectral heterogeneity should be lower. Otherwise, the objects will have the unbalanced geometrical shapes, and most of the shape and geometric properties will be lost. To choose the weights for smoothness and compactness parameters, allocating higher weights to compactness leads to compacting objects such as roads, buildings, etc. Also, it will be challenging to distinguish linear objects from nonlinear ones. Choosing a higher value for the weight parameter for shape heterogeneity, as well as, high values for the smoothness parameter give the best results.
2.2.4. Design of Hierarchical Model
The best strategy for road identification is based on a step-by-step model, similar to a decision tree procedure [22] . This model has some decision making nodes, in each a part of road pixels is separated from the non-road pixels. Primary, non-road image’s classes are including vegetation, buildings, and open spaces such as sidewalks and parking lots. The model produces the best possible results if the non-road classes are stepped through in an optimal order. In fact, the class that has maximum separability from the roads must be separated in the first stage. This will increase the possibility of distinguishing other classes from the roads in the next steps. To identify the order above, the sequential forward selection (SFS) method, which is based on the normalized Euclidian distance discrimination possibility criterion, is used. Figure 3 shows the suggested hierarchical model.
The presented model includes four nodes. In the first node, the image is classified into two classes: vegetation and non-vegetation. The remaining process steps are performed on non-vegetation classes. In the second node, the
Figure 3. The designed hierarchical model for road extraction and mapping.
non-vegetation area is divided into two classes: high and low regions. Geographic objects such as buildings, bridges, and interchange ramps belong to the high-region class, while sidewalks, parking lots, roads, and other open spaces are considered as a grounded and low-region class. In the third node, the low regions are again classified into two classes: low roads and open spaces. In the fourth node, high regions are divided into buildings and high roads. As a final step, the two road classes are merged to create a final road network.
2.2.5. Object-Based Feature Analysis
As was mentioned, the designed hierarchical model has the four nodes. For each node, based on the targeted objects, specific features can be extracted from the input data and can be employed for separating them from the rest of objects. Feature extractions at each node are described as following:
First node: the first node aims to divide the study area into vegetation and non-vegetation classes. Due to the specific characteristics of vegetation in the red and near-infrared spectral regions of the electromagnetic spectrum, the proper way to identify this class is through the use of vegetation indexes such as the normalized difference vegetation index (NDVI) [23] and the ratio vegetation index (RVI) [24] :
(8)
(9)
Second node: the second node intentions to identify and separate high region from low regions. Features used in this mode are the Mean Difference to Neighbor, the Mean difference to Darker Neighbor contains features f1, f2 and f3 respectively, as are presented below.
(10)
(11)
(12)
According to the wide variety of sizes and spectral properties of buildings in the study area, it is obvious that they cannot be placed in a single level of segmentation as one object. Therefore, in such cases, the lowest scale level has to be chosen for these elements. According to the wide variety of size and spectral properties of buildings in the study area, it is obvious that they cannot be placed in a single level of segmentation as one object. Therefore in such cases, the lowest scale level has to be chosen for these elements. Based on these features, some buildings, because of their large size are segmented as the multi-object. To resolve this problem, a post-processing strategy based on a conceptual feature (f4) has been applied. To do so, first, these two classes are classified. Then, for the objects of low region objects class, the perimeter percentage of each adjacent object with objects classified in high regions class is calculated using Equation (13). The result will have the values between 0 and 1. This feature, in fact, searches the objects in low regions class that are surrounded by the class of the high region.
(13)
In second feature (f5), in order to improve the results of each object in low regions class, the number of adjacent objects, classified as high regions, is divided by the whole number of adjacent objects and considered as a feature. The values of this feature are also scaled between 0 and 1 (Equation (14)). This feature, indeed, is looking for the objects in low regions class, which are statistically surrounded by high regions objects.
n: number of neighbors for object;
m: number of High Region Neighbor (14)
Third node: this node is for separating the class of the low region into two sub-classes of low roads and open space. The open space class includes sidewalks, spaces beside the high way, parking lots, and occasional soil coverage. Features used in this node include the average of return wave intensity, contour layer and slope (Equation (15) to (17)):
n: number of Pixels for each objects (15)
n: number of Pixels for each objects (16 )
n: number of Pixels for each objects (17)
Since there is always some spaces like sidewalks between roads and buildings, the following feature was applied to use its property.
(18)
Next feature, i.e. the distance to the nearest low regions, aims to classify and identify the previously classified objects based on f6, f7 and f8. Here, the ratio of distance between considered object centroid from length in low region, and the length of that object has been considered:
(19)
Fourth node: Similar to nodes two and three, in the fourth node, we want to identify and separate the objects of the highroads class from other objects in the high regions class. According to linear nature of objects in the roads class, following features, which determine the linear properties of objects, are used as well.
(20)
The asymmetry feature describes an object in comparison to a regular polygon. An ellipse encircles the object in a way that this feature becomes the ratio of minor radius to significant radius of the ellipse (Equation (21)).
(21)
The closer the objects shape to a regular polygon, the closer this value to zero. The next feature is the ratio of length to width for the main line of the object (Equation (22)).
(22)
The output of this step will be primary roads network.
2.2.6. Object-Based Post-Processing
Due to the complexity of urban areas and high objects’ density, it is necessary to perform a post-processing method, to improve initial results. To this end, several statistical, spatial and conceptual features, based on initial classification results, are used all the nodes in the hieratical model, except for the first node, as follow:
Second node: In this node, for the reduction of high objects surrounded by objects with the same height, inappropriate segmentation results have to be improved before classification using features (f1 - f5). Here, the objects, whose the absolute value of the difference between their DSM value and an average of this feature in neighbors is less than 30 centimeters, are merged with the merge region algorithm. After this relative improvement, Equation (23) is used to make a feature with more appropriate discrimination possibility.
(23)
Third node: here again, a composite feature, namely compactness, is used. This feature displays geometrical compactness of an object in some ways. This feature is produced by dividing the product of length (m) and width (n) of an object by object’s pixel number.
(24)
Compactness is equal to 1 when the object has a rectangular shape. This criterion feature has been designed by composing the compactness feature and the average distance of the object from the high regions class objects as follows:
(25)
Low road objects have lower compactness value due to their linear form. Moreover, logically among the low region class elements, they have more distance compared with high region elements. Accordingly, low road objects have a lower value of feature 15. It is obvious that the improvement of results in the second and third node, due to decreasing noise between the high region and low region, improves the result of node four.
3. Implementation and Experimental Results
3.1. Preparing Data
As it was mentioned, before image segmentation, the data, including satellite images and Lidar data, should be preprocessed. The preprocessing stage includes initial property detection from the TIN surface of the Lidar data, its transfer to raster space, and spatial enhancement of Quick Bird multispectral.
Octree filter was used for filtering of Lidar data. To do so and based on the spatial resolution or ground distance sampling (GSD) of the Lidar data, which is 50 centimeters, the noise removal is performed with a 1-meter threshold. After filtering, Delaunay method is used for triangulation of the height information and generation of a digital surface model (DSM), as well as the contours lines. Also, the triangulation of return wave intensity produces an interpolated raster intensity image. Finally, using bilinear interpolation, raster images are produced with a resolution of 60 cm from Lidar data sets. This value is selected to obtain raster elevation data with the same size and resolution of the satellite imagery. In parallel, the Gram-Schmidt method was used to produce the pan-sharpened image from the original satellite data. The output of this process is an image with four spectral bands and a spatial resolution of 60 cm.
3.2. Image Segmentation
E cognition is used in the segmentation step as an object-based image analysis tool, which uses Fractal Net Evolution Approach (FNEA) for segmentation. FNEA is a region growing technique based on local criteria and starts with one-pixel image objects [24] . For segmentation, the values of scale, shape, compactness and the weight of the spectral bands should be determined by the user. These properties are provided in Table 1. The last column of this table contains classes whose objects underwent segmentation at the relevant level. Indeed, at each level, the segmentation is performed on the objects of each class, which will be analyzed in the next level.
3.3. Design of Hierarchical Model
As was mentioned, SFS method, which is based on the normalized Euclidian distance discrimination possibility criterion, is used for the design of the hierarchical model. Table 2 shows the outcomes of this method.
As the table shows, the vegetation class has the highest discrimination possibility. Then, buildings and open spaces are second and the third classes to be separated first, respectively. According to these results, a model based on a masking strategy is designed to identify the roads. The hierarchical model indeed designs a rule-based system to categorize classes in an order that minimizes the noise and maximizes the discrimination possibility. The model arranges classes based on the ease detection of classes.
3.4. Implementation of Hierarchical Model
In this section, according to the hierarchical model, results of each node are presented. Features used in different classes are shown in Table 3.
According to the proposed model, the first node aims to divide the study area into vegetation and non-vegetation classes. Due to Table 3 and based on NDVI and RVI features, the separation of vegetation and non-vegetation classes is shown in Figure 4.
Table 1. The properties of segmenting different levels.
Table 2. Separability analysis of different classes from the roads.
Table 3. Different classes feature rules.
Figure 4. Results at first node: Vegetation vs. Non-vegetation.
In the second node, high regions are separated from the low regions. Therefore, segmentation was performed only on the non-vegetation class (Table 1). The result of this node has been shown in Figure 5.
In the third node, the class of the low region is classified into two sub-classes of the low road and open space classes. Segmentation was, then, performed on the low regions objects (Table 1). Figure 6 demonstrates the low road class objects after merging with adjacent objects and removing objects with unjustifiable areas.
In the fourth node, we aimed to identify and separate the objects of the high roads class from other objects in the class of the high region. Thus, segmentation was performed on high regions objects (Table 1). The results of this node have been shown in Figure 7.
The result of merging the high roads and low roads, before (Figure 8(a)) and after (Figure 8(b)) removing tiny objects, is presented in Figure 8.
3.5. Improvement of Initial Results
According to the discussions in the object-based post-processing season,
Figure 5. Initial results of low roads with removing objects with small area.
Figure 6. Initial results of low roads with removing objects with small area.
Figure 7. Initial results of the fourth node.


Figure 8. The initial result of merging high and low roads classes. (a) before removing tiny objects; (b) removing tiny objects.
Figure 9(a) in the second node and Figure 9(b) in the third node show the improved classification results. It can be seen from the classification results that the areas classified incorrectly in the first step, has been classified correctly.
The final results, as well as, merging of the high road and low roads are illustrated in Figure 10.


Figure 9. Improved classification results. (a) result in the second node ; (b) result in the third node.
Figure 10. Final merged results of high and low roads.
As it can be seen in Figure 10, there are some irregular areas, detected as roads, in the left part of the image. In the original image, this part contains the high dense roads. In other areas, roads have crinkles as well. The most important reason for this is the vehicles on the roads or beside and vegetation like trees and grasses along the roads.
4. Discussion
For analytical accuracy assessment, several test samples for each class from original data sets are visually extracted and used to calculate the confusion matrix. Table 4 shows the results of the error matrix produced for accuracy assessment. The number of control samples in the results evaluation was determined based on the coverage percentage of different classes.
The overall accuracy for identification of different classes is 89.2%, and the kappa value is 0.83. A detailed description and interpretation of each class will be provided subsequently. In the vegetation class, the accuracy was 99% and 79% for the producer and user accuracies respectively. This indicates the potential of well-known spectral indexes, such as NDVI and RV, using object-based classification for extracting vegetation land covers.
Table 4. Confusion matrix of different class’s identification results.
In the case of the high road class, the accuracy was 91% and 100% for the producer and user, respectively. The primary problem in this class is related to the producer accuracy and noise in some samples in the open space and building classes. Because of high road density in some parts of the image, an identification problem occurs at objects' boundaries in this class. On some edges, the error of merging of segmentation results led to the production of roads with edge regions including sidewalks and buildings. Although there are a few misclassifications between buildings with open space, vegetation, and low roads, the accuracy was 88% and 98% for the producer and user accuracies respectively. In the case of the open space class, the producer and user accuracies were 61% and 20% for respectively. Open space class is typically spectrally similar to roads and morphologically similar to building roofs. Therefore, the separation of this land cover class from two other classes is quite problematic. As well as, there are shadows caused by buildings or trees in some areas, has led to some open spaces are wrongly classified in the vegetation. In the low roads class, the producer and user accuracies are 93% and 93% respectively. The reason could be the performance of post-processing step. The appropriate separation of high and low regions classes has greatly facilitated low roads’ identification, as well as the buildings surrounded by low roads. The noise with high roads can be considered as leading noise of this class of objects. Also, roads become darker in some areas due to the shadows of adjacent trees or buildings. Because the nature of these classes, from textural spectral and geometrical point of views, they are similar. This causes so that those classes mistakenly are classified in the open space. Also, the incorrect merging of some other objects near to buildings, in the segmentation step, which affected slope values may be the reason if this miss-classification.
5. Conclusions
In this paper, an improved framework based on hieratical classification model was proposed to identify, extract and map the roads networks in a dense urban area. The proposed method was applied to multisource remote sensing data including high-resolution satellite imagery and Lidar points cloud. One of the essential issues in the study was the introduction of some post-processing operations for improving the results. Another issue was the design of a step by step hierarchical method based on analysis and optimization of feature space using discrimination possibility analysis of optimization method.
To obtain more reliable results, for each node, based on the targeted objects, specific features can be extracted from the input data and can be employed for separating them from the rest of objects. Here a question may arise as to why post-processing step is not considered as one of leading steps in this method. The reason can be as the following. First, the foundation of result improvement is the use of objects’ initial classification results and statistical, conceptual and even spatial analyses. Secondly, classification by proposed hierarchical model is entirely dependent on other classes. Therefore, it is impossible to realize an exact and step by step class separation; accordingly a post-processing operation on the results seems to be necessary. Although, the spectral and spatial complexity of urban scenes shows the great potential of combining Lidar data and high-resolution imagery and object-based image analysis for road detection. However, Lidar data may not be available for many urban areas. Utilizing more available ancillary data such as digital surface models extracted from stereo imagery is especially desirable and will be the focus of our future research.
Acknowledgements
The authors would like to thank the GSRS Data Fusion Contest committee and Digital Globe for providing and making the QuickBird and Lidar data sets from San Francisco area publicly available.
Cite this paper
Milan, A. (2018) An Integrated Framework for Road Detection in Dense Urban Area from High-Resolution Satellite Imagery and Lidar Data. Journal of Geographic Information System, 10, 175-192. https://doi.org/10.4236/jgis.2018.102009
References
- 1. Mena, J.B. (2003) State of the Art on Automatic Road Extraction for GIS Update: A Novel Classification. Pattern Recognition Letters, 24, 3037-3058. https://doi.org/10.1016/S0167-8655(03)00164-8
- 2. Baltsavias, E.P. (2004) Objection Extraction and Revision by Image Analysis Using Existing Geodata and Knowledge: Current Status and Steps towards Operational Systems. ISPRS Journal of Photogrammetry and Remote Sensing, 58, 129-151. https://doi.org/10.1016/j.isprsjprs.2003.09.002
- 3. Mokhtarzade, M. and Valadan Zoej, M.J. (2007) Road Detection from High-Resolution Satellite Images Using Artificial Neural Networks. International Journal of Applied Earth Observation and Geoinformation, 9, 32-40. https://doi.org/10.1016/j.jag.2006.05.001
- 4. Disha, T., Saroha, G.P. and Urvashi, B. (2012) Road Network Extraction from Satellite Images by Active Contour (Snake)Modeland Fuzzy C-Means. International Journal of Advanced Research in Computer Science and Software Engineering, 2, 195-198.
- 5. Bhirud, S.G. and Mangala, T.R. (2011) A New Automatic Road Extraction Technique Using Gradient Operation and Skeletal Ray Formation. International Journal of Computer Applications, 29, 0975-8887.
- 6. Maurya, R., Gupta, P.R. and Shukla, A.S. (2011) Road Extraction Using K-Means Clustering and Morphological Operations. International Conference on Image Information Processing (ICIIP), Shimla, 3-5 November, 2011, 1-6.
- 7. Li, H.Y., Xu, Y.J., Wang, Z. and Lu, Y.-N. (2012) Hierarchical Algorithm in DTM Generation and Automatic Extraction of Road from LIDAR Data. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 22 ISPRS Congress, 25 August-1 September 2012, Melbourne, 133-136.
- 8. You, S. and Zhao, J. (2012) Road Network Extraction from Airborne LiDAR Data Using Scene Context. IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Providence, RI, 16-21 June 2012.
- 9. Peng, J. (2011) A Method for Main Road Extraction from Airborne LiDAR Data in Urban Area. International Conference on Electronics, Communications and Control (ICECC), Ningbo, 9-11 September 2011, 2425-2428.
- 10. Silva, C. (2011) Automatic Road Extraction on Aerial Photo and Laser Scanner Data. International Conference on Environmental and Computer Science, IPCBEE 2011, IACSIT Press, Singapore, 19.
- 11. Hu, X., Li, Y., Shan, J., Zhang, J. and Zhang, Y. (2014) Road Centerline Extraction in Complex Urban Scenes from LiDAR Data Based on Multiple Features. IEEE Transactions on Geoscience and Remote Sensing, 52, 7448-7456. https://doi.org/10.1109/TGRS.2014.2312793
- 12. Wang, J., Qian, J. and Ma, R. (2013) Urban Road Information Extraction from High Resolution Remotely Sensed Image Based on Semantic Model. 21st International Conference on Geoinformatics, Kaifeng, 20-22 June 2013.
- 13. Laptev, I. (1997) Road Extraction Based on Line Extraction and Snakes. Master Thesis, Royal Institute of Technology, Stockholm, 71 p.
- 14. Yong, H. (2003) Automated Extraction of Digital Terrain Models, Roads and Buildings Using Airborne Lidar Data. PhD Thesis. http://www.geomatics.ucalgary.ca/links/GradTheses.html
- 15. Rottensteiner, F., Trinder, J., Clode, S. and Kubic, K. (2003) Building Detection Using LIDAR Data and Multispectral Images. Proceedings of the 7th International Conference on Digital Image Computing: Techniques and Applications, Sydney, 10-12 December 2003, 673-682.
- 16. Vosselman, G. (2002) On the Estimation of Planimetric Offsets in Laser Altimetry Data. ISPRS Commission III, Symposium 2002, Photogrammetric Computer Vision, Graz, 9-13 September 2002, 34 (3A), 375-380.
- 17. Tao, G. and Yasuoka, Y. (2002) Combining High Resolution Satellite Imagery and Airborne Laser Scanning Data for Generating Bare Land DEM in Urban Areas. Proceedings of International Workshop on Visualization and Animation of Landscape, International Archives of Photogrammetry, Remote Sensing and Spatial Information Science, Kunming, 26-28 February 2002.
- 18. Wang, M. and Tseng, Y.H. (2010) Automatic Segmentation of Li DAR Data into Coplanar Point Clusters using an Octree Based Split-and-Merge Algorithm. Photogrammetric Engineering and Remote Sensing, 76, 407-420. https://doi.org/10.14358/PERS.76.4.407
- 19. Qiang, D. and Wang, D. (2004) Constrained Boundary Recovery for Three Dimensional Delaunay Triangulations. International Journal for Numerical Methods in Engineering, 61, 1471-1500. https://doi.org/10.1002/nme.1120
- 20. Aiazz, B., Baronti, S., Selva, M. and Alparone, L. (2006) Enhanced Gram-Schmidt Spectral Sharpening Based on Multivariate Regression of MS and Pan Data. IGARSS IEEE International Conference on Geoscience and Remote Sensing Symposium, Denver, 31 July-4 August 2006, 3806-3809.
- 21. Benz, U.C., Hofmann, P., Willhauck, G., Lingenfelder, I. and Heynen, M. (2004) Multi-Resolution, Object-Oriented Fuzzy Analysis of Remote Sensing Data for GIS-Ready Information. ISPRS Journal of Photogrammetry and Remote Sensing, 58, 239-258. https://doi.org/10.1016/j.isprsjprs.2003.10.002
- 22. Skackelford, A.K. and Davis, C.H. (2003) A Combined Fuzzy Pixel-Based and Object-Based Approach for Classification of High Resolution Multispectral Data over Urban Areas. IEEE Transactions on Geoscience and Remote Sensing, 41, 2354-2363. https://doi.org/10.1109/TGRS.2003.815972
- 23. Rouse, J.W., Haas, R.H., Schell, J.A. and Deering, D.W. (1973) Monitoring Vegetation Systems in the Great Plains with ERTS. Goddard Space Flight Center, Washington DC, 309-317.
- 24. Jordan, C.F. (1969) Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology, 50, 663-666. https://doi.org/10.2307/1936256










