ABSTRACT

In a one-dimension Mauldin-Williams Random Cantor Set Universe, the Sigalotti topological speed of light is 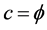where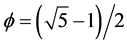. It follows then that the corresponding topological acceleration must be a golden mean downscaling of c namely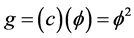. Since the maximal height in the one-dimensional universe must b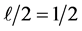e where 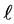is the unit interval length and note that the topological mass (m) and topological dimension (D) where m = D = 5 are that of the largest unit sphere volume, we can conclude that the potential energy of classical mechanics 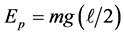translates to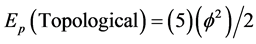. Remembering that the kinetic energy is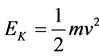, then by the same logic we see that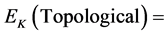 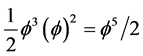when m = 5 is replaced by 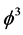for reasons which are explained in the main body of the present work. Adding both expressions together, we find Einstein’s maximal energy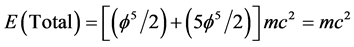. As a general conclusion, we note that within high energy cosmology, the sharp distinction between potential energy and kinetic energy of classical mechanics is blurred on the cosmic scale. Apart of being an original contribution, the article presents an almost complete bibliography on the Cantorian-fractal spacetime theory.

Keywords:

Potential Dark Energy, Kinetic Ordinary Energy, Motion as Illusion, Zenonparadoxa, E-Infinity Theory, Noncommutative Geometry, Topological Acceleration, Cantorian Universe, Accelerated Cosmic Expansion

1. Introduction

Space, time, matter and energy are concepts far from being trivial or obvious even within Newtonian classical mechanics [1] - [6] . This view was amply confirmed and deeply pondered in the wonderful writing of scientists such as H. Weyl and Max Jammar [1] [3] . Starting more or less from there it became the Author’s lifelong work and even magical fascination to incorporate the basic structure of quantum mechanics into the very topology and geometry of space and time [7] - [428] . To do this, the author followed a path inspired by the work of Richard Feynman and its development by the Canadian Physicist G. Ord and French Astrophysicist L. Nottale [7] [12] [13] .

The crucial turning point for E-infinity was when the Author’s basic work came in touch with the work on non-commutative geometry [14] [74] . In particular the superb analysis which the great French mathematician Alain Connes undertook on Penrose’s Fractal Tiling Universe using Von-Neumann’s pointless geometry [14] [140] is in retrospect the most important central piece in our current understanding of high energy physics and cosmology [7] - [270] . It turned out that the bijection formula which relates the Hausdorff dimension of an n-dimensional Cantor manifold to its topological dimension n [7]

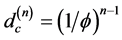(1)

where 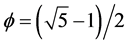is just a compact version of Von-Neumann-Connes’ dimensional function of a Penrose tiling universe [7] [14] [165] .

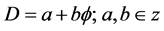(2)

In addition this dimensional function is generic and can be used to understand some of the most complex and difficult problems in Physics and Astrophysics [9] - [429] . In particular, it is easily shown using the above that the quantum particle may be described by the zero set as given by the bi-dimension [7] [27]

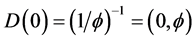(3)

while the quantum wave maybe modeled by the empty set given by the bi-dimension [7] [27]

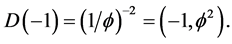(4)

In other words, the zero set quantum particle is described by a bi-dimension, zero for the topological dimension and 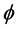for the Hausdorff dimension. On the other hand, the empty set quantum wave is fixed by the bi-dimension minus one for the topological dimension and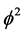 for the Hausdorff dimension [7] [9] [73] .

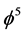
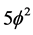
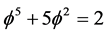
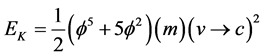
From this simple mental and mathematical picture, we were able to show that the volume of the quantum particle zero set in Kaluza-Klein spacetime is simply, while the corresponding volume of the quantum wave is [23] [24] . In other words, the measure of the particle is multiplicative while understandably the surface of this volume is a hyper-surface constituting the additive measure of the quantum wave. Since particle and wave in this picture, which is a ball, have a hyper spherical border and are therefore necessarily inseparable, it follows then that the total volume of the wave particle “quantum” structure is simply the sum. Inserting in Newton’s kinetic energy one finds [137] [138] [139]

(5)

where c is the speed of light. In that way, we were able to show that [48] - [400]

(6)

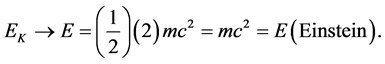
By contrast in the present work, we will take another route to arrive at the same result by stressing an optional separation between kinetic energy and potential energy in fractal spacetime.

2. Fractal Potential Energy and Fractal Kinetic Energy of Quantum Spacetime

The following is a “post-modern” and quite novel approach to the same fundamental problems connected to the total accepted theoretical energy density of the universe versus that which was measured and which gave rise to the new concepts of dark energy and dark matter. This problem was previously solved using a plethora of mathematical techniques. However and as we anticipated in the previous section, we are making in the present analysis a strict although optional distinction between potential energy and kinetic energy [430] .

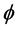
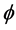
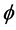
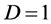
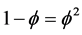
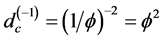
For this reason we start from a one-dimensional Cantor set. For this set everything is zero with the exception of one fundamental thing. The bi-dimension indicated already that the topological dimension is zero. The only thing which is not zero is the Hausdorff dimension which is equal to, but what about where is embedded? That means where is the nothingness which is left from removing iteratively but randomly parts of the unit interval? This zero set “nothing” is not really nothing but rather some- thing and is embedded in the complementary empty set. Since the dimension of the unit interval is, then the dimension of this complementary empty set must be a trivial. This agrees perfectly with the bijection formula and the dimensional function for n = −1 which gives [154] [155]

(7)

or equivalently

(8)

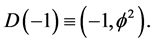
In addition the measure i.e. the length of the complementary set is a trivial 1 − 0 = 1. In other words this empty set is a fat Cantor set [7] [154] [155] .

Now let us look at the velocity in D(0). This was established by the work of the notable Italian physicist L. Sigalotti to be 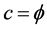which is not surprisingly the only non-zero quantity in the Cantor set. Next we like to determine the acceleration corresponding to V or say the acceleration analogous to Newtonian gravity on earth.

Now in E-Infinity we have a technique similar to non standard analysis were differentiation is equivalent to golden mean down scaling while integration is a golden mean scaling up [7] [9] [21] [28] .

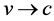
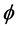
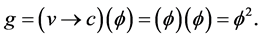
In this case we have to down scale by multiplication with. Therefore the acceleration is simply

(9)

Again, not surprisingly this corresponds in elasticity to a torsional term and is numerically equal to the Hausdorff dimension of the empty set quantum wave [19] [28] [119] .

Our next step is to determine the height of the mass in the gravity field which is endowed with a positive energy i.e. a potential energy. Since the edges of the unit Cantor interval corresponding to the limit of the universe at a nominal infinity, then the maximum length of the unit interval is simply one half (1/2).

Now we can write heuristically a fractal expression for conventional potential energy for

(10)

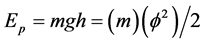
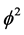
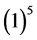
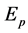
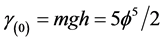
provided we know what m is. This is easily reasoned if we get access or an insight into the real meaning of mass. This is clearly connected to energy and energy is related to entropy. On the other hand entropy maybe measured via the Hausdorff dimension which is for the empty set. Now a mass in 5-dimensional spacetime becomes a Kaluza-Klein spacetime five dimensional mass. Consequently, our empty set mass cannot be which is nothing but 1. Therefore it must be m = (1) (5). Inserting in to, we find the familiar expression of ordinary cosmic energy density

(11)

exactly as shown previously using various other methods. Let us stress this point again. We have just established the potential energy nature of dark energy and squared it with the energy of the quantum particle via a mathematical tautology. This is because at the end of the day it is completely the same thing to say

(12)

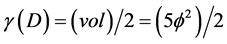
or to say

(13)

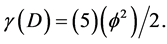
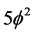
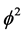
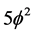
Thus could be interpreted as topological empty set mass m = 5 multiplied with the acceleration or as the volume of the 5D quantum wave empty set namely the additive volume. In other words we have a different mental picture leading to the same result [212] [426] .

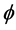
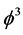
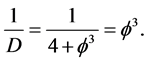
Returning to the kinetic energy, this is relatively simpler because real energy of real zero set quantum particles is sensibly interpreted as a 3D mass. In this case we have then to the power of 3D which give us as a multiplicative 3D mass i.e. volume. In turn this can be interpreted as the inverse of the spacetime core Hausdorff dimension [7] [9]

(14)

Inserting in Newton’s Kinetic energy, we find the expected result

(15)

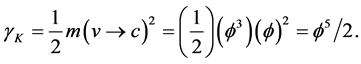
In agreement with expectations, the total energy which is the sum of the Kinetic and the potential energy is equal to Einstein’s maximal energy density [426] [427]

(16)

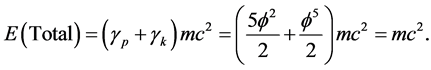
In concluding this part of our analysis we stress the subtlety of various interpretations of E(D) which could be potentially confusing. This is because 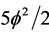could be interpreted

in equal measure as the quantum wave kinetic energy 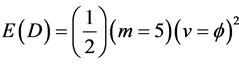or

the spacetime potential energy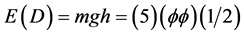. In both cases the result is the same but the “pictures” are different. In fact we could go as far as claiming that within quantum cosmology the difference between kinetic energy and potential energy is fuzzy and so is the difference between the state of motion or being at rest which resonates with the old philosophy of Zeno [430] .

3. Conclusion

We have come a long way in a relatively short time to recognize the depth and beauty involved in the discovery of the so-called missing dark energy of the cosmos. Dark energy is simply potential energy latent in the five-dimensional empty set spacetime. However, one could equally say that dark energy is the energy of quantum wave. Since it may be seen as a product of minus one dimensional empty set, it has a different sign to that of the ordinary energy. Consequently, the topological acceleration 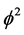when multiplied with the Kaluza-Klein topological mass and divided by the “height” 1/2 is the cause behind the accelerated expansion of the cosmos. As such our result reinforces recent exciting work reported in [424] [430] , and [429] [430] . However the mathematics and methodology used here are entirely different from the said references and therefore this agreement lends both theories considerable credibility.

Cite this paper

El Naschie, M.S. (2016) Cantorian-Fractal Kinetic Energy and Potential Energy as the Ordinary and Dark Energy Density of the Cosmos Respectively. Natural Science, 8, 511-540. http://dx.doi.org/10.4236/ns.2016.812052

References