Natural Science
Vol.06 No.17(2014), Article ID:52898,7 pages
10.4236/ns.2014.617117
Deriving of the Generalized Special Relativity (GSR) by Using Mirror Clock and Lorentz Transformations
M. H. M. Hilo1, R. Abd Elgani1, R. Abd Elhai1, M. D. Abd Allah1, Amel A. A. Elfaki2
1Department of Physics, Sudan University of Science and Technology, Khartoum, Sudan
2Department of Physics, Bahri University, Khartoum, Sudan
Email: mahmoudhilo@gmail.com, mahmoud1972@sustech.edu, rawia_abdalgani@yahoo.com, rawia@sustech.edu, rashaabdelhaye@sustech.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 October 2014; revised 28 October 2014; accepted 15 November 2014
ABSTRACT
Einstein relativity theory shows its high capability of promoting itself to solve the long stand physical problems. The so-called generalized special relativity (GSR) was derived later, using the beautiful Einstein relation between field and space-time curvature. In this work we re-derive (GSR) expression of time by incorporating the field effect in it, and by using mirror clock and Lorentz transformations. This expression reduces to that of (GSR) the previous conventional one, besides reducing to special relativistic expression. It also shows that the speed of light is constant inside the field and is equal to C. This means that the observed decrease of light in matter and field is attributed to the strong interaction of photons with particles and mediates which causes successive absorption and reemission processes that lead to time delay. This absorption process makes some particles appear to move faster than light within the field or medium. This new expression, unlike that of GSR, can describe time and coordinate relativistic expressions for strong as well as weak fields at constant acceleration.
Keywords:
Lorentz Transformations, Mirror Clock, Space-Time Curvature, Gravitational Field

1. Introduction
Einstein’s special relativity and general relativity represent one of the biggest achievements that change radically the space-time concept [1] . Special relativity (SR) succeeds in explaining the constancy of light speed in vacuum, long-time meson decay, and mass-energy conversion [2] .
SR shows that time, length, mass, and energy are velocity dependent [3] . Einstein extends his SR theory to the so-called general relativity theory (GR) which extends the space-time interval to the curved space GR succeeded in explaining a wide variety of astronomical phenomena. These include the Doppler red shift, which is interpreted as resulting from the universe expansion, the existence of relic microwave background, beside the gravitational red shift [4] .
These remarkable successes of SR and GR motivate some authors to promote SR within the frame of GR to produce the so-called Generalized Special Relativity (GSR) [5] .
Mubarak model, the matter energy-momentum tenser relation on the generalized Lorentz factor  derived from the space-time interval in the curve space, was utilized to construct the seminal EGSR model; time, length, mass and energy are dependent on the field potential as well as velocity [6] .
derived from the space-time interval in the curve space, was utilized to construct the seminal EGSR model; time, length, mass and energy are dependent on the field potential as well as velocity [6] .
In this work two mirrors of certain length, acting as time clock, are under the action of gravity. The motion of the two mirrors under gravity is utilized to find a useful expression of time in the presence of the gravitational field. The speed of light is assumed to be constant in the gravity field. This assumption is confirmed by obtaining the light speed in accursed space time [7] .
This paper, which is concerned with the derivation of time dilation in the gravitational field, consists of 3 sections; apart from introduction, Section 2 is devoted for presenting EGSR theory. The derivation of time dilation in the gravitational field for any field is done in Section 3. The speed of light in the gravitational field is found in Section 4. Sections 5 and 6 are devoted for discussion and conclusion (Generalized Special Relativity [8] ).
According to GSR the expressions of time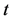 , length
, length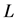 , and mass
, and mass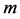 , are dependent on the velocity as well as field potential per unit mass and according to the relations.
, are dependent on the velocity as well as field potential per unit mass and according to the relations.
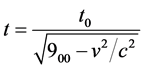 (1)
(1)
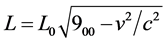 (2)
(2)
 (3)
(3)
where
 (4)
(4)
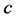 stands for light speed in vacuum, while
stands for light speed in vacuum, while 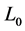 and
and 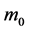 represent the rest time, length and mass respectively.
represent the rest time, length and mass respectively.
2. Time Dilation and Length Contraction
The expression of time in the presence of gravitational field can be found by considering two as a clock, with time intervals to representing the travel between the two mirrors as shown in Figure 1.
Figure 1. The mirror in free space.
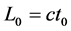 (5)
(5)
It moves with velocity up ward under gravity of acceleration g, the velocity of the lower mirror is given by
 (6)
(6)
where 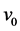 stands for the initial velocity, while
stands for the initial velocity, while  represents the displacement.
represents the displacement.
The vertical displacement 
The speed 
Thus

where:


where 

Inserting (9) in (6) yields as shown in Figure 2.

Since the point 


Figure 2. The mirror at t = 0.
Figure 3. The mirror displaced 
Speed 
In view of Equations (7)-(10), one gets

Thus:

Using relation (10)

If one consider 


Then relation (10) becomes

And relation (13) becomes
For weak field
Thus

Which coincides completed with the expression of time in the presence of the gravitational field obtain within the framework of GSR. Relation (14) it is important to note that of the factor 

According to Equations (9) and (10) this relation holds for any field other than the gravitational field.
The length contraction can be obtained by considering a clock falling by sliding on a rod of a height

where the rod is moving and accelerated w.r.t him, thus his length is



Thus, with the aid of Equations (18) (19) and (13).

This is in agreement with the corresponding expression in GSR.
3. Derivation of Time and Coordinate Expressions by Using Lorentz Transform
Using Lorentz transformation, the event at point 




Since the space is homogeneous it follows that

Consider ampoule of light emitted from a source when the origins 0 and 01 are in coincidence at
In this care

Substituting Equation (23) in Equations (22) and (21) yields


Inserting Equation (25) in Equation (24) yields

With the aid of Equation (8) and Equation (10)

When one consider the expression for the maximum speed in Equation (15), one gets

It is very striking to observe that when no field exist, i.e.

This is the usual SR expression.
For weak field
Therefore
Thus Equation (25) becomes

This is the usual expression of GSR for a weak field.
4. Discussion
In Section 3 time dilation expression in the presence of any field has been derived by using mirror, see Equations (11) and (14). The only assumption which causes a limitation to this expression is the constancy of acceleration. The mirror motion is described by using Newton’s Law of linear motion with constant acceleration.
The speed of light is assumed to be constant. The resulting expression for 
It also reduced to GSR form for a weak field as shown in Equation (16).
The expression of length contraction has been obtained as well. Again this expression reduced to SR and GSR also [9] .
Lorentz transformation is also utilized to find a relativistic expression for 

5. Conclusion
The expressions for time and length obtained by using Lorentz transformation and using mirror clock, for fields at constant acceleration, and by assuming the speed of light to be constant indicate that GSR rests on a solid ground. It also indicates that space and time are affected by any field, not gravity only. Unlike the curved space- time derivation, where the field is assumed to be week, this derivation holds for strong fields as well. By reducing to SR and GSR for a weak field, it indicates its self-consistency.
Cite this paper
M. H. M. Hilo,R. Abd Elgani,R. Abd Elhai,M. D. Abd Allah,Amel A. A. Elfaki, (2014) Deriving of the Generalized Special Relativity (GSR) by Using Mirror Clock and Lorentz Transformations. Natural Science,06,1275-1281. doi: 10.4236/ns.2014.617117
References
- 1. Lawdre, D.F. (1982) An Introduction to Tensor Calculus and Relativity. John Wiley and Sons, New York, Chapter 5, 6.
- 2. Weinberg, S. (1972) Gravitation and Cosmology. John Wiley and Sons, New York, Chapter 5, 6.
- 3. Savickas, D. (2002) Relation between Newtonian Mechanics, General Relativity and Quantum Mechanics. Journal of Physics, 70, 798-807.
- 4. Mubarak, D.A. and Ali, T. (2003) The Special Relativity in the Presence of Gravitation and Other Field. University of Khartoum, Khartoum.
- 5. Dirrar, M., Hilo, M.H.M., Abd Elgani, R. and Bakheet, A.M.A. (2013) Neutrino Speed Can Exceed the Speed of Light within the Frame Work of the Generalized Special Relativity and Savickas Model. Natural Science, 5, 685-688.
http://dx.doi.org/10.4236/ns.2013.56084 - 6. Hilo, M.H.M. (2011) Using of the Generalized Special Relativity in Deriving the Equation of the Gravitational Red-Shift. Journal of Modern Physics, 2, 370-373.
http://dx.doi.org/10.4236/jmp.2011.25045 - 7. Hilo, M.H.M., et al. (2011) Using of the Generalized Special Relativity (GSR) in Estimating the Neutrino Masses to Explain the Conversion of Electron Neutrinos. Natural Science, 3, 334-338.
http://dx.doi.org/10.4236/ns.2011.34044 - 8. Narlikar, J.V. (1993) Introduction to Cosmology. 2nd Edition, Cambridge University Press, Cambridge.
- 9. Xu, C., Uis, G.F.R.E., Xu, X.J. and El Tahir, A. (1992) The Generalized Field Equation. South African Journal of Physics, 15, 5.7.





















