Natural Science
Vol.6 No.2(2014), Article ID:42864,9 pages DOI:10.4236/ns.2014.62007
Solar radiation and atmospheric dynamics
Institute of Ionosphere, Almaty, Kazakhstan; vmsoms@rambler.ru
Copyright © 2014 Vyacheslav M. Somsikov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Vyacheslav M. Somsikov. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received 2 January 2014; revised 2 February 2014; accepted 9 February 2014
ABSTRACT
This paper studies the problems of mathematical description of physical processes in open non-equilibrium atmosphere. It is proposed that the mathematical description should be based on the idea that properties of an open system are determined by the properties of its elements and external constraints. It is also explained why atmosphere should be represented by an open non-equilibrium system of gas and radiation. Difference between physical processes in the above mentioned system and equilibrium atmosphere is given. The modification of equations of non-equilibrium thermodynamics for a system of gas and radiation is proposed. Possible ways for further development of tools of non-equilibrium thermodynamics are considered.
KEYWORDS
Radiation; Dynamics; Non-Equilibrium Systems; Thermodynamics; Entropy Production; Classical Mechanics
1. INTRODUCTION
The problem of the global change of the climate is a serious challenge to humanity and, above all, to the science [1]. But today we cannot even confidently answer, is this climate change connected with the anthropogenic factor or with the natural processes. The reason mostly lies in that that the present physical theory does not allow the strictly enough to describe the evolutionary processes in open non-equilibrium systems arising from the changes in external constraints. Our atmosphere is precisely such a system. i.e., the Earth’s atmosphere is an open non-equilibrium self-consistent system of “gas-radiation” (GRS). The non-equilibrium and openness of the atmosphere are determined by solar radiation and its interaction with the atmospheric gas. The radiation ensures a constant flow of energy into the atmosphere and sets the space-time structure of the gas, determines its composition and the deviation from equilibrium [2-6]. Therefore, to build a dynamic model of the atmosphere it should be seen as GRS.
Mathematical apparatus, which suitable for creating models of GRS, started to develop recently. Prior to this study of the atmosphere were carried out in the frame of the thermodynamic approach. The role of solar radiation was reduced to the source of atmospheric disturbances of different scales. The tides of the atmosphere caused by the motion of the sun across the sky were studied in the frame of this approach [4]. In this case, the solar radiation played the role of a regular source of large-scale atmospheric disturbances due to the heating. Thus the root cause of the occurrence of these disturbances is a diurnal variation of the solar radiation. The inhomogeneous structure of the atmosphere, created by such a source of disturbances, has a scale commensurate with the scale of the Earth and the period comparable to the period of the day.
In addition to the large-scale structure of the atmosphere, the solar radiation flux creates a fine-scale structure. This structure is created by the solar terminator (ST). The space-time structure of the perturbation parameters of the atmosphere, created by the ST, has periods ranging from several minutes to several hours and covers the entire globe. The nature of these irregularities is much more complicated than the nature of the tides. It is associated with sharp changes of photochemical and other parameters of the atmosphere due to the rapid change of the flux of solar radiation in the region of ST [7,8].
In recent decades mainly due to a sharp change in climate [1], the studies of the atmosphere as an open nonequilibrium system was started. In the first stage of this research, the questions about the role played in the dynamics of the atmosphere of openness and factor of non-equilibrium were studied. The estimations of the entropy production in the atmosphere during its interaction with solar radiation were performed [3]. The entropy production is the most important parameter indicating the degree of non-equilibrium of the atmosphere. These calculations confirmed the essential role of the openness of the atmosphere. Later the some peculiarities of the entropy balance have been studied [6]. The questions of the stability and properties of the climate models were considered [9]. A comprehensive analysis of observations on long-term changes in the radiation balance of the atmosphere in order to identify trends of climate change was carried out [10]. These studies have shown that the accounting of the non-equilibriums and openness of the atmosphere for improving the dynamic model of the atmosphere are requires.
To evaluate the contribution of the non-equilibrium processes into the dynamic structure of the atmosphere, the analysis of the dispersion relation for acoustic-gravity waves in view of their non-linear interaction with the solar radiation, was performed [11]. This analysis allowed us to determine the instability rate due to radiation. It was found that the instability of the atmosphere are exists for the waves with periods of 5 minutes during sunrise period at the altitudes 100 km.
As a next step in the development of studies of the atmosphere, the peculiarities in variations of the atmosphere due to the influence flows of the solar radiation on the dynamic properties of the atmospheric gas were investigated. Studies were carried out on the basis of the linearized empirical equations of non-equilibrium thermodynamics written for atmosphere as a GRS [12,13]. The result has been detected a significant shift of the spectrum of natural oscillations, determined by the interaction of radiation with the atmosphere. It was found that the spectrum of the acoustic-gravity waves in the atmosphere during the day have a higher frequency than at the night. Calculations well confirmed by experimental observations.
In consequence it became clear that on the way of creating an evolutionary model of the atmosphere have a lot of problems. One of the main challenges in building a model of the atmosphere as an open non-equilibrium system is that the existing mathematical tool, which is based on the equations of gas dynamics, is not suitable to describe the non-equilibrium processes. To create such mathematical tool the development of the physics of non-equilibrium systems is requires. i.e. the physics, which describes the time-dependent dissipative processes at the all hierarchically levels of the transformation of the incoming energy into open systems, in particular, the energy of solar radiation [14,15].
Here on the example of ST will be shown how to develop a model GRS. We are starting from the linear models of atmospheric disturbances. After that we will show; how to modify the equations of non-equilibrium thermodynamics for to use them to study the dynamic properties of the GRS; how the non-equilibrium processes in the atmosphere are connected with solar radiation; what are the difficulties in creating mathematical tools which lets describe open systems and how to overcome them; how to develop the evolution physics, i.e. the physics that will explore the processes of generation, development of the open non-equilibrium systems.
The Linear Model of the Atmosphereic Disturbances Generated by ST
As in the case of tides and in the case of small-scale inhomogeneities atmosphere generated by ST, perturbation calculations were based on the atmospheric gas dynamics equations in the thermodynamic approach. The general form a set of equations for the ST can be represented as follows [7,8]:
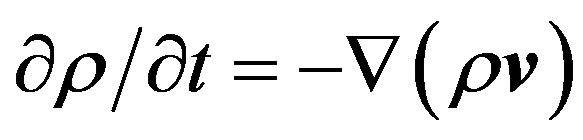 (1)
(1)
 (2)
(2)
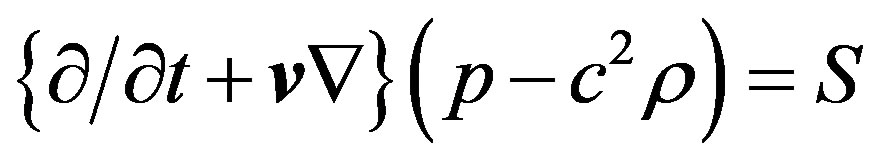 (3)
(3)
 (4)
(4)
Here t is the time;  is the atmospheric gas density; T is the atmospheric temperature;
is the atmospheric gas density; T is the atmospheric temperature; 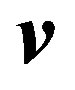 is the gas velocity;
is the gas velocity; 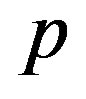 is the pressure;
is the pressure;  is the gravitational acceleration; R is the absolute gas constant reduced to molecular weight;
is the gravitational acceleration; R is the absolute gas constant reduced to molecular weight;  is a sound velocity;
is a sound velocity; 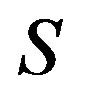 is a heat flow per unit volume per unit time;
is a heat flow per unit volume per unit time;  is external forces.
is external forces.
Since the ST has a global nature, the Eqs.1-4 should be solved in the spherical coordinate of system. Representing solution these equations in the form of the expansion in terms of harmonics:
 taking into account the smallness of the so-called sine terms, we can obtain the solution of the Eqs.1-4. For a pressure disturbance in an approximation, dictated by the ST characteristic dimensions, we will have [16]:
taking into account the smallness of the so-called sine terms, we can obtain the solution of the Eqs.1-4. For a pressure disturbance in an approximation, dictated by the ST characteristic dimensions, we will have [16]:
 (5)
(5)
Here,  are the height above the Earth’s surface, latitude, and longitude, respectively;
are the height above the Earth’s surface, latitude, and longitude, respectively; 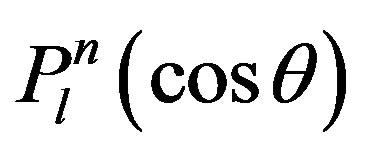 are the Legendre polynomials;
are the Legendre polynomials;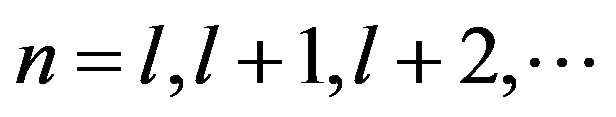 ;
;  is the harmonic of the source function expansion in terms of spherical functions;
is the harmonic of the source function expansion in terms of spherical functions;  is the undisturbed harmonic of atmospheric pressure;
is the undisturbed harmonic of atmospheric pressure;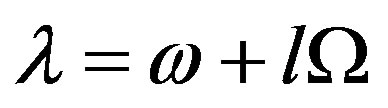 ;
;  is a frequency;
is a frequency;  is the Earth’s angular velocity of rotation;
is the Earth’s angular velocity of rotation;  is Green’s function determined by the ST spherical model;
is Green’s function determined by the ST spherical model;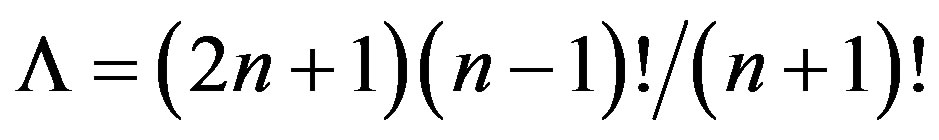 .
.
The calculation results of a pressure disturbance, generated by the spherical model of ST, on Figure 1 is illustrates. This calculation was performed using Formula (5), when the source function depends on the heat income into the atmosphere [17].
The interaction solar radiation with atmospheric gas in the ST region in some cases can lead to instability [8,18]. The mechanism of this instability is caused by the gradient of the solar radiation absorption coefficient during sunrise. This instability we call as “gradient-radiation instability”. The nature of this instability can be explained as follows: if any atmospheric element shifts in the region with a considerable radiation flux, e.g., under the action of the wave’s disturbance, this element will warm up and expand. If its expansion is sufficient, this element will start to float up. Because this elements falls in the region of stronger heating the process becomes exponentially unstable. The criterion for the “gradient-radiation instability” has the form [18]:
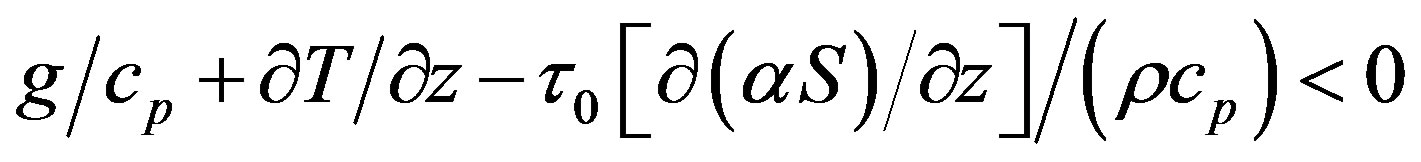 (6)
(6)
where  is the external wave period;
is the external wave period; 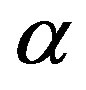 is the radiation absorption coefficient;
is the radiation absorption coefficient; 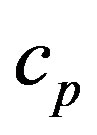 is the heat capacities at constant pressure.
is the heat capacities at constant pressure.
According to estimations, the radiation instability can originate in the dawn time in the thermosphere.
2. THE FIRST STEP TO GRS
For describing the evolutionary processes in the atmosphere, caused by solar radiation, must take into account the interdependence of the solar radiation and the state of the atmospheric gas. The analogue of the selfconsistent system of equations can serve as equations for the plasma in an electromagnetic field [19]. A similar

Figure 1. A pressure disturbance generated by the ST.
system of equations must be constructed for the atmosphere. This system of equations will allow in the given point of the atmosphere to take into account not only the dependence of the radiation flux from the parameters of the atmosphere but also the dependence of the parameters of the gas from the solar radiation flow. As such a system of the equations, which allows studying the nonequilibrium dynamic processes of an atmosphere, it is possible to use the modified equations of non-equilibrium thermodynamics [20], taking into account the interaction of atmospheric gas and radiation [21]. The solution of the equations of non-equilibrium thermodynamics is a very difficult task. Therefore simplification these equations are needed. We have done the maximum simplification of the original system of equations. At the same time the terms that determine the relationship of solar radiation and the gas state have been retained. In the new system, the Eqs.1, 2 and 4 are preserved. But the energy equation will differ (see (7)). These equations by the equations for the flow of solar radiation were supplemented (8), (9). The modification of the system of equations can be written as [12]:
 (7)
(7)
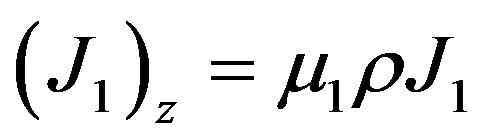 , (8)
, (8)
 (9)
(9)
Here 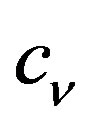 is the heat capacities at constant volume; Iv is the intensity of a beam of photons with frequency
is the heat capacities at constant volume; Iv is the intensity of a beam of photons with frequency ;
; 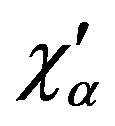 is the radiation absorption coefficient per unit gas density; L is the heat flux;
is the radiation absorption coefficient per unit gas density; L is the heat flux;  is the thermal radiation of the atmospheric gas;
is the thermal radiation of the atmospheric gas; 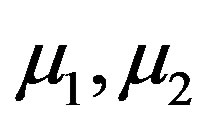 are the average coefficient of solar radiation flux absorption which going down and up consequently;
are the average coefficient of solar radiation flux absorption which going down and up consequently; 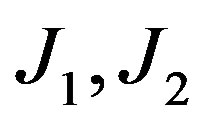 are the solar radiation flux are directed from top to bottom and vice versa; z is denote partial derivatives with respect to corresponding coordinate.
are the solar radiation flux are directed from top to bottom and vice versa; z is denote partial derivatives with respect to corresponding coordinate.
In the Eqs.1, 2, 4, 7-9 we saved only those terms which play a significant role in the generation of acoustic-gravity waves in atmosphere. The first two terms in Eq.7 correspond to the description of atmospheric perturbation in the linear approach [7]. These terms are responsible for acoustic-gravity wave’s generation in the equilibrium atmosphere. The last three terms appeared since the interaction between radiation and the atmospheric gas is taken into account. The third term is related to thermal conductivity. The fourth term is related to heating of the atmosphere by solar radiation, and the last term is related to infrared radiation outgoing into the space.
Since the coefficients of solar radiation flux absorption which going down and up consequently dependent on the atmospheric chemistry at different altitudes and have a very complicated character, the approximations of the Bouguer’s Eqs.8, 9 are used [3,6]. These equations have non-linear terms in the right-hand side which connect the atmospheric gas and solar radiation into the GRS.
The dispersion equation was determined in accordance with Eqs.1, 2, 4, 7-9. Its numerical calculations showed the shift of the spectrum of acousticgravity waves. This shift is appeared in the equilibrium atmosphere due to the interaction of the solar radiation and gas. It is directed towards the high-frequency region in the day time and caused by the solar radiation absorption and atmospheric emission of the radiations. These results are confirmed experimentally by the spectral analysis of the data of the pressure perturbation obtained during the period of August, September, and January in Antarctica [13]. This clearly demonstrates the fundamental role of coupling the gas and radiation.
Figure 2 is a diagram of deviation of the pressure values (in percentage) which obtained in accordance with the system of Eqs.1, 2, 4, 7-9 in the zero-order approximation. It is a deviation from the values calculated by the barometric formula.
Thus we obtain a good agreement between the theory results and experimental measurements for GRS model.
Since the effects due to non-equilibrium atmosphere and openness were significant it became apparent that for getting a real picture of the processes in the atmosphere, the atmosphere should be viewed as a GRS [12-14,21]. But to construct an evolutionary model of the atmosphere, the Eqs.1, 2, 4, 7-9 need to be modified in view of the more exactly nature of the energy exchange between the gas and radiation. As a next step to this aim we can use the non-equilibrium thermodynamics equations for atmospheric gas [21] and the equations for the solar radiation flux [3,6].
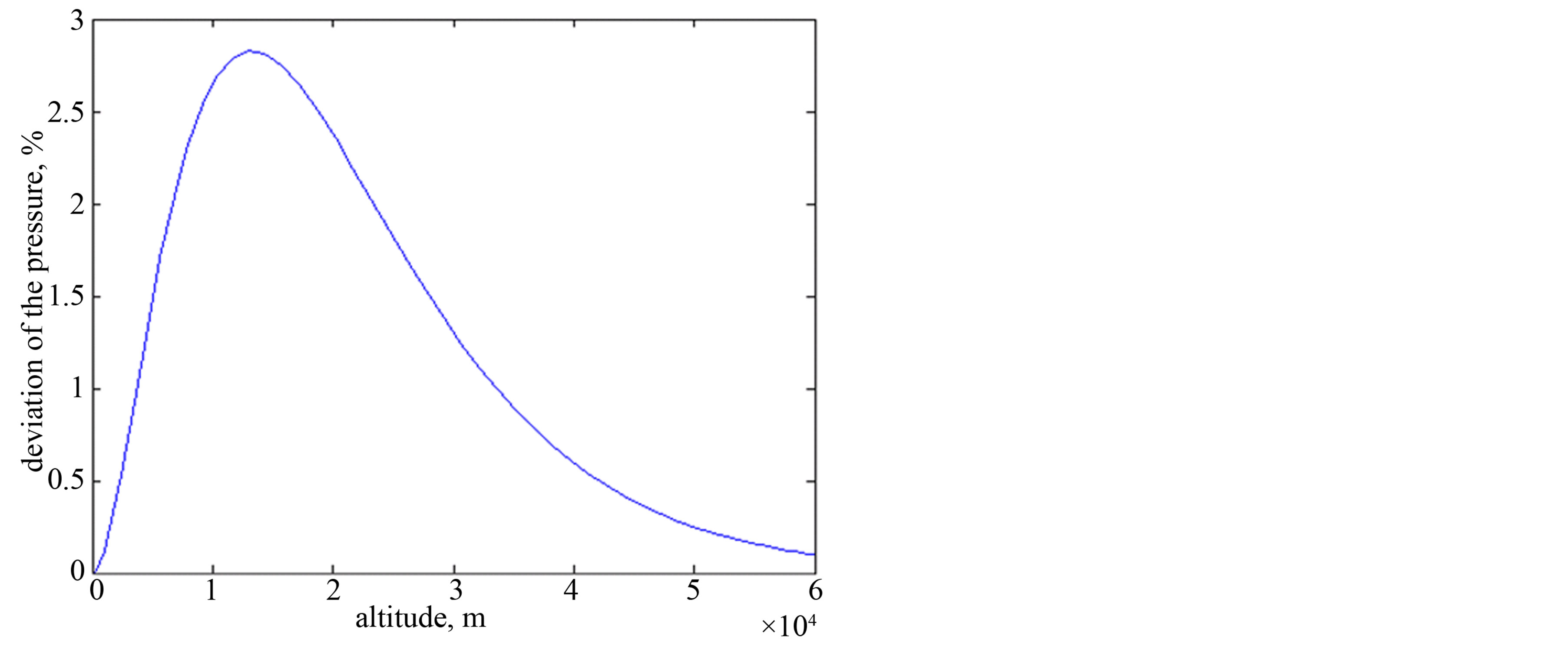
Figure 2. The deviation of the pressure in GRS from the barometric formula.
3. HOW TO CONSTRUCT THE NONEQUILIBRIUM THERMODYNAMICS EQUATION FOR GRS
The non-equilibrium thermodynamics equations there are equations which determine the change in mass, momentum, kinetic energy, internal energy and entropy in the non-equilibrium atmospheric gas of GRS [15]. But for GRS these equations must be modified taking into account the specific of the GRS. Let us show how it is possible to construct a system of equations for the GRS based on the classical equations of non-equilibrium thermodynamics [15,20]. We will start from the balance equation for the density of gas.
Atmospheric gas is a multicomponent. The balance between the different components is determined by photochemical reactions. Let the gas consists of m components of photochemical with the partial densities
 ,
, 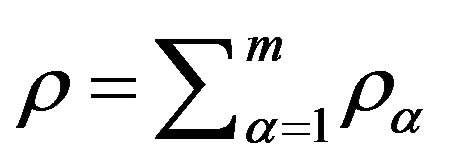 is a total density of the gas. The continuity equation for the density
is a total density of the gas. The continuity equation for the density 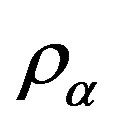 with the processes of photoionization and recombination can be obtained by taking into account the change in mass of the corresponding component as a result of photochemical reactions. It has the form:
with the processes of photoionization and recombination can be obtained by taking into account the change in mass of the corresponding component as a result of photochemical reactions. It has the form:
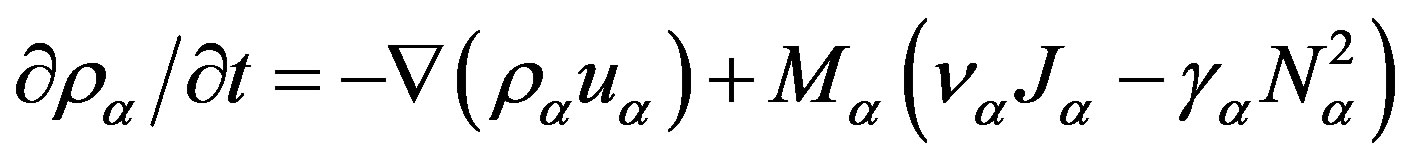 (10)
(10)
where  (а) is a photoionization rate, i.e. the number of acts of reaction per unit volume and per unit time,
(а) is a photoionization rate, i.e. the number of acts of reaction per unit volume and per unit time,  is an intensity of solar radiation, which determines the photoionization
is an intensity of solar radiation, which determines the photoionization  is a component,
is a component, 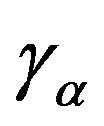 is a coefficient of photo recombination,
is a coefficient of photo recombination,  is a number of
is a number of 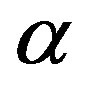 neutral gas component per volume unit. From the conservation of mass, we have:
neutral gas component per volume unit. From the conservation of mass, we have:
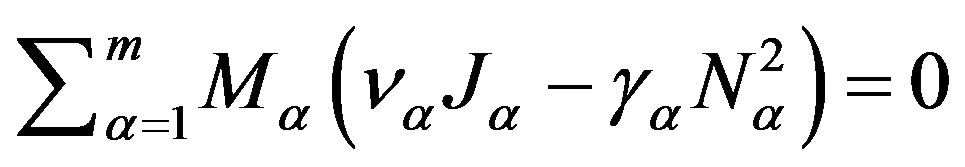 .
.
Although the condition (a) simplified, it allows taking into account the qualitative level of the photoionization process.
Let us introduce the local velocity of the center of mass for fluid particles:  and the local rate of diffusion of each component:
and the local rate of diffusion of each component: , and the diffusion fluxes
, and the diffusion fluxes , satisfying the condition:
, satisfying the condition: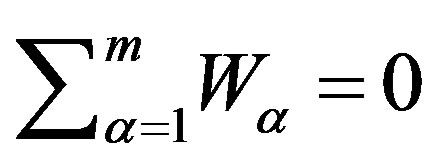 .
.
The equation describing the change in the total momentum per unit volume can be written as:
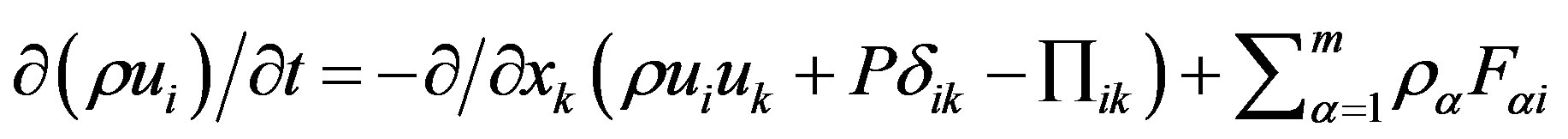 (11)
(11)
where  is a force, acting on a unit weight of
is a force, acting on a unit weight of  component of GRS.
component of GRS.
Here and after the indices “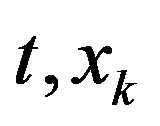 ”denote partial derivatives with respect to time and the corresponding coordinate.
”denote partial derivatives with respect to time and the corresponding coordinate.
The natural interpretation of (11) is that in addition to convective momentum flux with the projections 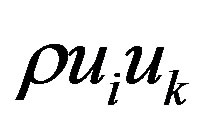 there is a “viscous” thread pulse:
there is a “viscous” thread pulse: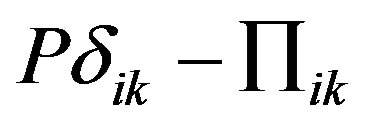 , not associated with the orderly movement of gas (convection) and with the random thermal motion. This movement also results to flow of the pulse through the boundary of the volume V and characterized by the values of the tensor
, not associated with the orderly movement of gas (convection) and with the random thermal motion. This movement also results to flow of the pulse through the boundary of the volume V and characterized by the values of the tensor  at the boundary of the volume V.
at the boundary of the volume V.
The source of the total momentum  is the total external force. In connection with estimations the main forces for the neutral atmosphere are gravity and pressure. Gravity causes the gravitational waves, and the pressure is source of the acoustic waves.
is the total external force. In connection with estimations the main forces for the neutral atmosphere are gravity and pressure. Gravity causes the gravitational waves, and the pressure is source of the acoustic waves.
In the ionosphere the essential role played by the ionized component of the atmospheric gas. Therefore the forces associated with the presence of electric and magnetic fields are appears. These forces can be written as:
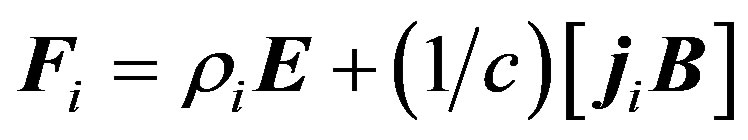 (12)
(12)
where  is external magnetic field,
is external magnetic field,  is electric field,
is electric field, 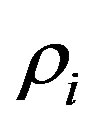 charge density for the i-th component of the charge,
charge density for the i-th component of the charge,  is ionospheric current.
is ionospheric current.
The first term in the expression for the force is due to external electric fields. Usually this term is significant in the area of the equator and the poles. In the mid latitudes electromagnetic force mainly is caused by the presence of a magnetic field. The expression for the current on the ionospheric heights ~200 km is [22]:
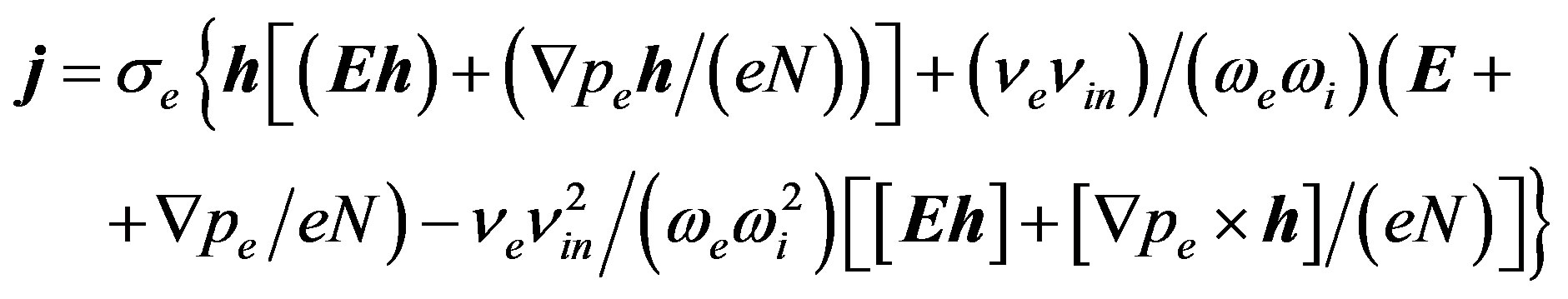 (13)
(13)
where  is characteristic frequency of collisions between ions and neutral component of the gas,
is characteristic frequency of collisions between ions and neutral component of the gas,  is the unit vector of the magnetic field of the earth,
is the unit vector of the magnetic field of the earth,  is a velocity of the charged components,
is a velocity of the charged components, 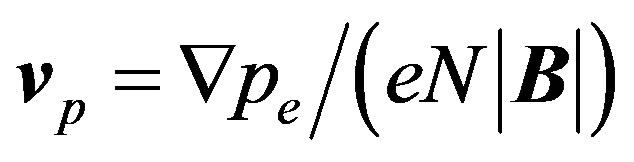 ,
,
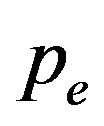 is a pressure of the electron gas,
is a pressure of the electron gas, 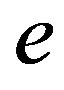 is electron charge,
is electron charge, 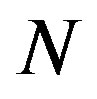 is a electron density,
is a electron density,  is a gyrofrequency of electrons and ions, respectively,
is a gyrofrequency of electrons and ions, respectively, 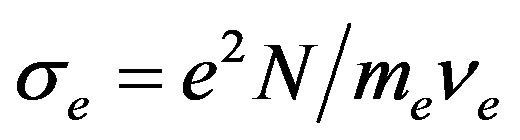 is a electronic conductivity,
is a electronic conductivity, 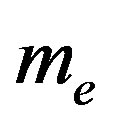 is a mass of the electron,
is a mass of the electron, 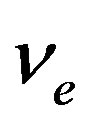 is a frequency of electron collisions with neutral particles.
is a frequency of electron collisions with neutral particles.
For the atmosphere above 300 km for the electromagnetic force can be writing:
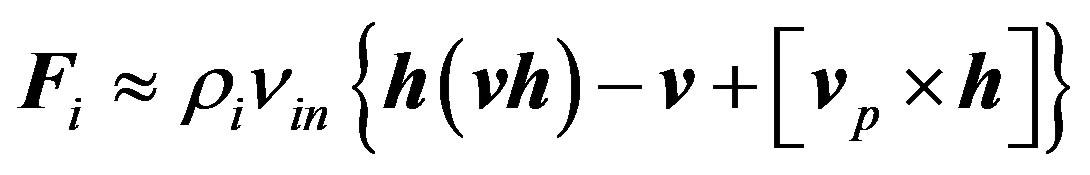 (14)
(14)
In according with (14) the forces in a first approximation due to the motion of the electron gas in the Earth’s magnetic field are proportional to the electron density.
In addition to the magneto-ionic forces, there are forces of friction in the ionospheric plasma due to collisions of ions and electrons and neutral particles. These forces are: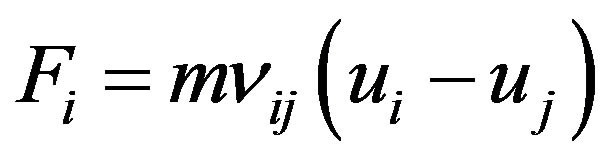 . Where
. Where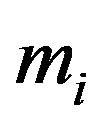 —is a mass of i—component of the gas,
—is a mass of i—component of the gas, 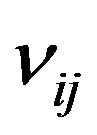 is a frequency of collisions
is a frequency of collisions  and
and —components of the ionospheric plasma,
—components of the ionospheric plasma,  ,
, 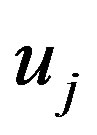 is a relative velocity.
is a relative velocity.
The energy of the atmospheric gas should be divided into three parts. There are kinetic, potential and internal energy per unit volume of the atmosphere. Kinetic energy equation is [20]:
 (15)
(15)
This form of the kinetic energy balance equation based on a physical hypothesis that the convective flow in addition to 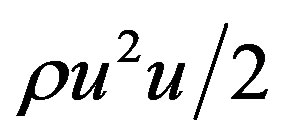 on the border of the volume there is a “viscous” thread of the kinetic energy with the projections
on the border of the volume there is a “viscous” thread of the kinetic energy with the projections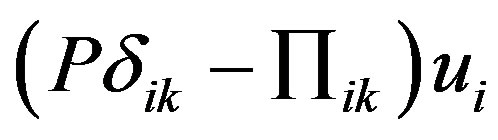 , and the sources of kinetic energy in addition to the work of external forces
, and the sources of kinetic energy in addition to the work of external forces 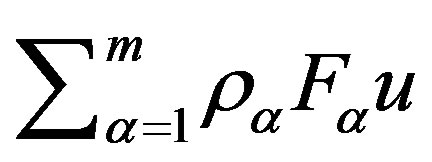 are the forces of pressure and viscous friction (the second term in the right-hand side of (15)).
are the forces of pressure and viscous friction (the second term in the right-hand side of (15)).
From the formula 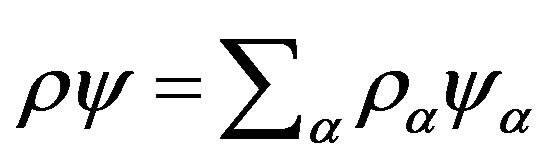 (
(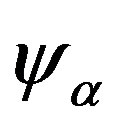 is a potential energy for
is a potential energy for  -component, per unit mass) in connection with Equation (10) we have:
-component, per unit mass) in connection with Equation (10) we have:
 (16)
(16)
Using the formula  and selecting convective flow
and selecting convective flow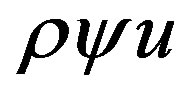 , the equation (16) becomes:
, the equation (16) becomes:
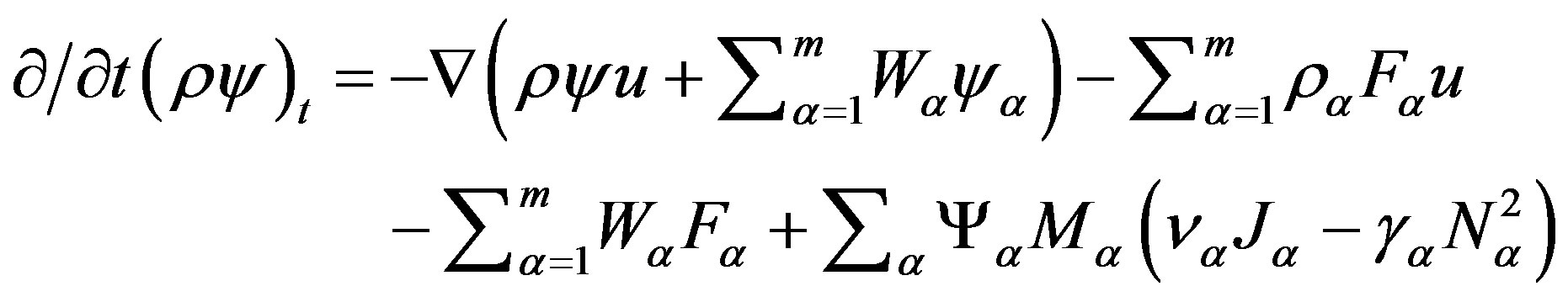
From (17) is following that the potential energy flux besides the convective “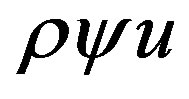 ” contains the diffusion flux:
” contains the diffusion flux: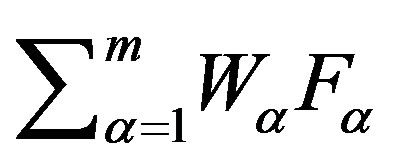 .
.
The balance of the total mechanical energy per unit volume  is determined by adding Eqs.15 and 17:
is determined by adding Eqs.15 and 17:
 (18)
(18)
Write down the equation for the balance of the internal energy density, defining it as the third component of the total energy density:
 .
.
The source of the total energy of the atmospheric gas is solar radiation . In addition it is necessary to take into account the radiative cooling of the atmosphere. In this case the total energy balance equation
. In addition it is necessary to take into account the radiative cooling of the atmosphere. In this case the total energy balance equation  becomes:
becomes:
 (19)
(19)
where the non-convective flow  equal to
equal to
 .
.
The non-convective flow 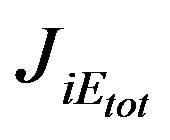 consists of “viscous” flow diffusion potential energy flux and heat flux (the first, second and third terms on the right side
consists of “viscous” flow diffusion potential energy flux and heat flux (the first, second and third terms on the right side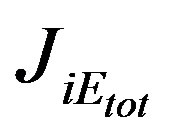 , respectively). This expression can be regarded as a phenomenological definition of the heat flux
, respectively). This expression can be regarded as a phenomenological definition of the heat flux . The contribution of radiation to the energy balance of the atmosphere is determined by the
. The contribution of radiation to the energy balance of the atmosphere is determined by the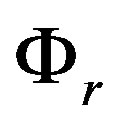 .
.
Balance equation for the internal energy in the approximation of stationary atmospheric is obtained by subtracting the expression (18) from (19) and using the expression :
:
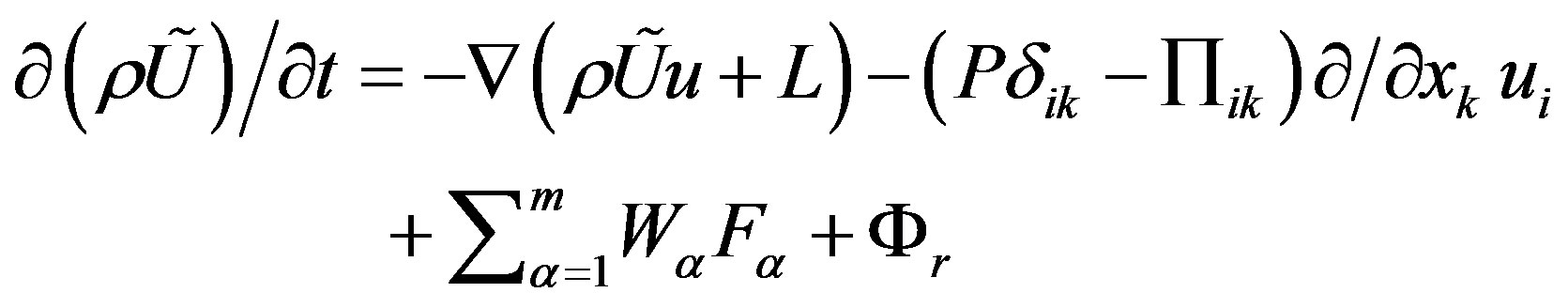 (20)
(20)
In addition to the convective flow of internal energy 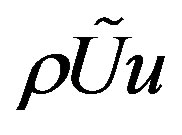 heat flux L is exists, and the density of sources in addition to the internal energy of the viscous forces and pressure contains a diffusion term
heat flux L is exists, and the density of sources in addition to the internal energy of the viscous forces and pressure contains a diffusion term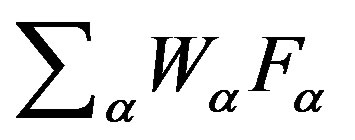 . That the balance equation for the internal energy stored in the form of (20) is due to the physical hypothesis that the force of viscous friction and pressure forces are responsible for the orderly transfer of mechanical energy of the gas and not the transfer of energy of random thermal motion.
. That the balance equation for the internal energy stored in the form of (20) is due to the physical hypothesis that the force of viscous friction and pressure forces are responsible for the orderly transfer of mechanical energy of the gas and not the transfer of energy of random thermal motion.
According to hypothesis of the existence of local equilibrium, the local molar thermodynamic entropy is defined by the equation:
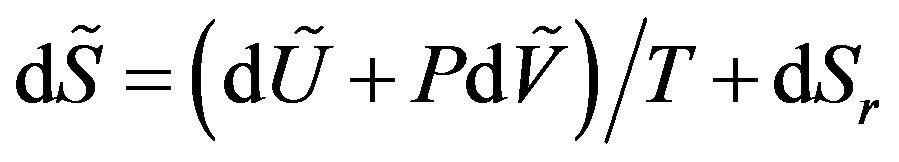 (21)
(21)
where  is increase of entropy due to the radiation fluxes.
is increase of entropy due to the radiation fluxes.
Assume that (21) holds true along the trajectory of the center of mass of small volumes of gas. Multiplying both sides of equation (21) by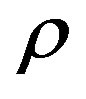 , replacing
, replacing 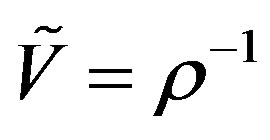 and going to the sub-stationary derivative with respect to time we obtain:
and going to the sub-stationary derivative with respect to time we obtain:
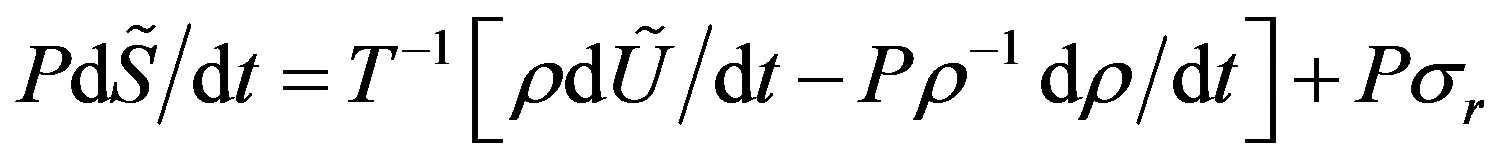 (22)
(22)
where 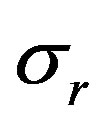 is entropy production in GRS due to the radiation fluxes [3,6].
is entropy production in GRS due to the radiation fluxes [3,6].
By doing in (22) the relevant transaction we arrive at the expression:
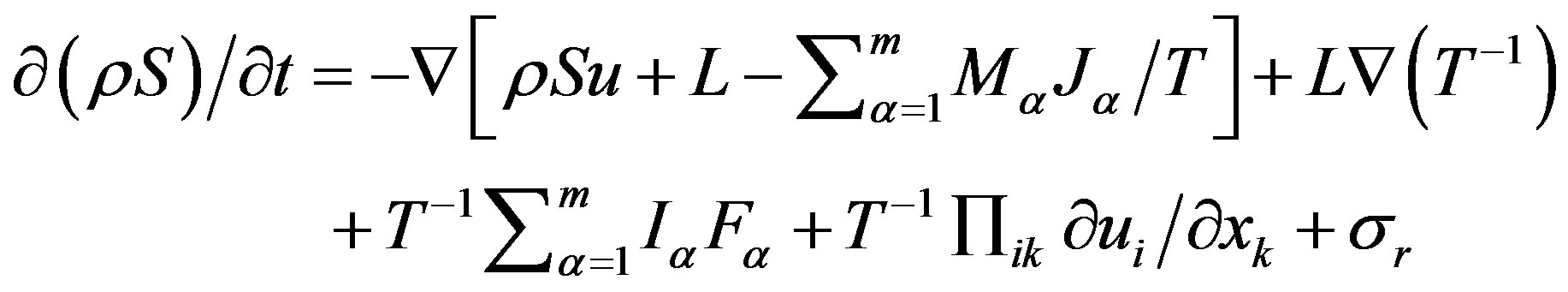 (23)
(23)
The interpretation of (23) is obvious: in addition to the convective flow of entropy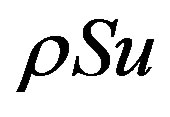 , there is heat flux
, there is heat flux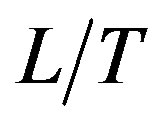 , and the density of the sources of entropy is given by:
, and the density of the sources of entropy is given by:
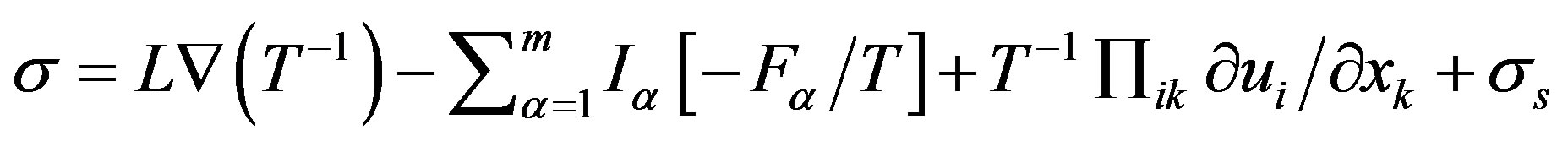
Consequently, the production of entropy in the atmosphere caused by thermal conductivity due to the existence of a temperature gradient (term “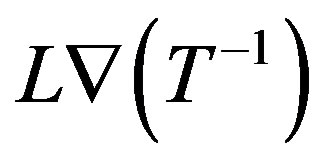 ”) diffusion caused by the presence of external forces, viscosity caused by the presence of velocity gradients (term
”) diffusion caused by the presence of external forces, viscosity caused by the presence of velocity gradients (term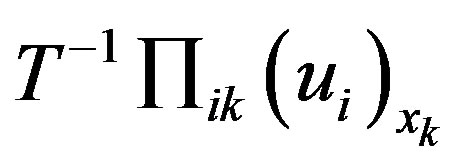 ), as well as its flow together with the solar radiation.
), as well as its flow together with the solar radiation.
Expression (24) is bilinear: each term is a factor of type of flow (heat flow L, diffusive flux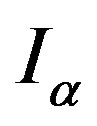 , momentum flux, or the viscosity tensor
, momentum flux, or the viscosity tensor 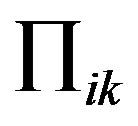 and the rate of a chemical reaction
and the rate of a chemical reaction ) and a factor proportional to the gradient of some value—temperature, potential energy (power
) and a factor proportional to the gradient of some value—temperature, potential energy (power ), velocity.
), velocity.
4. SOLAR RADIATION
The non-equilibrium thermodynamics equations for atmospheric gas of GRS must be supplemented by equations for the solar radiation. The solar energy leads to an increase of dynamic processes in the atmosphere, as is the case for the ST. The radiation changes the potential energy of the atmosphere by changing the temperature of the atmosphere in a gravitational field and by changing the chemical composition of the gas. It also changes the internal energy due to the heating of the atmosphere as a result of various dissipative processes. Moreover, it is stored in various inorganic and organic systems. Below we consider the simplest case, when the solar radiation changes the entropy and energy of the atmosphere.
According to Plank [6] the entropy density of the radiation with frequency 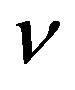 and intensity
and intensity  is equal to:
is equal to:
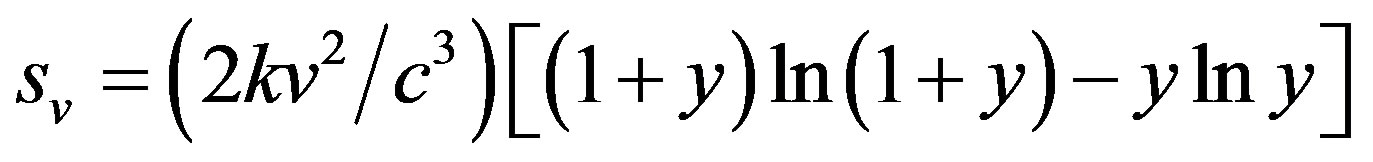 (25)
(25)
and their temperature:
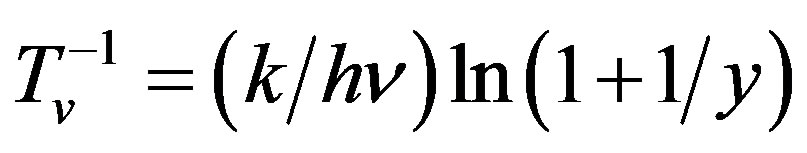 (26)
(26)
where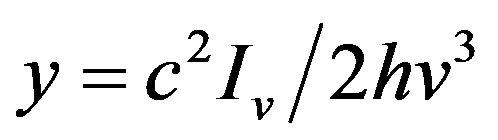 .
.
Formulas (25) and (26) can be obtained by considering the photons as particles obeying Bose-Einstein statistics [20].
Flows of energy and entropy of radiation per unit area ( and
and ) obtained by integrating the
) obtained by integrating the 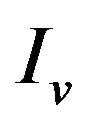 and
and  frequency and solid angle:
frequency and solid angle:
 (27)
(27)
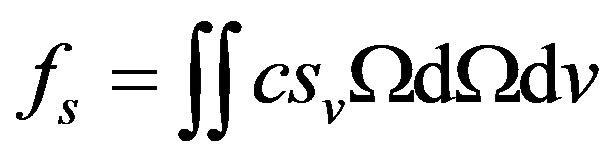 (28)
(28)
where  is a unit vector along the line,
is a unit vector along the line, 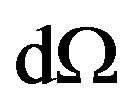 is differential solid angle.
is differential solid angle.
Differentiating (25) with respect to time t and the coordinate’s r, we obtain [6]:
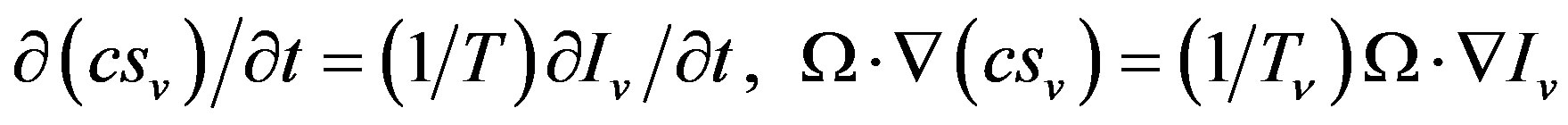 (29)
(29)
It follows that the entropy of the radiation transfer equation associated with conventional radiation transfer equation as follows:
 (30)
(30)
where 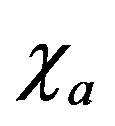 and
and 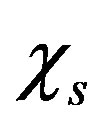 are the absorption and scattering of photons,
are the absorption and scattering of photons, 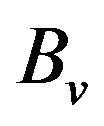 is a Planck’s radiation function. Due to the factor
is a Planck’s radiation function. Due to the factor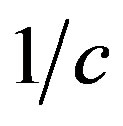 , in the derivatives on
, in the derivatives on 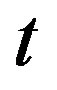 in (30) are generally negligibly small.
in (30) are generally negligibly small.
In particular, if the radiation emitted by a black body (in this case  constant), for (27), (28) we will have:
constant), for (27), (28) we will have:
 (31)
(31)
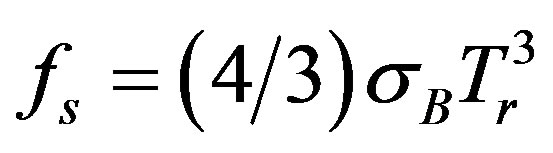 (32)
(32)
(where 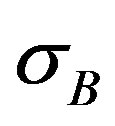 is a Stefan-Boltzmann constant).
is a Stefan-Boltzmann constant).
In non-equilibrium system, comprising a substance and radiation at different temperatures (e.g., molecules of the atmosphere, and solar photons), entropy density (with index m) and photon (with index r) its flow and production are formed:

At interaction photons with matter (absorption and scattering), the production of the entropy per unit volume is equal to:
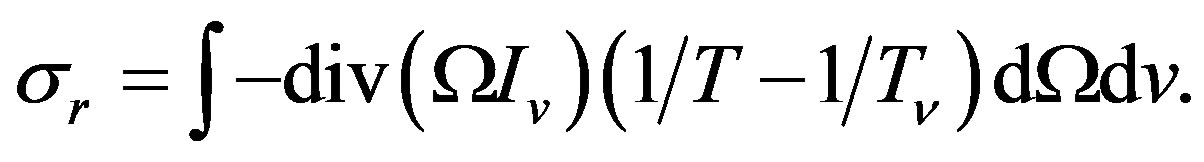 (33)
(33)
For black body radiation from (33) is obtained:
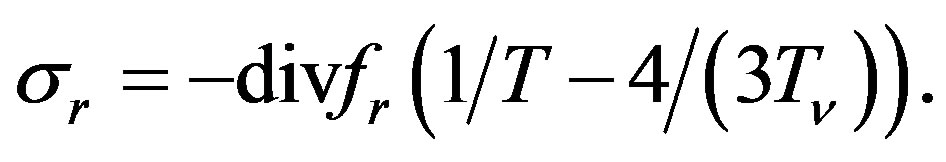 (34)
(34)
In (33), (34) the first term describes the change in entropy of matter, and the second—the photons. The fact that even for the non-equilibrium state of matter—a photon flux-entropy depends on the same parameters as the entropy of matter, S(E, T, V) (including the fact that the chemical potential of photons is zero [6,20]) confirms validity generalization of the above formulas for the radiation to non-equilibrium state.
Let us summarize the properties of entropy, defining its role in non-equilibrium systems. First of all, this is the only function of the state, which differs for irreversible and reversible processes: in the first case, it is growing, in the second case, does not change. The growth in total entropy of irreversible processes determines the direction of time (“arrow of time” [23]). Furthermore, the entropy is a measure of disorder macrostate which may be realized through various combinations of microstates. So it may serve as a measure reducing the ordering and increased—a measure of disorder. Finally, the entropy expresses the quality of energy. If the photon fluxes at a higher temperature than thermal radiation of the atmosphere, we have the increasing of the negentropy and increasing the order of the atmosphere.
It is believed that because the entropy of the system is not preserved, its plays a minor role compared with the energy. However the fact that the entropy is in contrast to the energy is not conserved, does not diminish its importance as a parameter characterizing the evolution of the systems. Its increase or decrease indicates the nature of the processes occurring in the system (ordering or disordering), and the magnitude of change may serve as their measure. When we say that the energy spent is actually spent negentropy. In this case, the energy comes and goes, but in different forms.
5. PROBLEMS AND PROSPECTS OF NONEQUILIBRIUM PHYSICS OF THE ATMOSPHERE
In general, the non-equilibrium thermodynamics equations allow us to study the GRS dynamics. But for it the knowledge of the various factors, such as thermal conductivity, coefficient of absorption of solar radiation, coefficients photochemical reactions, etc. is requires. Up to now these coefficients as usually take from the experiments. But they must be obtained rigorously on the basis of knowledge of equations defining the relationship of microscopic processes of interactions of substances and radiation with the collective properties of the medium. To find these coefficients need a theory that allows us to define the laws of systems dynamics on the basis of knowledge the law for dynamics their elements and external restrictions. One of the key problems constructing of this theory connected with that that the modern physical theories based on classical mechanics are not able to explain dissipative processes [23].
Indeed, all evolutionary phenomena in nature are related to the dissipative processes because attractors could not appear without dissipation. Boltzmann was the first who understood this problem and tried to solve it within the frames of the Newton’s laws. The conventional explanation of the mechanism of irreversibility is based on the property of exponential instability of Hamiltonian systems and the hypothesis of the existence of the fluctuations. The hypothesis of the existence of fluctuations provides breaking of the time symmetry of Hamiltonian systems. But this explanation does not give answer on the question, why in the frame of the Newton’s law the systems mechanics is reversible but in the nature all processes are irreversible.
In the recent years a deterministic solution of the ireversibility problem in the frame of the classical mechanics has been submitted. This solution has been found as a result of the removal of restrictions under which formalisms of classical mechanics was constructed [14,24,25]. The key idea which allowed to find this explanation consists in that that in the nature only bodies having the structure are exists. Presence of a structure causes a nonlinear transformation of the body’s motion energy into the internal energy. It is a cause of dissipation.
In the foundations of explanation of the mechanism of irreversibility the equation of motion system from potentially interacting material points is used. This motion equation has the form [25]:
 (35)
(35)
where 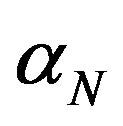 is a coefficient determined by the change in the internal energy of the system;
is a coefficient determined by the change in the internal energy of the system;  is a mass of the system;
is a mass of the system; 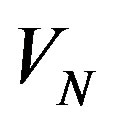 is a velocity of the center of mass of the system;
is a velocity of the center of mass of the system; 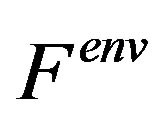 is a resultant force applied to the center of mass of the system.
is a resultant force applied to the center of mass of the system.
The first term on the right-hand side of (35) is a potent force that changes the kinetic energy of the system. The second term is measure of the internal energy change. Using the system’s motion eq.35 a generalized Liouville equations for non-equilibrium systems were obtained. It has the form [24]:
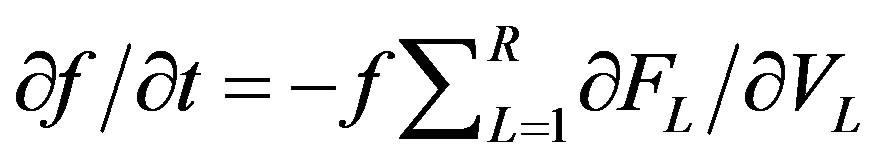 (36)
(36)
Here  is a distribution function for a set of subsystems, into which the non-equilibrium systems are divided;
is a distribution function for a set of subsystems, into which the non-equilibrium systems are divided; 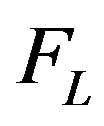 is a dissipative force;
is a dissipative force;  are a number of subsystems;
are a number of subsystems;  is
is 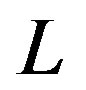 -subsystems velocity.
-subsystems velocity.
Eqs.35 and 36 show the possibility of extending the classical mechanics. This extending can be used for describe the dynamics of dissipative processes, to substantiate of the thermodynamics, statistical physics and kinetics. i.e. the possibility of using the laws of dynamics of elements to determined the laws of dynamics of their systems are opens.
6. CONCLUSION
Solar radiation is one of the main external factors that determine the spatial-time structure of the atmosphere and its dynamics. Solar radiation together with the atmospheric gas is a self-consistent non-equilibrium open system. It was found that the interaction of solar radiation with atmospheric gas leads to a shift of the spectrum of acoustic-gravitational waves. In the stationary case, the vertical structure of the atmosphere is determined not only by the composition of the atmospheric gas and the forces of gravity, but also by the spatial-time character of the energy exchange between the gas and radiation. Therefore for construct of atmospheric model, for studies of dynamical processes in the atmosphere and the climate change, etc., atmosphere should be considered as GRS.
For the study of the GRS, the equations of non-equilibrium dynamics can be used. In order to take into account the effects of photoionization and recombination, of multi-component of the atmospheric gas, the dependence of its spatio-temporal structure from the radiation, etc., the system equations of non-equilibrium dynamics need to be modified. This modification can be achieved by adding to the system of equations of gas dynamics the equations defining the radiation flux and accounting the terms in the gas-dynamic equations of conservation of mass, momentum and energy that govern the interaction of gas and radiation.
Solving of non-equilibrium thermodynamics equations faces a number of fundamental problems. First of all, to solve these equations the knowledge of the various factors such as thermal conductivity, coefficient of absorption of solar radiation, coefficients photochemical reactions etc., are required. Moreover these equation are not applicable to describe the fast processes in rarefied environments in systems far from equilibrium, in the high layers of the atmosphere, in the areas of sharp changes in environmental parameters, such as in the field of ST. For overcome these difficulties the development such a theoretical formalism which allows obtain non-equilibrium thermodynamics equations, describing the dynamics of the system, on the basis of the rigorous laws of dynamics of its elements are need. Such a theory should allow to link photochemical and other processes occurring at the micro-level, with macro-processes that determine the dynamics of a continuous medium, which is the GRS. The key idea the creation of this theory is to replace the mechanics of a material point on the mechanics, whose elements are the system. Such mechanics allow strictly bind micro-processes with dissipative macroprocesses. As a result the properties of the system from the properties of the structural elements under the existing external constraints can be found.
REFERENCES
- Obama, B. (2013) Administration calls for more action on climate change. EOS, 819, 78.
- Anthes, R.A., Panofsky, H.A., Cahir, J.J. and Rango, A. (1978) The atmosphere. 2nd Edition, Meteorology, London.
- Essex, C. (1984) Radiation and irreversible thermodynamics of climate. Journal of the Atmospheric Sciences, 12, 1985-1991. http://dx.doi.org/10.1175/1520-0469(1984)041<1985:RATITO>2.0.CO;2
- Ginsburg, E.I., Gulyaev, V.T. and Zhalkovskaya, L.V. (1987) Dynamic models of the free atmosphere. Russian Academy of Science (RAS), Novosibirsk.
- Wild, L.A. (1969) Theory of oscillations of the atmosphere, Gidrometizdat, Leningrad (L).
- Izakov, M.N. (1997) Self-organization and information on planets and ecosystems, UFN, 10, 1087-1094. http://dx.doi.org/10.3367/UFNr.0167.199710e.1087
- Somsikov, V.M. (1983) Solar terminator and dynamic of the atmosphere. Science, Alma-Ata.
- Somsikov, V.M. (2011) Solar terminator and dynamic phenomena in the atmosphere: A review. Geomagnetism and Aeronomy, 6, 707-719. http://dx.doi.org/10.1134/S0016793211060168
- Golitsyn, G.S. and Mokhov, I.I. (1978) The stability and properties of the extreme climate models. Atmospheric and Oceanic Physics, 4, 378-387.
- Zherebcov, G.A., Kovalenko, V.A. and Moloduh, S.I. (2004) The radiation balance of the atmosphere and climate manifestations of solar variability. Atmospheric and Ocean Optics, 12, 1003-1017.
- Arkhipov, Y.V., Ganguly, B., Namvar, R. and Somsikov, V.M. (1999) The influence of solar radiation on the vibrational spectrum of the atmosphere. Geomagnetism and Aeronomy, 4, 108-112.
- Somsikov, V.M., Dungenbaeva, K.E. and Ganguly, B. (2004) Acoustic-gravity waves in a non-equilibrium atmosphere. Geomagnetism and Aeronomy, 3, 407-411.
- Antonova, V.P., Dungenbaeva, K.E., Zalizovskii, A.V., Inchin, A.S., Kryukov, S.V., Somsikov V.M. and Yampol’skii, Yu.M. (2006) Difference between the spectra of acoustic gravity waves in daytime and nighttime hours due to nonequilibrium effects in the atmosphere. Geomagnetism and Aeronomy, 1, 101-109. http://dx.doi.org/10.1134/S0016793206010117
- Somsikov, V.M. (2006) By the beginning of the evolution of physics. PEOS, 2, 29-39. https://sites.google.com/site/peosrussian/home/zurnal-peos/vypuski/2006-god-tom-2
- Somsikov, V.M. (2010) Non-equilibrium atmosphere as a gas-radiation. Proceedings of the National Academy of Sciences of Kazakhstan. A Series of Physics & Mathimatics, 4. 148-154.
- Somsikov, V.M. (1987) A spherical model of wave generation in atmosphere by solar terminator. Journal of Atmospheric and Solar—Terrestrial Physics, 5, 433-438. http://dx.doi.org/10.1016/0021-9169(87)90037-7
- Kurmangaliev, D.A. and Somsikov, V.M. (1989) Structure of atmospheric pressure field waves generated by the solar terminator. Part 2. Calculations. Science, 2, 19-27.
- Somsikov, V.M. (1986) Radiation nonlinearity. VINITI, Alma-Ata.
- Vlasov, A.A. (2005) Macroscopic electrodynamics. 2nd Edition, Fizmatlit, Moscow (M).
- Rumer, Yu.B. and Ryvkin, M.Sh. (1977) Thermodynamics, statistical physics and kinematics. Science, Moscow (M).
- Somsikov, V.M., Andreev, A.B., Zhumabaew, B.T. and Sokolova, O.I. (2011) Analysis of diurnal dynamics of the geomag. Field variation spectrum. Geomagnetism and Aeronomy, 1, 68-72. http://elibrary.ru/item.asp?id=17218862
- Gershman, B.N. (1974) The dynamics of the ionospheric plasma. Science, Moscow (M).
- Nicolis, G. and Prigogine, I. (1990) Exploring complexity. Mir, Moscow (M).
- Somsikov, V.M. (2004) The equilibration of an hard-disks system. IJBC, 11, 4027-4033. http://www.worldscientific.com/doi/abs/10.1142/S0218127404011648
- Somsikov, V.M. (2013) Nonequilibrium systems and mechanics of the structured particles. Springer, London.

