Natural Science
Vol.6 No.7(2014), Article ID:45339,10 pages DOI:10.4236/ns.2014.67045
On the Role of the Entrostat in the Theory of Self-Organization
Viktor I. Shapovalov1, Nickolay V. Kazakov2
1The Volgograd Branch of Moscow Humanitarian-Economics Institute, Volgograd, Russia
2The Volgograd State Technical University, Volgograd, Russia
Email: shavi2011@yandex.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 25 December 2013; revised 25 January 2014; accepted 2 February 2014
ABSTRACT
The reasons for introducing the concept of the entrostat in statistical physics are examined. The introduction of the entrostat has allowed researchers to show the possibility of self-organization in open systems within the understanding of entropy as a measure of disorder. The application of the laws written down for the entrostat has also allowed us to formulate the “synergetic open system” concept. A nonlinear model of the activity of a medium-sized company in the market is presented. In the course of the development of this model, the concept of the entrostat was used. This model includes the equation of a firm’s market activity and condition of its stability. It is shown that this stability depends on the income of the average buyers of the firm’s goods and furthermore that the equation estimating the firm’s market activity includes the scenario of a subharmonic cascade, which ends in chaos for the majority of market participants, i.e., in an economic crisis. The feature of this paper is that the decision containing the scenario of the subharmonic cascade is found analytically (instead of numerically, as is customary in the current scientific literature).
Keywords:Entrostat, Entropy, Self-Organization, Synergetics, Economic Crisis

1. Introduction
The term “open system” is often used in scientific publications devoted to self-organization research. However, in most cases this concept is applied intuitively and it depends on a concrete situation. Still now, a general scientific explanation of the concept of an “open system” is absent.
For example, the studied system in physics is open if it interacts with (an) other system(s) and they together make a general isolated system. The requirement of the isolation of the general system is an indispensable condition. From a physical point of view, we cannot describe the behavior of an open system, disregarding the changes happening in systems with which it joins to make the general isolated system. This is connected with the fact that the main theoretical “tools” (conservation laws) in physics are formulated only for isolated systems. However, in this case, the self-organization phenomenon is inevitably excluded from this area of research. In particular, if a thermodynamic system were isolated, then it would be enough to use the known principles of thermodynamics for its complete description. Involving any processes of self-organization is not required for this purpose.
For non-physical systems (social, economic, etc.), the role of the laws of thermodynamics is the law of entropy increase (the law of entropy increase is the other name for the second law of thermodynamics in statistical physics). However, this is also carried out only in isolated systems. Thanks to Boltzmann and Gibbs’s works, we know that entropy is statistically expressed through the function of events probability. Therefore, entropy regularities work in any system in which it is possible to apply the concept of probability including social and economic ones (see [1] [2] ). At the same time, for example in the economy, it is very difficult to define all the systems that make the general isolated (closed) system by interacting. In the majority of real cases, the studied economic system interacts with many systems. We cannot consider all of them. As a result, we cannot make the general closed system. Here, the methods of synergetics come to the forefront. However, their scientific justification raises some questions.
Here, synergetic scientists, apparently, contradict physicists. The outside world influence is considered in synergetics by means of control parameters entering the evolutionary equation. These control parameters are considered to be constants [3] . This means that possible changes in external systems are not considered in synergetics. At the same time, from a physical point of view, these external systems together with the investigated have to make the general closed system. However, the self-organization of one part of the closed system has to be accompanied by the disorganization of its other part. Therefore, the statement about the invariance of any its part is incorrect. The specified statement can be correct only in one case—if the studied system represents an infinitesimal part of the general closed system. But then the general system cannot be considered to be closed as the infinitesimal part adds nothing and cannot close the final system by itself.
Thus, although practice has shown the efficiency of synergetic approaches, the legitimacy of their methods has still not yet been proved scientifically. In our opinion, this problem is allowed by means of the entrostat concept. As a result, the “open system” term has received natural-science justification.
2. Need of Entrostat Introduction for the Correct Description of Self-Organization in Statistical Physics
More than twenty years ago, precisely in 1990, the first article was published introducing the concept of the entrostat with regard to open systems [4] . At that time, almost no one paid attention to the importance of this concept to explain the phenomenon of self-organization. In recent years, at least in Russia, there has been a noticeable increase in the number of publications mentioning the term “entrostat”. However, sometimes authors do not use the term correctly. The impression is that they do not fully understand its meaning. In this vein, in this paper we would like to, first of all, recall the reasons why the concept of the entrostat was introduced in statistical physics; secondly, we examine its features more fully; and thirdly, we show the advantage that the researcher gets when using this term in the study of the self-organization of systems.
The concept of the entrostat appeared in order to resolve the crisis in statistical physics that called into question the interpretation of entropy as a measure of disorder. The main argument of the opponents of this interpretation was the fact that statistical physics failed to provide an explanation of the phenomenon of self-organization. The problem was only exacerbated by the apparent successes made in this direction by the part of synergetics based on the methods of nonlinear dynamics.
The main obstacle to the explanation of self-organization in statistical theory is the difficulty comparing the entropies of different states of an open system (see [2] [3] [5] ). What do we mean by this? If the system under study interacts with another system, changes occur in both of them. To describe these changes, the appropriate variables are required. If these two systems constitute a general closed system, then in principle we can determine all the changes in each of them. Herewith, in the statistical expression of entropy (Boltzmann-Gibbs entropy) written for the system under study, the distribution function (the probability density) becomes conventional, depending on the variables of both systems. However, in most real cases, the system under study is affected by a very large number of external systems—the external environment. In such cases, it is almost impossible to consider all the required variables and, therefore, it is impossible to record properly the statistical expression of entropy. The introduction of the concept of the entrostat allowed researchers to address the issue of comparing the entropies of different states from an unexpected viewpoint. As a result, the study of self-organization within statistical theory made headway.
An entrostat is a system whose entropy does not change during the interaction with the system under study [6] [7] . In practice, the property of an entrostat belongs to the environment for which the condition is fulfilled [8] -[10] : , where ΔS and ΔSe are the entropy changes of the system under study and the external environment respectively, caused by their interaction. As we can see, the external environment acts as the entrostat if its entropy change is neglectably small in comparison with the entropy change of the system under study. For example, in thermal conductivity tasks, the entrostat is represented by the thermostat—the environment that maintains a constant temperature at the system’s boundaries.
, where ΔS and ΔSe are the entropy changes of the system under study and the external environment respectively, caused by their interaction. As we can see, the external environment acts as the entrostat if its entropy change is neglectably small in comparison with the entropy change of the system under study. For example, in thermal conductivity tasks, the entrostat is represented by the thermostat—the environment that maintains a constant temperature at the system’s boundaries.
In the world around us, we can consider as the entrostat the environment whose influence upon the system greatly exceeds the reverse influence of the system upon the environment. For example, a strong wind blowing against the walking man forces him to lean forward, i.e., to perform certain actions. Since these actions do not affect the atmosphere, the atmosphere is the entrostat in relation to the man. A loud noise outside an open window created by the traffic will force us to close the window, while the traffic—the entrostat—won’t even notice this action. It is well known that it is easier to follow bureaucratic regulations than to procure their cancellation, i.e., the laws of society are the rules that one person interacting with society (the entrostat) is almost unable to change. And such examples abound.
According to the authors of the present paper, the phenomenon of the entrostat occurs when the impact of the system under study upon the entrostat is so small that it is comparable to disorderly structural noise in the entrostat (i.e., the impact is infinitely small in relation to the entrostat).
The main advantage of introducing the concept of the entrostat is that it excludes the external environment when studying the behavior of an open system. In particular, all the changes that occur during the interaction of the system with the entrostat relate to the system. Therefore, all the new variables that describe these changes will relate to the system. The latter means that we do not need to build a general closed system. According to this, on the basis of the analysis of conventional entropy properties, the following relation was proved (the proof can be found in [7] -[9] [11] [12] ):
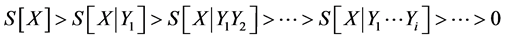 , (1)
, (1)
where the square brackets are the designation but are not the functional dependency; X is the variable characterizing the state of the system;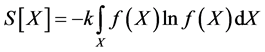 —the closed system’s entropy in the equilibrium state; and
—the closed system’s entropy in the equilibrium state; and
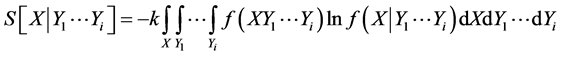 (2)
(2)
—the entropy of the open system in the i-th stationary state (the i-th stationary state differs from the closed state by the changes in the structure that arise due to the influence of the entrostat and the described variables Y1, Y2,···, Yi); and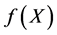 ,
, 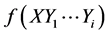 and
and  are distribution functions (probability densities).
are distribution functions (probability densities).
Note that expression (2) characterizes the system’s entropy only if it interacts with the entrostat. Otherwise, for the distribution functions appearing in (2), it would be necessary, in addition to the variables X, Y1, Y2,···,Yi, to take into account the variables that describe the changes in all the systems with which the system under study presumably interacts. The latter, as noted above, is almost impossible. In other words, in (1) the comparison of the open states of the system is correct when we speak of the system’s interaction with the entrostat. Neglecting this circumstance may lead to inconsistencies [9] .
It is necessary to distinguish the situations in which neither of the two interacting systems can be considered to be the entrostat. Imagine that a hot object has been carried into a thermally insulated room. After some time, the temperature of the object and the air temperature in the room become equal. Herewith, the change in temperature will be noticeable in both systems. Consequently, none of them can act as the entrostat. Now suppose that there is a window wide open in the room. After a while, the hot object inevitably cools, its temperature will be exactly equal to the air temperature outside. As the temperature of the air remains the same after the object cools, in this case the air must be considered to be the entrostat.
Let us discuss some important consequences of inequality (1). The entropies presented in (1) correspond to stationary states and differ in the number of variables. However, as noted above, the number of variables is determined by the value of the external influence, i.e., the value of the system’s openness. Therefore, for each inequality in (1), we assign a specific value of some phenomenological parameter called the system’s degree of openness.
The degree of openness α is a parameter characterizing the value of the structural changes that take place in the system as a result of its interaction with the entrostat. The extreme positions of (1) hold the boundary states of the system. For the leftmost position, ![]() is carried out, which means an absolutely closed state; for the extreme right position,
is carried out, which means an absolutely closed state; for the extreme right position, 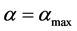 , which should mean a maximally open state. Let us denote the entropy value in the i-th stationary state with a degree of openness
, which should mean a maximally open state. Let us denote the entropy value in the i-th stationary state with a degree of openness ![]() as
as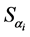 ; then, (1) can be rewritten as follows:
; then, (1) can be rewritten as follows:
 . (3)
. (3)
where .
.
Inequality (3) suggests the concept of the system-critical level of the organization. Let ![]() be the value of the system’s entropy at the beginning of some process. Let us introduce the designations:
be the value of the system’s entropy at the beginning of some process. Let us introduce the designations: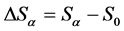 —the change of the entropy of the system that has reached the stationary state (herewith, the system has a degree of openness α);
—the change of the entropy of the system that has reached the stationary state (herewith, the system has a degree of openness α); —the entropy change of an absolutely closed system that has reached the equilibrium;
—the entropy change of an absolutely closed system that has reached the equilibrium; —the negative entropy change by which the stationary value
—the negative entropy change by which the stationary value 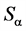 decreases with an increase in
decreases with an increase in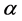 . It is easy to see that
. It is easy to see that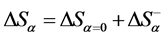 . We have found that in an open system the overall change in the entropy
. We have found that in an open system the overall change in the entropy  consists of the positive
consists of the positive 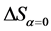 and the negative
and the negative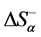 . The value
. The value  is called the critical level of the system’s organization (for more details, see [6] [11] -[13] ). In other words, we consider
is called the critical level of the system’s organization (for more details, see [6] [11] -[13] ). In other words, we consider 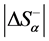 to be the quantitative measure of the organization of the system in the stationary state. According to (1), by the organization of the system, we understand the structural connections described by the macroscopic variables X, Y1, Y2,···, Yi,···.
to be the quantitative measure of the organization of the system in the stationary state. According to (1), by the organization of the system, we understand the structural connections described by the macroscopic variables X, Y1, Y2,···, Yi,···.
As seen from (3), the value  uniquely corresponds to the system’s degree of openness
uniquely corresponds to the system’s degree of openness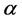 :
: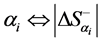 . This implies an important conclusion: to increase or decrease the value of the system’s critical level of organization
. This implies an important conclusion: to increase or decrease the value of the system’s critical level of organization , it is necessary to correspondingly increase or decrease its degree of openness.
, it is necessary to correspondingly increase or decrease its degree of openness.
Summing up, let us formulate the laws of the behavior of open systems under the influence of the entrostat (the detailed proof can be found in [6] [11] [12] ):
1) Each open system has a critical level of organization. If the system is organized below this level1, the processes of self-organization prevail; if it is organized above this level, the processes of disorganization prevail; at the critical level, these processes balance each other, and the state of the system becomes stationary.
2) The value of the critical level uniquely corresponds to the system’s degree of openness.
3) To increase order in the system, it is necessary to increase its degree of openness. The new value of the degree of openness will match a new higher critical level . As a result, the system will be dominated by the processes of self-organization, thereby increasing its organization to a new critical level.
. As a result, the system will be dominated by the processes of self-organization, thereby increasing its organization to a new critical level.
4) To disorganize the system, it is necessary to reduce its degree of openness. Herewith, the critical level will fall, causing a predominance of disorganization processes that reduce order in the system to a new value of the critical level.
According to the well-known statistical expression of entropy, the latter is rigidly connected with the probability of events through the distribution function. Therefore, in practice entropy laws manifest themselves as an increase in the probability of the corresponding events. In other words, the events contributing to these laws will occur more frequently than others. However, to what extent more frequently? At least, so that the requirements of entropy laws are fulfilled. In particular, in any system (e.g., in a city), if we construct so much that it exceeds its critical level of system organization, the probability of events leading to disorganization will increase. In the case of a city, environmental problems will worsen, the number of accidents will increase, the number of causes for social unrest will grow, and so on. Unfortunately, no major construction includes a preliminary assessment of the entropy changes that may occur in the environment as a result of this construction.
A great number of facts in the surrounding world illustrate these four laws.
For example, in a closed vessel completely filled with some fluid, the motion of the molecules is equiprobable in all directions. Let us make a hole in the vessel. If the pressure in the vessel is higher than that in the external environment, the molecules will quickly form a new structure—the fluid stream in the direction of the hole, i.e., self-organization takes place. To keep ourselves in good physical shape, we execute various power exercises. In other words, we expose ourselves to external influences, causing self-organizing processes within the organism. The easing of physical activity inevitably leads to some disorganization of the organism. The living organism infected with a virus gets ill. However, even in this case there are powerful processes of self-organization going on in its organism, as a result of which, firstly, it recovers, and secondly, it becomes immune to the virus for a certain period. Of course, later, because of the absence of the virus in the environment, the organism will disorganize a bit, and it will again be able to contract the disease. Medical vaccinations are in fact that small external influence that causes the organism to self-organize to a level sufficient to resist the virus.
What do parents do to reduce the disorder that constantly appears around growing children? They educate the children, that is, they influence them by creating in their consciousness the processes of self-organization. But once they get a little distracted from child education and let their kids become more reserved (closed) in relation to the parents, the processes of disorganization inevitably start dominating in them, and the result is what we call “getting out of hand”.
Human society is also a system, so the described regularities exist in it, too. For example, without delving into the history of different states, you can still note that states that tend to toughen access control at their borders (a decrease in the degree of openness) experience within themselves an increase in the destructive processes in the economy and culture as well as in other areas of human activity that fall under customs pressure. Conversely, the weakening of access control at the borders (an increase in the degree of openness) leads to strengthening progressive processes.
The application of the laws formulated for the entrostat to the system “Earth” has allowed us to distinguish the fundamental causes of global trends. A relatively constant degree of openness of Earth (in relation to the cosmos entrostat) sets a certain critical level of order on the planet. Below its critical level, humankind increases order in the environment compared with disorder, and as result inevitably exceeds this level. When this happens, the processes of disorganization should prevail on Earth, i.e., the probability of any events leading to destruction should increase. At the same time, increasing the planet’s degree of openness (e.g., as a result of large-scale cosmos exploration, i.e., exploration of the Moon, the Mars, etc.) would increase the value of its critical level. The latter will form strong creative trends (for more details, see [6] [13] ).
In [8] [9] [12] , there are other examples of the above-stated provisions.
Important note: while opening the system with the aim of its ordering and self-organization, one should ensure that the intensity of the opening does not exceed a certain threshold above which the system is not in time to self-organize and will be destroyed. For example, a military intervention is also an opening of the state that has been attacked. According to the above-stated regularities, powerful self-organization processes occur in this state, such as the mobilization, intensification of all productive forces, and so on. However, if the intervention is fast and the state is small, it will not have the time to build an effective defense and will be destroyed [9] .
Thus, the introduction of the concept of the entrostat has allowed us to show the possibility of self-organization in open systems within the understanding of entropy as a measure of disorder.
3. Synergetic Open System
As noted in the Introduction, the influence of the outside world is considered in synergetics through the control parameters, which are considered to be constants. In other words, synergetic scientists, unlike physicists, do not join studied systems with the outside world (or its part) in order to make a general closed system. The legitimacy of such a, more likely intuitive, approach received fundamental justification with the introduction of the entrostat concept.
Let us remind ourselves that the environment in which entropy change can be neglected in comparison with a change in studied system entropy (see the previous section) acts in the entrostat role. The main reason for this is the circumstance that the result of the influence of the studied system on the entrostat does not exceed the chaotic structural noise in the entrostat, representing the infinitesimal size for the latter. Therefore, the studied system interacting with the entrostat cannot together make the closed general system (the studied system does not exist as it does for the entrostat).
When the researcher addresses the entrostat, he (or she) deals with the so-called limit transition from one level of the description to another. For example, the approach of the continuous media in hydrodynamics assumes that an element of the media is the point that, in turn, has to consist (and it is considered to be essentially important) of a large number of liquid molecules. Nobody considers each molecule while writing down the equation of the liquid flow for a closed system. It is not a proper level of the description. In other words, the addition of any one molecule does not absolutely influence the behavior of the continuous media. The reason here can be only one: the continuous media is an infinitely large system for a separate molecule, i.e., it is the entrostat.
As an investigating system, synergetic scientists do not unite system with the environment in order to make the general closed system. In our opinion, they only do so if the environment is the entrostat. Let us note that such a synergetic open system has to differ from a physical open system. Really, physical systems open in relation to each other make the closed system together. The laws of thermodynamics are sufficient to describe the processes that occur in them; there is no required application of the synergetic principles. However, it is impossible to construct the closed system if the studied system interacts with the entrostat. The synergetic regularities move to the forefront in this case.
Therefore, we will call a synergetic open system or simply a synergetic system the system interacting with the entrostat.
In synergetics, a change in the external influence corresponds to a change in the values of the control parameters. Therefore, the entrostat influences the system through these control parameters. As a result, by choosing these or those values of control parameters, we act in an entrostat role and can control the tendencies in the system in order to change the probability of events in the necessary direction for us. For example, we can make the current steady system state unstable and vice versa. In the following section, we illustrate this situation, having defined the borders of a steady state of an economic system “market” and having pointed to the possible reasons for its crisis. When the number of market participants is rather insignificant, they can try to agree. By considering them as a closed system, we can formulate a number of rules to promote the benefit for each participant. However, such a market will not be steady as entropy (disorder) increases in the closed system. The same is clear from the economic point of view, too. Really, in a closed market, the profit of one participant is accompanied by the expenses of others. Therefore, we will consider the market for which it is impossible to consider all participants—the “spontaneous” market. In such a market, each participant interacts with a very large number of sellers and consumers, i.e., with the entrostat.
4. Nonlinear Model of an Economic Crisis
As a rule, the expected volume of the next sale is estimated by the results of the previous sale, corresponding to Markov processes. For Markov processes, it is convenient to carry out a search of steady states by means of a discrete map (Poincaré map). Suppose the firm of interest to us sells goods X in some market. Let these goods compete with the goods Y sold in the same market by other firms.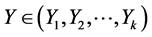 , where “k” is the number of all firms with competing goods in this market. Let us remind that we suppose k to be a very large number. We consider the case of maximum competition: X and Y are equal or substitutable goods. We choose the volumes of realized goods as variables:
, where “k” is the number of all firms with competing goods in this market. Let us remind that we suppose k to be a very large number. We consider the case of maximum competition: X and Y are equal or substitutable goods. We choose the volumes of realized goods as variables: 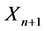 is the expected volume of the next sale and
is the expected volume of the next sale and 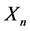 is the volume of the previous sale. The units of measurement do not have a basic value. We find the concrete expression for the discrete map by calculating ratios that are characteristic of the actions of the studied system, in this case, operations in the market.
is the volume of the previous sale. The units of measurement do not have a basic value. We find the concrete expression for the discrete map by calculating ratios that are characteristic of the actions of the studied system, in this case, operations in the market.
1) The expected volume of the next sale  is proportional, first, to the volume
is proportional, first, to the volume ![]() bought in the sale, and second, to demand
bought in the sale, and second, to demand 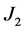 for commodity X, i.e.,
for commodity X, i.e., 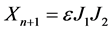 , where e is some coefficient of proportionality.
, where e is some coefficient of proportionality.
2) As a rule, when defining the quantity of goods offered for sale, businesspeople are guided by the quantity sold on the previous occasion. Therefore, volume ![]() is proportional to
is proportional to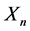 , i.e.,
, i.e., 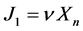 , where n is some coefficient of proportionality.
, where n is some coefficient of proportionality.
3) We believe that the main factor causing average demand (in the region considered) for goods is the income  of the average buyer (in the same region). Therefore, demand
of the average buyer (in the same region). Therefore, demand  for goods X is proportional to income
for goods X is proportional to income . To take account of competition, we subtract
. To take account of competition, we subtract ![]() from this proportion, where
from this proportion, where ![]() is a part of demand that was satisfied by the purchase of Y instead of X:
is a part of demand that was satisfied by the purchase of Y instead of X: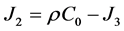 , where r is the coefficient of proportionality.
, where r is the coefficient of proportionality.
4) In turn, ![]() is proportional to the price
is proportional to the price 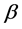 of goods X (i.e., the higher price
of goods X (i.e., the higher price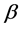 , the more Y will be bought instead of X) and the number of crossing of goods X and Y (
, the more Y will be bought instead of X) and the number of crossing of goods X and Y (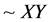 , see Figure 1). Under the crossing of these goods, we understand the joint presence of goods X and Y in the market, due to which the buyer has the opportunity to make a choice in favor of one of them (e.g., they are located in the same market area).
, see Figure 1). Under the crossing of these goods, we understand the joint presence of goods X and Y in the market, due to which the buyer has the opportunity to make a choice in favor of one of them (e.g., they are located in the same market area).
As a result, we derive the following equation:
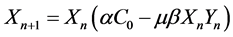 (4)
(4)
which represents the discrete map, describing the process of firm trade in the market (a and m are the proportionality coefficients). As we can see,  and
and 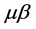 are the control parameters.
are the control parameters.
Let us use the known equation of fixed points: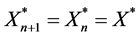 ;
;  (“*” is a designation of a fixed point). By applying this to Equation (4), we find
(“*” is a designation of a fixed point). By applying this to Equation (4), we find
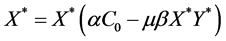 , (5)
, (5)
from which
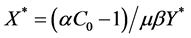 (6)
(6)
representing the fixed point of map (4) (i.e., the stationary volume of the firm’s sales). We do not consider the trivial solution  as we assume that the firm has non-zero sales.
as we assume that the firm has non-zero sales.
Further, we want to find the condition for the stability for (6). Let us remind ourselves that in Equations (4) and (5),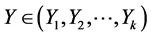 . In this case, the standard approach recommends that we find out the Jacobian for the kD dynamical system. However, in our model k is a very large number and the Jacobian can only be solved numerically. Therefore, we use another approach including the concept of entrostat. We hypothesize that the difficulties of one company have almost no influence on the total sales
. In this case, the standard approach recommends that we find out the Jacobian for the kD dynamical system. However, in our model k is a very large number and the Jacobian can only be solved numerically. Therefore, we use another approach including the concept of entrostat. We hypothesize that the difficulties of one company have almost no influence on the total sales 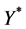 of other companies in the market because of their great amount (k is a very large number). Therefore, this
of other companies in the market because of their great amount (k is a very large number). Therefore, this 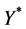 with high reliability can be considered to be constant, i.e., as an entrostat.
with high reliability can be considered to be constant, i.e., as an entrostat.
Let us make the perturbation of the stationary solution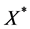 , leaving fixed the
, leaving fixed the 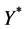 of other companies. Then, Equation (5) can be written for the perturbed variable X as follows:
of other companies. Then, Equation (5) can be written for the perturbed variable X as follows:
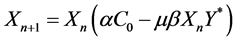 . (7)
. (7)

Figure 1. Number of crossings definition. Let X be a set of four values and Y a set of three values. As we see, the number of not repeated crossings (the crossing is designated by an arrow) is equal to 12, i.e., it is equal to the multiplication XY.
We use the well-known condition of the stability of the fixed point in the theory of discrete maps: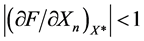 , where F is the right-hand side of the discrete map (in our model, F is the right-hand side of the discrete map (7)). We calculate a partial derivative:
, where F is the right-hand side of the discrete map (in our model, F is the right-hand side of the discrete map (7)). We calculate a partial derivative:
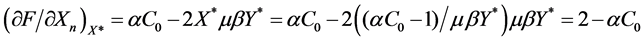 .
.
By substituting this into the condition of stability, we find [14]
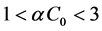 , (8)
, (8)
i.e., the condition of stability for the stationary volume of firm sales. As we can see, the average buyer income  is the control parameter that affects the stability of the average firm in the market.
is the control parameter that affects the stability of the average firm in the market.
The inequality on the right-hand side of (8) seems to be a contradiction: in the case of the growth of average buyer income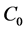 , the firm may lose its stability. To understand this, we perform the following replacement of variables [14] :
, the firm may lose its stability. To understand this, we perform the following replacement of variables [14] : 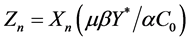 and
and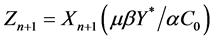 , and enter the designation:
, and enter the designation:
 . (9)
. (9)
As a result, the discrete map (7) takes the form
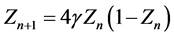 .
.
As we see, this equation coincides with square map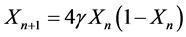 . It is known that the systems described by this map develop according to the scenario of the subharmonic cascade [15] [16] . The stationary state of this discrete map loses stability if
. It is known that the systems described by this map develop according to the scenario of the subharmonic cascade [15] [16] . The stationary state of this discrete map loses stability if  (first cascade). Therefore, from (9) we derive
(first cascade). Therefore, from (9) we derive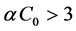 . This in turn corresponds to a violation of the right-hand side of condition (8).
. This in turn corresponds to a violation of the right-hand side of condition (8).
Thus, the market activity of the firm develops according to the scenario of the subharmonic cascade. As it is known, this scenario inevitably results in chaos. In our opinion, in practice, the latter manifests itself in the form of an economic crisis.
The model we have developed allows us to see the details of the origin of an economic crisis. Owing to the increase in the control parameter 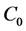 (i.e., average buyer income), a violation of the upper limit of the stability condition (8) by the majority of market participants takes place. According to the scenario of the subharmonic cascade, two new stable states appear. One of these corresponds to a higher volume of sales than in (6), as occurs with the increased buyer income
(i.e., average buyer income), a violation of the upper limit of the stability condition (8) by the majority of market participants takes place. According to the scenario of the subharmonic cascade, two new stable states appear. One of these corresponds to a higher volume of sales than in (6), as occurs with the increased buyer income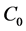 . In the case of a further
. In the case of a further 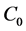 increase, we must expect the serial doubling of the quantity of steady
increase, we must expect the serial doubling of the quantity of steady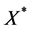 , which ends in a chaotic state.
, which ends in a chaotic state.
In our opinion, the main cause of the crisis can be summarized in economic terms as follows: growth in salaries outpaces labor productivity growth. Indeed, labor productivity is determined by technological progress, but growth in salaries is influenced by ideas such as the quality of life for the majority of workers. If employees consider their lives to be poor, then they stage a strike. As a result, they obtain an increase in salary, but labor productivity remains the same. To obtain a growth in worth, it is necessary to transfer part of the production of goods to countries in which salaries are relatively low. The resulting profit helps cover the costs of the unjustified salaries of native employees. However, over time, strikes also begin in the lower cost countries and end in salary growth. As a result, production costs increase and profits fall in these countries. The latter factor forces companies to restructure their debts to banks. If this happens to many firms, banks will receive less money in real terms. Increasing loan interest only increases the amount of bad debt. This puts the banks under the threat of bankruptcy and marks the beginning of an economic crisis.
5. Conclusions
1) The external system whose entropy change can be neglected in comparison with the entropy change of the system under study acts as the entrostat. The main reason for this is the fact that the impact of the system under study upon the entrostat does not exceed the disorderly structural noise in the entrostat, i.e., this impact represents an infinitely small value for the entrostat. According to authors of the present paper, when a researcher refers to the entrostat, he (or she) has to deal with transition from one level of description to another.
2) The introduction of the concept of the entrostat has allowed us to show the possibility of self-organization in open systems within the statistical understanding of entropy as a measure of disorder.
3) The modern market includes many links between its components. The specificity of these links generates various types of markets. Many researchers seek to more accurately account for this specificity. However, increasing the model’s accuracy is limited to taking into account the large number of relationships between variables. This leads to great mathematical non-linearity of the market models. As a result, the numerical components of these models increase considerably. The processing power of modern computers contributes to this approach, too. However, in our opinion, conclusions based on analytical solutions allow us to formulate a qualitative picture of the phenomenon better than conclusions based on numerical ones. In order to create an analytical model, we consider only main kinds of the firm activity that are always presented in any market. In addition, we have made two obvious assumptions. First, any average firm determines the range and quantity of goods for the current sales, considering first of all the results of the immediate previous sales. This fact points to a discrete Markov process, which is well described by discrete mappings. Second, since any average firm competes with a large number of other firms, the oscillations of its sales have almost no influence on the summary sales of the remaining firms. This means mathematically that if we set a perturbation for a stationary firm state to investigate it for stability, then we can neglect the influence of this perturbation on the behavior of other firms as a whole (i.e., we can consider other firms’ stationary sales volumes to be the entrostat). This removes the multidimensionality and, as a consequence, the model solutions are analytic.
4) According to one of our model conclusions, the stability of average firm in the market depends on the income of the average (in this region) buyer of its goods. It was found that this income has an upper value that the firm (and thus the market, as the firm is arbitrarily, randomly chosen) loses stability. By investigating this question in an analytical way, we found that the reason for this is the subharmonic cascade. It is known that the subharmonic cascade is a typical chaos scenario. This means that we have proved a very important conclusion: the market economy has to be accompanied by crises. The presence of the subharmonic cascade in market activity has also been noted by other researchers. However, their conclusions have been based on numerical calculations (e.g., [17] ). Our approach provides an analytical solution to this problem and thus opens a new direction for economic research.
References
- Prigogine, I. (1980) From Being to Becoming: Time and Complexity in the Physical Sciences. W. H. Freeman and Company, San Francisco.
- Klimontovich, Yu.L. (1996) Relative Ordering Criteria in Open Systems. Uspekhi Fizicheskikh Nauk, 166, 1231-1243. http://dx.doi.org/10.3367/UFNr.0166.199611f.1231
- Haken, H. (1988) Information and Self-Organization. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-662-07893-8
- Shapovalov, V.I. (1990) Synergetics Aspect of the Law of the Entropy Growth. In: Pleskachevskiy, U.M., Ed., Non-Traditional Scientific Ideas about Nature and Its Phenomena, Club FENID, Homel, 370-372.
- Klimontovich, Yu.L. (1987) Entropy Evolution in Self-Organization Processes H-Theorem and S-Theorem. Physica, 142A, 390-404. http://dx.doi.org/10.1016/0378-4371(87)90032-X
- Shapovalov, V.I. (1995) Entropiyny Mir (The Entropy World). Peremena, Volgograd.
- Shapovalov, V.I. (2001) Formation of System Properties and Statistical Approach. Automation and Remote Control, 62, 909-918. http://dx.doi.org/10.1023/A:1010245619531
- Shapovalov, V.I. (2004) To the Question on Criteria of Order Change in Open System: The Statistical Approach. Applied Physics, 5, 25-33.
- Shapovalov, V.I. (2005) Basis of Ordering and Self-Organization Theory. ISPO-Service, Moscow.
- Shapovalov, V.I. (2011) Entrostat. http://arxiv.org/ftp/arxiv/papers/1103/1103.1139.pdf
- Shapovalov, V.I. (2008) The Criteria of Order Change in Open System: The Statistical Approach. http://arxiv.org/ftp/arxiv/papers/0801/0801.2126.pdf
- Shapovalov, V.I. (2012) The Criterion of Ordering and Self-Organization of Open System. Entropy Oscillations in Linear and Nonlinear Processes. International Journal of Applied Mathematics and Statistics, 26, 16-29.
- Shapovalov, V.I. and Kazakov, N.V. (2013) The Fundamental Reasons for Global Catastrophes. Natural Science, 5, 673-677. http://dx.doi.org/10.4236/ns.2013.56082
- Shapovalov, V.I. (2008) Steady Coexistence of the Subjects of the Market Representing the Private and State Capital. http://arxiv.org/ftp/arxiv/papers/0812/0812.4028.pdf
- Haken, H. (1978) Synergetics: An Introduction. Springer, Berlin, New York. http://dx.doi.org/10.1007/978-3-642-96469-5
- Berge, P., Pomeau, Y. and Vidal, Ch. (1988) L’ordre dans le chaos. Hermann, Paris.
NOTES

1Let us remind that according to (1), by the organization of the system, we understand the structural connections described by the macroscopic variables X, Y1, Y2,···, Yi,···.

