Natural Science
Vol.5 No.2(2013), Article ID:27834,5 pages DOI:10.4236/ns.2013.52028
Curvature mass inside hadrons: Linking gravity to QCD
![]()
School of Information Management, Nanjing University, Nanjing, China; yye@nju.edu.cn
Received 7 November 2012; revised 10 December 2012; accepted 23 December 2012
Keywords: Curvature Mass; Geometric Field; Unified Field Theory; Gravity; Dark Matter; Dark Energy; QCD
ABSTRACT
Following the basic ideas of general relativity and quantum field theory, combing two kinds of standard models, the curvature mass inside hadrons is discussed and developed, in which the standard model of particle physics and the standard model of cosmos are naturally unified under the mathematical framework of geometric field theory, where the phenomena of dark matter and dark energy could get naturally theoretical interpretation.
1. INTRODUCTION
There have been two standard models in physics, in which one is the standard model of particle physics based on gauge quantum field theory [1], for unifying strong (theoretically approached by QCD), weak and electromagnetic interactions; and another is the standard model of cosmos based on general relativity [2], for explaining expanding cosmos and gravity. The standard models are verified by experiments very well [3]. When the Higgs boson was discovered at 126 GeV by LHC [4,5] recently, the standard model of particle physics is completed.
However, the two kinds of standard models are so different that they can’t reach complete physical unification. Following general relativity, the mass distribution determines the curvature of space-time (equivalence principle). According to QCD, the quarks in hadrons are abided in a small space-time (space radium about 10−18 m) with large mass (around 1 TeV). As we think gravity is too weak to care before, we always ignore gravity in particle physics. But, inside hadrons, since large mass could introduce high curvature of space-time, the effects of general relativity can’t be ignored, i.e. we can’t ignore gravity inside hadrons where large mass would produce high spacetime curvature.
Logically, if the standard model of particle physics and the standard model of cosmos are correct meantime, there will be a combination of gravity and strong interaction in a small space-time, which is just inside hadrons, where quarks possess high mass and act each other in very small space-time. Let us consider the situation.
2. THEORETICAL FRAMEWORK: CURVATURE MASS LINKING TO STRONG INTERACTION
For measuring physical world, basic physical measures include mass m, energy E and momentum p. According to relativity, under Lorentz invariance, we have their relation
 (1)
(1)
where c is velocity of light. If we choose physical unit and let c = h = 1 where 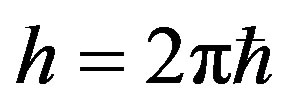 is Planck’s constant, it is
is Planck’s constant, it is
 (2)
(2)
This means mass distribution is proportional to the distribution of energy and momentum, i.e. energy and momentum tensor Tμν.
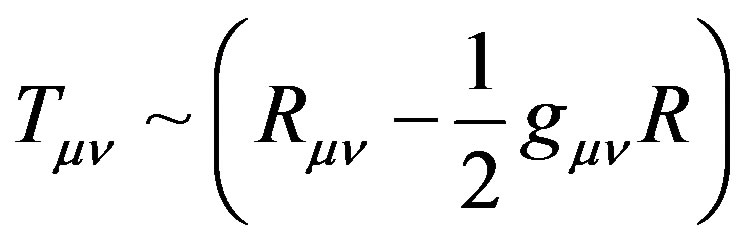 (3)
(3)
where gμν is metric tensor, Rμν Ricci tensor and R scalar curvature.
According to general relativity, Tμν is equivalent to the curvature of space-time. If we introduce the distribution of mass, i.e. the tensor of mass mμν, we obtain
 (4)
(4)
With introducing the wave function Ψ and considering its normalization, we have
 (5)
(5)
in which ψL and ψR are left-handed and right-handed parts of a Dirac spinor respectively and <|> are Dirac notations as left-vector and right-vector [5]. Then we obtain
 (6)
(6)
where m is Eigenvalues of mμν and k is a real constant. As the dimension of curvature is radium−1, 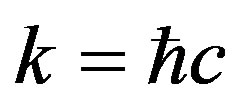 is a natural choice for matching physical dimensions, which just combines micro-quantum theory and macro-relativity.
is a natural choice for matching physical dimensions, which just combines micro-quantum theory and macro-relativity.
Meanwhile, following the Lagrangian in QCD [1,6], we see
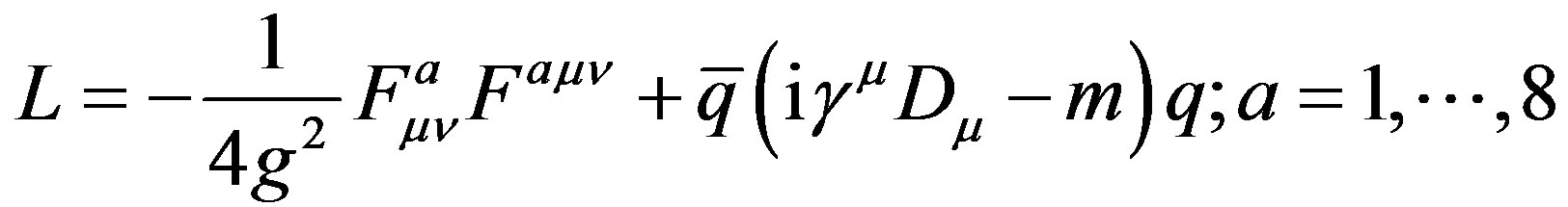 (7)
(7)
where the first item describes gluons and second item quarks and g is gauge factor, while F means field strength and γμ denotes Dirac matrices (c.f. Appendix).
Replacing q with wave function Ψ and introducing Eqs. 6-7, we obtain the Lagrangian of strong interaction with curvature mass in hadrons
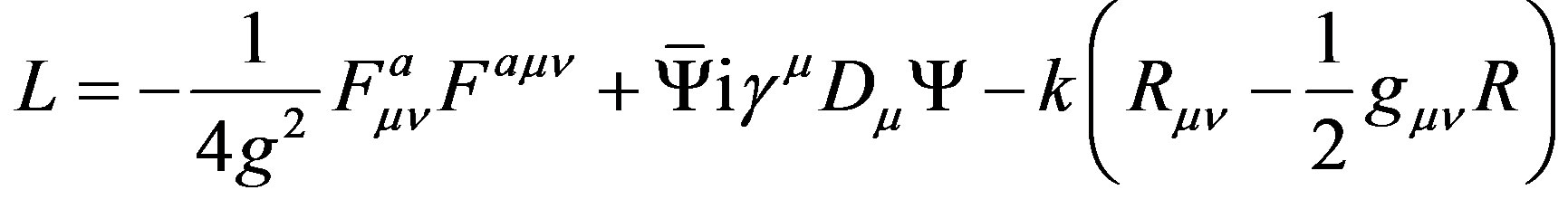 (8)
(8)
This constructs fundamental theoretical analytical framework.
3. MATHEMATICAL STRUCTURE: GEOMETRIC UNIFIED FIELD
Using multi-vector Mk (k = 0, 1, 2, 3, 4) [7-9] as field measures, where Mk is a multi-vector of grade k. k = 0 is scalar, k = 1 vector, k = 2 bivector, k = 3 pseudovector and k = 4 pseudoscalar, we have
 (9)
(9)
in which Ψ = φ − iθ constructs a complex wave function of matter, while A = V − iU forms a complex vector function of matter particles in space-time and B keeps a bivector as interaction. The Eq.6 means that matter combines wave function and vector function in their interacttion, which is just an image fitting the duality of waveparticle, within combining mass and energy as matter.
The conjuncture of M is
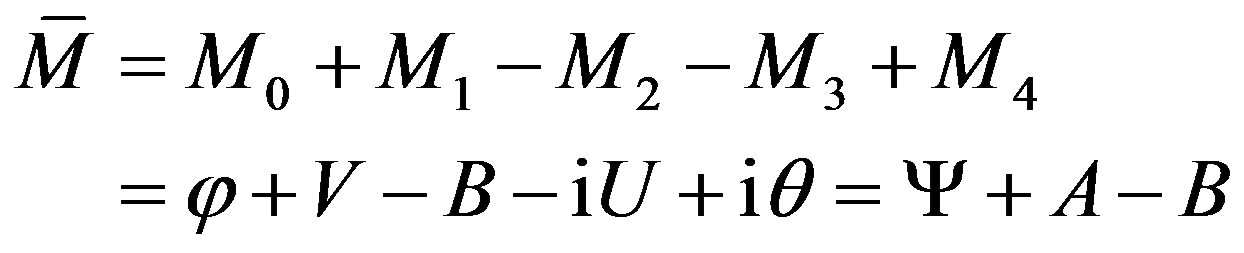 (10)
(10)
And the reversion of multi-vector M, denoted by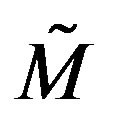 , becomes
, becomes
 (11)
(11)
Introducing differential operators
 (12)
(12)
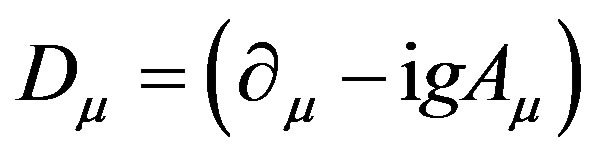 (13)
(13)
where Eq.13 means covariant derivative and g denotes gauge factor, we have
 (14)
(14)
 (15)
(15)
So we set up the necessary mathematical foundations. Since we apply the mathematics of geometric algebra and geometric calculus, we can call the following physical unification as geometric field.
Synthesizing above mathematical notations, the mathematical framework for the world is constructed as follows.
 (16)
(16)
 (17)
(17)
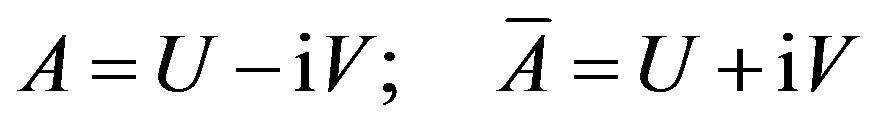 (18)
(18)
The unified Lagrangian contains all elements of geometric field [9,10], characterized by multi-vector 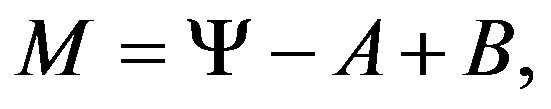
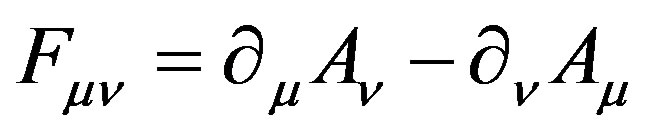 and
and . So, in Eqs. 9-18, all elements of the geometric unified field are included.
. So, in Eqs. 9-18, all elements of the geometric unified field are included.
When one ignores G and introduce F
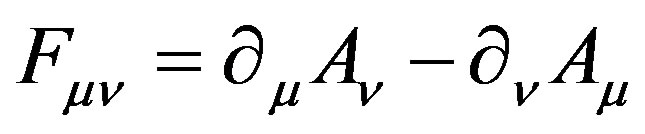 (19)
(19)
and 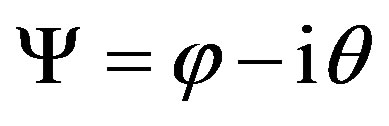 and A are linked by following equation
and A are linked by following equation
 (20)
(20)
one can choose Lagrangian
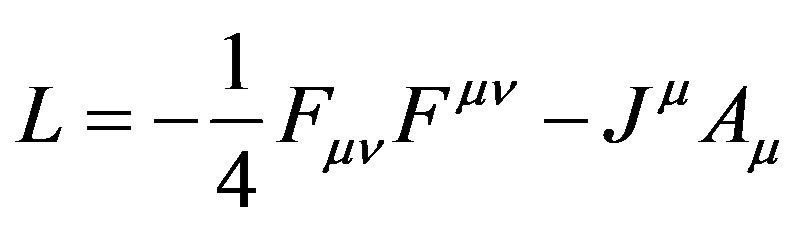 (21)
(21)
where 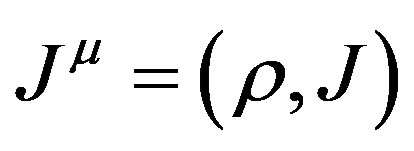 is current.
is current.
As action 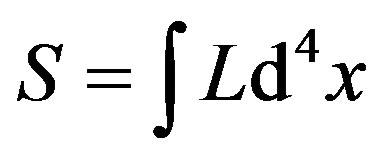 and
and , one obtains classical Maxwell’s equations under gauge group U(1)
, one obtains classical Maxwell’s equations under gauge group U(1)
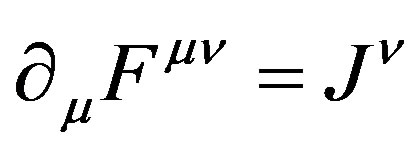 (22)
(22)
or equivalent form of geometric algebra
 (23)
(23)
When we notice

the left and right wave functions fit following coupled two-component equations, which are equivalent to Diractype equation as 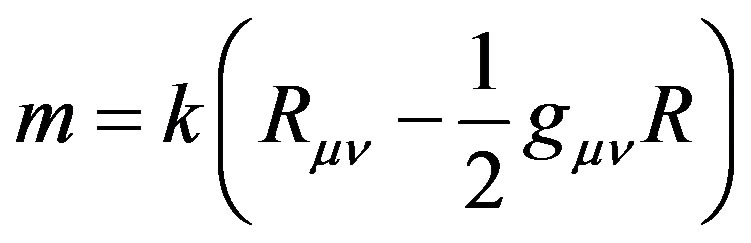
 (24)
(24)
Let us introduce gauge fields Wμ, stemming from group SU(2), with the field strength tensor
 (25)
(25)
we can choose Lagrangian
 (26)
(26)
Combining Eqs.21 and 26, we have electroweak Lagrangian
 (27)
(27)
If we ignore A, G becomes dominated. Then we have Lagrangian fitting QCD model under SU(3) invariance
 (28)
(28)
where the first item describes gluons and second item quarks, which is just (7), with .
.
When Eqs.21, 27 and 28 act together in a particle system, SUC(3) × SUL(2) × UY(1) symmetry had been embedded. Meanwhile, as the m is substituted by curvature of space-time according to , the unified physics covers gravity, strong and electroweak interaction in it, with holding unified Lagrangian as
, the unified physics covers gravity, strong and electroweak interaction in it, with holding unified Lagrangian as
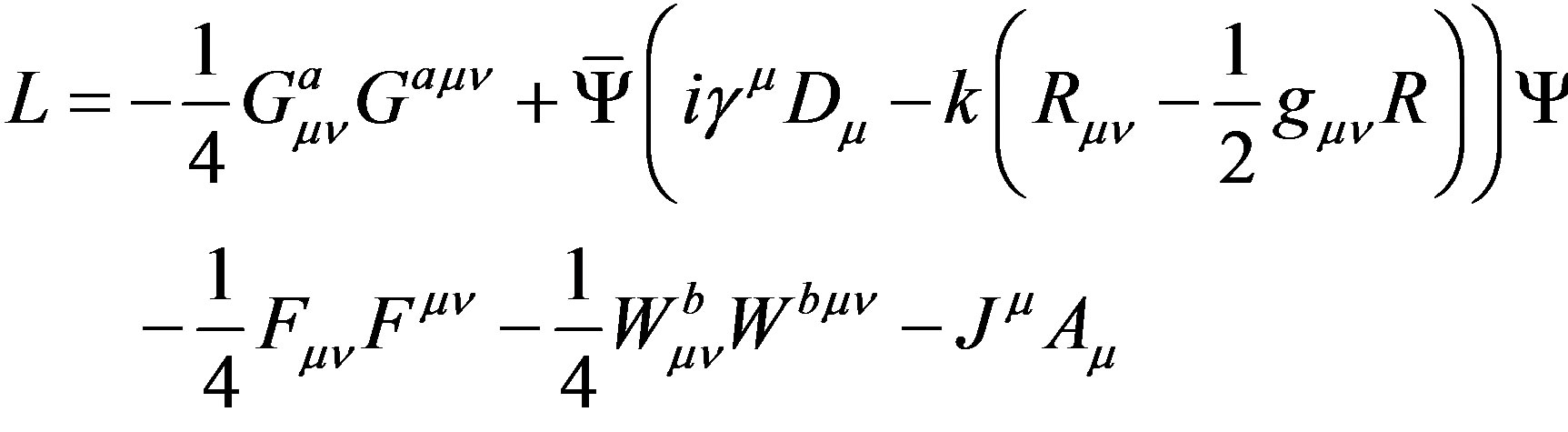 (29)
(29)
Now, we have the geometric unified field, where mass can be replaced by curvature of space-time, which provides a mathematical structure for unified physics.
4. GENERAL PHYSICAL PRINCIPLES
While the standard model of particles is characterized by gauge symmetry with SUC(3) × SUL(2) × UY(1), the standard model of cosmos and general relativity are characterized by big-bang cosmology and the mass being equivalent to the curvature of space-time, based on the general equivalence principle. They constructed a theoretical frame-work for understanding physical reality [11, 12].
Therefore, all fields and their phenomena will be interpreted by the unified mechanism, and the unified physical mechanism can be induced into ACC (Action, Connection and Construction) principles [13].
The action principle acts on action S, revealing the dynamic mechanism of a physical system
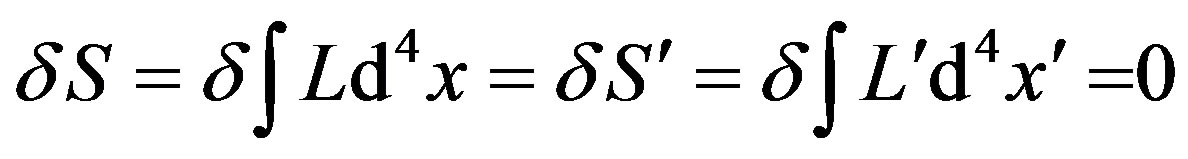 (30)
(30)
The action principle is the first physical principle in geometric unified field, which originates from the Lagrange-Hamilton principle and the Nöther theorem and determines the dynamic evolution of a physical system.
The first key physical idea retains the relativity principle of local gauge invariance, which includes that a phase change and a rotation or a displacement never change physical laws, in following gauge trans-formation
 (31)
(31)
 (32)
(32)
where Λ denotes an arbitrary function of space and time and g is gauge factor.
The connection principle links physical potential with mathematical connection, physical field strength and mathematical curvature, as shown with the following mathematical structure
 (33)
(33)
in which P is multi-vector potential, ω multi-vector connection, and k1 a real constant; F multi-vector field strength, Ω multi-vector curvature, and k2 another real constant.
The connection principle is the second physical principle in geometric unified field, which originates in Newton’s 2nd law and Einstein’s equivalence principle and encompass the kinematical characteristics and the dynamic structure of a physical system.
The second key physical idea focuses on matter and energy being equivalent to the curvature of space-time locally. This is the general equivalence principle in both micro-world and macro-cosmos. As we knew that the world was a duality combining wave with particle, as well as space-time curvature, when we apply M as the measure of matter and energy, Ω as curvature of spacetime, the core idea becomes Distribution of mass = Curvature of space-time The construction principle links inner geometric structure with outer topological index as
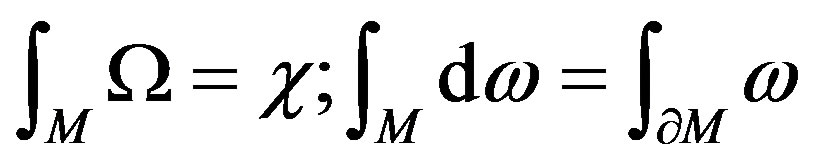 (34)
(34)
where Ω is curvature and ω connection, while χ denotes characteristic index and M as manifold on multivector.
Originated from the Gauss-Bonnet formula and Stokes theorem, the construction principle is the third physical principle in geometric unified field, which links inner structure with surface parameters, so that it reveals the constructure of the world for unified physics.
One can apply the above three principles to any physical system as a general approach to physical unification, which constructs the overall dynamics of the world.
The above physical unification retains all ideas from both quantum field theory and general relativity in it, while the duality of wave and particle as well as mass and curvature are combined in a unified physics.
5. GRAVITY MERGING INTO STRONG INTERACTION: LINKING TO PHYSICAL UNIFICATION
Applying Lagrange equation to the Lagrangian (29), we find
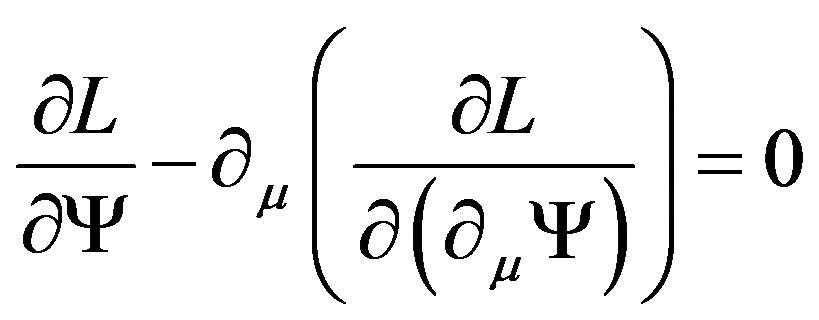 (35)
(35)
And remember energy-momentum tensor to be
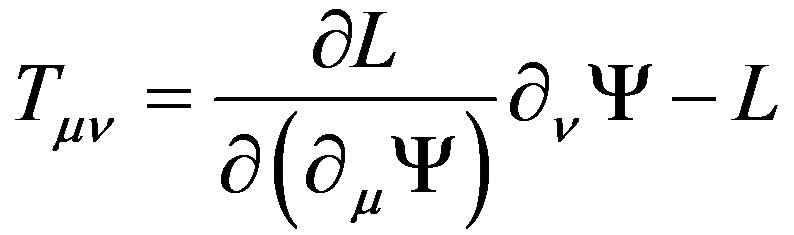 (36)
(36)
As  and
and
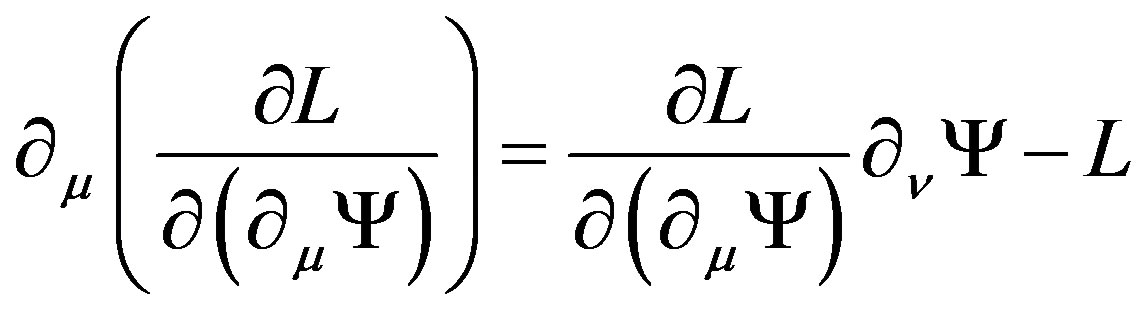 , supposing
, supposing 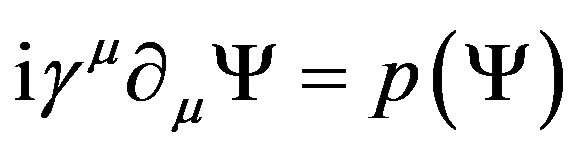 and
and , we obtain
, we obtain
 (37)
(37)
And varying the  in Eq.29, we have
in Eq.29, we have
 (38)
(38)
The variation causes
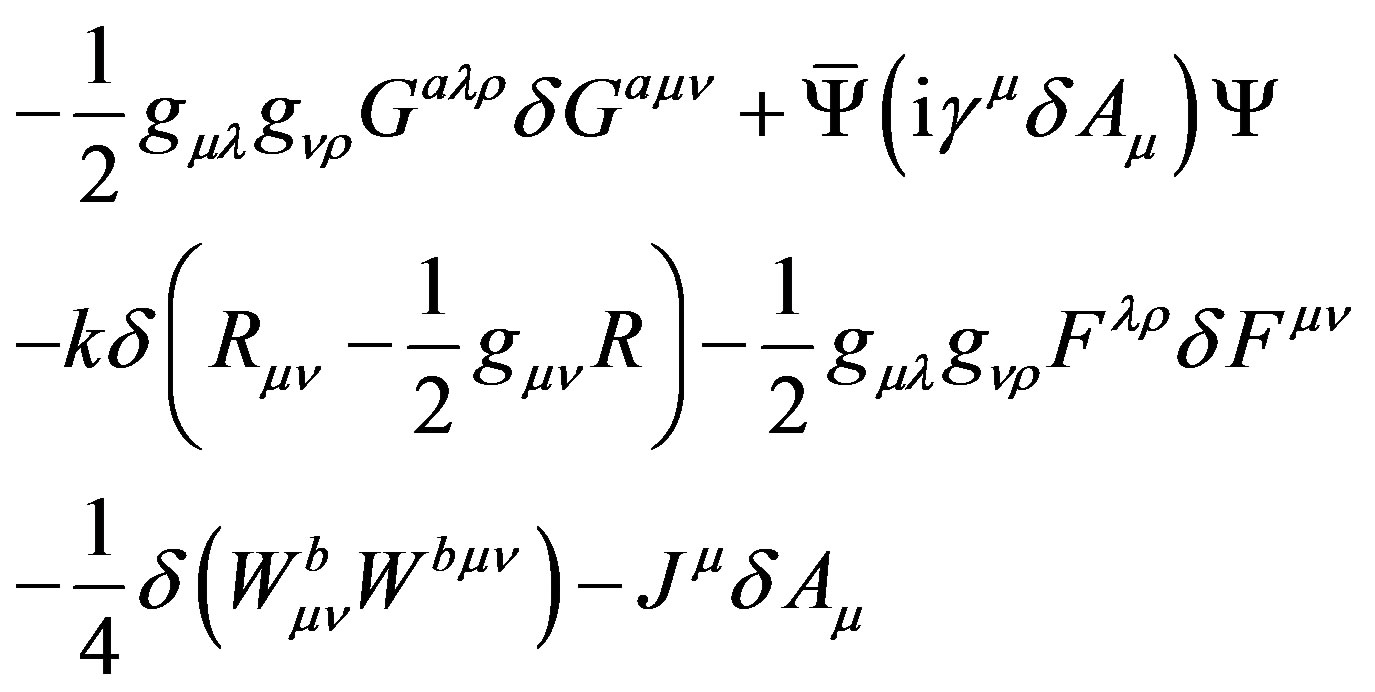 (39)
(39)
as
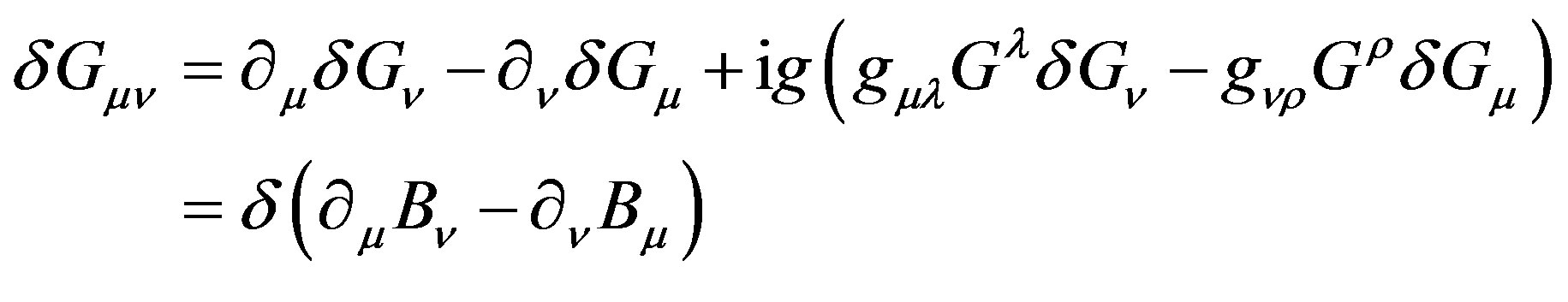 and
and , Eq.39 could be divided into two parts, particle phase and wave phase, and result in following combined equations
, Eq.39 could be divided into two parts, particle phase and wave phase, and result in following combined equations
 (40)
(40)
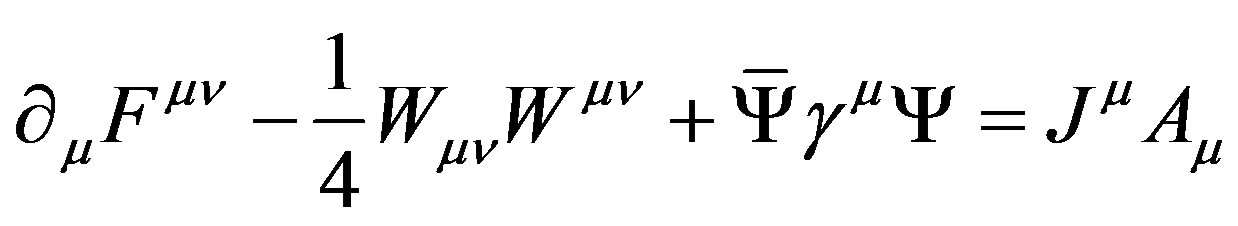 (41)
(41)
Eqs.37 and 40 unify strong interaction and gravity while Eq.41 links electroweak interaction where Higgs mechanism remains.
If we introduce linkage between 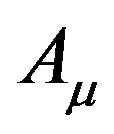 and
and 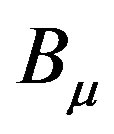 as
as
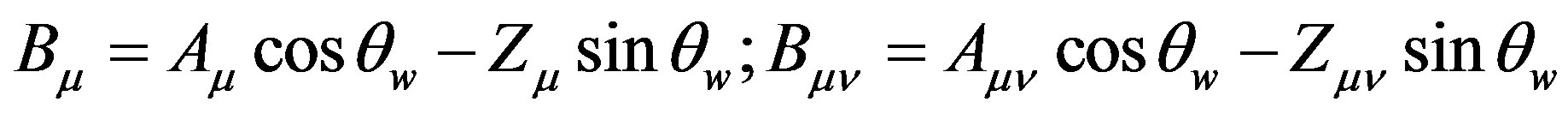 (42)
(42)
electroweak model is maintained by linking to strong interaction.
6. POTENTIAL APPLICATION: EXPLANATION OF DARK MATTER & ENERGY
Based on Eq.37, we can also provide a theoretical interpretation of dark matter and dark energy [14], where p (Ψ) item indicates dark matter and E(Ψ) item denotes dark energy. Thus, unknown dark matter and dark energy originate from theoretical flaws, and they are phenomenological effects in the physical unification of geometric field.
When we combine  with
with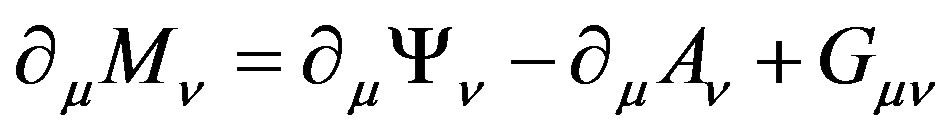 , we obtain
, we obtain
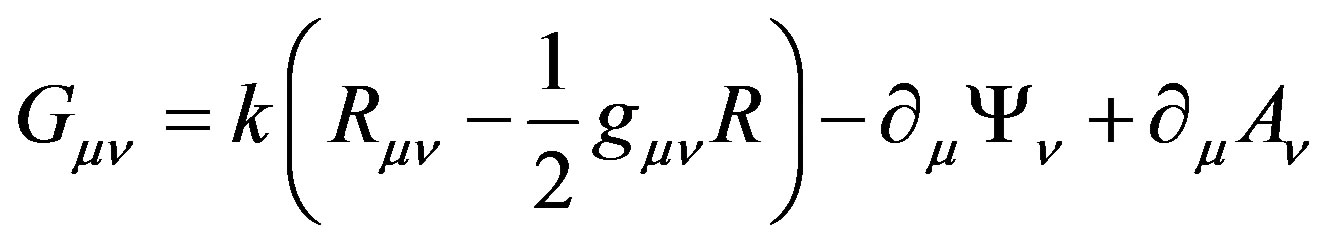 (43)
(43)
So, we know that the essences of dark matter and dark energy are effects of scalar and vector functions mathematically. Meanwhile, complement to Higgs mechanism, the mass also originated from curvature inside hadrons.
7. CONCLUDING REMARKS
Combining quantum field theory and general relativity, geometric field did unify the two standard models together, which provided another way to consider physical unification, where the distribution of matter-energy is proportional to the curvature of space-time and waveparticle duality is embedded into multi-vector functions. The unified physical framework looks good in both mathematics and physics, with retaining and matching all results of present physics, which is another U-theory [15].
While Higgs boson was found in LHC, we would provide this way to introduce mass inside hadrons. Following this nonlinear physical unification, dark matter and energy might also be naturally interpreted, which could stimulate further studies.
8. ACKNOWLEDGEMENTS
The author is grateful to the anonymous reviewer for helpful comments.
REFERENCES
- Chou Cottingham, W. N. and Greenwood, D. A. (2007) An introduction to the Standard Model of Particle Physics. 2nd Edition, Cambridge University Press, Cambridge. doi:10.1017/CBO9780511791406
- Weinberg, S. (1972) Gravitation and cosmology. Wiley, New York.
- Nakamura, K., et al., Particle Data Group (2010) Review of particle physics. Journal of Physics G: Nuclear and Particle Physics, 37, 075021. doi:10.1088/0954-3899/37/7A/075021
- The ATLAS Collaboration (2012) Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Physics Letters B, 716, 1-29.
- The CMS Collaboration (2012) Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Physics Letters B, 716, 30-61.
- Dirac, P. A. M. (1935) The principles of quantum mechanics. Oxford University Press, Oxford.
- Hestenes, D. (2003) Spacetime physics with geometric algebra. American Journal of Physics, 71, 691-714. doi:10.1119/1.1571836
- Doran, C. J. L. and Lasenby, A. N. (2003) Geometric algebra for physicists. Cambridge University Press, Cambridge.
- Lasenby, A., Doran, C. and Gull, S. (1998) Gravity, gauge theories and geometric algebra. Philosophical Transactions of the Royal Society of London, A356, 487-582.
- Zee, A. (2010) Quantum field theory in a nutshell. 2nd Edition, Princeton University Press, Princeton.
- Penrose, R. (2004) The road to reality: A complete guide to the laws of the universe. Jonathan Cape, London.
- Connes, A. (1995) Noncommutative geometry and reality. Journal of Mathematical Physics, 36, 6194-6231. doi:10.1063/1.531241
- Ye, F. Y. (2009) A Clifford-Clifford-Riemannian physical unification and fractal dynamics. Chaos, Solitons and Fractals, 41, 2301-2305. doi:10.1016/j.chaos.2008.09.004
- Li, M., et al. (2011) Dark energy. Communications in Theoretical Physics, 56, 525-604. doi:10.1088/0253-6102/56/3/24
- Ye, F. Y. (2009) From chaos to unification: U Theory vs. M Theory. Chaos, Solitons and Fractals, 42, 89-93. doi:10.1016/j.chaos.2008.10.030
APPENDIX
Dirac matrices are defined as
 (A.1)
(A.1)
Mostly their Weyl or chiral representation of Dirac matrices are applied as
 (A.2)
(A.2)
The standard complex Pauli matrices  with conjuncture
with conjuncture 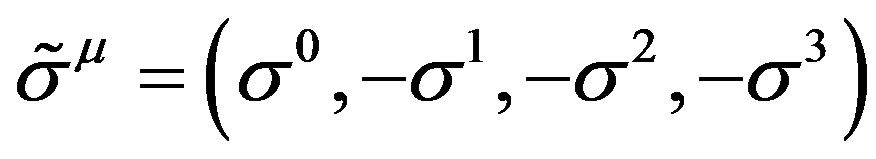 keep following forms
keep following forms
 (A.3)
(A.3)
For numerical estimation of curvature mass, as the curvature is proportional to the radium−1, we can estimate the gravity strength with mass in a space with radium at 10−15 m referring to Eq.6
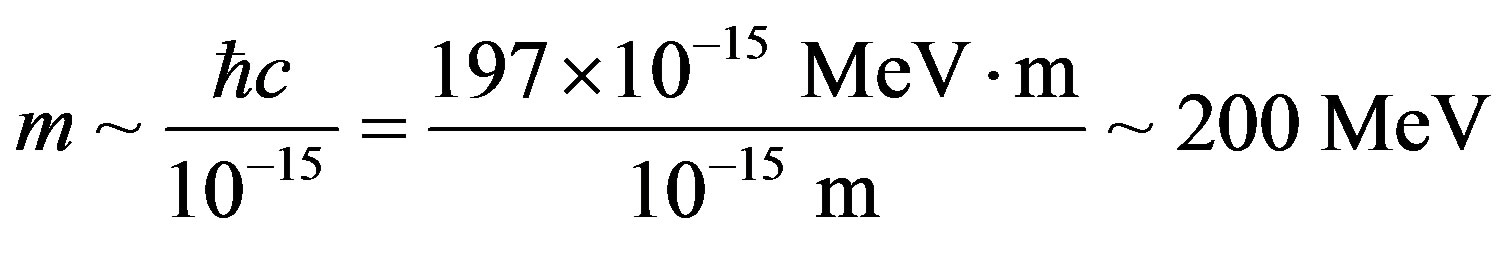 .
.

