Natural Science
Vol.4 No.12A(2012), Article ID:26121,12 pages DOI:10.4236/ns.2012.412A138
The LBFGS quasi-Newtonian method for molecular modeling prion AGAAAAGA amyloid fibrils
![]()
1Centre for Informatics and Applied Optimization, Graduate School of Sciences, Information Technology and Engineering, The University of Ballarat, Victoria, Australia; *Corresponding Author: j.zhang@ballarat.edu.au
2School of Management Science, Qufu Normal University, Rizhao, China
3Department of Applied Mathematics, Hong Kong Polytechnic University, Hong Kong, China
4Institute of Applied Mathematics, Academia Sinica, Beijing, China
5Department of Applied Mathematics, Dalian University of Technology, Dalian, China
Received 23 October 2012; revised 22 November 2012; accepted 8 December 2012
Keywords: Protein 3D Structure; Computational Approaches; Optimization Method; Molecular Modelling; Prion AGAAAAGA Amyloid Fibrils
ABSTRACT
Experimental X-ray crystallography, NMR (Nuclear Magnetic Resonance) spectroscopy, dual polarization interferometry, etc. are indeed very powerful tools to determine the 3-Dimensional structure of a protein (including the membrane protein); theoretical mathematical and physical computational approaches can also allow us to obtain a description of the protein 3D structure at a submicroscopic level for some unstable, noncrystalline and insoluble proteins. X-ray crystallography finds the X-ray final structure of a protein, which usually need refinements using theoretical protocols in order to produce a better structure. This means theoretical methods are also important in determinations of protein structures. Optimization is always needed in the computer-aided drug design, structure-based drug design, molecular dynamics, and quantum and molecular mechanics. This paper introduces some optimization algorithms used in these research fields and presents a new theoretical computational method—An improved LBFGS Quasi-Newtonian mathematical optimization method—to produce 3D structures of prion AGAAAAGA amyloid fibrils (which are unstable, noncrystalline and insoluble), from the potential energy minimization point of view. Because the NMR or X-ray structure of the hydrophobic region AGAAAAGA of prion proteins has not yet been determined, the model constructed by this paper can be used as a reference for experimental studies on this region, and may be useful in furthering the goals of medicinal chemistry in this field.
1. INTRODUCTION
Neurodegenerative diseases including Parkinson’s, Alzheimer’s, Huntington’s, and Prion’s were found they all featured amyloid fibrils [1-6]. Amyloid is characterized by a cross-β sheet quaternary structure and recent X-ray diffraction studies of microcrystals revealed atomistic details of core region of amyloid [7,8]. All the quaternary structures of amyloid cross-β spines can be reduced to one of the 8 classes of steric zippers of [8], with strong van der Waals (vdW) interactions between β- sheets and hydrogen bonds (HBs) to maintain the β- strands. A new era in the structural analysis of amyloids started from the “steric zipper”-β-sheets [7]. As the two β-sheets zip up, Hydrophobic Packings (HPs & vdWs) have been formed. The extension of the “steric zipper” above and below (i.e. the β-strands) is maintained by Hydrogen Bonds (HBs) (but usually there is no HB between the two β-sheets). This is the common structure associated with some 20 neurodegenerative amyloid diseases.
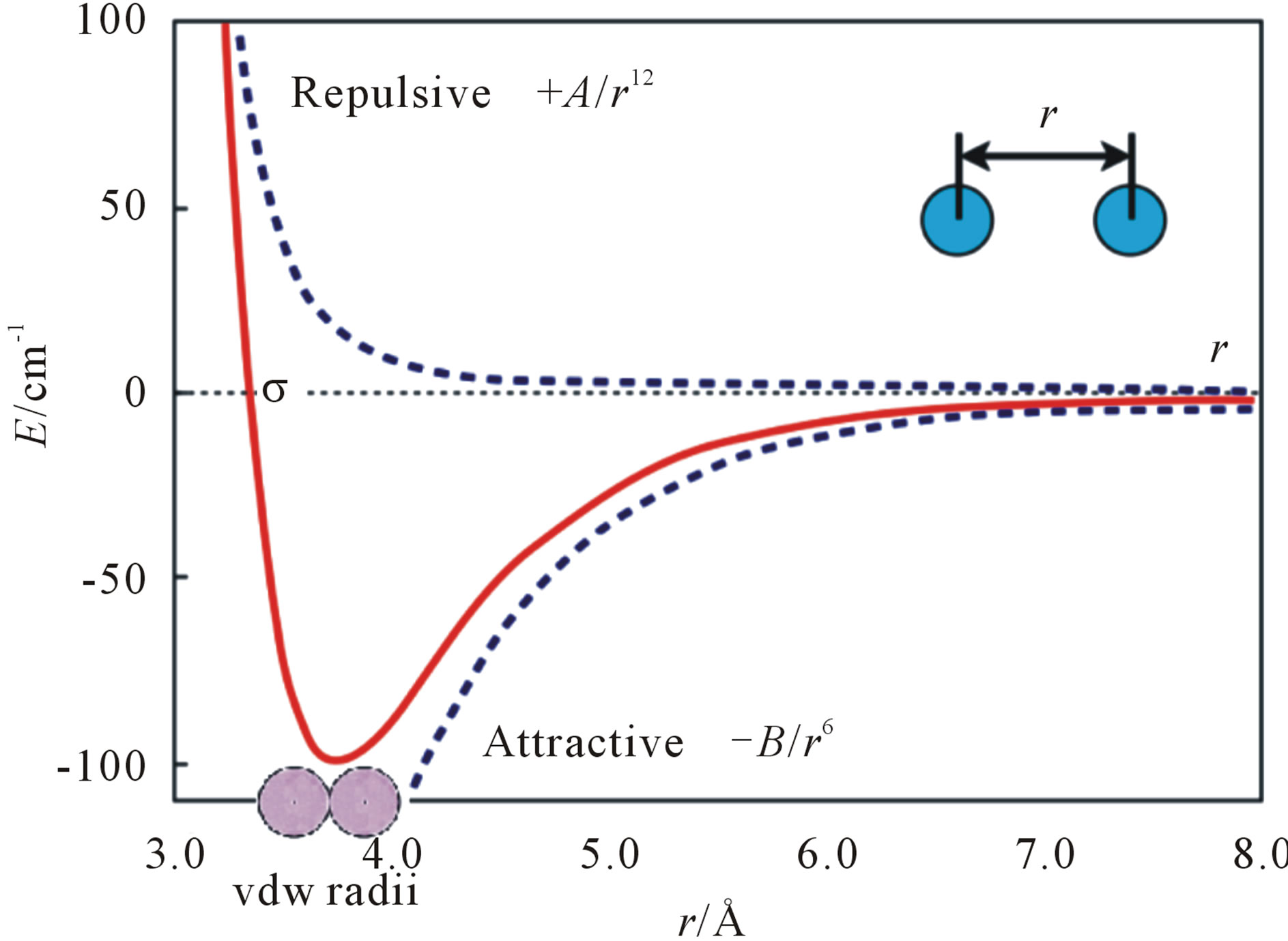
We first do some mathematical analysis for the common structure. The vdW contacts of the two atoms can be described by the Lennard-Jones (LJ) potential energy, where the parameters on the depth of the potential well and the atom diameter can be fitted to reproduce experimental data or deduced from results of accurate quantum chemistry calculations. There are two parts describing LJ potential energy: the repulsion and the attraction (Figure 1). The minimization of LJ potential energy is an optimization problem, which is a well-known and challenging test problem for global optimization [10-14]. It is very hard for global optimization to directly solve this problem even with a small number of atoms. Similarly,
the potential energy for the HBs between β-strands has a similar mathematical formula, and usually most of the HBs are still kept during the phase of molecular modelling of amyloid fibrils. Thus, the amyloid fibril molecular modelling problem can be reduced to solve the optimization problem of minimizing LJ potential energy though it is not easy to accurately solve for a large molecule.
Alternatively, we have found another way to solve the problem of minimizing LJ potential energy [15]. Seeing Figure 1, we may know that this optimization problem reaches its optimal value at the bottom of the LJ potential well, where the distance between two atoms equals to the sum of vdW radii of the two atoms. Hence, the amyloid fibril molecular modelling problem can be looked as a molecular distance geometry problem (MDGP) [16-18]. As an example to explain MDGP, the problem of locating sensors in telecommunication networks is a DGP. In such a case, the positions of some sensors are known (which are called anchors) and some of the distances between sensors (which can or cannot be anchors) are known. The DGP is to locate the positions of all the sensors. The MDGP looks sensors as atoms and their telecommunication network as a molecule. In this paper, we aim to solve the alternative MDGP problem (i.e. Eq.11 of [15]) for modelling amyloid fibril molecular 3D structures.
Neurodegeneration is the progressive loss of structure or function of neurons, including death of neurons. A prion is a misshapen protein that acts like an infectious agent (but not requiring either DNA, RNA, or both) to cause a number of fatal diseases. Prion diseases are rich in β-sheets (compared with the normal prion protein PrPC in rich of α-helices) and are so-called “protein structural conformational” diseases. The normal hydrophobic region 113-120 AGAAAAGA peptide of prion proteins is an inhibitor/blocker of prion diseases. PrP lacking this palindrome could not convert to prion diseases. Brown et al. pointed out that the AGAAAAGA peptide was found to be necessary (though not sufficient) for blocking the toxicity and amyloidogenicity of PrP 106-126, and the peptide AGAA does not form fibrils [19]. The minimum sequence necessary for fibril formation should be AGAAA, AGAAAA, AGAAAAG, AGAAAAGA and GAAAAGA, but the molecular structures of these fibrils have not known yet. This paper addresses an important problem on modelling the 3D molecular structures of prion AGAAAAGA amyloid fibrils of neurodegenerative diseases. The rest of this paper is arranged as follows. In the next section, i.e. Section 2, an improved LBFGS Quasi-Newtonian method is presented for solving Eq.11 of [5]. Section 3 implements this Quasi-Newtonian method by constructing a 3D molecular structure of prion AGAAAAGA amyloid fibrils of neurodegenerative prion diseases. Numerical results of computations show that the method designed in Section 2 is very effective and successful. This concluding remark will be made in the last section, i.e. Section 4.
2. METHODS
In a (macro) molecular system, if it is very far from equilibrium, then the forces may be excessively large, a robust energy minimization (EM) is required; another reason to perform an EM is the removal of all kinetic energy from the system: EM reduces the thermal noise in the structures and potential energies [20]. EM, with the images at the endpoints fixed in space, of the total system energy provides a minimum energy path. EM can be done using steepest descent (SD), conjugate gradient (CG), and Limited-memory Broyden Fletcher Goldfarb Shanno (LBFGS) methods.
Three kinds of possible EM methods are: 1) Derivative-free methods—that require only function evaluations, e.g. the simplex method and its variants; 2) derivative information methods—the partial derivatives of the potential energy with respect to all coordinates are known and the forces are minimized, e.g. SD, CG methods; and 3) second derivative information methods, e.g. LBFGS method. “SD is based on the observation that if the real-valued function  is defined and differentiable in a neighbourhood of a point x0 then
is defined and differentiable in a neighbourhood of a point x0 then 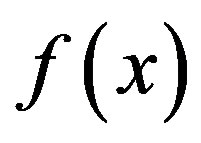 decreases fastest if one goes from x0 in the direction of the negative gradient of
decreases fastest if one goes from x0 in the direction of the negative gradient of 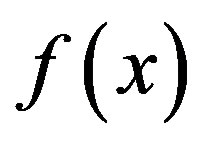 at x0 and SD local search method converges fast [21]. SD is robust and easy to implement but it is not most efficient especially when closer to minimum; at this moment, we may use the efficient CG. CG is slower than SD in the early stages but more efficient when closer to minimum. CG algorithm adds an orthogonal vector to the current direction of the search, and then moves them in another direction nearly perpendicular to this vector. The hybrid of SD-CG will make SD or CG more efficient than SD or CG alone. However, CG cannot be used to find the EM path, for example, when “forces are truncated according to the tangent direction, making it impossible to define a Lagrangian” [22,23]. In this case, the powerful and faster quasiNewtonian method (e.g. the LBFGS quasi-Newtonian minimiser) can be used [22,24-28]. We briefly introduce the LBFGS quasi-Newtonian method as follows.
at x0 and SD local search method converges fast [21]. SD is robust and easy to implement but it is not most efficient especially when closer to minimum; at this moment, we may use the efficient CG. CG is slower than SD in the early stages but more efficient when closer to minimum. CG algorithm adds an orthogonal vector to the current direction of the search, and then moves them in another direction nearly perpendicular to this vector. The hybrid of SD-CG will make SD or CG more efficient than SD or CG alone. However, CG cannot be used to find the EM path, for example, when “forces are truncated according to the tangent direction, making it impossible to define a Lagrangian” [22,23]. In this case, the powerful and faster quasiNewtonian method (e.g. the LBFGS quasi-Newtonian minimiser) can be used [22,24-28]. We briefly introduce the LBFGS quasi-Newtonian method as follows.
Newton’s method in optimization explicitly calculates the Hessian matrix of the second-order derivatives of the objective function and the reverse of the Hessian matrix [29]. The convergence of this method is quadratic, so it is faster than SD or CG. In high dimensions, finding the inverse of the Hessian is very expensive. In some cases, the Hessian is a non-invertible matrix, and furthermore in some cases, the Hessian is symmetric indefinite. QuasiNewton methods thus appear to overcome all these shortcomings.
Quasi-Newton methods (a special case of variable metric methods) are to approximate the Hessian. Currently, the most common quasi-Newton algorithms are the SR1 formula, the BHHH method, the widespread BFGS method and its limited/low-memory extension LBFGS, DFP, MS, and Broyden’s methods [30-33]. In Amber [23] and Gromacs [20], LBFGS is used, and the hybrid of LBFGS with CG—a Truncated Newton linear CG method with optional LBFGS Preconditioning [25]— is used in Amber [23].
For BFGS method, whether it converges at all on nonconvex problems is still an open problem. In fact, Powell (1984) gave a counter-example that shows that BFGS with an inexact line-search search may fail to converge [34-36]. Li and Fukushima (2001) proposed a modified BFGS method for non-convex objective function [37]. Basing on [24,25,37-39], in this paper we present an improved LBFGS method described as follows [40]— which presents the non-monotone line search technique [41,42] for the Wolfe-type search. The improved LBFGS method presented in this paper is much better than the standard BFGS method in view of the CPU time (see Figure 2) tested through more than 30 nonlinear programming problems (where each selected problem is regular, that is, its first and second derivatives exist and are continuous everywhere, and each problem is with different dimensions, i.e., 100, 500, 1000 and 10,000 dimensions) and its mathematical theory to support this algorithm can be seen from [40]. This paper implements the Wolfe-type search by the approximation technique of piecewise linear or quadratic function [43].
Algorithm 1: An Improved LBFGS Optimization Method for minimizing a non-convex function [40].
Step 0: Choose an initial point , an initial positive definite matrix H0, and choose constants σ1, σ2 such that 0 < σ1 < σ2 < 1, and choose an positive integer m1. Let k = 0.
, an initial positive definite matrix H0, and choose constants σ1, σ2 such that 0 < σ1 < σ2 < 1, and choose an positive integer m1. Let k = 0.
Step 1: If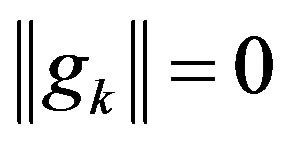 , then output xk and stop; otherwise,
, then output xk and stop; otherwise,
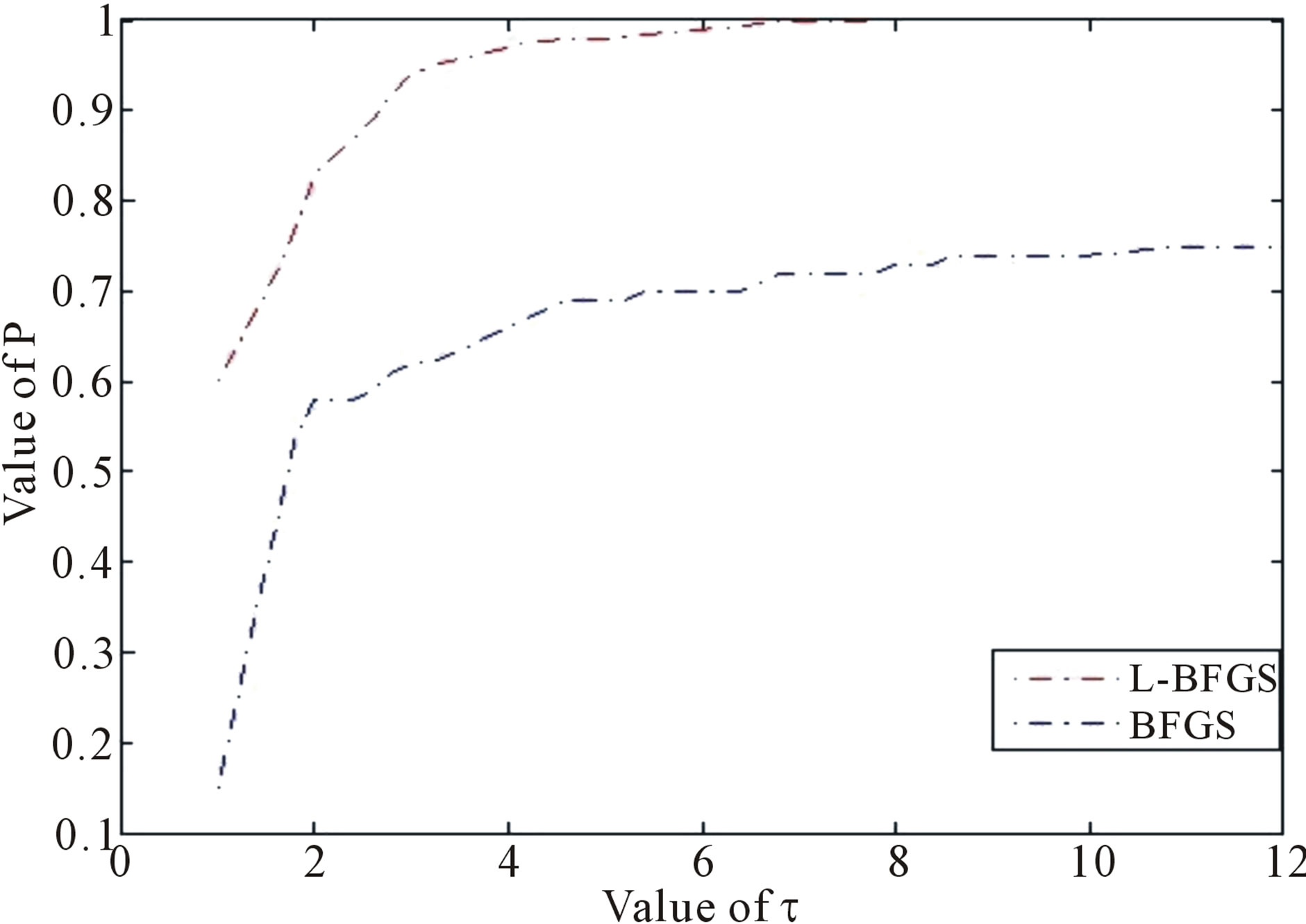
Figure 2. Performance based on CPU time, where 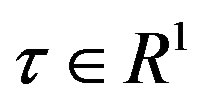 is a factor of the best possible ratio for CPU performance ratio of solvers L-BFGS and BFGS, and P is the probability distribution of the CPU performance ratio. Detailed mathematical formula for P can be seen in [44].
is a factor of the best possible ratio for CPU performance ratio of solvers L-BFGS and BFGS, and P is the probability distribution of the CPU performance ratio. Detailed mathematical formula for P can be seen in [44].
go to Step 2.
Step 2: Solve the following linear equation to get dk:

Step 3: Find a step-size λk > 0 satisfying the Wolfetype line search conditions:
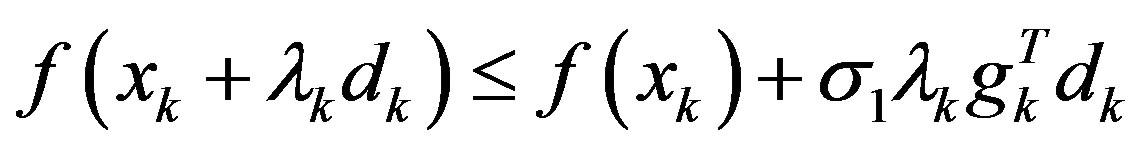 ,
,
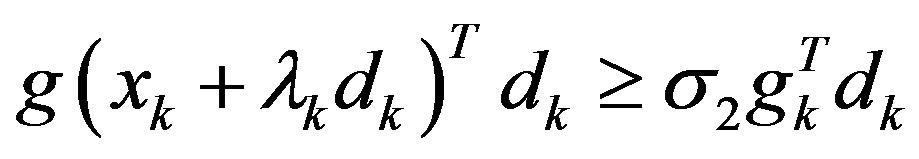 .
.
Step 4: Let 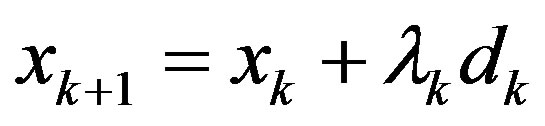 be the next iteration. Calculate gk+1 and ||gk+1||.
be the next iteration. Calculate gk+1 and ||gk+1||.
Step 5: Let ,
, 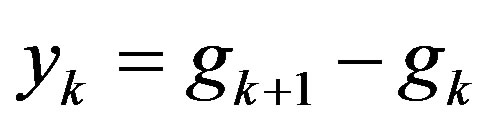 ,
, 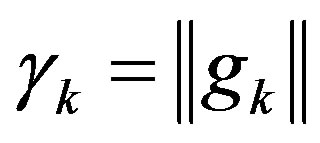 , then
, then .
.
Step 6: Let ḿ = min{k + 1, m1}. Update Hk following the formula
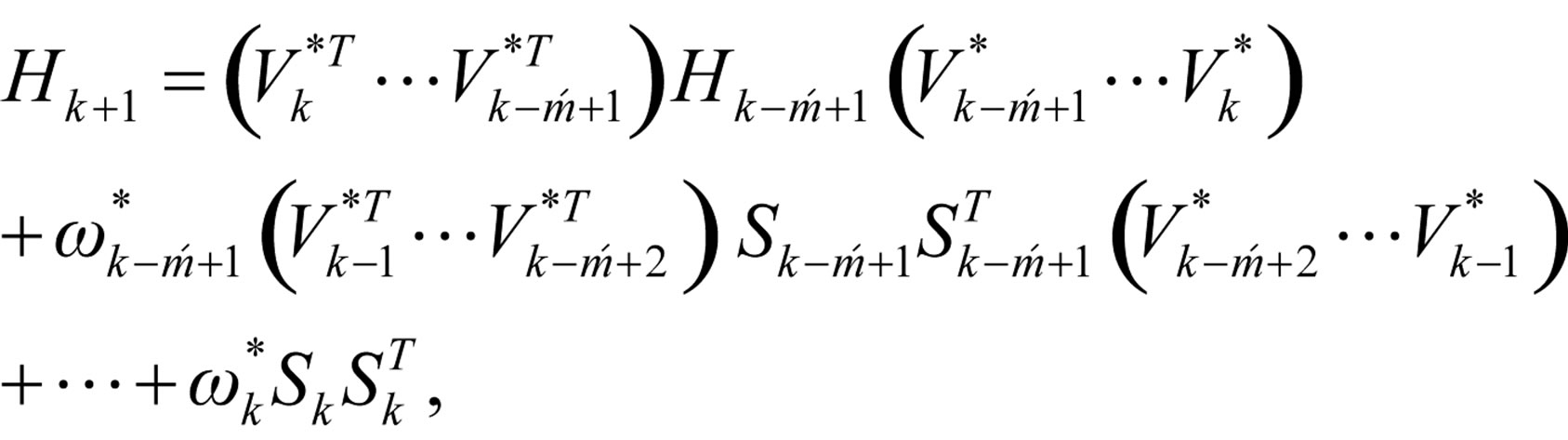
where 
 (when k = 0,
(when k = 0,
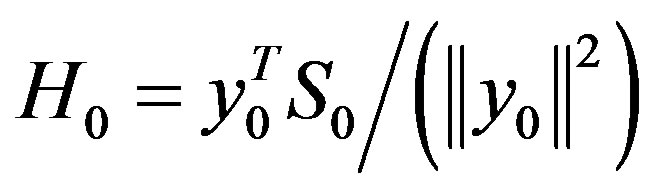 ,
, 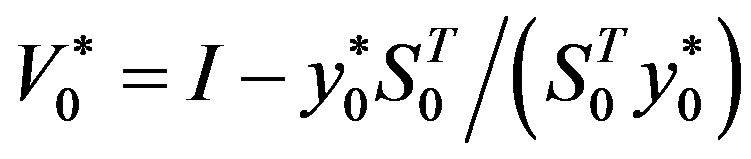 ,
,
Step 7: Let k = k + 1 and go to Step 1.
In Algorithm 1, gk denotes the gradient of  at xk, and the convergence and the R-linear convergent rate of Algorithm 1 are guaranteed by the following assumptions: (A1) f is twice continuously differentiable, (A2) f has Lipschitz continuous gradients and Hessians, (A3) the Hessian at the stationary point is always positively definite, and (A4) the level set of f is bounded. The detailed proof of the convergence and R-linear convergent rate of Algorithm 1 can be found in [40].
at xk, and the convergence and the R-linear convergent rate of Algorithm 1 are guaranteed by the following assumptions: (A1) f is twice continuously differentiable, (A2) f has Lipschitz continuous gradients and Hessians, (A3) the Hessian at the stationary point is always positively definite, and (A4) the level set of f is bounded. The detailed proof of the convergence and R-linear convergent rate of Algorithm 1 can be found in [40].
In [40], the non-monotone line search technique for step-size λk is used. This is a difference between the algorithm of [40] and this paper. All in all, it is well known that quasi-Newton method is an efficient solution method for unconstrained and continuously differentiable minimization problem [45-47]. However, it needs computing and storage of the updated matrix which is an approximation to the Hessian matrix in each iteration of the method. Hence, its efficiency may decrease when it is applied to large scale optimization problem. To overcome the drawback, limited memory quasi-Newton method is proposed [48]. The main ideal of this method is nearly identical to that of the standard BFGS method, and the only difference is that the inverse Hessian approximation is not formed explicitly, but defined by a small number, say ḿ, of BFGS updates. This technique received much attention in recent years and numerical experiments show that it is very competitive [24,49], and its global convergence and R-linear convergence rate with Wolfe line search are established for the uniformly convex case [24,26]. Since the limited memory BFGS method may suffer from ill-conditions for small value of ḿ, Al-Baali (1999) [50] made some modifications to the method and establish its global convergence based on the same assumptions, and Byrd et al. (1994) [51] derives new representation of limited memory quasi-Newton matrices for the benefit of computing the updated matrix. Recently, a non-monotone line search is introduced, see e.g., [41,42]. Then it is showed to be more competitive and practical for solving nonlinear optimization problems, and [52] established the global convergence of this line search applied to limited memory BFGS method based on the uniformly convex assumption. Motivated by the above observation, it turns out that in two respects the limited memory BFGS method is much less effective. First, we note that the convergence analysis of the method is focused on the uniformly convex assumption and little is known for non-convex case. Second, numerical experiments have suggested the main weakness of limited memory method is that it may converge very slowly in terms of number of iterations for ill-conditioned problems. The purpose of the above Algorithm 1 is to reduce these defects and Figure 2 shows the effectiveness of the proposed algorithm. We will apply it into the molecular modelling of prion AGAAAAGA amyloid fibrils in the next section.
3. RESULTS AND DISCUSSION
From their research of prion, scientists found that the cross-β structure of peptides is with the nature of selfaggregation, the self-aggregating to form fibers. This provides us a new research idea for nanomaterials. HBs can be formed between peptide β-strands, and one peptide monomer connects together with another in accordance with the specific structure to form fibers. Many laboratories in the world are synthesizing peptides that can self-aggregate to form fibers, and want to be able to control the growth of the fiber to find out new functional materials [53,54]. The studies of this paper not only benefit nanometerials research, but also benefit the research on neurodegenerative amyloid fibril diseases. Prion AGAAAAGA peptide has been reported to own an amyloid fibril forming property (initially described in 1992 by Gasset et al. of Prusiner’s Group) [19,55-78], but there has not been experimental structural bioinformatics for this segment yet due to the unstable, noncrystalline and insoluble nature of this region. Furthermore, Zhang (2011) did accurate calculations to confirm the amyloid fibril property at this region (Figure 3) [79] in the use of the fibril prediction program of [80].
3.1. Material for the Molecular Modeling
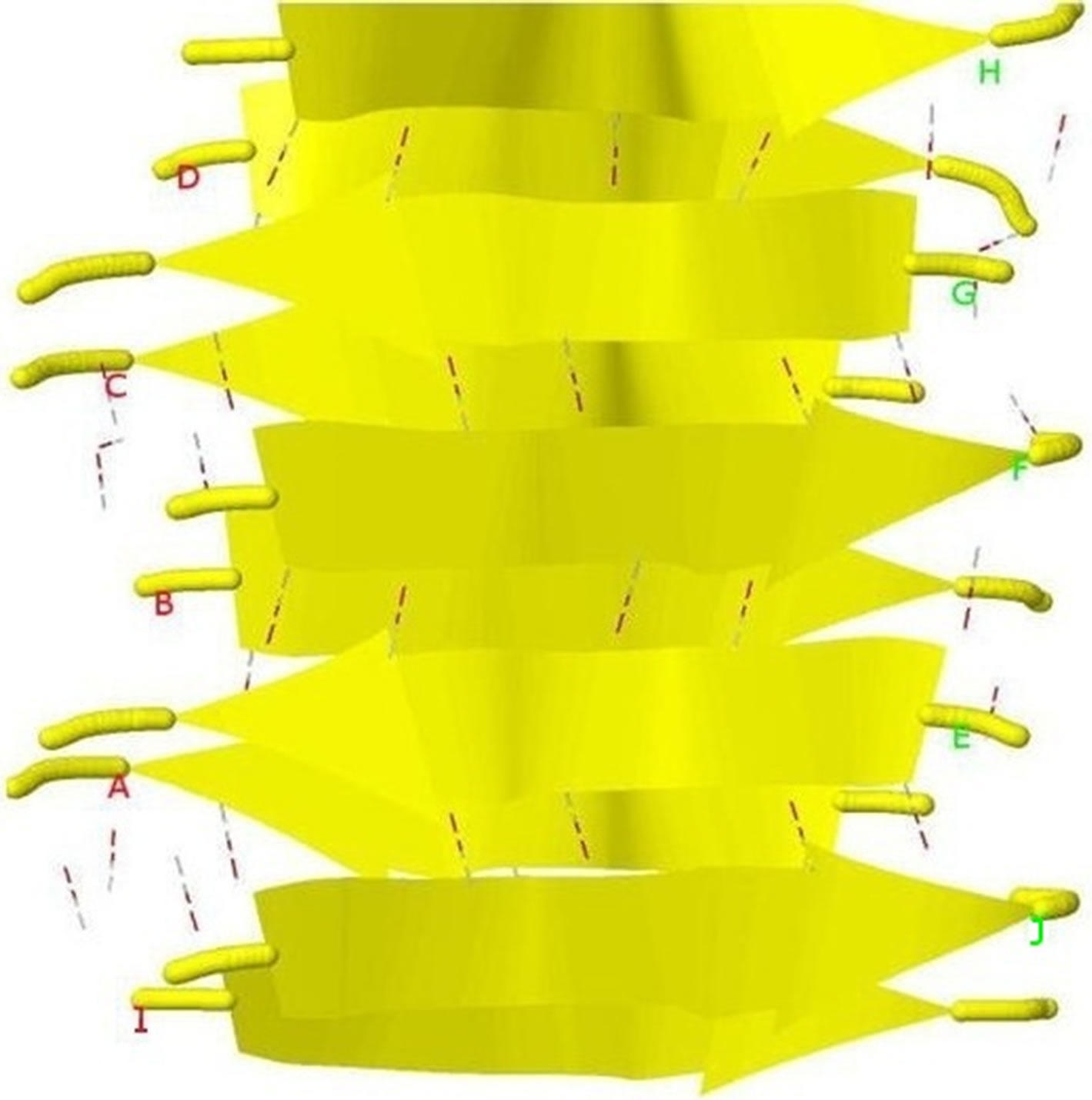
This paper uses a suitable pdb file template 2OMP.pdb (the LYQLEN peptide derived from human insulin residues 13-18 [8]) from the Protein Data Bank to build an 8-chain AGAAAAGA prion amyloid fibril molecular model to illuminate Algorithm 1 works very well. To choose 2OMP.pdb (Figure 4) as the modeling template is due to it can pass all the long procedures of SDCG-SA (equilibrations & productions)-SDCG of [79] in the use of the fibril prediction program of [80]. By observations of Figure 4 and the 2nd column of coordinates of 2OMP.pdb, we know that E(F) chains can be calculated on the XZ-plane from A(B) chains by Eq.3.1 and other chains can be got by a parallel up (or down) along the X-axis by Eqs.3.2-3.3:
 , (3.1)
, (3.1)
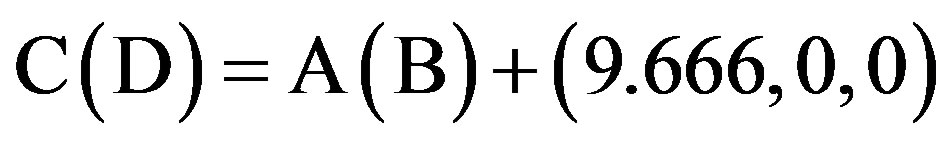 (3.2)
(3.2)
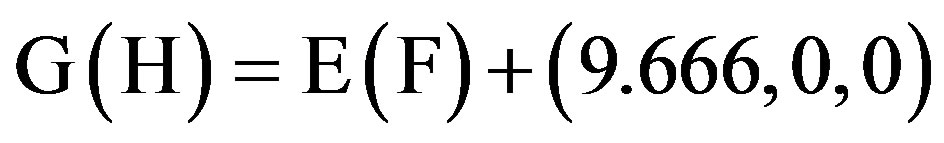 (3.3)
(3.3)
3.2. New Molecular Modeling Homology Model
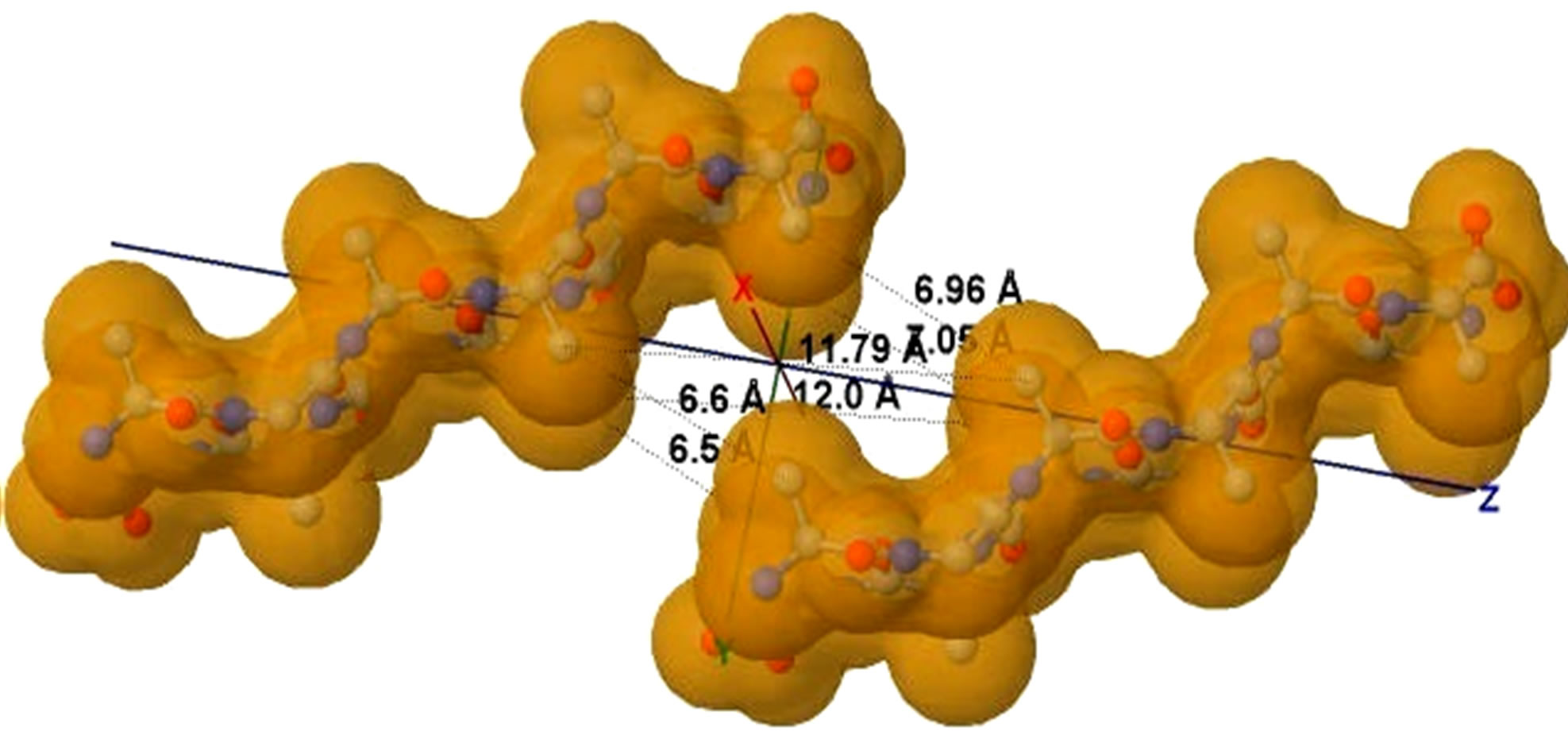
Basing on the template 2OMP.pdb from the Protein Data Bank (Figure 4), the AGAAAAGA palindrome amyloid fibril model of prions (denoted as Model 1) will be constructed. Chains AB of Model 1 will be got from AB Chains of 2OMP.pdb using themutatemodule of the free package Swiss-PdbViewer (SPDBV Version 4.01). It is pleasant to see that some HBs are still kept after the mutations; thus we just need to consider the vdWs only. Making mutations for EF Chains of 2OMP.pdb, we can get the EF Chains of Model 1. Then we add GLY and ALA residues by XLEaP module of Amber 11. However, the vdWs between Chain A and Chain E, between B Chain and F Chain are too far at this moment (Figure 5, where the twice of the vdWradius of CB atom is 3.4 angstroms).
In [79] the commercial package InsightII (accelrys. com) is used to build models. Instead of InsightII, because this package is not available by the authors, this paper uses Algorithm 1 to build and optimize Model 1. In “Zipper 1”, fixing the coordinates of A.ALA3.CB, A.ALA1.CB and letting the coordinates of E.ALA6.CB, E.ALA4.CB be variables, we may get an optimization problem:
 (3.4)
(3.4)
or
 (3.5)
(3.5)
Figure 3. Prion AGAAAAGA (113 - 120) segment is clearly and surely identified as the amyloid fibril formation region, because its energy is less than the amyloid fibril formation threshold energy −26 kcal/mol.

Figure 4. Protein fibril structure of human insulin LYQLEN (13 - 18) (PDB id: 2OMP). Dashed lines denote the HBs between the pairs of β-strands. A, B, C, D, E, F, G, H denote the chains of the fibril. The pair of β-sheets 1 & 2 forms a completely dry interface by vdWs, and between many pairs of β-sheets wet interfaces are formed with water molecules.
 (a)
(a)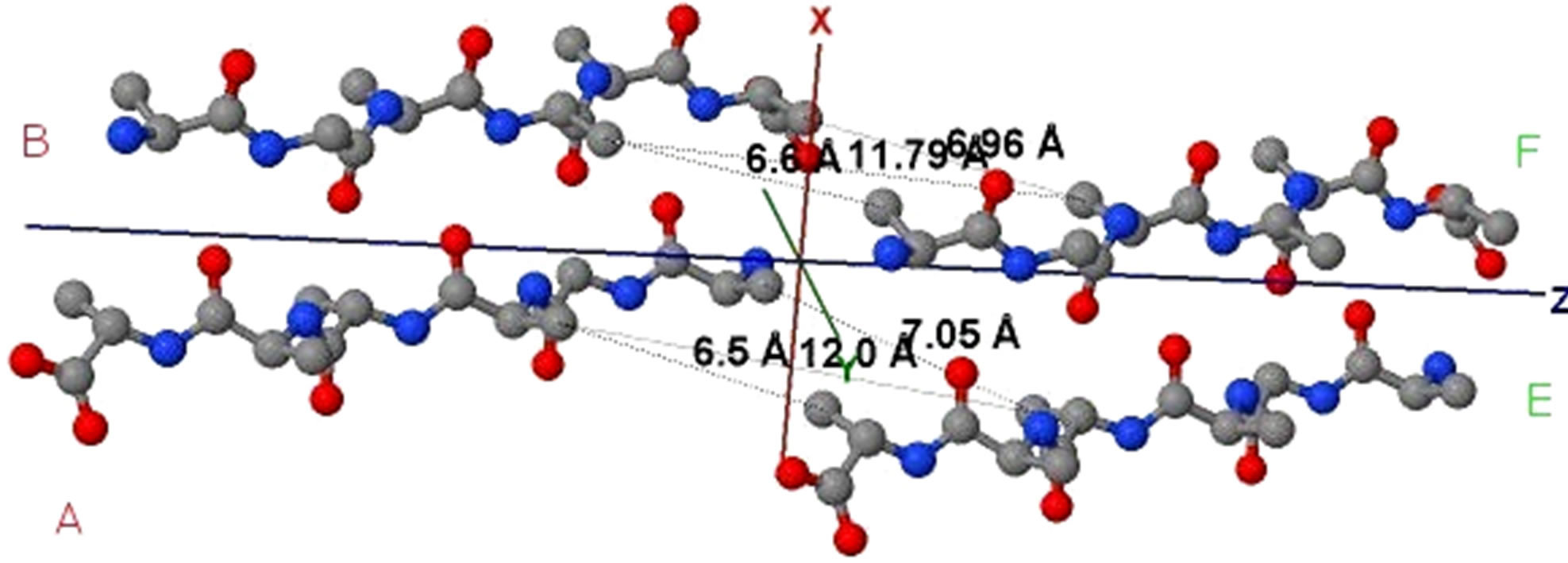 (b)
(b)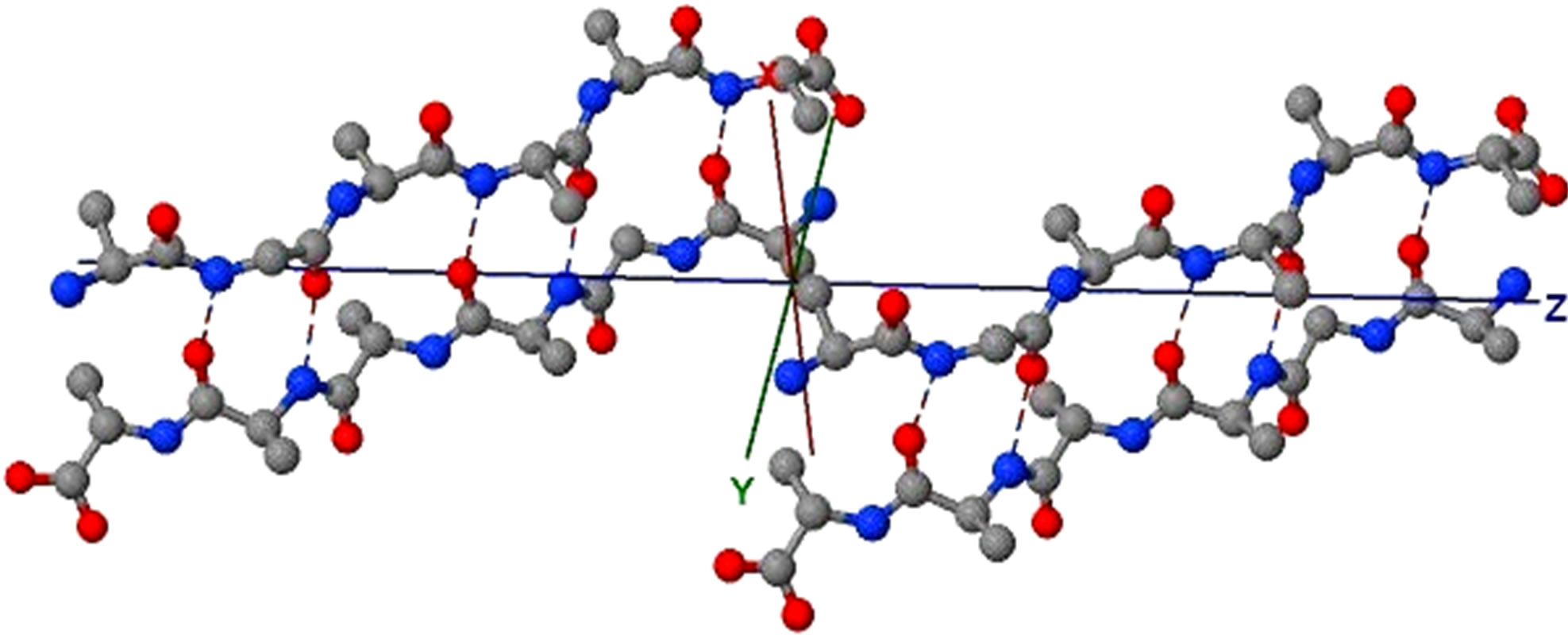 (c)
(c)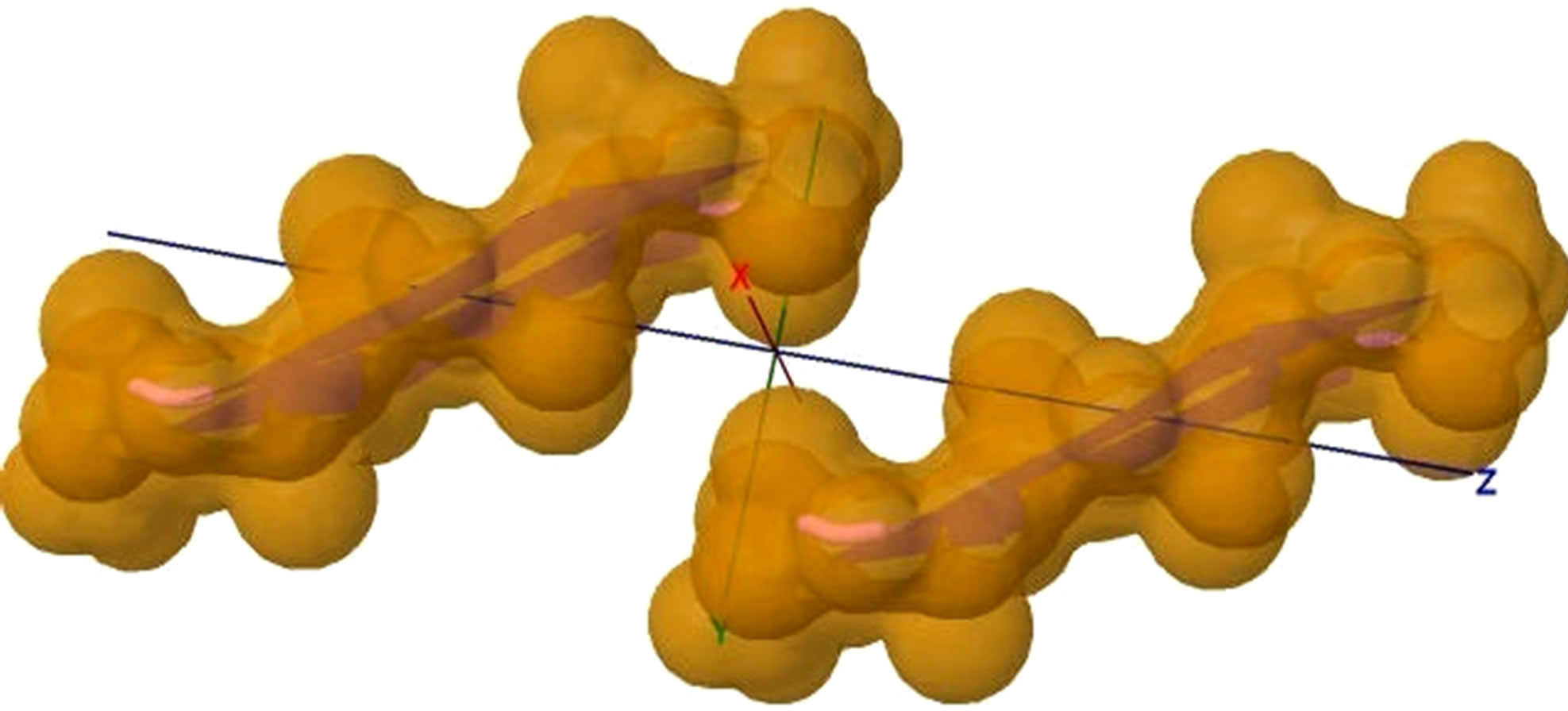 (d)
(d)
Figure 5. (a) shows the distances of “Zipper 1”-E.ALA6.CB-A.ALA3.CBE.ALA4.CB-A.ALA1.CB are 6.5, 12.0 and 7.05 angstroms respectively, and the distances of “Zipper 2”-F.ALA1.CB-B.ALA4.CB-F.ALA3.CB-B.ALA6.CB are 6.6, 11.79, 6.96 angstroms respectively. In (a), A, B, E, F denote A, B, E, F Chains, the red colored spheres are oxygen atoms, the blue colored spheres are nitrogen atoms, and the gray colored spheres are carbon atoms; (b) shows the far vdW surface; (c) shows the violet colored A, B, E, F Chains of Figure 4; (d) shows HBs (in turns from left to right): A/E.ALA5.O-B/F.GLY2.N, A/E.ALA5.N-B/F.GLY2.O, A/E. ALA3.O-B/F.ALA4.N, A/E.ALA3.N-B/F.ALA4.O, A/E.ALA1.O-B/F.ALA6.N.
with an initial solution (–0.067, 5.274, 7.860; –1.119, 1.311, 13.564). Similarly, in “Zipper 2”, fixing the coordinates of B.ALA4.CB, B.ALA6.CB and letting the coordinates of F.ALA1.CB, F.ALA3.CB be variables, we get another optimization problem:
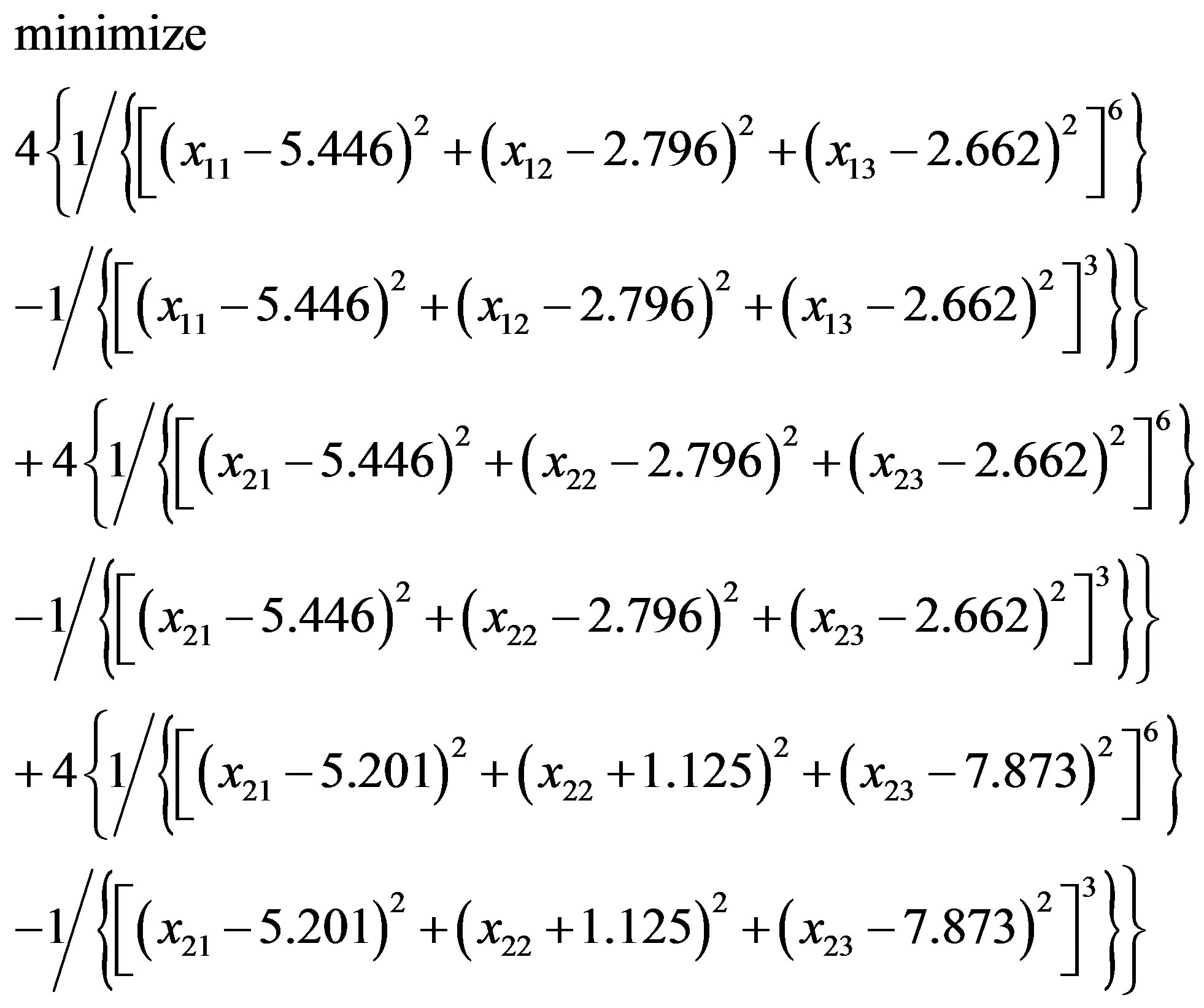 (3.6)
(3.6)
or
 (3.7)
(3.7)
with an initial solution (4.714, 4.878, 8.881; 4.170, 1.360, 14.292). Next, we solve Eqs.3.5 and 3.7 by Algorithm 1.
We first solve Eq.3.5 in the use of Algorithm 1. We set σ1 = 10−4, σ2 = 0.1 - 0.9, m1 = 3 - 7, take the initial solution x0 = (−0.067, 5.274, 7.860; −1.119, 1.311, 13.564) and calculate its gradient g0 = (−69.7747, 140.135, 365.852, −752.075, −285.005, 3576.69) and its Hessian matrix
 (3.8)
(3.8)
which is a positive definite matrix with eigenvalues (1085.02, 372.093, 341.157, 230.049, 61.2695, 61.2695). Then Algorithm 1 hybridized with simulated annealing global optimal search (in order to bring local optimal solutions to jump out of local traps, replacing the discrete gradient local optimal search method in Algorithm 1 of [14] by the Algorithm 1 of this paper) is executed and the optimal solution (3.027, 4.954, 3.856; 1.679, 1.777, 5.011) for Eq.3.5 is got.
Similarly, for Eq.3.7, we take the initial solution x0 = (4.714, 4.878, 8.881; 4.170, 1.360, 14.292) and calculate its gradient g0 = (−46.8782, 133.142, 397.798, −401.192, −182.604, 3436.46) and its Hessian matrix
 (3.9)
(3.9)
which is a positive definite matrix with eigenvalues (1044.83, 361.8, 328.538, 238.159, 63.973, 63.973). The optimal solution got for Eq.3.7 is (7.412, 4.760, 4.624; 5.887, 1.451, 5.757).
We set (3.027, 4.954, 3.856; 1.679, 1.777, 5.011) as the coordinates of E.ALA6.CB and E.ALA4.CB, (7.412, 4.760, 4.624; 5.887, 1.451, 5.757) as the coordinates of F.ALA1.CB and F.ALA3.CB, and taking the average value we get
 . (3.10)
. (3.10)
By Eq.3.10 we can get very close vdW contacts between A(B) chains and E(F) chains (Figure 5(b)), and other chains of Model 1 can be got by Eqs.3.2, 3.3 and Eq.3.11:
 . (3.11)
. (3.11)
The initial structure of Model 1 illuminated in Figures 6(a) and (b) is not the optimal structure with the lowest total potential energy. The initial structure also has no hydrogen atoms (so no hydrogen bonds existed) and water molecules added. For each Chain, the C-terminal and N-terminal atoms also have problems. Clearly there are a lot of close/bad contacts between β-strand atoms as illuminated in Figures 6(a) and (b). We used the ff03 force field of AMBER 11, in a neutral pH environment. The amyloid fibrils were surrounded with a 8 angstroms layer of TIP3PBOX water molecules using the XLEaP module of AMBER 11. 1944 waters and 408 hydrogen atoms were added for Model 1 byt he XLEaP module. solvated amyloid fibril was inimized by the method.
The LJ potential energy of atoms’ vdW interactions is just a part of the total potential energy of a protein, and by observations from Model 1 computed by Eqs.3.2, 3.3, 3.10 and 3.11 we can see that the contacts between β-strand atoms and β-sheet atoms are too close/bad. Thus, we need to relax Model 1 computed. The relaxation is done in the use of local search LBFGS Quasi-Newton method (lbfgs_memory_depth = 3) within AMBER 11 [23]. The relaxed/optimized Model 1 is illuminated in Figure 6(c). Seeing Figure 6(d) compared with Figure 6(b), we may know the vdW interactions between the two β-sheets are very relaxed/optimized now. Figure 6(c) shows the Model 1 of optimal molecular structure for prion AGAAAAGA amyloid fibrils.
4. CONCLUSIONS
In a (macro) molecular system, a robust energy mini-
 (a)
(a) (c)
(c) (b)
(b) (d)
(d)
Figure 6. Left: The close vdW surface contacts between Chains A(B) and E(F) of Model 1 after solving Eqs.3.5 and 3.7; Right: The constructed Model 1 with 10 chains. The dashed lines denote HBs.
mization is very necessarily required. Mathematical optimization minimization methods find a place to apply in these systems. Because in physics the (macro) molecular system usually is not a simple two-body problem of system, local search optimization methods are very useful in the applications to the (macro) molecular system. On anther sense, when a protein is unstable, noncrystalline or insoluble and very difficult to detect its 3D structure by the expensive and costly NMR and X-ray, theoretical mathematical or physical computational method can be used to produce the 3D structure of the protein. Moreover, even though the X-ray crystallography finds the X-ray final structure of a protein, we still need refinements using theoretical protocols in order to produce a better structure. The theoretical computational method—an improved LBFGS Quasi-Newtonian mathematical optimization method-presented in this paper and other mathematical optimization methods mentioned in this paper should be very useful in the protein molecular modeling research field.
This paper also shows the effectiveness of the improved LBFGS mathematical optimization method presented. Prion AGAAAAGA amyloid fibrils have not much structural information. This paper presents some bioinformatics on the molecular structures of prion AGAAAAGA amyloid fibrils in the sense of theoretical emphasis. The structures may be helpful in the advance in the biochemical knowledge of prion protein misfolding or instability and in the future applications for therapeutic agent design.
5. ACKNOWLEDGEMENTS
This research was supported by the National Natural Science Foundation of China (No. 11171180), the National Basic Research Program of China (2010CB732501), and a Victorian Life Sciences Computation Initiative (VLSCI) grant numbered VR0063 & 488 on its Peak Computing Facility at the University of Melbourne, an initiative of the Victorian Government (Australia). The first author appreciates the financial support by Professors Changyu Wang and Yiju Wang for his visits to Qufu Normal University (China), and by Professor Xiangsun Zhang for his visits to Chinese Academy of Sciences (Beijing); the first author also appreciates Professor Adil M. Bagirov (University of Ballarat) for his instructions to implement the Wolfe-type search. This paper is dedicated to Professor Xiangsun Zhang (Academia Sinica, Beijing) on the occasion of his 70th birthday. The authors appreciate the anonymous referees for their comments on this paper.
REFERENCES
- Chiang, P.K., Lam, M.A. and Luo, Y. (2008) The many faces of amyloid beta in Alzheimer’s disease. Current Molecular Medicine, 8, 580-584. doi:10.2174/156652408785747951
- Irvine, G.B., El-Agnaf, O.M., Shankar, G.M. and Walsh, D.M. (2008) Protein aggregation in the brain: The molecular basis for Alzheimer’s and Parkinson’s diseases. Molecular medicine (Cambridge, Mass), 14, 451-464.
- Ferreira, S.T., Vieira, M.N. and De Felice, F.G. (2007) Soluble protein oligomers as emerging toxins in Alzheimer’s and other amyloid diseases. IUBMB Life, 59, 332-345. doi:10.1080/15216540701283882
- Nature Editorial (2001) More than just mad cow disease. Nature Structural & Molecular Biology, 8, 281. doi:10.1038/86132
- Truant, R., Atwal, R.S., Desmond, C., Munsie, L. and Tran, T. (2008) Huntington’s disease: Revisiting the aggregation hypothesis in polyglutamine neurodegenerative diseases. FEBS Journal, 275, 4252-4262. doi:10.1111/j.1742-4658.2008.06561.x
- Weydt, P. and La Spada, A.R. (2006) Targeting protein aggregation in neurodegeneration—lessons from polyglutamine disorders. Expert Opinion on Therapeutic Targets, 10, 505-513. doi:10.1517/14728222.10.4.505
- Nelson, R., Sawaya, M.R., Balbirnie, M., Madsen, A., Riekel, C., Grothe, R. and Eisenberg, D. (2005) Structure of the cross-beta spine of amyloid-like fibrils. Nature, 435, 773-778. doi:10.1038/nature03680
- Sawaya, M.R., Sambashivan, S., Nelson, R., Ivanova, M.I., Sievers, S.A., Apostol, M.I., Thompson, M.J., Balbirnie, M., Wiltzius, J.J., McFarlane, H.T., Madsen, A., Riekel, C. and Eisenberg, D. (2007) Atomic structures of amyloid cross-beta spines reveal varied steric zippers. Nature, 447, 453-457. doi:10.1038/nature05695
- Zhang, J.P. (2011) The Lennard-Jones potential minimization problem for prion AGAAAAGA amyloid fibril molecular modeling. arXiv:1106.1584.
- Kolossvry, I. and Bowers, K.J. (2010) Global optimization of additive potential energy functions: Predicting binary Lennard-Jones clusters. Physical Review E, 82, Article ID: 056711. doi:10.1103/PhysRevE.82.056711
- Sicher, M., Mohr, S. and Goedecker, S. (2010) Efficientmoves for global geometry optimization methods and their application to binary systems. Journal of Chemical Physics, 134, 44-106.
- Strodel, B., Lee, J.W., Whittleston, C.S. and Wales, D.J. (2010) Transmembrane structures for Alzheimer’s Aβ (1-42) oligomers. Journal of the American Chemical Society, 132, 13300-13312. doi:10.1021/ja103725c
- Ye, T., Xu, R. and Huang, W. (2011) Global optimization of binary Lennard-Jones clusters using three perturbation operators. Journal of Chemical Information and Modeling, 51, 572-577. doi:10.1021/ci1004256
- Zhang, J.P., Sun, J. and Wu, C.Z. (2011) Optimal atomicresolution structures of prion AGAAAAGA amyloid fibrils. Journal of Theoretical Biology, 279, 17-28. doi:10.1016/j.jtbi.2011.02.012
- Zhang, J.P., Gao, D.Y. and Yearwood, J. (2011) A novel canonical dual computational approach for prion AGAAAAGA amyloid fibril molecular modeling. Journal of Theoretical Biology, 284, 149-157. doi:10.1016/j.jtbi.2011.06.024
- Grosso, A., Locatelli, M. and Schoen, F. (2009) Solving molecular distance geometry problems by global optimization algorithms. Computational Optimization and Applications, 43, 23-37. doi:10.1007/s10589-007-9127-8
- More, J.J. and Wu, Z.J. (1997) Global continuation for distance geometry problems. SIAM Journal on Optimization, 7, 814-836. doi:10.1137/S1052623495283024
- Zou, Z.H., Bird, R.H. and Schnabel, R.B. (1997) A stochastic/perturbation global optimization algorithm for distance geometry problems. Journal of Global Optimization, 11, 91-105. doi:10.1023/A:1008244930007
- Brown, D.R. (2000) Prion protein peptides: Optimal toxicity and peptide blockade of toxicity. Molecular and Cellular Neuroscience, 15, 66-78. doi:10.1006/mcne.1999.0796
- van der Spoel, D., Lindahl, E., Hess, B., van Buuren, A.R., Apol, E., Meulenhoff, P.J., Tieleman, D.P., Sijbers, A.L.T.M., Feenstra, K.A., van Drunen, R. and Berendsen, H.J.C. (2010) Gromacs User Manual Version 4.5.4. www.gromacs.org
- Snyman, J.A. (2005) Practical mathematical optimization: An introduction to basic optimization theory and classical and new gradient-based algorithms. Springer Publishing, New York.
- Chu, J., Trout, B.L. and Brooks, B.R. (2003) A superlinear minimization scheme for the nudged elastic band method. Journal of Chemical Physics, 119, 12708-12717. doi:10.1063/1.1627754
- Case, D.A., Darden, T.A., Cheatham, T.E., Simmerling III, C.L., Wang, J., Duke, R.E., Luo, R., Walker, R.C., Zhang, W., Merz, K.M., Roberts, B.P., Wang, B., Hayik, S., Roitberg, A., Seabra, G., Kolossvary, I., Wong, K.F., Paesani, F., Vanicek, J., Liu, J., Wu, X., Brozell, S.R., Steinbrecher, T., Gohlke, H., Cai, Q., Ye, X., Wang, J., Hsieh, M.-J., Cui, G., Roe, D.R., Mathews, D.H., Seetin, M.G., Sagui, C., Babin, V., Luchko, T., Gusarov, S., Kovalenko, A. and Kollman, P.A. (2010) AMBER 11. University of California, San Francisco.
- Liu, D.C. and Nocedal, J. (1989) On the limited memory method for large scale optimization. Math Programming B, 45, 503-528. doi:10.1007/BF01589116
- Nocedal, J. and Morales, J. (2000) Automatic preconditioning by limited memory quasi-Newton updating. SIAM Journal on Control and Optimization, 10, 1079-1096. doi:10.1137/S1052623497327854
- Byrd, R.H., Nocedal, J. and Zhu, C. (1995) Towards a discrete Newton method with memory for large-scale optimization. Optimization Technology Center Report OTC- 95-1, North-western University, Evanston and Chicago.
- Byrd, R.H., Lu, P. and Nocedal, J. (1995) A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing, 16, 1190-1208. doi:10.1137/0916069
- Zhu, C., Byrd, R.H. and Nocedal, J. (1997) L-BFGS-B: Algorithm 778: L-BFGSB, FORTRAN routines for large scale bound constrained optimization. ACM Transactions on Mathematical Software, 23, 550-560. doi:10.1145/279232.279236
- Dennis, J.E., Robert, J.R. and Schnabel, B. (1996) Numerical methods for unconstrained optimization and nonlinear equations. SIAM. doi:10.1137/1.9781611971200
- Nocedal, J. and Wright, S.J. (1999) Numerical Optimization. 2nd Edition, Springer-Verlag, Berlin and New York.
- Berndt, E., Hall, B., Hall, R. and Hausman, J. (1974) Estimation and Inference in nonlinear structural models. Annals of Economic and Social Measurement, 3, 653-665.
- Luenberger, D.G. and Ye, Y.Y. (2008) Linear and nonlinear programming. 3rd Edition, International Series in Operations Research & Management Science, Springer, New York.
- Wang, Y.J. and Xiu, N.H. (2012) Nonlinear optimization theory and methods. Science Press, Beijing.
- Powell, M.J.D. (1984) Nonconvex minimization calculations and the conjugate gradient method. In: Griffiths, D.F., Ed., Numerical Analysis, Springer Verlag, Berlin, 122-141.
- Mascarenhas, W.F. (2004) The BFGS method with exact line searches fails for non-convex objective functions. Mathematical Programming, 99, 49-61. doi:10.1007/s10107-003-0421-7
- Dai, Y.H. (2002) Convergence properties of the BFGS algorithm. SIAM Journal on Optimization, 13, 693-701. doi:10.1137/S1052623401383455
- Li, D.H. and Fukushima, M. (2001) A modified BFGS method and its global convergence in nonconvex minimization. Journal of Computational and Applied Mathematics, 129, 15-35. doi:10.1016/S0377-0427(00)00540-9
- Xiao, Y.H., Wei, Z.X. and Wang, Z.G. (2008) A limited memory BFGS-type method for large-scale unconstrained optimization. Journal of Computational and Applied Mathematics, 56, 1001-1009. doi:10.1016/j.camwa.2008.01.028
- Yang, Y.T. and Xu, C.X. (2007) A compact limitedmemory method for large scale unconstrained optimization. European Journal of Operational Research, 180, 48-56. doi:10.1016/j.ejor.2006.02.045
- Hou, Y.T. and Wang, Y.J. (2012) The modified limited memory BFGS method for large-scale optimization. MSc Degree Thesis, Qufu Normal University, Qufu.
- Grippo, L., Lamparello, F. and Lucidi, S. (1986) A nonmonotone line search technique for Newton’s method. SIAM Journal on Numerical Analysis, 23, 707-716. doi:10.1137/0723046
- Han, J.Y. and Liu, G.H. (1997) Global convergence analysis of a new nonmonotone BFGS algorithm on convex objective Functions. Computational Optimization and Applications, 7, 277-289. doi:10.1023/A:1008656711925
- Bagirov, A.M., Karaszen, B. and Sezer, M. (2008) Discrete gradient method: Derivative-free method for nonsmooth optimization. Journal of Optimization Theory and Applications, 137, 317-334. doi:10.1007/s10957-007-9335-5
- Dolan, E.D. and Mor, J.J. (2002) Benchmarking optimization software with performance profiles. Mathematical Programming 91, 201-213. doi:10.1007/s101070100263
- Byrd, R.H. and Nocedal, J. (1989) A tool for the analysis of quasi-Newton methods with application to unconstrained minimization. SIAM Journal on Numerical Analysis, 26, 727-739. doi:10.1137/0726042
- Byrd, R.H., Nocedal, J. and Yuan, Y.X. (1987) Global convergence of a class of quasi-Newton methods on convex problems. SIAM Journal on Numerical Analysis, 24, 1171-1189. doi:10.1137/0724077
- Dennis, J.E. and More, J.J. (1977) Quasi-Newton method, motivation and theory. SIAM Review, 19, 46-89. doi:10.1137/1019005
- Nocedal, J. (1980) Updating quasi-Newton matrices with limited storage. Mathematics of Computation, 35, 773- 782. doi:10.1090/S0025-5718-1980-0572855-7
- Gilbert, J.C. and Lemarichal, C. (1989) Some numerical experiments with variable storage quasi-Newton algorithms. Mathematical Programming, 45, 407-435. doi:10.1007/BF01589113
- Al-Baali, M. (1999) Improved Hessian approximations for the limited memory BFGS method. Numerical Algorithms, 22, 99-112. doi:10.1023/A:1019142304382
- Byrd, R.H., Nocedal, J. and Schnabel, R.B. (1994) Representations of quasi-Newton matrices and their use in limited memory methods. Math Programming, 63, 129- 156. doi:10.1007/BF01582063
- Yuan, G.L., Wei, Z.X. and Wu, Y.L. (2010)Modified limitedmemory BFGS method with nonmonotone line search for unconstrained optimization. Journal of the Korean Mathematical Society, 47, 767-788. doi:10.4134/JKMS.2010.47.4.767
- Alper, T., Cramp, W., Haig, D. and Clarke, M. (1967) Does the agent of scrapie replicate without nucleic acid? Nature, 214, 764-766. doi:10.1038/214764a0
- Griffith, J. (1967) Self-replication and scrapie. Nature, 215, 1043-1044. doi:10.1038/2151043a0
- Brown, D.R. (2001) Microglia and prion disease. Microscopy Research and Technique, 54, 71-80. doi:10.1002/jemt.1122
- Brown, D.R., Herms, J. and Kretzschmar, H.A. (1994) Mouse cortical cells lacking cellular PrP survive in culture with a neurotoxic PrP fragment. Neuroreport, 5, 2057-2060. doi:10.1097/00001756-199410270-00017
- Cappai, R. and Collins, S.J. (2004) Structural biology of prions. In: Rabenau, H.F., Cinatl, J. and Doerr, H.W., Eds., Prions A Challenge for Science, Medicine and the Public Health System, Karger, Basel, 14-32.
- Chabry, J., Caughey, B. and Chesebro, B. (1998) Specific inhibition of in vitro formation of protease-resistant prion protein by synthetic peptides. The Journal of Biological Chemistry, 273, 13203-13207. doi:10.1074/jbc.273.21.13203
- Cheng, H.M., Tsai, T.W.T., Huang, W.Y.C., Lee, H.K., Lian, H.Y., Chou, F.C., Mou, Y., Chu, J. and Chan, J.C. (2011) Steric zipper formed by hydrophobic peptide fragment of Syrian hamster prion protein. Biochemistry, 50, 6815-6823. doi:10.1021/bi200712z
- asset, M., Baldwin, M.A., Lloyd, D.H., Gabriel, J.M., Holtzman, D.M., Cohen, F., Fletterick, R. and Prusiner, S.B. (1992) Predicted alpha-helical regions of the prion protein when synthesized as peptides form amyloid. Proceedings of the National Academy of Sciences of the United States of America, 89, 10940-10944. doi:10.1073/pnas.89.22.10940
- Haigh, C.L., Edwards, K. and Brown, D.R. (2005) Copper binding is the governing determinant of prion protein turnover. Molecular and Cellular Neuroscience, 30, 186- 196. doi:10.1016/j.mcn.2005.07.001
- Harrison, C.F., Lawson, V.A., Coleman, B.M., Kim, Y.S., Masters, C.L., Cappai, R., Barnham, K.J. and Hill, A.F. (2010) Conservation of a glycine-rich region in the prion protein is required for uptake of prion infectivity. The Journal of Biological Chemistry, 285, 20213-20223. doi:10.1074/jbc.M109.093310
- Holscher, C., Delius, H. and Burkle, A. (1998) Overexpression of nonconvertible PrPC delta114-121 in scrapieinfected mouse neuroblastoma cells leads to transdominant inhibition of wild-type PrPSc accumulation. Journal of Virology, 72, 1153-1159.
- Jobling, M.F., Huang, X., Stewart, L.R., Barnham, K.J., Curtain, C., Volitakis, I., Perugini, M., White, A.R., Cherny, R.A., Masters, C.L., Barrow, C.J., Collins, S.J., Bush, A.I. and Cappai, R. (2001) Copper and Zinc binding modulates the aggregation and neurotoxic properties of the prion peptide PrP 106-126. Biochemistry, 40, 8073- 8084. doi:10.1021/bi0029088
- Jobling, M.F., Stewart, L.R., White, A.R., McLean, C., Friedhuber, A., Maher, F., Beyreuther, K., Masters, C.L., Barrow, C.J., Collins, S.J. and Cappai, R. (1999) The hydrophobic core sequence modulates the neurotoxic and secondary structure properties of the prion peptide 106- 126. Journal of Neurochemistry, 73, 1557-1565. doi:10.1046/j.1471-4159.1999.0731557.x
- Jones, E.M., Wu, B., Surewicz, K., Nadaud, P.S., Helmus, J.J., Chen, S., Jaroniec, C.P. and Surewicz, W.K. (2011) Structural polymorphism in amyloids: New insights from studies with Y145Stop prion protein fibrils. The Journal of Biological Chemistry, 286, 42777-42784. doi:10.1074/jbc.M111.302539
- Kourie, J.I. (2001) Mechanisms of prion-induced modific tions in membrane transport properties: implications for signal transduction and neurotoxicity. Chemico-Biological Interactions, 138, 1-26. doi:10.1016/S0009-2797(01)00228-9
- [Kourie, J.I., Kenna, B.L., Tew, D., Jobling, M.F., Curtain, C.C., Masters, C.L., Barnham, K.J. and Cappai, R. (2003) Copper modulation of ion channels of PrP[106-126] mutant prion peptide fragments. Journal of Membrane Biology, 193, 35-45. doi:10.1007/s00232-002-2005-5
- Kuwata, K., Matumoto, T., Cheng, H., Nagayama, K., James, T.L. and Roder, H. (2003) NMR-detected hydrogen exchange and molecular dynamics simulations provide structural insight into fibril formation of prion protein fragment 106-126. Proceedings of the National Academy of Sciences of the United States of America, 100, 14790- 14795. doi:10.1073/pnas.2433563100
- Laganowsky, A., Liu, C., Sawaya, M.R., Whitelegge, J.P., Park, J., Zhao, M., Pensalfini, A., Soriaga, A.B., Landau, M., Teng, P.K., Cascio, D., Glabe, C. and Eisenberg, D. (2012) Atomic view of a toxic amyloid small oligomer. Science, 335, 1228-1231. doi:10.1126/science.1213151
- Lee, S.W., Mou, Y., Lin, S.Y., Chou, F.C., Tseng, W.H., Chen, C.H., Lu, C.Y., Yu, S.S. and Chan, J.C. (2008) Steric zipper of the amyloid fibrils formed by residues 109-122 of the Syrian hamster prion protein. Journal of Molecular Biology, 378, 1142-1154. doi:10.1016/j.jmb.2008.03.035
- Ma, B.Y. and Nussinov, R. (2002) Molecular dynamics simulations of alanine rich β-sheet oligomers: Insight into amyloid formation. Protein Science, 11, 2335-2350. doi:10.1110/ps.4270102
- Norstrom, E.M. and Mastrianni, J.A. (2005) The AGAAAAGA palindrome in PrP is required to generate a productive PrPSc-PrPC complex that leads to prion propagation. The Journal of Biological Chemistry, 280, 27236-27243. doi:10.1074/jbc.M413441200
- Sasaki, K., Gaikwad, J., Hashiguchi, S., Kubota, T., Sugimura, K., Kremer, W., Kalbitzer, H.R. and Akasaka, K. (2008) Reversible monomer-oligomer transition in human prion protein. Prion, 2, 118-122. doi:10.4161/pri.2.3.7148
- Wagoner, V.A. (2010) Computer simulation studies of self-assembly of fibril forming peptides with an Intermediate resolution protein model. Ph.D. Thesis, North Carolina State University, Raleigh.
- Wagoner, V.A., Cheon, M., Chang, I. and Hall C.K. (2011) Computer simulation study of amyloid fibril formation by palindromic sequences in prion peptides. Proteins: Structure, Function, and Bioinformatics, 79, 2132-2145. doi:10.1002/prot.23034
- Wegner, C., Romer, A., Schmalzbauer, R., Lorenz, H., Windl, O. and Kretzschmar, H.A. (2002) Mutant prion protein acquires resistance to protease in mouse neuroblastoma cells. Journal of General Virology, 83, 1237- 1245.
- Zanuy, D., Ma, B. and Nussinov, R. (2003) Short peptide amyloid organization: Stabilities and conformations of the islet amyloid peptide NFGAIL. Biophysical Journal, 84, 1884-1894. doi:10.1016/S0006-3495(03)74996-0
- Zhang, J.P. (2011) Optimal molecular structures of prion AGAAAAGA palindrome amyloid fibrils formatted by simulated annealing. Journal of Molecular Modeling, 17, 173-179. doi:10.1007/s00894-010-0691-y
- Zhang, Z.Q., Chen, H. and Lai, L.H. (2007) Identification of amyloid fibril-forming segments based on structure and residue-based statistical potential. Bioinf, 23, 2218- 2225.