Natural Science
Vol.5 No.3(2013), Article ID:29020,7 pages DOI:10.4236/ns.2013.53045
Analytical expression of concentrations of adsorbed CO molecules, O atoms and oxide oxygen
![]()
Department of Mathematics, The Madura College, Madurai, India; *Corresponding Author: raj_sms@rediffmail.com
Received 12 October 2012; revised 15 November 2012; accepted 27 November 2012
Keywords: Oscillatory Dynamics; Reaction-Diffusion; Boundary Value Problems; Homotopy Perturbation Method
ABSTRACT
A mathematical model of the oscillatory regimes of CO oxidation over plantinum-group metal catalysts are discussed. The model is based on nonstationary diffusion equation containing a nonlinear term related to Michaelis-Menten kinetics of the enzymatic reaction. This paper presents the analytical and numerical solution of the system of non-linear differential equations. Here the Homotopy perturbation method (HPM) is used to find out the analytical expressions of the concentration of CO molecules, O atom and oxide oxygen respectively. A comparison of the analytical approximation and numerical simulation is also presented. A good agreement between theoretical and numerical results is observed.
1. INTRODUCTION
Rate auto-oscillations in a heterogeneous catalytic reaction were first discussed more than two decades ago [1-3]. Some heterogeneous systems which show oscillatory behaviour on catalysts with various structures in a wide pressure range are presently known. One of the most extensively studied heterogeneous catalytic reactions exhibiting oscillatory dynamics is CO oxidation on platinum catalysts.
Various mathematical models are used in detailed analysis of the mechanism of the rate oscillations in catalytic CO oxidation. These models are based on a set of nonlinear ordinary differential equations [4-12]. Microscopic stochastic models by using the Monte Carlo method [13-18] one of the most interesting in theoretical investigation of the dynamics of fluctuating reaction systems. These stochastic models are based on detailed information concerning the elementary steps of the reaction, the structure of the catalyst surface, and the mobility of species in the adsorption layer.
Therefore, the theoretical investigation and explanation of complex dynamic phenomena on a catalyst surface cannot be comprehensive. It is necessary to develop systems of consistent mathematical models describing the evolution of reaction systems on different spatial scales. This would allow the advantages of different classes of mathematical models.
Recently Kurkina and Semendyaeva [3] described the oscillatory dynamical system which includes a Monte Carlo simulation and adsorption layer approximation. To our knowledge no analytical expressions of the concentration of CO molecules, O atom and oxide oxygen have been derived from the system. The purpose of the communication is to derive the analytical expression of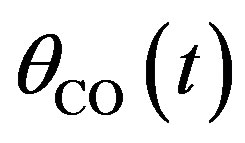 ,
, 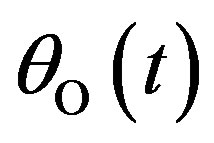 , and
, and 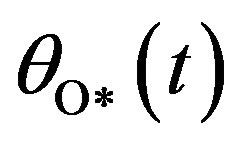 by solving the system of non-linear differential equation using Homotopy perturbation method.
by solving the system of non-linear differential equation using Homotopy perturbation method.
2. MATHEMATICAL FORMULATION OF BOUNDARY VALUE PROBLEM
The oscillatory dynamics of the thickness shear model (TSM) kinetic network will be described using Lattice gas model. In this model any lattice site may be free (*) or occupied by an adsorbed carbon monoxide molecule COads, an adsorbed oxygen atom Oads or an adsorbed oxide oxygen atom . The thickness shear mode (TSM) kinetic network includes the Langmuir-Hinshelwood mechanism [3].
. The thickness shear mode (TSM) kinetic network includes the Langmuir-Hinshelwood mechanism [3].
 (1)
(1)
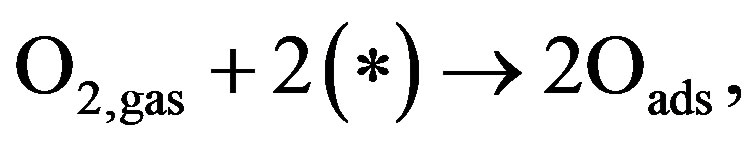 (2)
(2)
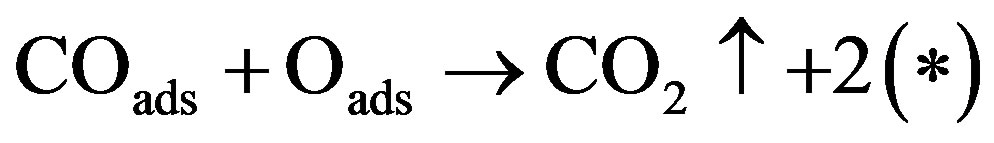 (3)
(3)
and the formation and removal of surface oxide,
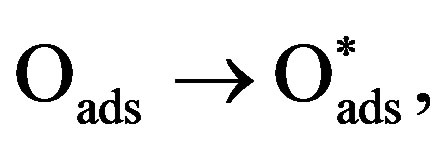 (4)
(4)
 (5)
(5)
Furthermore, we consider the migration of adsorbed species via a vacant-site mechanism:
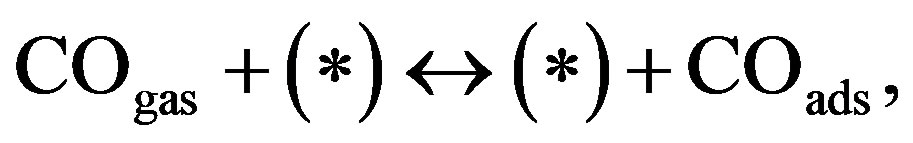 (6)
(6)
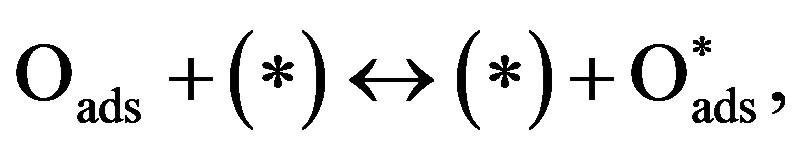 (7)
(7)
 (8)
(8)
Here, 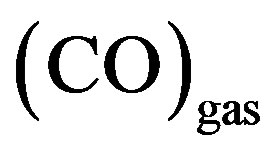 and
and 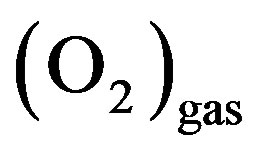 are molecules in the gas phase. Two-site process occurs on adjacent lattice sites. The rate of a two-site process is defined for a pair of sites, and the rate of a one-site process is defined for one site. The surface oxide formation step (4) is viewed as a one-site process, and step (5) is a two-site process. It is assumed that oxide oxygen retains its reactivity (see step (5)) and markedly decreases the activity of the catalyst in reactant adsorption from the gas phase.
are molecules in the gas phase. Two-site process occurs on adjacent lattice sites. The rate of a two-site process is defined for a pair of sites, and the rate of a one-site process is defined for one site. The surface oxide formation step (4) is viewed as a one-site process, and step (5) is a two-site process. It is assumed that oxide oxygen retains its reactivity (see step (5)) and markedly decreases the activity of the catalyst in reactant adsorption from the gas phase.
3. STOCHASTIC AND DETERMINISTIC MODELS
The basic kinetic equations in a multidimensional system will be solved by approximate methods. In Monte Carlo stochastic modelling, state trajectories are constructed for the reaction system in the state space. Stochastic models describe the evolution of a selected lattice fragment at the atomic level. According to the above kinetic network, the variation of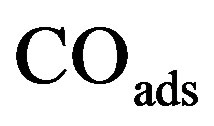 ,
, 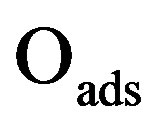 and
and  concentrations are described by a set of following nonlinear differential equations [4]:
concentrations are described by a set of following nonlinear differential equations [4]:
 (9)
(9)
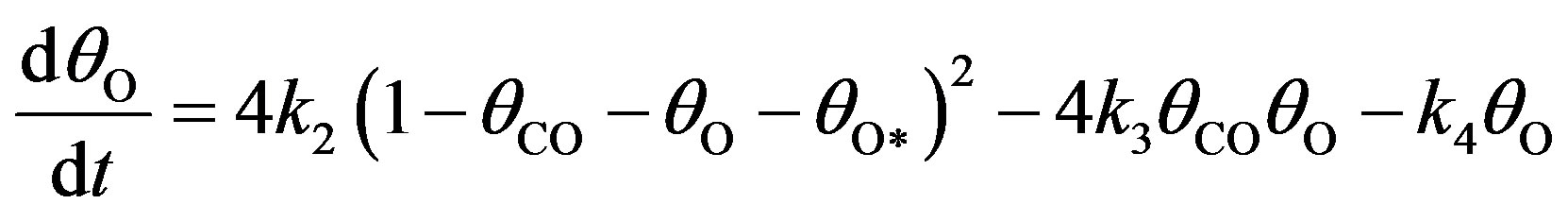 (10)
(10)
 (11)
(11)
The initial conditions are as follows:
 (12)
(12)
Here, 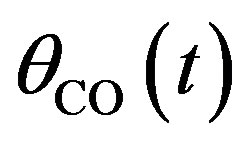 ,
, 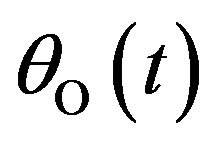 , and
, and 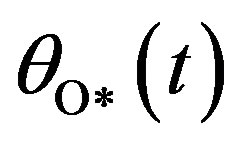 are the concentrations of adsorbed CO molecules and O atoms and oxide oxygen, respectively, and
are the concentrations of adsorbed CO molecules and O atoms and oxide oxygen, respectively, and 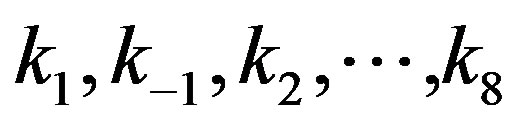 are the rate constants of elementary steps. The normalization conditions are as follows:
are the rate constants of elementary steps. The normalization conditions are as follows:
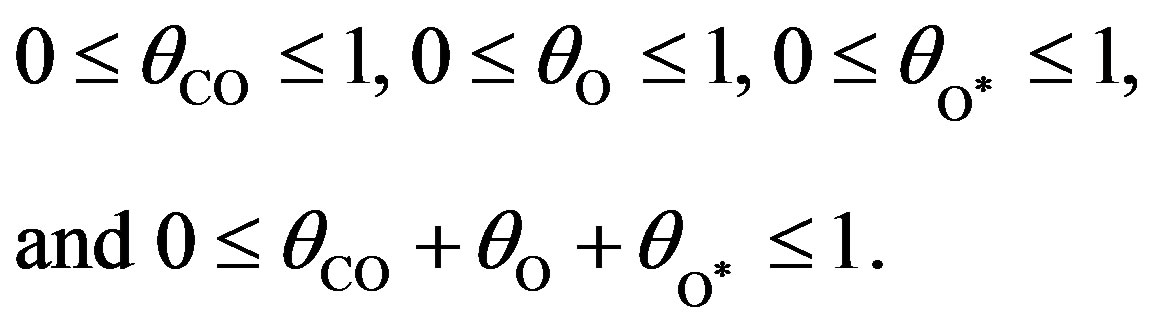 (13)
(13)
To simplify, we can assume that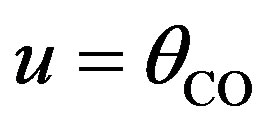 ,
, 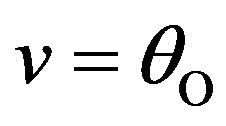 and
and 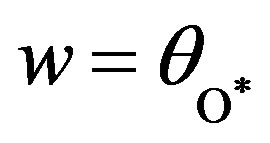 The above Eqs.9-11 become
The above Eqs.9-11 become
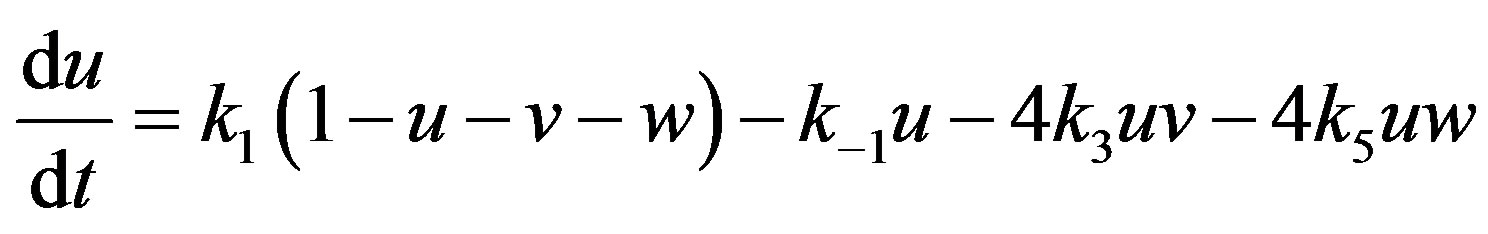 (14)
(14)
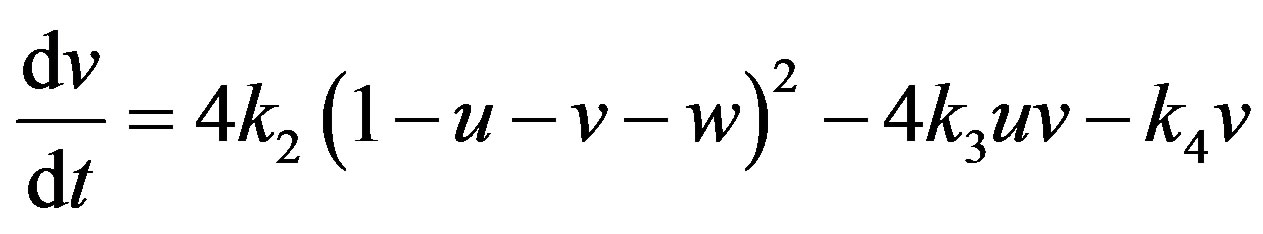 (15)
(15)
 (16)
(16)
Now the boundary condition (12) (or initial conditions) becomes
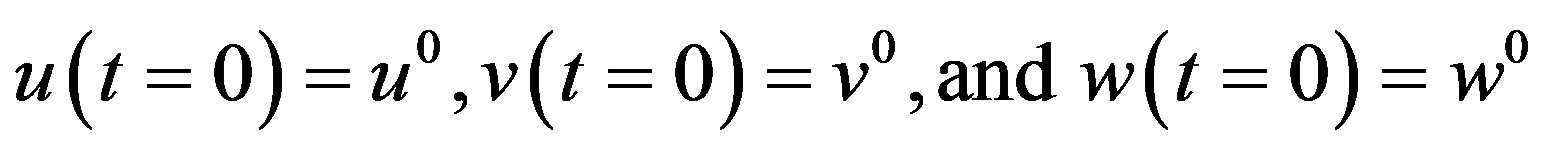
where
 (17)
(17)
4. ANALYTICAL EXPRESSIONS OF CONCENTRATIONS USING HOMOTOPY PERTURBATION METHOD [HPM]
Recently, many authors have applied the HPM to various problems by demonstrating the efficiency of the HPM in handling non-linear structures and solving various physics and engineering problems [16-19]. This method is a combination in topology and classic perturbation techniques. Ji Huan He used the HPM to solve the light hill equation [20], the Duffing equation [21] and the Blasius equation [22]. The idea has been used to solve non-linear boundary value problems, integral equations and many other problems [23-27]. The HPM is unique in its applicability, accuracy and efficiency. The HPM uses the imbedding parameter p as a small parameter and only a few iterations are needed to search for an asymptotic solution. Using this method (see Appendix A), we can obtain the following solution to Eqs.14-16 for the given boundary conditions (Eq.17).
 (18)
(18)
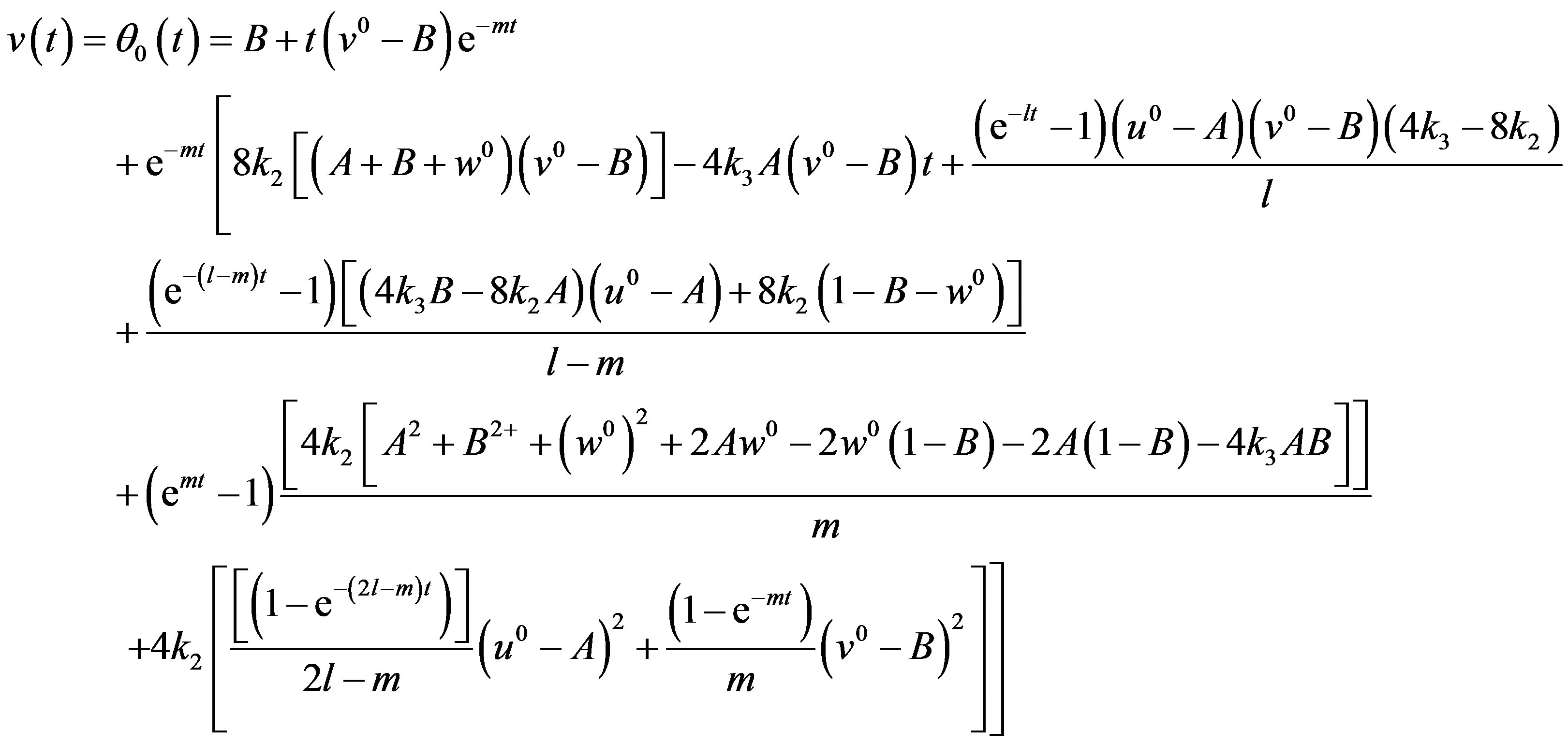 (19)
(19)
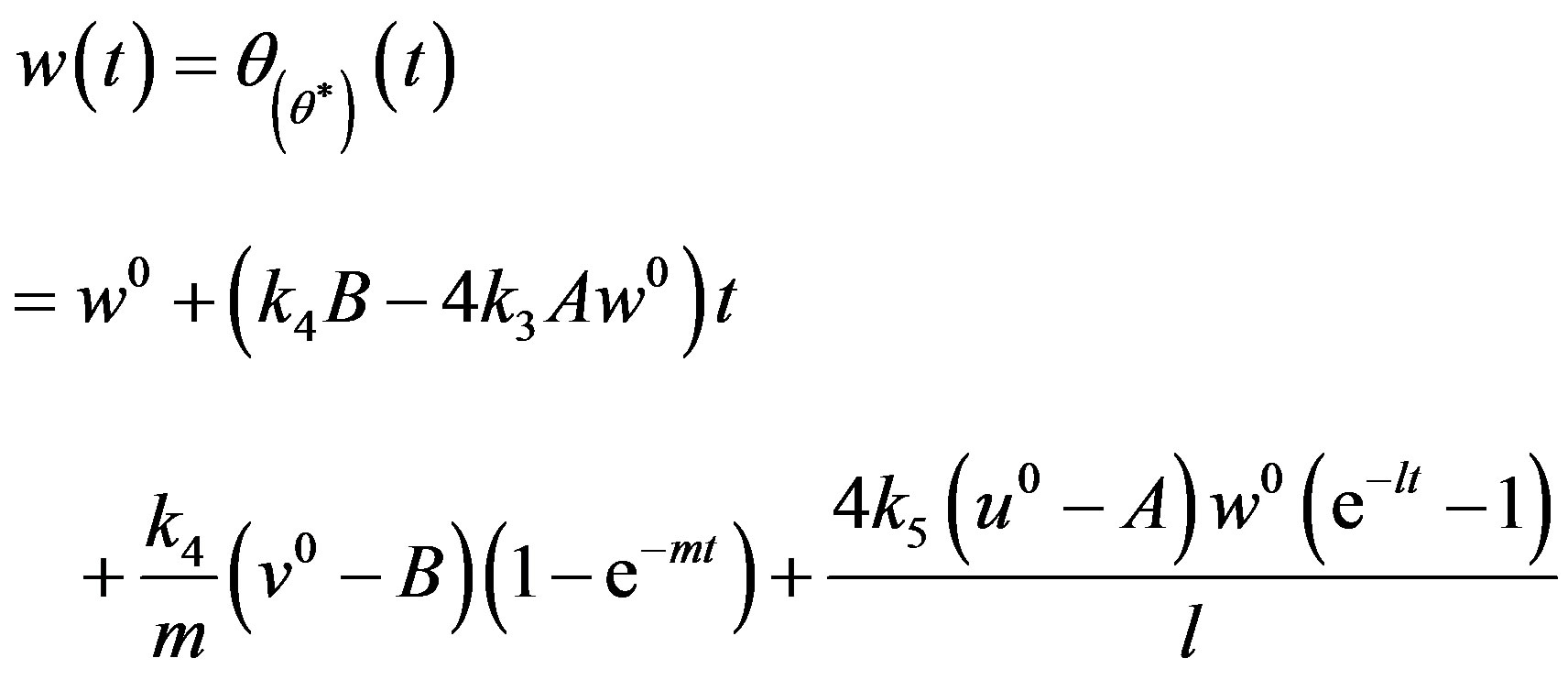 (20)
(20)
where
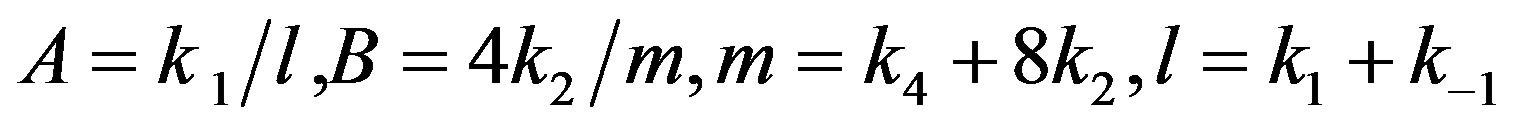 (21)
(21)
The Eqs.18-20 represent the new closed form of analytical expression of concentrations of CO molecules, O atom and oxide oxygen for all values of rate constant and time.
5. ANALYTICAL EXPRESSION OF CONCENTRATION FOR STEADY STATE CONDITION
For the case of steady state, the Eqs.14-16 become
 (22)
(22)
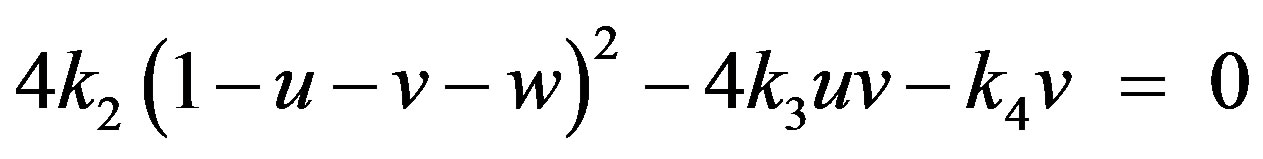 (23)
(23)
 (24)
(24)
Solving the above non-linear algebraic equation by using Maple software, we can obtain the concentration of CO molecule, O atom and oxide oxygen as follows:
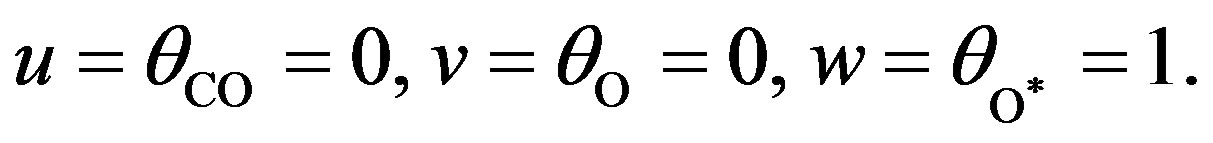 (25)
(25)
6. NUMERICAL SOLUTION
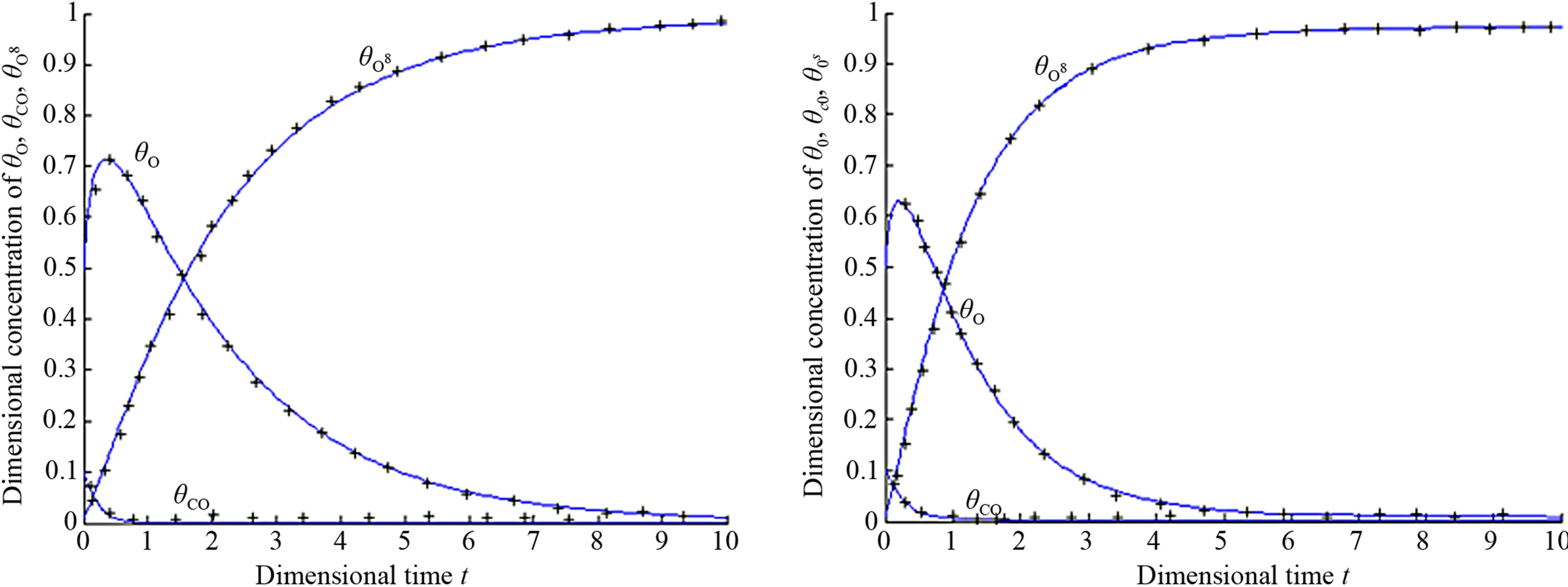
In order to test accuracy of this method the non-linear differential Eqs.14-16 for the boundary conditions (Eq.17) are solved by numerical methods. The function pdex4 in Matlab software was used to solve these equations. It is a function of solving the initial boundary value problems for non-linear differential equations. The Matlab program is also given in Appendix B. The numerical results are also compared with our analytical results in Figures 1(a)-(d). A satisfactory agreement is noted here.
7. DISCUSSION
Figures 1(a)-(d) represent the non steady state concentration of CO molecules u(t) or , O atom v(t) or
, O atom v(t) or 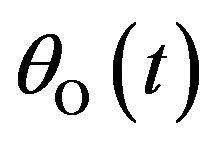 and oxide oxygen w(t) or
and oxide oxygen w(t) or 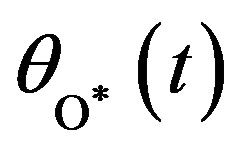 for all values of rate constant and time. From the figure it is evident that the value of the concentration of CO molecule decrease from its initial value of concentration and reaches the steady state value zero when t = 2 sec for all values of rate constant. From the figures it is also inferred that the value of concentration of O atom rises initially and reaches the maximum value when t » 0.5 sec and then decreases gradually. The concentration of O atom attains the steady state value when t = 10 sec. From this figure it is also observed that the concentration of oxide oxygen always increases when time increases and reaches the steady state value 1 when t = 5 sec for all values of rate constant. From this figure it is to conclude that
for all values of rate constant and time. From the figure it is evident that the value of the concentration of CO molecule decrease from its initial value of concentration and reaches the steady state value zero when t = 2 sec for all values of rate constant. From the figures it is also inferred that the value of concentration of O atom rises initially and reaches the maximum value when t » 0.5 sec and then decreases gradually. The concentration of O atom attains the steady state value when t = 10 sec. From this figure it is also observed that the concentration of oxide oxygen always increases when time increases and reaches the steady state value 1 when t = 5 sec for all values of rate constant. From this figure it is to conclude that 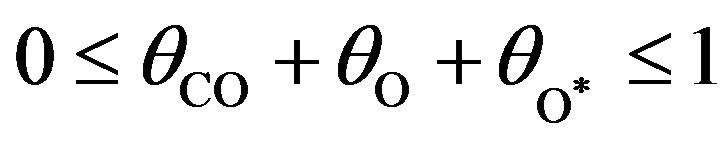 for all values of time and rate constant.
for all values of time and rate constant.
8. CONCLUSION
The theory of the dynamics of catalysts CO oxidation in the frame work of the Thickness shear mode kinetic is described. Approximate analytical solutions to the system of non-linear reaction equations are presented using Homotopy perturbation method. A simple, straight forward and a new method of estimating the concentrations of CO molecules, O atom and Oxide oxygen are derived. This analytical result will be useful to know the behaviour of the reaction system. A good agreement with the numerical simulation data is also noted. The extension of
 (a)
(a)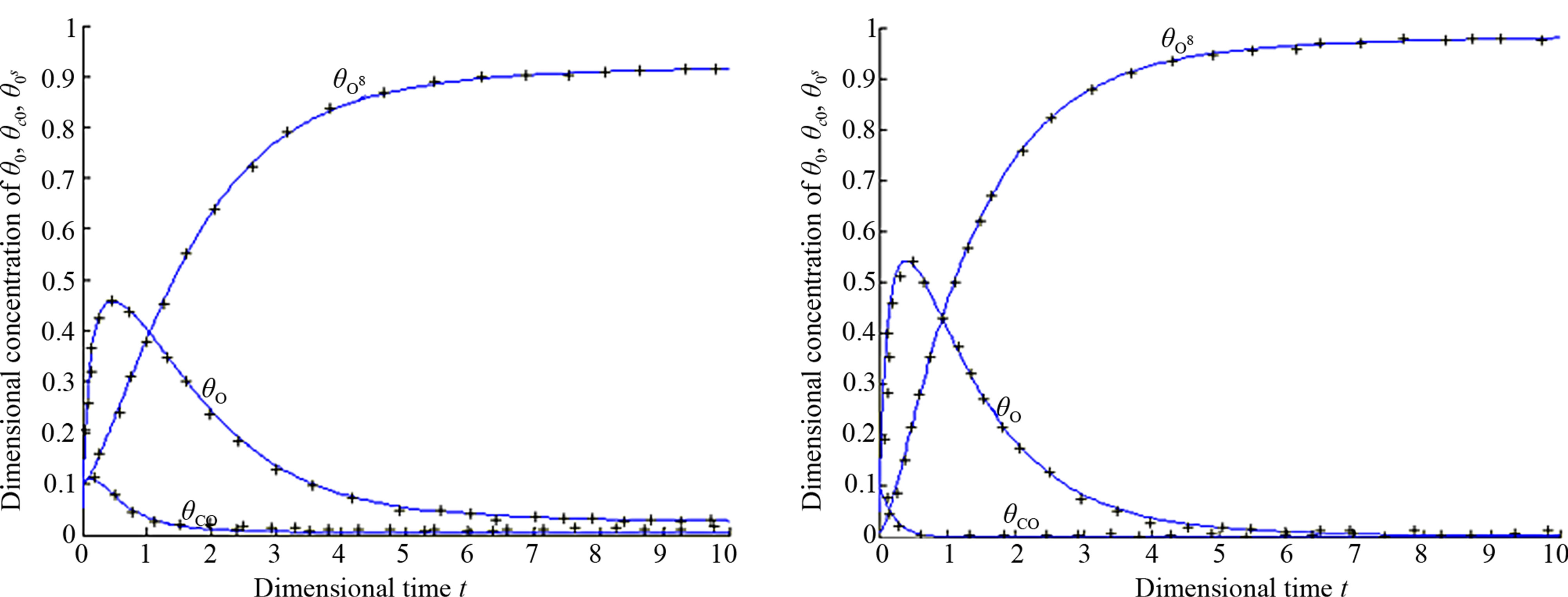 (b)
(b)
Figure 1. Dimensional concentration profile of adsorbed CO molecules θCO, O atom θO and oxide oxygen 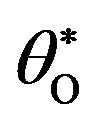 for various values of parameters and initial concentration. (a) k1 = 0.1, k−1 = 2, k2 = 5, k4 = 0.5, k5 = 2, k3 = 1,
for various values of parameters and initial concentration. (a) k1 = 0.1, k−1 = 2, k2 = 5, k4 = 0.5, k5 = 2, k3 = 1,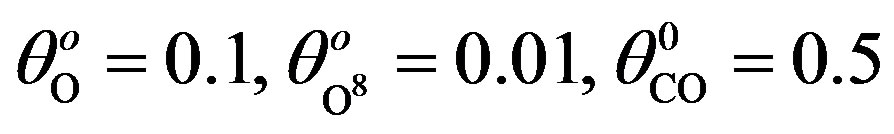 ; (b) k1 = 0.5, k−1 = 2, k2 = 5, k4 = 1, k5 = 2, k3 = 1,
; (b) k1 = 0.5, k−1 = 2, k2 = 5, k4 = 1, k5 = 2, k3 = 1,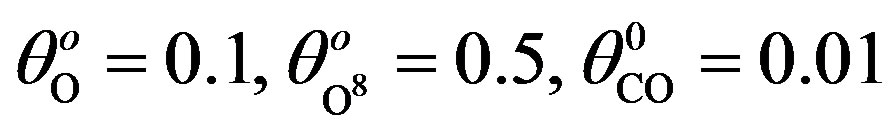 ; (c) k1 = 0.5, k−1 = 1, k2 = 2, k4 = 1, k5 = 2, k3 = 0.1,
; (c) k1 = 0.5, k−1 = 1, k2 = 2, k4 = 1, k5 = 2, k3 = 0.1,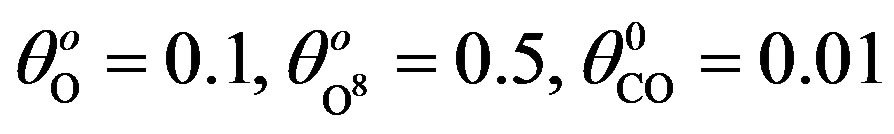 ; (d) k1 = 0.1, k−1 = 4, k2 = 2, k4 = 1, k5 = 2, k3 = 0.1,
; (d) k1 = 0.1, k−1 = 4, k2 = 2, k4 = 1, k5 = 2, k3 = 0.1, .
.
this method with more modelling and simulation procedure to the some of the non-linear reaction diffusion mechanism in biosensor [28] seems possible.
9. ACKNOWLEDGEMENTS
This work is supported by the University Grants Commission (UGC) (Ref. No. F. No. 39 - 58/2010(SR)) and Council of Scientific and Industrial Research (CSIR) (No.01 (2442)/10/EMR-II), Government of India. The authors are thankful to the Secretary, the Principal, The Madura College, Madurai, India for their constant encouragement.
REFERENCES
- Hugo, P. and Jakubith, M. (1972) Dynamic behavior and kinetics of carbon monoxide-oxidation at the platinum catalyst. Chemie Ingenieur Technik, 44, 383-387. doi:10.1002/cite.330440608
- Beusch, H., Fieguth, P. and Wicke, E. (1972) Kinetically and thermally induced instabilities in reaction behavior of individual catalyst particles. Chemie Ingenieur Technik, 44, 445-451. doi:10.1002/cite.330440702
- Kurkina, E.S. and Semendyaeva, N.L. (2005) Oscillatory dynamics of co oxidation on platinum-group metal catalysts. Kinetics and Catalysis, 46, 453-463. doi:10.1007/s10975-005-0098-4
- Sales, B.C., Turner, J.E. and Maple, M.B. (1982) Oscillatory oxidation of CO over Pt, Pd and Ir catalysts: Theory. Surface Science, 114, 381-394. doi:10.1016/0039-6028(82)90692-6
- Eigenberger, G. (1978) Steady state multiplicity of the kinetic model of CO oxidation reaction. Chemical Engineering Science, 33, 1255-1263. doi:10.1016/0009-2509(78)85091-X
- Bykov, V.I., Yablonskii, G.S. and Elokhin, V.I. (1981) Steady state multiplicity of the kinetic model of CO oxidation reaction. Surface Science Letters, 107, 334-338.
- Yablonskii, G.S., Bykov, V.I. and Elokhin, V.I. (1984) Kinetics of model reactions of heterogeneous catalysis. Nauka, Novosibirsk. (in Russian)
- Slin’ko, M.M. and Slin’ko, M.G. (1982) Rate oscillations in heterogeneous catalyzed reactions. Kinetics and Catalysis, 23, 1421.
- Makeev, A.G. and Semendyaeva, N.L. (1996) A note on g-derivative and g-integral. Tatra Mountains Mathematical Publications, 8, 76.
- Slinko, M.M., Kurkina, E.S., Liauw, M.A. and Jaeger, N.J. (1999) Mathematical modeling of complex oscillatory phenomena during CO oxidation over Pd zeolite catalysts. Journal of Chemical Physics, 111, 8105-8114. doi:10.1063/1.480144
- Peskov, N.V., Slinko, M.M. and Jaeger, N.I. (2002) Stochastic model of reaction rate oscillations in the CO oxidation on nm-sized palladium particles. Journal of Chemical Physics, 116, 2098-2106. doi:10.1063/1.1429234
- Zhdanov, V.P. (2002) Monte carlo simulations of oscillations, chaos and pattern formation in heterogeneous catalytic reactions. Surface Science Reports, 45, 231-326. doi:10.1016/S0167-5729(01)00023-1
- Latkin, E.I., Elokhin, V.I. and Gorodetskii, V.V. (2001) Monte carlo model of oscillatory CO oxidation having regard to the change of catalytic properties due to the adsorbate-induced Pt(1 0 0) structural transformation. Journal of Molecular Catalysis A: Chemical, 166, 23-30. doi:10.1016/S1381-1169(00)00468-4
- Elokhin V.I. and Latkin E.I. (1995) Statistic lattice model of oscillating and wave phenomena over the catalyst surface during CO oxidation. Doklady Akademii Nauk, 344, 56-61. (in Russian)
- Elokhin, V.I., Latkin, E.I., Matveev, A.V. and Gorodetskii, V.V. (2003) Application of statistical lattice models to the analysis of oscillatory and auto wave processes on the reaction of carbon monoxide oxidation over platinum and palladium surfaces. Kinetics and Catalysis, 44, 672-700. doi:10.1023/A:1026106509151
- Haario, H. and Seidman, T.I. (1994) Reaction and diffusion at a gas/liquid interface, II. SIAM Journal on Mathematical Analysis, 25, 1069-1084. doi:10.1137/S0036141092234712
- He, J.H. (1999) Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262. doi:10.1016/S0045-7825(99)00018-3
- He, J.-H. (2000) A coupling method of homotopy technique and a perturbation technique for non-linear problems. Computer Methods in Applied Mechanics and Engineering, 35, 37-43. doi:10.1016/S0020-7462(98)00085-7
- He, J.-H. (2003) Homotopy perturbation method: A new nonlinear analytical technique. Applied Mathematics and Computation, 135, 73-79. doi:10.1016/S0096-3003(01)00312-5
- He, J.-H. (2006) Homotopy perturbation method for solving boundary value problems. Physics Letters A, 350, 87- 88. doi:10.1016/j.physleta.2005.10.005
- He, J.-H. (2006) Some asymptotic methods for strongly nonlinear equations. International Journal of Modern Physics B, 20, 1141-1199. doi:10.1142/S0217979206033796
- Kalachev, L.V. and Seidman, T.I. (2003) Singular perturbation analysis of a stationary diffusion/reaction system exhibiting a corner-type behavior in the interval interior. Journal of Mathematical Analysis and Applications, 288, 722-743. doi:10.1016/j.jmaa.2003.09.024
- Li, S.J. and Liu, Y.X. (2006) An improved approach to nonlinear dynamical system identification using pid neural networks. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 177-182.
- Loghambal, S. and Rajendran, L. (2010) Mathematical modeling of diffusion and kinetics of amperometric immobilized enzyme electrodes. Electrochim Acta, 55, 5230-5238. doi:10.1016/j.electacta.2010.04.050
- Meena, A. and Rajendran, L. (2010) Mathematical modeling of amperometric and potentiometric biosensors and system of non-linear equations—Homotopy perturbation approach. Journal of Electroanalytical Chemistry, 644, 50-59. doi:10.1016/j.jelechem.2010.03.027
- Anitha, S., Subbiah, A., Subramaniam S. and Rajendran, L. (2011) Analytical solution of amperometric enzymatic reactions based on Homotopy perturbation method. Electrochimica Acta, 56, 3345-3352. doi:10.1016/j.electacta.2011.01.014
- Ananthaswamy, V. and Rajendran, L. (2012) Analytical solution of two-point non linear boundary value problems in a porous catalyst particles. International Journal of Mathematical Archieve, 3, 810-821.
- Baronas, R., Ivanauskas, F. Kulys, J. (2010) Mathematical modelling of biosensors: An Introduction for chemists and mathematicians. Springer, Dordrecht, Heidelberg, London, New York.
APPENDIX A
Analytical Solution of the Nonlinear Equations Using Homotopy Perturbation Method
In this appendix, we indicate how Eqs.14-16 may be solved using HPM. To find the solution of Eqs.14-16, we first construct a homotopy as follows [16-19]:
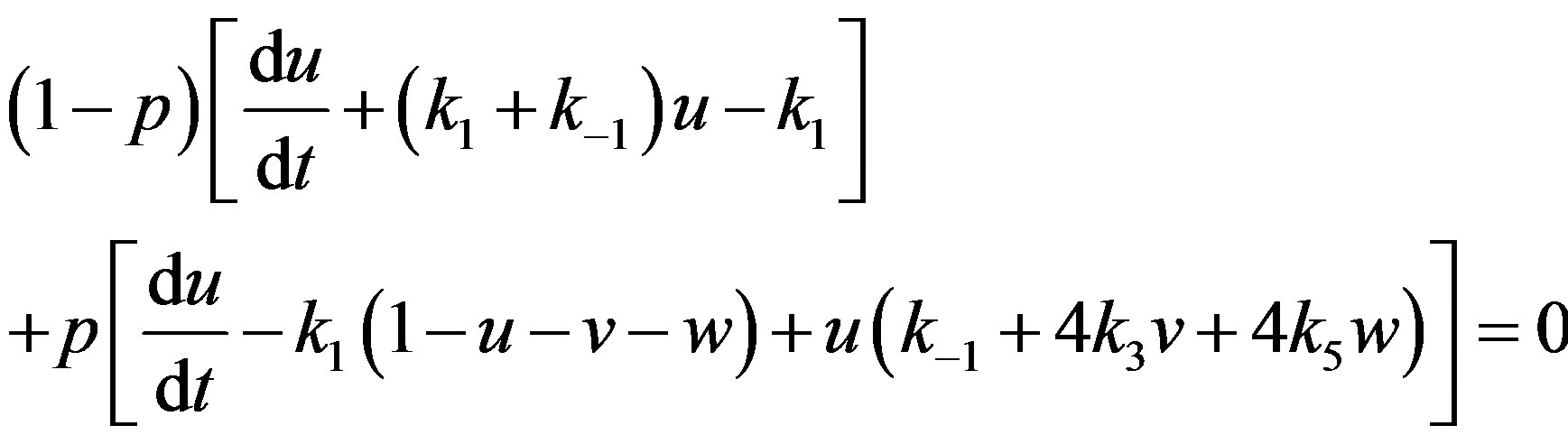 (A1)
(A1)
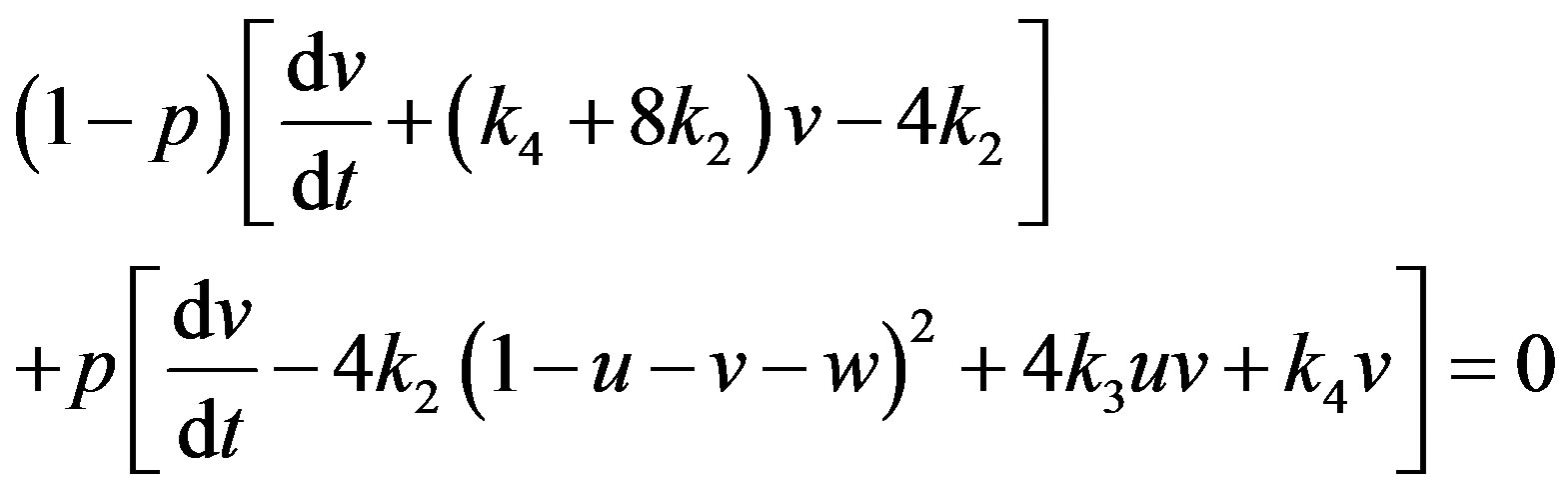 (A2)
(A2)
 (A3)
(A3)
where 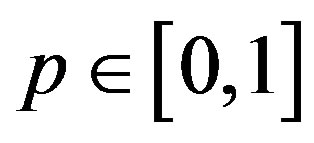 is an embedding parameter. According to HPM, we can first use the parameter p as a “small parameter” and assume that the solution of Eqs.14-16 can be written as a power series in p.
is an embedding parameter. According to HPM, we can first use the parameter p as a “small parameter” and assume that the solution of Eqs.14-16 can be written as a power series in p.
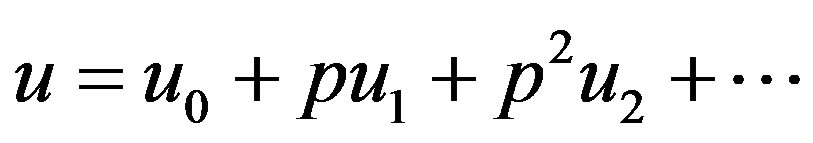 (A4)
(A4)
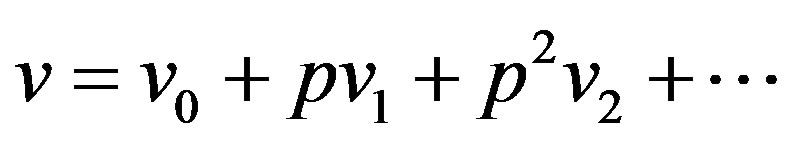 (A5)
(A5)
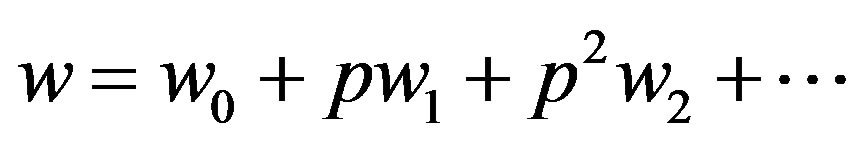 (A6)
(A6)
where 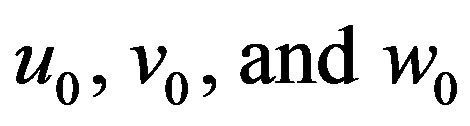 are zero-order solution (initial approximation) and
are zero-order solution (initial approximation) and 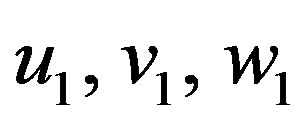 are the first order approximate solution. When p = 0, we get zero-order solution (initial approximate solution or solution of linear terms). Setting p = 1, results in the approximate solution of Eqs.14-16. Substituting Eqs.A4-A6 into Eqs.A1-A3 and comparing the coefficients of like powers of p we obtain the following differential equations.
are the first order approximate solution. When p = 0, we get zero-order solution (initial approximate solution or solution of linear terms). Setting p = 1, results in the approximate solution of Eqs.14-16. Substituting Eqs.A4-A6 into Eqs.A1-A3 and comparing the coefficients of like powers of p we obtain the following differential equations.
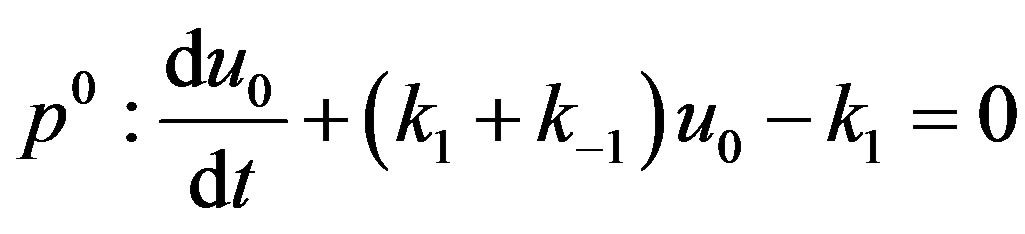 (A7)
(A7)
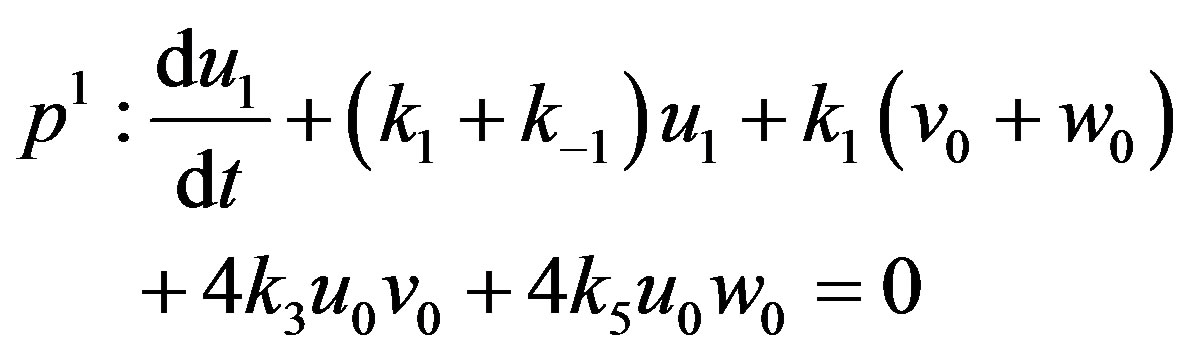 (A8)
(A8)
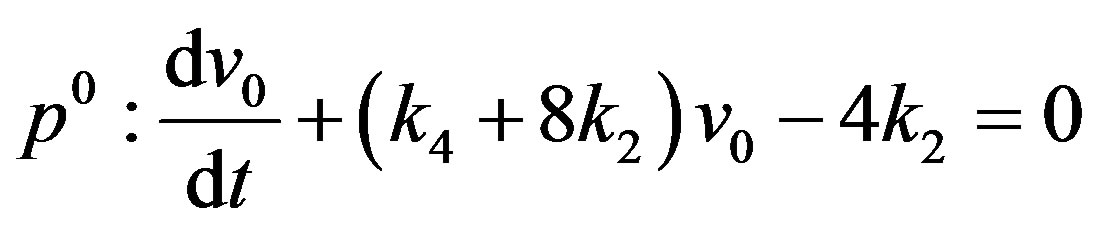 (A9)
(A9)
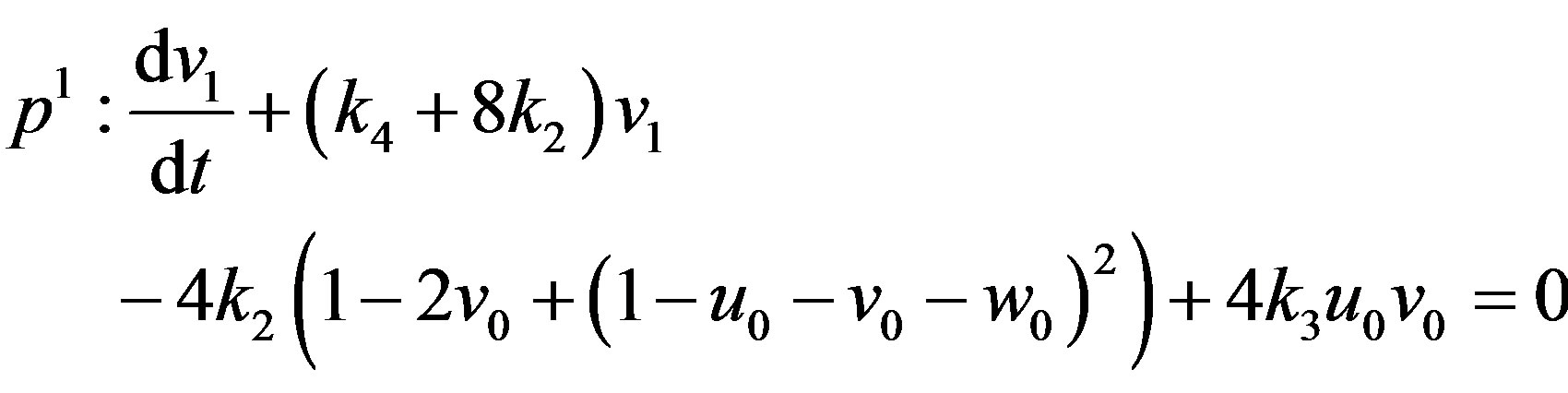 (A10)
(A10)
and
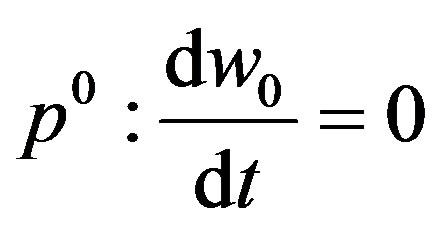 (A11)
(A11)
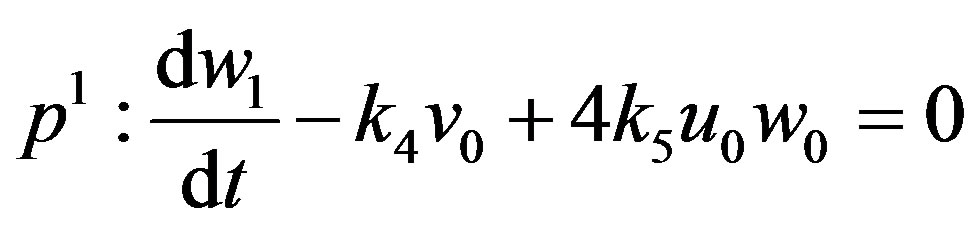 (A12)
(A12)
The initial conditions in Equation (17) becomes
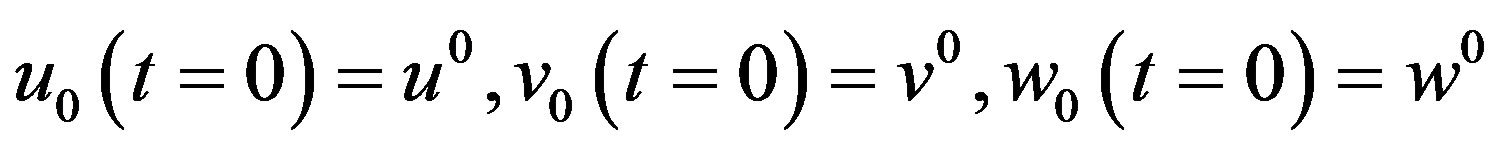 (A13)
(A13)
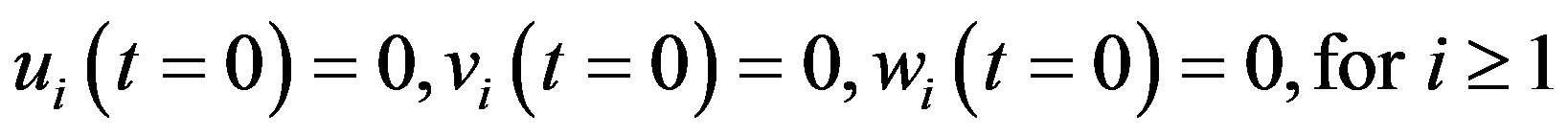 (A14)
(A14)
Solving the equations using the initial conditions Equation (A14), we obtain the following results.
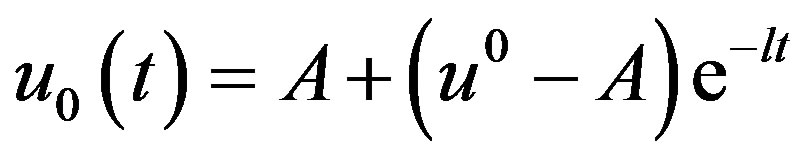 (A15)
(A15)
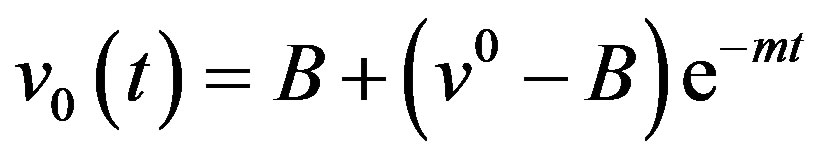 (A16)
(A16)
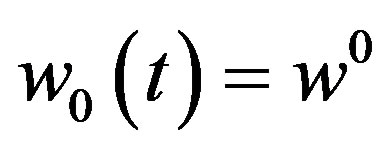 (A17)
(A17)
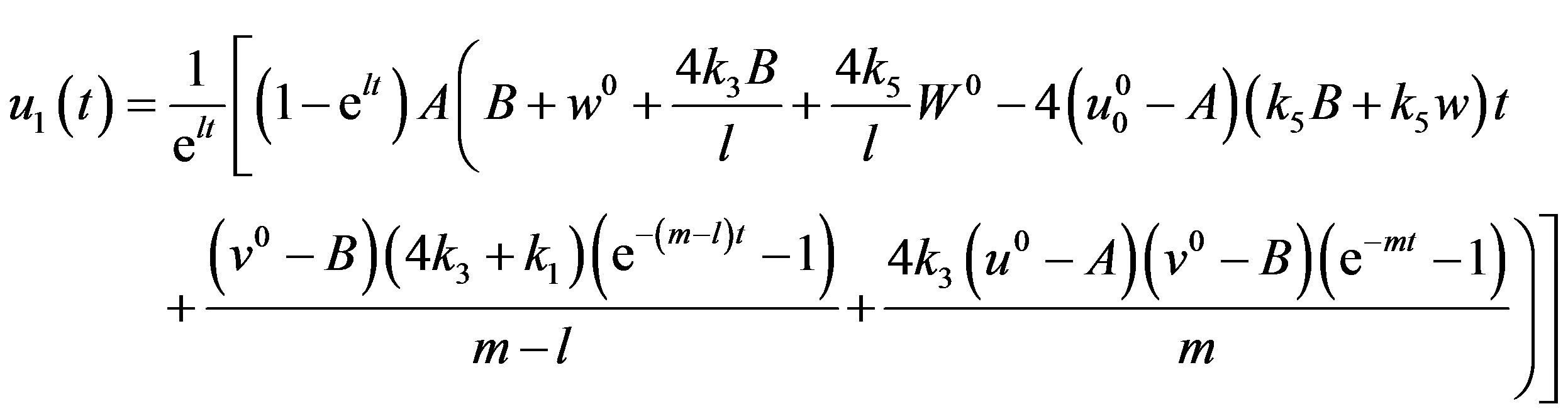 (A18)
(A18)
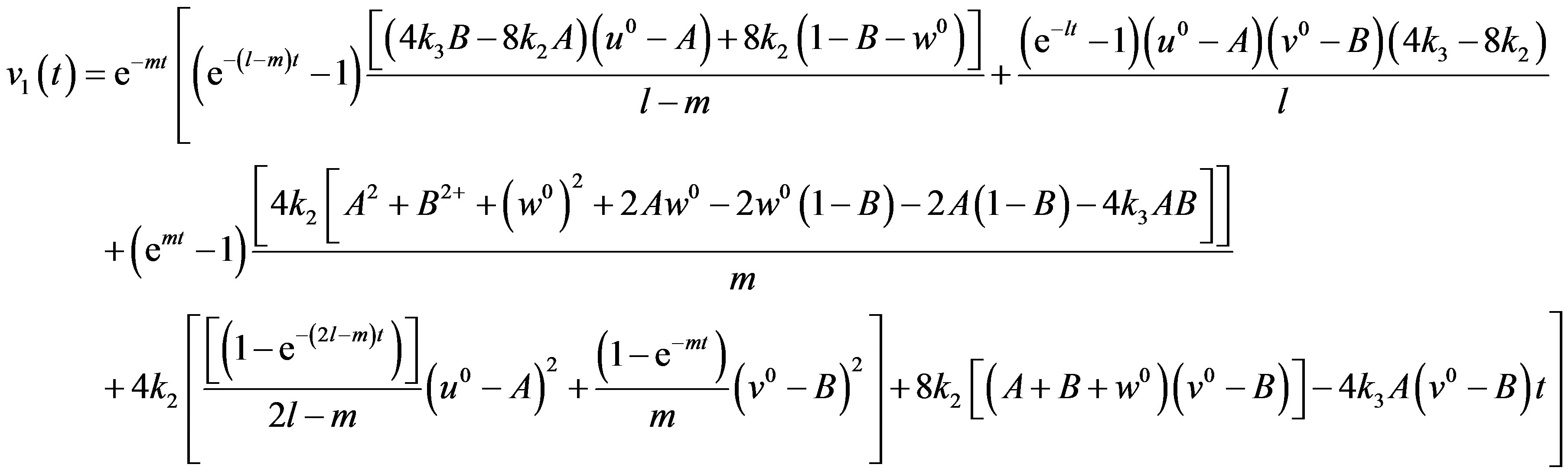 (A19)
(A19)
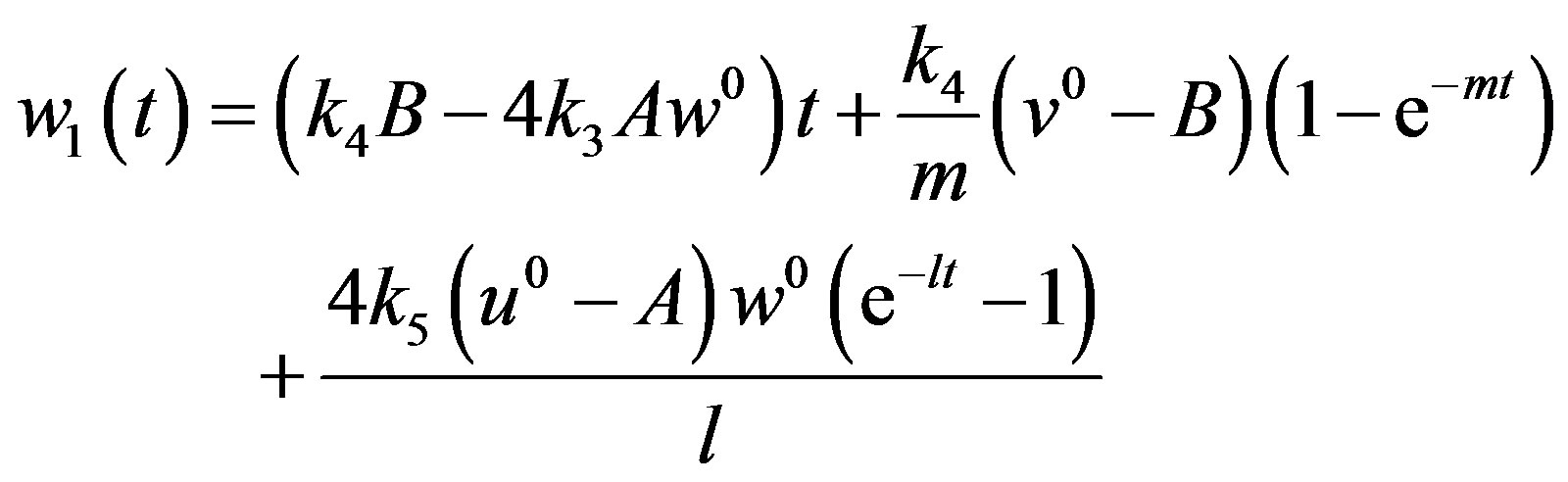 (A20)
(A20)
According to the HPM, we can conclude that
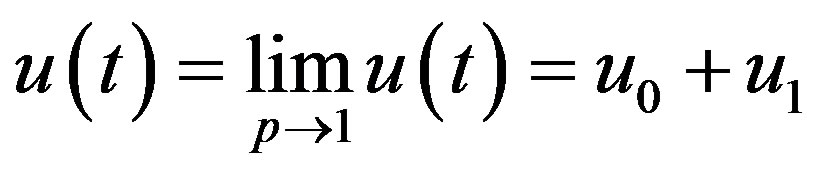 (A21)
(A21)
 (A22)
(A22)
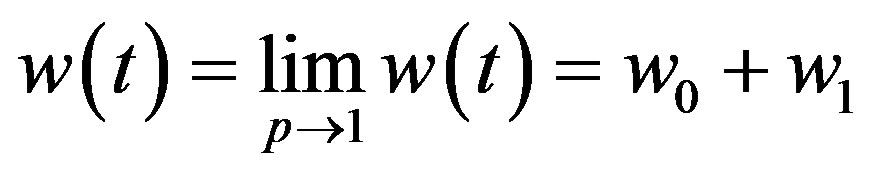 (A23)
(A23)
where
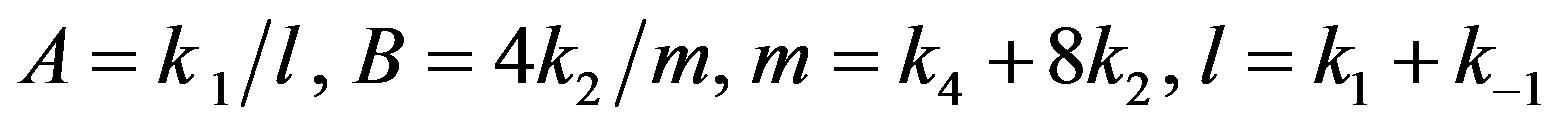 (A24)
(A24)
After putting the Eqs.A15-A20 in the Eqs.A21-A24 we get the Eqs.18-20 in the text.
APPENDIX B
Matlab Program to Find the Numerical Solution of Eqs.14-16
function main1 options = odeset ('RelTol',1e-6,'Stats','on');
%initial conditions T=100;
Xo = [0.1; 0.5; 0.01];
tspan = [0,10];
tic
[t,X] = ode45(@TestFunction,tspan,Xo,options);
toc figure hold on plot(t, X(:,1))
plot(t, X(:,2))
plot(t, X(:,3),'.')
legend('x1','x2','x3')
ylabel('x')
xlabel('t')
return function [dx_dt]= TestFunction(t,x)
a=0.9,b=0.002,k2=0.5,k4=0.03,k5=0.2,k3=1,c=0.1,d=0.01,O=0.5dx_dt(1) =a*(1-x(1)-x(2)-x(3))-b*x(1)-4*k3*x(1)*x(2)-4*k5*x(1)*x(3);
dx_dt(2) =4*k2*(1-x(1)-x(2)-x(3))^2-4*k3*x(1)*x(2)-k4*x(2);
dx_dt(3)=k4*x(2)-4*k5*x(1)*x(3);
dx_dt = dx_dt';
return

