Health
Vol. 4 No. 9A (2012) , Article ID: 23238 , 10 pages DOI:10.4236/health.2012.429108
A new index for measuring aging inequality: An application to Asian countries
![]()
1Department of Statistics, Shahjalal University of Science and Technology, Sylhet, Bangladesh; *Corresponding Author: mtajstat@yahoo.com
2Department of Statistics, Gauhati University, Guwahati, India
Received 25 May 2012; revised 22 June 2012; accepted 30 June 2012
Keywords: Inequality; Aging; Gini Index; Geometric Measure
ABSTRACT
Although the Gini coefficient is an ideal measure of income inequality, it may be applied to measure the aging inequality in a society. In this paper, an attempt has been made to develop alternative measures of aging inequality based on the Gini index. The study uses the secondary population data of Asian countries collected from the international data base, US census Bureau. From the analysis it is observed that the Gini coefficient shows equally sensitivity at all levels. The coefficient is more concern for the country which is closed to the line of absolute equality. For example, the sensitivity level in the Gini coefficient is observed much higher in Israel than in Qatar. The logarithmic transformation of Gini coefficient does not work well because it violates the transfer principle. The Geometric measure of Gini coefficient fails to measure inequality because of violating the transfer principle. On the other hand, the logarithmic transformation of geometric equivalent of the Gini coefficient works better because it shows more sensitivity than the Gini coefficient and satisfies the transfer principle. From the analysis it is also found that the trigonometric measure of Gini coefficient works better than the logarithmic transformation of geometric equivalent of the Gini coefficient because it satisfies transfer principle as well as shows higher sensitivity. Therefore, the trigonometric measure of the Gini coefficient is the best measure of aging inequality among the measures considered in the study.
1. INTRODUCTION
Inequality is a fundamental characteristics of all graduated social parameters and conceptualized as ‘‘the average difference in the status between any pairs relative to the average status’’ [1]. The overall level of inequality in a country, region or population group and more generally the distribution of consumption, income or other attributes is also in itself an important dimension of welfare in that group. Inequality measures can be calculated for any distribution not just for consumption, income or other monetary variables but also for land, other continuous and cardinal variables [2].
Although inequality has long been topic of interest to sociologists, few have bothered to carefully specify what they mean by the term. It is easy, of course, to distinguish perfect equality from a state of inequality. The lack of rigor created difficulty so long as research on inequality emphasized the determinants of individual attainments. But recent efforts to test of hypothesis explaining why some societies are less equal than others have necessitated the adoption of precise measures of inequality, such as the Gini index or the standard deviation [3-5]. In the absence of clear criteria for choosing among the numerous measures of inequality, researchers have usually based their choice on convenience, familiarity, or on vague methodological grounds. Nevertheless, the decision to rank one distribution is more unequal than another has theoretical as well as methodological implications. In fact, the choice of an inequality measures is properly regarded as a choice among alternative definition of inequality rather than a choice among alternative ways of measuring a single theoretical construct [2]. Although measures of inequality are increasingly used to compare nations, cities, and other social units, the properties of alternative measures have received little attention in the sociological literature.
While studying the traditional measures, it is observed that there are basically two shortcomings of traditional measures of population aging. First one is the use of cut off point for old and young age of population. For example, the cut off point of old age is 65 for developed countries and 60 years for developing countries. Similarly, the cut off point of young age is 15 in developing country and 20 in developed country. Second, the accuracy of any measure increases as the observable range of variability increases. The traditional measures consider the change of age cohorts but ignore the total pattern of the age structure of population. It is observed that when the slope of trend line (the regression coefficient) was used to measure of aging that overcome the shortcoming of traditional measures of aging [6].
Nath and Nazrul [7] proposed new indices taking into account both tails of age distribution and investigated the aging process of some Asian countries especially focusing with Bangladesh population. An improved measure of aging speed with its application for Bangladesh population has been proposed by Islam and Nath [8]. Both the studies indicate the aging as one of the emerging problems in Bangladesh.
The Gini index satisfies the basic criteria of scale invariance and the principle of transfers, but two other measures: the coefficient of variation and Theil’s measure are usually preferable. While none of these measures is strictly appropriate for interval-level data, valid comparisons can be made in special circumstances. The social welfare function is considered as an alternative approach for developing measures of inequality and methods of estimation, testing, and decomposition [2].
Though the Gini index of concentration appeal to most economist who rank income distribution in empirical studies, but it was also used in risk analysis and financial theory. Hence it is not surprising to see that the Gini index use as a measure of dispersion in portfolio analysis [9-12].
For variables like age, where utility is neither strictly increasing nor especially relevent, the flat sensitivity of the coefficient of variation makes it appropriate choice [2]. An empirical example of the frequency distribution among 12 occupational categories of US men at selected ages in 1952, 1962 and 1972 was given by Hauser et al. [13]. The Gini index values for US men aged 35 - 44 during the three periods were 0.353, 0.300 and 0.318 respectively, a decline in inequality over time [14].
The measures, the coefficient of variation and the Gini index (G) in statistics texts are only appropriate for variables measured on a ratio scale, like income or age, which have a theoretically fixed zero point [15]. While developing the Gini index of inequality for individual data, it is observed that this index is a simple measure of dispersion and concentration whose fields of application are not confined to income distribution [12].
Optimal grouping techniques (OGT) were first used for income distribution to determine Gini index [16,17]. The OGT were also used to determine the cut off point to age distribution of population. By using OGT to the US population, it is found that the age at which one becomes an older person has dramatically increased. For example, the entry age into oldness was 48.7 years in 1930 while 57.6 years in 2004. The values of Gini index that address in the contex of age distribution of US population was 0.42 in 1950 and 0.36 in 2000 [18]. The existing formula of Gini coefficient was used to develop some alternative measure of economic inequality. The developed measures were applied to the data set of 96 countries on distribution of income from world development indicator [19].
Dalton [20] proposed that measures of inequality ought to increase whenever income is transferred from poorer person to a richer person, regardless of how poor or how rich or the amount of income transferred. Following a suggestion by Pigou [21], Dalton also proposed the condition that a transfer of income from a richer to a poorer person, so long as that transfer does not reverse the ranking of the two, will result in decrease inequity. This is known as the Pigou-Dalton principle [22].
Gini coefficient is the most common statistical index of diversity or inequality in social sciences [2,23]. It is widely used in econometrics as a standard measure of inter-individual or inter-household inequality in income or wealth [9,22,24]. In some studies, Gini coefficient was used to measure variability in levels of mortality among socio-economic groups. It has also been employed for analyses of the variation in degree of people's inequality in the face of death over time and across countries. In some studies, Gini coefficient was used to measure variability in levels of mortality among socio-economic groups [25].
Gini coefficient is computed from distributions of deaths by age in real populations. In order to avoid a bias due to different age structures, a standard population age structure was used for weighting. This approach is the same as that in economics since age at death and population distributions are independent from each other, exactly like income and population in econometrics. The use of Gini coefficient for the analysis of inequality in health in the 1980s, stressed that the individual-based measurement of inequality in health is a way to a universal comparability of degrees of inequality over time and across countries [26].
If we consider a particular distribution of age with n-number of groups or individuals, for same amount of transfer of ages between any two groups, Gini coefficient shows equal sensitivity provided the transfer occurs between two successive groups or individual. Moreover, we can observe that the Gini coefficient shows more concern for countries, which are close to the line of absolute equality. In order to address some of the above mentioned issues, the other indices like variance, coefficient of variation and standard deviation have also been considered, but those have incompetent either because of their total concentration on differences around mean or beacause of violating the Pigou-Dalton condition. The Pigou-Dalton condition implies that any transfer from smaller group (poor group) to higher group (rich group), other thing remaining the same, would always increase the inequality measure. In line with the same one may also think that any transfer from higher group (rich group) to smaller group (poor group), other thing remaining the same, would always decrease the inequality measure [27]. In the above situation, it is necessary to develop some measures or modify the usual formula of Gini coefficient that fulfil the mentioned issues. In this paper, an attempt is made to develop some alternative measures of population aging inequality based on Gini coefficient by using secondary data for Bangladesh and some other selected countries of the world.
2. DATA AND METHOD
The study uses the secondary population data collected from international data base, US census Bureau (www. census.gov/population/data/idb) for 2011. Alternative aging indices have been applied along with conventional aging indices: proportion of older people, proportion of persons aged less than 15 years, proportion of person aged between 15 and 59 years to the Bangladesh population as well as 50 Asian countries. To see the sensitivity level of the alternative measures, special focus is given on Bangladesh, China, India, Israel, North Korea, Nepal, Qatar, Singapore, Sri Lanka and Thailand.
2.1. Gini-Coefficient of Inequality
The Gini coefficient is usually defined in terms of the Lorenz curve [28]. It is the most popular measure of distributional inequality. The Lorenz curve is a graphical device used to represent distributional inequality. The Gini coefficient is a numerical measure of inequality based on the Lorenz curve. Much of the literature is concerned with income inequality. With a few notable exceptions, the result of Gini coefficients also can be applied to other quantitative variables [2]. The Gini coefficient varies between 0 (complete equality) and 1 (complete inequality). There are a number of ways in which the Gini coefficient can be expressed and interpreted. Many researchers derived it as a measure of inequality as it satisfies the axioms (criteria) of an ideal measure. The existing formula for Gini coefficients are as follows:
 (1)
(1)
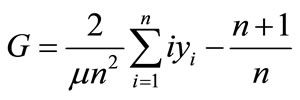 (2)
(2)
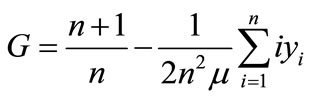 (3)
(3)
where,  is the income/age of the i-th person,
is the income/age of the i-th person,  is the income/age of the j-th person,
is the income/age of the j-th person,  is the average income/age and
is the average income/age and 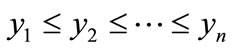 . Eq.1 is a measure of dispersion divided by twice the mean. It is the average absolute difference between all pairs of individuals. Specifically (1) is known as Gini coefficient of mean difference given by Kendall and Stuart [29]. They also define this coefficient as “one half of the average value of absolute differences between all pairs of incomes divided by the mean income”. We will apply this measure to estimate the aging inequality of population. Eq.2 is given by Dasgupta et al. [30] which is more mathematically tractable and computationally convenient for individual level data. Note that the first term in (2) involves a weighted sum of all the scores, where the weight applied to each score is its rank in the distribution. Eq.3 is due to Sen [22] and it shows the income-waiting system in the welfare function behind the Gini coefficient.
. Eq.1 is a measure of dispersion divided by twice the mean. It is the average absolute difference between all pairs of individuals. Specifically (1) is known as Gini coefficient of mean difference given by Kendall and Stuart [29]. They also define this coefficient as “one half of the average value of absolute differences between all pairs of incomes divided by the mean income”. We will apply this measure to estimate the aging inequality of population. Eq.2 is given by Dasgupta et al. [30] which is more mathematically tractable and computationally convenient for individual level data. Note that the first term in (2) involves a weighted sum of all the scores, where the weight applied to each score is its rank in the distribution. Eq.3 is due to Sen [22] and it shows the income-waiting system in the welfare function behind the Gini coefficient.
2.2. Modification of the Formula of Gini Coefficient
Researchers [31-34] in the field of measurement of inequality have always been in the quest of presenting of simple and easy way to calculate Gini coefficient keeping its objective. Milanovic [32] claims that the formula developed by him to measure the inequality is easy to calculate even in using a simple hand calculator. We are trying to modify the existing formula of Gini coefficient. The formulas given in Eqs.1-3 are almost same [35]. Therefore we can choose any one of them for modification. We choose expression (1) for modification among existing formulas. In this paper we are working with the distribution of age. Let 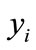 and
and 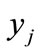 is the share/proportion of persons belonging to one particular age group and we assume that
is the share/proportion of persons belonging to one particular age group and we assume that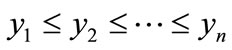 . Thusmean of
. Thusmean of  is
is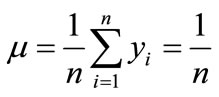 , as
, as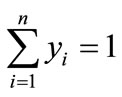 .
.
The Eq.1 can be modified as follows:
 (4)
(4)
Age structure of population can be categoried into three broad groups namely children, active force and elderly.
Since the data set consists of 3 different age groups (i = j = 3), the expression (4) can be rewritten as
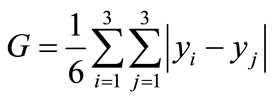 (5)
(5)
After some straight forward simplication, the expression (5) can be written as follows:
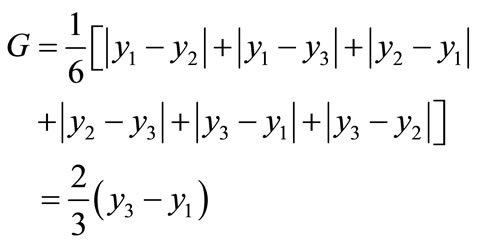
i.e.
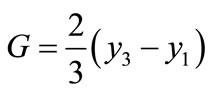 (6)
(6)
Ignoring the multiplier, the expression becomes
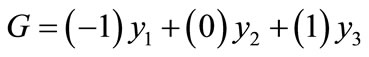 (7)
(7)
where 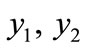 and
and 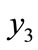 represent the proportion of elderly, the proportion of children and the proportion of active population as these supports for Bangladesh as well as developing countries.
represent the proportion of elderly, the proportion of children and the proportion of active population as these supports for Bangladesh as well as developing countries.
2.3. Logarithmic Transformation of Gini Coefficient
In order to make Gini coefficient more rational in terms of sensitivity, we take the natural logarithm and modify the Eq.4 and Eq.5 as follows:
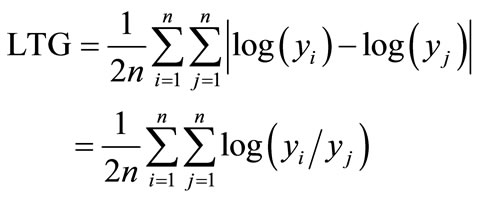
i.e.
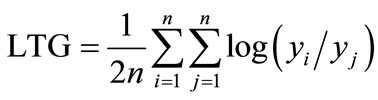 (8)
(8)
For 3 different groups, the expression becomes
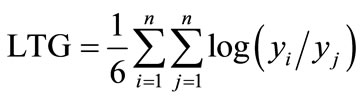 (9)
(9)
Since it violates the transfer principle of an ideal measure of inequality, we should look for other measures.
2.4. Geometric Equivalent of Gini Coefficient
Majumder [19] developed a geometric formula of Gini coefficient based on the Lorenz curve and the line of absolute equality. In order to find a simple and alternative derivation of Gini’s coefficient with robustness and accuracy, we will look forward to some other alternative geometric measure as follows.
From the Figure 1, it is clear that the diagonal line has
divided the rectangle into two equal triangles. For each triangle, base = height = 1, as sum of proportion equal to unity. The area of triangle is
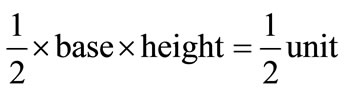
From the figure 1, it shows that the area beyond the Lorenz curve is the sum of area of n small triangles and (n – 1) rectangles. The area of each triangle is:
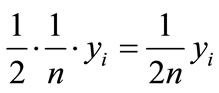
and the sum of n triangles is
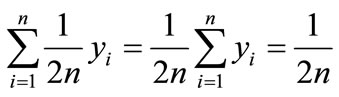 , since
, since 
Similarly, the sum of (n – 1) rectangles is
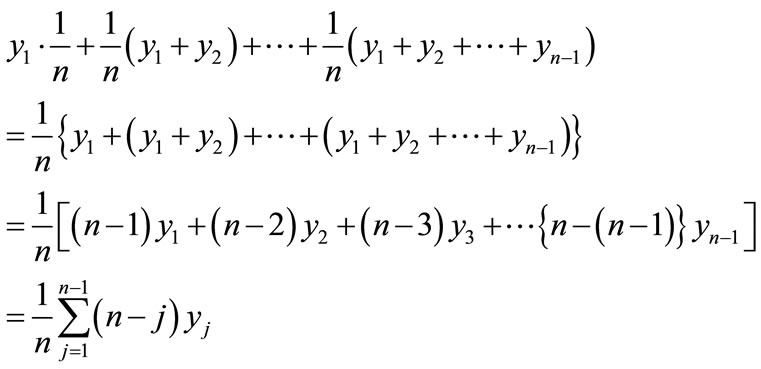
The total area beyond the Lorenz curve is
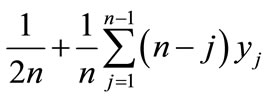
Now the area between the diagonal line and the Lorenz curve is
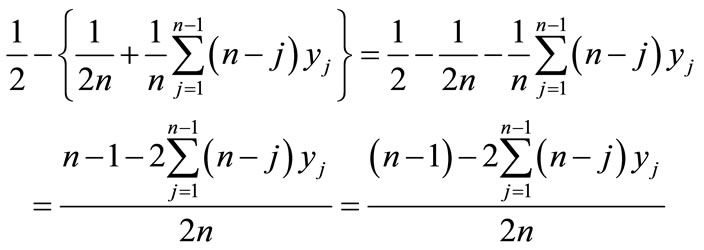 (10)
(10)
We may standardise the above expression (10) with the multiplier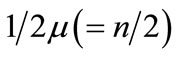 .
.
Therefore Eq.10 may considered as an alternative geometric measure of Gini’s coefficient and written as
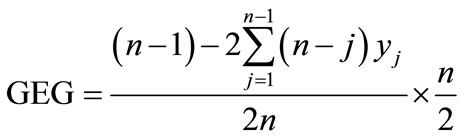
Therefore,
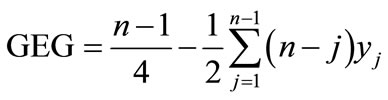 (11)
(11)
For 3 different groups, the expression (11) becomes
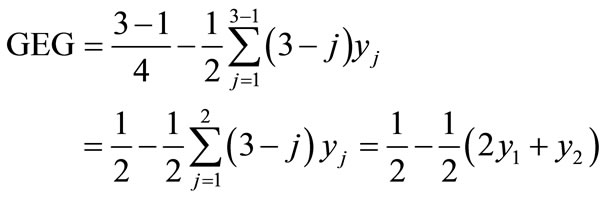
Therefore,
 (12)
(12)
2.5. Logarithmic Transformation of Geometric Equivalent of Gini Coefficient (LTGEG)
Taking logarithm the expression (11) and (12) become
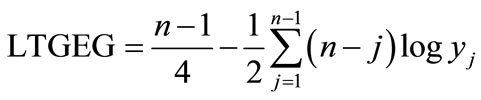 (13)
(13)
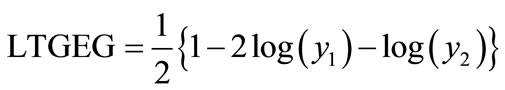 (14)
(14)
2.6. Trigonometric Measures of Gini Coefficient (TMG)
We have developed arithmetic and geometric derivation of Gini coefficient for measuring aging inequality. In order to find simpler and alternative derivation of Gini coefficient to measure aging inequality, it is tried to develop trigonometric measure of inequality. Mojumder [19] has developed Trigonometric measure of Gini coefficient to estimate income inequality. We demonstrate in a formalized manner how to apply the TMG to the age distribution. It is seen that there are n-numbers of rightangled triangles below the Lorenz curve corresponding to n number of individuals/groups. The Cotangent is computed and added them to get a measure of inequality. By looking at the left hand side complementary angle of each right-angled triangle, one can measure cotangent of it, which is nothing but the base of the triangle divided by the perpendicular of it. Therefore, the Trigonometric measure based on cotangent is as follows:
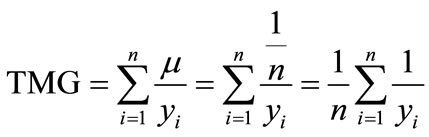 (15)
(15)
We can standardise the expression (15) by substracting n from it and multiplying by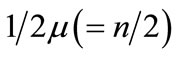 . Thus we have
. Thus we have
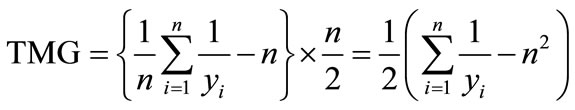
i.e.
 (16)
(16)
For 3 different individuals/groups, the TMG becomes
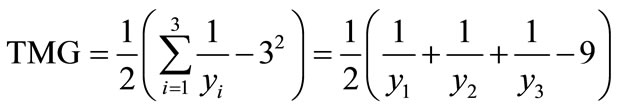
i.e.
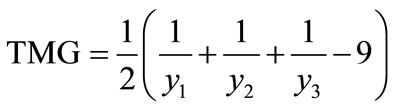 (17)
(17)
3. RESULTS AND DISCUSSION
The developed measures of inequality of population aging have been applied to Bangladesh population as well as some other selected countries. We have chosen those countries of Asia which satisfy the rank order condition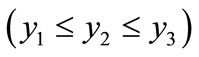 . The results of the measures of inequality of population aging have been displayed in Tables 1 and 2. For convenience of the analysis, it is assumed that
. The results of the measures of inequality of population aging have been displayed in Tables 1 and 2. For convenience of the analysis, it is assumed that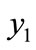 ,
, 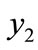 and
and  represent lower end, middle end and higher end of the distribution.
represent lower end, middle end and higher end of the distribution.
3.1. Gini Coefficient (G)
Table 1 shows Gini coefficient (G) values for 50 selected countries in Asia. The G is computed by using the Eq.6. The minimum and maximum observed value of G is 0.439 (in Israel) and 0.837 (in Qatar) respectively which satisfies the hypothetical values (minimum and maximum) of Gini coefficient. Table 2 shows the sensitivity level of indices in responses to 1 percent transfer of ages from one group to another group for few selected countries in Asia. Gini coefficient satisfies Pigou-Dalton condition. When reorganisation of ages takes place from the smaller group to higher group, value of G increases and vice verca. It is equally sensitive within the country in upward direction and downward direction. For example, if we consider Bangladesh, we see that for 1 percent
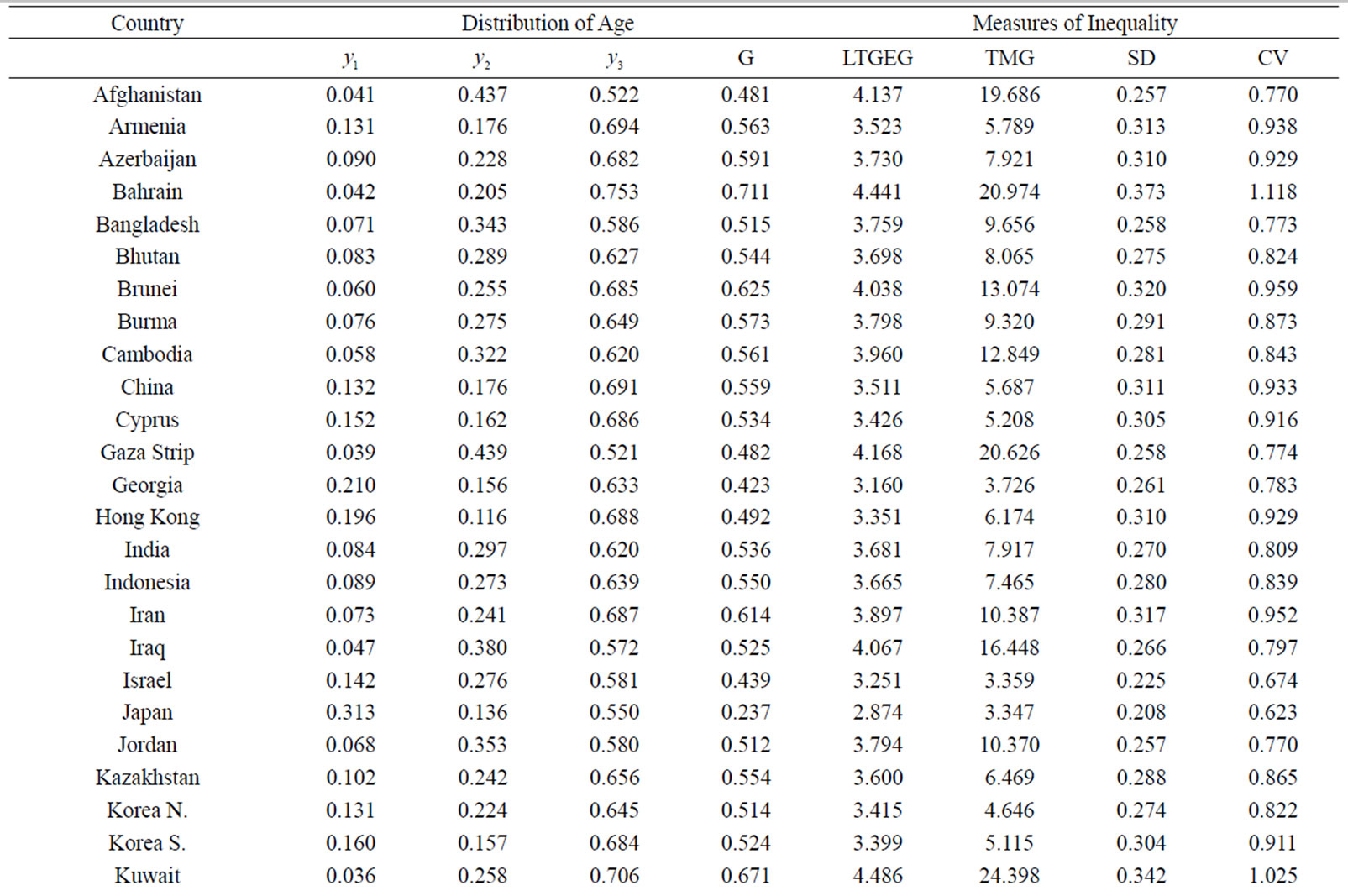
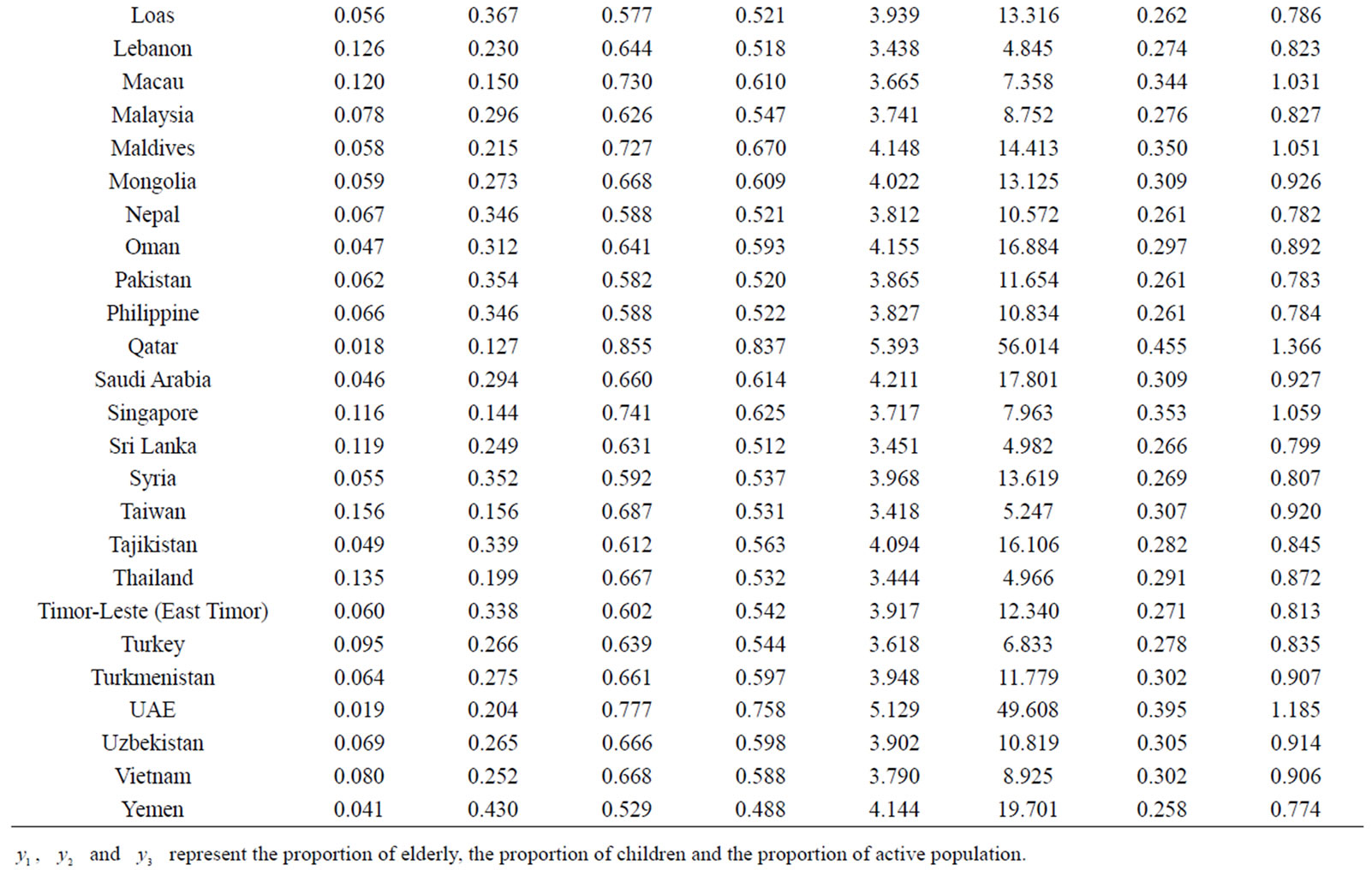
Table 1. Distribution of ages and different measures of inequality.

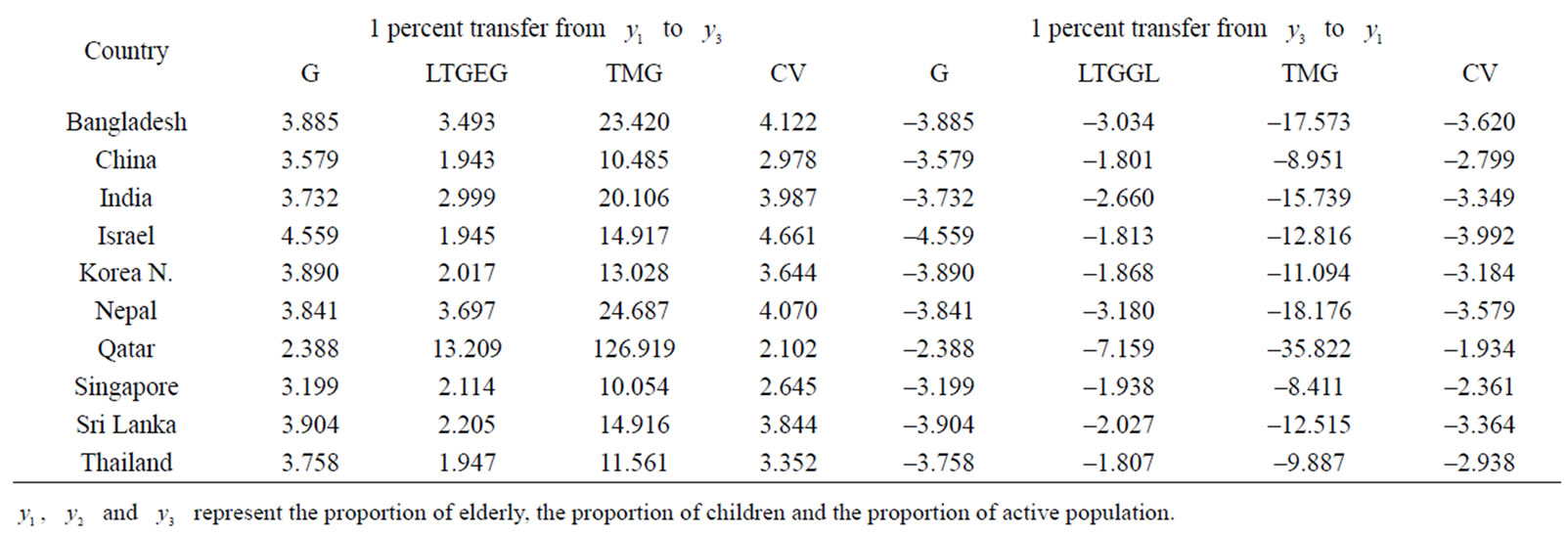
Table 2. Sensitivity of different measures of inequality.
transfer of ages between two consecutive groups G changes by 1.942 percent from Table 2. This is true for all other countries also. It implies that the sensitivity of Gini coefficient within a country or for a particular distribution is constant at all levels. Thus it follows from the property of Gini coefficient that equal transfer of amount between any two successive groups/individuals changes the Gini coefficient in the same manner but for different countries changes may be different.
From the expression (7), it may be realised that the value of G may be higher in a country where share at the lower end are comparatively smaller than the other. Our data support this claim. For example, the G value of Israel, Bangladesh and Qatar are 0.439, 0.515 and 0.837 respectively. Their corresponding share of the lower end are 0.142, 0.071 and 0.018 respectively (Table 1). It is clear from the analysis that the smaller value of G implies more aging society.
It is also observed that changes of G may be higher in a country where the values of G are comparatively smaller than others. For example, when transfer of person (1 percent) belongs to specific age interval takes place between any two consecutive groups in Israel and Singapore, G changes by 2.28 percent and 1.60 percent respectively in these two countries as shown in Table 2. When reorganisations take place between higher group and lower group (Table 2), G changes by 4.56 percent and 3.20 percent respectively in these two countries. It conveys that Gini coefficient is more concern for Israel than for Singapore. Therefore it is said that the changes of Gini coefficient is higher in comparatively equal distribution of ages. If we compare the age distribution of Bangladesh and North Korea (Table 1), we observe that the distribution of age is more equal in the latter than in the former. However changes of G are higher for Noth Korea than Bangladesh (Table 2).
3.2. Logarithmic Transformation of Geometric Equivalent of Gini Coefficient (LTGEG)
It is observed that the minimum and maximum value of the logarithmic transformation of the geometric index (LTGEG) are 3.251 (in Israel) and 5.393 (in Qatar) as displayed in Table 1. The LTGEG is computed by using the expression (14). This index (LTGEG) satisfies Pigoudalton condition. From the sensitivity analysis of the index, it is found that for 1 percent transfer of person belongs to specific age interval from 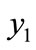 to
to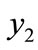 , LTGEG increases by 1.47 percent and 2.61 percent in Israel and India respectively (Table 2). Similarly if we transfer 1 percent people belongs to specific age interval between two consecutive groups in upward direction, the sensitivity of LTGEG increases gradually. It tells us that the index is not equally sensitive at all levels within a country. On the other hand, the index, G is equally sensitive al all level. Also we observe that for 1 percent transfer from the lowest group (
, LTGEG increases by 1.47 percent and 2.61 percent in Israel and India respectively (Table 2). Similarly if we transfer 1 percent people belongs to specific age interval between two consecutive groups in upward direction, the sensitivity of LTGEG increases gradually. It tells us that the index is not equally sensitive at all levels within a country. On the other hand, the index, G is equally sensitive al all level. Also we observe that for 1 percent transfer from the lowest group (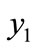 ) to the highest group (
) to the highest group (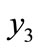 ), changes of LTGEG is higher where the variation (inequality) is higher than other (Table 2). For example, LTGEG increases by 1.95 percent (in Israel) and 3.00 percent (in India). Again if we compare the sensitivity levels of the LTGEG in the two countries, we observe that those are much higher in India than in Israel. It confirms that the index has more concerned for the countries which are far from the line of equality.
), changes of LTGEG is higher where the variation (inequality) is higher than other (Table 2). For example, LTGEG increases by 1.95 percent (in Israel) and 3.00 percent (in India). Again if we compare the sensitivity levels of the LTGEG in the two countries, we observe that those are much higher in India than in Israel. It confirms that the index has more concerned for the countries which are far from the line of equality.
When transfer of ages takes place in downward direction from 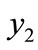 to
to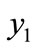 ,
, 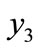 to
to 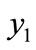 and so on, sensitivity level gradually decreases (Table 2). However, the extent of increase and decrease in both directions are not equal. For example, in India, for 1 percent transfer of person belongs to specific age interval from
and so on, sensitivity level gradually decreases (Table 2). However, the extent of increase and decrease in both directions are not equal. For example, in India, for 1 percent transfer of person belongs to specific age interval from 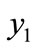 to
to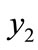 , the LTGEG increases by 2.61 percent (Table 2). On the other hand, for 1 percent transfer of person from
, the LTGEG increases by 2.61 percent (Table 2). On the other hand, for 1 percent transfer of person from 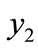 to
to 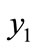 the LTGEG decreases by 2.26 percent (Table 2). From the sensitivity analysis, it is observed that, the index, LTGEG satisfies the Pigou-dalton condition as well as the rank order condition (
the LTGEG decreases by 2.26 percent (Table 2). From the sensitivity analysis, it is observed that, the index, LTGEG satisfies the Pigou-dalton condition as well as the rank order condition ( ).
).
It is also observed that changes of LTGEG are higher, where share at the lower end is comparatively smaller. For example, the changes of LTGEG in Qatar and Israel are 12.60 and 1.47 respectively whereas the share at the lower end are 0.018 and 0.142 for these two countries. Therefore it can be said that share of the elderly population is higher where the sensitivity of index is higher. It is also clear that this index (LTGEG) is more sensitive than the Gini coefficient (G).
3.3. Trigonometric Measures of Gini Coefficient (TMG)
The TMG is computed by using the expression (17). The observed minimum and maximum values of trigonometric measure (TMG) are 3.359 (in Israel) and 56.014 (in Qatar) respectively (Table 1). So this measure (TMG) satisfies the hypothetical values. It shows more sensitivity than any other measures as presented in the paper. For example, for 1 percent transfer of person belongs to specific age interval from 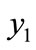 to
to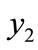 , the index increases by 12.03 percent in Israel, 19.04 percent in India and 125.92 percent in Qatar (Table 2). Qatar has the most unequal distribution of age because of the higher value of the measures (Table 2). Again, when 1 percent transfer of person takes place from
, the index increases by 12.03 percent in Israel, 19.04 percent in India and 125.92 percent in Qatar (Table 2). Qatar has the most unequal distribution of age because of the higher value of the measures (Table 2). Again, when 1 percent transfer of person takes place from 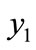 to
to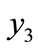 , the changes of TMG are 14.92 percent in Israel, 20.11 percent in India and 126.92 percent in Qatar (Table 2). So it is clear that the sensitivity of TMG is higher when transfer takes place between the lowest group and the highest group than the transfer of consecutive groups. From the sensitivity analysis of the index, one can say that the sensitivity is smaller where the share of the lower end is comparatively higher. This indirectly implies that Israel has more elderly than India and Qatar. Again, it is clear that trigonometric measure (TMG) satisfies the Pigou-dalton condition as well as the rank order condition (
, the changes of TMG are 14.92 percent in Israel, 20.11 percent in India and 126.92 percent in Qatar (Table 2). So it is clear that the sensitivity of TMG is higher when transfer takes place between the lowest group and the highest group than the transfer of consecutive groups. From the sensitivity analysis of the index, one can say that the sensitivity is smaller where the share of the lower end is comparatively higher. This indirectly implies that Israel has more elderly than India and Qatar. Again, it is clear that trigonometric measure (TMG) satisfies the Pigou-dalton condition as well as the rank order condition (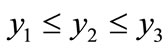 ) of age group. Because when 1 percent transfer of person takes place in upward direction, the TMG increases and in downward direction the index decreases.
) of age group. Because when 1 percent transfer of person takes place in upward direction, the TMG increases and in downward direction the index decreases.
4. CONCLUSION
All the measures (G, LTGEG and TMG) satisfy the rank-order condition (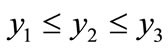 ). An inequality index satisfies the three basic properties: rank-order condition, mean or scale independence and population size independence (Anand, 1997). The two of above properties tell that if every one’s age is changed in the same proportion and similarly if number of individual/person at each age level is changed by the same proportion, the index remain invariant. It is observed that all the measures (G, LTGEG and TMG) discussed here satisfy these properties. Therefore, this measure may be considered as an alternative measure of inequality of aging. Again, from the performance of the measures CV, G and LTGEG, it is clear that LTGEG is better one. Because it overcomes all the difficulties face by other measures CV and G. Again the trigonometric measure (TMG) works very well because it follows all the properties of an ideal measure. Also its sensitivity level is higher than other measures. Considering the criteria of measure and the degree of sensitivity, TMG is the best measure of aging inequality.
). An inequality index satisfies the three basic properties: rank-order condition, mean or scale independence and population size independence (Anand, 1997). The two of above properties tell that if every one’s age is changed in the same proportion and similarly if number of individual/person at each age level is changed by the same proportion, the index remain invariant. It is observed that all the measures (G, LTGEG and TMG) discussed here satisfy these properties. Therefore, this measure may be considered as an alternative measure of inequality of aging. Again, from the performance of the measures CV, G and LTGEG, it is clear that LTGEG is better one. Because it overcomes all the difficulties face by other measures CV and G. Again the trigonometric measure (TMG) works very well because it follows all the properties of an ideal measure. Also its sensitivity level is higher than other measures. Considering the criteria of measure and the degree of sensitivity, TMG is the best measure of aging inequality.
5. ACKNOWLEDGEMENTS
We are grateful to the reviewers of this article who have given valuable suggestions.
![]()
![]()
REFERENCES
- Blau, P.M. (1977) A macrosociological theory of social structure. American Journal of Sociology, 83, 26-54. doi:10.1086/226505
- Allison, P.D. (1978) Measures of inequality. American Sociological Review, 43, 865-880. doi:10.2307/2094626
- Jackman, R. (1974) Political democracy and social inequality: a comparative analysis. American Journal of Sociology, 83, 78-99.
- Hewitt, C. (1977) The effect of political democracy and social democracy on inequality in industrial societies. American Sociological Review, 42, 450-465. doi:10.2307/2094750
- Kelley, J. and Klein, H.S. (1977) Revolution and rebirth of inequality. A theory of stratification in post revolutionary society.
- Kii, T. (1982) A new index for measuring demographic aging. The Gerontologist, 22, 438-442. doi:10.1093/geront/22.4.438
- Nath, D.C. and Islam, M.N. (2009) New indices. An application of measuring the aging process of some Asian countries with special reference to Bangladesh. Population Ageing, 2, 23-39. doi:10.1007/s12062-009-9016-2
- Islam, M.N. and Nath, D.C. (2010) Application of demographic components for measuring the ageing velocity: An explanation with Bangladesh context. Demography India, 39, 297-313.
- Atkinson, A.B. (1970) On the measurement of inequality. Journal of Economic Theory, 2, 244-263. doi:10.1016/0022-0531(70)90039-6
- Shalit, H. And Yitzhaki, S. (1984) Mean gini, portfolio theory and pricing of risky assets. Journal of Finance, 39, 1449-1468. doi:10.1111/j.1540-6261.1984.tb04917.x
- Yitzhaki, S. (1982) Stochastic dominance, mean, variance and Gini’s mean difference. American Economic Review, 72, 178-185.
- Shalit, H. (1985) Calculating the Gini index of inequality for individual data. Oxford Bulletion of Economics and Statistics, 47, 185-189.
- Hauser, R.M., Dickinson, P.J., Travis, H.P. and Kaffel, J.M. (1975) Structural changes in occupational mobility among men in the United States. American Sociological Review, 40, 585-598. doi:10.2307/2094197
- Blau, P.M. (1977) Inequality and heterogeneity. Free Press, New York.
- Mueller, J.H., Schuessler, K.F. and Costner, H.L. (1977) Statistical reasonining in socilogy. 3rd edition, Houghton-Mifflin, Boston.
- Aghevli, B.B. and Mehran, F. (1981) Optimal grouping of income distribution data. Journal of the American Statistical Association, 76, 22-26. doi:10.1080/01621459.1981.10477596
- Davies, J.B. and Shorrocks, A.F. (1989) Optimal grouping of income and wealth data. Journal of Econometrics, 42, 97-108. doi:10.1016/0304-4076(89)90078-X
- D’Albis, H. and Collard, F. (2011) Age grouping and the measurement of population aging’ paper presented in the seminar at IZA. Universities of Montpellier and ParisDauphine for Insightful Discussions.
- Majumder, A. (2007) Alternative measures of economic inequality. Artha Beekshan, 16, 3-20
- Dalton, H. (1920) The measurement of the inequality of income. Economic Journal, 30, 348-361. doi:10.2307/2223525
- Pigou, A.C. (1912) Wealth and Welfare.
- Sen, A. (1973) On economic inequality. Norton, New york. doi:10.1093/0198281935.001.0001
- Kendall, M.G. and Stuart, A. (1969) The advanced theory of statistics. Charles Griffin, London.
- Anand, S. (1983) Inequality and poverty in Malaysia: Measurement and decomposition. Oxford University Press, New York.
- Leclerc, A., Lert, F. and Fabien, C. (1990) Differential mortality: some comparisons between England and Wales, Finland and France, based on inequality measures. International Journal of Epidemiology, 19, 1001-1010. doi:10.1093/ije/19.4.1001
- Illsey, R. and Le Grand, J. (1987) The measurement of inequality in health. In: Williams, A., Ed., Health and economics, Macmillan, London, 13-36.
- Sen, A. (1999) On economic inequality (expended edition with a substantial annexure by James, E. and Amartya Sen). Oxford University Press, New Delhi.
- Ray, J.L. and Singer, J.D. (1973) Measuring the concentration of power in the international system. Sociological Methods and Research, 1, 403-437. doi:10.1177/004912417300100401
- Kendall, M. and Stuart, A. (1977) The advance theory of statistics. Vol. 1. 4th edition, Macmillan, New York.
- Partha, D., Sen, A. and Starrett, D. (1973) Notes on the measurement of inequality. Journal of Economic Theory, 6, 180-187. doi:10.1016/0022-0531(73)90033-1
- Yitzhaki, S. (1994) Economic distance and overlapping of distributions. Journal of Econometrics, 61, 147-159. doi:10.1016/0304-4076(94)90081-7
- Milanovic, B. (1997) A simple way to calculate the Gini coefficient and some implications. Economic Letters, 56, 45-49. doi:10.1016/S0165-1765(97)00101-8
- Lerman, R. and Yitzhaki, S. (1985) Income inequality effects by income source: A new approach and applications to the US. The Review of Economics and Statistics, 63, 151-156.
- Pyatt, D., Chen, C.N. and Fei, J. (1980) The distribution of income by factor components. Quarterly Journal of Economics, 451-473. doi:10.2307/1885088
- Anand, S. (1997) The measurement of income inequality’ in measurement of inequality and poverty. Oxford University Press, New Delhi.


