Engineering
Vol.5 No.5A(2013), Article ID:31798,5 pages DOI:10.4236/eng.2013.55A002
The Optimal Inventory Policy of Production Management
1Department of Applied Mathematics and Business Administration, Chung Yuan Christian University, Chung-Li City, Taiwan
2Department of Banking and Finance, Takming University of Science and Technology, Taipei City, Taiwan
Email: *shyder@cycu.edu.tw, a9601103@gmail.com, shyder@cycu.edu.tw
Copyright © 2013 Shou-Mei Su, Shy-DerLin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 25, 2013; revised March 27, 2013; accepted April 6, 2013
Keywords: EPQ; Raw Materials; Reusable; Imperfect-Quality Items
ABSTRACT
The traditional Economic Production Quantity (EPQ) assumes that the replenishments are instantaneous and the relevant cost only consists of setup cost, stock-holding cost of the finished goods and the purchasing cost of raw materials. As a manager of a manufactory, there is a problem that must be taken into consideration. If the establishment buys all of the raw materials at the beginning, the stock-holding cost for the raw materials should be accounted into the relevant cost. The main purpose of this paper will add the stock-holding cost of raw materials to the EPQ model. Base on this new modified EPQ model, two more useful models are established. One of the new models contains the reusable raw materials instead of the raw materials. The other one considers the stock-holding cost of the raw materials and the imperfect-quality items are considered. We present the optimal cycle length from each of these three models.
1. Introduction
The EPQ model was developed by E. W. Taft [1] in 1918. The EPQ model is a well-known and commonly used inventory control technique. E. W. Taft [1] did not consider the stock-holding cost for the raw materials. In today’s factory, producers are required to prepare raw materials, parts, ... etc. that will be used in the production in order to finish the operation schedule. These prepared raw materials, parts, ... etc. that cause extra stock-holding cost and must be paid by the producers. Therefore, we add the stock-holding cost in the EPQ model. Up to now Lin [2] is the first one to establish an EPQ model taking the stockholding cost of raw materials into consideration.
There are three EPQ models concerning about the total relevant costs in this paper. The first EPQ model (called model 1) is based on Lin’s [2] model that takes the stockholding cost of raw materials into consideration.
We are attempting to reduce the impact of environmental impairment and increasing competition capabilities of business by recycling the repair and waste disposal which were enthusiastically concerned in the past years. So the second EPQ model (called model 2) is based on model 1 and Richter’s [3] ideas. We assume that all the raw materials are reusable raw materials and the stockholding cost of raw materials is taken into consideration. For making sure the quality of products, we assume all the products are screened. So the third EPQ model (called model 3) is based on model 1 and Salameh and Jaber’s [4] ideas. We assume that all products are screened in the process of making. The proportion of imperfect-quality items is fixed and the stock-holding cost of raw materials is taken into consideration.
2. The Models
The mathematical models developed in this study are based on the following definitions and assumptions.
2.1. Definition
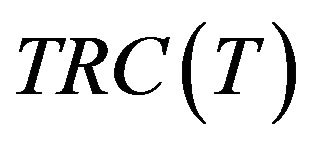 : the annual total relevant cost per unit time;
: the annual total relevant cost per unit time;
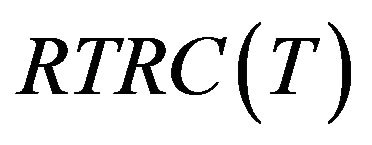 : the annual total relevant cost containing reusable raw materials per unit time;
: the annual total relevant cost containing reusable raw materials per unit time;
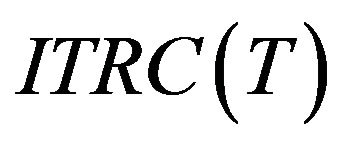 : the annual total relevant cost containing imperfect-quality items per unit time;
: the annual total relevant cost containing imperfect-quality items per unit time;
 : the order size;
: the order size;
S: the setup cost;
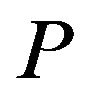 : the production rate;
: the production rate;
 : the demand rate;
: the demand rate;
 : the purchasing cost per unit raw materials;
: the purchasing cost per unit raw materials;
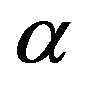 : the reusable rate;
: the reusable rate;
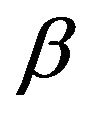 : the percentage of defective items in finished productions;
: the percentage of defective items in finished productions;
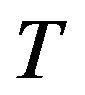 : the cycle length;
: the cycle length;
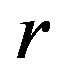 : the discount rate;
: the discount rate;
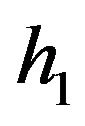 : the stock holding cost of raw materials per item per unit time;
: the stock holding cost of raw materials per item per unit time;
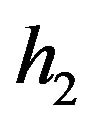 : the stock holding cost of finished products per item per unit time;
: the stock holding cost of finished products per item per unit time;
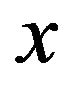 : the screening rate;
: the screening rate;
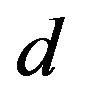 : the unit screening cost;
: the unit screening cost;
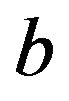 : the selling price of unit imperfect-quality items;
: the selling price of unit imperfect-quality items;
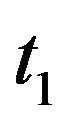 : the screening time.
: the screening time.
2.2. Assumptions
(1) Production rate P is greater than demand rate D(2) Production rate P and demand rate D are known and constant(3) Shortage is not allowed(4) A single item is considered,
(5)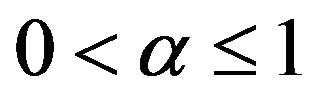 ,
,
(6)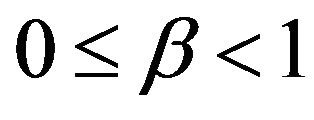 (7) The imperfect-quality items are sold at the end of the screening time(8)
(7) The imperfect-quality items are sold at the end of the screening time(8) 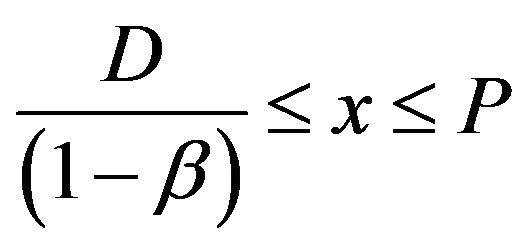 and
and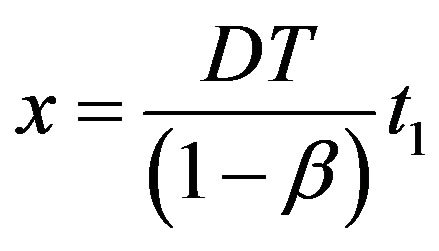 .
.
There are three models considered in this paper.
Model 1: Using the total relevant cost per unit time to find the optimal cycle length (It is shown in Figure 1).
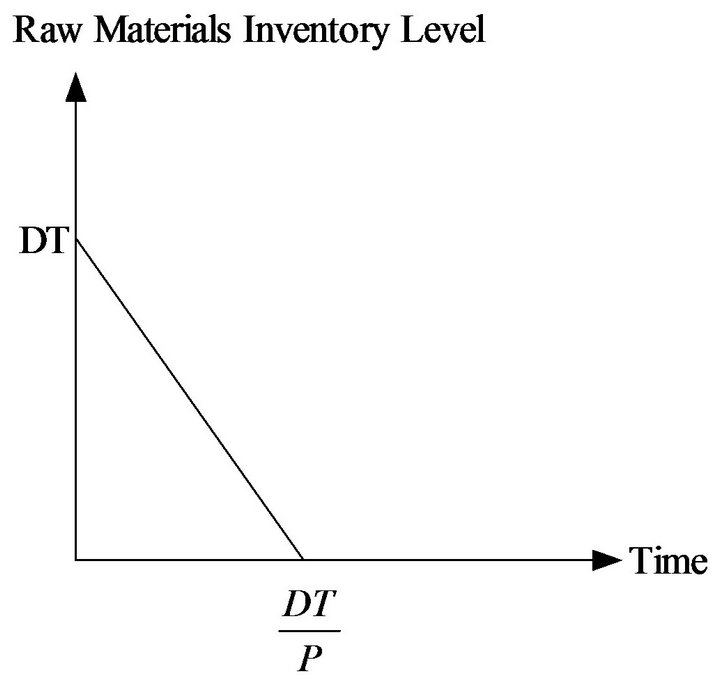
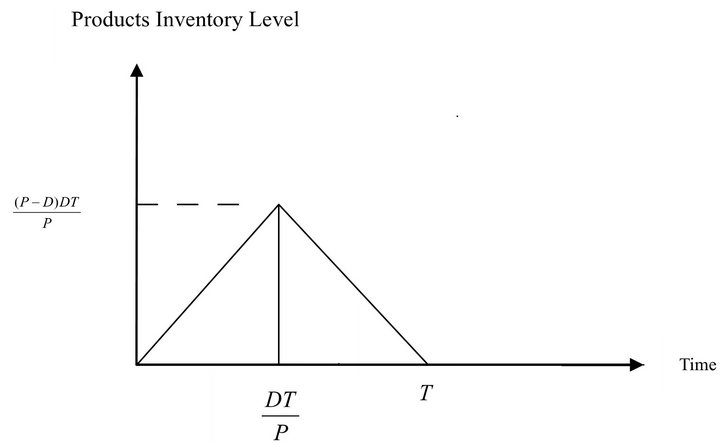
Figure 1. The EPQ model containing raw material.
The annual total relevant cost TRC(T) consists of the following elements:
The ordering cost per unit time 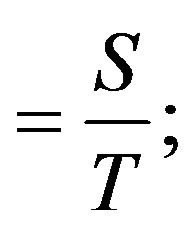 (1)
(1)
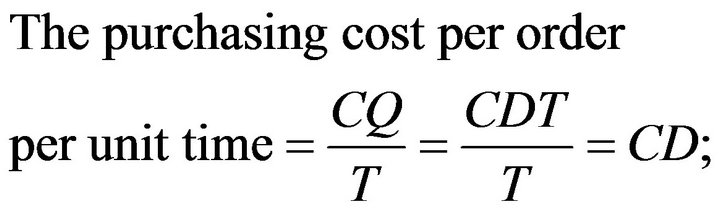 (2)
(2)
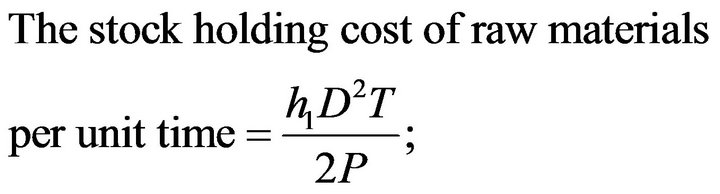 (3)
(3)
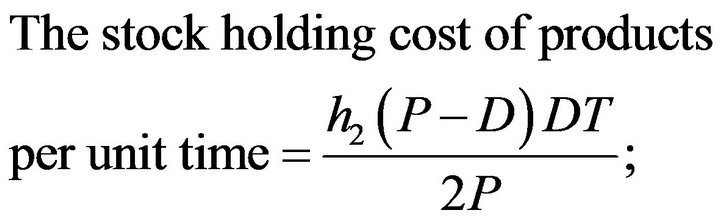
The total relevant cost per unit time can be expressed as follows:
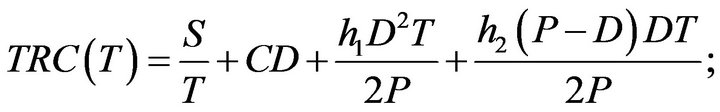
The unique solution of above equation is
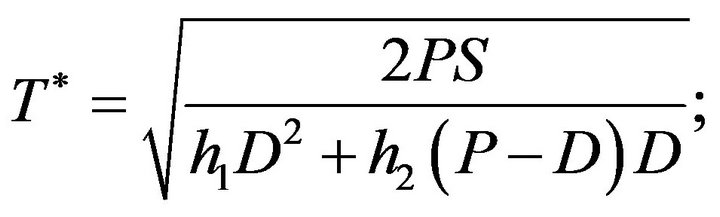
The optimal order quantity is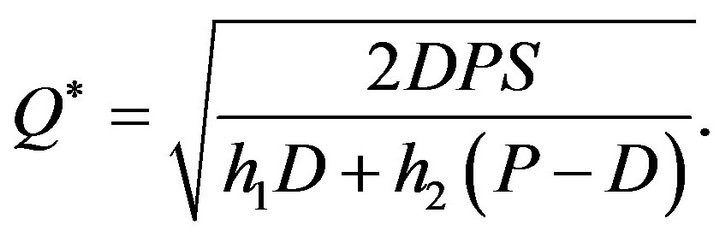
At time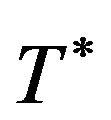 , the
, the 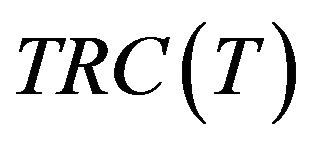 has a global minimum on
has a global minimum on 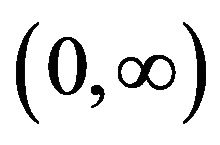
If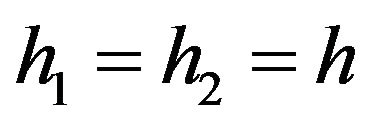 then
then 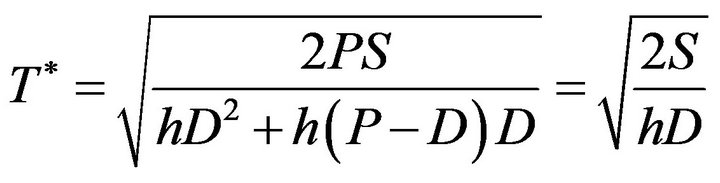
and 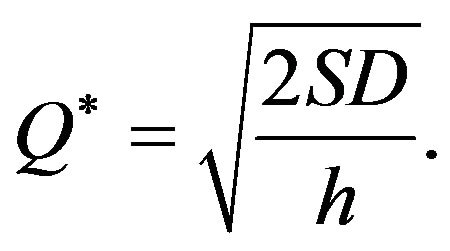
The optimal quantity of this model is the same as that of the traditional EOQ inventory model.
Model 2: Using the annual total relevant cost using 100% reusable raw materials to find the optimal solution (It is shown in Figure 2).
The topic of environmental protection in the world is enthusiastically concerned in recent years. So, by the recycle of the repair and waste disposal productions, we can reduce the impact to environment and increase the ability of competition in business. Also the amount of reused raw materials at the beginning is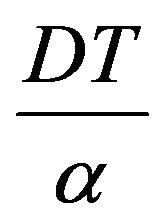 , then the amount of
, then the amount of 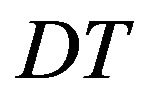 of usable raw materials can be got.
of usable raw materials can be got.
The annual total relevant cost with 100% reusable raw materials 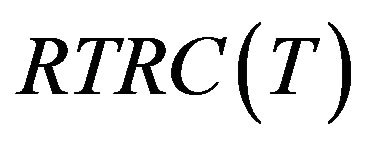 consists of the following elements:
consists of the following elements:
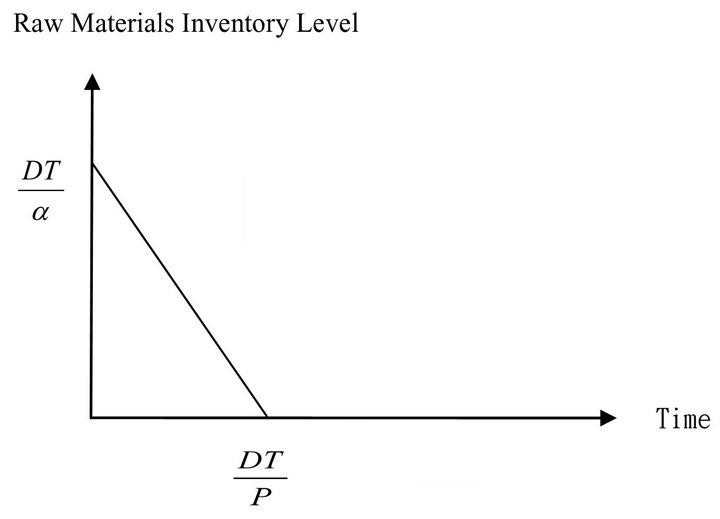
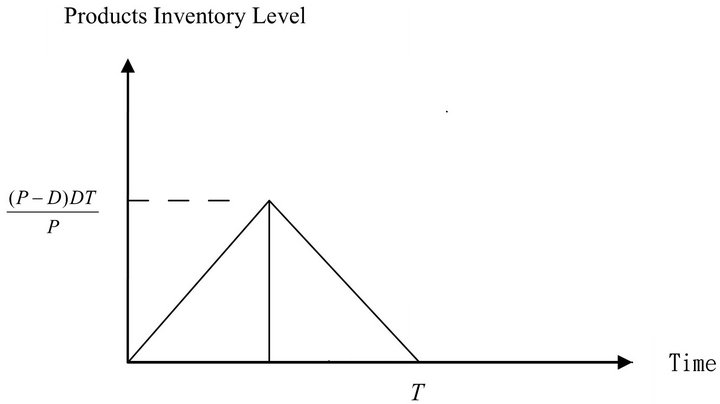
Figure 2. The EPQ model containing reusable raw material.
The setup cost per unit time 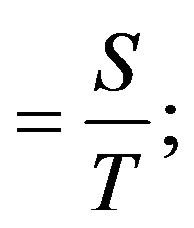
The purchasing cost per order per unit time 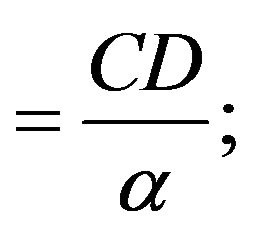
The stock holding cost of raw materials per unit time
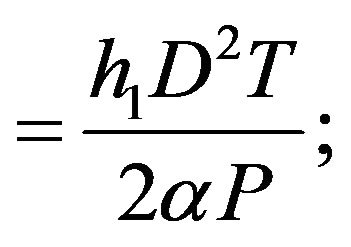
The stock holding cost of products per unit time
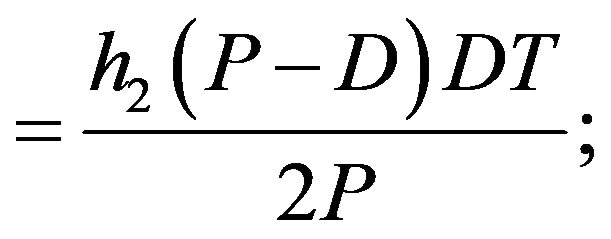
The total relevant cost per unit time can be expressed as follows:
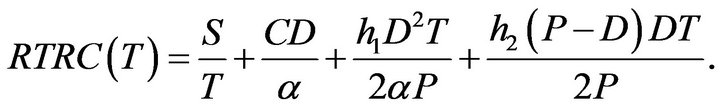
And the first and second derivatives of  are
are
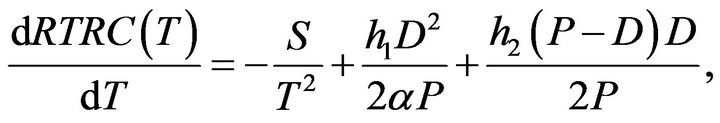
and
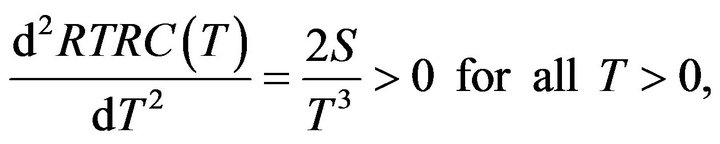 respectively Set
respectively Set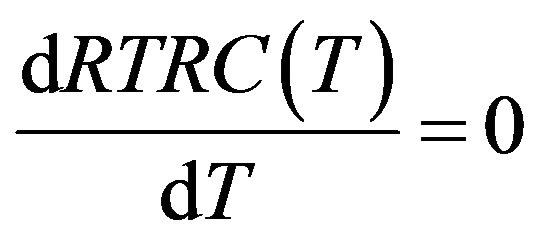 , then we have the following result:
, then we have the following result:
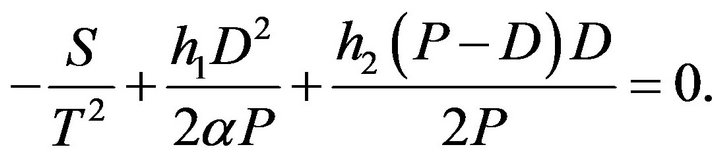
The unique solution of above equation is
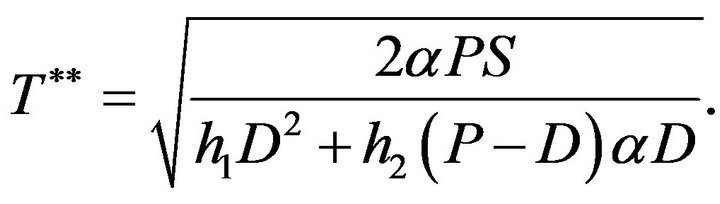
At time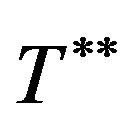 , the
, the 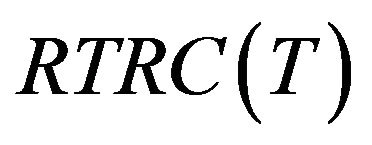 has a global minimum on
has a global minimum on  since
since 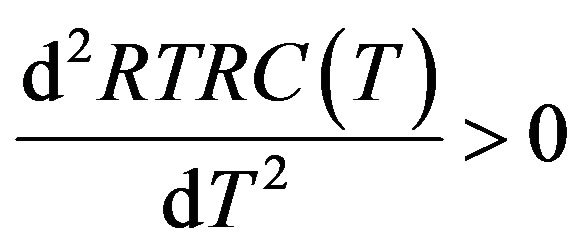 for all
for all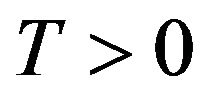 .
.
Model 3: Using the annual total relevant cost containing imperfect-quantity items to find the optimal cycle length (It is shown in Figure 3).
This is an EPQ model by accounting for fixed percentage imperfect-quality items and considering the issue that poor quality items were sold as a single batch with lower price than it of good quality items at the end of the screening time.
The annual total relevant costs 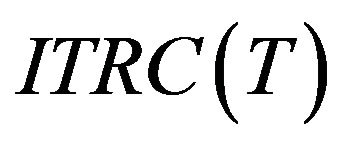 consists of the following elements:
consists of the following elements:
The ordering cost per unit time 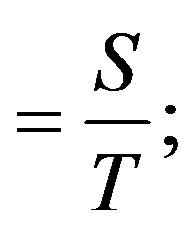
The purchasing cost per order per unit time 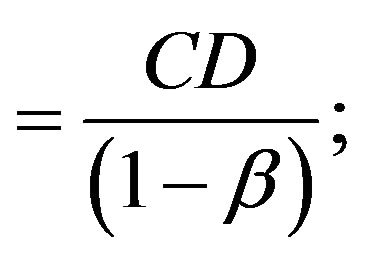
The screening cost per unit time 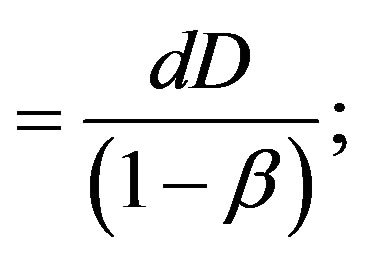
The stock holding cost of raw materials per unit time
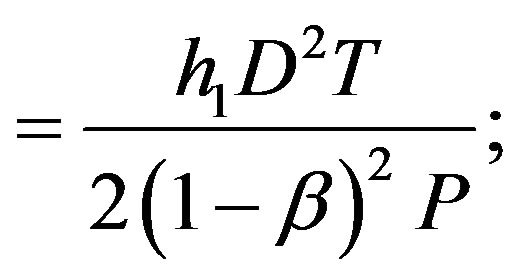
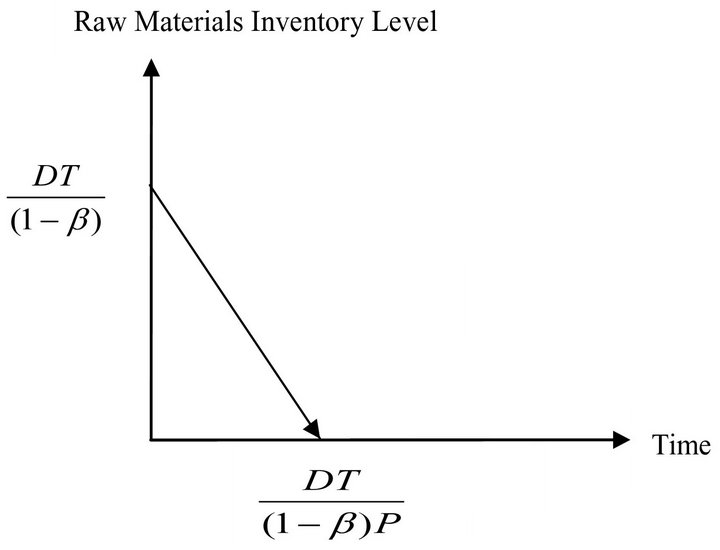
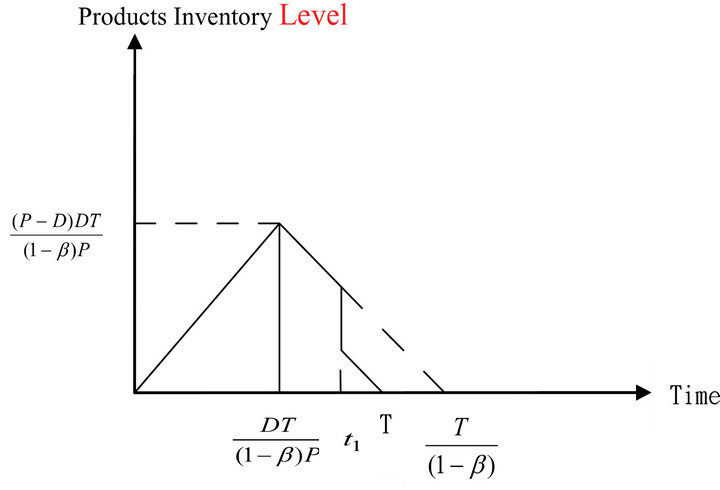
Figure 3. The EPQ model containing imperfect-quality items.
The stock holding cost of products per unit time
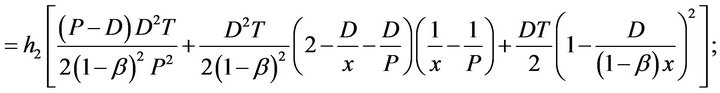
The money earned from selling the imperfect-quality items per unit time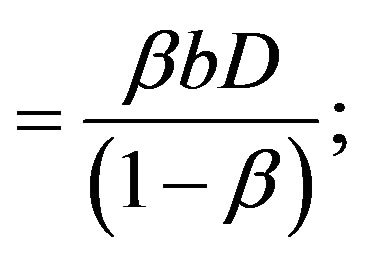
The total relevant cost per unit time can be expressed as follows:
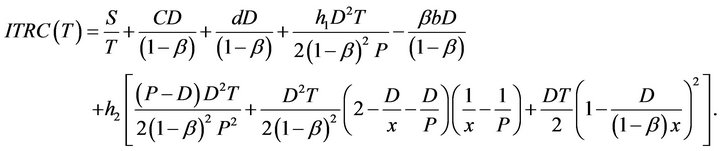
And the first and second derivatives of 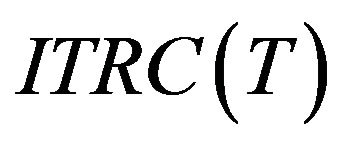 are
are
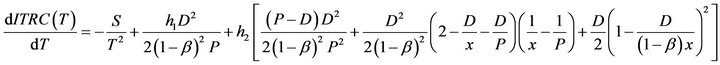 .
.
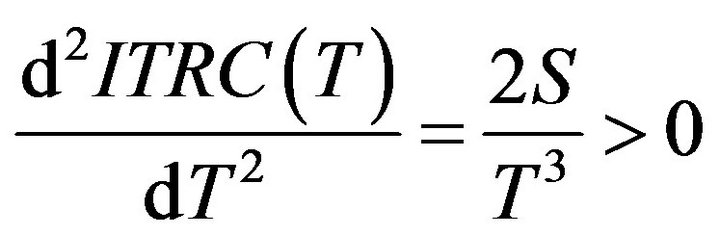 for all
for all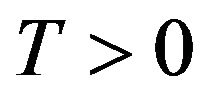 , respectively.
, respectively.
Set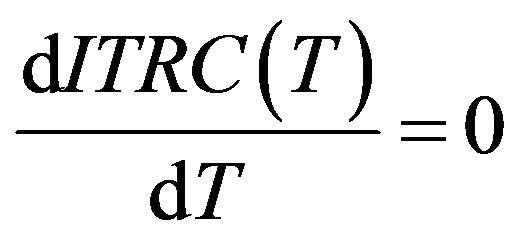 , and set
, and set
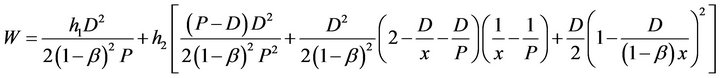
then we have the following result:
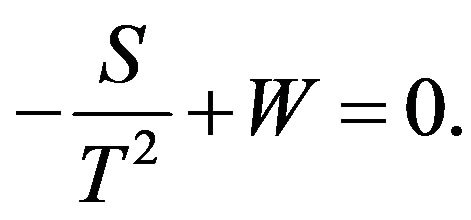
The unique solution of above equation is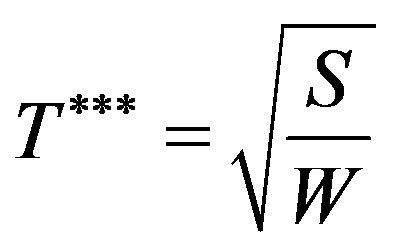 .
.
At the time of T***, the 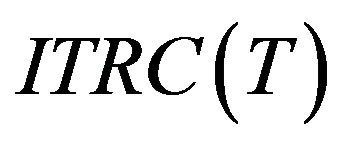 has a global minimum on
has a global minimum on 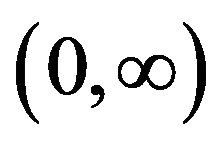 since
since 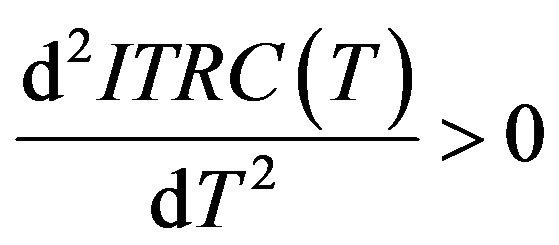 for all
for all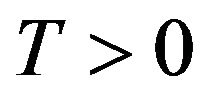 .
.
3. Numerical Examples
Example 1. If we set the numbers as
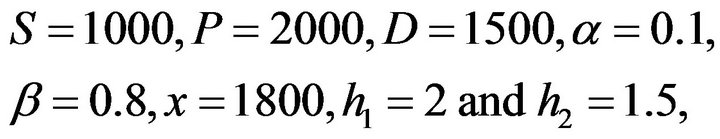
then we have

Example 2. If we set the numbers as
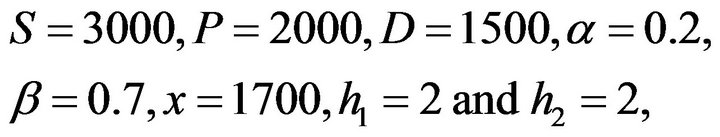
then we have

4. Conclusion
In this paper, we add the stock-holding cost of raw materials into this EPQ model to obtain the optimal inventory policy. This is an idea about modifying the traditional EPQ model. To academic researches and practices, the stock-holding cost of raw material has been added to the EPQ model, the result of adding the stock-holding cost of raw materials into the EPQ model is more useful and practical.
REFERENCES
- E. W. Taft, “The Most Economical Production Lot,” The Iron Age, Vol. 101, 1918, pp. 1410-1412.
- S.-D. Lin, “The Optimal Inventory Policy of Production Management,” Across-Straits Academic Conference Proceedings in Management Theories and Practices, Vol. 213, 2010, pp. 199-202.
- K. Richter, “The Extended EOQ Repair and Waste Disposal Model,” International Journal of Production Economics, Vol. 46, No. 1-3, 1996, pp. 443-447. doi:10.1016/0925-5273(95)00143-3
- M. K. Salameh and M. Y. Jaber, “Economic Reduction Quantity Model for Items with Imperfect Quality,” International Journal of Production Economics, Vol. 64, 2000, pp. 59-64. doi:10.1016/S0925-5273(99)00044-4
NOTES
*Corresponding author.

