Engineering
Vol.5 No.2(2013), Article ID:27728,11 pages DOI:10.4236/eng.2013.52024
Finite Element Analysis of In-Plane Displacements and Von-Mises Stresses in Ellipsoidal and Circular Cylinderical Petroleum Tankers
Mechanical Engineering Department, University of Ibadan, Ibadan, Nigeria
Email: *oluwoleo2@asme.org
Received October 16, 2012; revised December 16, 2012; accepted December 26, 2012
Keywords: Von-Mises Stress; Petrol Tanks; Finite Element Analysis
ABSTRACT
Road tankers are the most used means of transporting petroleum product to end users due to its cost effectiveness and energy-efficiency. The cylindrical tank has been well designed for by ASME VIII divisions 1 and 2 using analytical equations. Petrol tankers are not circular but elliptical probably for stability during transportation. This paper has used the finite element method to investigate in-plane displacements and Von-Mises stresses in both circular and elliptical cylindrical tanks under full loading. An elliptical OANDO® tanker of 66.78 m3 volume and shell thickness of 0.2 mm and an equivalent volume circular cylindrical tank was used for the simulation. MATLAB® was used to generate geometrical mesh model of the petroleum tankers, extract element coordinates and conduct the finite element analysis. Plane strain condition was used in analyzing a section of the petroleum tanker. It was observed that an equivalent volume circular cylindrical tank was under a higher internal pressure (16,858 N/m2) compared to the elliptical cylinder (14,480 N/m2). Von-Mises stress and in-plane displacements showed direct linear relationships with internal fluid pressure. Von-Mises stress in the elliptical tank was found to be lower (5.7 × 106 N/m2) than for the circular tank (8 × 106 N/m2). In plane displacements was zero in the longitudinal direction for both tanks and of the order of 10−4 mm in the y-direction for both tanks with the circular larger by about 2.5 × 10−3 cm. So in addition to tank stability on the lorry, the Von-Mises stresses were lower as well for the elliptical tank. It was also observed that Von-Mises stresses were far below the yield stress of the steel plate. However, the effect of weldment area on lowering of yield stress was not studied. Stress values were validated using analytical method and found to be insignificantly different (P > 0.05).
1. Introduction
Road tankers are cylindrical or ellipsoidal pressure vessels used to convey liquids especially petroleum products. Petroleum tanker is widely used over other means of transporting petroleum products (pipeline, trains, badges and trucks) due to its cost effectiveness and energy-efficiency [1]. According to the projection of Ekpen [2], Nigeria’s petroleum product consumption will rise to about 300 Kb/day, a large part ofher total energy consumption in the country. Recently, there has been increasing number of reports of tanker explosion during transit, claiming several lives and properties [3-9]. There is therefore need to consider petroleum tanker safety in line with design.
Road tankers constructed locallyare designed based on ASME standards for pressure vessels (ASME VIII divisions 1 and 2). The ASME standard presents design formulae that are simple to use, but limited to specific geometries and geometry details such as welded supports and openings. It does not put into consideration several actions or combination of actions such as local loads, seismic load, wind loads and external pressure in its design formula. A better approach is the design by analysis. According to Josef et al. [10], design by analysis is very flexible, it allows for any combination of actions, it can be used for complicated geometry, and it addresses directly the creativity of the designer. Finite element method is an efficient technique of design by analysis as it gives result close to corresponding experimental values.
The Finite Element Method is a numerical technique ideally suited to digital computers in which a continuous elastic structure (continuum) is divided (discretized) into smaller but finite well defined sub-structures (element) that can be represented by simple equations [11]. According to George [12], it represents an approximate numerical solution of a boundary value problem described by a differential equation.
There are several publications on application of Finite element analysis of specific pressure vessels. Mirko et al., [13] applied Finite element method in the determination of the stress state of a cylindrical vessel with variable thickness. The stress distribution of deformed tank i.e. a tank with part that has been formally repaired was analyzed [14]. Jaroslav [15], In his work made a listings of over 865 papers and conference proceedings on finite element in the analysis of pressure vessels and pipelines which he classified into the following categories: linear and nonlinear, static and dynamic; stress and deflection analyses; stability problems; thermal problems; fracture mechanics problems; contact problems; fluid-structure interaction problems; manufacturing of pipes and tubes; welded pipes and pressure vessel components; development of special finite elements for pressure vessels and pipes; finite element software.
Most Finite element analysts develop own codes using MATLAB, C++, or FORTRAN. Meshing of geometrical models is done manually giving poor results. Other challenges faced by finite element analysts include: high cost of acquiring CAD software for numerical simulation, difficulty in managing read data from standard CAD programs such as dwg format (AutoCAD file) when using own code, and erroneous results, due to improper use of commercial software.
MATLAB is a computer language and the software has an interactive computing environment that enables numerical computation, analysis and data visualization [16]. This work has explored MATLAB’s plotting capability and powerful computational tools to generate the geometrical mesh model of a petroleum tanker, extract element coordinates and conduct a finite element analysis of Von-Mises stress on a loaded tanker. The values obtained were compared with ASME standard.
2. Methodology
2.1. Automated Mesh Generator
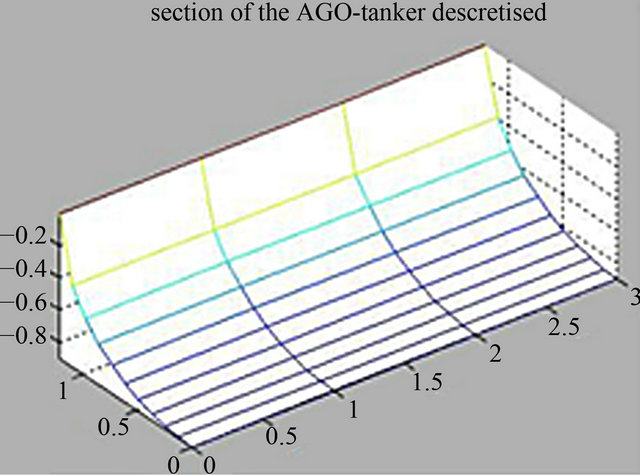
The ellipsoidal tanker which is predominantly more common compared to the cylindrical ones has three inner segments (Figures 1 and 2). Each segment can be divided into four symmetrically similar sections (Figure 3). For ease and simplicity, the left bottom section was considered (Figure 4), and an automated mesh generation code was written with MATLAB®.
The common ellipse (Figure 5) and the ellipse Equation (1) was used in the development of the code. The automated mesh generator was developed using piecewise straight lines to approximate the curve and element continuity created during the meshing relations. The flowchart for the automated mesh generator is shown (Figure 6). Figure 7 shows meshing of the quarter section.

Figure 1. The tank model.
Figure 2. The tanker model divided into 3 parts initially joined together.
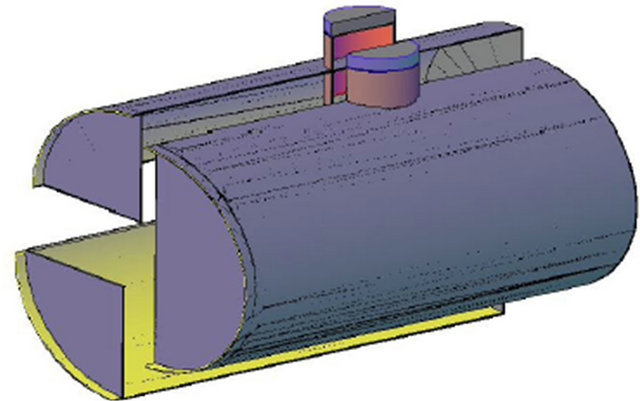

Figure 3. A part of the tanker further sectioned into parts.

Figure 4. Section for automated meshing.
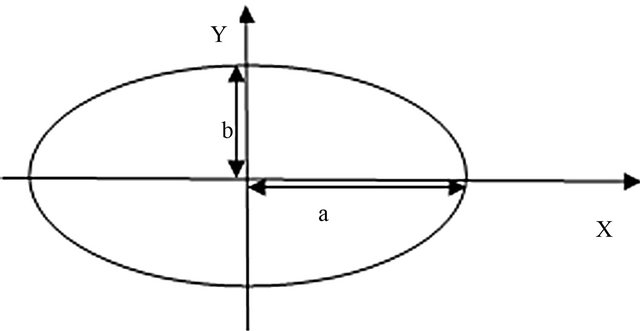
Figure 5. An ellipse with its dimension.
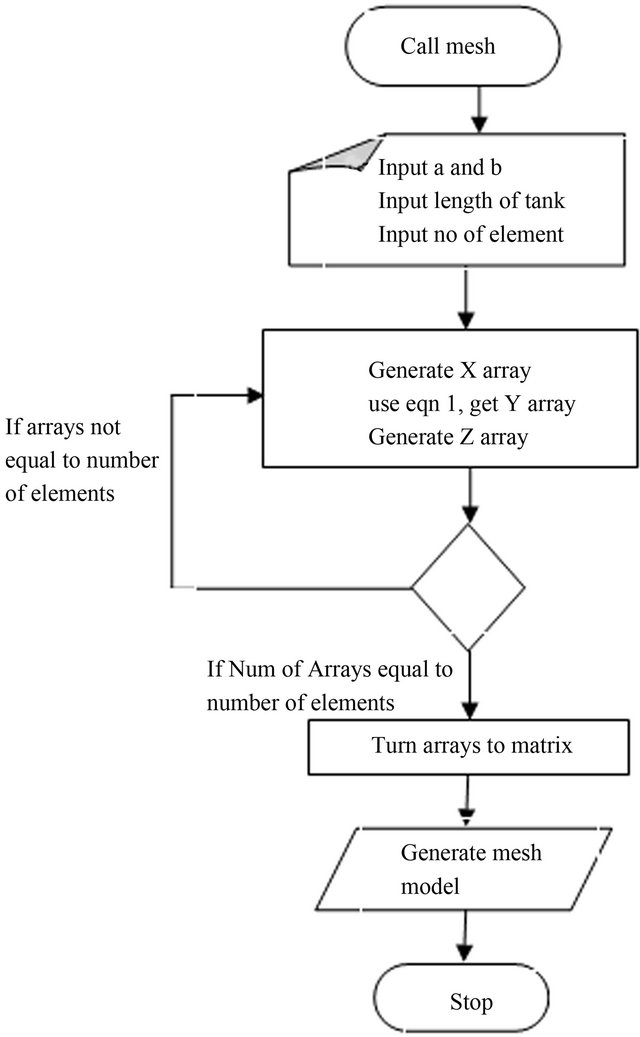
Figure 6. Algorithm for automatic mesh generator.
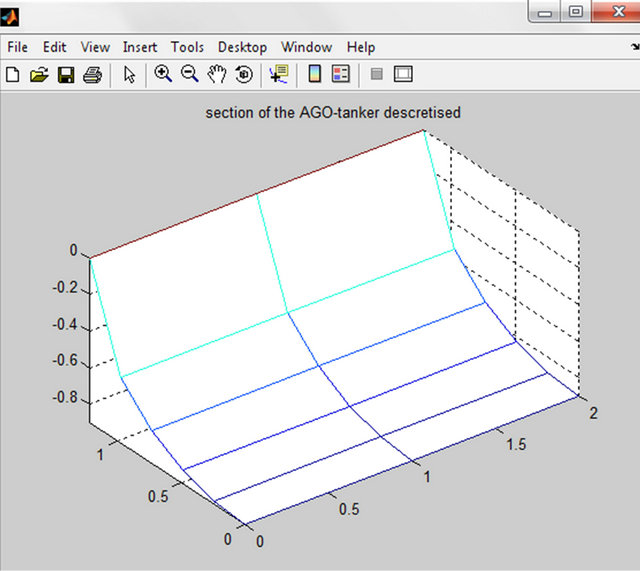 (a)
(a)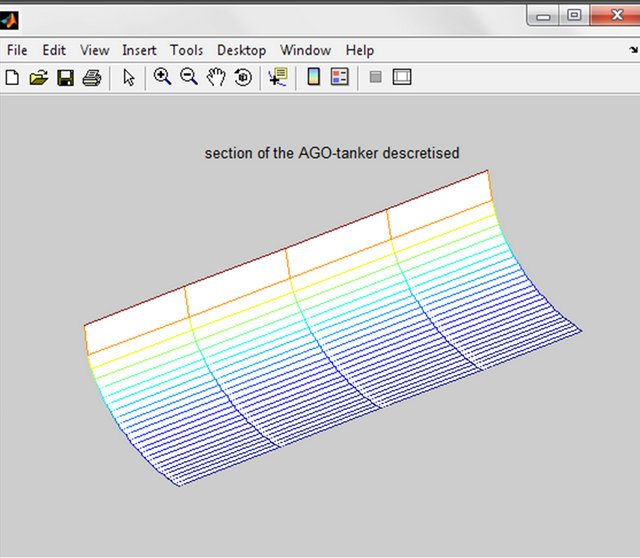 (b)
(b)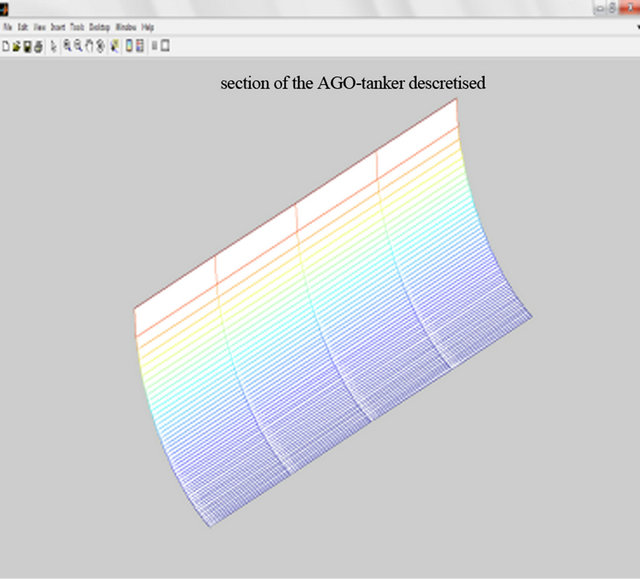 (c)
(c)
Figure 7. (a) 10 elements mesh; (b) 200 elements mesh; (c) 500 elements mesh.
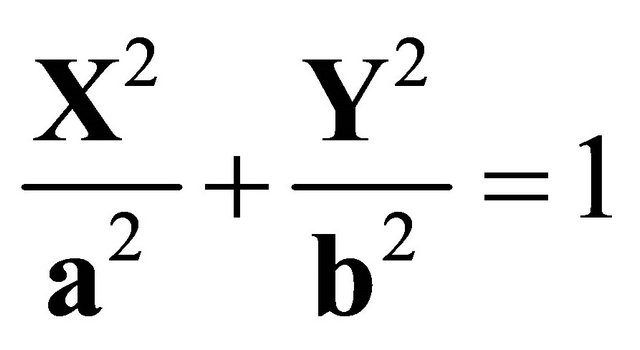 also was written as
also was written as
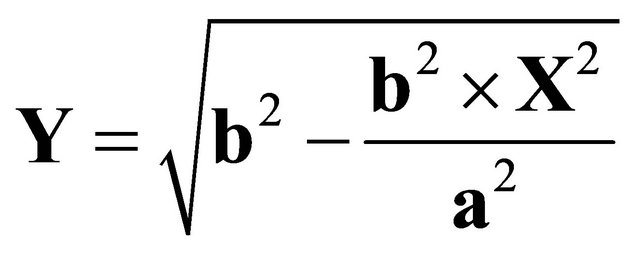 (1)
(1)
where a represents half the horizontal axis, and b half the vertical axis as shown in Figure 5.
2.2. Estimation of Stiffness Matrix and Force Vector
After generating the meshed model, an element was extrapolated and used in developing the stiffness matrix and force vector, needed to evaluate the displacement vector for plane strain elasticity of the model and VonMises stress.
The equation for the rectangular shell elements was derived by combining the linear rectangular element (membrane element) and the plate element (bending element).
2.2.1. Membrane Element
The equilibrium equations for a three-dimensional linear elasticity express in terms of stress is given [17,18] as;
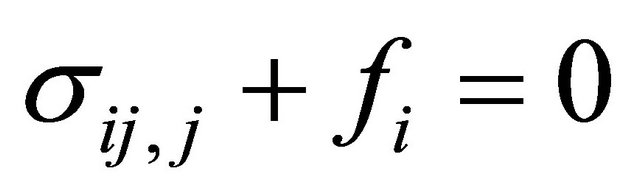
where 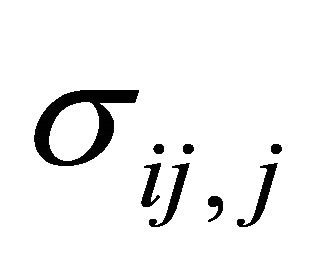 are the stress components,
are the stress components, 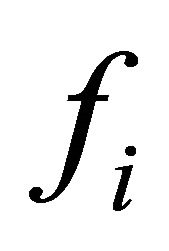 are the body forces.
are the body forces.
The above equilibrium equation expressed in terms of displacement for two dimensional analyses is given as follows. The equation was reduced to two dimensional since plane strain condition is being considered.
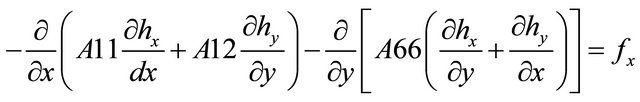
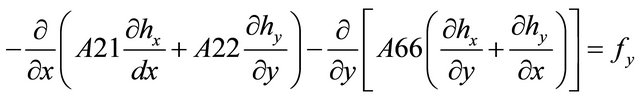
hx and hy are the in-plane displacement in the x and y directions respectively of the Cartesian coordinate system.
2.2.2. Weak Formulation of the Membrane Element Equation
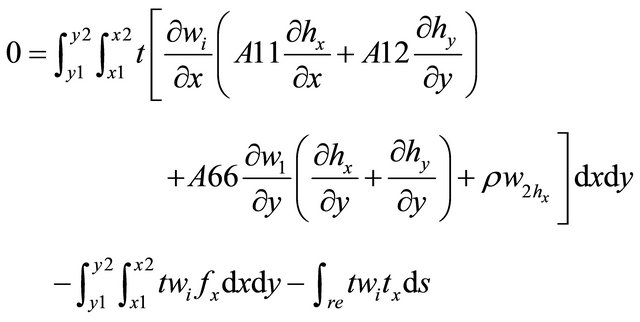
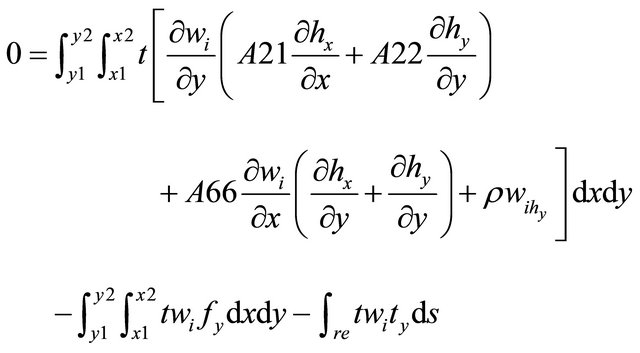
2.2.3. Stiffness Matrix for the Membrane Element
The finite element equation is expressed as
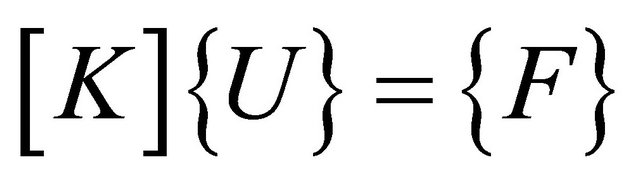
[K] is the stiffness matrix, {F} is the force vector and {U} is the displacement vector.
For plane strain condition, assuming homogeneity of material,
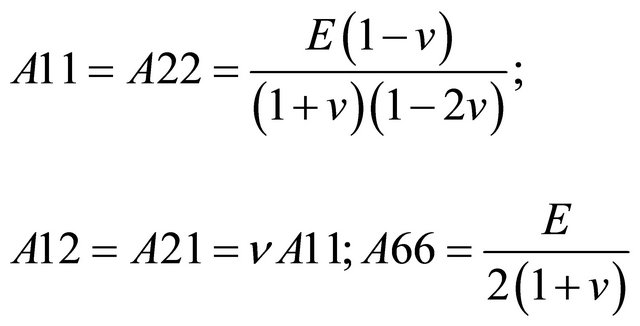
E and v are the material elastic constant and poison ratio respectively.
2.2.4. Interpolating Function for the Membrane Element
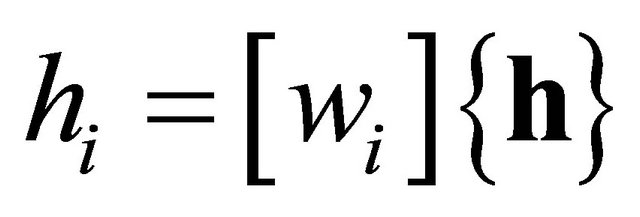 where
where  is the in-plane displacement vector,
is the in-plane displacement vector, 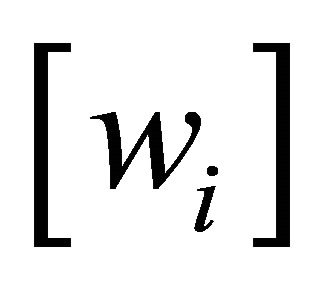 are the weight functions. The weight function for the rectangular element was used in the analysis.
are the weight functions. The weight function for the rectangular element was used in the analysis.
2.2.5. Bending Element
The standard equation governing plate bending [19] is given as follows;
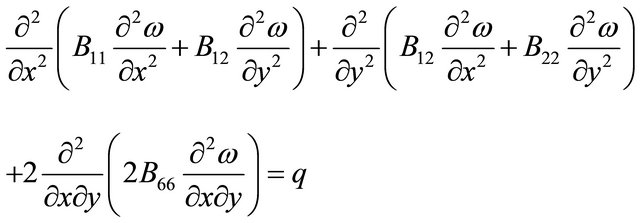
Bij is the bending stiffness matrix for the shell element. E, v and t are the elastic modulus, poison ratio and thickness respectively of the tanker being considered.
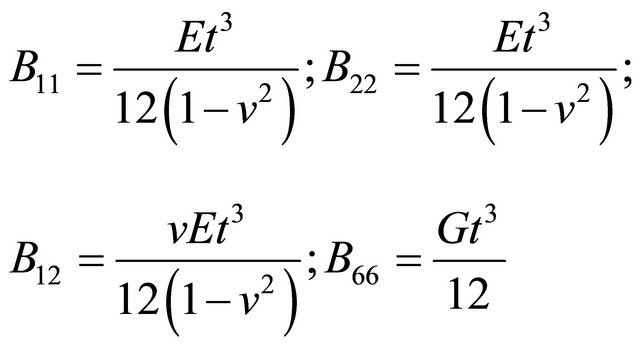
2.2.6. Weak Formulation of the Bending Element
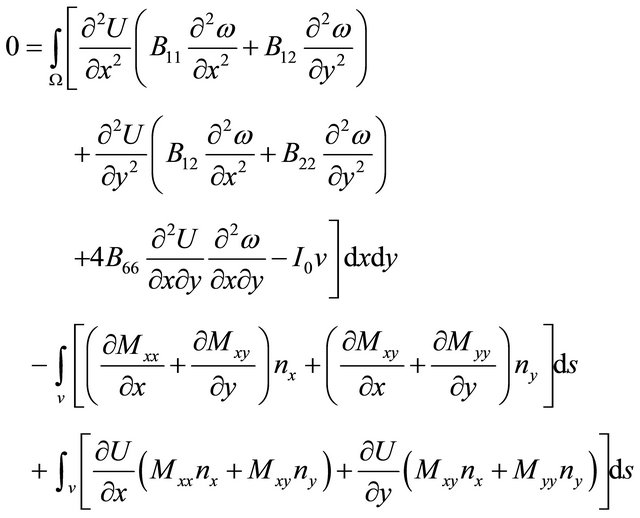
2.2.7. Stiffness Matrix for the Bending Element
For the plate element, on application of the classical plate theory [19], the Finite Element Model is given as follows
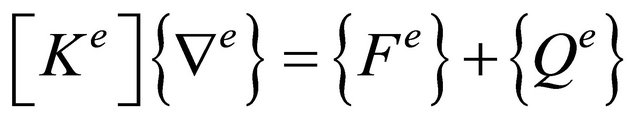
Every term retains their meaning as above except for  which is used to represent one out-of-plane displacement in the thickness axis and two rotations. Mass matrix was neglected since dynamics of the system was not considered.
which is used to represent one out-of-plane displacement in the thickness axis and two rotations. Mass matrix was neglected since dynamics of the system was not considered.
2.2.8. Interpolation Function for the Bending Element
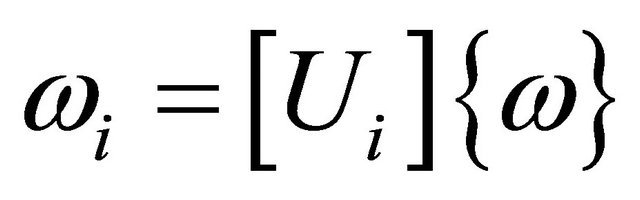 . Where
. Where  represents one out-of-plane displacement in the thickness direction and two rotations and
represents one out-of-plane displacement in the thickness direction and two rotations and 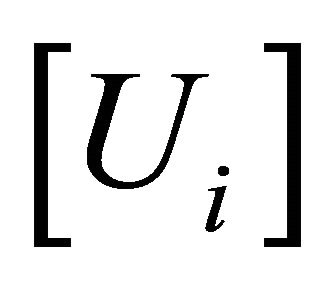 are the weight functions. Bij’ are the material elasticity matrices for the bending element.
are the weight functions. Bij’ are the material elasticity matrices for the bending element.
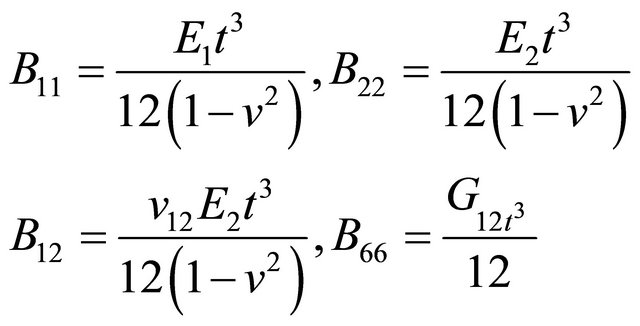
2.3. Calculation of p and q for Each Element
The stiffness matrices, and force vectors are basically a function of the side length of the rectangular element (Figures 8(a) and (b)) used to form the tanker model. From Figure 8, the values of p and q were calculated applying coordinate geometry as follows:
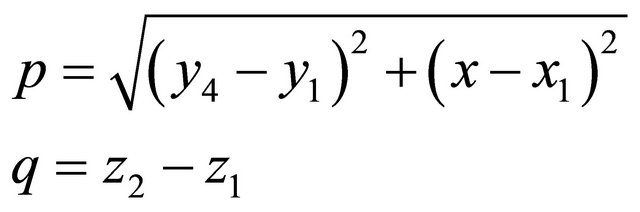
xi, yi and zi are the coordinate locations of each element. I = 1 to 4 represents the four nodes of a 4 nodal rectangular element.
 (a)
(a)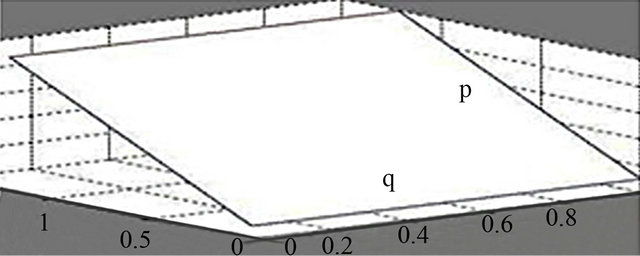 (b)
(b)
Figure 8. (a) Element mesh of the section; (b) An element showing dimensions for FEA.
2.4. Combination of Membrane and Bending Stiffness Matrices and Force Vectors
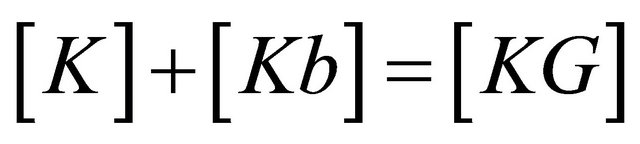
where [K] is the 8 × 8 membrane stiffness matrix and [Kb] is the 12 × 12 bending stiffness matrix, both combining to give the total elemental stiffness matrix [KG] in the form shown below
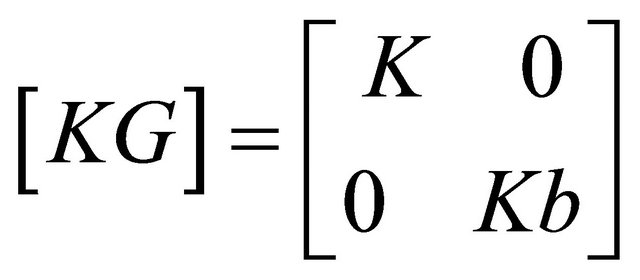
The force vectors were combined in similar manner to form the total elemental force vector as follows
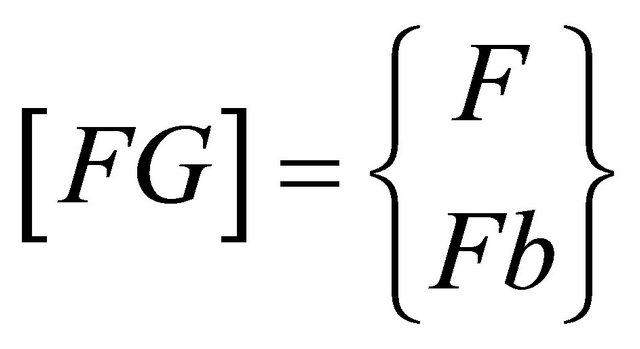
2.5. Boundary Conditions and Calculation of Displacement
Each element has five degrees of freedom (two in-plane displacements u and v, one out-of-plane displacements w, and two rotations. The displacements and bending at the edges were given zero since they are fixed.
Code for evaluating the finite element equation {U} =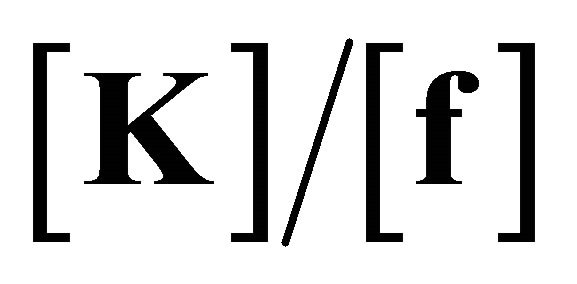 , introducing boundary conditions and estimating the displacement was done using the flow algorithm (Figure 9).
, introducing boundary conditions and estimating the displacement was done using the flow algorithm (Figure 9).
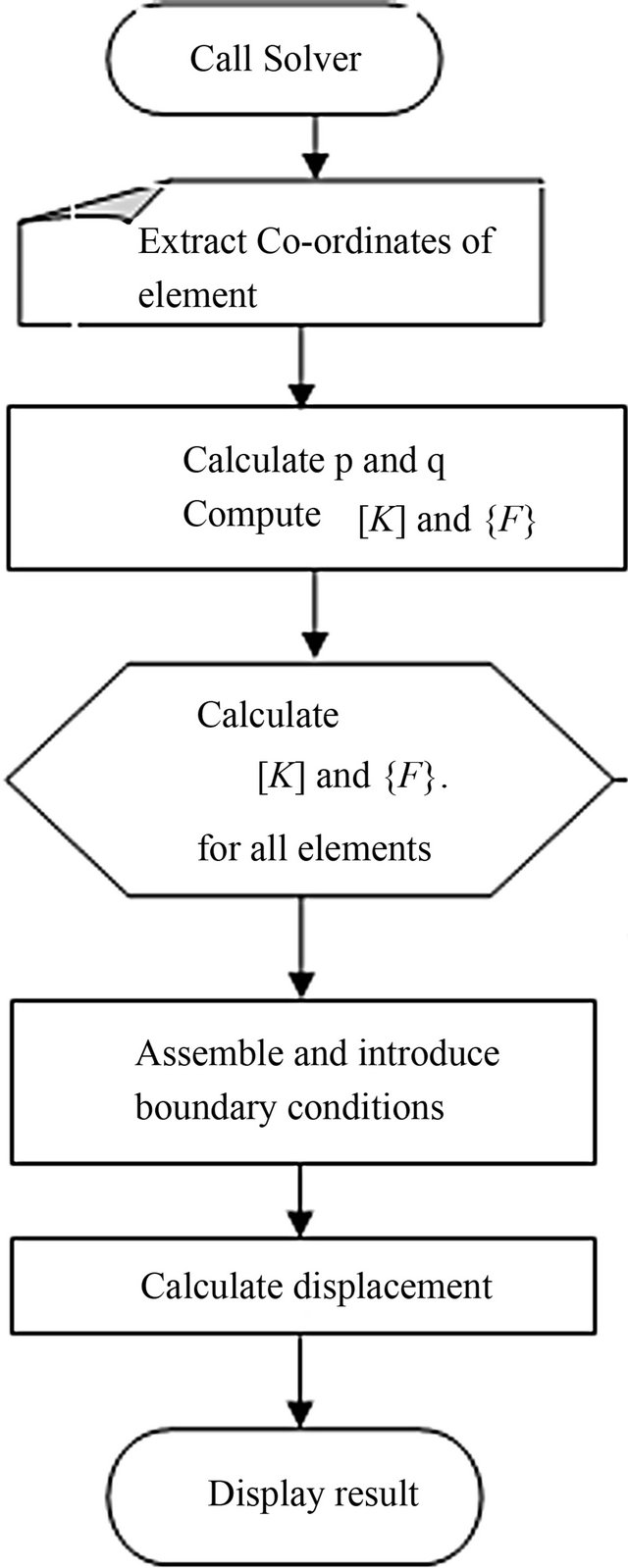
Figure 9. Algorithm applying extracted elemental coordinate for FE analysis.
2.6. Calculation of Stresses and Von-Mises Stress
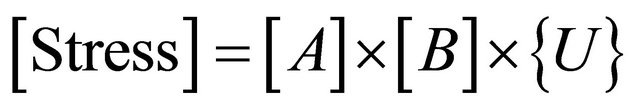
Aij represent the elasticity matrices for both the membrane element and bending element respectively.
[B] Represents the strain vectors and moment vector for membrane and bending element respectively.
[Stress] is the bending and membrane stress being computed.
2.7. Analytical Von-Mises Stress Calculation To compute the Von-Mises stress analytically, there are three principal stresses which are all functions of the pressure.
P1 = Principal stress 1 = Hoop stress = pressure × horizontal radii axis/t;
P2 = Principal stress 2 = Hoop stress/2;
P3 = Principal stress 3 = radial stress pressure;
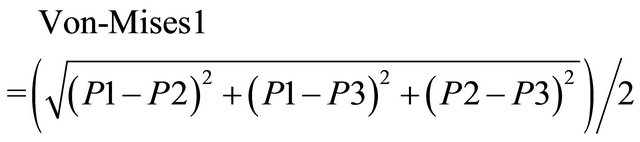
2.8. Dimensions Used for Analysis
Length of tanker = 485 cm;
Vertical axis of tanker = 180 cm;
Horizontal axis of tanker = 244 cm;
Thickness of tanker = 0.2 cm;
Poison ratio = 0.3;
Material of construction = A516M Grade 70;
Specified minimum yield stress = 25 × 107 N/m2;
Maximum allowable stress = 13.8 × 107 N/m2;
Elastic modulus = 200 × 109 N/m2.
3. Results and Discussions
3.1. Results
Figure 10 shows Von-Moses stress variation with loading. At full loading, Von-Mises stress was 5.7 × 106 N/m2 and this decreased linearly to zero as the tank is offloaded until there is an empty tank with zero VonMises stress.
Figure 11 shows Von-Mises stress converge to a consistent value at large mesh elements for both elliptical and circular tanks. It also shows Von-Mises stress for circular tanks slightly higher than for the elliptical tank. Both FEM computed values converged to the analytical values for both circular and elliptical. ASME values tallied with the values for circular tank which are the same as the analytical values for the circular tank.
Figure 12 shows the effect of tanker internal pressure on in-plane displacement in the longitudinal (x) direction of elliptical cylindrical tankers. It shows a linear relationship between both parameters consistent with Hooke’s law at elastic dimensions.
Figure 13 shows the effect of variation in internal pressure in elliptical tank on in-plane circumferential (y) displacements. It shows as well a linear relationship between both parameters.
Figure 14 shows the combined plots of in-plane longitudinal displacements for both circular and elliptical cylindrical tanks at full loading. The plots show that longitudinal displacements were the same for both tanks and were as it were non-existent (zero).
Figure 15 shows the combined plot of the circumferential in-plane displacements for both tanks at full loading. The plots show that the circumferential in-plane displacements were existent but at an order of 10−4 cm. The circular cylindrical tank showed higher circumferential displacement than the elliptical with a difference of about 2.5 × 10−3 cm.
Figure 16 shows Von-Mises stress variation with tanker shell thickness. It shows an increasing stress as shell thickness is reduced and after 5.0 × 10−2 m shell thickness, Von-Mises stress increased rapidly till yield stress is reached.
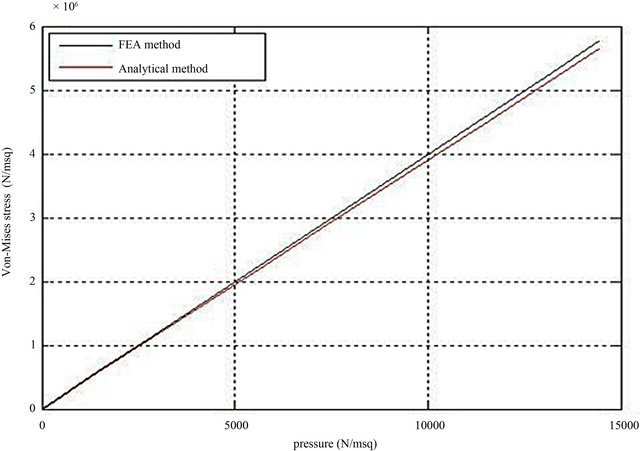
Figure 10. Von-Mises stress variation with internal tank pressure for elliptical cylindrical tank using 800 element meshes.
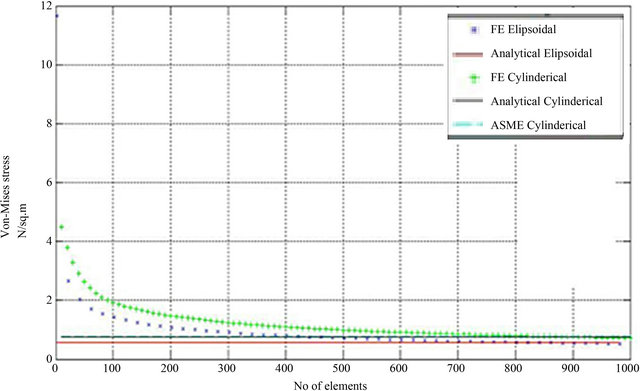
Figure 11. Von-Mises stress variation with no of meshing elements for cylindrical and elliptical cylindrical tank at 16,858 N/m2 and 14,480 N/m2 loading pressure respectively.
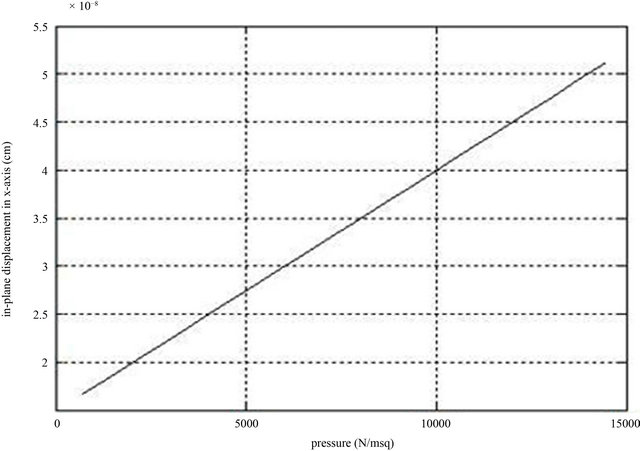
Figure 12. Variation of in-plane displacement in the longitudinal (x) direction of elliptical cylindrical tankers with internal load pressure.
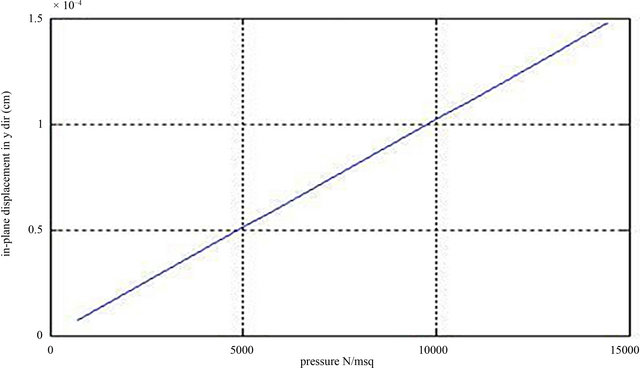
Figure 13. Variation of in-plane displacement in the circumferential (y) direction of Elliptical cylindrical tankers with internal load pressure.
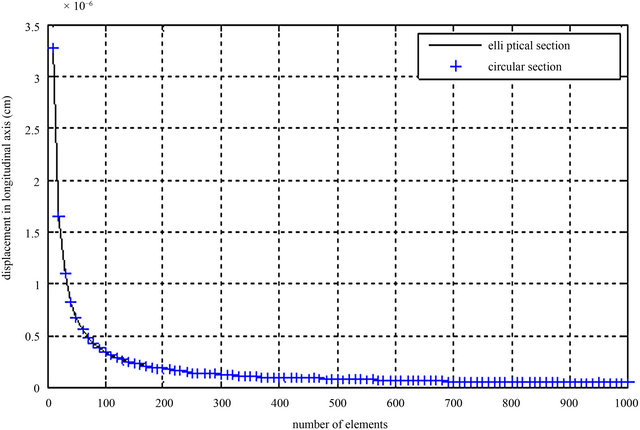
Figure 14. In plane displacement in the longitudinal (x) directionof elliptical and circular cylindrical tankers at full loading.
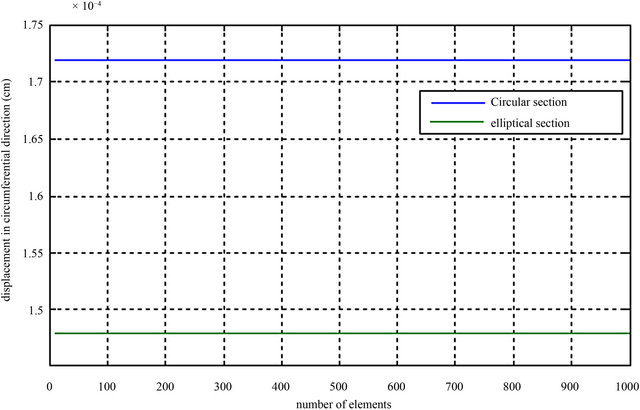
Figure 15. In plane displacement in the circumferential (y) direction of elliptical and circular cylindrical tankers at full loading.
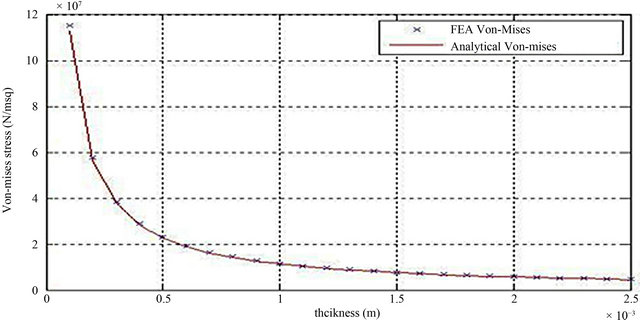
Figure 16. Von-Mises variation with tanker shell thickness.
3.2. Discussion of Results
The direct linear relationships between internal loading pressure and Von-Mises stress (Figure 10) and that between in-plane displacements and internal pressure (Figures 12 and 13) are not unexpected because of the linearity of the stress-strain relationship in the elastic region. The result clearly showed that at full load Von-Mises stress is maximum (Figures 10 and 11). However, the Von-Mises stress for the fully loaded tanker still fell far below the yield stress of the material and the maximum allowable stress (Figure 11). This showed that the tanker will not yield during transportation from the loading pressure. However, since the tanks are always welded and not seamless, the tanks are susceptible to yield stress lowering effect of heat-affected-zone (HAZ) from welding. The HAZ causes embrittlement, hence a lowering of yield stress and if care is not taken, there could be microhole defects from where rapid crack propagation could develop causing catastrophic failure of the tank. If this effect is coupled to the corrosive effect of the petroleum product over time causing what can be termed stresscorrosion effect on the welded portion could as well cause failure over time. However, these issues were not addressed in this paper and are concerns for future work.
The results also show that circular cylinderical tanks have higher internal pressures as well as higher VonMises stresses than elliptical tanks of the same loading volume (Figure 13). The lower Von-Mises stresses developed in elliptical cylindrical tanks as well as their stability during transportation gives the elliptical tank a big edge over the circular cylindrical tank.
The in-plane displacements (Figures 14 and 15) showed good tanker material integrity and nullifies any idea of failure by yielding but just as had been mentioned earlier future work on weldment defects coupled with stresscorrosion need to be done to investigate what is transpiring here which could lead to other types of failure over time.
The inverse and non-linear relationship between tank shell thickness and Von-Mises stress (Figure 16) was also not surprising because of the relations between hoop/longitudinal stresses and shell thickness. This result showed clearly that it is important to design for a thickness that would guarantee a sufficient factor of safety especially since the effect of the welded parts’ heat affected zone (HAZ) on lowering of yield stress must be considered.
4. Conclusion
Von-Mises stresses in circular and elliptical petroleum tankers under full loading have been obtained using the finite element method. It was observed that an equivalent volume circular cylindrical has a higher internal pressure (16,858 N/m2) compared to the elliptical cylinder (14,480 N/m2). Von-Mises stresses showed a linear relationship with variation in internal fluid pressure. Von-Mises stresses in the elliptical tank were found to be lower (5.7 × 106 N/m2) than for the circular tank (8 × 106 N/m2. VonMises stresses were far below the yield stress of the steel plate (25 × 107 N/m2). However, the effect of weldment area and stress corrosion on lowering of yield stress was not studied. Values obtained for the circular cylindrical tank were compared with ASME VIII divisions 1 and 2 standard values and found not to be significantly different (P > 0.05).
REFERENCES
- KSP 10-K, “Transportation of Petroleum Products,” 2012. www.wikinvest.com/stock/KSea_ Transportation_Partners_ LP_%28KSP%29/Transportation
- J. O. Ekpen, “Oil Refinery in Nigeria. (Myths and Truths),” NAEE Conference, Abuja, 28-29 April 2011, 2012. http://naee.org.ng/files/
- K. Babasoki, “Abuja Tanker Explosion,” 2012. Fromogala.wrodpress.com/2011/11/16/latest-news-fromthe-abuja-tanker explosion
- A. Ola and O. David, “10 Killed in Multiple Tanker Explosions, Building Collapse,” 2012. wwww.vanguardngr.com/2012/06/10-killed-in multiple-tanker-explosion-building-collapse
- Daily Mail Reporter, “86,000 Gallon Oil Tanker Bursts into Flames in Highway Crash Caused by Drunken Driver,” 2012. www.wdailymail.co.uk/news/article-2126891/fuel-tanker-bursts-into-flames-us-freeway-crash-caused-by-drunken-driver
- M. Emeka, “Ogun State Government Silent on Fuel Tanker Explosion,” Vanguard, 2012, 6 Pages.
- O. Uchechukwu and A. Boila, “Vehicles Burnt at Ibadan Tanker Explosion,” 2012. www.tribune.com/ng/.../37648-12vehiclesburnt-inibadan-tanker
- C. Miley, “Melborne Tanker Explosion Burns 9,” 2012. news ninemsn.com.all/ national/8387836/petrol-tanker-explodes-in-melborne-suburb
- B. Godfey and O. Ifeyinwa, “Oil Tanker Explosion Destroys Containers, Cars at Apapa Port,” 2012. www.vanguardngr.com/2012/04/oil-tanker explosion-destroys-containers-cars-at-apapa-port
- L. Z. Josef, R. Franz and S. Sebastian, “Pressure Vessel Design—The Direct Route,” 1st Edition’ Elsevier ltd., Oxford, 2006.
- G. B. Richard, “Advance Strength and Applied Stress Analysis,” 2nd Edition, McGraw Hill Publishing Companies Inc., New York, 1999.
- R. B. George, 1995. “Finite Element Analysis,” Shaum’s Outline Series, McGraw-Hill, New York, 1995, 73 Pages.
- Đ. Mirko, P. Dragan and B. Milan, “Identification of the Stress-Strain State of a Cylindrical Tank with Walls of Variable Thickness,” FME Transactions, Vol. 39, No. 1, 2011, pp. 25-32.
- V. P. Anatoly, Y. F. Sergiy, S. K. Viktor and Z. K. Edward, “Analysis of the Stressed State of Cylindrical Tanks with Defects of Geometrical Shape,” SCAD Group, Kiev, 2003.
- M. Jaroslav, 1996. “Finite Elements in the Analysis of Pressure Vessels and Piping—A Bibliography (1976- 1996),” International Journal of Pressure Vessels and Pipings, Vol. 69, No. 3, 1996, pp. 273-339.
- M. Patrick and A. O. Thomos, “Graphics and GUIs with Matlab,” Chapman & Hall CRC Press Company, London, 2003.
- T. Timoshenko and J. Goodier, “Theory of Elasticity,” McGraw Hill Books Company Inc., New York, 1951.
- C. Ross, “Advance Stress Analysis,” Ellis Horwood Limited, New York, 1987.
- J. N. Ready, “An Introduction to Finite Element Method,” 3rd Edition, McGraw Hill, New York, 2006.
NOTES
*Corresponding author.

