Engineering
Vol. 3 No. 12 (2011) , Article ID: 9208 , 6 pages DOI:10.4236/eng.2011.312143
Numerical Analysis on Static Mechanical Properties of the Periodic Multilayer Lattice Material
1School of Mechanical Engineering, Nanjing University Science & Technology, Nanjing, China
2Department of Chemical Engineering, Nanjing University Science & Technology, Nanjing, China
3Department of Physics, Nanjing University Science & Technology, Nanjing, China
E-mail: *guoruid@163.com
Received July 8, 2011; revised September 6, 2011; accepted September 13, 2011
Keywords: Metal Matrix, Honeycombs, Mechanical, Selection for Material Properties
ABSTRACT
Lattice material is a typical periodic structural material, and the gaps of the lattice material are often used to carry filling materials. In order to satisfy the load-carrying requirements of a certain multifunction/structure integrated composite material, four different 3D periodic multilayer lattice materials were proposed in this paper, such as the square, the quadrate, the tetrahedron and the hexagon. The BEAM189 element in ANSYS was adopted to predict their static mechanical properties, and the Mises strength criterion was taken as the failure criterion. Based on the solution of FEM, the axial stress and displacement of the top surface were obtained. The results indicated that adopting the relative stiffness and the load-mass ratio as the overall assessment is effective to evaluate the overall bearing capacity of the multilayer lattice materials. Given the same cross-section size of the cellular configuration, the hexagon multilayer lattice material shows the relatively optimal overall bearing capacity in the four configurations, while the tetrahedron configuration performs the worst.
1. Introduction
The lattice material is a kind of periodic structural material composed by nodes and joint trusses, which mesoscopic configuration is 2D or 3D spatial configuration, and the gaps of the trusses can be used to carry filling materials. Compared with traditional materials, lattice material possesses various microstructures and the higher porosity which can reduce the weight and improve the stiffness and strength. Meanwhile, the microstructure of lattice material is much more order, and its mechanical properties are better than the foam metal. So, the lattice material is the popular subject in the recent engineering research field [1-9].
Compared with traditional materials, lattice material has better designability. According to different requirements, it can be filled with varied functional materials, such as materials of anti-projectile, materials of energy absorption, materials of heat insulation, materials of sound absorption, and so on. Hence, it can help to meet the multi-functional requirements of the composite materials, and it also helps to further reduce the structure’s overall weight [10]. The function precondition of materials is determined by the structure design, and the topological configuration of the skeleton is the key factor. The mechanical properties of the lattice material are directly related to its porosity and pore structure. By changing the porosity and the morphology of the pore, the overall performances of the lattice material would be affected. In this paper, we try to provide a kind of multifunction/ structure integrated composite material, as shown in the Figure 1. Its base frame is a kind of lattice metal skeleton, and its gaps are filled with ceramic materials, highstrength fiber materials and wave absorbing materials to satisfy the multi-functional requirement of a certain armor protection material. For providing some valuable theoretical references to improve the quality and the efficiency of the structure design and process for the composite material, we mainly focused on the optimized mechanical performances of its lattice metal skeleton. In order to satisfy the load-carrying requirements of the composite material, we proposed four different 3D periodic multilayer lattice materials with different spatial configurations. Based on the static structural simulation method with ANSYS, the static mechanical properties of the four multilayer lattice materials were analyzed and compared.
2. Theoretical Analysis Method
Static mechanical properties of the periodic lattice materials are always concerned in the academe and engineering [11]. Based on strain energy method and homogeneous theory, Noor and Straalen proposed an equivalent computation model for the substitute core [12,13]. Wang systematically summarized the elastic properties of the typical two-dimensional lattice materials [14,15]. Based on micromechanics, Delpande and Fleck put forward an octahedral lattice material and its elastic constitutive relationship [16]. Liu established a more simplified micromechanical model and its applicability was verified with numerical simulations [17,18]. Mohr and Rabczuk proposed constitutive models for the two-dimensional porous materials and the lattice truss sandwich materials [19,20]. Given six spindle orientation yield strength theory, XUE proposed a phenomenological yield surface ellipsoid criterion [21,22]. Commonly, the relative density of lattice material is less than 30%, and its thickness of the microstructure truss is usually much less than its length. Thus, the structure can be simplified as the beam model for mechanical analysis [11]. There are some routine theoretical analysis methods for the lattice materials’ mechanical properties, such as, the coordinate transform method, the finite element method (FEM), the homogenization method and so on [23].
• Using the coordinate transform method, the rigidity coefficient of the anisotropic cell is obtained through the transformation of orthogonal Cartesian coordinate system.
• FEM is a discrete numerical method, a combination of finite elements is used to substitute the continuous body, so the infinite freedom issue is changed to a finite freedom issue. Based on the equivalent stiffness matrix model, the equivalent mechanical parameters can be calculated respectively.
• Homogenization method evolves some macroscopic structure’s mechanical parameters (such as displacement and stress) on the microscopic scales, the characterization parameter asymptotic technology and the perturbation technology is used to establish the control equations and finally to get the macroscopic mechanical parameters of the material.
With the thorough theoretical research on lattice materials, FEM is adopted by many scholars to calculate the equivalent mechanical parameters of truss structure, and FEM can simultaneity analyze the stiffness and the bearing capacity of the materials. Using ANSYS, the static mechanical properties of different 3D periodic multilayer lattice materials are analyzed in this paper.
3. FEM Model
3.1. Topology Configurations
For the limits of the process technics, four different configurations are mainly focused in the preliminary design period. All of the four types of configurations are bending dominated materials. The space characteristics of the configuration and its cell are shown in Figure 2.
3.2. Finite Element Model
In order to analyze the bearing capacity and structural stiffness of the lattice material, BEAM189 element was adopted. In ANSYS, the BEAM189 is a quadratic (3- node) beam element in 3-D. The BEAM189 is based on Timoshenko beam theory, shear deformation effects are included, and it is well-suited for linear, large rotation, and/or large strain nonlinear applications.
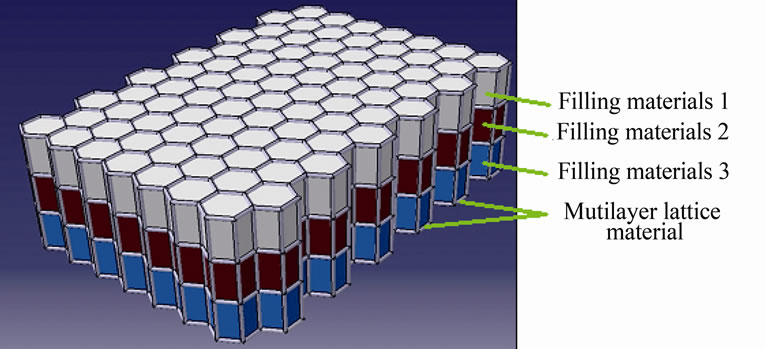
Figure 1. The hexagon multilayer composite material.
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 2. The space characteristics of different configuretions and its cells. (a) The square cell; (b) The quadrate cell; (c) The hexagon cell; (d) The tetrahedron cell.
The structural dimension of the multilayer lattice material was defined as 100 mm × 100 mm × 30 mm. Introducing the warping freedom of the truss’s cross-section, the cross-section shape of the beam element was circular, and the size was defined as Φ4 mm. the steel was chosen as the material, its density is 7830 kg/cm3, the compressive strength is 735 MPa, the elastic modulus is 210 GPa, and the Poisson’s ratio is 0.3. The axial compression load was imposed evenly on the top surface of the lattice material, and the freedom of the bottom surface was fixed. The node’s radial displacement of the top surface was limited, and the nodes’ axial displacement of the top surface was coupled. The ANSYS FEM model was shown in Figure 3.
Zhang [24] pointed that the failure type of lattice material was mostly the compression fracture. So, we took the Mises strength criterion as the failure criterion. After the solution of the FEM, the axial stress and displacement of the top surface were obtained to analyze the material’s bearing capacity. The simulation result was shown in Figure 4.

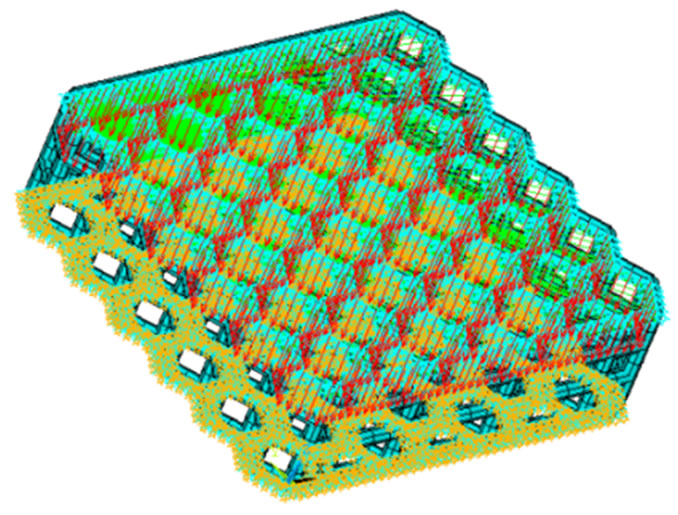
Figure 3. FEM model and loading model of the hexagon multilayer lattice material.
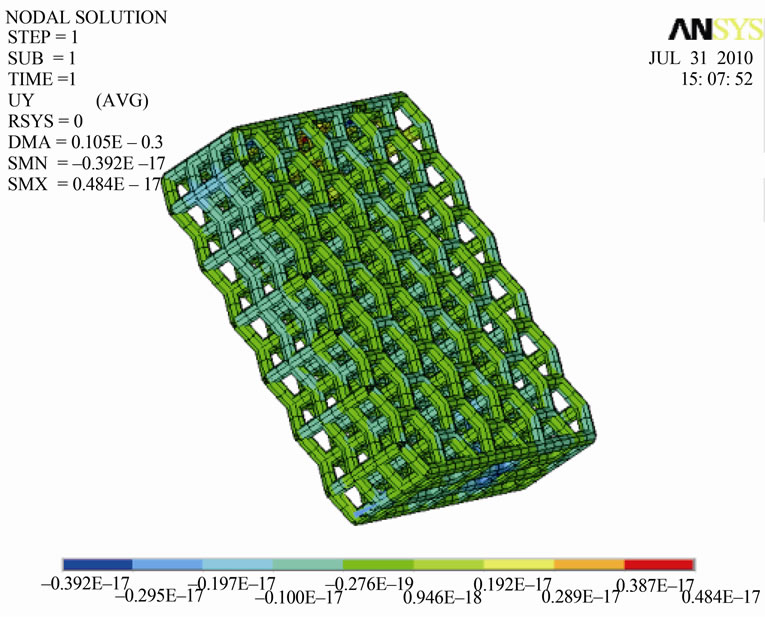

Figure 4. Axial stress and displacement of the hexagon multilayer lattice material.
4. Simulation Results and Analysis
When the load forces change from 100 KN to 1600 KN, the axial stress and displacement of the top surface can be simulated with the FEM. For the square multilayer lattice material, the load started from 100 KN, when it reached 1179 KN, the compression stress was increased to 735 Mpa, and the material lapsed. Meanwhile, the maximum axial displacement of the top surface reached 0.105 mm. Similarly, the quadrate multilayer lattice material, the hexagon multilayer lattice material, and the tetrahedral multilayer lattice material were also calculated and analyzed. Finally, the comparative result curve was obtained, as shown in Figures 5 and 6.
It can be seen from Figure 5 that the axial stress of the multilayer lattice materials is linearly enhanced along with the increasing load. Additional, when the axial stress reaches 735 MPa, the maximum compression loads of the four multilayer lattice materials are 1179 KN, 1090 KN, 1025 KN and 1550 KN. As the result, the load-mass ratio could be obtained (maximum compression load divided the overall structure mass), and we can use this ratio to measure the bearing capacity of the multilayer lattice materials.
Also, as shown in Figure 6, the maximum axial displacement of the multilayer lattice materials is enhanced along with the increasing load. Before the structure fracture occurred, the maximum displacement of the top surface linearly depends on the load. So, the slope of the curves, which stands for the structure stiffness of the material, can be also obtained. Compared the obtained structure stiffness with the material’s overall mass, the relative stiffness is deduced, and we can use this relative value to measure the stiffness of the multilayer lattice materials.
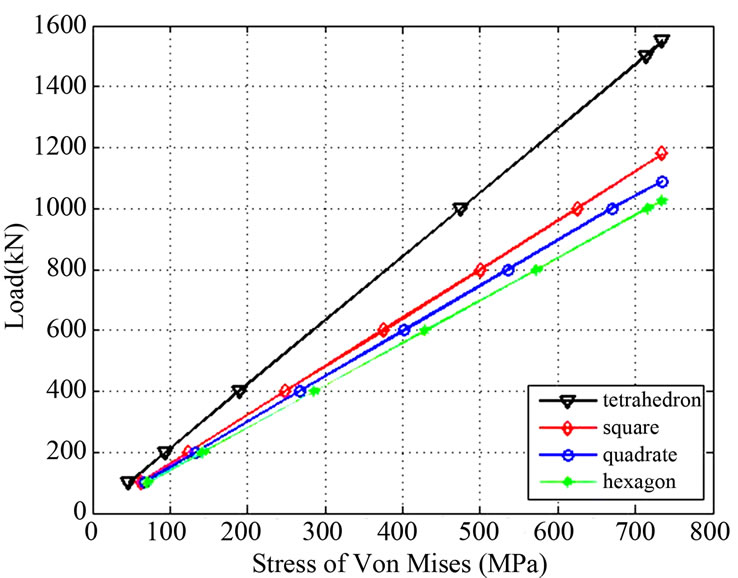
Figure 5. Load-stress curve of different multilayer lattice materials.

Figure 6. Load-displacement curve of different multilayer lattice materials.
It can be seen from Table 1 that different configuretional multilayer lattice materials possess the different RD, RS and LM Ratio. The failure load of the tetrahedron configuration is the maximum 1550 KN, and its relative density is also the maximum 0.8595. But, if we take the relative stiffness and load-mass ratio in consideration to assess the material’s overall bearing capacity, the tetrahedron configuration’s performance is the worst. Also, the four different multilayer lattice materials can be ranked according to its respective bearing capacity. That is, the hexagon configuration is better than the quadrate configuration, and the worst is the tetrahedron configuretion. So, the hexagon multilayer lattice material performs much better than other type of material in the overall assessment.
5. Conclusions
Generally speaking, the static mechanical properties of the lattice material can be expediently analyzed with FEM, and the results can provide some valuable theoretical references for the preliminary structural design of the lattice composite material. In addition, it can both save the study time and the experimental funds. Based on the analysis results of the four types of multilayer lattice materials, it can be concluded that:
• In the FEM analysis, the relative stiffness and the load-mass ratio as the overall assessment is effective to evaluate the overall bearing capacity of the multilayer lattice materials, when the fourth strength theory is taken as the failure criterion.
• Given the same cross-section size of the cellular configuration, the hexagon multilayer lattice material shows the relatively optimal overall bearing capacity in the four configurations, while the tetrahedron configuration is the worst.
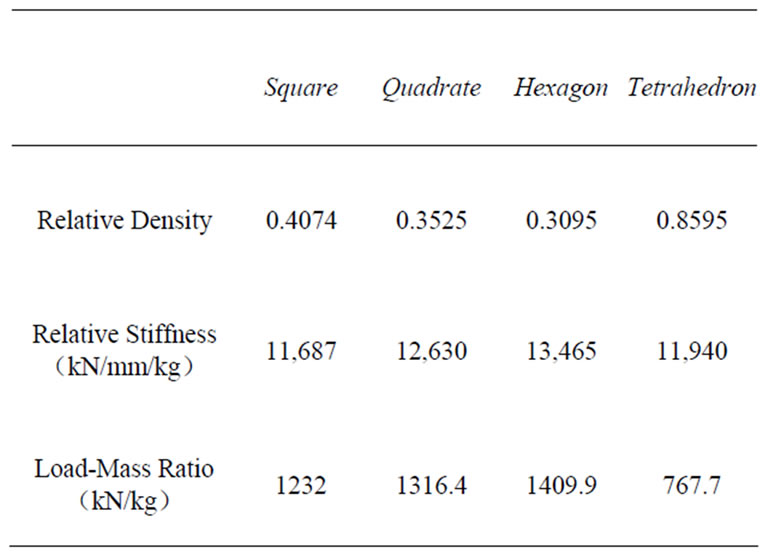
Table 1. Different lattice structure’s overall bearing capacity.
• Only the different configurations are considered to measure the materials’ bearing capacity in this paper, while other factors, including the size and shape of the beam element are ruled out in the FEM analysis. The conclusion can only provide some helpful references for the preliminary structure design of the multilayer lattice material.
• In further research, either the dimensional parameters of the cell or the overall configuration can be changed to adapt for the optimization of the multilayer lattice material.
6. Acknowledgements
This research has been supported by NUST Research Funding under Grant 2010ZDJH06. The program manager was Dr. Jiang Wei. The authors also wish to express their gratitude to Dr. Zhu Rong for his contribution to the preliminary process of the multilayer lattice materials.
7. REFERENCES
- A. G. Evans, “Lightweight Materials and Structures,” MRS Bulletin, Vol. 10, 2001, pp. 790-797.
- A. G. Evans, J. W. Hutchinson, N. A. Fleck, et al., “The Topological Design of Multifunctional Cellular Materials,” Progress in Materials Science, Vol. 46, 2001, pp. 309-327. doi:10.1016/S0079-6425(00)00016-5
- T. J. Lu, L. Valdevit and A. G. Evans, “Active Cooling by Metallic Sandwich Structures with Periodic Cores,” Progress in Materials Science, Vol. 50, No. 7, 2005, pp. 789-815. doi:10.1016/j.pmatsci.2005.03.001
- H. N. G. Wadley, “Multifunctional Periodic Cellular Metals,” Philosophical Transactions of the Royal Society A, Vol. 364, No. 1838, 2006, pp. 31-68.
- J. Y. Christian, D. R. Darren, A. Mark and N. G. W. Haydn, “Experiment Assessment of the Ballistic Response of Composite Pyramidal Lattice Truss Structures,” Composites: Part B, Vol. 39, 2008, pp. 556-569. doi:10.1016/j.compositesb.2007.02.029
- Z. Y. Xue and J. W. Hutchinson, “Preliminary Assessment of Sandwich Plates Subject to Blast Loads,” International Journal of Mechanical Sciences, Vol. 45, 2003, pp. 687-705. doi:10.1016/S0020-7403(03)00108-5
- H.-L. Fan, W. Yang, D.-N. Fang and Z. Zhuang, “Interlacing Technique for New Carbon Fiber Lattice Materials,” Journal of Aeronauticalmaterials, Vol. 27, No. 1, 2007, pp. 46-50.
- Y.-Z. Yang, J.-L. Yang, T. Zheng and D.-N. Fang, “Progress in Research Work of Light Materials,” Chinese Quarterly of Mechanics, Vol. 28, No. 4, 2007, pp. 503-516.
- Q. Wang and G. Xu, “Theoretical Basis of Beam Elements in ANSYS and Application,” Journal of China Three Gorges University (Natural Sciences), Vol. 27, No. 4, 2005, pp. 336-340.
- Q. C. Zhang, T. J. Lu and T. Wen, “Process in the Study on Enhanced Mechanical Properties of High-Performance Lightweight Lattice Metallic Materials,” Advances in Mechanics, Vol. 40, No. 2, 2010, pp. 157-169.
- D.-N. Fang, Y.-H. Zhang and X.-D. Cui, “Mechanical Properties and Multifunctional Design of the Lightweight Lattice Materials,” The Publishing House of Science, Beijing, 2009.
- A. K. Noor, W. S. Burton and C. W. Bert, “Computational Models for Sandwich Panels and Shells,” Applied Mechanics Reviews, Vol. 4, No. 3, 1996, pp. 155-199. doi:10.1115/1.3101923
- I. J. V. Straalen, “Comprehensive Overview of Theories for Sandwich Panels,” Workshop on Modeling of Sandwich Structures and Adhesive Bonded Joints, Porto, 2000.
- A. J. Wang, R. S. Kumar and D. L. McDowell, “Mechanical Behavior of Extruded Prismatic Cellular Metals,” Mechanics of Advanced Materials and Structures, Vol. 12, No. 3, 2005, pp. 185-200. doi:10.1080/15376490590928534
- A. J. Wang and D. L. McDowell, “Yield Surfaces of Various Periodic Metal Honeycombs at Intermediate Relative Density,” International Journal of Plasticity, Vol. 21, No. 2, 2005, pp. 285-320. doi:10.1016/j.ijplas.2003.12.002
- V. S. Deshpande and N. A. Fleck, “Isotropic Constitutive Models for Metallic Foams,” Journal of the Mechanics and Physics of Solids, Vol. 48, No. 6-7, 2000, pp. 1253- 1283. doi:10.1016/S0022-5096(99)00082-4
- J. S. Liu and T. J. Lu, “Multi-Objective and Multi-Loading Optimization of Ultralightweight Truss Materials,” International Journal of Solids and Structures, Vol. 41, 2004, pp. 618-635. doi:10.1016/j.ijsolstr.2003.10.003
- J. S. Liu, Z. C. Deng and T. J. Lu, “Analytical Modeling and Finite Element Simulation of the Plastic Collapse of Sandwich Beams with Pin-Reinforced foam Cores,” International Journal of Solids and Structures, Vol. 45, 2008, pp. 5127-5151.
- D. Mohr, “Mechanism Based Multi-Surface Plasticity Model for Ideal Truss Lattice Materials,” International Journal of Solids and Structures, Vol. 42, No. 11-12, 2005, pp. 3235-3260. doi:10.1016/j.ijsolstr.2004.10.032
- T. Rabczuk, J. Y. Kim, E. Samaniego and T. Belytschko, “Homogenization of Sandwich Structures,” International Journal for Numerical Methods in Engineering, Vol. 61, No. 7, 2004, pp. 1009-1027. doi:10.1002/nme.1100
- Z. Xue and J. W. Hutchinson, “Constitutive Model for Quasistatic Deformation of Metallic Sandwich Cores,” International Journal for Numerical Methods in Engineering, Vol. 61, No. 13, 2004, pp. 2205-2238. doi:10.1002/nme.1142
- Z. Xue, A. Vaziri and J. W. Hutchinson, “Non-Uniform Hardening Constitutive Model for Compressible Orthotropic Materials with Application to Sandwich Plate Cores,” Computer Modeling in Engineering and Sciences, Vol. 10, No. 1, 2005, pp. 79-95.
- Z.-D. Zhou, “FEM and Multi-Objective Optimization of Light Sandwich Structures,” Dalian University of Technology, Daliang, 2008.
- C.-T. Zhang, “Manufacturing and Properties of TwoDimension Lattice Composite Structures,” Graduate School of National University of Defense Technology, Changsha, 2008.

